Study on the Mathematical Model of Vacuum Breaker Valve for Large Air Mass Conditions
Abstract
1. Introduction
2. Methods
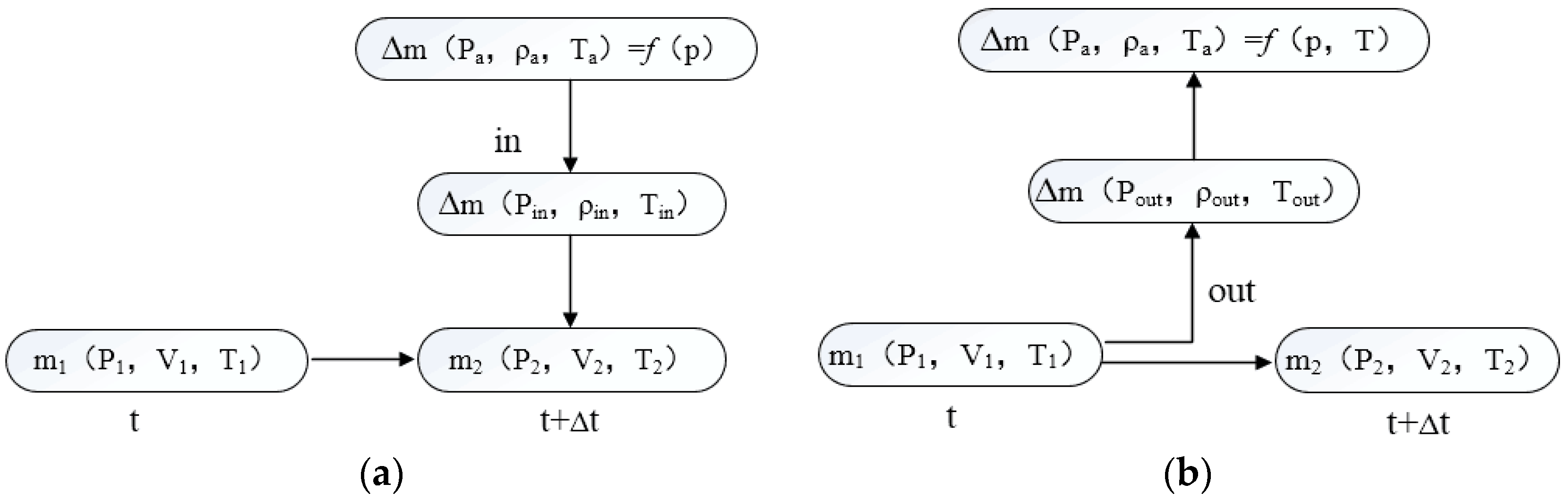
2.1. Problems with the Air Valve Mathematical Model
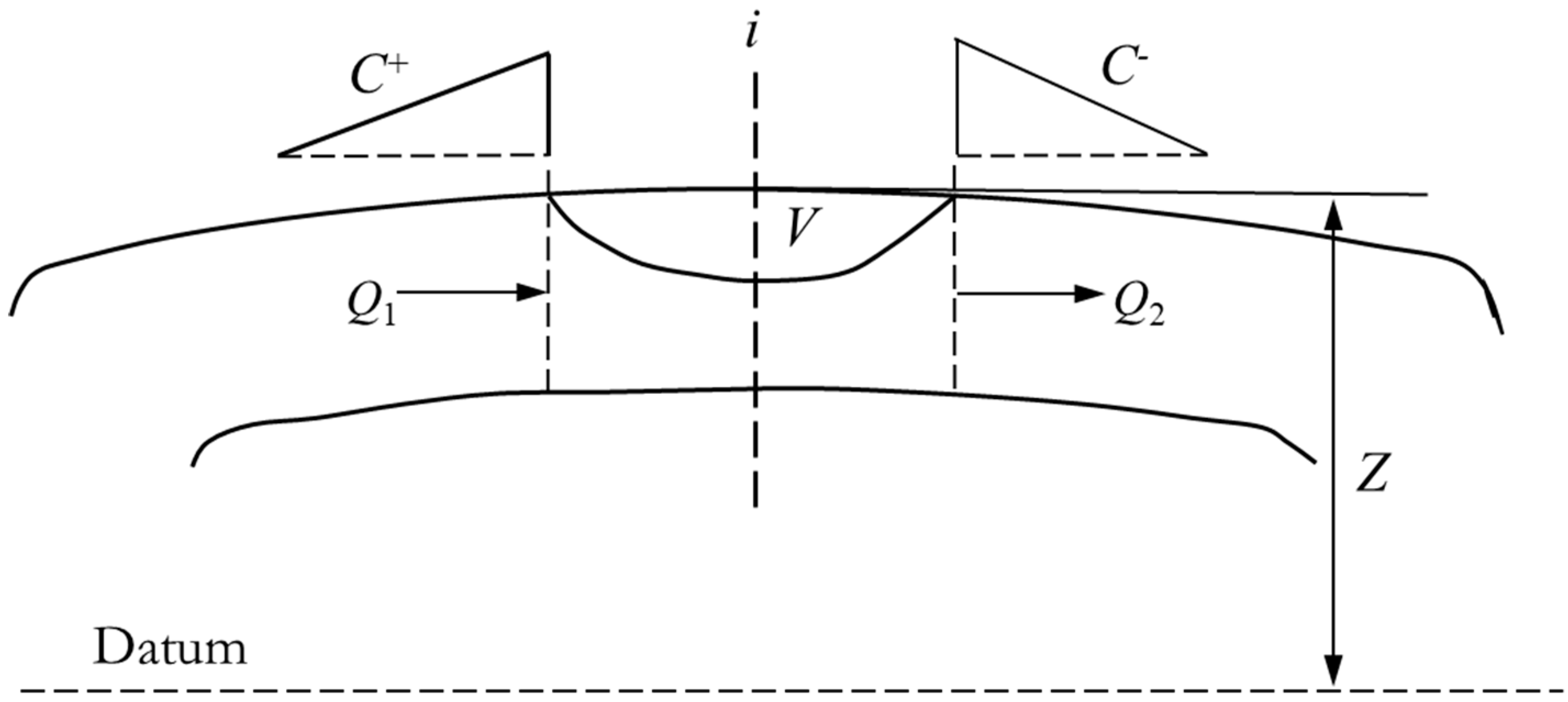
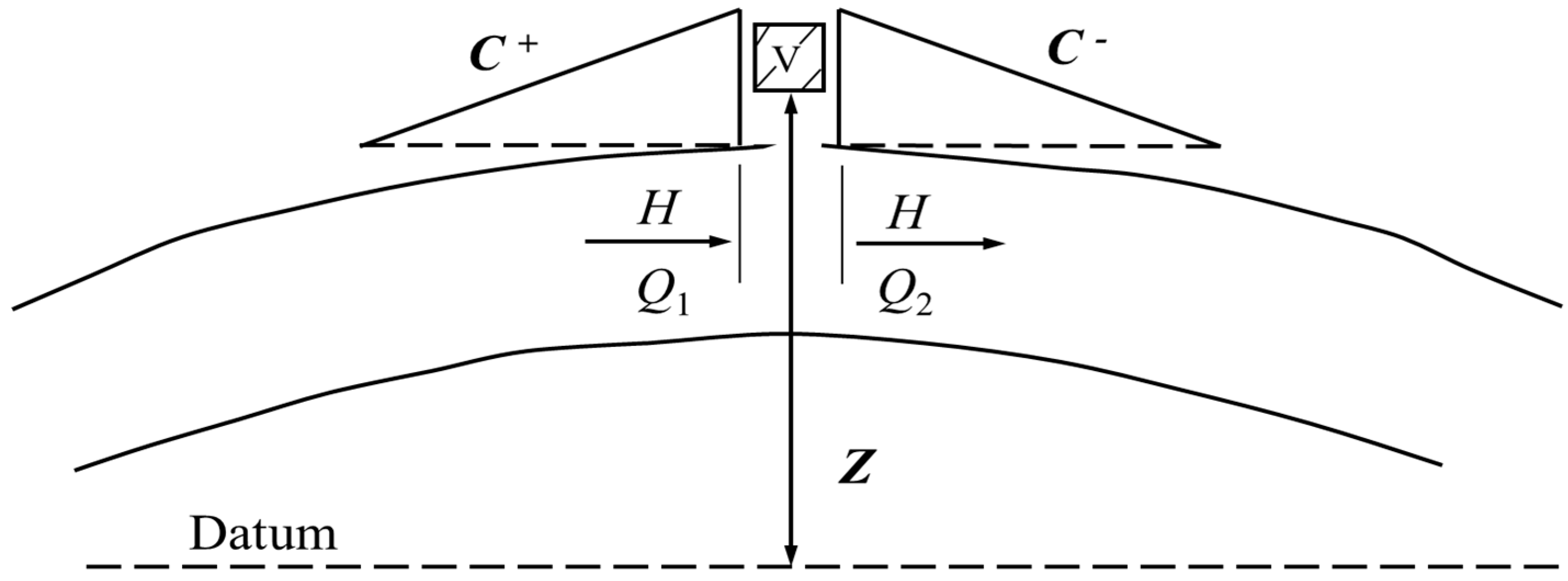
2.2. Mathematical Model of the Vacuum Breaker Valve
3. Results
3.1. Project Description
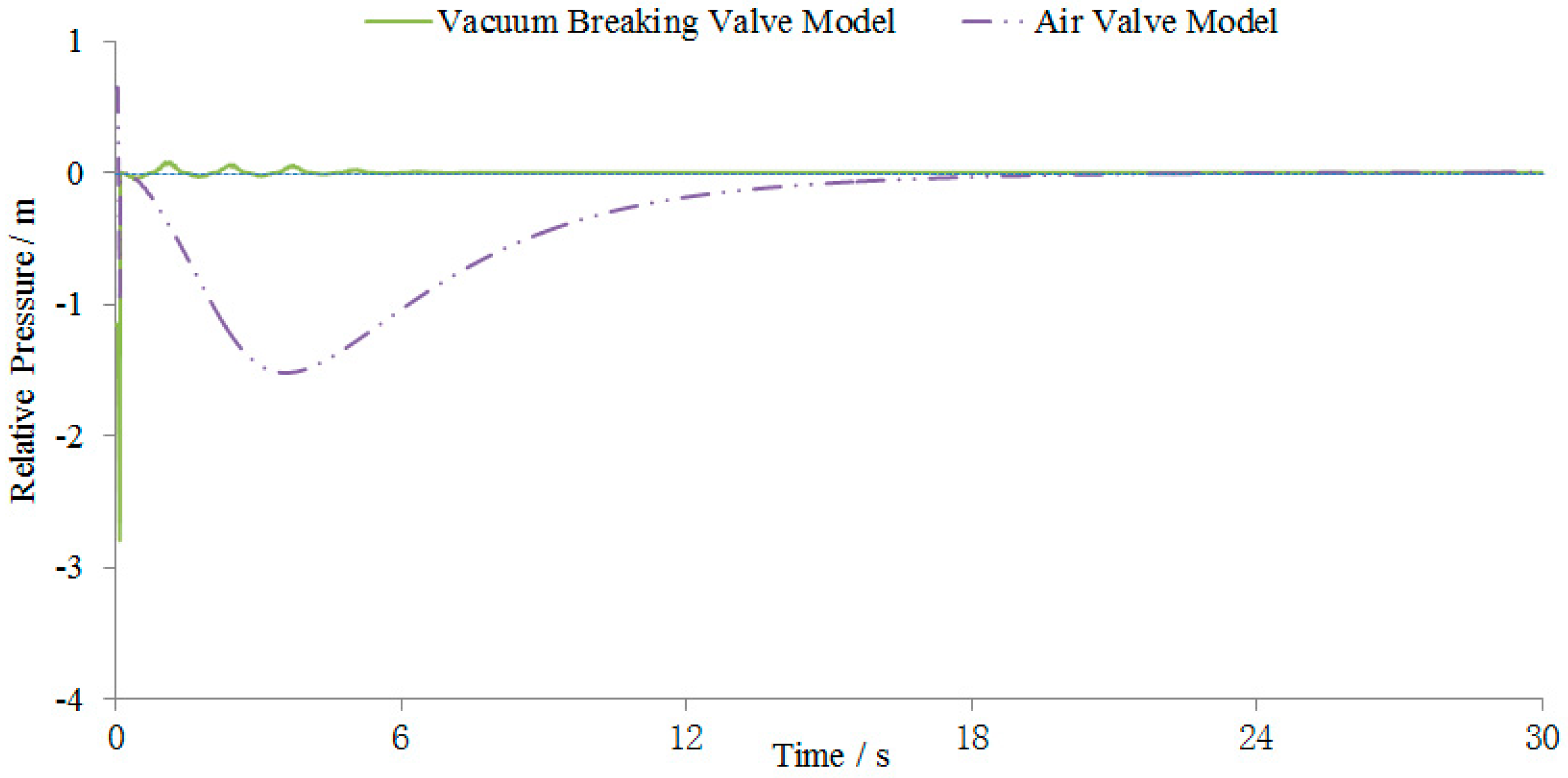
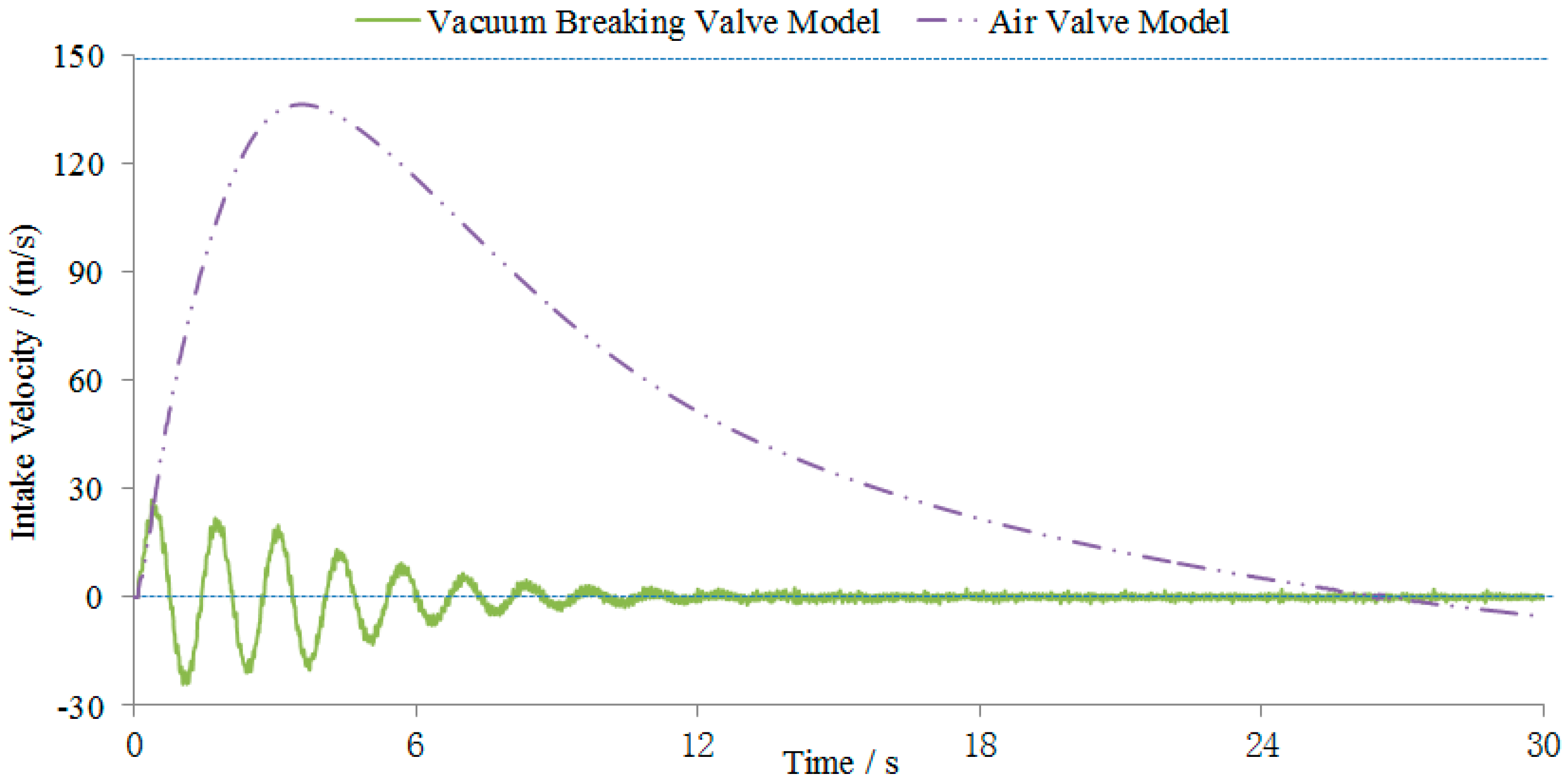
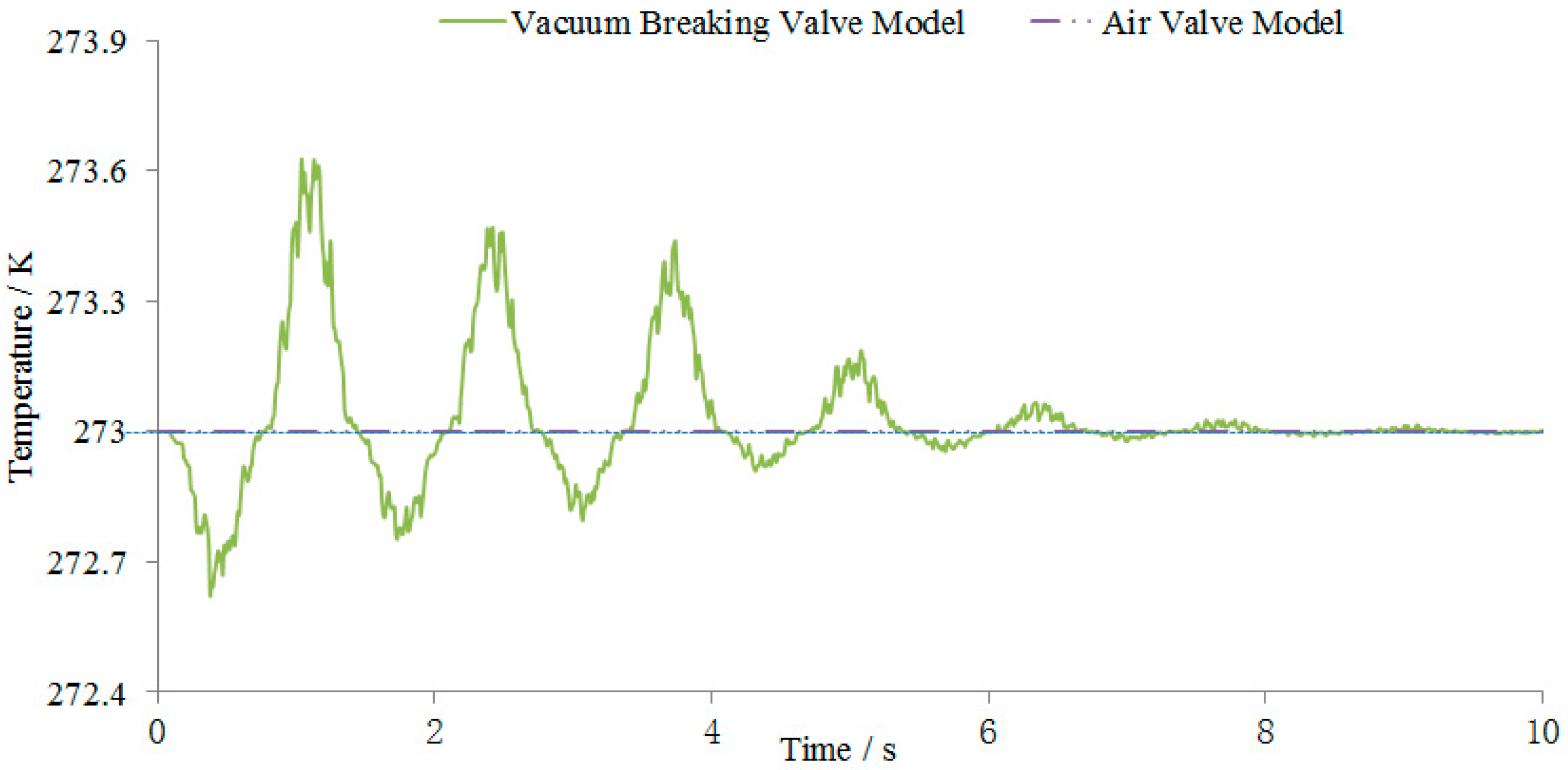
3.2. Numerical Simulation of the Air Valve and Vacuum Breaker Valve
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lescovich, J.E. Locating and Sizing Air-Release Valves. J. Am. Water Works Ass. 1972, 64, 457–461. [Google Scholar] [CrossRef]
- McPherson, D.L. Air valve sizing and location: A prospective. In Proceedings of the Pipelines Specialty Conference 2009, San Diego, CA, USA, 15–19 August 2009; pp. 905–919. [Google Scholar]
- Coronado-Hernández, O.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Experimental and Numerical Analysis of a Water Emptying Pipeline Using Different Air Valves. Water 2017, 9, 98. [Google Scholar]
- Manual of Water Supply Practices—M51: Air-Release, Air-Vacuum, and Combination Air Valves, 1st ed.; American Water Works Association: Denver, CO, USA, 2001.
- Bergant, A.; Kruisbrink, A.; Arregui, F. Dynamic behavior of air valves in a large-scale pipeline apparatus. J. Mech. Eng. 2012, 58, 225–237. [Google Scholar] [CrossRef]
- Lucca, Y.F.L.D.; Aquino, G.A.; Filho, J.G.D. Experimental apparatus to test air trap valves. IOP Conf. Ser. Earth Environ. 2010, 12, 1–8. [Google Scholar] [CrossRef]
- Arregui, F.J. Air Valves Dynamic Behavior; ITA, Universitat Polytecnica Valencia: Valencia, Spain, 2012. [Google Scholar]
- Lee, T.S.; Leow, L.C. Numerical study on the effects of air valve characteristics on pressure surges during pump trip in pumping systems with air entrainment. Int. J. Numer. Meth. Fl. 1999, 29, 645–655. [Google Scholar] [CrossRef]
- Lubbers, C.; Clemens, F. Detection of gas pockets in pressurized waste water mains using dynamic system response analysis. Water Sci. Tech. 2007, 55, 31–38. [Google Scholar] [CrossRef]
- Ramezani, L.; Karney, B.; Malekpour, A. The challenge of air valves: A selective critical literature review. J. Water Resour. Plan. Manag. 2015, 141, 04015017. [Google Scholar] [CrossRef]
- Bergant, A.; Tijsseling, A.S.; Vitkovsy, J.P.; Covas, D.I.C.; Simpson, A.R.; Lambert, M.F. Parameters affecting water-hammer wave attenuation, shape and timing-Part 2: Case studies. J. Hydraul. Res. 2008, 46, 382–391. [Google Scholar] [CrossRef]
- De Martino, G.; Fontana, N.; Giugni, M. Transient flow caused by air expulsion through an orifice. J. Hydraul. Eng. 2008, 134, 1395–1399. [Google Scholar] [CrossRef]
- Fontana, N.; Galdiero, E.; Giugni, M. Pressure surges caused by air release in water pipelines. J. Hydraul. Res. 2016, 54, 461–472. [Google Scholar] [CrossRef]
- Lingireddy, S.; Wood, D.J.; Zloczower, N. Pressure surges in pipeline systems resulting from air releases. J. Am. Water Works Ass. 2004, 96, 88–94. [Google Scholar] [CrossRef]
- Li, G.; Baggett, C.C.; Rosario, R.A. Air/vacuum valve breakage caused by pressure surges—Analysis and solution. In Proceedings of the World Environmental and Water Resources Congress 2009, Kansas City, MO, USA, 2009, 17–21 May; pp. 112–121.
- Ramezani, L.; Karney, B. Water column separation and cavity collapse for pipelines protected with air vacuum valves: Understanding the essential wave processes. J. Hydraul. Eng. 2017, 143, 04016083. [Google Scholar] [CrossRef]
- Cabrera, E.; Fuertes, V.S.; García-Serra, J.; Arregui, F.; Gasc, L.; Palau, V. Reviewing air valves selection. In Proceedings of the Pumps, Electromechanical Devices and Systems Applied to Urban Water Management, Valencia, Spain, 22–25 April 2003; pp. 633–640. [Google Scholar]
- Miao, D.; Zhang, J.; Chen, S.; Yu, X.D. Water hammer suppression for long distance water supply systems by combining the air vessel and valve. J. Water Supply: Res. T. 2017, 66, 319–326. [Google Scholar] [CrossRef]
- De Aquino, G.A.; De Lucca, Y.D.F.L.; Dalfre Filho, J.G. The importance of experimental tests on air valves for proper choice in a water supply project. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 403. [Google Scholar] [CrossRef]
- Bianchi, A.; Mambretti, S.; Pianta, P. Practical formulas for the dimensioning of air valves. J. Hydraul. Eng. 2007, 133, 1177–1180. [Google Scholar] [CrossRef]
- JÖNSSON, L. Maximun transients’ pressures in a conduit with check valve and air entrainment. In Proceedings of the International Conference on the Hydraulics of Pumping Stations, Manchester, UK, 17–19 September 1985. [Google Scholar]
- Zhou, L.; Liu, D.; Karney, B. Investigation of hydraulic transients of two entrapped air pockets in a water pipeline. J. Hydraul. Eng. 2013, 139, 949–959. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D.; Karney, B.; Wang, P. Phenomenon of white mist in pipelines rapidly filling with water with entrapped air pockets. J. Hydraul. Eng. 2013, 139, 1041–1051. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D.; Karney, B.; Zhang, Q. Influence of entrapped air pockets on hydraulic transients in water pipelines. J. Hydraul. Eng. 2011, 137, 1686–1692. [Google Scholar] [CrossRef]
- Tran, P.D. Pressure Transients Caused by Air-Valve Closure while Filling Pipelines. J. Hydraul. Eng. 2016, 143, 04016082. [Google Scholar]
- Albertson, M.L.; Andrews, J.S. Transients Caused by Air Release. In Control of Flow in Closed Conduits; Colorado State Univ.: Fort Collins, CO, USA, 1971; pp. 315–340. [Google Scholar]
- Carlos, M.; Arregui, F.J.; Cabrera, E.; Palau, C.V. Understanding air release through air valves. J. Hydraul. Eng. 2011, 137, 461–469. [Google Scholar] [CrossRef]
- Zhou, F.; Hicks, F.E.; Steffler, P.M. Observations of air water interaction in a rapidly filling horizontal pipe. J. Hydraul. Eng. 2002, 128, 635–639. [Google Scholar] [CrossRef]
- Zhou, F.; Hicks, F.E.; Steffler, P.M. Transient flow in a rapidly filling horizontal pipe containing trapped air. J. Hydraul. Eng. 2002, 128, 625–634. [Google Scholar] [CrossRef]
- Izquierdo, J.; Fuertes, V.S.; Cabrera, E.; Iglesias, P.L.; Garcia-Serra, J. Pipeline start-up with entrapped air. J. Hydraul. Res. 1999, 37, 579–590. [Google Scholar] [CrossRef]
- Wylie, E.B.; Streeter, V.L.; Suo, L.S. Fluid Transients in Systems; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients; Springer: New York, NY, USA, 2014. [Google Scholar]
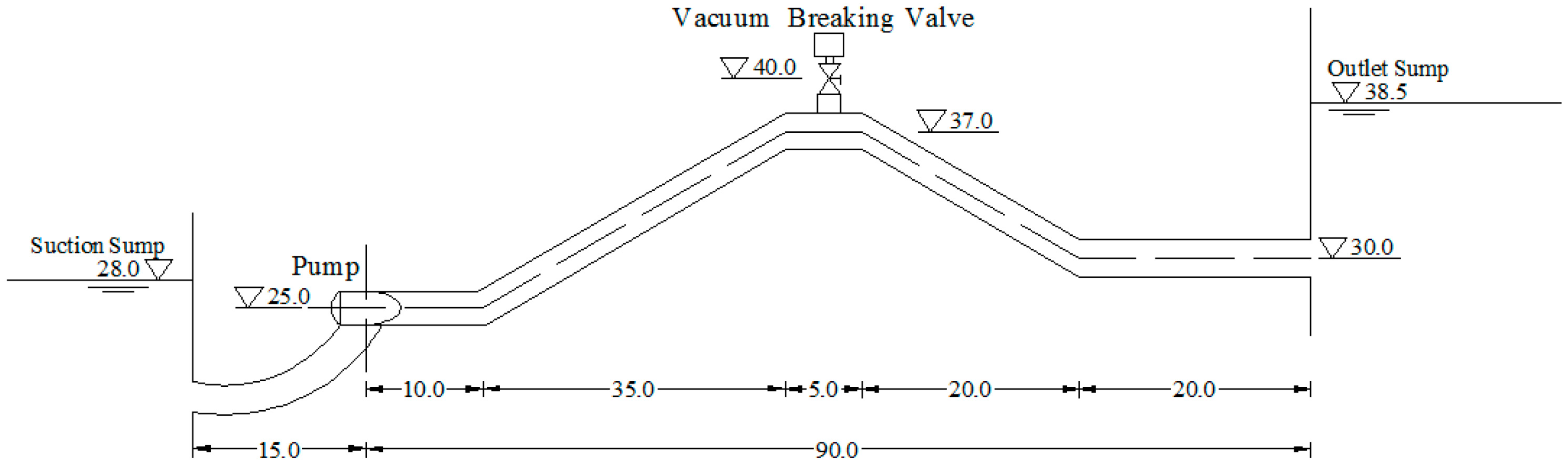
| Water Level of Suction Sump (m) | 28.0 | Diameter of Vacuum Breaker Valve (m) | 0.3 |
|---|---|---|---|
| Water level of outlet sump (m) | 38.5 | Intake pressure of vacuum breaker valve (m) | −3.0 |
| Quantity of pipes | 1 | Quantity of pumps | 1 |
| Elevation of pipe center at outlet sump end (m) | 30.0 | Elevation of pump (m) | 25.0 |
| Elevation of pipe center at top of siphon pipe (m) | 37.0 | Rated head (m) | 12 |
| Horizontal length of pipe (m) | 105.0 | Rated flow (m3/s) | 10 |
| Pipe diameter (m) | 2.4 | Rated rotational speed (r/min) | 250 |
| Design flow (m3/s) | 10 | Rated motor power (kW) | 1600 |
| Elevation of vacuum breaker valve (m) | 40.0 | Flywheel moment (kg·m2) | 3800 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.-y.; Fan, C.-y.; Yu, X.-d.; Zhang, J.; Lv, J.-w.; Xu, T.-y. Study on the Mathematical Model of Vacuum Breaker Valve for Large Air Mass Conditions. Water 2019, 11, 1358. https://doi.org/10.3390/w11071358
Zhang X-y, Fan C-y, Yu X-d, Zhang J, Lv J-w, Xu T-y. Study on the Mathematical Model of Vacuum Breaker Valve for Large Air Mass Conditions. Water. 2019; 11(7):1358. https://doi.org/10.3390/w11071358
Chicago/Turabian StyleZhang, Xiao-ying, Cheng-yu Fan, Xiao-dong Yu, Jian Zhang, Jia-wen Lv, and Ting-yu Xu. 2019. "Study on the Mathematical Model of Vacuum Breaker Valve for Large Air Mass Conditions" Water 11, no. 7: 1358. https://doi.org/10.3390/w11071358
APA StyleZhang, X.-y., Fan, C.-y., Yu, X.-d., Zhang, J., Lv, J.-w., & Xu, T.-y. (2019). Study on the Mathematical Model of Vacuum Breaker Valve for Large Air Mass Conditions. Water, 11(7), 1358. https://doi.org/10.3390/w11071358






