Simultaneous Sensor Placement and Pressure Reducing Valve Localization for Pressure Control of Water Distribution Systems
Abstract
1. Introduction
2. Pressure Sensor Placement
2.1. Problem Description
2.2. The K-Means++ Method to Determine the Regions
- Randomly select K points as starting centers of the clusters.
- Allocate the data points to the nearest clusters based on their distance from the center.
- The mean of each of the K clusters becomes the new center.
- Repeat from step 2 until the locations of the centers do not change.
- The number of clusters needs to be given a priori, which is a difficult task in practice.
2.3. Determining the Number of Clusters K
2.4. The Accuracy of Representation (AOR)
2.4.1. Definition of AOR
2.4.2. Improving the AOR with a Partition Matrix
3. Localization of PRVs
3.1. Pressure Analysis on the Edges of the Regions
3.2. Placement of the PRVs
- Since a PRV works with its water flow only in one direction, a pipe in which the water flow direction alters during the operation should not be selected for the valve placement. Otherwise, there will be no assurance to meet the pressure demand.
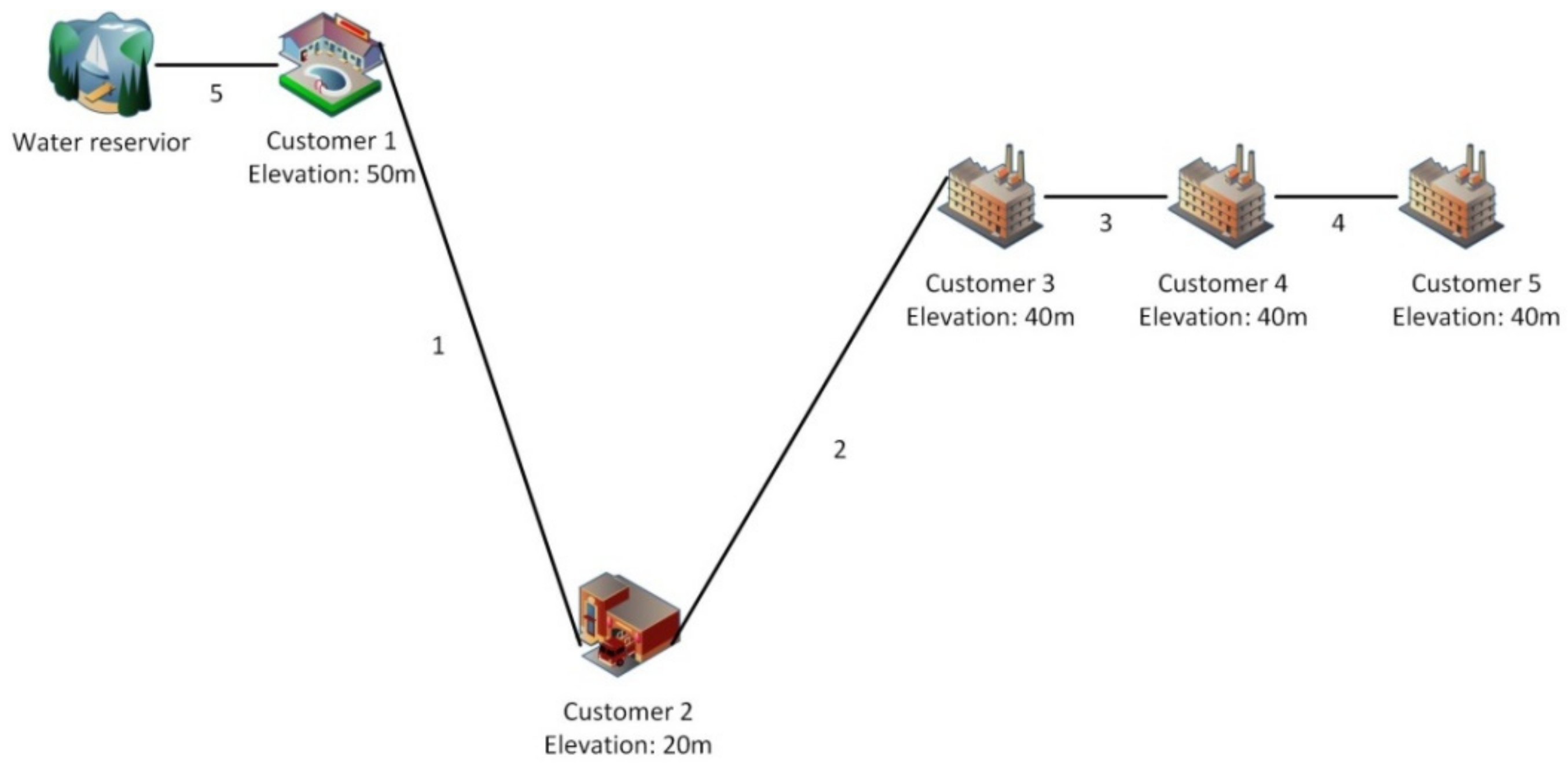
- For PRV placement, the downstream elevation should be considered to ensure the pressure demand at the downstream nodes. For example, if the main source of pressure difference is from the elevation difference, and if a downstream node is lower in elevation, its pressure will usually be greater than the upstream pressure. In this case, if the PRV is placed on this link due to the large pressure difference, the pressure at the downstream nodes can be lower than the pressure demand.For example, as shown in Figure 2, the elevations at nodes 1, 2, 3, 4 and 5 are 50 m, 20 m, 40 m, 40 m and 40 m, respectively. Node 2 is the downstream node of pipe 1 and the upstream node of pipes 2, 3 and 4. A PRV may be installed on pipe 1 and its setting of the valve is determined to reduce the external pressure at node 2 so that the pressure meets the lowest pressure requirement at node 2. Then, the head of node 2 will be lowered, and therefore, the minimum pressure requirement for nodes 3, 4 and 5 may not be met. Thus, a PRV should not be installed on pipe 1, in spite of its high pressure difference.
- Pipes directly connected to a water tank or a pump should not be selected as candidates for placing PRVs. This is due to the fact that the elevation generated by a water tank or a pump is the only energy source ensuring the consumer demands. Installing a valve there may degrade proper delivery of the water to some consumers.
3.3. Determining the Setting Values for PRVs
- Partially opened (active mode): water flows through the valve and the downstream pressure is reduced to the setting value of the PRV, when the upstream pressure is above the setting value.
- Fully open (open mode): the PRV is entirely open and acts as if it is not present, when the upstream pressure is below the setting value.
- Fully closed (closed mode): the PRV closes completely and acts as a check valve, when the pressure on the downstream side exceeds that on the upstream side, or if reverse flow in the pipe is incipient.
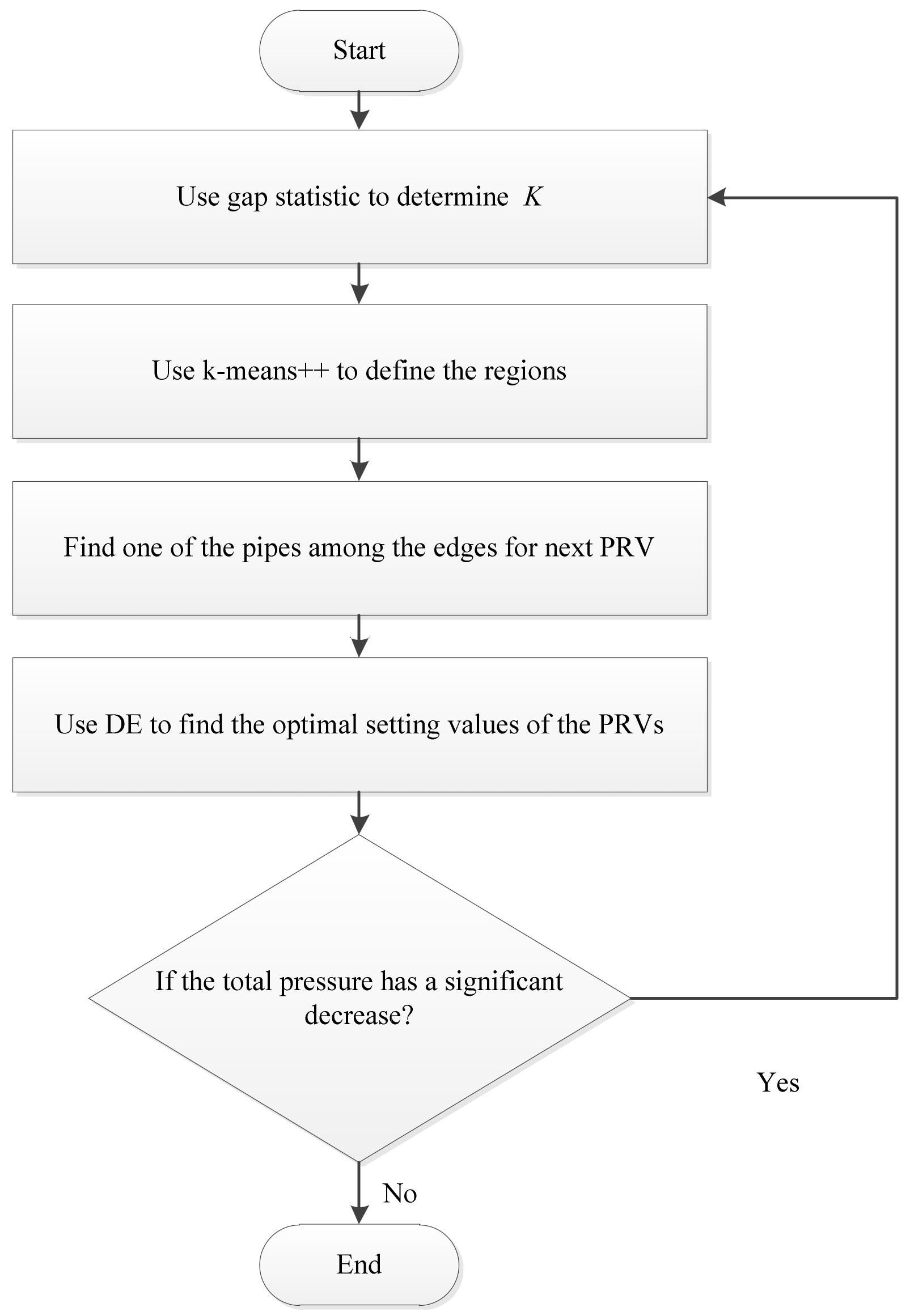
4. Implementation of the Proposed Approach
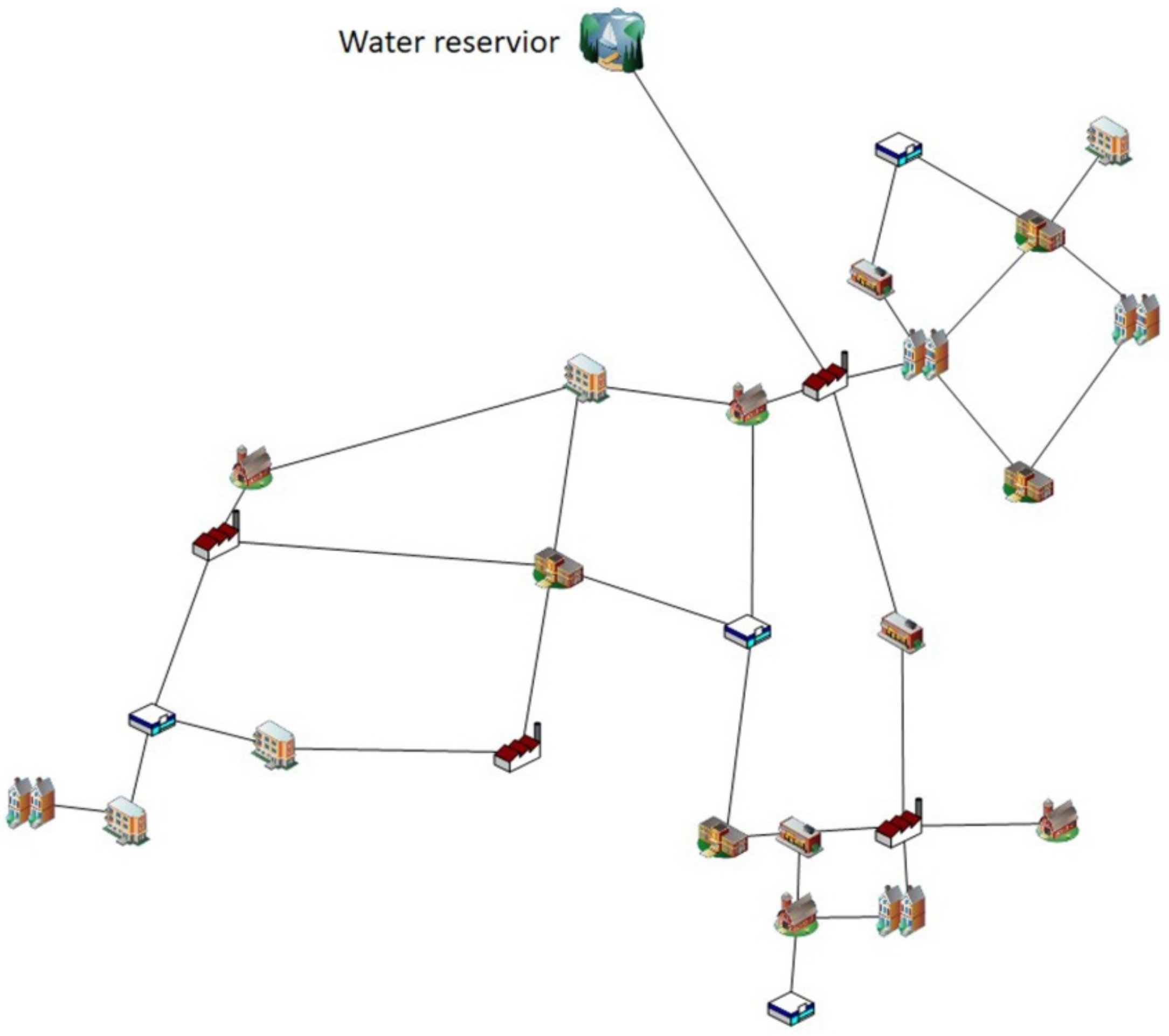
5. Case Studies
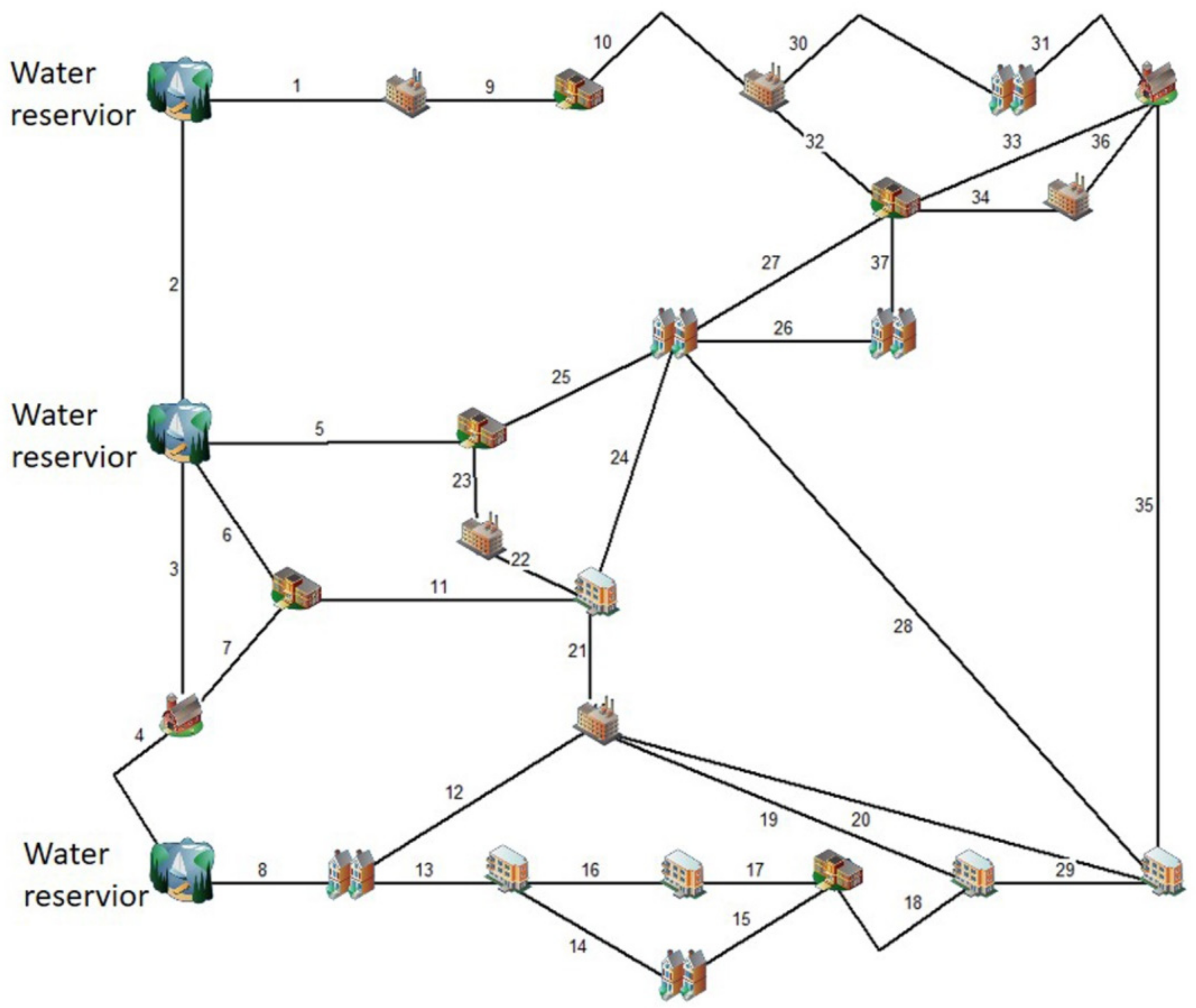
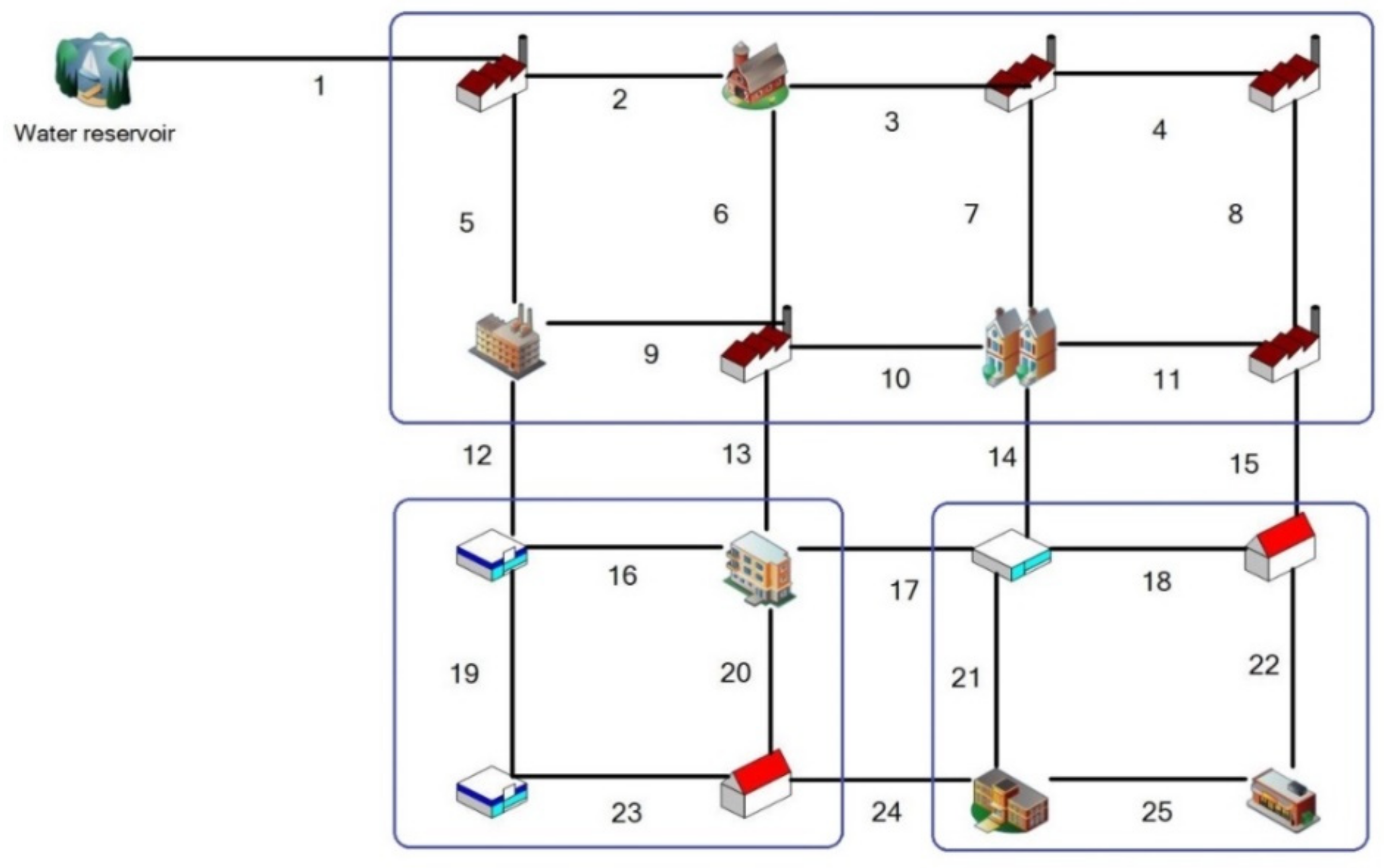
5.1. Case Study 1: Jilin Network
5.2. Case Study 2: A Benchmark WDS
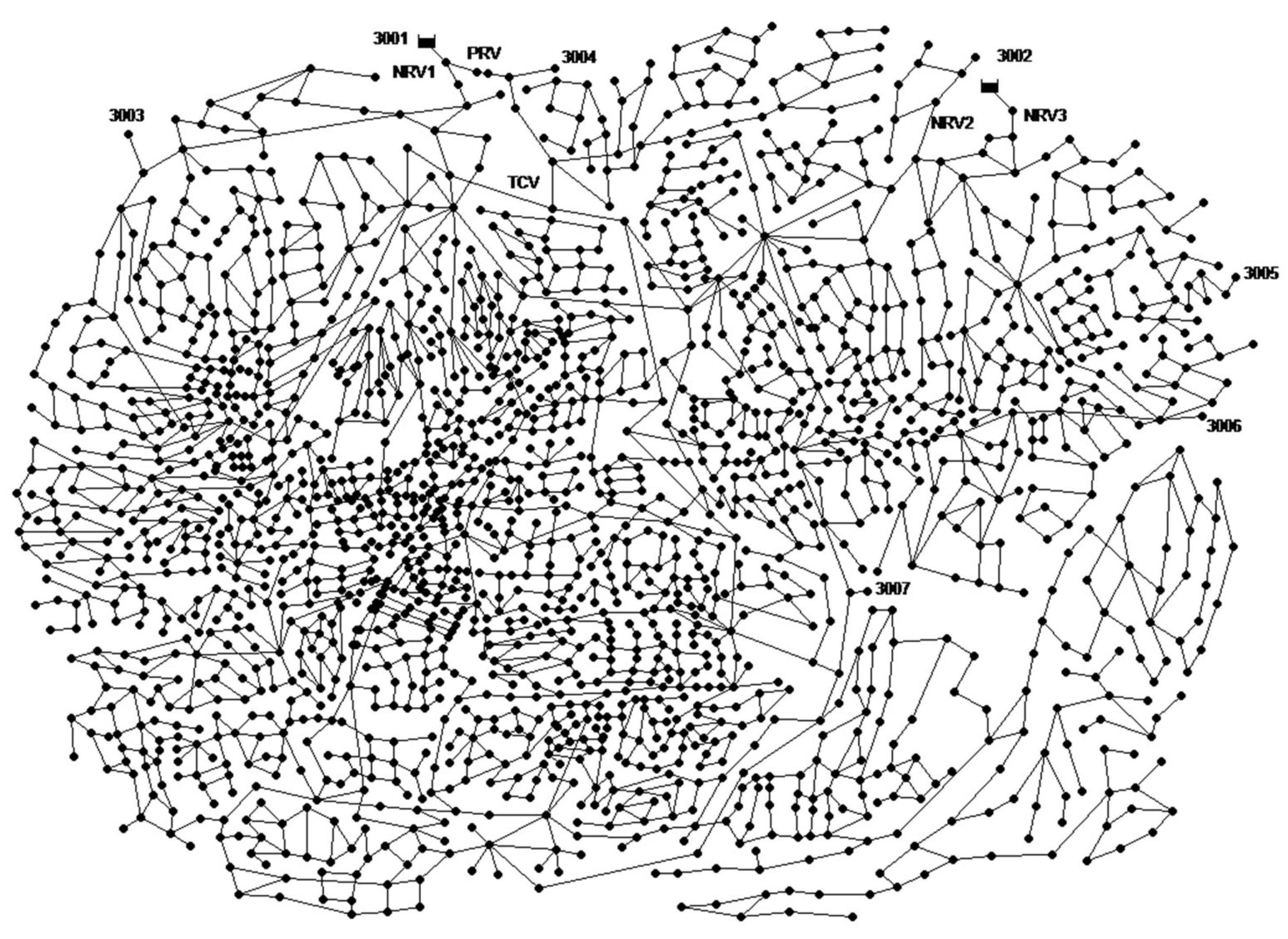
5.3. Case Study 3: Sensor and PRV Localization for EXNET
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lambert, A.O. International report: Water losses management and techniques. Water Sci. Technol. Water Supply 2002, 2, 1–20. [Google Scholar] [CrossRef]
- Savic, D.A.; Walters, G.A. Integration of a model for hydraulic analysis of water distribution networks with an evolution program for pressure regulation. Comput. Aided Civ. Infrastruct. Eng. 1996, 11, 87–97. [Google Scholar] [CrossRef]
- Vicente, D.J.; Garrote, L.; Sanchez, R.; Santillan, D. Pressure management in water distribution systems: Current status, proposals, and future trends. J. Water Resour. Plan. Manag. 2016, 142, 04015061. [Google Scholar] [CrossRef]
- Ulanicki, B.; Bounds, P.L.M.; Rance, J.P.; Reynolds, L. Open and closed loop pressure control for leakage reduction. Urban Water 2000, 2, 105–114. [Google Scholar] [CrossRef]
- Fontana, N.; Giugni, M.; Glielmo, L.; Marini, G.; Zollo, R. Real-time control of pressure for leakage reduction in water distribution network: Field experiments. J. Water Resour. Plan. Manag. 2018, 144. [Google Scholar] [CrossRef]
- Wang, Y.; Puig, V.; Cembrano, G. Non-linear economic model predictive control of water distribution networks. J. Process Control 2017, 56, 23–34. [Google Scholar] [CrossRef]
- Sun, C.; Morley, M.; Savic, D.; Puig, V.; Cembrano, G.; Zhang, Z. Combining model predictive control with constraint-satisfaction formulation for the operative pumping control in water networks. Procedia Eng. 2015, 119, 963–972. [Google Scholar] [CrossRef][Green Version]
- Baunsgaard, K.M.H.; Ravn, O.; Kallesøe, C.S.; Poulsen, N.K. MPC control of water supply networks. In Proceedings of the 2016 European Control Conference (ECC), Aalborg, Denmark, 29 June–1 July 2016; pp. 1770–1775. [Google Scholar]
- Renaud, E.; Sissoko, M.T.; Clauzier, M.; Gilbert, D.; Sandraz, A.C.; Pillot, J. Comparative study of different methods to assess average pressures in water distribution zones. Water Util. J. 2015, 10, 25–35. [Google Scholar]
- Halkijevic, I.; Vouk, D.; Posavcic, H. Average pressure in a water supply system. In Proceedings of the 15th International Symposium on Water Management and Hydraulic Engineering, Primošten, Croatia, 6–8 September 2017; pp. 1–11. [Google Scholar]
- Isovitsch, S.L.; VanBriesen, J.M. Sensor placement and optimization criteria dependencies in a water distribution system. J. Water Resour. Plan. Manag. 2008, 134, 186–196. [Google Scholar] [CrossRef]
- Krause, A.; Leskovec, J.; Guestrin, C.; VanBriesen, J.; Faloutsos, C. Efficient sensor placement optimization for securing large water distribution networks. J. Water Resour. Plan. Manag. 2008, 134, 516–526. [Google Scholar] [CrossRef]
- Aral, M.M.; Guan, J.; Maslia, M.L. Optimal design of sensor placement in water distribution networks. J. Water Resour. Plan. Manag. 2010, 136, 5–18. [Google Scholar] [CrossRef]
- Casillas, M.V.; Puig, V.; Garza-Castañón, L.E.; Rosich, A. Optimal sensor placement for leak location in water distribution networks using genetic algorithms. Sensors 2013, 13, 14984–15005. [Google Scholar] [CrossRef] [PubMed]
- Perez, R.; Sanz, G.; Puig, V.; Quevedo, J.; Escofet, M.A.C.; Nejjari, F.; Meseguer, J.; Cembrano, G.; Tur, J.M.M.; Sarrate, R. Leak localization in water networks: A model-based methodology using pressure sensors applied to a real network in Barcelona [applications of control]. IEEE Control Syst. Mag. 2014, 34, 24–36. [Google Scholar]
- Yoo, D.G.; Chang, D.E.; Song, Y.H.; Lee, J.H. Optimal placement of pressure gauges for water distribution networks using entropy theory based on pressure dependent hydraulic simulation. Entropy 2018, 20, 576. [Google Scholar] [CrossRef]
- Steffelbauer, D.; Neumayer, M.; Günther, M.; Fuchs-Hanusch, D. Sensor placement and leakage localization considering demand uncertainties. Procedia Eng. 2014, 89, 1160–1167. [Google Scholar] [CrossRef]
- Christodoulou, S.E.; Gagatsis, A.; Xanthos, S.; Kranioti, S.; Agathokleous, A.; Fragiadakis, M. Entropy-based sensor placement optimization for waterloss detection in water distribution networks. Water Resour. Manag. 2013, 27, 4443–4468. [Google Scholar] [CrossRef]
- Soldevila, A.; Blesa, J.; Tornil-Sin, S.; Fernandez-Canti, R.M.; Puig, V. Sensor placement for classifier-based leak localization in water distribution networks using hybrid feature selection. Comput. Chem. Eng. 2017, 108, 152–162. [Google Scholar] [CrossRef]
- Covelli, C.; Cimorelli, L.; Cozzolino, L.; Morte, R.D.; Pianese, D. Reduction in water losses in water distribution systems using pressure reduction valves. Water Supply 2016, 16, 1033–1045. [Google Scholar] [CrossRef]
- Creaco, E.; Alvisi, S.; Franchini, M. Multistep approach for optimizing design and operation of the C-Town pipe network model. J. Water Resour. Plan. Manag. 2016, 142, C4015005. [Google Scholar] [CrossRef]
- Prescott, S.L.; Ulanicki, B. Improved control of pressure reducing valves in water distribution networks. J. Hydraul. Eng. 2008, 134, 56–65. [Google Scholar] [CrossRef]
- Hindi, K.S.; Hamam, Y.M. Locating pressure control elements for leakage minimization in water supply networks: An optimization model. Eng. Optim. 1991, 17, 281–291. [Google Scholar] [CrossRef]
- Araujo, L.S.; Ramos, H.; Coelho, S.T. Pressure control for leakage minimisation in water distribution systems management. Water Resour. Manag. 2006, 20, 133–149. [Google Scholar] [CrossRef]
- Nicolini, M.; Zovatto, L. Optimal location and control of pressure reducing valves in water networks. J. Water Resour. Plan. Manag. 2009, 135, 178–187. [Google Scholar] [CrossRef]
- Dai, P.D.; Li, P. Optimal localization of pressure reducing valves in water distribution systems by a reformulation approach. Water Resour. Manag. 2014, 28, 3057–3074. [Google Scholar] [CrossRef]
- Savic, D.A.; Walters, G.A. An evolution program for optimal pressure regulation in water distribution networks. Eng. Optim. 1995, 24, 197–219. [Google Scholar] [CrossRef]
- Dai, P.D.; Li, P. Optimal pressure regulation in water distribution systems based on an extended model for pressure reducing valves. Water Resour. Manag. 2016, 30, 1239–1254. [Google Scholar] [CrossRef]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Wu, X.; Kumar, V.; Quinlan, J.R.; Ghosh, J.; Yang, Q.; Motoda, H.; McLachlan, G.J.; Ng, A.; Liu, B.; Yu, P.S.; et al. Top 10 algorithms in data mining. Knowl. Inf. Syst. 2008, 14, 1–37. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. k-Means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Sieranoja, S.; Fränti, P. Random projection for k-means clustering. In Artificial Intelligence and Soft Computing, Proceedings of ICAISC 2018, Zakopane, Poland, 3–7 June 2018; Springer: Berlin/Heidelberg, Germany, 2018; pp. 680–689. [Google Scholar]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. Ser. B 2001, 63, 411–423. [Google Scholar] [CrossRef]
- Yan, M.; Ye, K. Determining the number of clusters using the weighted gap statistic. Biometrics 2007, 63, 1031–1037. [Google Scholar] [CrossRef]
- Scott, A.J.; Symons, M.J. Clustering methods based on likelihood ratio criteria. Biometrics 1971, 27, 387–397. [Google Scholar] [CrossRef]
- Dunn, J.C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Khezzar, L.; Harous, S.; Benayoune, M. Steady-state analysis of water distribution networks including pressure-reducing valves. Comput. Aided Civ. Infrastruct. Eng. 2001, 16, 259–267. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, Z.; Zhang, Q. Differential evolution with composite trial vector generation strategies and control parameters. IEEE Trans. Evol. Comput. 2011, 15, 55–66. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET 2 Users Manual; US Environmental Protection Agency: Washington, WA, USA, 2000.
- Bi, W.; Dandy, G.C. Optimization of water distribution systems using online retrained metamodels. J. Water Resour. Plan. Manag. 2014, 140. [Google Scholar] [CrossRef]
- Sterling, M.J.H.; Bargiela, A. Leakage reduction by optimised control of valves in water networks. Trans. Inst. Meas. Control 1984, 6, 293–298. [Google Scholar] [CrossRef]
- Jowitt, P.W.; Xu, C. Optimal valve control in water-distribution networks. J. Water Resour. Plan. Manag. 1990, 116, 455–472. [Google Scholar] [CrossRef]
- Reis, L.; Porto, R.; Chaudhry, F. Optimal location of control valves in pipe networks by genetic algorithm. J. Water Resour. Plan. Manag. 1997, 123, 317–326. [Google Scholar] [CrossRef]
- Eck, B.; Mevissen, M. Valve Placement in Water Networks: Mixed-Integer Mon-Linear Optimization with Quadratic Pipe Friction; IBM Research Report No. RC25307(IRE1209-014); IBM Research Smarter Cities Technology Centre: Dublin, Ireland, 28 September 2012. [Google Scholar]

| No. of PRVs | Total Pressure (m) | Min. Pressure (m) | Setting Value of PRVs | No. of PSs | AOR |
|---|---|---|---|---|---|
| 0 | 20.1063 | 6 | 93.04% | ||
| 1 | 20.0160 | 29.93 | 6 | 84.46% | |
| 2 | 20.0123 | 32.01; 27.83 | 6 | 82.72% | |
| 3 | 20.0489 | 35.65; 24.3; 32.91 | 7 | 80.67% | |
| 4 | 20.2887 | 35.32; 37.26; 28.43; 34.55 | 7 | 84.35% | |
| 5 | 20.2836 | 33.44; 28.06; 29.70; 38.7; 23.41 | 9 | 81.27% |
| No. of PRVs | Link IDs [Current Study] | Link IDs [26] | Link IDs [25] |
|---|---|---|---|
| 1 | 11 | 11 | 11 |
| 2 | 11,9 | 11,20 | 11,20 |
| 3 | 11,9,20 | 11,20,21 | 11,20,1 |
| 4 | 11,9,20,21 | 11,20,21,1 | 1,11,20,21 |
| No. of PRVs | Total Pressure (m) |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 |
| No. of PRVs | Link IDs [Current Study] | Link IDs [24] | Link IDs [26] |
|---|---|---|---|
| 2 | 11,10 | 1,11 | 1,11 |
| 3 | 11,10,20 | 11,21,29 | 11,20,21 |
| 4 | 11,10,20,21 | 1,8,11,20 | 1,11,20,29 |
| 5 | 11,10,20,21,18 | 1,8,11,21,29 | 1,11,20,21,29 |
| 6 | 11,10,20,21,18,16 | 1,5,11,8,20,21 | 1,11,20,21,29,31 |
| No. of PRVs | Total Pressure (m) | No. of PSs | AOR |
|---|---|---|---|
| 0 | 11 | 98.07% | |
| 1 | 11 | 81.27% | |
| 2 | 13 | 84.81% | |
| 3 | 11 | 70.36% | |
| 4 | 13 | 66.33% | |
| 5 | 13 | 59.83% | |
| 6 | 9 | 55.27% |
| No. of PRVs | Total Pressure (m) | Min. Pressure (m) | Link IDs |
|---|---|---|---|
| 1 | 3.4560 | 25.2948 | 3026 |
| 2 | 3.4493 | 25.1376 | 3026; 2490 |
| 3 | 2.8942 | 8.0330 | 3026; 2490; 2341 |
| 4 | 2.7625 | 8.0398 | 3026; 2490; 2341; 4908; |
| 5 | 2.7585 | 8.2901 | 3026; 2490; 2341; 4908; 2714; |
| 6 | 2.7404 | 8.1232 | 3026; 2490; 2341; 4908; 2714; 2512; |
| 7 | 2.7431 | 8.2778 | 3026; 2490; 2341; 4908; 2714; 2512; 4854; |
| 8 | 2.7124 | 8.1086 | 3026; 2490; 2341; 4908; 2714; 2512; 4854; 4898 |
| Burst Scene | Without Burst | Place 1 | Place 2 | Place 3 | Place 4 | Place 5 |
|---|---|---|---|---|---|---|
| AOR | 80.63% | 79.89% | 80.51% | 80.49% | 80.49% | 79.94% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Hopfgarten, S.; Ostfeld, A.; Salomons, E.; Li, P. Simultaneous Sensor Placement and Pressure Reducing Valve Localization for Pressure Control of Water Distribution Systems. Water 2019, 11, 1352. https://doi.org/10.3390/w11071352
Cao H, Hopfgarten S, Ostfeld A, Salomons E, Li P. Simultaneous Sensor Placement and Pressure Reducing Valve Localization for Pressure Control of Water Distribution Systems. Water. 2019; 11(7):1352. https://doi.org/10.3390/w11071352
Chicago/Turabian StyleCao, Hao, Siegbert Hopfgarten, Avi Ostfeld, Elad Salomons, and Pu Li. 2019. "Simultaneous Sensor Placement and Pressure Reducing Valve Localization for Pressure Control of Water Distribution Systems" Water 11, no. 7: 1352. https://doi.org/10.3390/w11071352
APA StyleCao, H., Hopfgarten, S., Ostfeld, A., Salomons, E., & Li, P. (2019). Simultaneous Sensor Placement and Pressure Reducing Valve Localization for Pressure Control of Water Distribution Systems. Water, 11(7), 1352. https://doi.org/10.3390/w11071352