Estimation of Reservoir Sediment Flux through Bottom Outlet with Combination of Numerical and Empirical Methods
Abstract
1. Introduction
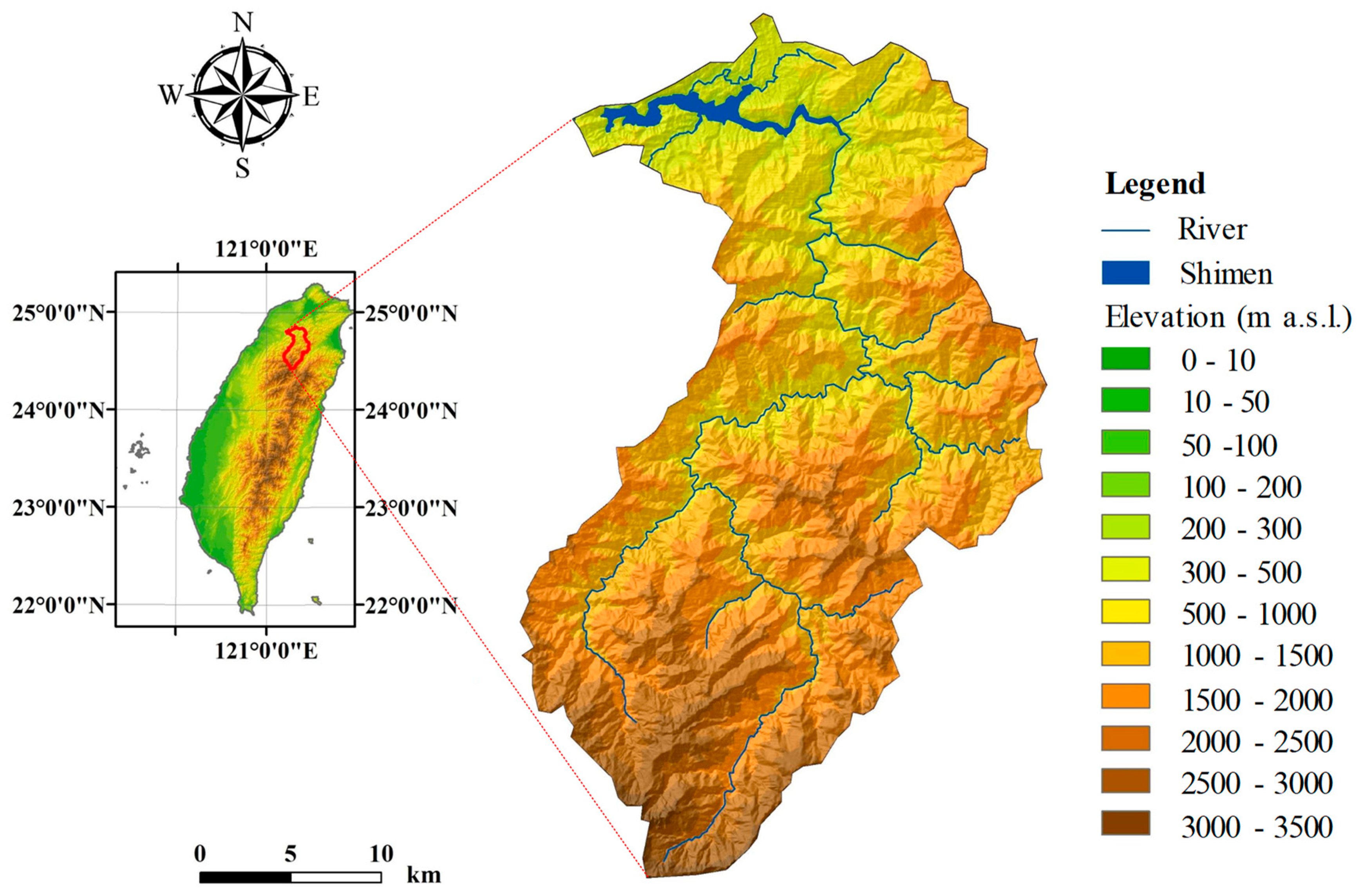
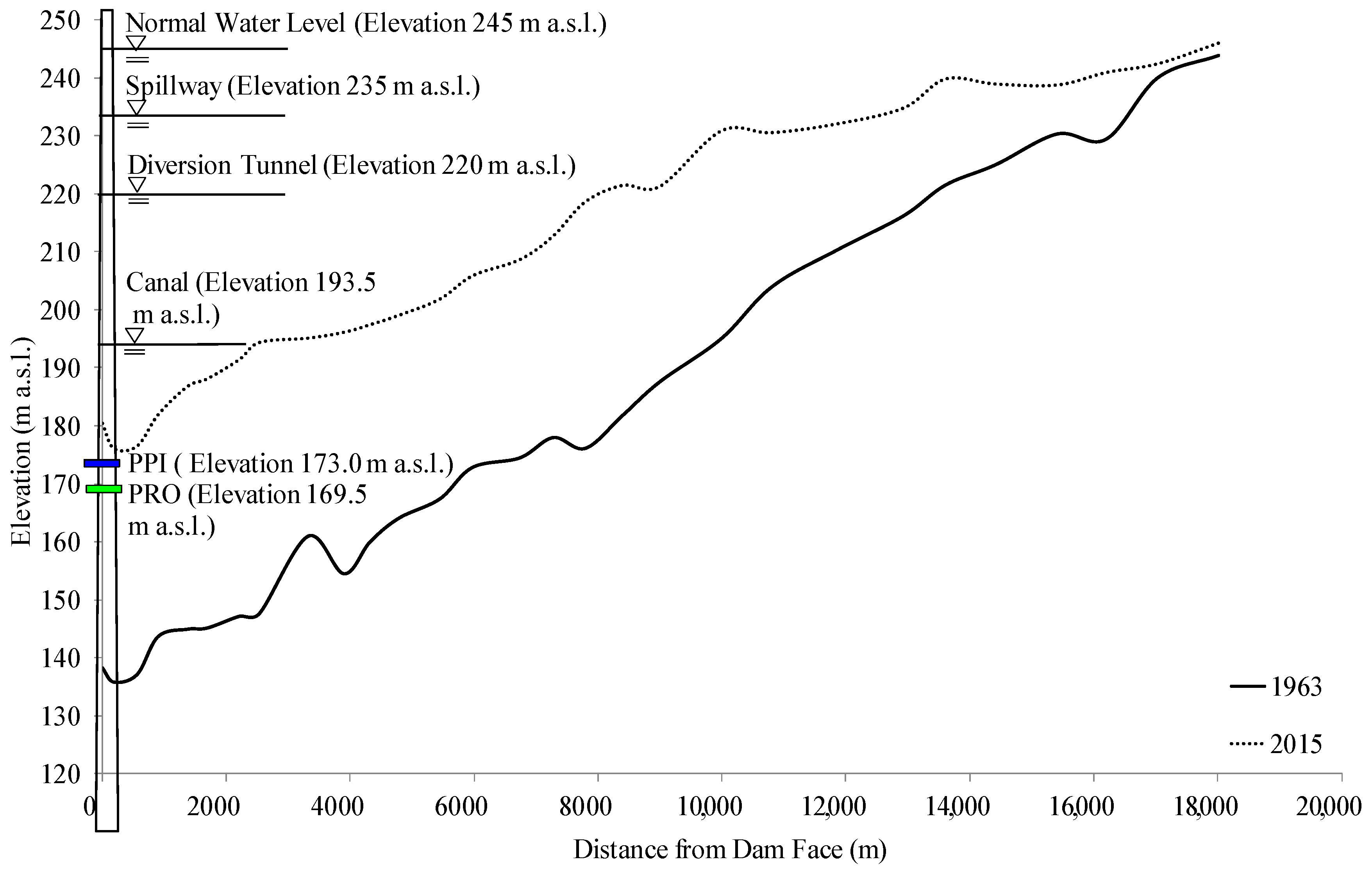
2. Study Site
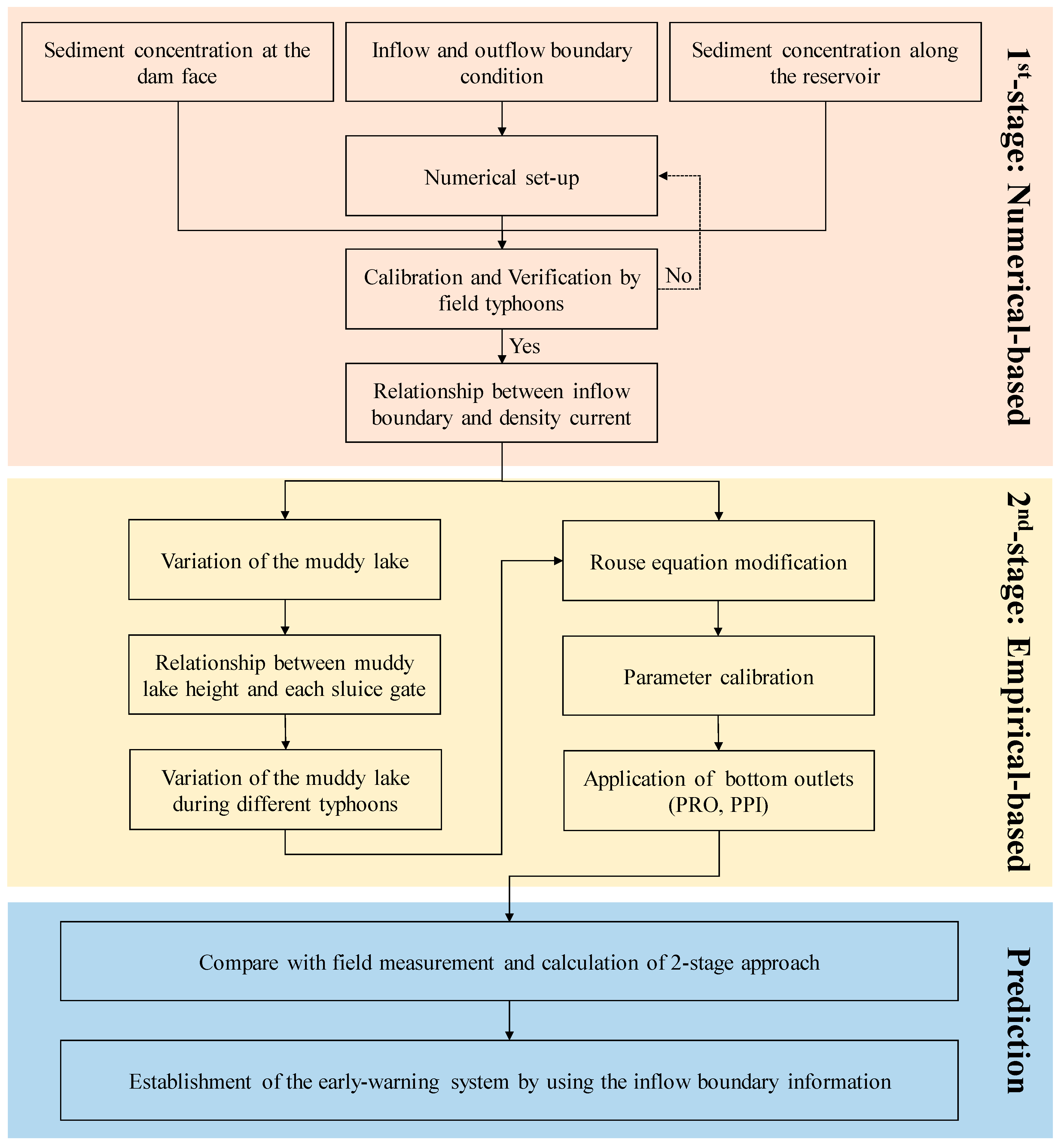
3. Estimated Method
3.1. Governing Equations for Density Current Flow
3.2. Variation of Muddy Lake
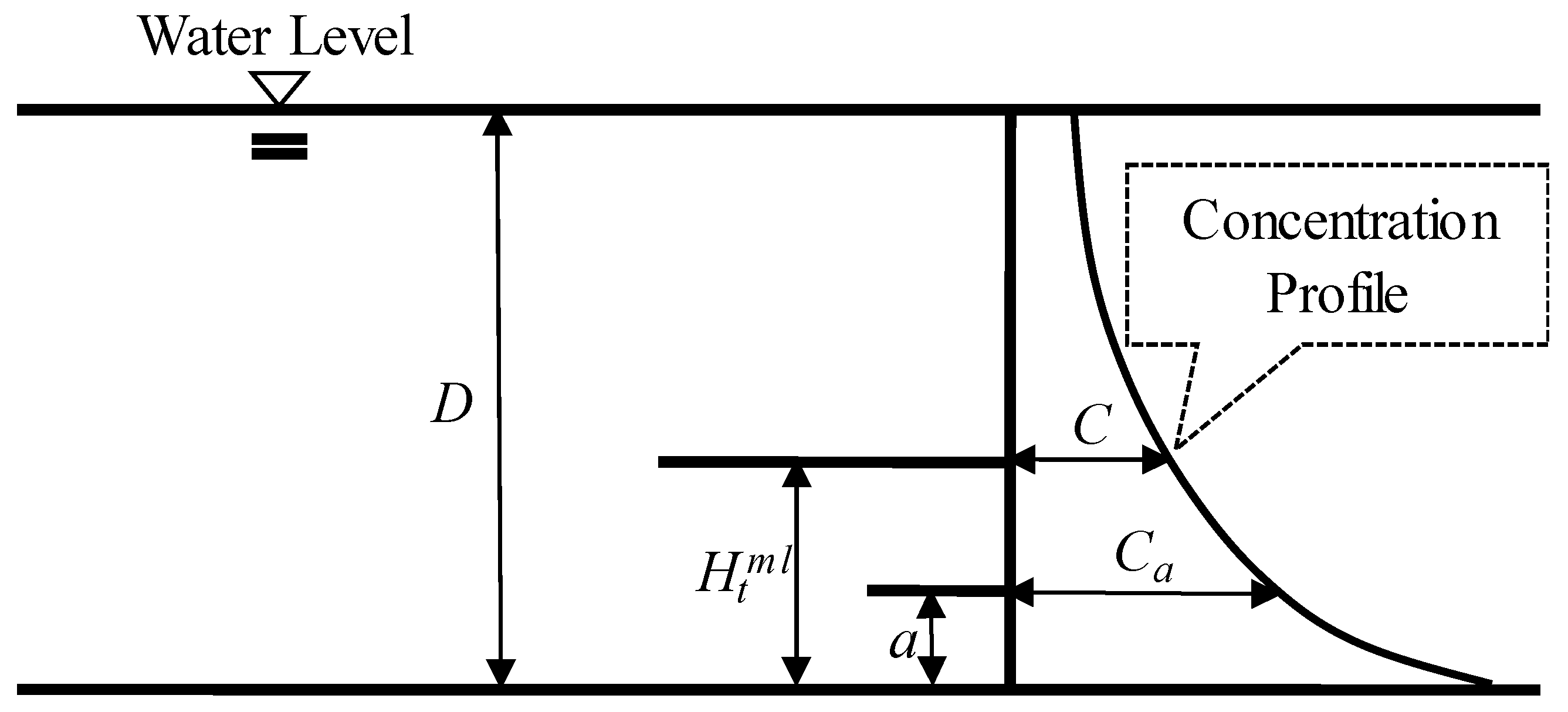
3.3. Concentration Calculation
3.4. Height of Aspiration
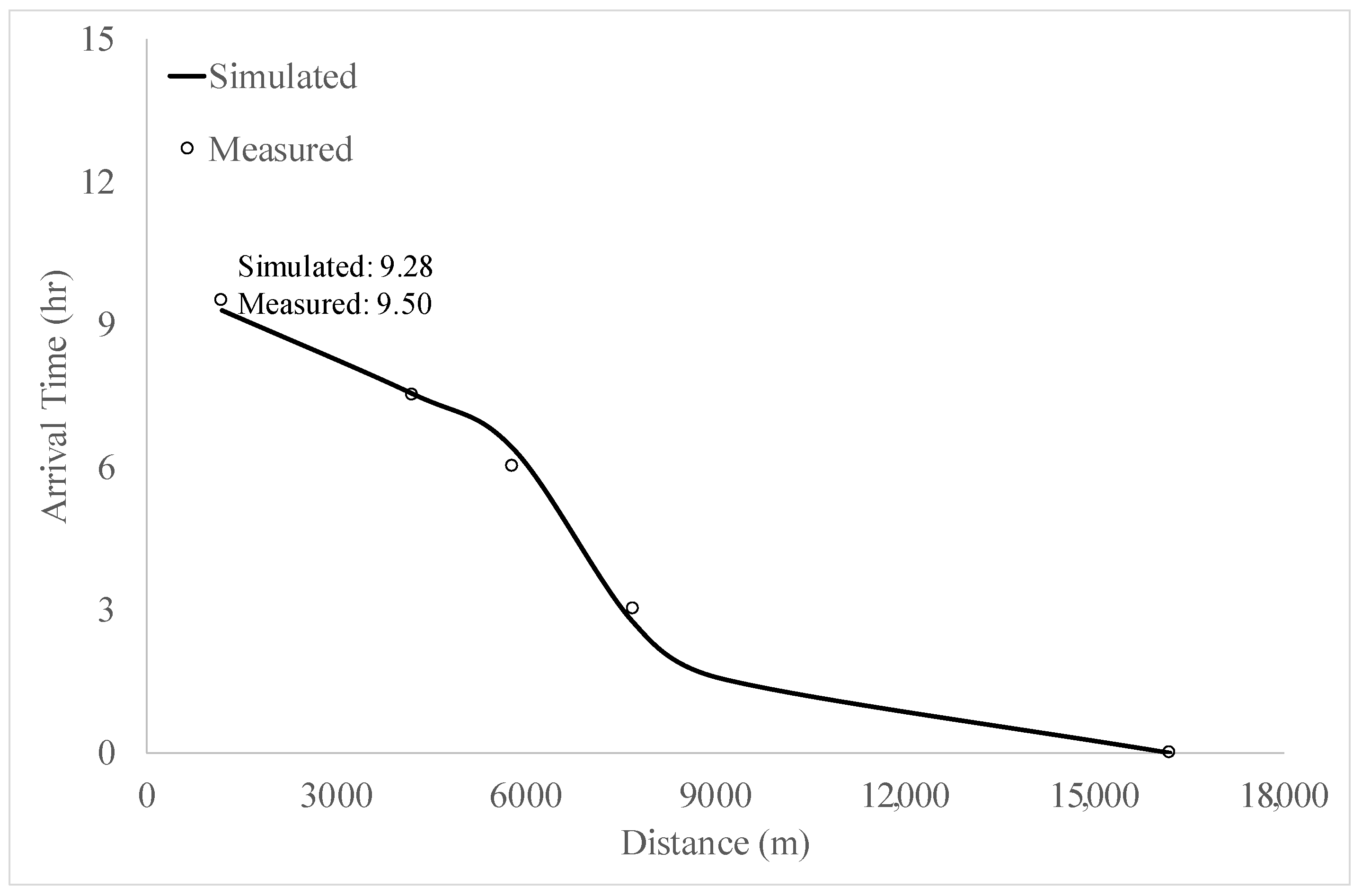
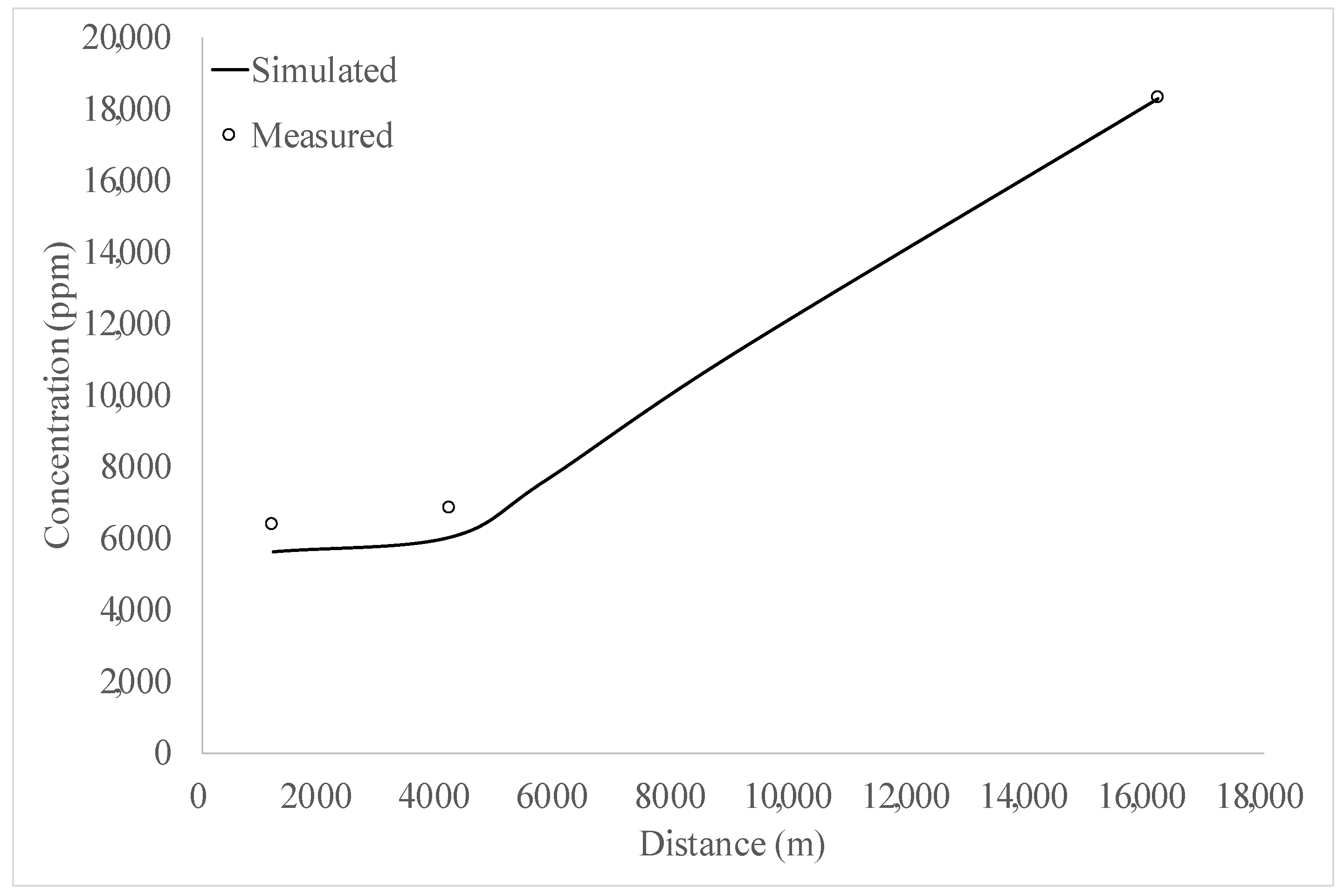
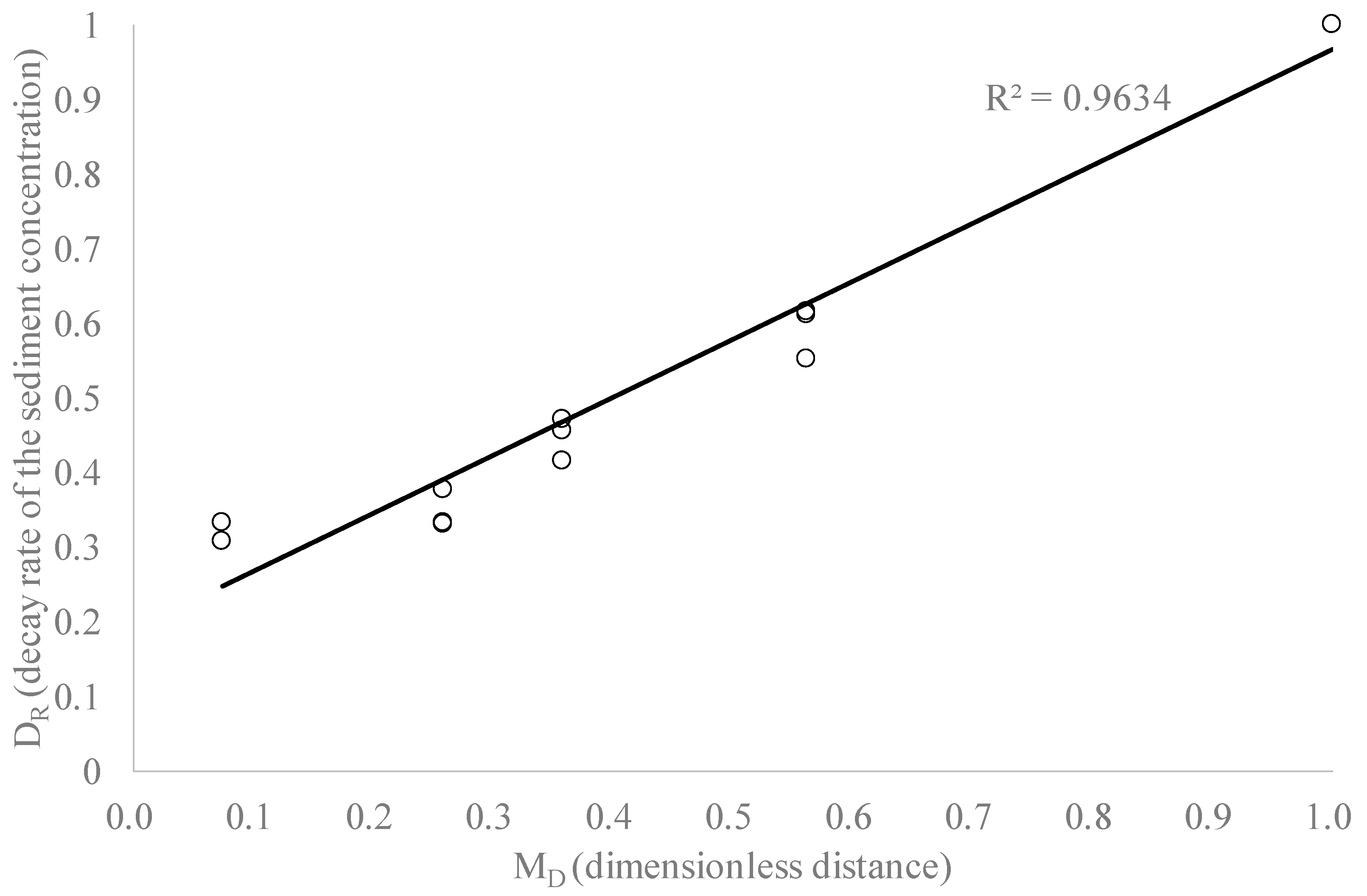
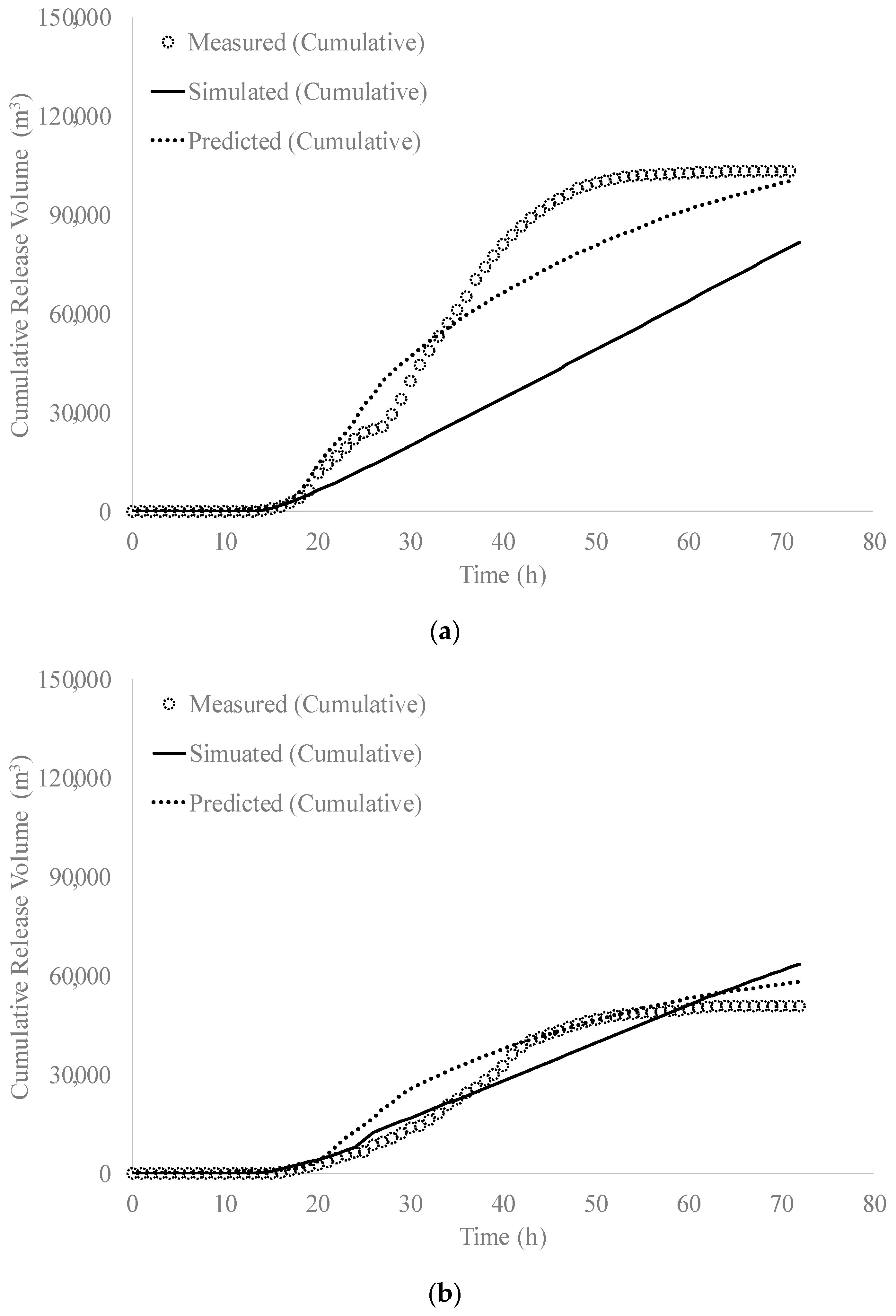
4. Research Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Notation
| distances between reservoir bed and the centerline of bottom outlet | |
| storage area in different elevation | |
| concentration at distances | |
| concentration at distances | |
| near-bed concentration of the kth size class | |
| drag coefficient | |
| constant and ranges from 0.05–1.00 | |
| total suspended sediment concentration defined as | |
| layer-averaged volumetric concentration of the kth sediment size class | |
| geometric mean diameter | |
| diameter of sediment size k | |
| water depth | |
| decay rate | |
| exponent of concentration distribution | |
| dimensionless entrainment coefficient | |
| erosion rate potential | |
| Froude number | |
| densimetric Froude number | |
| acceleration of gravity | |
| current thickness | |
| height of aspiration | |
| height of clear lake at corresponding time | |
| height of muddy lake at corresponding time | |
| kth | sediment size class |
| dimensionless distance | |
| volume fraction of the kth sediment size class | |
| total discharge through orifice | |
| inflow discharge and represents as turbidity water | |
| outflow discharge through different sluice gates | |
| outflow discharge of Diversion Tunnel | |
| dimensionless peak discharge of density current | |
| outflow discharge of PPI | |
| outflow discharge of PRO | |
| outflow discharge of Canal | |
| concentration of the peak discharge | |
| outflow discharge of Spillway | |
| shape factor of sediment particle | |
| friction between upper ambient water and the turbidity current | |
| current specific gravity | |
| bulk Richardson number | |
| , , | depth-averaged stresses due to turbulence and dispersion |
| time | |
| layer-averaged velocity in -direction | |
| shear velocity in the -direction | |
| average velocity | |
| layer-averaged velocity in -direction | |
| velocity of clear lake movement | |
| velocity of muddy lake movement | |
| dimensionless travel velocity of peak concentration of density current | |
| shear velocities in the -direction | |
| bed frictional velocity | |
| -direction in Cartesian coordinate | |
| -direction in Cartesian coordinate | |
| current top elevation | |
| bed elevation | |
| mixture density | |
| density of sediment | |
| density of ambient water | |
| bed shear stresses in -direction | |
| bed shear stresses in -direction | |
| kinematic viscosity of water | |
| fall velocity of the kth sediment size class | |
| turbulent eddy viscosity | |
| porosity of bed sediment |
References
- Hanjra, M.A.; Qureshi, M.E. Global water crisis and future food security in an era of climate change. Food Policy 2010, 35, 365–377. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Gao, Y.X.; Annandale, G.W.; Morris, G.L.; Jiang, E.; Zhang, J.H.; Cao, Y.T.; Carling, P.; Fu, K.D.; Guo, Q.C.; et al. Sustainable sediment management in reservoirs and regulated rivers: Experiences from five continents. Earth’s Future 2014, 2, 256–280. [Google Scholar] [CrossRef]
- Ercin, A.E.; Hoekstra, A.Y. Water footprint scenarios for 2050: A global analysis. Environ. Int. 2014, 64, 71–82. [Google Scholar] [CrossRef] [PubMed]
- Wisser, D.; Frolking, S.; Hagen, S.; Bierkens, F.P.M. Beyond peak reservoir storage? A global estimate of declining water storage capacity in large reservoirs. Water Resour. Res. 2013, 49, 5732–5739. [Google Scholar] [CrossRef]
- Oehy, C.; Schleiss, A. Control of turbidity currents in reservoirs by solid and permeable obstacles. J. Hydraul. Eng. 2007, 133, 637–648. [Google Scholar] [CrossRef]
- Shiklomanov, I.A.; Rodda, J.C. World Water Resources at the Beginning of the Twenty-First Century; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Lehner, B.; Liermann, C.R.; Revenga, C.; Vörösmarty, C.; Fekete, B.; Crouzet, P.; Döll, P.; Endejan, M.; Frenken, K.; Magome, J.E.A. Global Reservoir and Dam (GRanD) Database; Global Water System Project: Bonn, Germany, 2014. [Google Scholar]
- Chen, C.Y.; Chen, L.K.; Yu, F.C.; Lin, Y.C.; Lee, C.L.; Wang, Y.T. Landslides affecting sedimentary characteristics of reservoir basin. Environ. Earth Sci. 2010, 59, 1693–1702. [Google Scholar] [CrossRef]
- Water Resources Agency. Maintaining a Sustainable Tsengwen Reservoir Planning Report; Water Resources Agency: Taipei, Taiwan, 2014.
- Wang, H.W.; Kondolf, M.; Tullos, D.; Kuo, W.C. Sediment management in Taiwan’s reservoir and barriers to implementation. Water 2018, 10, 1034. [Google Scholar] [CrossRef]
- Forel, F.A. Les ravins sous-lacustre des fleuves glaciaires: Acad. Sci. Paris C. R. 1885, 101, 725–728. [Google Scholar]
- Lane, E.W. Some Hydraulic Engineering Aspects of Density Currents; Hydraulic Laboratory Report No. Hyd-373; U.S. Bureau of Reclamation: Denver, CO, USA, 1954.
- Grover, N.C.; Howard, C.S. The passage of turbid water through Lake Mead. Trans. Am. Soc. Civ. Eng. 1938, 103, 720–781. [Google Scholar]
- Water Resources Planning Institute. Hydraulic Model Studies for Sediment Sluicing and Flood Diversion Engineering of Shihman Reservoir; Water Resources Agency: Taichung, Taiwan, 2012.
- National Chiao Tung University. Long-Term Measurement of Sediment Transport and Density Current Simulation in Shihmen Reservoir; Water Resources Planning Institute: Hsinchu, Taiwan, 2014.
- National Chiao Tung University. Long-Term Monitoring of Sediment Transport in Shihmen Reservoir; Water Resources Planning Institute: Hsinchu, Taiwan, 2015.
- Ren, Z.; Ning, Q. Lecture Notes of the Training Course on Reservoir Sedimentation; IRTCES: Beijing, China, 1985. [Google Scholar]
- Müller, P.J.; De Cesare, G. Sedimentation problems in the reservoirs of the Kraftwerke Sarganserland-Venting of turbidity currents as the essential part of the solution. Q.89-R.21. In Proceedings of the 23rd Congress of the International Commission on Large Dams CIGB-ICOLD, Brasilia, Brazil, 25–29 May 2009; Volume 2. [Google Scholar]
- Wang, Z.; Xia, J.; Deng, S.; Zhang, J.; Li, T. One-dimensional morphodynamic model coupling open-channel flow and turbidity current in reservoir. J. Hydrol. Hydromech. 2017, 65, 68–79. [Google Scholar] [CrossRef]
- Feng, W.; Lin, C.-P.; Deschamps, R.J.; Drnevich, V.P. Theoretical model of a multisection time domain reflectometry measurement system. Water Resour. Res. 1999, 35, 2321–2331. [Google Scholar] [CrossRef]
- Huang, A.-B.; Lin, C.-P.; Chung, C.-C. TDR/DMT characterization of a reservoir sediment under water. J. GeoEng. 2008, 3, 61–66. [Google Scholar]
- Lin, C.-P.; Tang, S.-H.; Lin, C.-H.; Chung, C.-C. An improved modeling of TDR signal propagation for measuring complex dielectric permittivity. J. Earth Sci. 2015, 26, 827–834. [Google Scholar] [CrossRef]
- Luthi, S. Experiments on non-channelized turbidity currents and their deposits. Mar. Geol. 1981, 40, M59–M68. [Google Scholar] [CrossRef]
- Parker, G.; Garcia, M.; Fukushima, Y.; Yu, W. Experiments on turbidity currents over an erodible bed. J. Hydraul. Res. 1987, 25, 123–147. [Google Scholar] [CrossRef]
- Lee, H.Y.; Yu, W.S. Experiment study of reservoir density current. J. Hydraul. Eng. 1997, 123, 520–528. [Google Scholar] [CrossRef]
- Wu, C.H. A Study on Flood-Induced Sediment Transport and Its Sluicing Methods in a Reservoir. Ph.D. Thesis, Department of Hydraulic and Ocean Engineering, National Cheng Kung University, Tainan, Taiwan, 2015. [Google Scholar]
- Toniolo, H.; Parker, G.; Voller, V. Role of ponded turbidity currents in reservoir trap efficiency. J. Hydraul. Eng. 2007, 133, 579–595. [Google Scholar] [CrossRef]
- Gessler, D.; Hall, B.; Spasojevic, M.; Holly, F.; Pourtaheri, H.; Raphelt, N. Application of 3D mobile bed, hydrodynamic model. J. Hydraul. Eng. 1999, 125, 737–749. [Google Scholar] [CrossRef]
- Choi, S.-U.; Garcia, M. Turbulence modeling of density currents developing two dimensionally on a slope. J. Hydraul. Eng. 2002, 128, 55–63. [Google Scholar] [CrossRef]
- Firoozabadi, B.; Farhanieh, B.; Rad, M. Hydrodynamics of two-dimensional, laminar turbid density currents. J. Hydraul. Res. 2003, 41, 623–630. [Google Scholar] [CrossRef]
- Lai, Y.G.; Huang, J.C.; Wu, K.W. Reservoir turbidity current modeling with a two-dimensional layer-averaged model. J. Hydraul. Eng. 2015, 141, 04015029. [Google Scholar] [CrossRef]
- Huang, C.C.; Lai Yong, G.; Lai, J.S.; Tan, Y.C. Field and numerical modeling study of turbidity current in Shimen Reservoir during typhoon events. J. Hydraul. Eng. 2019, 145, 05019003. [Google Scholar] [CrossRef]
- Rouse, H. Modern conceptions of the mechanics or fluid turbulence. Trans. Am. Soc. Civ. Eng. 1937, 102, 463–505. [Google Scholar]
- Huang, C.-C.; Lai, J.-S.; Lee, F.-Z.; Tan, Y.-C. Physical model-based investigation of reservoir sedimentation processes. Water 2018, 10, 352. [Google Scholar] [CrossRef]
- Yu, G.-H. The essentiality of water resource development in Taiwan. Taiwan Water Conserv. 2016, 64, 1–8. [Google Scholar]
- Lai, Y.G.; Greimann, B.P. Predicting contraction scour with a two-dimensional depth averaged model. J. Hydraul. Res. 2010, 48, 383–387. [Google Scholar] [CrossRef]
- García, M.H. Depositional turbidity currents laden with poorly sorted sediment. J. Hydraul. Eng. 1994, 120, 1240–1263. [Google Scholar] [CrossRef]
- Fan, J.H. Experimental studies on density currents. Sci. Sin. 1960, 4, 275–303. [Google Scholar]





| Year, Typhoon | 2015, Soudelor | 2015, Dujuan | 2016, Megi |
|---|---|---|---|
| Total inflow (106 m3) | 247.15 | 196.00 | 248.60 |
| Total outflow (106 m3) | 211.27 | 165.28 | 258.12 |
| Peak inflow (m3/s) | 5634 | 3802 | 4267 |
| Total inflow sediment (106 m3) | 0.91 | 0.69 | 1.30 |
| Total outflow sediment (106 m3) | 0.33 | 0.26 | 0.26 |
| Spillway (Fluid/sediment) (%) | 57.95/10.37 | 39.49/3.87 | 48.00/6.67 |
| Diversion tunnel (Fluid/sediment) (%) | 21.68/0.87 | 33.44/3.21 | 25.91/0.80 |
| Canal (Fluid/sediment) (%) | 1.62/0.54 | 1.36/2.34 | 0.79/0.28 |
| PPI (Fluid/sediment) (%) | 7.43/5.35 | 8.01/10.85 | 5.74/3.24 |
| PRO (Fluid/sediment) (%) | 4.16/11.35 | 2.58/7.05 | 2.83/3.21 |
| Total release sediment (%) | 36.27 | 37.33 | 19.92 |
| Year, Typhoon | PRO (Permanent River Outlet) | PPI (Power Plant Intake) | ||||
|---|---|---|---|---|---|---|
| Measured | Simulated | Predicted | Measured | Simulated | Predicted | |
| 2015, Soudelor | 103,323 | 81,715 | 101,402 | 50,882 | 63,527 | 58,019 |
| 2015, Dujuan | 47,638 | 22,506 | 50,451 | 72,323 | 59,387 | 68,000 |
| 2016, Megi | 41,616 | 63,238 | 42,230 | 41,940 | 51,720 | 45,333 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-C.; Lin, W.-C.; Ho, H.-C.; Tan, Y.-C. Estimation of Reservoir Sediment Flux through Bottom Outlet with Combination of Numerical and Empirical Methods. Water 2019, 11, 1353. https://doi.org/10.3390/w11071353
Huang C-C, Lin W-C, Ho H-C, Tan Y-C. Estimation of Reservoir Sediment Flux through Bottom Outlet with Combination of Numerical and Empirical Methods. Water. 2019; 11(7):1353. https://doi.org/10.3390/w11071353
Chicago/Turabian StyleHuang, Cheng-Chia, Wen-Cheng Lin, Hao-Che Ho, and Yih-Chi Tan. 2019. "Estimation of Reservoir Sediment Flux through Bottom Outlet with Combination of Numerical and Empirical Methods" Water 11, no. 7: 1353. https://doi.org/10.3390/w11071353
APA StyleHuang, C.-C., Lin, W.-C., Ho, H.-C., & Tan, Y.-C. (2019). Estimation of Reservoir Sediment Flux through Bottom Outlet with Combination of Numerical and Empirical Methods. Water, 11(7), 1353. https://doi.org/10.3390/w11071353





