Interplays between State and Flux Hydrological Variables across Vadose Zones: A Numerical Investigation
Abstract
1. Introduction
2. Methods and Materials
2.1. Model Setup and Data Inputs
2.2. Generation of Soil Hydraulic Parameters
2.3. Temporal Stability Analysis of Soil Moisture
3. Results and Discussion
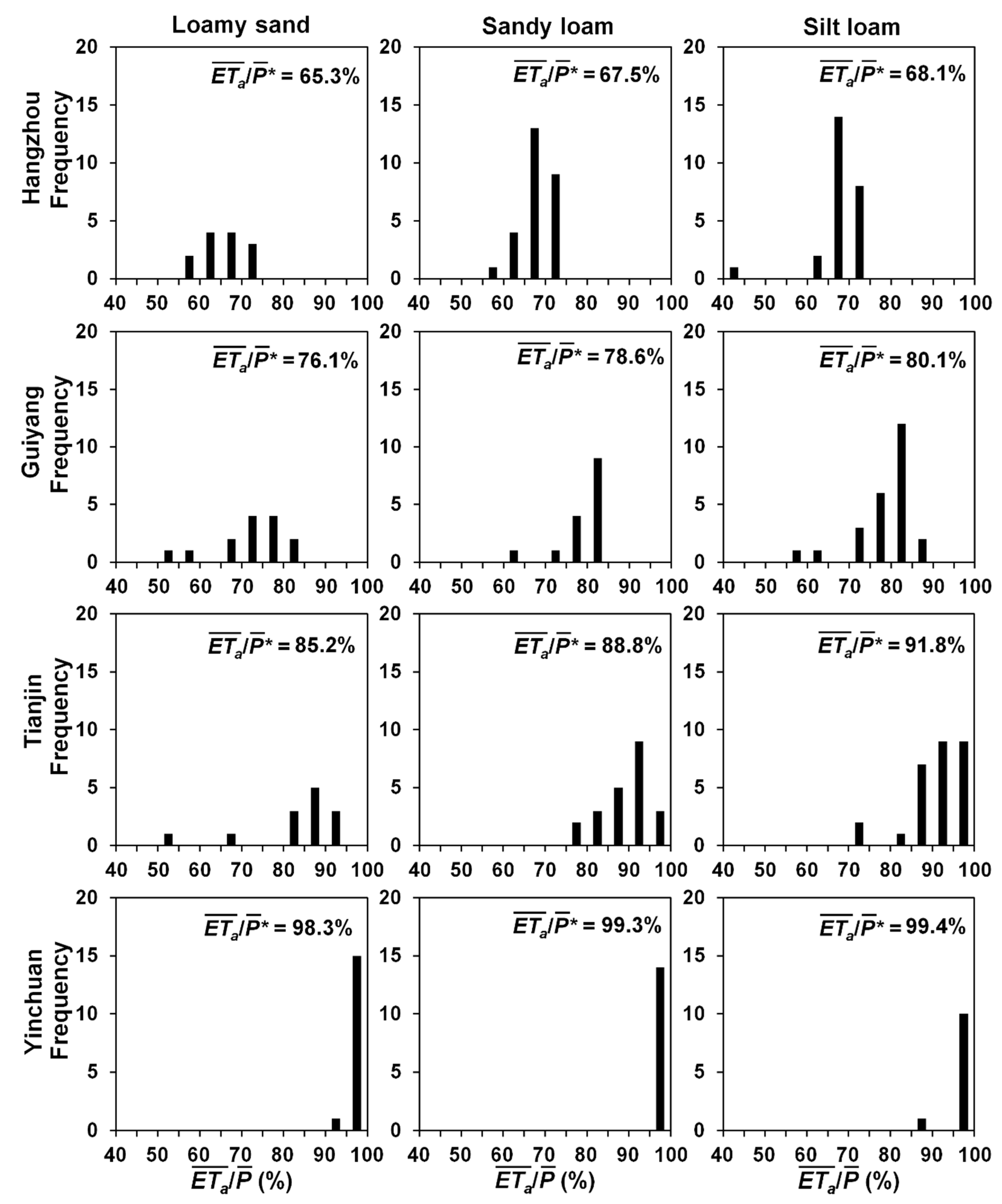
3.1. Comparison of Hydroclimatic Conditions across the Study Sites
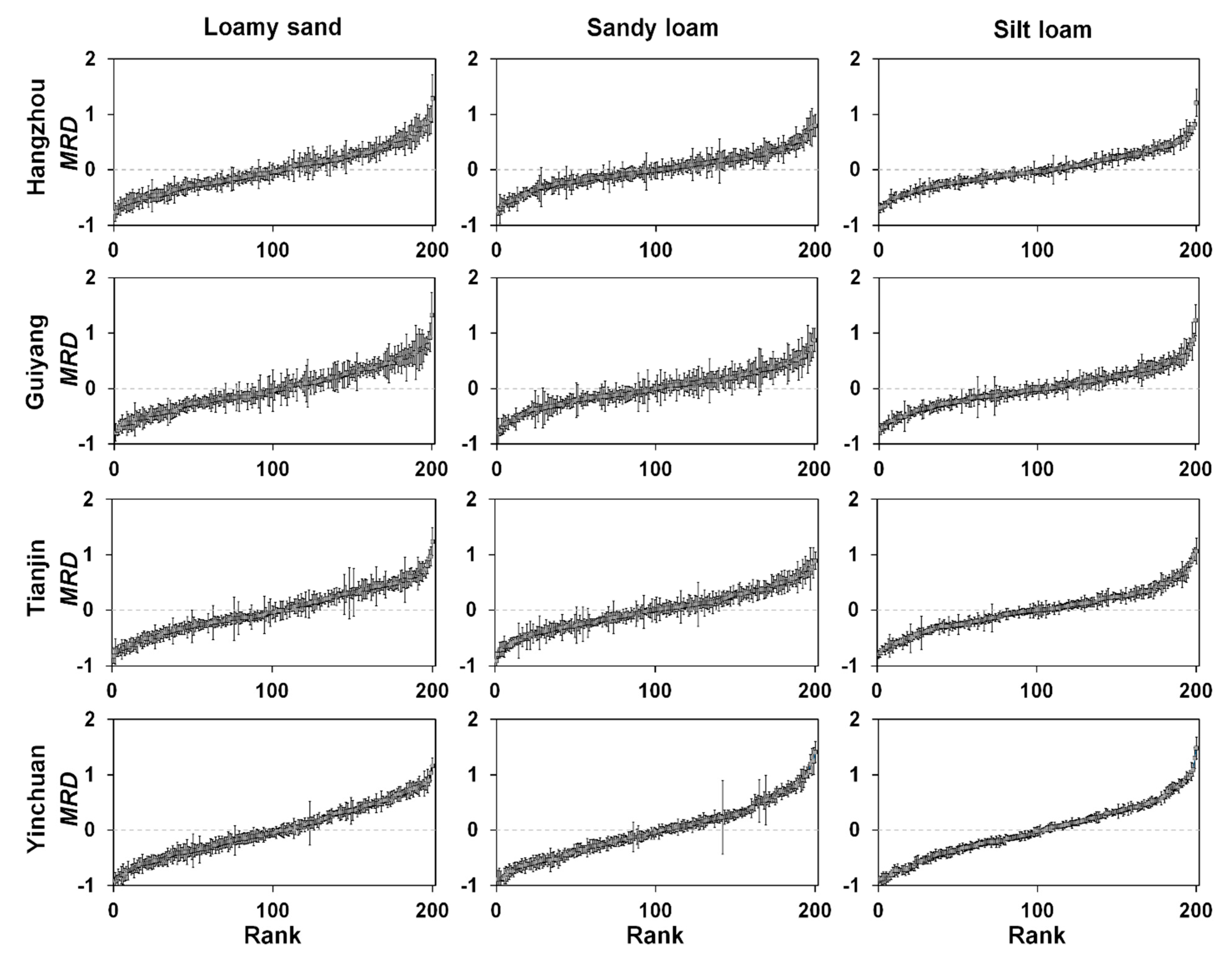
3.2. Simulated Patterns of MRD
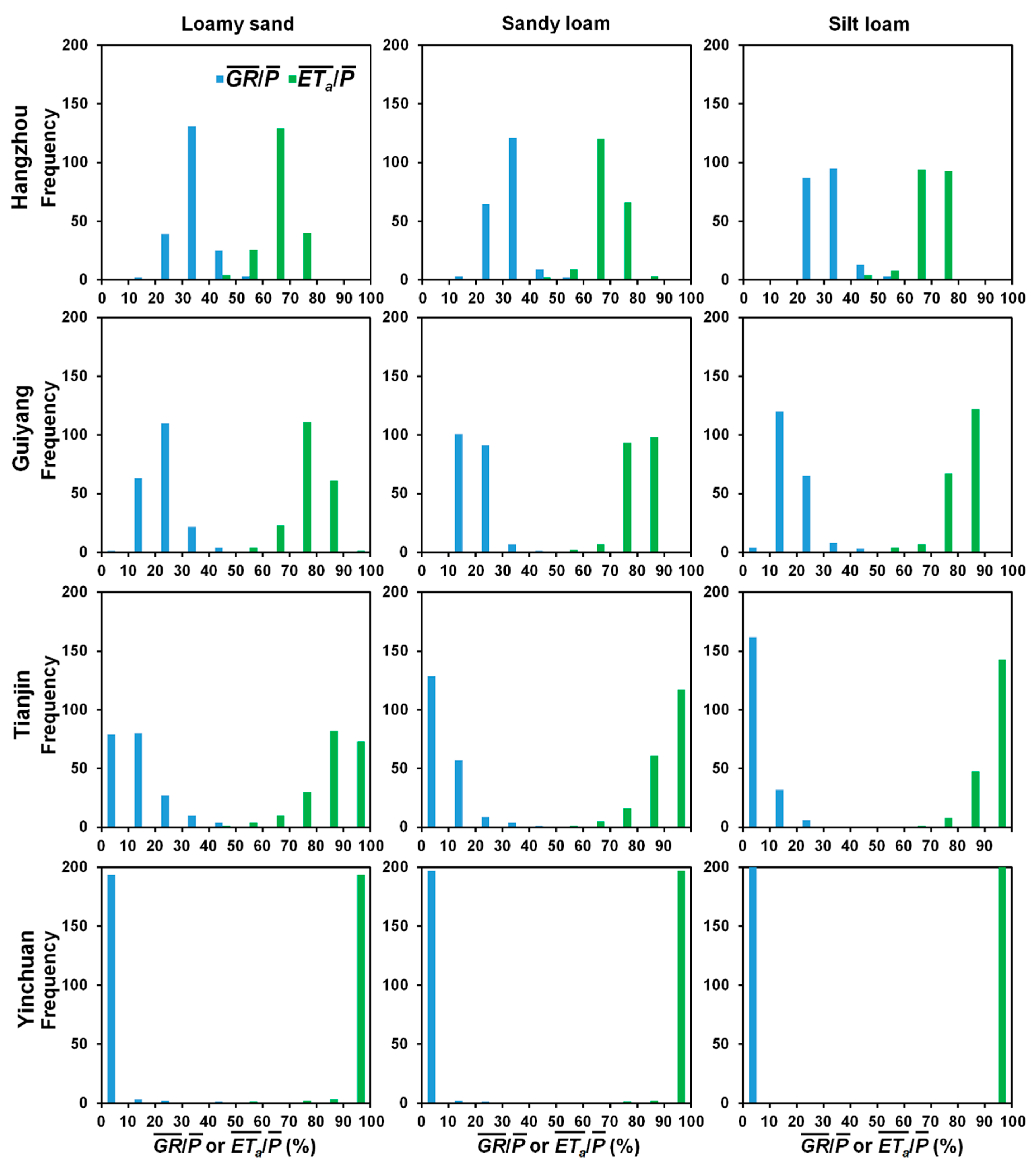
3.3. Distribution Patterns of and
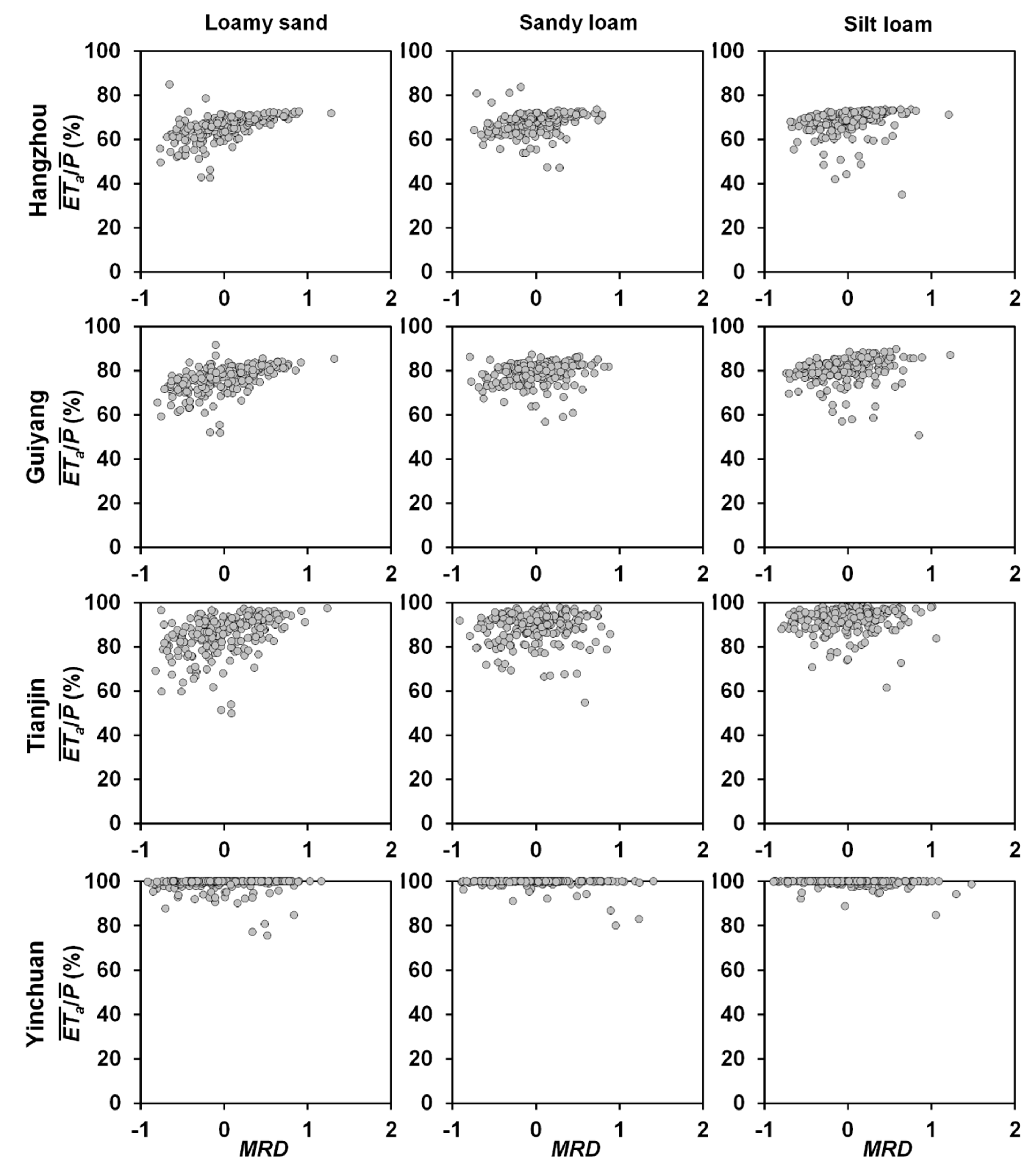
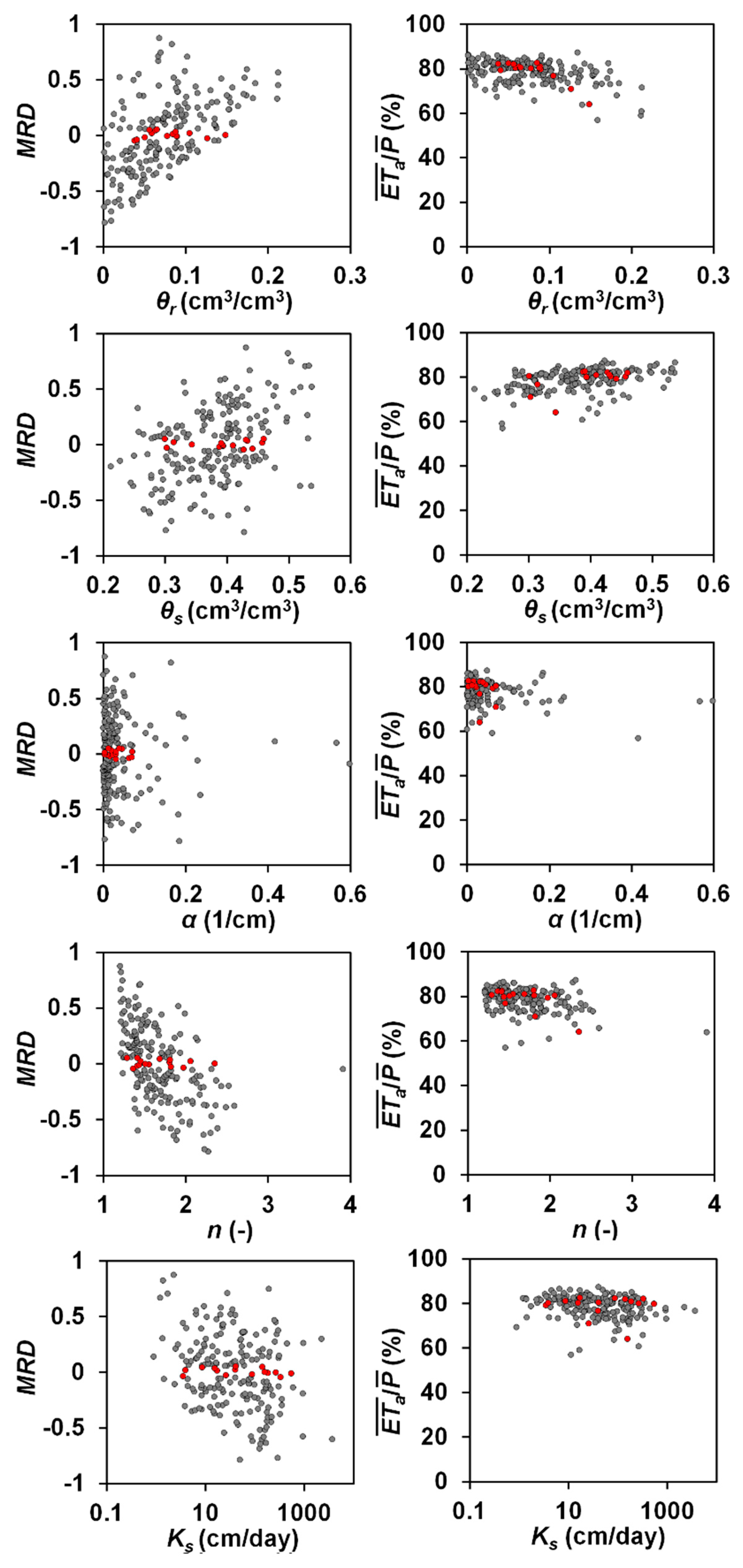
3.4. Relationships of MRD with and
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil moisture measurement for ecological and hydrological watershed-scale observatories: A review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Vereecken, H.; Huisman, J.A.; Pachepsky, Y.; Montzka, C.; van der Kruk, J.; Bogena, H.; Weihermüller, L.; Herbst, M.; Martinez, G.; Vanderborght, J. On the spatio-temporal dynamics of soil moisture at the field scale. J. Hydrol. 2014, 516, 76–96. [Google Scholar] [CrossRef]
- Keese, K.E.; Scanlon, B.R.; Reedy, R.C. Assessing controls on diffuse groundwater recharge using unsaturated flow modeling. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Szilagyi, J.; Zlotnik, V.A.; Gates, J.B.; Jozsa, J. Mapping mean annual groundwater recharge in the Nebraska Sand Hills, USA. Hydrogeol. J. 2011, 19, 1503–1513. [Google Scholar] [CrossRef]
- Trambauer, P.; Dutra, E.; Maskey, S.; Werner, M.; Pappenberger, F.; van Beek, L.P.H.; Uhlenbrook, S. Comparison of different evaporation estimates over the African continent. Hydrol. Earth Syst. Sci. 2014, 18, 193–212. [Google Scholar] [CrossRef]
- Wang, T.; Franz, T.E.; Zlotnik, V.A. Controls of soil hydraulic characteristics on modeling groundwater recharge under different climatic conditions. J. Hydrol. 2015, 521, 470–481. [Google Scholar] [CrossRef]
- Daly, E.; Porporato, A. A review of soil moisture dynamics: From rainfall infiltration to ecosystem response. Environ. Eng. Sci. 2005, 22, 9–24. [Google Scholar] [CrossRef]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Moreno, H.A.; Mascaro, G.; Rodriguez, J.C.; Watts, C.J.; Garatuza-Payan, J.; Scott, R.L. Observed relation between evapotranspiration and soil moisture in the North American monsoon region. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Peters-Lidard, C.D.; Clark, M.; Samaniego, L.; Verhoest, N.E.C.; van Emmerik, T.; Uijlenhoet, R.; Achieng, K.; Franz, T.E.; Woods, R. Scaling, similarity, and the fourth paradigm for hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 3701–3713. [Google Scholar] [CrossRef] [PubMed]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; de Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951. [Google Scholar] [CrossRef]
- Wang, T.; Franz, T.E.; Yue, W.; Szilagyi, J.; Zlotnik, V.A.; You, J.; Chen, X.; Shulski, M.D.; Young, A. Feasibility analysis of using inverse modeling for estimating natural groundwater recharge from a large-scale soil moisture monitoring network. J. Hydrol. 2016, 533, 250–265. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; de Rosnay, P.; Ryu, D.; Walker, J.P. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Song, L.; Zhao, Q.; Ge, Y.; Xu, T.; Ma, Y.; Zhu, Z.; Jia, Z.; Zhang, F. Upscaling evapotranspiration measurements from multi-site to the satellite pixel scale over heterogeneous land surfaces. Agric. For. Meteorol. 2016, 230–231, 97–113. [Google Scholar] [CrossRef]
- Vachaud, G.; Passerat De Silans, A.; Balabanis, P.; Vauclin, M. Temporal stability of spatially measured soil water probability density function1. Soil Sci. Soc. Am. J. 1985, 49, 822–828. [Google Scholar] [CrossRef]
- Vanderlinden, K.; Vereecken, H.; Hardelauf, H.; Herbst, M.; Martínez, G.; Cosh, M.H.; Pachepsky, Y.A. Temporal stability of soil water contents: A review of data and analyses. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Pachepsky, Y.A.; Guber, A.K.; Jacques, D. Temporal persistence in vertical distributions of soil moisture contents. Soil Sci. Soc. Am. J. 2005, 69, 347–352. [Google Scholar] [CrossRef]
- Starr, G.C. Assessing temporal stability and spatial variability of soil water patterns with implications for precision water management. Agric. Water Manag. 2005, 72, 223–243. [Google Scholar] [CrossRef]
- Guber, A.K.; Gish, T.J.; Pachepsky, Y.A.; van Genuchten, M.T.; Daughtry, C.S.T.; Nicholson, T.J.; Cady, R.E. Temporal stability in soil water content patterns across agricultural fields. Catena 2008, 73, 125–133. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Morbidelli, R. Spatial-temporal variability of soil moisture and its estimation across scales. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Wang, T.; Liu, Q.; Franz, T.E.; Li, R.; Lang, Y.; Fiebrich, C.A. Spatial patterns of soil moisture from two regional monitoring networks in the United States. J. Hydrol. 2017, 552, 578–585. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Turkeltaub, T.; Kurtzman, D.; Bel, G.; Dahan, O. Examination of groundwater recharge with a calibrated/validated flow model of the deep vadose zone. J. Hydrol. 2015, 522, 618–627. [Google Scholar] [CrossRef]
- Foolad, F.; Franz, T.E.; Wang, T.; Gibson, J.; Kilic, A.; Allen, R.G.; Suyker, A. Feasibility analysis of using inverse modeling for estimating field-scale evapotranspiration in maize and soybean fields from soil water content monitoring networks. Hydrol. Earth Syst. Sci. 2017, 21, 1263–1277. [Google Scholar] [CrossRef]
- Martínez, G.; Pachepsky, Y.A.; Vereecken, H. Temporal stability of soil water content as affected by climate and soil hydraulic properties: A simulation study. Hydrol. Process. 2014, 28, 1899–1915. [Google Scholar] [CrossRef]
- Wang, T. Modeling the impacts of soil hydraulic properties on temporal stability of soil moisture under a semi-arid climate. J. Hydrol. 2014, 519, 1214–1224. [Google Scholar] [CrossRef]
- Vereecken, H.; Kamai, T.; Harter, T.; Kasteel, R.; Hopmans, J.; Vanderborght, J. Explaining soil moisture variability as a function of mean soil moisture: A stochastic unsaturated flow perspective. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Wang, T.; Zlotnik, V.A.; Šimunek, J.; Schaap, M.G. Using pedotransfer functions in vadose zone models for estimating groundwater recharge in semiarid regions. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Simunek, J.; Sejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1 D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Media; Version 4.17; Depart. of Environ. Sci., University of California Riverside: Riverside, CA, USA, 2013; p. 308. [Google Scholar]
- Zlotnik, V.A.; Wang, T.; Nieber, J.L.; Šimunek, J. Verification of numerical solutions of the Richards equation using a traveling wave solution. Adv. Water Resour. 2007, 30, 1973–1980. [Google Scholar] [CrossRef]
- Neuman, S.P.; Feddes, R.A.; Bresler, E. Finite Element Simulation of Flow in Saturated-Unsaturated Soils Considering Water Uptake by Plants; Third Annual Report; Proj. A10-SWC-77; Hydraul. Eng. Lab., Technion: Haifa, Israel, 1974. [Google Scholar]
- Feddes, R.A.; Kowalik, P.J.; Neuman, S.P. Simulation of Field Water Use and Crop Yield; John Wiley and Sons: New York, NY, USA, 1978. [Google Scholar]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef]
- Wang, T.; Zlotnik, V.A. A complementary relationship between actual and potential evapotranspiration and soil effects. J. Hydrol. 2012, 456–457, 146–150. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar] [CrossRef]
- Jackson, R.B.; Canadell, J.; Ehleringer, J.R.; Mooney, H.A.; Sala, O.E.; Schulze, E.D. A global analysis of root distributions for terrestrial biomes. Oecologia 1996, 108, 389–411. [Google Scholar] [CrossRef]
- Small, E.E. Climatic controls on diffuse groundwater recharge in semiarid environments of the southwestern United States. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Available online: http://www.ncdc.noaa.gov/cdo-web/ (accessed on 19 June 2019).
- Hargreaves, G.H.; Samani, Z.A. Estimation potential evapotranspiration. J. Irrig. Drain. Eng. ASCE 1982, 108, 223–230. [Google Scholar]
- Gutiérrez-Jurado, H.A.; Vivoni, E.R.; Harrison, J.B.J.; Guan, H. Ecohydrology of root zone water fluxes and soil development in complex semiarid rangelands. Hydrol. Process. 2006, 20, 3289–3316. [Google Scholar] [CrossRef]
- Vogel, T.; Dohnal, M.; Dusek, J.; Votrubova, J.; Tesar, M. Macroscopic modeling of plant water uptake in a forest stand involving root-mediated soil water redistribution. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Wesseling, J.G. Meerjarige Simulatie van Grondwaterstroming voor Verschillende Bodemprofielen, Grondwatertrappen en Gewassen Met Het Model SWATRE. Rapport 152; Wageningen, DLO-Staring Centrum. 1991, p. 63. Available online: https://library.wur.nl/WebQuery/wurpubs/fulltext/304226 (accessed on 19 June 2019).
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Lawrence, J.E.; Hornberger, G.M. Soil moisture variability across climate zones. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Teuling, A.J.; Hupet, F.; Uijlenhoet, R.; Troch, P.A. Climate variability effects on spatial soil moisture dynamics. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Weighted recalibration of the Rosetta pedotransfer model with improved estimates of hydraulic parameter distributions and summary statistics (Rosetta3). J. Hydrol. 2017, 547, 39–53. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G.; Guadagnini, A.; Neuman, S.P. Inverse modeling of unsaturated flow using clusters of soil texture and pedotransfer functions. Water Resour. Res. 2016, 52, 7631–7644. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; Ceballos, A. Temporal stability of soil moisture in a large-field experiment in Spain. Soil Sci. Soc. Am. J. 2003, 67, 1647–1656. [Google Scholar] [CrossRef]
- Wang, T.; Franz, T.E. Field observations of regional controls of soil hydraulic properties on soil moisture spatial variability in different climate zones. Vadose Zone J. 2015, 14. [Google Scholar] [CrossRef]
- Yokoo, Y.; Sivapalan, M.; Oki, T. Investigating the roles of climate seasonality and landscape characteristics on mean annual and monthly water balances. J. Hydrol. 2008, 357, 255–269. [Google Scholar] [CrossRef]
- Cosh, M.H.; Jackson, T.J.; Moran, S.; Bindlish, R. Temporal persistence and stability of surface soil moisture in a semi-arid watershed. Remote Sens. Environ. 2008, 112, 304–313. [Google Scholar] [CrossRef]
- Zhao, Y.; Peth, S.; Wang, X.Y.; Lin, H.; Horn, R. Controls of surface soil moisture spatial patterns and their temporal stability in a semi-arid steppe. Hydrol. Process. 2010, 24, 2507–2519. [Google Scholar] [CrossRef]
- Zhang, L.; Dawes, W.R.; Walker, G.R. Response of mean annual evapotranspiration to vegetation changes at catchment scale. Water Resour. Res. 2001, 37, 701–708. [Google Scholar] [CrossRef]
- Wang, T.; Istanbulluoglu, E.; Lenters, J.; Scott, D. On the role of groundwater and soil texture in the regional water balance: An investigation of the Nebraska Sand Hills, USA. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Chen, X.; Rubin, Y.; Ma, S.; Baldocchi, D. Observations and stochastic modeling of soil moisture control on evapotranspiration in a Californian oak savanna. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Hu, W.; Shao, M.; Han, F.; Reichardt, K.; Tan, J. Watershed scale temporal stability of soil water content. Geoderma 2010, 158, 181–198. [Google Scholar] [CrossRef]
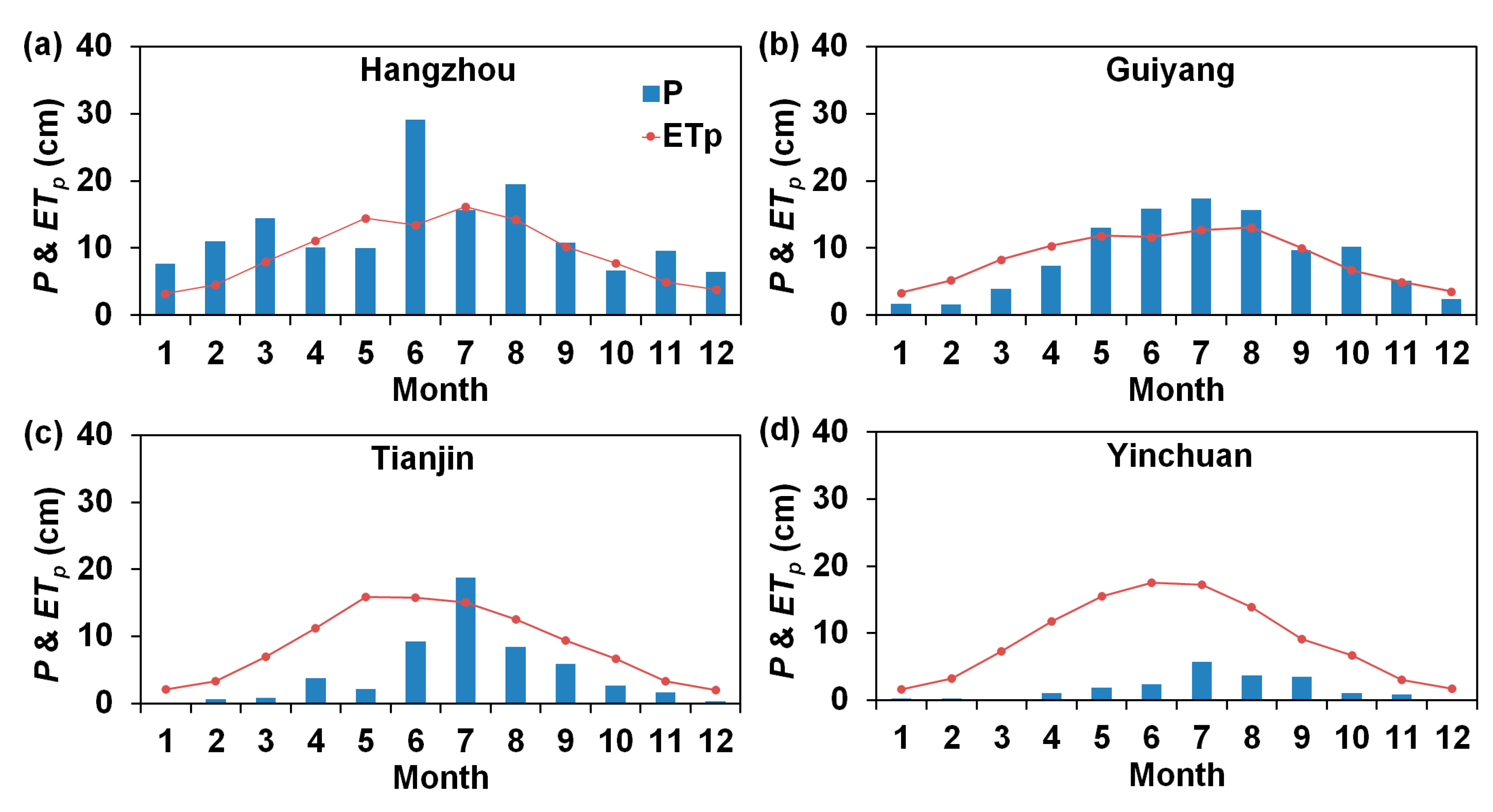
| Location | Latitude | Longitude | (-) | ||
|---|---|---|---|---|---|
| Hangzhou | 30.23°N | 120.17°E | 150.9 (127.4–172.9) * | 111.8 (108.0–115.1) | 0.74 (0.62–0.89) |
| Guiyang | 26.58°N | 106.73°E | 103.8 (73.5–137.1) | 101.7 (95.9–104.6) | 0.98 (0.74–1.40) |
| Tianjin | 39.10°N | 117.17°E | 54.3 (35.6–75.7) | 104.1 (99.9–107.2) | 1.92 (1.37–2.81) |
| Yinchuan | 38.47°N | 106.20°E | 20.8 (16.6–29.2) | 108.6 (106.8–110.5) | 5.22 (3.74–6.43) |
| Soil Texture | θr (cm3 cm−3) | θs (cm3 cm−3) | α (1/cm) | n (-) | Ks (cm/day) |
|---|---|---|---|---|---|
| Loamy sand | 0.064 (0.035) * | 0.386 (0.063) | 0.036 (0.039) | 1.908 (0.580) | 342.5 (864.1) |
| Sandy loam | 0.076 (0.047) | 0.381 (0.068) | 0.040 (0.075) | 1.673 (0.359) | 125.4 (334.1) |
| Silt loam | 0.098 (0.057) | 0.432 (0.077) | 0.006 (0.007) | 1.790 (0.475) | 62.8 (180.9) |
| Location | Loamy Sand | Sandy Loam | Silt Loam | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Range of MRD | Range of SDRD | Mean SDRD | Range of MRD | Range of SDRD | Mean SDRD | Range of MRD | Range of SDRD | Mean SDRD | |
| Hangzhou | −0.765–1.287 | 0.046–0.428 | 0.139 | −0.741–0.799 | 0.041–0.402 | 0.131 | −0.690–1.210 | 0.022–0.264 | 0.085 |
| Guiyang | −0.797–1.324 | 0.037–0.486 | 0.158 | −0.789–0.873 | 0.049–0.430 | 0.159 | −0.732–1.230 | 0.027–0.370 | 0.112 |
| Tianjin | −0.819–1.237 | 0.043–0.462 | 0.133 | −0.977–0.891 | 0.053–0.397 | 0.134 | −0.793–1.064 | 0.032–0.301 | 0.091 |
| Yinchuan | −0.912–1.166 | 0.035–0.397 | 0.114 | −0.889–1.410 | 0.043–0.664 | 0.111 | −0.890–1.485 | 0.024–0.199 | 0.073 |
| Location | Loamy Sand | Sandy Loam | Silt Loam | |||
|---|---|---|---|---|---|---|
| Hangzhou | 0.679 | −0.668 | 0.431 | −0.429 | 0.461 | −0.462 |
| Guiyang | 0.630 | −0.623 | 0.288 | −0.279 | 0.378 | −0.393 |
| Tianjin | 0.482 | −0.478 | 0.123 | −0.145 * | 0.188 ** | −0.258 |
| Yinchuan | 0.255 | −0.297 | 0.227 ** | −0.241 | 0.089 | −0.158 * |
| Soil Hydraulic Parameters | Hangzhou | Guiyang | Tianjin | Yinchuan | ||||
|---|---|---|---|---|---|---|---|---|
| MRD | MRD | MRD | MRD | |||||
| θr | 0.411 | −0.372 | 0.573 | −0.369 | 0.734 | −0.356 | 0.920 | −0.018 |
| θs | 0.497 | 0.481 | 0.398 | 0.422 | 0.219 ** | 0.351 | 0.026 | −0.095 |
| α | −0.012 | −0.176 * | 0.026 | −0.307 | 0.038 | −0.443 | 0.061 | −0.493 |
| n | −0.568 | −0.270 | −0.578 | −0.351 | −0.548 | −0.363 | −0.294 | −0.156 * |
| Ks | −0.357 | −0.406 | −0.263 | −0.301 | −0.109 | −0.172 * | 0.008 | 0.286 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Wang, T.; Zhang, Y. Interplays between State and Flux Hydrological Variables across Vadose Zones: A Numerical Investigation. Water 2019, 11, 1295. https://doi.org/10.3390/w11061295
Wang Z, Wang T, Zhang Y. Interplays between State and Flux Hydrological Variables across Vadose Zones: A Numerical Investigation. Water. 2019; 11(6):1295. https://doi.org/10.3390/w11061295
Chicago/Turabian StyleWang, Zhaoxin, Tiejun Wang, and Yonggen Zhang. 2019. "Interplays between State and Flux Hydrological Variables across Vadose Zones: A Numerical Investigation" Water 11, no. 6: 1295. https://doi.org/10.3390/w11061295
APA StyleWang, Z., Wang, T., & Zhang, Y. (2019). Interplays between State and Flux Hydrological Variables across Vadose Zones: A Numerical Investigation. Water, 11(6), 1295. https://doi.org/10.3390/w11061295




