Impacts of Spatial Heterogeneity and Temporal Non-Stationarity on Intensity-Duration-Frequency Estimates—A Case Study in a Mountainous California-Nevada Watershed
Abstract
1. Introduction
2. Materials and Methods
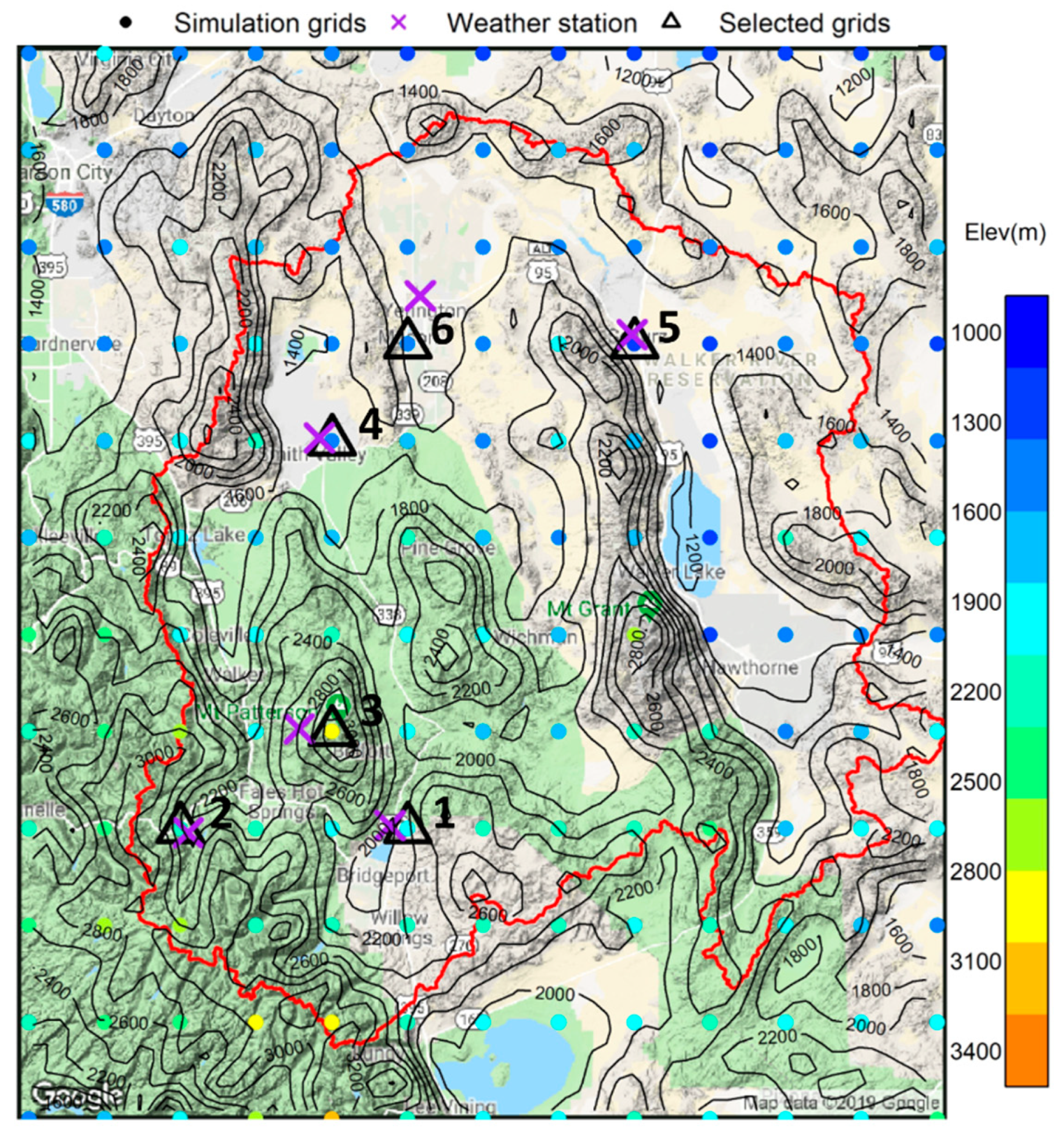
2.1. Research Area
2.2. Method
2.3. Trend Analysis
2.4. Quasi-Stationary and Non-Stationary IDFs
2.5. Geostatistics: (Variogram and Kriging)
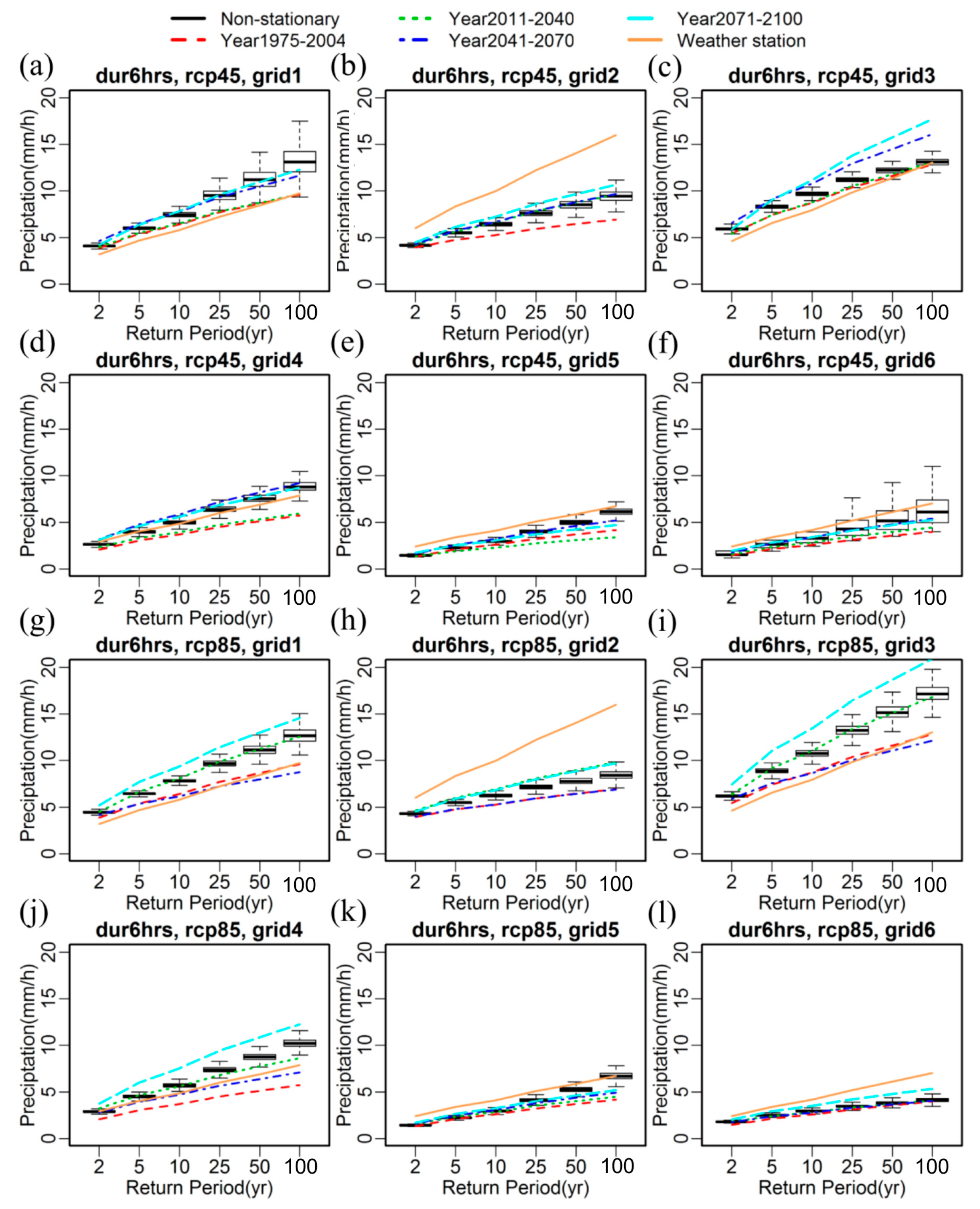
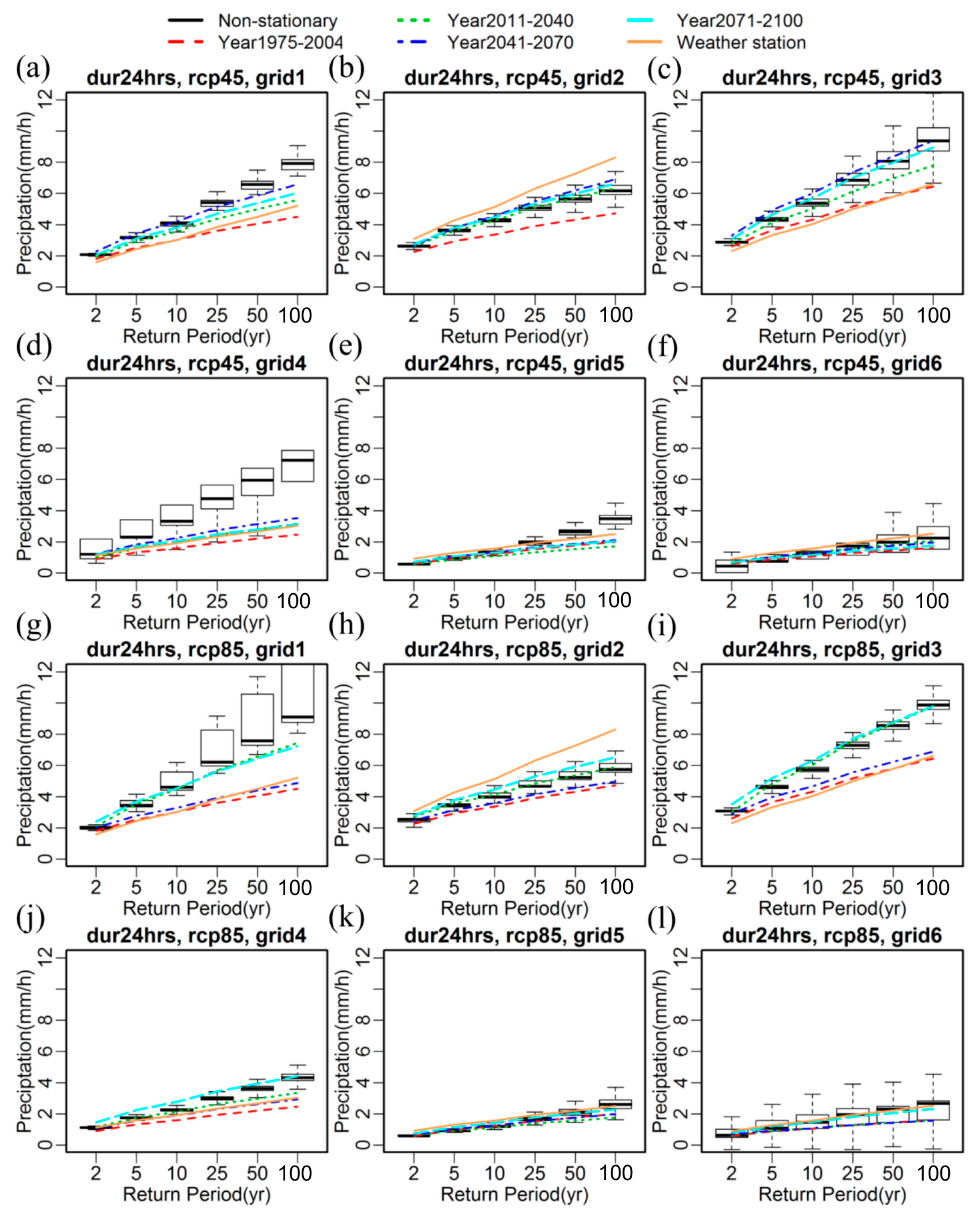
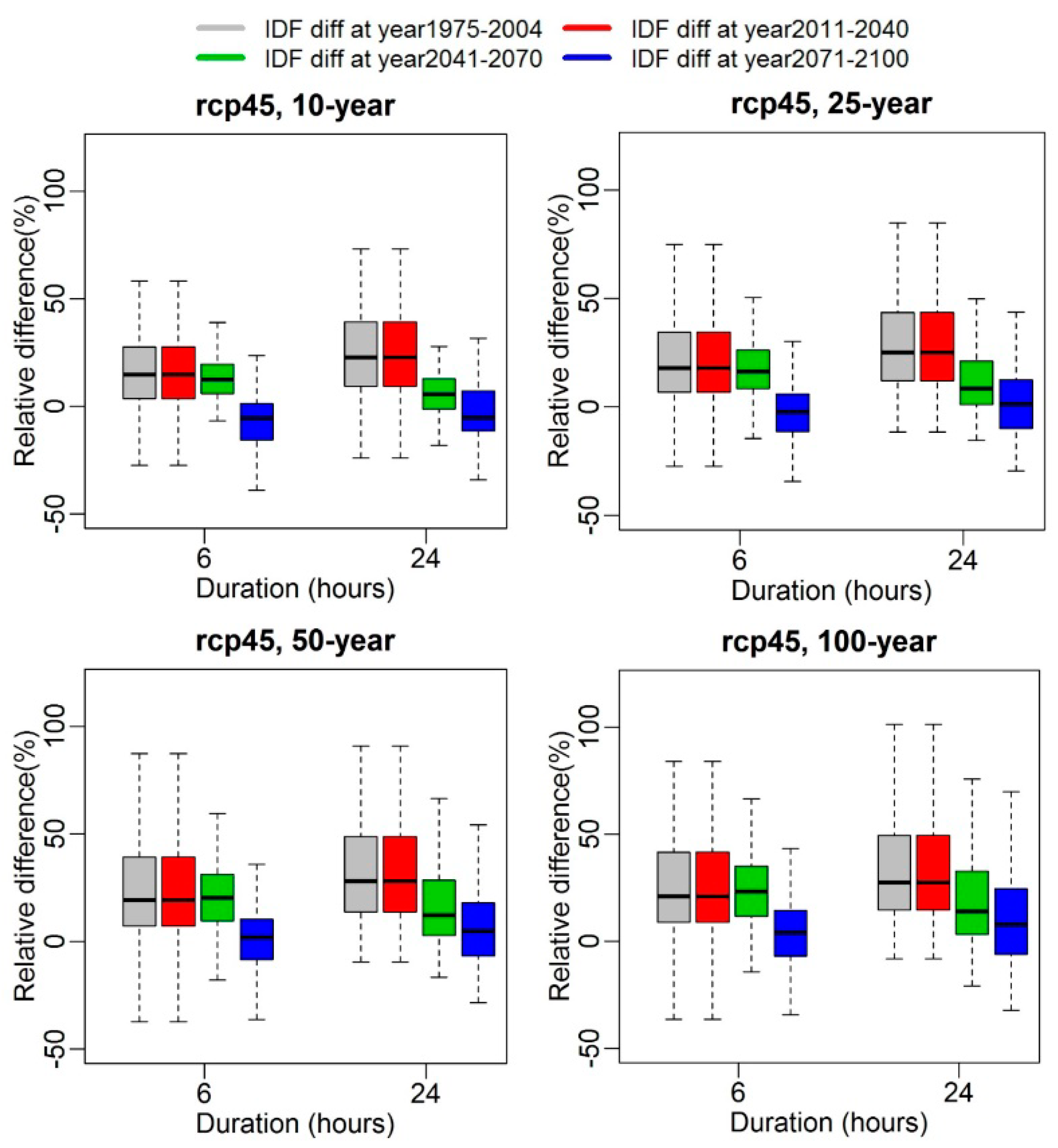
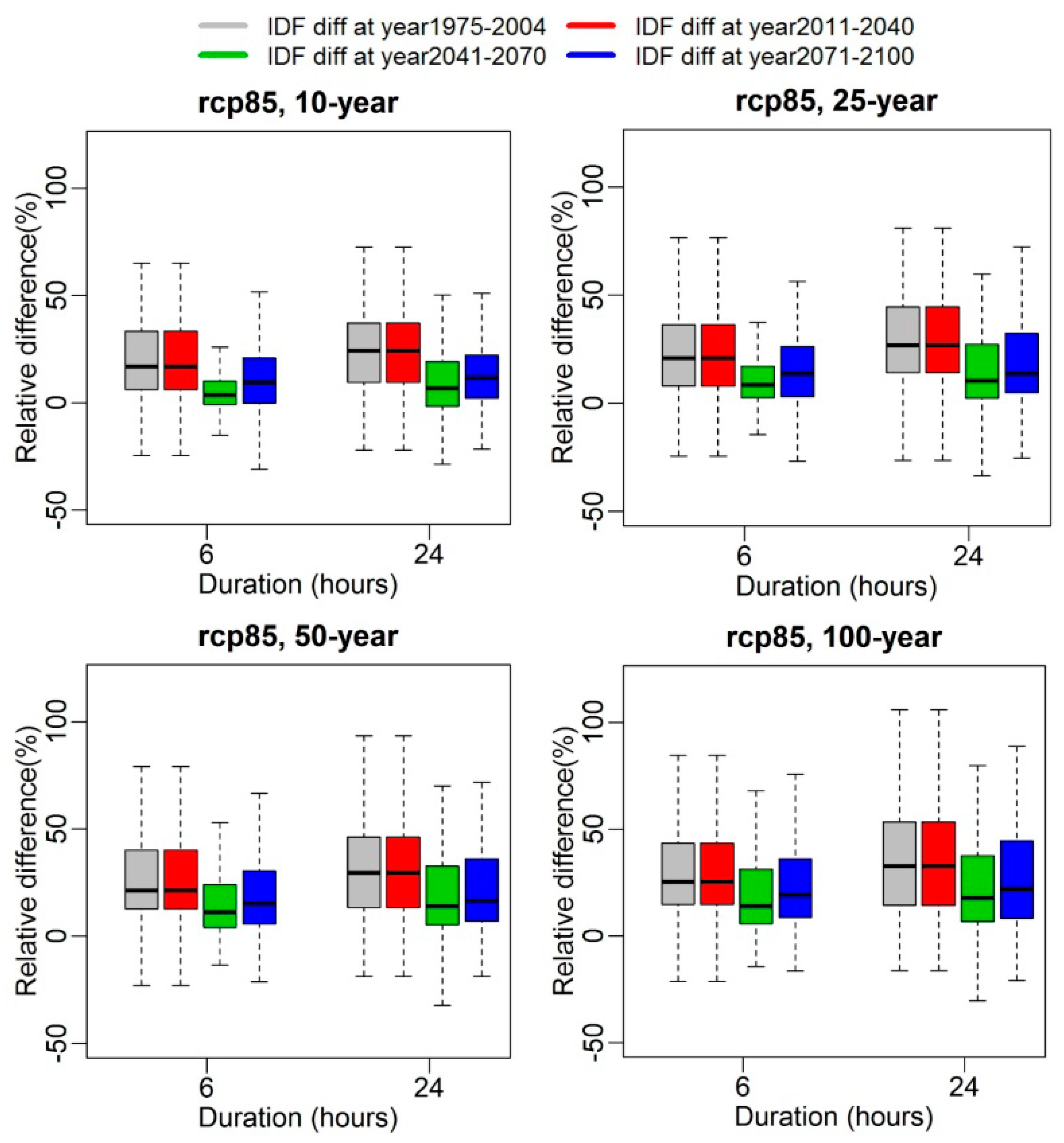
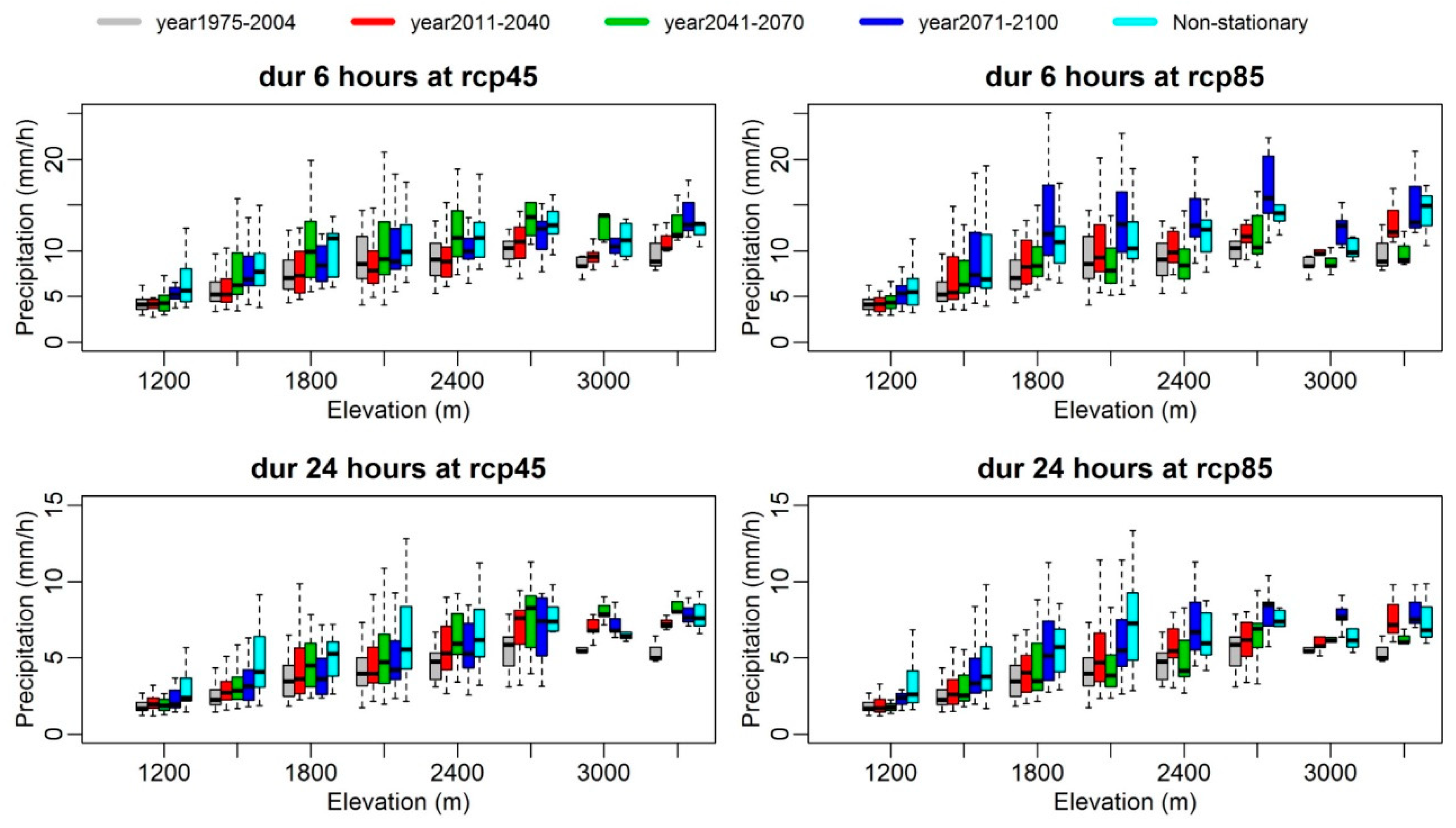
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Watt, E.; Marsalek, J. Critical review of the evolution of the design storm event concept. Can. J. Civ. Eng. 2013, 40, 105–113. [Google Scholar] [CrossRef]
- Endreny, T.A.; Imbeah, N. Generating robust rainfall intensity–duration–frequency estimates with short-record satellite data. J. Hydrol. 2009, 371, 182–191. [Google Scholar] [CrossRef]
- Saghafian, B.; Golian, S.; Ghasemi, A. Flood frequency analysis based on simulated peak discharges. Nat. Hazards 2014, 71, 403–417. [Google Scholar] [CrossRef]
- Eagleson, P.S. Dynamics of Flood Frequency. Water Resour. Res. 1972, 8, 878–898. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Chang, E.K.; Guo, Y.; Xia, X. CMIP5 multimodel ensemble projection of storm track change under global warming. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Li, W.; Li, L.; Ting, M.; Liu, Y. Intensification of Northern Hemisphere subtropical highs in a warming climate. Nat. Geosci. 2012, 5, 830. [Google Scholar] [CrossRef]
- Peck, A.; Prodanovic, P.; Simonovic, S.P. Rainfall Intensity Duration Frequency Curves Under Climate Change: City of London, Ontario, Canada. Can. Water Resour. J. 2012, 37, 177–189. [Google Scholar] [CrossRef]
- Westra, S.; Fowler, H.; Evans, J.; Alexander, L.; Berg, P.; Johnson, F.; Kendon, E.; Lenderink, G.; Roberts, N. Future changes to the intensity and frequency of short-duration extreme rainfall. Rev. Geophys. 2014, 52, 522–555. [Google Scholar] [CrossRef]
- Sarhadi, A.; Soulis, E.D. Time-varying extreme rainfall intensity-duration-frequency curves in a changing climate. Geophys. Res. Lett. 2017, 44, 2454–2463. [Google Scholar] [CrossRef]
- Mailhot, A.; Duchesne, S.; Caya, D.; Talbot, G. Assessment of future change in intensity–duration–frequency (IDF) curves for Southern Quebec using the Canadian Regional Climate Model (CRCM). J. Hydrol. 2007, 347, 197–210. [Google Scholar] [CrossRef]
- Sugahara, S.; Da Rocha, R.P.; Silveira, R. Non-stationary frequency analysis of extreme daily rainfall in Sao Paulo, Brazil. Int. J. Clim. 2009, 29, 1339–1349. [Google Scholar] [CrossRef]
- Lima, C.H.R.; Kwon, H.H.; Kim, J.Y. A Bayesian beta distribution model for estimating rainfall IDF curves in a changing climate. J. Hydrol. 2016, 540, 744–756. [Google Scholar] [CrossRef]
- Mondal, A.; Mujumdar, P.P. Modeling non-stationarity in intensity, duration and frequency of extreme rainfall over India. J. Hydrol. 2015, 521, 217–231. [Google Scholar] [CrossRef]
- De Paola, F.; Giugni, M.; Topa, M.E.; Bucchignani, E. Intensity-Duration-Frequency (IDF) rainfall curves, for data series and climate projection in African cities. SpringerPlus 2014, 3, 133. [Google Scholar] [CrossRef] [PubMed]
- Gilroy, K.L.; McCuen, R.H. A nonstationary flood frequency analysis method to adjust for future climate change and urbanization. J. Hydrol. 2012, 414, 40–48. [Google Scholar] [CrossRef]
- Modesto Gonzalez Pereira, M.J.; Sanches Fernandes, L.F.; Barros Macário, E.M.; Gaspar, S.M.; Pinto, J.G.; Engineering, D. Climate change impacts in the design of drainage systems: Case study of Portugal. J. Irrig. Drain. Eng. 2014, 141, 05014009. [Google Scholar] [CrossRef]
- Sanches Fernandes, L.; Pereira, M.; Morgado, S.; Macário, E. Influence of Climate Change on the Design of Retention Basins in Northeastern Portugal. Water 2018, 10, 743. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. Statistics of extremes and estimation of extreme rainfall: I. Theoretical investigation/Statistiques de valeurs extrêmes et estimation de précipitations extrêmes: I. Recherche théorique. Hydrol. Sci. J. 2004, 49. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Montanari, A. Negligent killing of scientific concepts: The stationarity case. Hydrol. Sci. J. 2015, 60, 1174–1183. [Google Scholar] [CrossRef]
- De Luca, D.; Galasso, L. Stationary and non-stationary frameworks for extreme rainfall time series in southern Italy. Water 2018, 10, 1477. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Stationarity is undead: Uncertainty dominates the distribution of extremes. Adv. Water Resour. 2015, 77, 17–36. [Google Scholar] [CrossRef]
- Chan, S.C.; Kendon, E.J.; Fowler, H.J.; Blenkinsop, S.; Roberts, N.M.; Ferro, C.A. The value of high-resolution met office regional climate models in the simulation of multihourly precipitation extremes. J. Clim. 2014, 27, 6155–6174. [Google Scholar] [CrossRef]
- Pavelko, M.T.; Orozco, E.L. Hydrologic Data for the Walker River Basin, Nevada and California, Water Years 2010–14; US Geological Survey: Reston, VA, USA, 2015; ISSN 2327-638X.
- Gao, Y.; Leung, L.R.; Lu, J.; Liu, Y.; Huang, M.; Qian, Y.J.G.R.L. Robust spring drying in the southwestern US and seasonal migration of wet/dry patterns in a warmer climate. Geophys. Res. Lett. 2014, 41, 1745–1751. [Google Scholar] [CrossRef]
- Kraucunas, I.; Clarke, L.; Dirks, J.; Hathaway, J.; Hejazi, M.; Hibbard, K.; Huang, M.; Jin, C.; Kintner-Meyer, M.; van Dam, K.K.J.C.C. Investigating the nexus of climate, energy, water, and land at decision-relevant scales: The Platform for Regional Integrated Modeling and Analysis (PRIMA). Clim. Chang. 2015, 129, 573–588. [Google Scholar] [CrossRef]
- Skamarock, W.; Klemp, J.; Dudhia, J.; Gill, D.; Barker, D.; Dudha, M.; Huang, X.; Wang, W.; Powers, Y. A Description of the Advanced Research WRF Version 3; NCAR Technical Note; Mesoscale and Microscale Meteorology Division; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Lawrence, D.; Oleson, K.W.; Flanner, M.G.; Thorton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.-L.; Levis, S.; Skaguchi, K.; et al. Parameterization Improvements and Functional and Structural Advances in Version 4 of the Community Land Model. J. Adv. Model. Earth Syst. 2011, 3, 27. [Google Scholar] [CrossRef]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The Community Climate System Model Version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Pingale, S.M.; Khare, D.; Jat, M.K.; Adamowski, J. Spatial and temporal trends of mean and extreme rainfall and temperature for the 33 urban centers of the arid and semi-arid state of Rajasthan, India. Atmos. Res. 2014, 138, 73–90. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, S.; Fu, S.L.; Liu, J.S.; Wang, G.Q.; Zhou, G.Y. Trends of precipitation in Beijiang River basin, Guangdong Province, China. Hydrol. Process. 2008, 22, 2377–2386. [Google Scholar] [CrossRef]
- Zhang, X.B.; Zwiers, F.W.; Li, G.L. Monte Carlo experiments on the detection of trends in extreme values. J. Clim. 2004, 17, 1945–1952. [Google Scholar] [CrossRef]
- Patra, J.P.; Mishra, A.; Singh, R.; Raghuwanshi, N. Detecting rainfall trends in twentieth century (1871–2006) over Orissa State, India. Clim. Chang. 2012, 111, 801–817. [Google Scholar] [CrossRef]
- Seleshi, Y.; Zanke, U. Recent changes in rainfall and rainy days in Ethiopia. Int. J. Clim. 2004, 24, 973–983. [Google Scholar] [CrossRef]
- Yilmaz, A.; Perera, B. Extreme rainfall nonstationarity investigation and intensity–frequency–duration relationship. J. Hydrol. Eng. 2013, 19, 1160–1172. [Google Scholar] [CrossRef]
- Agilan, V.; Umamahesh, N. Modelling nonlinear trend for developing non-stationary rainfall intensity–duration–frequency curve. Int. J. Clim. 2017, 37, 1265–1281. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Da Silva, R.M.; Santos, C.A.; Moreira, M.; Corte-Real, J.; Silva, V.C.; Medeiros, I.C. Rainfall and river flow trends using Mann–Kendall and Sen’s slope estimator statistical tests in the Cobres River basin. Nat. Hazards 2015, 77, 1205–1221. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend analysis in Turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Chang. 2016, 6, 508. [Google Scholar] [CrossRef]
- Appel, U.; Brandt, A.V. Adaptive sequential segmentation of piecewise stationary time series. Inf. Sci. 1983, 29, 27–56. [Google Scholar] [CrossRef]
- Michelangeli, P.-A.; Vautard, R.; Legras, B. Weather regimes: Recurrence and quasi stationarity. J. Atmos. Sci. 1995, 52, 1237–1256. [Google Scholar] [CrossRef]
- Patel, A.P.; Timbadiya, P.; Patel, P. Development of IDF curves under non-stationary meteorological condition. In Proceedings of the 36th IAHR World Congress, The Hague, The Netherlands, 28 June–3 July 2015. [Google Scholar]
- AghaKouchak, A.; Easterling, D.; Hsu, K.; Schubert, S.; Sorooshian, S. Extremes in a Changing Climate: Detection, Analysis and Uncertainty; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 65. [Google Scholar]
- Cheng, L.; AghaKouchak, A. Nonstationary precipitation intensity-duration-frequency curves for infrastructure design in a changing climate. Sci. Rep. 2014, 4, 7093. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.Y.; AghaKouchak, A.; Gilleland, E.; Katz, R.W. Non-stationary extreme value analysis in a changing climate. Clim. Chang. 2014, 127, 353–369. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Naveau, P.J. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Coles, S.; Bawa, J.; Trenner, L.; Dorazio, P. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001; Volume 208. [Google Scholar]
- Melchers, R.E.; Beck, A.T. Structural Reliability Analysis and Prediction; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Renard, B.; Sun, X.; Lang, M. Bayesian methods for non-stationary extreme value analysis. In Extremes in a Changing Climate; Springer: Dordrecht, The Netherlands, 2013; pp. 39–95. [Google Scholar]
- Gilleland, E.; Katz, R.W. New software to analyze how extremes change over time. Eostrans. Am. Geophys. Union 2011, 92, 13–14. [Google Scholar] [CrossRef]
- Shaw, E.M.; Beven, K.J.; Chappell, N.A.; Lamb, R. Hydrology in Practice; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Bhagat, N. Flood Frequency Analysis Using Gumbel’s Distribution Method: A Case Study of Lower Mahi Basin, India. J. Water Resour. Ocean Sci. 2017, 6, 51. [Google Scholar] [CrossRef]
- Zelenhasic, E.F. Theoretical Probability Distributions for Flood Peaks; Hydrology Papers (Colorado State University); No. 42; Colorado State University: Fort Collins, CO, USA, 1970. [Google Scholar]
- Sarma, P. Flood risk zone mapping of Dikrong sub basin in Assam. In Proceedings of the Map India 1999 Conference, New Delhi, India, 24–26 August 1999. [Google Scholar]
- Ward, R. Hydrology of Floods in Canada: A Guide to Planning and Design; National Research Council Canada, Associate Committee on Hydrology: Ottawa, ON, Canada, 1989. [Google Scholar]
- Solaiman, T.A.; Simonovic, S.P. Development of Probability Based Intensity-Duration-Frequency Curves under Climate Change; Department of Civil and Environmental Engineering, The University of Western Ontario City: London, ON, Canada, 2011. [Google Scholar]
- Chow, V.T. Statistical and probability analysis of hydrologic data. In Handbook of Applied Hydrology; McGraw-Hill Book Company: New York, NY, USA, 1964; pp. 8.1–8.91. [Google Scholar]
- Cheng, L. Frameworks for Univariate and Multivariate Non-Stationary Analysis of Climatic Extremes; UC Irvine: Irvine, CA, USA, 2014. [Google Scholar]
- Katz, R.W. Statistics of extremes in climate change. Clim. Chang. 2010, 100, 71–76. [Google Scholar] [CrossRef]
- Ragno, E.; AghaKouchak, A.; Love, C.A.; Cheng, L.; Vahedifard, F.; Lima, C.H.J. Quantifying changes in future intensity-duration-frequency curves using multimodel ensemble simulations. Water Resour. Res. 2018, 54, 1751–1764. [Google Scholar] [CrossRef]
- Rosbjerg, D.; Madsen, H. Design with uncertain design values. In Proceedings of the International Conference on Hydrology in a Changing Environment, Exeter, England, 6–10 July 1998; pp. 155–163. [Google Scholar]
- Ter Braak, C.J.; Vrugt, J.A. Differential evolution Markov chain with snooker updater and fewer chains. Stat. Comput. 2008, 18, 435–446. [Google Scholar] [CrossRef]
- Ter Braak, C.J. A Markov Chain Monte Carlo version of the genetic algorithm Differential Evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- Vrugt, J.A.; ter Braak, C.J.F.; Diks, C.G.H.; Robinson, B.A.; Hyman, J.M.; Higdon, D. Accelerating Markov Chain Monte Carlo Simulation by Differential Evolution with Self-Adaptive Randomized Subspace Sampling. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 273–290. [Google Scholar] [CrossRef]
- Olea, R.A. Geostatistics for Engineers and Earth Scientists; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Ribeiro, P.J., Jr.; Diggle, P.J. geoR: A package for geostatistical analysis. R News 2001, 1, 14–18. [Google Scholar]
- Sugarbaker, L.J.; Constance, E.W.; Heidemann, H.K.; Jason, A.L.; Lukas, V.; Saghy, D.L.; Stoker, J.M. The 3D Elevation Program Initiative: A Call for Action; US Geological Survey: Reston, VA, USA, 2014; pp. 2330–5703.
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, H.; Hou, Z.J.; Wigmosta, M.; Liu, Y.; Leung, L.R. Impacts of Spatial Heterogeneity and Temporal Non-Stationarity on Intensity-Duration-Frequency Estimates—A Case Study in a Mountainous California-Nevada Watershed. Water 2019, 11, 1296. https://doi.org/10.3390/w11061296
Ren H, Hou ZJ, Wigmosta M, Liu Y, Leung LR. Impacts of Spatial Heterogeneity and Temporal Non-Stationarity on Intensity-Duration-Frequency Estimates—A Case Study in a Mountainous California-Nevada Watershed. Water. 2019; 11(6):1296. https://doi.org/10.3390/w11061296
Chicago/Turabian StyleRen, Huiying, Z. Jason Hou, Mark Wigmosta, Ying Liu, and L. Ruby Leung. 2019. "Impacts of Spatial Heterogeneity and Temporal Non-Stationarity on Intensity-Duration-Frequency Estimates—A Case Study in a Mountainous California-Nevada Watershed" Water 11, no. 6: 1296. https://doi.org/10.3390/w11061296
APA StyleRen, H., Hou, Z. J., Wigmosta, M., Liu, Y., & Leung, L. R. (2019). Impacts of Spatial Heterogeneity and Temporal Non-Stationarity on Intensity-Duration-Frequency Estimates—A Case Study in a Mountainous California-Nevada Watershed. Water, 11(6), 1296. https://doi.org/10.3390/w11061296





