2.2.2. Explaining Model Parameters
Usually, the best-fit model parameters (m
1, m
2) are unknown. To establish them (without using an inverse problem-solving method), it is necessary to find the relationship between the search parameters and other explanatory variables. Spatial terrain characteristics can be used as possible explanatory variables [
21,
26]. The overall curvature, planar curvature, profile curvature, overall slope, slope in the x-direction, and slope in the y-direction were, in the present case, selected for predicting individual model parameters. The characteristics were determined as described by Zevenbergen and Thorne [
29]. The source of terrain characteristics was the DEM input. Terrain characteristics were calculated for the all raster cells located behind the bank lines around the river. The terrain characteristics of the nearest raster cell were used to estimate the parameters of a given endpoint. As explanatory variables, the left bank terrain characteristics for model parameter m
1 and the right bank terrain characteristics for parameter
m2 were used.
Statistical learning methods were used for finding the dependence between model variables and terrain characteristics. Those statistical learning methods studied were multiple linear regression, extended linear regression, and random forest (RF).
A simple linear model (LM) is used for finding a linear relationship between a response and its predictor, and, in the case of multiple linear regressions, this relationship is based upon more than a single predictor. The LM is described in Equation (1):
where
βx are the linear parameters,
xi are predictor variables,
εi is the error term, and
M is the number of predictor variables. A mixed selection procedure, as described by Gareth et al. [
30], was adopted for choosing the optimal number of variables.
An extended linear model with no random effects (GLS) was also used. This method extends linear regression with an ability to fit models with heteroscedastic and correlated within-group errors, but with no random effects [
31]. The extended formula of the LM is described in Equation (2):
where
Ai are positive-definite matrices composed using variance and covariance matrices,
βx are the linear parameters,
xi are predictor variables,
εi is the error term, and
M is the number of predictor variables. Again, the mixed selection procedure, as described by Gareth et al. [
30], was adopted for choosing the optimal number of variables.
Random forest (RF) is a combined machine learning method for classification and regression. This method is based on an ensemble of a regression tree (RT) algorithm. RT deals with tree structure by dividing the dataset into homogenous groups. That division is driven by some classification criterion, such as minimizing the variance of a given set of variables. In the case of RF, a dataset is divided into multiple sub-datasets by a bootstrap aggregating algorithm. For each sub-dataset, an RF of its own is constructed. This creates a group of random trees, termed RF. For each predictor variable, a measure of variable importance can be determined. Based on variable importance values, it is possible to decide which variables have significant impact for the response and which can be omitted [
32].
All statistical analyses in this work were performed using statistical software R. The extended linear model with no random effects was applied using the package nlme [
33], and the package randomForest [
34] was used for random forests.
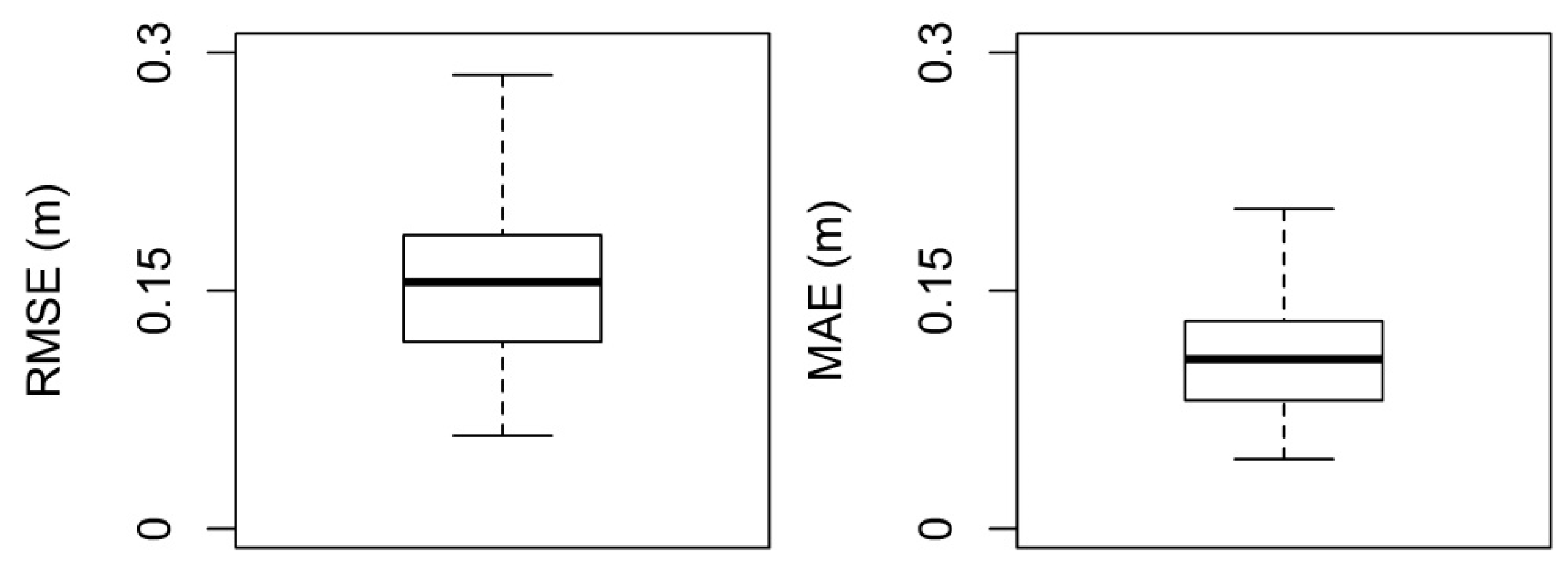
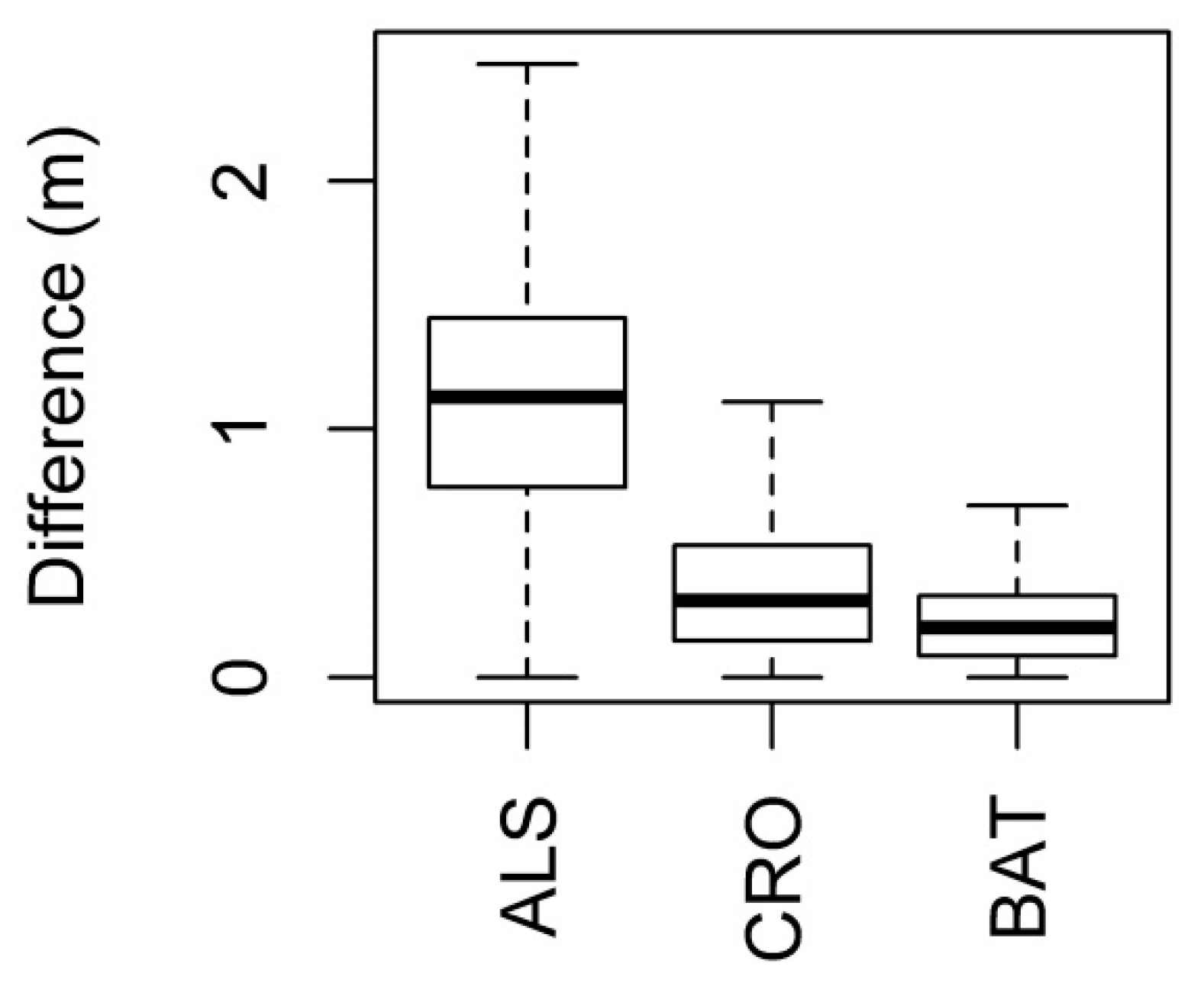
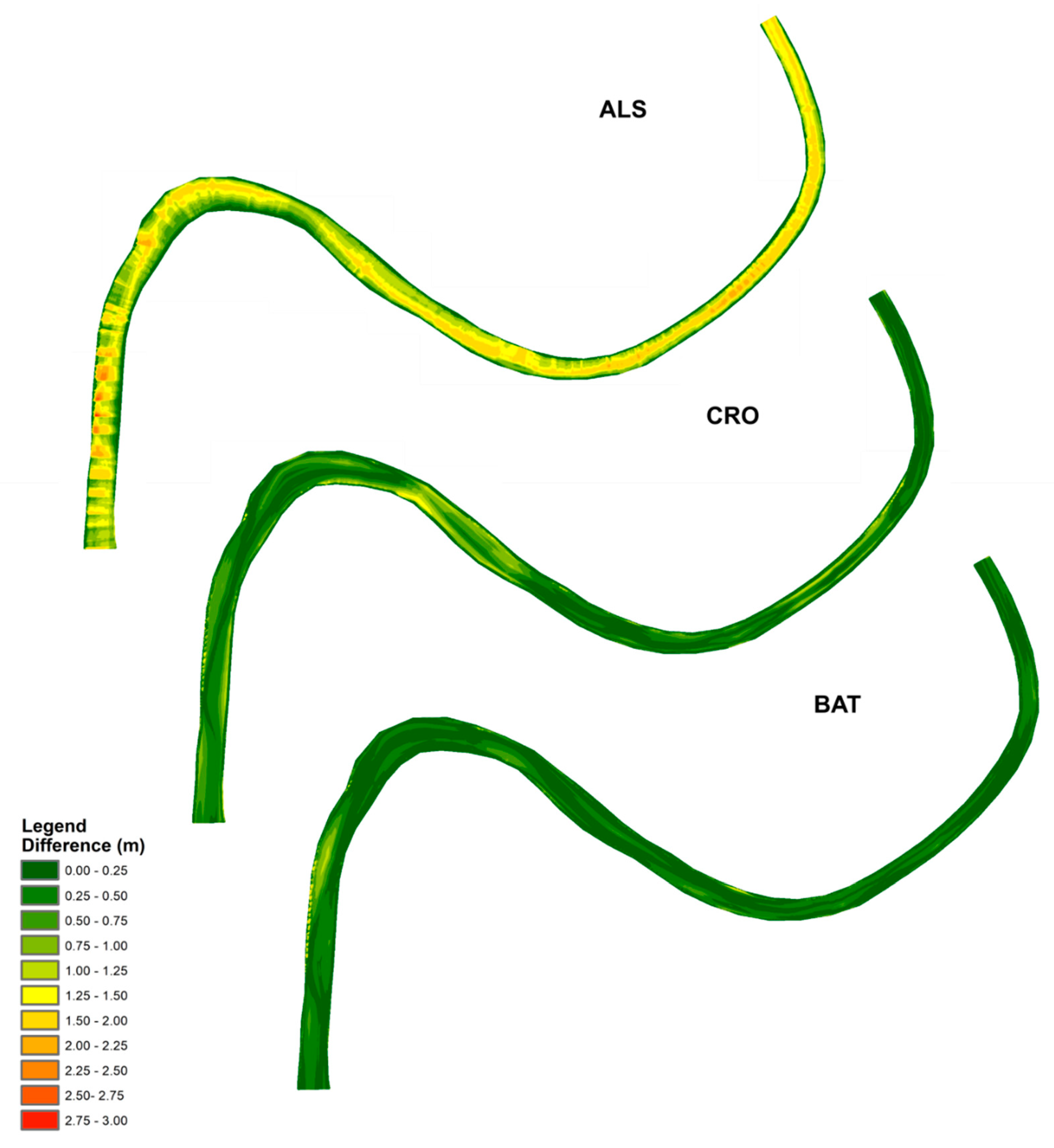
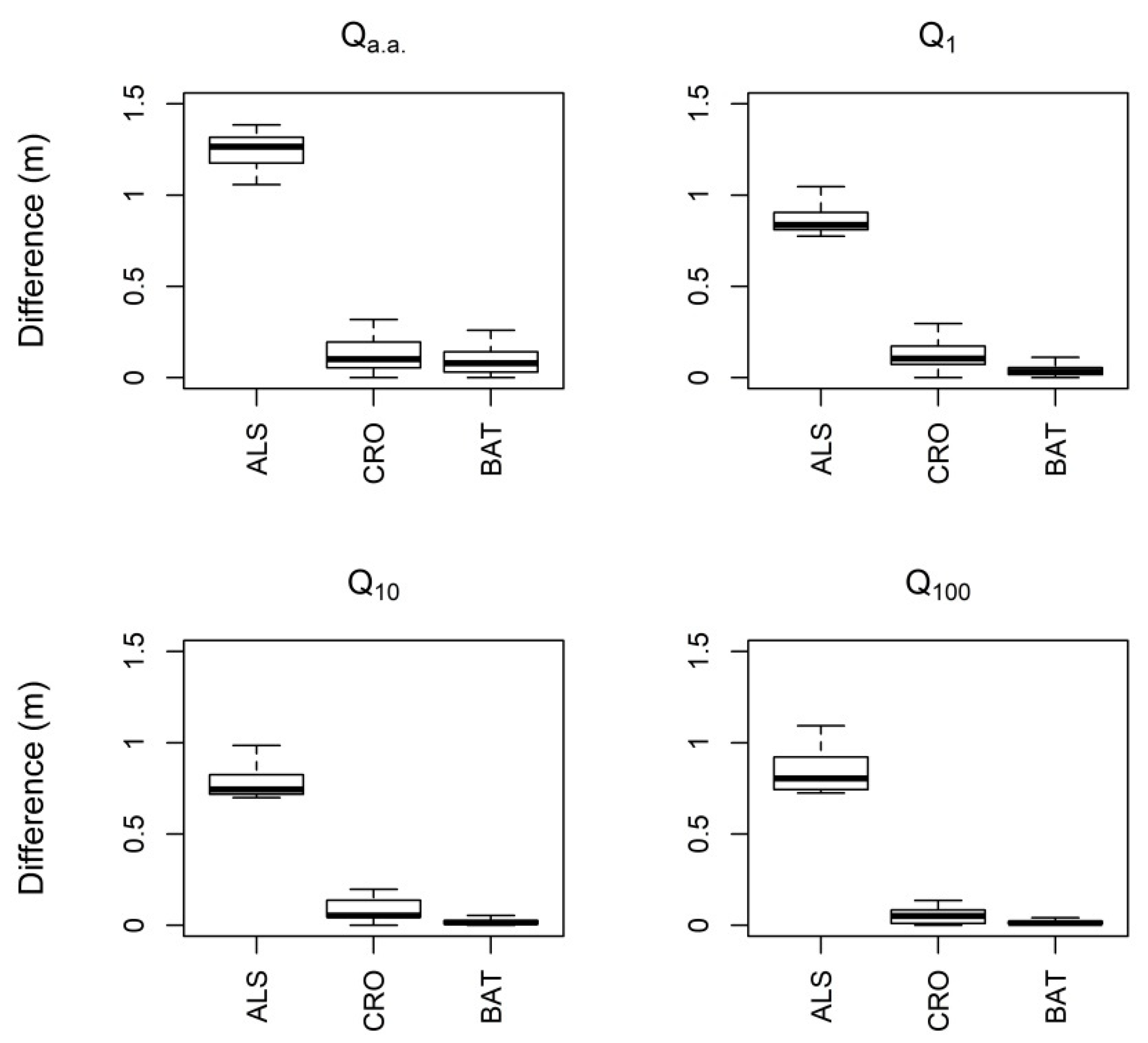
The coefficient of determination (
R2) was used to evaluate the reliability of model parameters. As a second quality assessment, vertical differences between models based on the best model parameters and a model based on estimated parameters were calculated. For this comparison, a similar approach is used in
Section 2.1.
2.2.3. Cross-Section Construction and Transformation
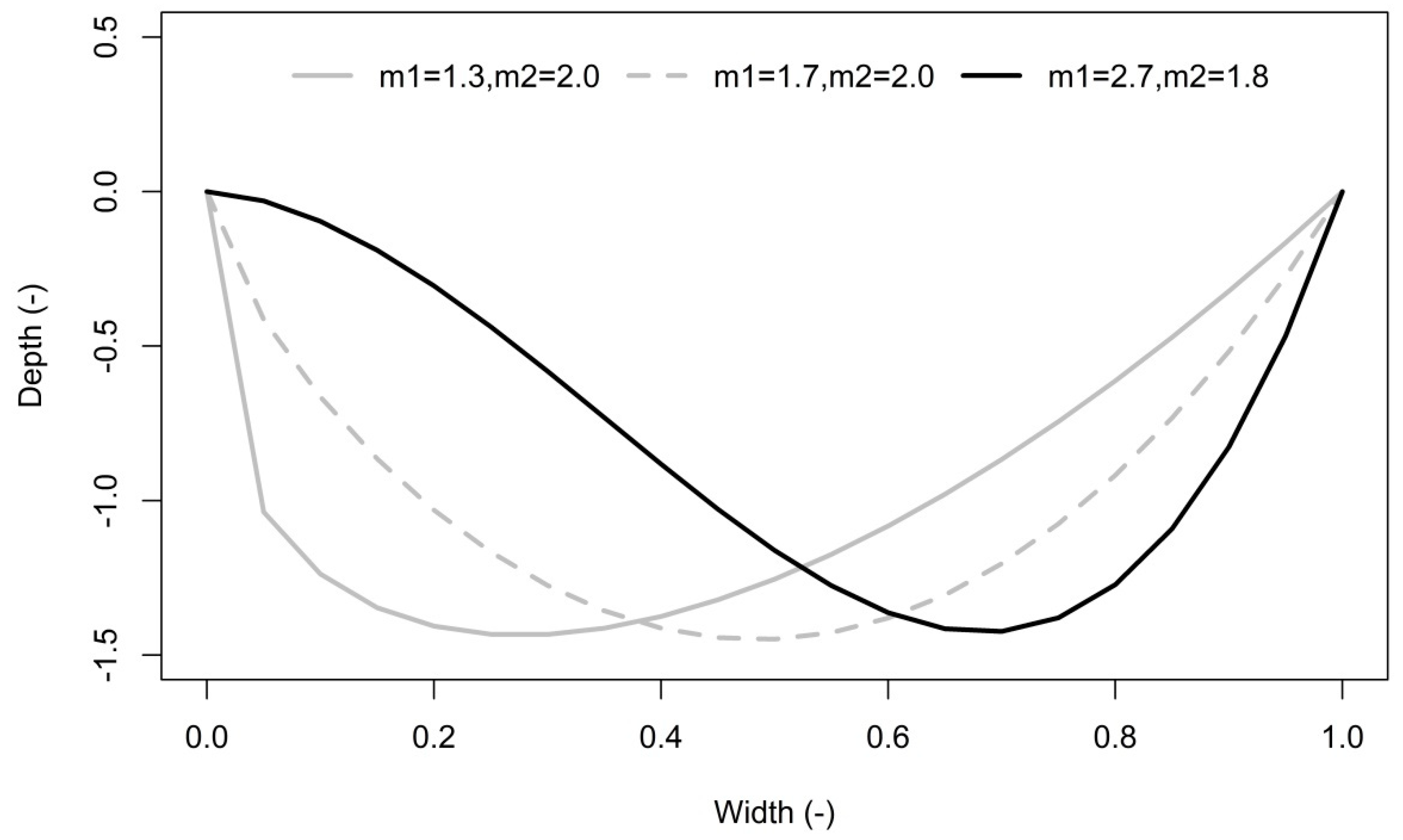
Once the model parameters are estimated, new cross-sections can be constructed. A tested theoretical cross-section model Equation (3) is able to estimate the natural river cross-section on the basis of estimated parameters [
35]. The studied theoretical model of the river cross-section is explained as:
where
z(d) is the depth of water at a distance d from the left endpoint of the cross-section, while m
1 and m
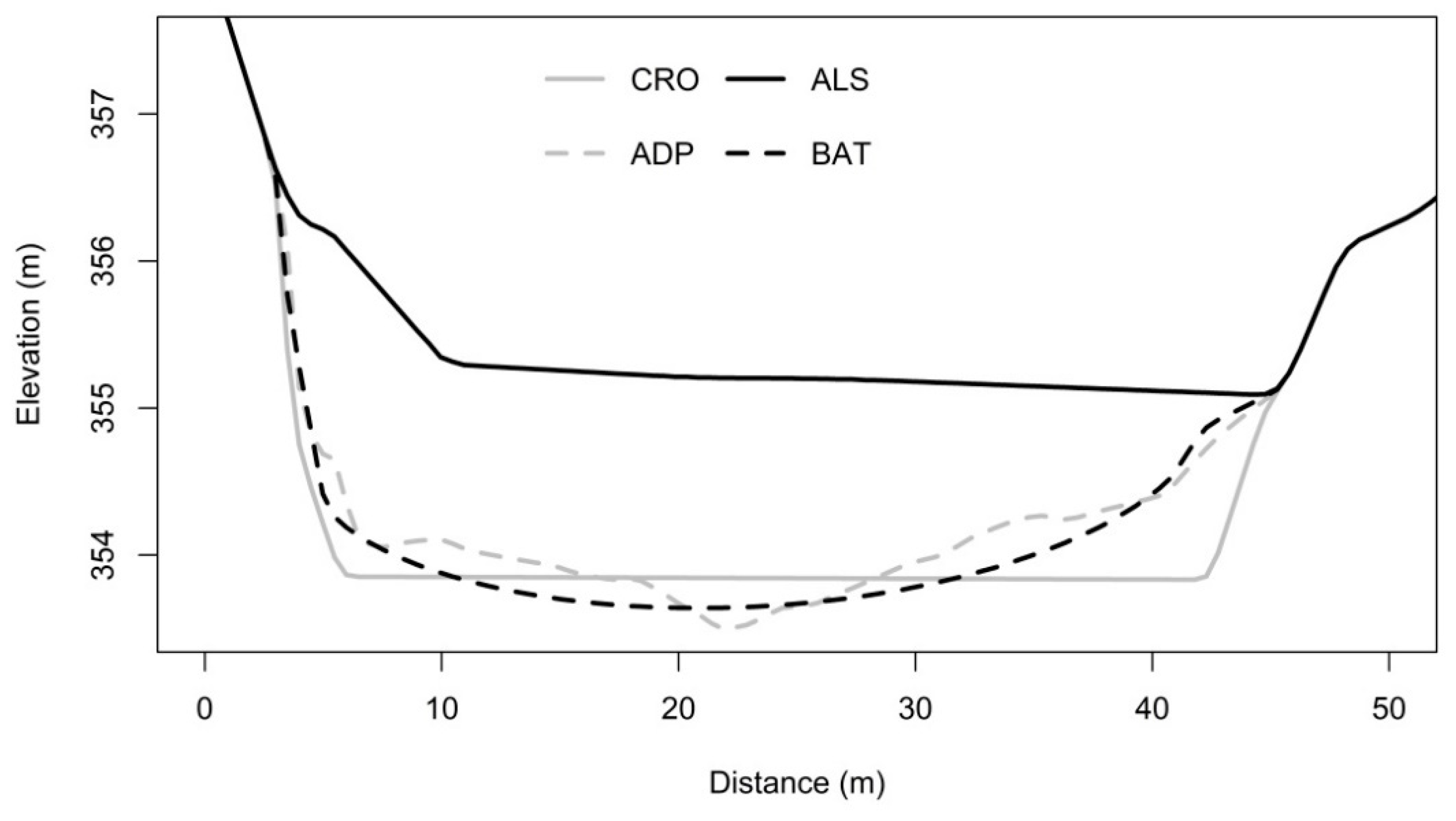
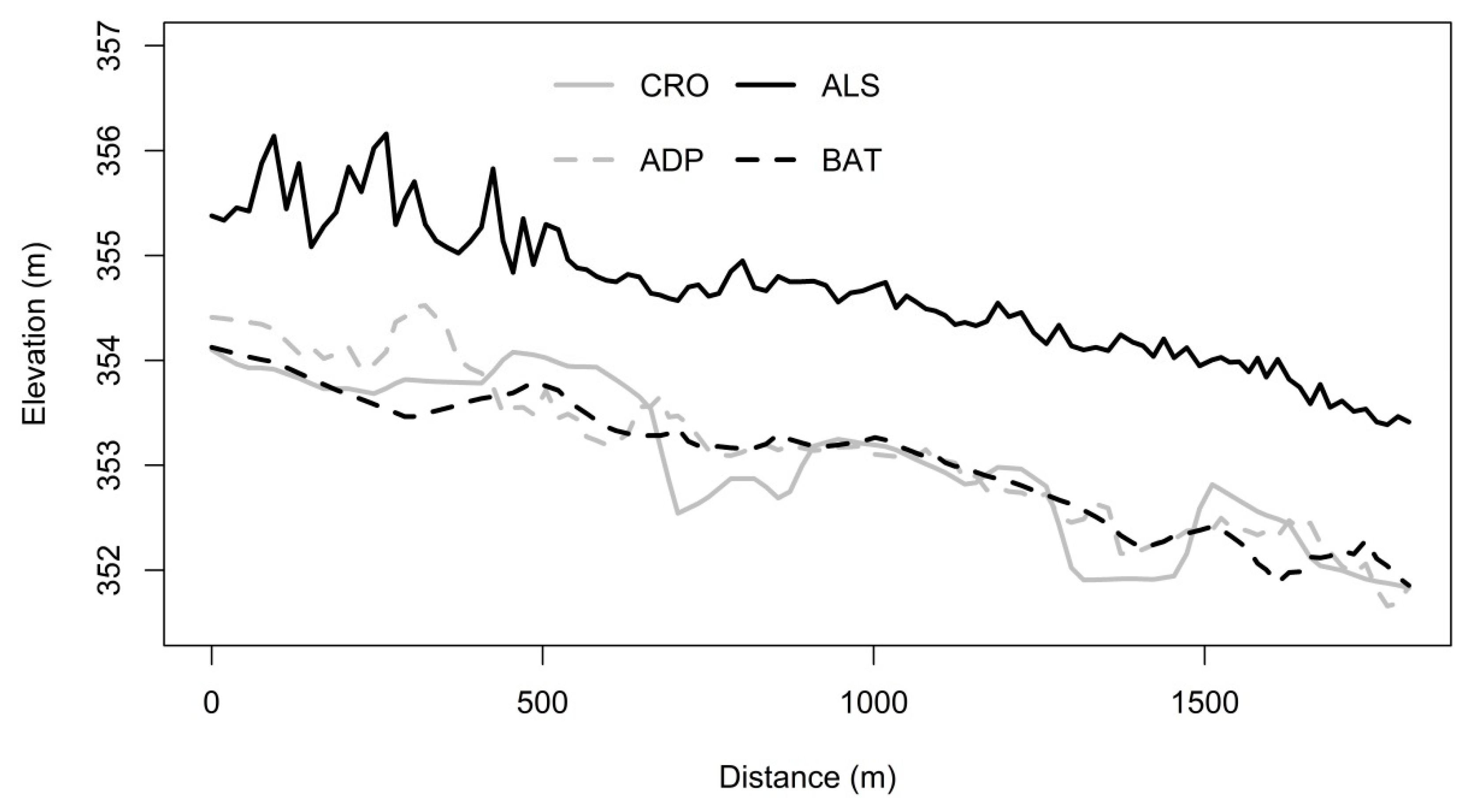
2 are theoretical model parameters that are unique for each river cross-section. An example of the estimated shapes of the cross-section is shown in
Figure 2.
Due to the mathematical nature of the proposed model, a new cross-section width of 0–1 [
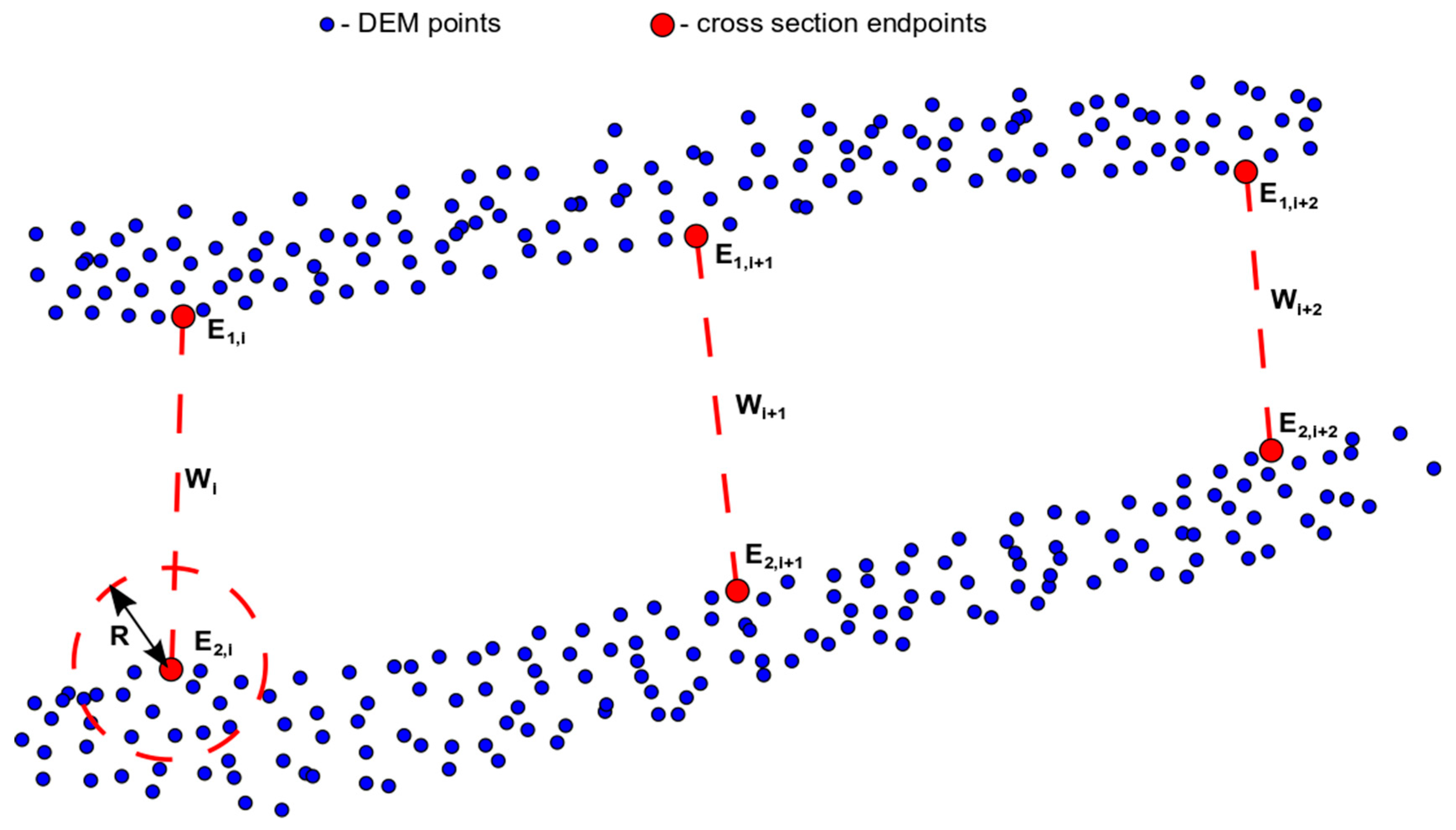
35] must be selected in the first step. Note that the value 0 represents the left side of the cross-section. Additional points are inserted between the points 0 and 1. The user decides upon the number of points to insert. Once new stationing is defined, the depth value for each cross-section point is computed by applying Equation (3). New cross-sections produced by the proposed bathymetric model are in normative state (width and flow area are equal to (1)). Width transformation is simple. Stationing of the new cross-section is multiplied by the distance (W) between its endpoints (
Figure 1). For the flow area transformation, an adequate flow area must be identified. This adequate flow area defines the flow area of the river channel required for the transfer of the design flow. The adequate flow area is determined using Chezy’s equation on the basis of Manning’s roughness coefficient, water surface slope, and design flow rate. This adequate flow area is compared with the area of the new cross-section. If the adequate flow area is smaller than the cross-sectional area, then the depths of the cross-section points are multiplied by the area multiplication parameter. This step is repeated until the adequate flow area is equal to or less than the area of the cross-section. Manning’s coefficient, design flow rate, and area multiplication parameter are the input parameters. The water longitudinal surface slope and water surface elevation of each cross-section are extracted from the DEM. A similar approach had been used in the work of Roub et al. [
28].
The final transformation step is to add the new cross-section into the coordinate system used. The XY coordinates of the first and last point of the cross-section correspond to the coordinates of the endpoints E1 and E2, for which the cross-section has been created. All internal points are placed on the line connecting the endpoints. Therefore, the coordinates of the internal points can be calculated based on the coordinates of the endpoints and its station value. The method of calculating the coordinates of internal points may vary depending on the coordinate system used. The lower of the altitudes of both endpoints is determined as the water level of this cross-section. The altitude (Z value) of each point is obtained by subtracting the water level and its depth. All cross-section points have coordinates X, Y, and Z and stationing after transformation.