A Comparative Analysis of the Historical Accuracy of the Point Precipitation Frequency Estimates of Four Data Sets and Their Projections for the Northeastern United States
Abstract
1. Introduction
2. Data and Methodologies
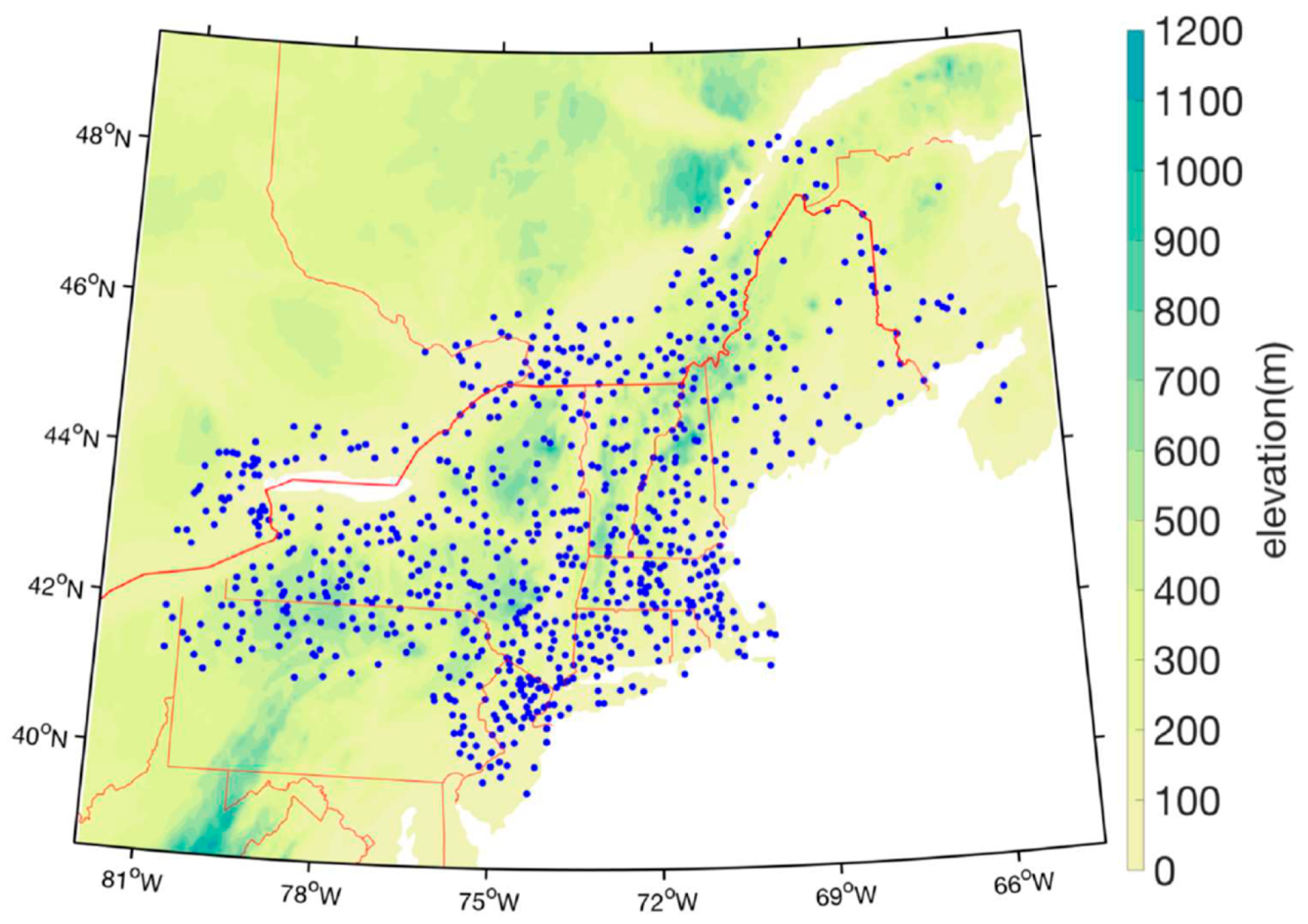
2.1. The Observational and Downscaled Model Data Sets
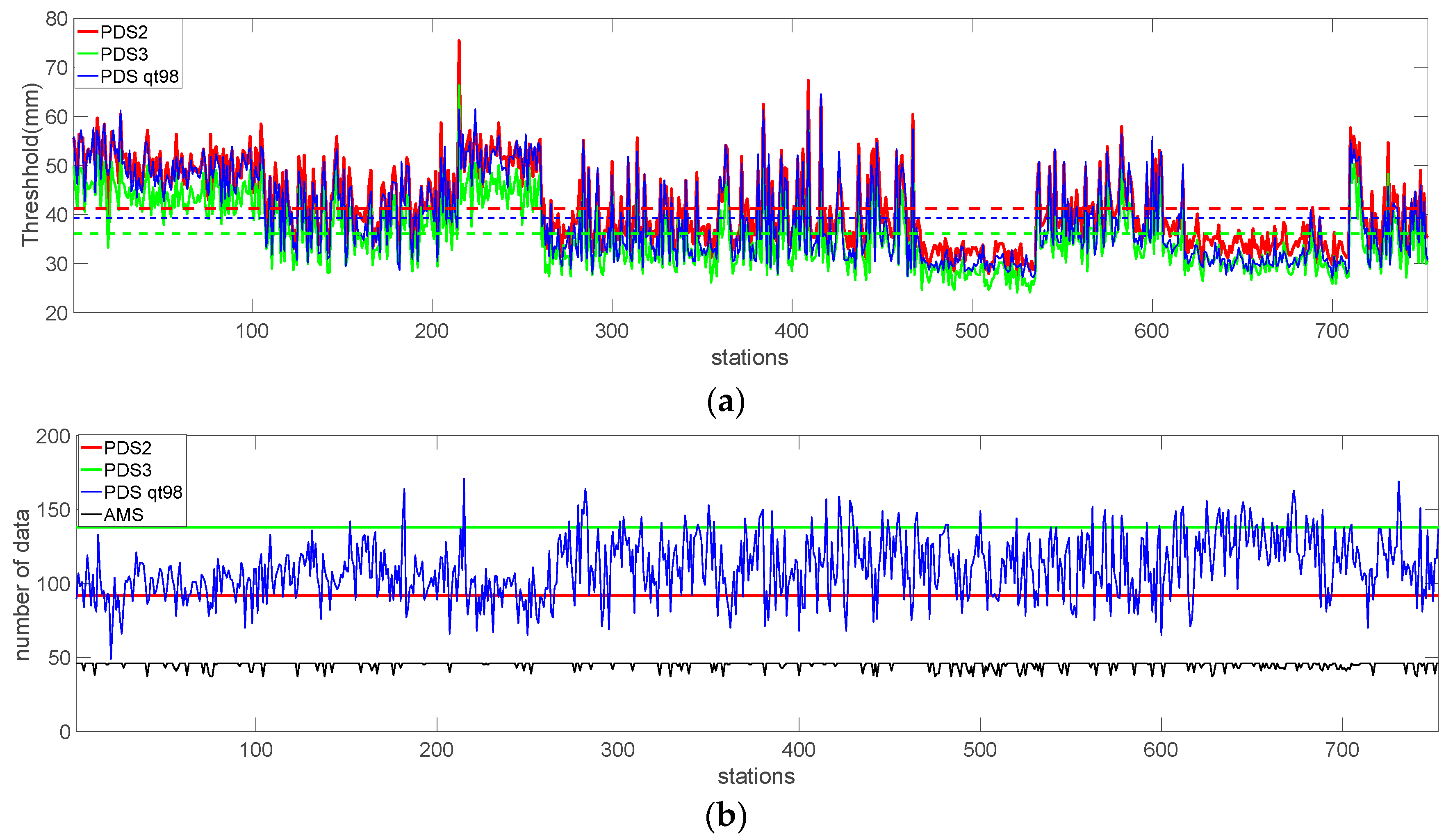
2.2. Methodologies
3. Evaluations of the Downscaled Model Data for the Historical Period of 1960–2005
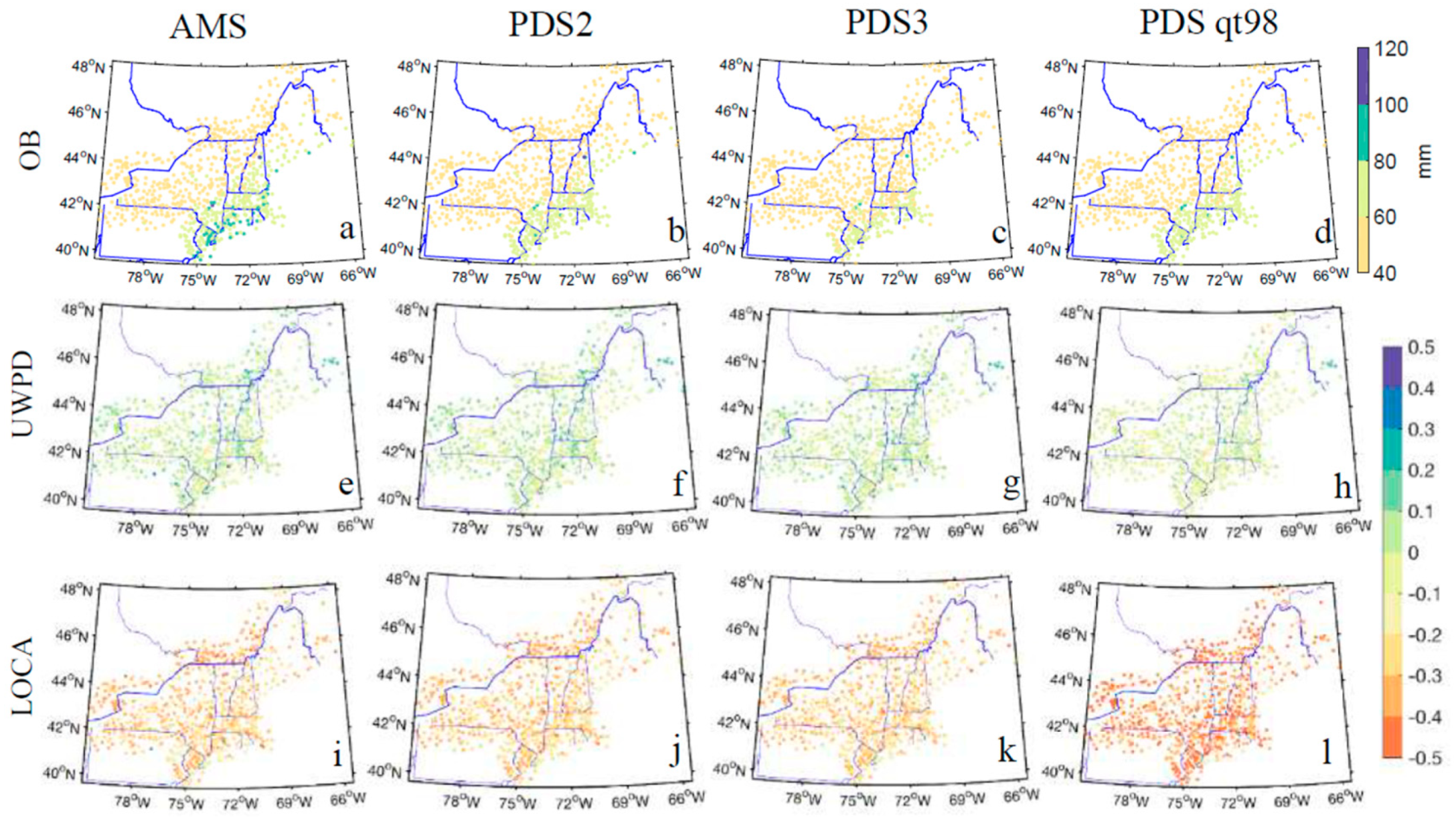
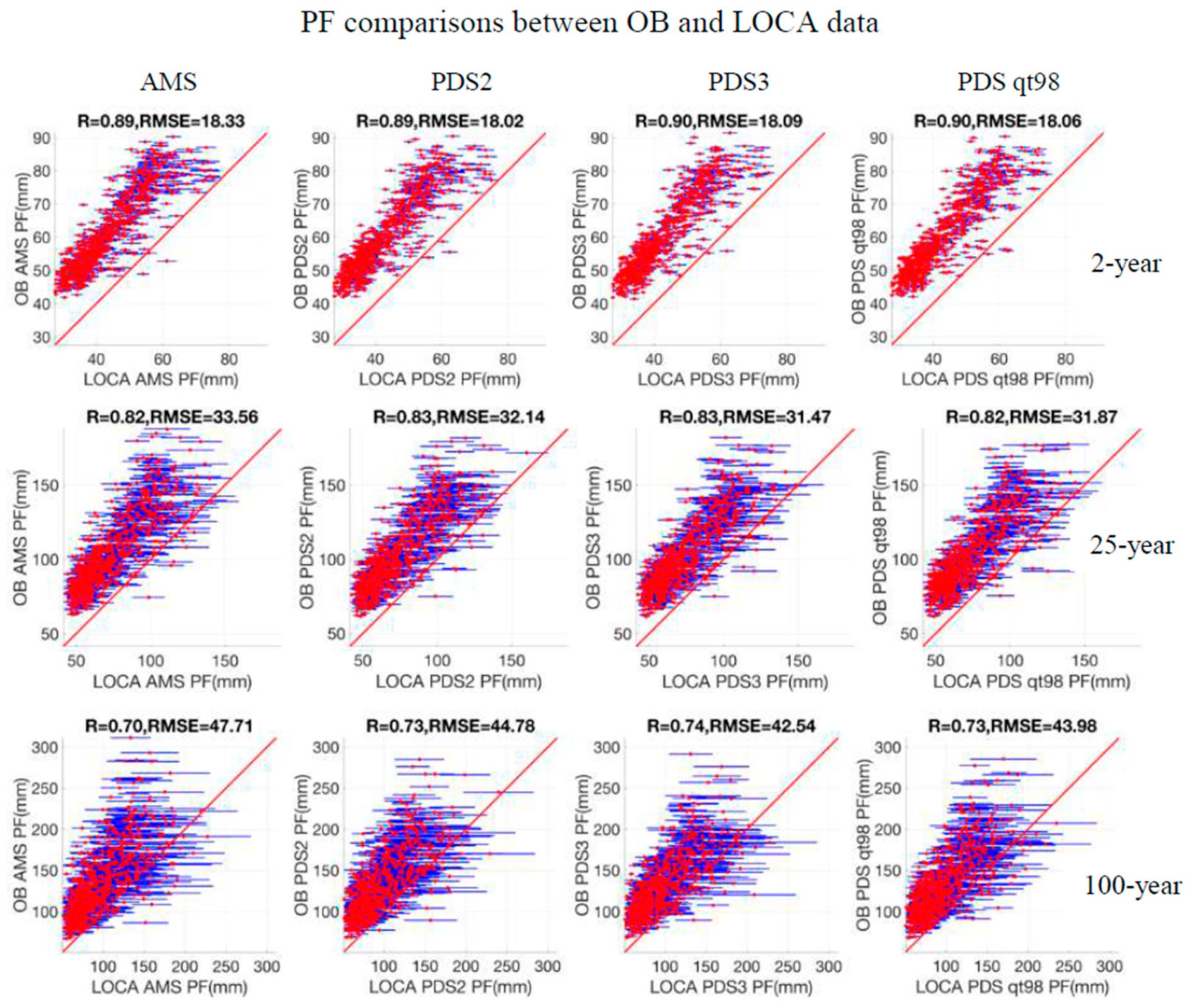
3.1. Comparison of the Climatology of AMS and PDS of the Observed and Modeled Data
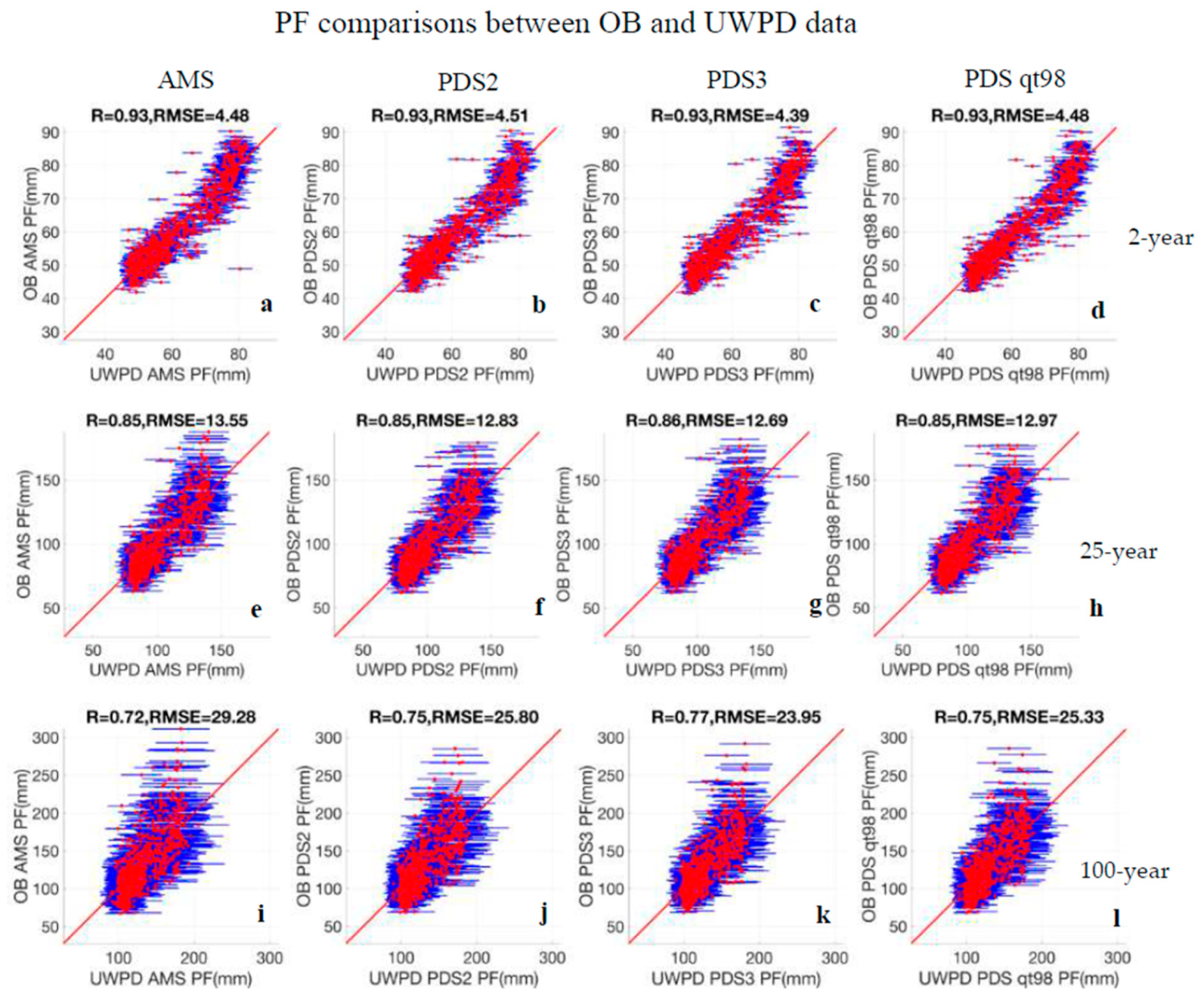
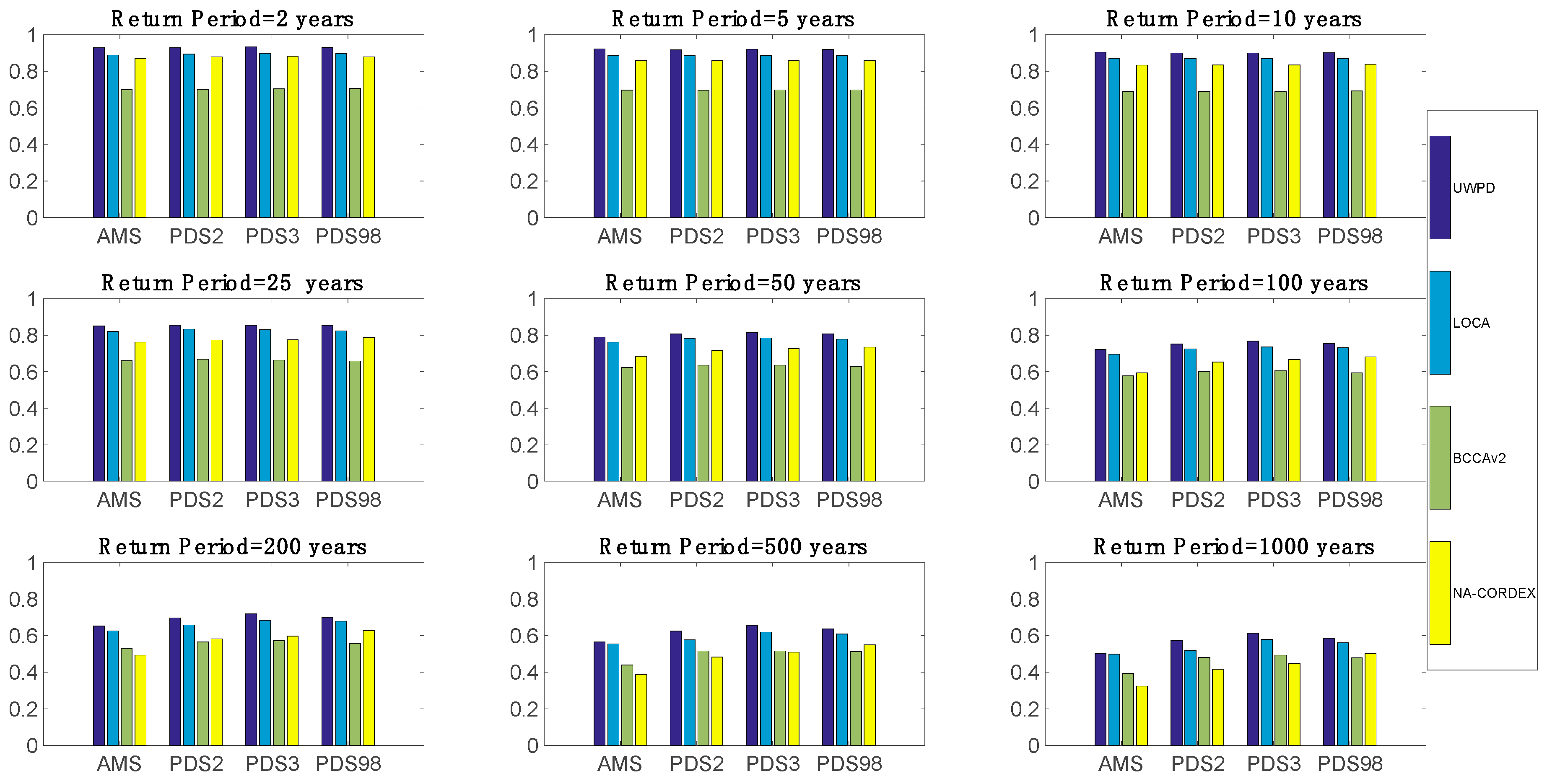
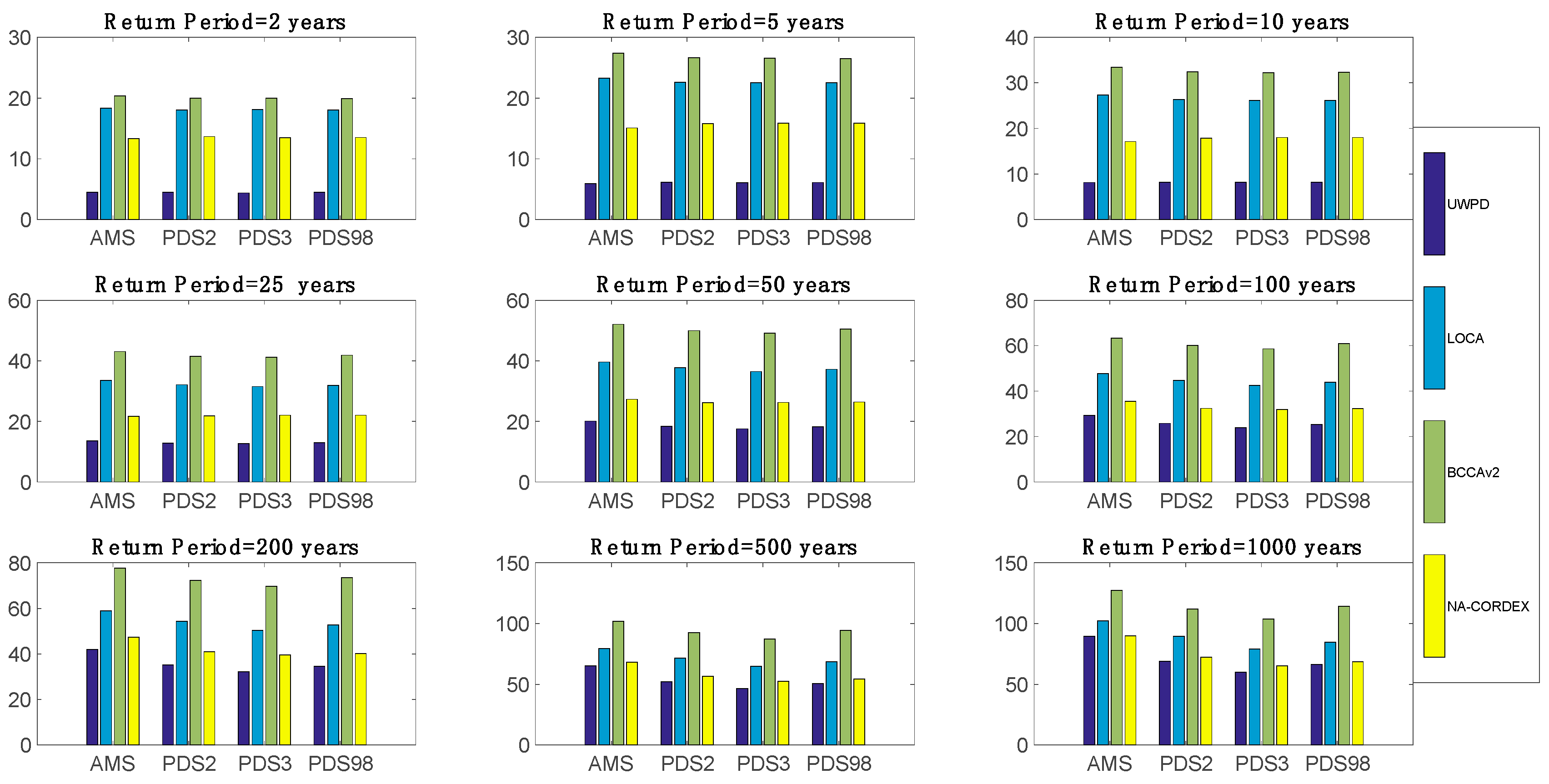
3.2. Comparison of PF Estimates of the Observed and Modeled Data
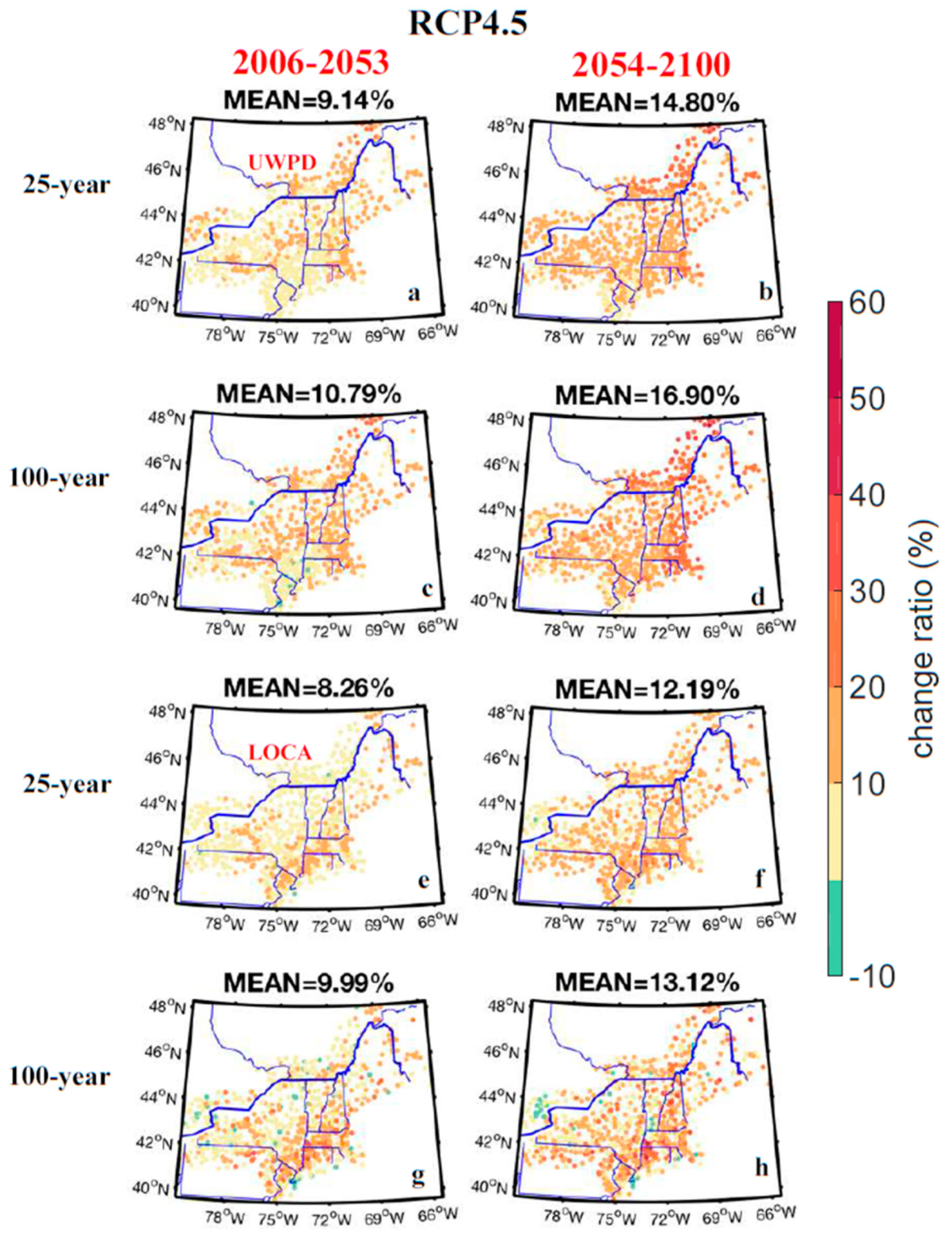
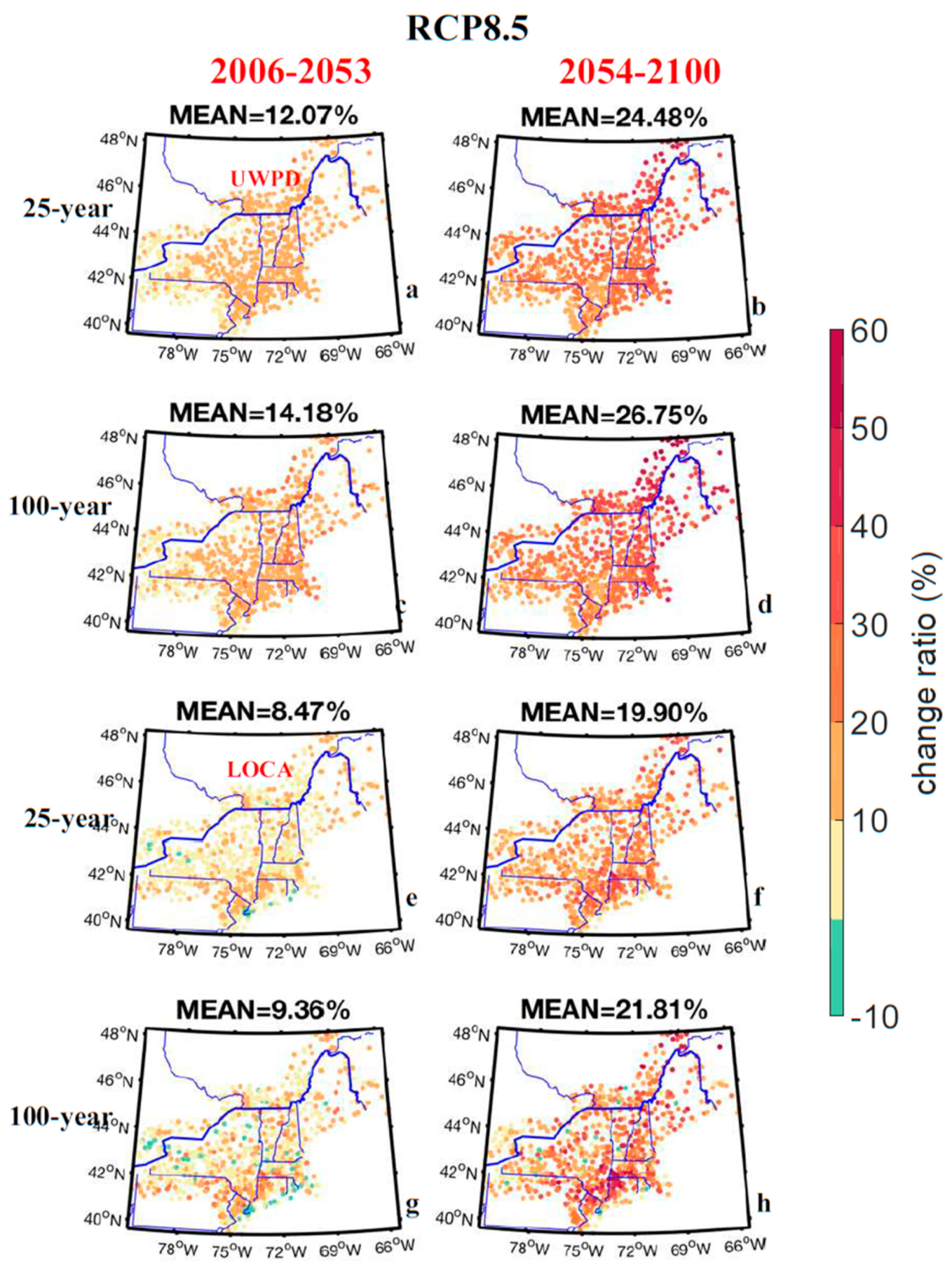
4. Projected PF Estimates
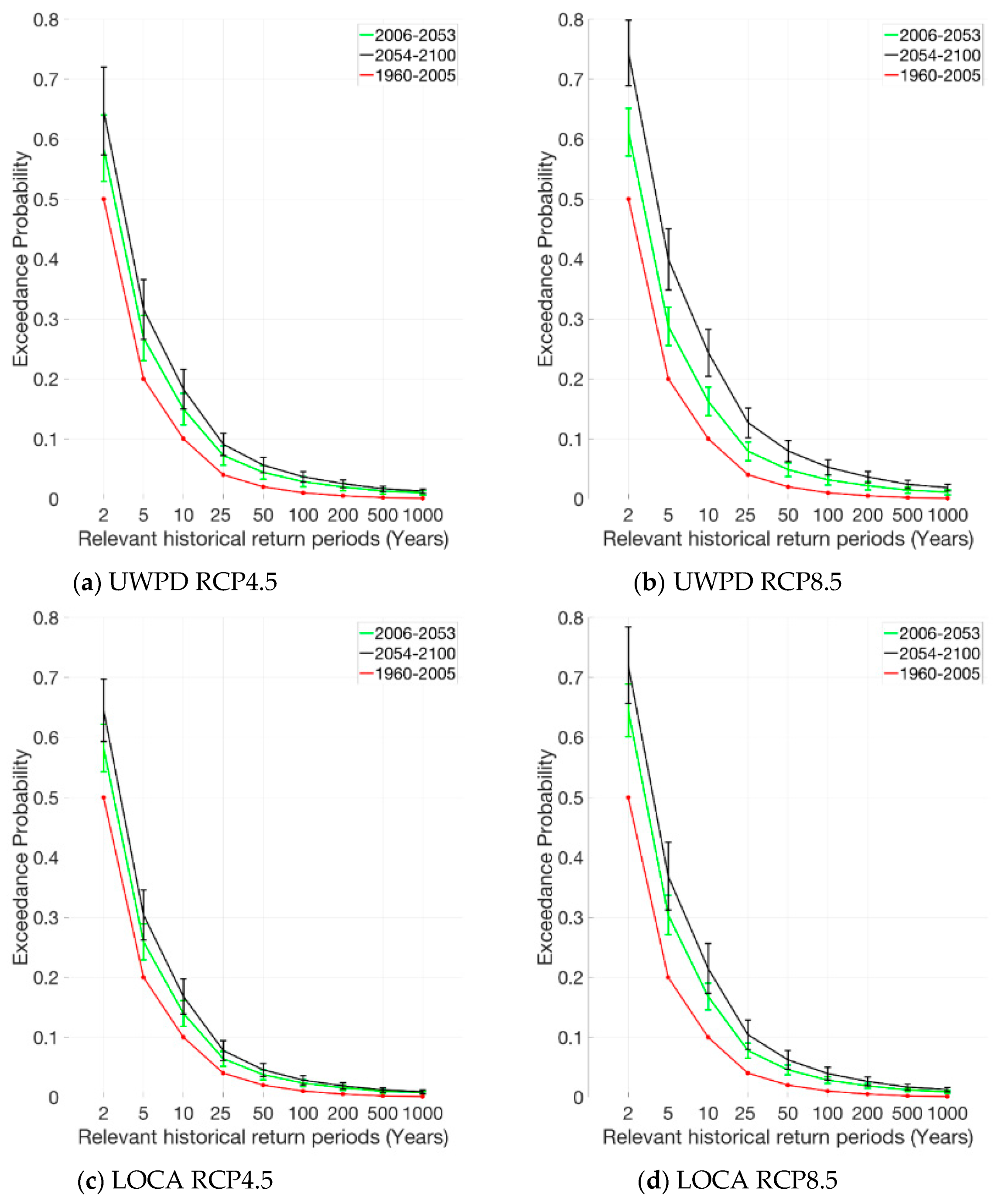
5. Changes to Exceedance Probabilities
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Easterling, D.R.; Kunkel, K.E.; Arnold, J.R.; Knutson, T.; LeGrande, A.N.; Leung, L.R.; Vose, R.S.; Waliser, D.E.; Wehner, M.F. Precipitation change in the United States. In Climate Science Special Report: Fourth National Climate Assessment; Wuebbles, D.J., Fahey, D.W., Hibbard, K.A., Dokken, D.J., Stewart, B.C., Maycock, T.K., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2017; Volume, I, pp. 207–230. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- Kunkel, K.E.; Stevens, L.E.; Stevens, S.E.; Sun, L.Q.; Janssen, E.; Wuebbles, D.; Rennells, J.; Degaetano, A.; Dobson, J.G. Regional climate trends and scenarios for the U.S. National Climate Assessment: Part. 1—Climate of the Northeast; NOAA Technical report NESDIS 142-1; U.S. Department of Commerce: Washington, DC, USA, 2013.
- Melillo, J.M.; Richmond, T.C.; Yohe, G.W. Climate Change Impacts in the United States: The Third National Climate Assessment; U.S. Government Printing Office: Washington, DC, USA, 2014; p. 841.
- Hoerling, M.J.; Eischeid, J.; Perlwitz, X.W.; Quan, K.W.; Cheng, L. Characterizing recent trends in U.S. heavy precipitation. J. Clim. 2016, 29, 2313–2332. [Google Scholar] [CrossRef]
- Huang, H.P.; Winter, J.M.; Osterberg, E.C.; Horton, R.M.; Beckage, B. Total and extreme precipitation changes over the Northeastern United States. J. Hydr. 2017, 18, 1783–1798. [Google Scholar] [CrossRef]
- Maidment, D.R. Handbook of Hydrology; McGraw-Hill, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Markus, M.; Wuebbles, D.J.; Liang, X.-Z.; Hayhoe, K.; Kristovich, D.A.R. Diagnostic analysis of future climate scenarios applied to urban flooding in the Chicago metropolitan area. Clim. Chang. 2012, 111, 879–902. [Google Scholar] [CrossRef]
- Katz, R.W. Statistical methods for nonstationary extremes. In Extremes in a Changing Climate: Detection, Analysis and Uncertainty; Kouchak, A., Easterling, D., Hsu, K., Schubert, S., Sorooshian, S., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 15–37. [Google Scholar]
- Cheng, L.; AghaKouchak, A.; Gilleland, E.; Katz, R.W. Non-stationary Extreme Value Analysis in a Changing Climate. Clim. Chang. 2014. [Google Scholar] [CrossRef]
- Janssen, E.; Wuebbles, D.J.; Kunkel, K.E.; Olsen, S.C.; Goodman, A. Observational- and model-based trends and projections of extreme precipitation over the contiguous United States. Earth’s Future 2014, 2, 99–113. [Google Scholar] [CrossRef]
- Markus, M.; Angel, J.; Byard, G.; McConkey, S.; Zhang, C.; Cai, X.; Notaro, M.; Ashfaq, M. Communicating the Impacts of Projected Climate Change on Heavy Rainfall Using a Weighted Ensemble Approach. J. Hydrol. Eng. 2018, 23, 04018004. [Google Scholar] [CrossRef]
- Randall, D.A.; Wood, R.A.; Bony, S.; Colman, R.; Fichefet, T.; Fyfe, J.; Kattsov, V.; Pitman, A.; Shukla, J.; Srinivasan, J.; et al. Cilmate Models and Their Evaluation. In Climate Change 2007: The Physical Science Basis; Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Kunreuther, H.; Gupta, S.; Bosetti, V.; Cooke, R.; Dutt, V.; Ha-Duong, M.; Held, H.; Llanes-Regueiro, J.; Patt, A.; Shittu, E.; et al. Integrated Risk and Uncertainty Assessment of Climate Change Response Policies. In Climate Change 2014: Mitigation of Climate Change; Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Notaro, M.; Lorenz, D.J.; Hoving, C.; Schummer, M. Twenty-first-century projections of snowfall and winter severity across central-eastern North America. J. Clim. 2014, 27, 6526–6550. [Google Scholar] [CrossRef]
- Vavrus, S.J.; Notaro, M.; Lorenz, D.J. Interpreting climate model projections of extreme weather events. Weather Clim. Extrem. 2015, 10, 10–28. [Google Scholar] [CrossRef]
- Ashfaq, M.; Ghosh, S.; Kao, S.C.; Bowling, L.C.; Mote, P.; Touma, D.; Rauscher, S.A.; Diffenbaugh, N.S. Near-term acceleration of hydroclimatic change in the western U.S. J. Geophys. Res. 2013, 118, 10676–10693. [Google Scholar] [CrossRef]
- Ashfaq, M.; Bowling, L.C.; Cherkauer, K.; Pal, J.S.; Diffenbaugh, S.N. Influence of climate model biases and daily-scale temperature and precipitation events on hydrological impacts assessment: A case study of the United States. J. Geophys. Res. Atmos. 2010, 115, D14116. [Google Scholar] [CrossRef]
- Whetton, P.; Macadam, I.; Bathols, J.; O’Grady, J. Assessment of the use of current climate patterns to evaluate regional enhanced greenhouse response patterns of climate models. Geophys. Res. Lett. 2007, 34, L14701. [Google Scholar] [CrossRef]
- Knutti, R. The end of model democracy? Clim. Chang. 2010, 102, 395–404. [Google Scholar] [CrossRef]
- Perica, S.; Pavlovic, S.; Laurent, M.S.; Trypaluk, C.; Unruh, D.; Martin, D.; Wilhite, O. Precipitation-Frequency Atlas of the United States. Version 3.0: Northeastern Statates; National Weather Service: Silver Spring, MD, USA, 2019.
- Stacy, E.W. A generalization of the gamma distribution. Ann. Math. Stat. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Kirchmeier, M.C.; Lorenz, D.J.; Vimont, D.J. Statistical downscaling of daily wind speed variations. J. Appl. Meteor. Climatol. 2014, 53, 660–675. [Google Scholar] [CrossRef]
- Daly, C.; Gibson, W.P.; Taylor, G.H.; Doggett, M.K.; Smith, J.I. Observer bias in daily precipitation measurements at United States cooperative network stations. Bull. Amer. Meteor. Soc. 2007, 88, 899–912. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteor. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Kirchmeier-Young, M.C.; Lorenz, D.J.; Vimont, D.J. Extreme Event Verification for Probabilistic Downscaling. J. Appl. Meteor. Climatol. 2016, 55, 2411–2430. [Google Scholar] [CrossRef]
- Downscaled Climate Projections introduction. Available online: https://djlorenz.github.io/downscaling2/main.html (accessed on 17 June 2019).
- Pierce, D.W.; Cayan, D.R.; Thrasher, B.L. Statistical downscaling using Localized Constructed Analogs (LOCA). J. Hydrometeorol. 2014, 15, 2558–2585. [Google Scholar] [CrossRef]
- U.S. Global Change Research Program (USGCRP). Impacts, Risks, and Adaptation in the United States: Fourth National Climate Assessment; U.S. Global Change Research Program: Washington, DC, USA, 2018; Volume II, p. 1515. [CrossRef]
- LOCA Statistical Downscaling (Localized Constructed Analogs). Available online: http://loca.ucsd.edu/ (accessed on 17 June 2019).
- Maraun, D.; Wettterball, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Theme, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48, RG3003. [Google Scholar] [CrossRef]
- Downscaled CMIP3 and CMIP5 Climate and Hydrology Projections. Available online: https://gdo-dcp.ucllnl.org/downscaled_cmip_projections/dcpInterface.html (accessed on 17 June 2019).
- Mearns, L.; McGinnis, S.; Korytina, D.; Scinocca, J.; Kharin, S.; Jiao, Y.; Qian, M.; Lazare, M.; Biner, S.; Winger, K.; et al. The NA-CORDEX dataset, version 1.0. In NCAR Climate Data Gateway; The National Center for Atmospheric Research: Boulder, CO, USA, 2017. [Google Scholar] [CrossRef]
- The North American CORDEX Program—Regional Climate Change Scenario Data and Guidance for North America, for Use in Impacts, Decision-Making, and Climate Science. Available online: https://na-cordex.org/ (accessed on 17 June 2019).
- Miller, J.F.; Frederick, R.H.; Tracey, R.J. Precipitation Frequency Atlas of the Western United States; National Technical Information Service: Springfield, VA, USA, 1973; Volume 11.
- Perica, S.; Pavlovic, S.; Laurent, M.S.; Trypaluk, C.; Unruh, D.; Wilhite, O. NOAA Atlas 14 Precipitation-Frequency Atlas of the United States; Version 2.0; National Weather Service: Silver Spring, MD, USA, 2018; Volume 11.
- Madsen, H.; Pearson, C.P.; Rosbjerg, D. Comparison of annual maximum series and partial duration series methods for modeling extreme hydrologic events regional modeling. Water Resour. Res. 1997, 33, 759–769. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modelling of Extreme Values; Springer: Berlin, Germany, 2001. [Google Scholar]
- Langbein, W.B. Annual floods and the partial-duration flood series. Transactions. Am. Geophys. Union 1949, 30, 879–881. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Easterling, D.R.; Kristovich, D.A.R.; Gleason, B.; Stoecker, L.; Smith, R. Meteorological causes of the secular variations in observed extreme precipitation events for the conterminous United States. J. Hydrometeor. 2012, 13, 1131–1141. [Google Scholar] [CrossRef]
- Ulbrich, U.; Leckebusch, G.C.; Grieger, J.; Schuster, M.; Akperov, M.; Bardin, M.Y.; Feng, Y.; Gulev, S.; Inatsu, M.; Keay, K.; et al. Are Greenhouse Gas Signals of Northern Hemisphere winter extra-tropical cyclone activity dependent on the identification and tracking algorithm? Meteorol. Z. 2013, 22, 61–68. [Google Scholar] [CrossRef]
- Serinaldi, F. Dismissing return periods! Stoch. Environ. Res. Risk Assess. 2015, 29, 1179–1189. [Google Scholar] [CrossRef]
- McFadden, D. Modeling the Choice of Residential Location. Transp. Res. Record. 1978, 673, 72–77. [Google Scholar]
- Hosking, J.R.M. Moments or L moments? An example comparing two measures of distributional shape. Am. Stat. 1992, 46, 186–189. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Global Warming of 1.5 °C; An IPCC Special Report on the impacts of global warming of 1.5 °C above pre-industrial levels and related global greenhouse gas emission pathways, in the context of strengthening the global response to the threat of climate change, sustainable development, and efforts to eradicate poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; World Meteorological Organization: Geneva, Switzerland, 2018; 32p. [Google Scholar]
- Kunkel, K.E.; Karl, T.R.; Brooks, H.; Kossin, J.; Lawrimore, J.H.; Arndt, D.; Bosart, L.; Changnon, D.; Cutter, S.L.; Doesken, N.; et al. Monitoring and understanding trends in extreme storms: State of knowledge. Bull. Amer. Meteor. Soc. 2013, 94, 499–514. [Google Scholar] [CrossRef]
- Wang, C.Z.; Zhang, L.P.; Lee, S.K.; Wu, L.X.; Mechoso, C.R. A global perspective on CMIP5 climate model biases. Nat. Clim. Chang. 2014, 4, 201–205. [Google Scholar] [CrossRef]
- Sharifi, E.; Steinacher, R.; Saghafian, B. Multi time-scale evaluation of high-resolution satellite-based precipitation products over northeast of Austria. Atmos. Res. 2018, 206, 46–63. [Google Scholar] [CrossRef]
| Data Set | Models Used |
|---|---|
| UWPD (24) | ACCESS1-0; ACCESS1-3; CanESM2; CMCC-CESM; CMCC-CM CMCC-CMS; CNRM-CM5; CSIRO-Mk3-6-0; GFDL-CM3; GFDL-ESM2G GFDL-ESM2M; HadGEM2-CC; inmcm4; IPSL-CM5A-LR; IPSL-CM5A-MR IPSL-CM5B-LR; MIROC5; MIROC-ESM; MIROC-ESM-CHEM; MPI-ESM-LR MPI-ESM-MR; MRI-CGCM3; MRI-ESM1; NorESM1-M |
| LOCA (32) | ACCESS1-0; ACCESS1-3; bcc-csm1-1; bcc-csm1-1-m; CanESM2 CCSM4; CESM1-BGC; CESM1-CAM5; CMCC-CM; CMCC-CMS CNRM-CM5; CSIRO-Mk3-6-0; EC-EARTH; FGOALS-g2; GFDL-CM3 GFDL-ESM2G; GFDL-ESM2M; GISS-E2-H; GISS-E2-R; HadGEM2-AO HadGEM2-CC; HadGEM2-ES; inmcm4; IPSL-CM5A-LR; IPSL-CM5A-MR MIROC5; MIROC-ESM; MIROC-ESM-CHEM; MPI-ESM-LR; MPI-ESM-MR MRI-CGCM3; NorESM1-M |
| BCCAv2 (20) | ACCESS1-0; bcc-csm1-1; CanESM2; CCSM4; CESM1-BGC CNRM-CM5; CSIRO-Mk3-6-0; GFDL-CM3; GFDL-ESM2G; GFDL-ESM2M inmcm4; IPSL-CM5A-LR; IPSL-CM5A-MR; MIROC5; MIROC-ESM; MIROC-ESM-CHEM; MPI-ESM-LR; MPI-ESM-MR; MRI-CGCM3; NorESM1-M |
| NA-CORDEX (6) | CanESM2: {CRCM5(0.44°); RCA4(0.44°); CanRCM4(0.22°, 0.44°)}; EC-EARTH: {HIRHAMS(0.44°); RCA4(0.44°)} |
| Relevant Historical Return Periods (Years) | 2 | 5 | 10 | 25 | 50 | 100 | 200 | 500 | 1000 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Projected return periods (UWPD) | RCP4.5 | 2006–2053 | 1.7 [1.6–1.9] | 3.7 [3.3–4.3] | 6.7 [5.7–8.1] | 13.8 [11.3–17.8] | 22.7 [18.0–30.6] | 34.9 [27.0–49.5] | 50.9 [38.5–75.3] | 77.2 [56.9–120.1] | 100.4 [72.9–161.3] |
| 2054–2100 | 1.5 [1.4–1.7] | 3.2 [2.7–3.8] | 5.5 [4.6–6.7] | 11.0 [9.1-13.9] | 17.8 [14.5–22.9] | 27.2 [22.0–36.0] | 39.5 [31.5–53.2] | 59.9 [47.0–82.5] | 77.8 [60.6–108.8] | ||
| RCP8.5 | 2006–2053 | 1.6 [1.5–1.7] | 3.5 [3.1–3.9] | 6.2 [5.3–7.2] | 12.6 [10.5–15.7] | 20.6 [16.6–27.0] | 31.6 [24.8–43.6] | 45.9 [34.9–66.9] | 69.4 [51.0–108.3] | 90.0 [64.7–147.7] | |
| 2054–2100 | 1.3 [1.2–1.5] | 2.5 [2.2–2.9] | 4.1 [3.5–4.9] | 7.9 [6.6–9.8] | 12.5 [10.3–16.0] | 19.0 [15.3–25.0] | 27.4 [21.8–37.0] | 41.4 [32.3–57.8] | 53.9 [41.6–76.5] | ||
| Projected return periods (LOCA) | RCP4.5 | 2006–2053 | 1.7 [1.6–1.8] | 3.9 [3.5–4.4] | 7.1 [6.2–8.4] | 15.6 [13.1–19.4] | 26.7 [21.7–34.5] | 42.7 [34.1–57.1] | 64.5 [50.7–88.7] | 102.0 [78.8–144.7] | 136.2 [104.0–197.1] |
| 2054–2100 | 1.5 [1.4–1.7] | 3.3 [2.9–3.8] | 5.9 [5.1–7.2] | 12.9 [10.6–16.4] | 22.0 [17.7–28.9] | 35.2 [27.9–47.9] | 53.3 [41.4–74.8] | 84.1 [63.6–123.9] | 112.0 [83.2–171.1] | ||
| RCP8.5 | 2006–2053 | 1.7 [1.6–1.8] | 3.7 [3.3–4.2] | 6.9 [5.9–8.1] | 15.1 [12.7–18.7] | 26.0 [21.5–33.0] | 42.0 [34.1–54.6] | 63.7 [51.0–84.7] | 101.1 [79.8–138.0] | 135.2 [105.6–187.9] | |
| 2054–2100 | 1.4 [1.3–1.5] | 2.7 [2.4–3.2] | 4.7 [3.9–5.8] | 9.6 [7.8–12.5] | 16.1 [12.8–21.5] | 25.4 [20.1–34.7] | 38.2 [29.9–52.9] | 60.0 [46.6–84.3] | 79.8 [61.7–113.1] | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Markus, M.; Lorenz, D.; Angel, J.R.; Grady, K. A Comparative Analysis of the Historical Accuracy of the Point Precipitation Frequency Estimates of Four Data Sets and Their Projections for the Northeastern United States. Water 2019, 11, 1279. https://doi.org/10.3390/w11061279
Wu S, Markus M, Lorenz D, Angel JR, Grady K. A Comparative Analysis of the Historical Accuracy of the Point Precipitation Frequency Estimates of Four Data Sets and Their Projections for the Northeastern United States. Water. 2019; 11(6):1279. https://doi.org/10.3390/w11061279
Chicago/Turabian StyleWu, Shu, Momcilo Markus, David Lorenz, James R. Angel, and Kevin Grady. 2019. "A Comparative Analysis of the Historical Accuracy of the Point Precipitation Frequency Estimates of Four Data Sets and Their Projections for the Northeastern United States" Water 11, no. 6: 1279. https://doi.org/10.3390/w11061279
APA StyleWu, S., Markus, M., Lorenz, D., Angel, J. R., & Grady, K. (2019). A Comparative Analysis of the Historical Accuracy of the Point Precipitation Frequency Estimates of Four Data Sets and Their Projections for the Northeastern United States. Water, 11(6), 1279. https://doi.org/10.3390/w11061279






