Abstract
Traditional reservoir operation mainly focuses on economic benefits, while ignoring the impacts on navigation. Thus, the economic operation of reservoirs considering navigational demands is of great significance for improving benefits. A navigation capacity evaluation method (NCEM), which evaluates the navigation capacity considering the influence of flow velocity and water level variation on navigation, is proposed to more effectively evaluate the navigation capacity. Based on two-dimensional hydrodynamic numerical simulation, the NCEM accurately calculates the navigation capacity according to detailed flow velocity and water level changes. In addition, a short-term multi-objective optimal operation model considering the upstream and downstream navigation and power generation is established. Then, the Strength Pareto Evolutionary Algorithm (SPEA2) is used to solve the model. To verify the rationality of the method and model, they are applied to the case study of the Xiangjiaba reservoir. The results demonstrate that the method and model can not only provide a series of operation schemes for decision makers of reservoirs, but also direct the ship to pass safely through the approach channel, implying a certain practical value and significance as a reference for the short-term optimal operation of reservoirs in the future.
1. Introduction
Hydropower is an important clean and renewable energy source, and increasing numbers of hydropower stations have been built in recent years to meet economic needs worldwide [1,2,3,4,5,6]. In order to explore resources more efficiently, many scholars have carried out studies on the optimal operation of reservoirs [7,8,9]. Furthermore, some useful optimal models and algorithms which comprehensively consider the benefits of reservoirs are proposed [10,11,12,13]. However, there are relatively few studies on the operation of reservoir considering navigation demands.
During the daily operation of the reservoir, scheduling schemes are developed to take into account power generation needs [14], peak load regulation [15], and storage water demands etc., which will result in daily cyclical changes in the discharge volume and water level [16]. The fluctuation is transmitted downstream, causing a complex unsteady flow [17]. Moreover, due to the special topography of some rivers, the large discharge volume of the reservoir can cause a large surface velocity and reflux in the local area of the river reaches [18]. These phenomena seriously hinder the navigation of ships [19]. Consequently, in order to ensure the safe and stable operation of the reservoir, it is necessary to implement an evaluation of the navigation capacity of the channel, laying a foundation for a comprehensive optimization of the operation of the reservoir [20].
Defining and quantifying navigation capacity is the premise for the short-term optimal operation of reservoirs to meet the requirements of navigation, and it is also the basis for assessing the impact of operation of the reservoir on navigation. There are many studies on the operation mode of ship locks in order to increase navigation benefits [21,22,23,24], defining and quantifying the navigation capacity to a certain extent so that the navigation objective can be integrated into the optimization model. Ji et al. [25,26,27] used the weighted total tardiness of the ships as the navigation objective to solve the problem of ship lock scheduling, increasing the interests of shippers and owners of the lock. To maximize navigation benefits, the Non-Dominated Sorting Genetic Algorithm III (NSGA-III) was used to optimize the operation mode of the ship lock and the order of the ship passing through the ship lock. However, this method mainly focuses on the navigation efficiency and the operation mode of the ship lock. It does not highlight the operation effect of the reservoir and lacks a comprehensive consideration of the multiple benefits of the reservoir.
Taking the hydraulic factors of the reservoir and river reaches as indicators of navigation capacity, the navigation objective and other objectives (power generation, flood control, ecological environment, etc.) of the reservoir can be combined to form a multi-objective optimization model. The influencing factors of the navigation are complex, and parameters such as flow velocity, water surface gradient, variation of daily water level, and variation of hourly water level are usually used as the evaluation indicators at present. Ackermann et al. [28] used the sum of water level variability and flow variability with different weighting factors as the navigation objective based on the result of the one-dimensional hydrodynamic simulation. Wang and Zhang [29] proposed a single objective optimization model considering navigation demands (using the maximum amount of power generation as the objective), and took flow ramping as the constraint. Ma et al. [30] used the comprehensive influence of multiple hydraulic factors for the evaluation of navigability, defining the navigation capacity as zero (not satisfying the navigation requirements) or one (satisfying the navigation requirements) when the navigation capacity could not be evaluated in detail. Liu et al. [31] used the guarantee rate of navigation to quantify the navigation objective, which is related to the discharge volume. This method combines well with the flood control objective and navigation objective, meets the demands for the multiple benefits of reservoir, and achieves good results.
In summary, the above studies analyze the influence of reservoir scheduling on navigation, and use intelligent optimization algorithms to solve optimization problems. In addition, optimal operation schemes are achieved for both single-objective and multi-objective models. Nevertheless, the above methods and models at least have one of the following shortcomings. Firstly, the navigation objective may not be defined and quantified, and the navigation conditions are treated as constraints rather than objectives in the model. The obtained optimization results thus do not reflect the navigation benefits. Secondly, the quantization of the navigation objective may be too rough to consider the impact of some hydraulic factors on navigation accurately. Thirdly, the evaluation of the navigation capacity may not consider the impact of flow velocity on navigation, and may not take into account the combined effects of various hydraulic factors (flow rate, water level, etc.) on navigation. Fourthly, a single-objective model may be used to analyze the comprehensive benefits of navigation and power generation, which has great limitations in exploring the relationship between multiple objectives.
To this end, this paper proposes a navigation capacity evaluation method which evaluates the navigation capacity considering the comprehensive influence of flow velocity and water level variation on navigation. Moreover, a short-term multi-objective optimal operation model considering the upstream and downstream navigation and power generation is established.
The rest of this paper is organized as follows. Section 2 firstly analyzes the impact of the flow velocity and water level on navigation, and a navigation capacity evaluation method (NCEM) is proposed for defining and quantifying the navigation objective. In Section 3, the multi-objective operation model of reservoir is established. Section 4 briefly shows the algorithm and flowchart of the multi-objective model adopted in this study. Section 5 presents the case study of the Xiangjiaba reservoir, with calculation results and discussions. Finally, the conclusions are given in Section 6.
3. Multi-Objective Reservoir Operation Model
The short-term multi-objective optimal operation model of reservoir considers economic and navigation benefits in this paper. The model consists of three objectives: the economic objective, the upstream navigation capacity objective, and the downstream navigation capacity objective. The decision variables in this paper are set to the upstream water level () of the reservoir.
The power generation of the reservoir is directly related to the flow used to generate electricity, and has an indirect relationship with the discharge volume. The navigation capacity is directly related to the discharge volume. Therefore, the discharge volume is used as the link to analyze the influence of short-term reservoir operation on power generation and navigation.
3.1. Objective Function
3.1.1. Economic Objective: Maximizing the Daily Total Power Generation
Maximizing the total daily power generation is a necessary objective to guarantee economic benefits [37]. For short-term optimal operation problem, the formula for economic objective can be written as follows:
where is the total number of periods in the operation period; is the length of time in each period; is the total power generation; is the output of hydroelectric generators in the -th stage; and and are the power discharge and net head in the -th stage, respectively.
Moreover, depends on , , and the energy loss, and the energy loss is determined by the efficiency of the hydroelectric generator. The formula can be expressed as follows:
where and are the water level in the upstream and downstream of the reservoir in the -th stage, respectively; and is the water head loss.
3.1.2. Navigation Objective: Maximizing the Navigation Capacity
To maximize the navigation capacity is an important objective, which is beneficial to navigation. Besides, the navigation capacity is a comprehensive evaluation indicator, taking into account the influence of flow velocity and water level variation on the ship according to Section 2. The formula to calculate the navigation objective is defined as follows:
where represents the navigation capacity; and and are weighting factors. According to Formulas (7) and (9), Formula (13) can also be written as the following form:
3.2. Constraints
Due to the operation of reservoir and the demands of navigation, the optimization of three objectives is restricted due to the following constraints [38].
(1) Water volume balance
where is the storage volume of the reservoir in the -th stage and is the inflow in the -th stage.
(2) Constraints on the reservoir volume
where is the minimum limit of the in the -th stage and is the maximum limit of the in the -th stage.
(3) Water head constraint of hydropower station:
where and are the minimum and maximum limit of work head level in the -th stage respectively, which depends on the hydroelectric generator.
(4) Power generation constraint:
where and are the lower and upper limit of in the -th stage, respectively.
(5) Navigable discharge volume constraint
where and are minimum and maximum navigable discharge volume in the -th stage, respectively.
(6) Boundary conditions constraint
where is the upstream water level in the beginning of the scheduling period; is the upstream water level in the end of the scheduling period.
4. Methodology
Studying the relationship between power generation, the upstream navigation capacity, and the downstream navigation capacity is a multi-objective optimization problem (MOP) [39,40]. There are several multi-objective evolutionary algorithms to solve the complicated multi-objective problem, such as the Strength Pareto Evolutionary Algorithm (SPEA2) [41]; the Non-Dominated Sorting Genetic Algorithm II (NSGA-II) [42]; the Multi-Objective Bee Colony Optimization algorithm (EMOBCO) [43]; and the Multi-Objective Artificial Sheep Algorithm (MOASA) [44], etc. Besides, maintaining a good distribution of solutions is a challenge for the optimization algorithms. Therefore, the SPEA2, which is a multi-objective evolutionary algorithm based on elitist strategy, is used to solve the MOP problem with three objectives in this study. The SPEA2 employs an enhanced fitness assignment strategy for archive truncation and density-based selection in order to obtain the Pareto frontier with uniform distribution. In the algorithm, the archive is used to store all non-dominated solutions generated in the optimization process, and the advantage of the archive is to obtain the Pareto front with better distribution. To start with an initial population and an empty archive, all non-dominated individuals are copied to the archive, and the dominated population members are removed from the archive under the update strategy of the archive set for each iteration. The update strategy of the archive set is as follows:
- (1)
- When there are no individuals in the external archive set, the non-dominated solutions generated in the iteration are stored directly in the archive set;
- (2)
- If the newly generated individuals are dominated by the individuals in the archive set, the new individuals will be deleted. Conversely, individuals can be deleted from the original archive set and new individuals added to the archive set;
- (3)
- When the number of individuals in the archive set reaches the preset maximum capacity, the individuals with smaller crowding distance are deleted.
Therefore, the Pareto solution set is stored in the archive, and the archive set is output as the optimization result finally.
Coupled with the above SPEA2 and NCEM, the flowchart of the multi-objective model is shown in Figure 2.
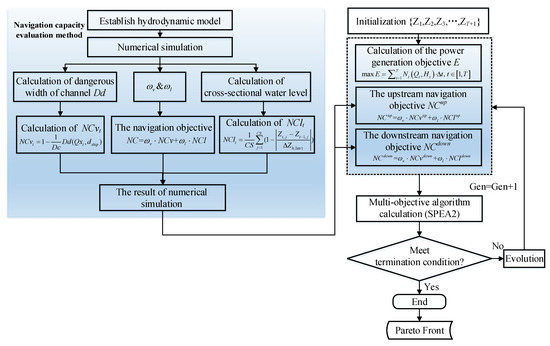
Figure 2.
Flowchart of proposed method and model. (Gen represents the generation).
The calculation steps are as follows:
Step 1: Establish the hydrodynamic model
Two two-dimensional hydrodynamic models (upstream and downstream river reaches) are established according to Section 2.1. The flow profile in the unsteady flow condition is used as the upstream boundary, and the water level profile is used as the downstream boundary in both models [17]. Based on the results of the numerical simulation, the value of and the cross-sectional water level corresponding to different operation conditions are calculated. Therefore, the value of and under different operation conditions can be determined according to Formulas (6) and (8).
Step 2: Determine the weighting factors
and are weighting factors that determine the effect of flow velocity and water level variation on navigation capacity in Formula (13).
The value of and can be determined according to Step 1. If there is very large flow velocity in the river reach during the operation of reservoir, then the flow velocity is considered to be the main obstacle to navigation, and the value of is set greater than . If there is no large flow velocity, the water level variation is the main factor affecting navigation, and the value of is greater than .
Step 3: Determine the navigation objective functions
According to Formula (13), the parameters () and () of the upstream and downstream navigation objective functions are determined in Step 2. In the calculation of each navigation objective function of the following algorithm, the value of and under different operation conditions calculated in Step 1 will be imposed in the navigation objective function to determine the specific value of navigation capacity.
Step 4: Initialization
A series of individuals which represent the upstream water level are generated, and these individuals are randomly generated according to maximum and minimum limits in the algorithm. Besides, the parameters of SPEA2 are initialized, including the population size, the maximum number of generations, the size of the archive, the crossover rate, the mutation rate, etc.
Step 5: Solution algorithm
In this step, the multi-objective problem is solved by SPEA2. Among them, the expression form of the navigation objective function is determined by the result calculated in Step 3. The value of and in different operation conditions can be obtained by the numerical simulation in Step 1, providing a basis for the calculation of each navigation objective function.
Step 6: The output
The archive set is output as the optimization result if the termination condition is met, and the Pareto solution set is obtained finally.
5. Case Study
5.1. Case Description
The Xiangjiaba (XJB) reservoir is located at the juncture of Shuifu city and Yibin city in China, which is the last level reservoir of Jinsha River hydropower base, as shown in Figure 3a,b. With a multi-year average runoff of 3810 m3/s, the XJB reservoir can control a basin area of 458,800 square kilometers, accounting for 97% of the Jinsha River basin area. In addition, the total storage capacity of the XJB reservoir is 5.163 billion cubic meters, and the regulating storage volume is 900 million cubic meters. The main parameters of XJB reservoir is shown in Table 1.
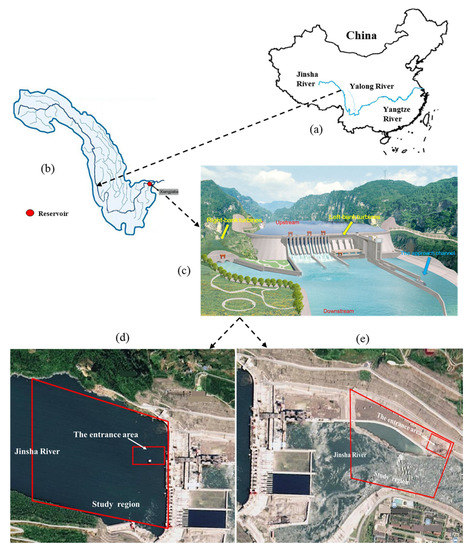
Figure 3.
Study area: (a,b) The location of the Xiangjiaba (XJB) reservoir; (c) The layout of turbines in the XJB reservoir; (d) The upstream reaches of the reservoir; (e) The downstream reaches of the reservoir.

Table 1.
Basic parameters of the XJB reservoir.
The XJB reservoir not only has the function of generating electricity, but also regulating navigation. It is the third largest hydropower station in China and the fifth largest in the world, for which the total installed capacity for power generation is 6 × 106 kW, and the annual average power generation is 3.013 × 1010 kWh. Furthermore, it is the only dam in the Jinsha River hydropower base to build a ship lift with a very efficient ship navigation rate. Its scale is equivalent to that of the Three Gorges reservoir, and it takes only 15 min for a ship of one kiloton to cross the dam. Compared with the average dam time of the Three Gorges reservoir of 5 h, the navigation efficiency of XJB reservoir is quite high.
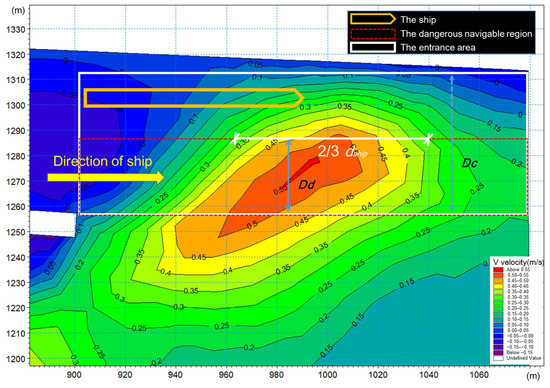
However, due to the operation of reservoir, the navigation of the upstream and downstream reaches of the reservoir is seriously affected by the unsteady flow and the navigational is impeded. Besides, the difficulty of upstream and downstream navigation of the reservoir is both caused by the water flow at the entrance area of the approach channel. When the ship passes through the entrance area, care should be taken to avoid the influence of the large transverse velocity near the dike on the navigation. Therefore, it is of great practical significance to formulate optimization decisions to ensure economic benefits and navigation safety.
There are a total of eight turbines in XJB reservoir, four of which are located on the right-bank underground powerhouse, with the other four located on the left-bank power house at the dam toe, as shown in the Figure 3c. Besides, the left-bank turbines are about 900 m away from the entrance area of approach channel, with an interval of 36 m for each turbine. The right-bank turbines are about 1300 m away from the entrance area of approach channel, and each turbine is about 39 m apart.
In order to build the economic/navigation multi-objective model, the initial water level and the final water level of a day are both set as 379.5 m in this study. The average hourly inflow remains at 5000 m3/s. Moreover, the allowed navigation period of the XJB reservoir is from 08:00 to 18:00 h in a day, and a typical ship with a size of 85.0 m × 10.8 m × 2.0 m (length × width × draft depth) is selected for analysis. For the short-term optimization operation problem in this case study, the length of time in each period is set to one hour.
5.2. Parameter Settings and Simulation Working Conditions
5.2.1. Model Parameter Setting
According to the measured sections data of Jinsha River, two two-dimensional hydrodynamic models for the upstream and downstream reaches, respectively, are established by the software Mike21 FM to analyze the navigation capability. Moreover, the study regions of two models are selected, as shown in Figure 3d,e.
The width of the study region of the upstream reaches is 590 m and the length is 910 m. Besides, the total number of model grids is 1227, and the number of grid nodes is 690.
The size of the study area of the downstream model is m. Also, the total number of grid cells and the number of grid nodes is 1698 and 1008, respectively. The generated mesh of the upstream and downstream reservoir is shown in Figure 4.
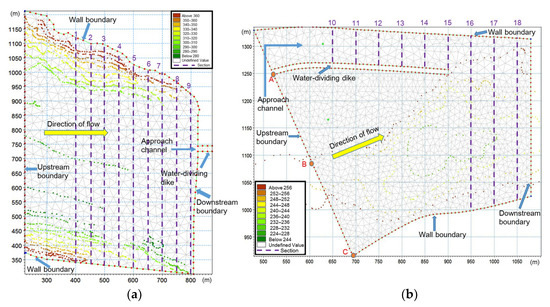
Figure 4.
Generated mesh of the reservoir upstream (a) and downstream (b).
Then, the numerical simulation results of the water level is compared with the measured data. In addition, the parameters of the model are modified by the result of the comparison until the simulated result matches the measured data within an acceptable range.
In order to explore the influence of the water level variation on navigation, the cross-section is set every 50 m in two models; finally, 18 cross-sections are set in the upstream and downstream models.
5.2.2. Simulation Working Conditions
According to the layout of turbines in Section 5.1, during the actual operation when all the turbines work normally, the symmetric flow will be generated in the downstream river reaches, because the discharge is uniformly distributed in the downstream reaches. In this condition, the upstream boundary line in the downstream model is AC, as shown in Figure 4, which means that the discharge is evenly distributed on the AC boundary.
However, if only some of the turbines work, then there will be asymmetric flow in the downstream river reaches because of the uneven discharge distribution. In order to explore the influence of asymmetric flow on the downstream navigation capacity, two typical working conditions are selected for research, as shown in Table 2.

Table 2.
Three simulation working conditions.
Whether the symmetric flow or the asymmetric flow is determined by the outflow condition of the two sections AB and BC, as shown in Figure 4, which are on the two sides of the midpoint B of the boundary line on the downstream model. If there is outflow on both sections (AB and BC), a symmetric flow will be generated. If there is outflow on the only section (AB or BC), an asymmetric flow will be generated.
Thus, three simulations are performed in the case study, which are the preliminary simulation of symmetric flow, and the elaborate simulation of symmetric flow and asymmetric flow, respectively. Among them, Condition 1 is performed in the preliminary simulation and elaborate simulation, and Conditions 2 and 3 are completed in the asymmetric flow simulation.
5.3. Results
5.3.1. Numerical Simulation Results
(1) Preliminary simulation of symmetric flow
To briefly study the navigation capacity and determine the weighting factors ( and ) for the above two hydrodynamic models, four working conditions (two upstream conditions and two downstream conditions) are selected to simulate the influences of flow velocity and water level on ship navigation, as shown in Table 3. The value of discharge volume and water level are used to the upstream and downstream boundary conditions of the two models in the Table 3, respectively.

Table 3.
The working conditions and results of preliminary simulation of symmetric flow.
The upstream water level of Condition P1 is 380 m, which is the normal water storage level (September–December of this year, January and June of the following year). The highest flow occurs in September, and the average annual flow is 9880 m3/s. Besides, in Condition P2 the upstream water level is 370 m in July–September, the highest flow is in August, and the average annual flow is 9970 m3/s. Finally, Condition P3 and Condition P4 show the minimum and maximum navigable flow in the downstream reaches of the reservoir, respectively.
According to the model parameter settings listed in Section 5.2, the numerical simulation of the two hydrodynamic models is implemented separately. The research results are as follows:
- (1)
- The numerical simulation results of Condition P1 and Condition P2 are shown in Table 3, Figure 5, and Figure 6. It can be seen that the longitudinal velocity and transverse velocity of the upstream entrance area of approach channel satisfy the navigation requirements. Therefore, it can be inferred that the upstream navigation capacity () is less affected by the flow velocity. In this study case, is mainly related to the water level variation, and the formula for is expressed as follows:where: = 12 and = 1.5 m/h.
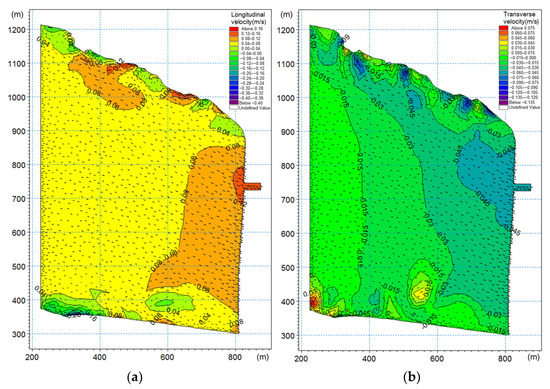 Figure 5. Longitudinal velocity (a) and transverse velocity (b) diagram under Condition P1 of the upstream model.
Figure 5. Longitudinal velocity (a) and transverse velocity (b) diagram under Condition P1 of the upstream model.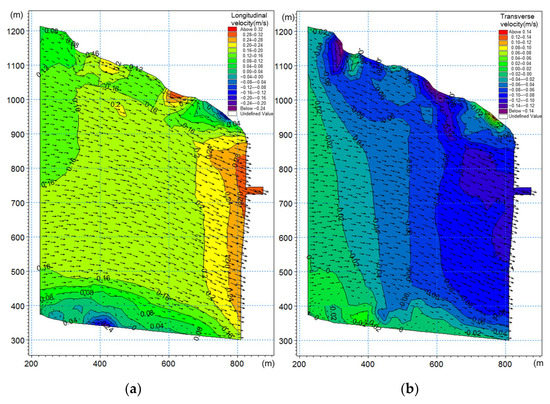 Figure 6. Longitudinal velocity (a) and transverse velocity (b) diagram under Condition P2 of the upstream model.
Figure 6. Longitudinal velocity (a) and transverse velocity (b) diagram under Condition P2 of the upstream model. - (2)
- The transverse velocity and longitudinal velocity in Condition P3 and the longitudinal velocity in the Condition P4 are all satisfied by the navigation requirement, as shown in Figure 7 and Table 3. However, the local transverse velocity exceeds the limit value of 0.3 m/s in the Condition P4, which seriously hinders the navigation in the entrance area of the approach channel. As a result, the transverse velocity is the most important factor affecting the downstream navigation, which is considered in this case.
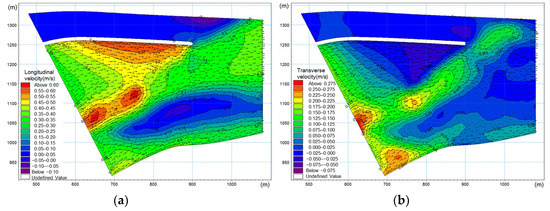 Figure 7. Longitudinal velocity (a) and transverse velocity (b) diagram under Condition P3 of the downstream model.
Figure 7. Longitudinal velocity (a) and transverse velocity (b) diagram under Condition P3 of the downstream model.
The downstream navigation should first consider the influence of the flow velocity and then consider the influence of the water level variation. Therefore, in the objective of the downstream navigation capacity (), the weight of the flow velocity accounts for a larger proportion ( = 0.95), and the water level variation accounts for a relatively small proportion ( = 0.05). Finally, the formula for is expressed as follows:
where = 22 and = 57 m.
(2) Elaborate simulation of symmetric flow
To explore the different values of and the cross-sectional water level under different discharge volume in the downstream model, 23 sets of numerical simulations with different discharge volumes () are implemented. The boundary conditions of simulations and the simulated results are shown in Table 4. According to the water level–flow relationship of XJB reservoir, the discharge volume () profile is applied as the upstream boundary condition, and the downstream water level () profile is used as the downstream boundary condition in the downstream model.

Table 4.
The results of numerical simulations in the downstream model.
Taking the discharge volume of 5700 m3/s as an example, = 0.403 is obtained through the calculation, as shown in Figure 8.
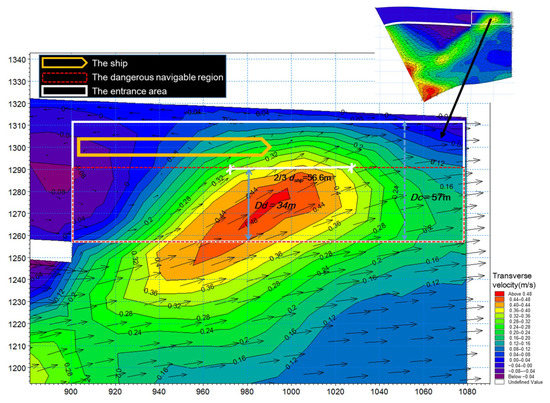
Figure 8.
Transverse velocity diagram in the entrance area of approach channel in the upstream model (where = 0.403, = 5700 m3/s).
In order to calculate the value of cross-sectional water level under different conditions in the upstream model, 21 sets of numerical simulations are completed, and the results are shown in Table 5. According to the average hourly inflow (I) set in Section 5.1, the inflow profile is used as the upstream boundary condition, and the upstream water level () profile is applied as the downstream boundary condition in the upstream model. Therefore, the water levels of the downstream boundary condition are selected between the dead water level (370 m) and the normal height (380 m), with an interval of 0.5 m.

Table 5.
The results of numerical simulations in the upstream model.
(3) Asymmetric flow simulation
To study the influence of asymmetric flow on the of XJB reservoir, Conditions 2 and 3 in Table 2 are simulated by the same downstream model with different boundary lines.
Twenty-three sets of numerical simulations are carried out, and their boundary conditions are the same as those in the elaborate simulation of symmetric flow, as shown in Table 4. The calculation results are shown in Figure 9.
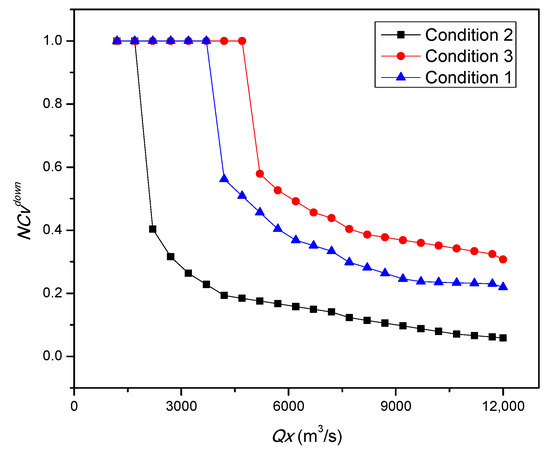
Figure 9.
The value of under different discharge volume (three working conditions).
Through the simulation results, the following conclusions can be drawn:
- (1)
- For downstream navigation of XJB reservoir, when the discharge volume (less than 1700 m3/s) is relatively small, the downstream navigation capacity considering the flow velocity () of the three working conditions is the same ( = 1);
- (2)
- When the discharge volume is large (greater than 1700 m3/s), the is the poorest in Condition 1 (only left-bank turbines work), better in Condition 2 (all turbines work), and the best in Condition 3 (only right-bank turbines work).
Due to the fact that the left-bank turbines are close to the entrance area of approach channel, if only the left-bank turbines are working, then a larger area where the transverse velocity exceeds the limit value will be generated, and there will be a greater dangerous navigation width (). In contrast, the right-bank turbines are far away from the entrance area and have less impact on the navigation of the entrance area. Therefore, the study and results of asymmetric flow can provide useful suggestions for the unit commitment problem [45]. For example, when less power generation is required by XJB reservoir, it is preferable to only operate the right-bank turbines in order to satisfy the navigation demands.
The length of time in each period is set to 1 h in this paper, so the symmetric flow is selected as the study object in the short-term optimal operation problem. Besides, the study results of asymmetric flow can provide guidance for future ultra-short term optimal operation problems or inner-plant economical operations [46].
5.3.2. Multi-Objective Model Results
Based on the simulation results of symmetric flow in the two models (Table 4 and Table 5) and the determination of weighting factors ( and ), the objective functions of and are expressed by Formulas (22) and (23), respectively. Then, the multi-objective optimal operation model is calculated according to the process of Figure 2. The algorithm parameters are set as follows: the population size is set to 200, the size of the archive is set to 100, the number of iterations is set to 20,000 generations, the mutation rate is set to 0.04, and the crossover rate is set to 0.85.
The Pareto optimal front of three objectives is acquired as given in Figure 10a; the optimal results of any two of the objectives are also expressed in Figure 10b–d. All the operation schemes results of the reservoir are shown in Table 6. The three conclusions drawn from the Figure 10 are as follows:
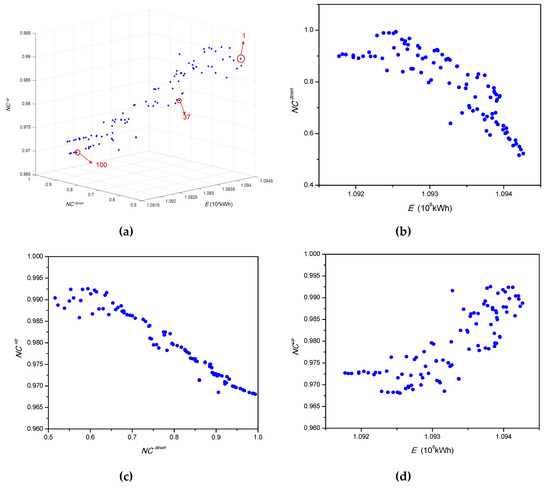
Figure 10.
The Pareto optimal front. (a) The optimal results of three objectives (E, NCdown and NCup); (b) The optimal results of two objectives (E and NCdown); (c) The optimal results of two objectives (NCdown and NCup); (d) The optimal results of two objectives (E and NCup).

Table 6.
Operation schemes of reservoir (arranged in ascending order of ).
- (1)
- There is an obvious inverse relationship between the total power generation () and the downstream navigation capacity () from the results of Figure 10b. The larger the total power generation (), the smaller the downstream navigation capacity () in a day. The minimum value of is 0.52, and the maximum value is 0.99 with a growth of 90.38%, which varies greatly. At the same time, there is a drop of from the maximum value at 10,942.07 × 104 kWh to the minimum value at 10,925.44 × 104 kWh.
- (2)
- As shown in the Figure 10c, there is a certain inverse trend between the upstream navigation capacity () and the downstream navigation capacity (). When the upstream navigation capacity increases, the downstream navigation capacity declines. The minimum value of in all the schemes is 0.968, and the maximum value is 0.992 with a smaller growth compared to the change in .
- (3)
- Finally, it can be seen that the relationship between the total power generation () and the upstream navigation capacity () is not obvious shown in the Figure 10d. There is little interaction between these two elements.
5.4. Discussion
To further understand the relationship between three objectives and explain the cause of this phenomenon, typical schemes are selected to be discussed and analyzed in depth. Because and have no obvious relationship and the change of in all schemes is relatively small, the three schemes which mainly consider the relationship between and are selected. The schemes consist of the maximum of the total power generation (Scheme 1), the extreme point of the maximum of the downstream navigation capacity (Scheme 100), and the relative intermediate point (Scheme 37) compared to other schemes. The comparison of the objective values of the three schemes is expressed in Figure 11a, and the specific power generation and navigation processes of the three schemes are shown in Figure 11b–d, respectively.
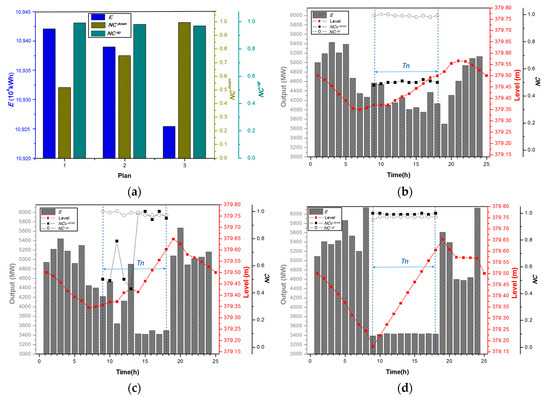
Figure 11.
Operation schemes. (a) The comparison of the objective values of the three schemes; (b) Scheme 1; (c) Scheme 37; (d) Scheme 100.
The common feature of the three schemes is that the water level drops from 00:00 h to 0:00 h (the start of navigation), and is in a state of gradual drainage before navigation. Then the reservoir begins to store the water and the water level grows between 08:00 and 18:00 h (the end of navigation), thus decreasing the amount of the discharge volume in the navigable period in order to establish a favorable navigation environment. After the navigation ends, the water level drops to the end water level in the following hours, which will maximize the amount of power generation after the navigation process.
In Scheme 1, the water level falls from 00:00 to 08:00 h to 379.37 m slowly, with a moderate drop, followed with a slight rise during the navigation time. However, during the navigation period, the average discharge volume of the reservoir is maintained at 4602 m3/s, and the average output is maintained at 4213 MW, resulting in a large amount of electricity during this period. In the meantime, the value of per hour is maintained between 0.48 and 0.52, resulting in a large transverse velocity in the entrance area of approach channel, which is not conducive to navigation according to the numerical simulation results in Section 5.3.1. This scheme significantly rises the total power generation, but reducing the downstream navigation capacity in contrast.
In Scheme 100, after the water level sharply declines from 00:00 to 08:00 h, the reservoir strengthens the water storage, and the water level increases rapidly. During the navigation time, the average output and discharge volume are maintained at 3430 MW and 3708 m3/s, respectively. Consequently, the value of per hour is also the highest with an average value of 1, and it builds beneficial condition for navigations while decreasing the economic benefits of the reservoir.
Scheme 37 represents a compromise that considers both economics and navigation. It can provide short-term power generation operation advice for reservoir managers, and it can also guide ship operators to safely pass through dangerous areas.
6. Conclusions
In the past, most navigation capacity evaluation methods neglected the influence of flow velocity on navigation of ships. Based on the two-dimensional hydrodynamic numerical simulation, a navigation capability evaluation method that considers the flow velocity and water level comprehensively is proposed in this paper. In addition, a short-term multi-objective optimal operation model considering the upstream and downstream navigation and power generation of the reservoir is established and solved by SPEA2. To verify the reasonableness and practicability of the method and model, an example of short-term optimal operation of the Xiangjiaba reservoir in China is studied. Based on the case study, this paper analyzes in depth the impact of various operation processes of reservoir on economic and navigable benefits. The following conclusions can be drawn:
- (1)
- The proposed NCEM to evaluate the navigation capability is reasonable and effective, and can comprehensively analyze the influence of flow velocity and water level variation on navigation accurately.
- (2)
- The proposed multi-objective model can obtain a favorable Pareto frontier and explore the relationship between objectives. In the case study of the XJB reservoir, there is an obvious inverse relationship between power generation and the downstream navigation capacity. Also, the relationship between downstream navigation capacity and upstream navigation capability is inverse. However, there is little interaction between power generation and upstream navigation capability.
- (3)
- The results illustrate that the method and model are reasonable and effective, and also indicate that they can provide a series of favorable optimal operation schemes for the reservoir to obtain economic and navigational benefits.
Author Contributions
This paper was carried out with collaboration between all authors. T.J. and H.Q. contributed to modeling and finalized the manuscripts. D.Y., J.Z., and Z.Z. guided the experiments. C.L., J.W., and B.L. contributed to data analysis. All authors contributed to the literature review and prepared the figures.
Funding
This research was funded by the National Key R&D Program of China (No. 2016YFC0401910), the National Natural Science Foundation of China (No. 91647114, 91547208), the Fundamental Research Funds for the Central Universities (HUST: 2019JYCXJJ036), and the Graduates’ Innovation Fund, Huazhong University of Science and Technology (No. 2019YGSCXCY008, 2019YGSCXCY018, 2019YGSCXCY023, 2019YGSCXCY036).
Acknowledgments
The authors greatly appreciate the anonymous reviewers and academic editor for their constructive comments and valuable suggestions to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhao, J.S.; Wang, Z.J.; Weng, W.B. Study on the holistic model for water resources system. Sci. China Ser. E-Eng. Mater. Sci. 2004, 47S, 72–89. [Google Scholar] [CrossRef]
- Cai, X.M.; McKinney, D.C.; Lasdon, L.S. Solving nonlinear water management models using a combined genetic algorithm and linear programming approach. Adv. Water Resour. 2001, 24, 667–676. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, J.; Mo, L.; Zhang, R.; Zhang, Y. Short-term hydrothermal generation scheduling using differential real-coded quantum-inspired evolutionary algorithm. Energy 2012, 44, 657–671. [Google Scholar] [CrossRef]
- Mo, L.; Lu, P.; Wang, C.; Zhou, J. Short-term hydro generation scheduling of Three Gorges-Gezhouba cascaded hydropower plants using hybrid MACS-ADE approach. Energy Convers. Manag. 2013, 76, 260–273. [Google Scholar] [CrossRef]
- Mahor, A.; Rangnekar, S. Short term generation scheduling of cascaded hydro electric system using novel self adaptive inertia weight PSO. Int. J. Electr. Power Energy Syst. 2012, 34, 1–9. [Google Scholar] [CrossRef]
- Barros, M.; Tsai, F.; Yang, S.L.; Lopes, J.; Yeh, W. Optimization of large-scale hydropower system operations. J. Water Resour. Plan. Manag. ASCE 2003, 129, 178–188. [Google Scholar] [CrossRef]
- Zhang, X.; Luo, J.; Sun, X.; Xie, J. Optimal reservoir flood operation using a decomposition-based multi-objective evolutionary algorithm. Eng. Optim. 2019, 51, 42–62. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Zhou, J.; Cheng, C. Multi-objective operation optimization of a cascaded hydropower system. J. Water Resour. Plan. Manag. 2017, 143, 05017010. [Google Scholar] [CrossRef]
- Nilsson, O.; Sjelvgren, D. Hydro unit start-up costs and their impact on the short term scheduling strategies of Swedish power producers. IEEE Trans. Power Syst. 1997, 12, 38–43. [Google Scholar] [CrossRef]
- Cheng, C.; Liao, S.; Tang, Z.; Zhao, M. Comparison of particle swarm optimization and dynamic programming for large scale hydro unit load dispatch. Energy Convers. Manag. 2009, 50, 3007–3014. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, Y.; Wang, L.; Yuan, Y. An enhanced differential evolution algorithm for daily optimal hydro generation scheduling. Comput. Math. Appl. 2008, 55, 2458–2468. [Google Scholar] [CrossRef]
- Yuan, X.; Ji, B.; Chen, Z.; Chen, Z. A novel approach for economic dispatch of hydrothermal system via gravitational search algorithm. Appl. Math. Comput. 2014, 247, 535–546. [Google Scholar] [CrossRef]
- Castelletti, A.; Pianosi, F.; Restelli, M. A multiobjective reinforcement learning approach to water resources systems operation: Pareto frontier approximation in a single run. Water Resour. Res. 2013, 49, 3476–3486. [Google Scholar] [CrossRef]
- Wu, X.; Cheng, C.; Lund, J.R.; Niu, W.; Miao, S. Stochastic dynamic programming for hydropower reservoir operations with multiple local optima. J. Hydrol. 2018, 564, 712–722. [Google Scholar]
- Xie, M.; Zhou, J.; Li, C.; Lu, P. Daily generation scheduling of cascade hydro plants considering peak shaving constraints. J. Water Resour. Plan. Manag. 2016, 142, 04015072. [Google Scholar] [CrossRef]
- Kalumba, M.; Nyirenda, E. River flow availability for environmental flow allocation downstream of hydropower facilities in the Kafue Basin of Zambia. Phys. Chem. Earth 2017, 102, 21–30. [Google Scholar] [CrossRef]
- Shang, Y.; Li, X.; Gao, X.; Guo, Y.; Ye, Y.; Shang, L. Influence of daily regulation of a reservoir on downstream navigation. J. Hydrol. Eng. 2017, 22, 05017010. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, M.; Zhu, L.; Liu, W.; Han, J.; Yang, Y. Influence of large reservoir operation on water-levels and flows in reaches below dam: Case study of the Three Gorges Reservoir. Sci. Rep. 2017, 7, 15640. [Google Scholar] [CrossRef]
- Wagenpfeil, J.; Arnold, E.; Linke, H.; Sawodny, O. Modelling and optimized water management of artificial inland waterway systems. J. Hydroinformat. 2013, 15, 348–365. [Google Scholar] [CrossRef]
- Jia, T.; Zhou, J.; Liu, X. A daily power generation optimized operation method of hydropower stations with the navigation demands considered. MATEC Web Conf. 2018, 246, 01065. [Google Scholar] [CrossRef]
- Caris, A.; Limbourg, S.; Macharis, C.; van Lier, T.; Cools, M. Integration of inland waterway transport in the intermodal supply chain: A taxonomy of research challenges. J. Transp. Geogr. 2014, 41, 126–136. [Google Scholar] [CrossRef]
- Ceylan, H.; Bell, M.G.H. Genetic algorithm solution for the stochastic equilibrium transportation networks under congestion. Transp. Res. Part Methodol. 2005, 39, 169–185. [Google Scholar]
- Bugarski, V.; Bačkalić, T.; Kuzmanov, U. Fuzzy decision support system for ship lock control. Expert Syst. Appl. 2013, 40, 3953–3960. [Google Scholar] [CrossRef]
- Bierwirth, C.; Meisel, F. A survey of berth allocation and quay crane scheduling problems in container terminals. Eur. J. Oper. Res. 2010, 202, 615–627. [Google Scholar] [CrossRef]
- Ji, B.; Yuan, X.; Yuan, Y. Orthogonal design-based NSGA-III for the optimal lockage co-scheduling problem. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2085–2095. [Google Scholar]
- Ji, B.; Yuan, X.; Yuan, Y.; Lei, X.; Fernando, T.; Lu, H.H. Exact and heuristic methods for optimizing lock-quay system in inland waterway. Eur. J. Oper. Res. 2019, 277, 740–755. [Google Scholar]
- Yuan, X.; Ji, B.; Yuan, Y.; Wu, X.; Zhang, X. Co-scheduling of lock and water–land transshipment for ships passing the dam. Appl. Soft Comput. 2016, 45, 150–162. [Google Scholar]
- Ackermann, T.; Loucks, D.P.; Schwanenberg, D.; Detering, M. Real-time modeling for navigation and hydropower in the River Mosel. J. Water Resour. Plan. Manag. ASCE 2000, 126, 298–303. [Google Scholar]
- Wang, J.; Zhang, Y. Short-Term optimal operation of hydropower reservoirs with unit commitment and navigation. J. Water Resour. Plan. Manag. ASCE 2012, 138, 3–12. [Google Scholar] [CrossRef]
- Ma, C. Fast optimal decision of short-term dispatch of Three Gorges and Gezhouba cascade hydropower stations with navigation demand considered. Syst. Eng. Theory Pract. 2013, 33, 1345–1350. (In Chinese) [Google Scholar]
- Liu, Y.; Qin, H.; Mo, L.; Wang, Y.; Chen, D.; Pang, S.; Yin, X. Hierarchical flood operation rules optimization using multi-objective cultured evolutionary algorithm based on decomposition. Water Resour. Manag. 2018, 33, 337–354. [Google Scholar] [CrossRef]
- Nithiarasu, P.; Zienkiewicz, O.C.; Sai, B.; Morgan, K.; Codina, R.; Vazquez, M. Shock capturing viscosities for the general fluid mechanics algorithm. Int. J. Numer. Methods Fluids 1998, 28, 1325–1353. [Google Scholar] [CrossRef]
- Casulli, V.; Walters, R.A. An unstructured grid, three-dimensional model based on the shallow water equations. Int. J. Numer. Methods Fluids 2000, 32, 331–348. [Google Scholar] [CrossRef]
- Erpicum, S.; Pirotton, M.; Archambeau, P.; Dewals, B.J. Two-dimensional depth-averaged finite volume model for unsteady turbulent flows. J. Hydraul. Res. 2014, 52, 148–150. [Google Scholar] [CrossRef]
- Kuiry, S.N.; Pramanik, K.; Sen, D. Finite volume model for shallow water equations with improved treatment of source terms. J. Hydraul. Eng. ASCE 2008, 134, 231–242. [Google Scholar] [CrossRef]
- Lu, W.L.; Chen, Z.Q. Study on navigational flow conditions of port areas and connection sections of navigation buildings. Southwest Highw. 2008. (In Chinese) [Google Scholar] [CrossRef]
- Feng, Y.; Zhou, J.; Mo, L.; Yuan, Z.; Zhang, P.; Wu, J.; Wang, C.; Wang, Y. Long-term hydropower generation of cascade reservoirs under future climate changes in Jinsha River in southwest China. Water 2018, 10, 235. [Google Scholar] [CrossRef]
- Wen, X.; Zhou, J.; He, Z.; Wang, C. Long-term scheduling of large-scale cascade hydropower stations using improved differential evolution algorithm. Water 2018, 10, 383. [Google Scholar] [CrossRef]
- Chang, L.; Chang, F. Multi-objective evolutionary algorithm for operating parallel reservoir system. J. Hydrol. 2009, 377, 12–20. [Google Scholar] [CrossRef]
- Zhao, T.T.G.; Zhao, J.S. Improved multiple-objective dynamic programming model for reservoir operation optimization. J. Hydroinformat. 2014, 16, 1142–1157. [Google Scholar] [CrossRef]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the strength pareto evolutionary algorithm. ETH Zur. Res. Collect. 2001. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhou, J.; Lu, P.; Li, Y.; Wang, C.; Yuan, L.; Mo, L. Short-term hydro-thermal-wind complementary scheduling considering uncertainty of wind power using an enhanced multi-objective bee colony optimization algorithm. Energy Convers. Manag. 2016, 123, 116–129. [Google Scholar] [CrossRef]
- Lai, X.; Li, C.; Zhang, N.; Zhou, J. A multi-objective artificial sheep algorithm. Neural Comput. Appl. 2018. [Google Scholar] [CrossRef]
- Wang, W.; Li, C.; Liao, X.; Qin, H. Study on unit commitment problem considering pumped storage and renewable energy via a novel binary artificial sheep algorithm. Appl. Energy 2017, 187, 612–626. [Google Scholar] [CrossRef]
- Li, C.; Wang, W.; Chen, D. Multi-objective complementary scheduling of hydro-thermal-RE power system via a multi-objective hybrid grey wolf optimizer. Energy 2019, 171, 241–255. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).