Small-Scale Rainfall Variability Impacts Analyzed by Fully-Distributed Model Using C-Band and X-Band Radar Data
Abstract
1. Introduction
2. Materials and Methods
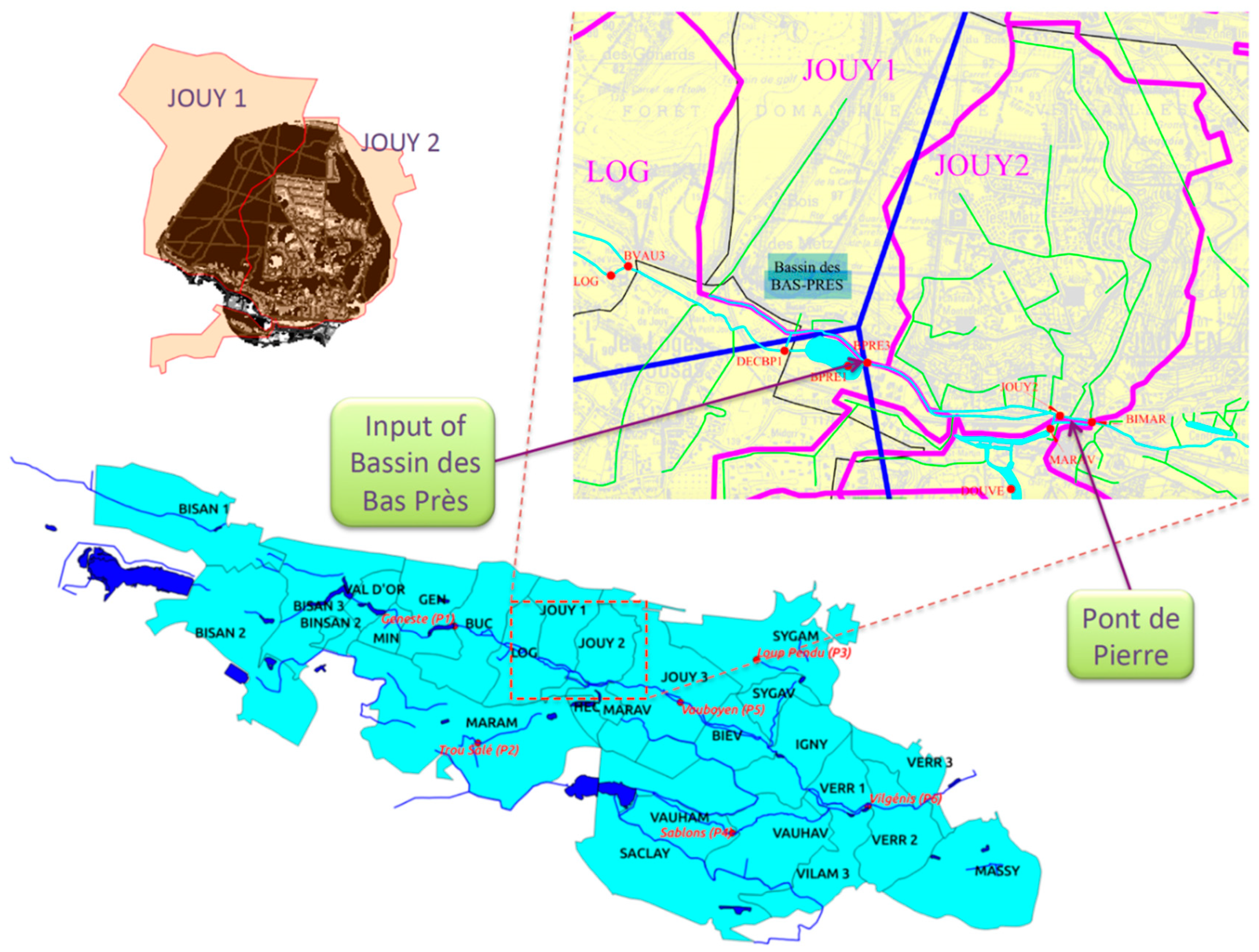
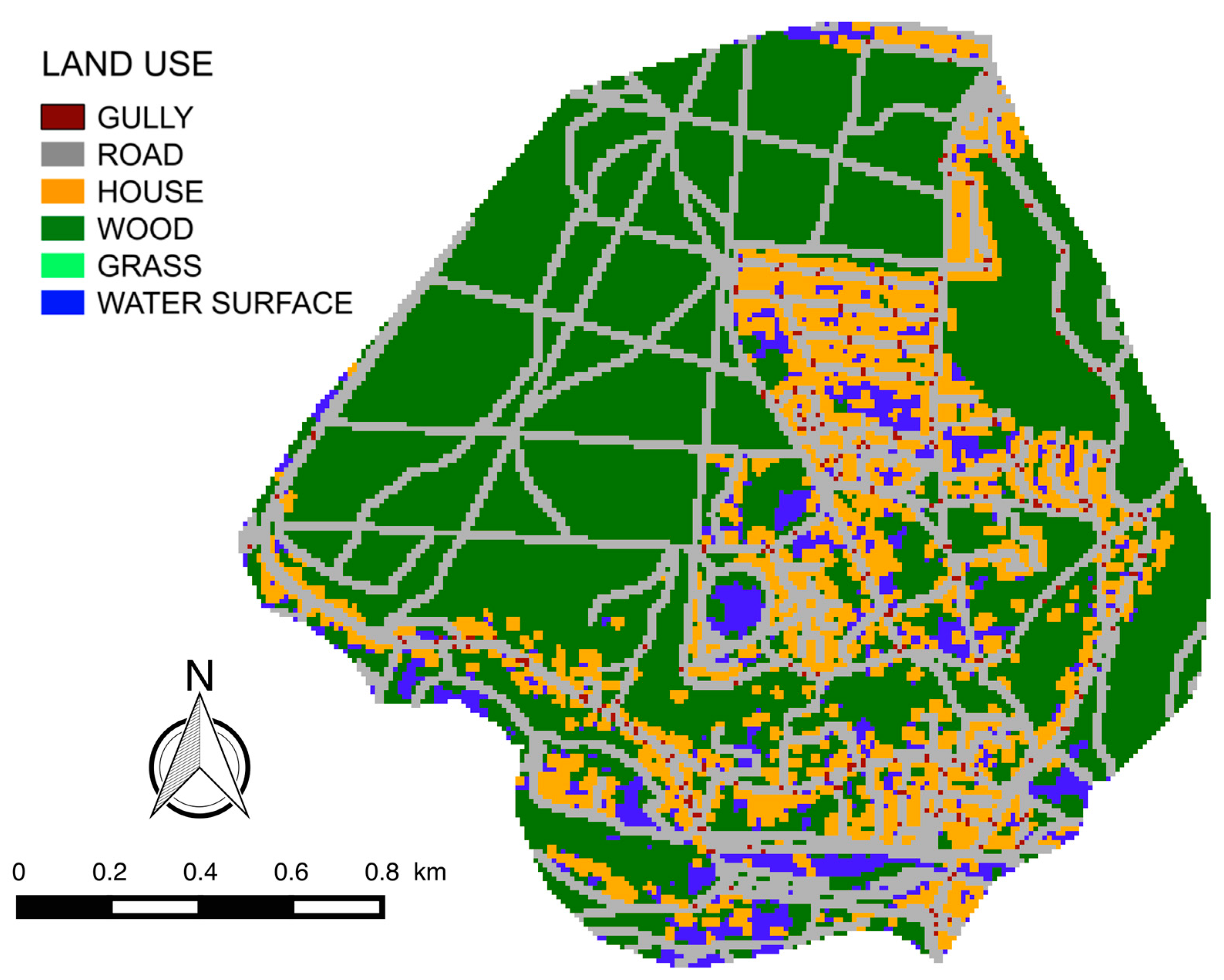
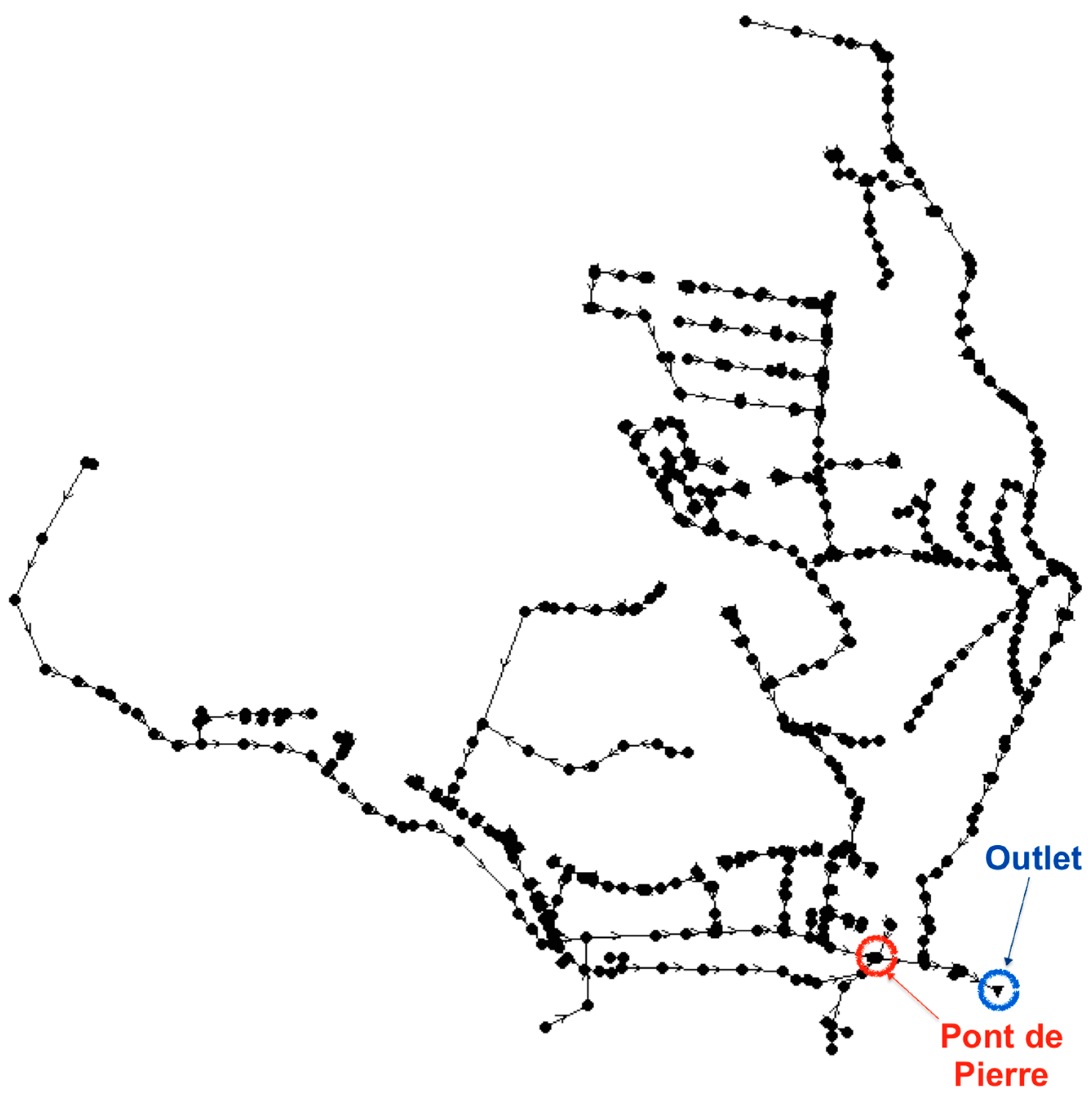
2.1. Case Study
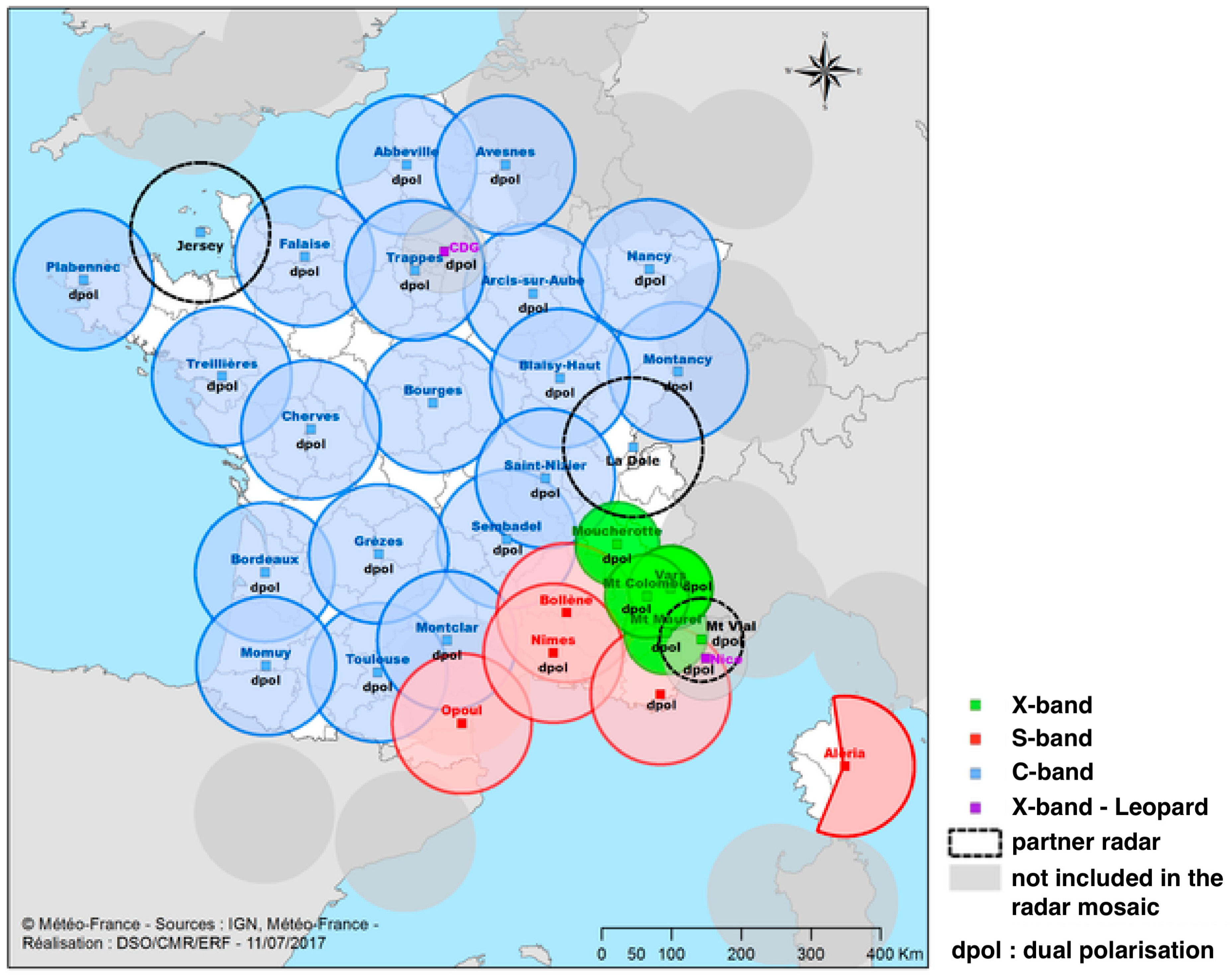
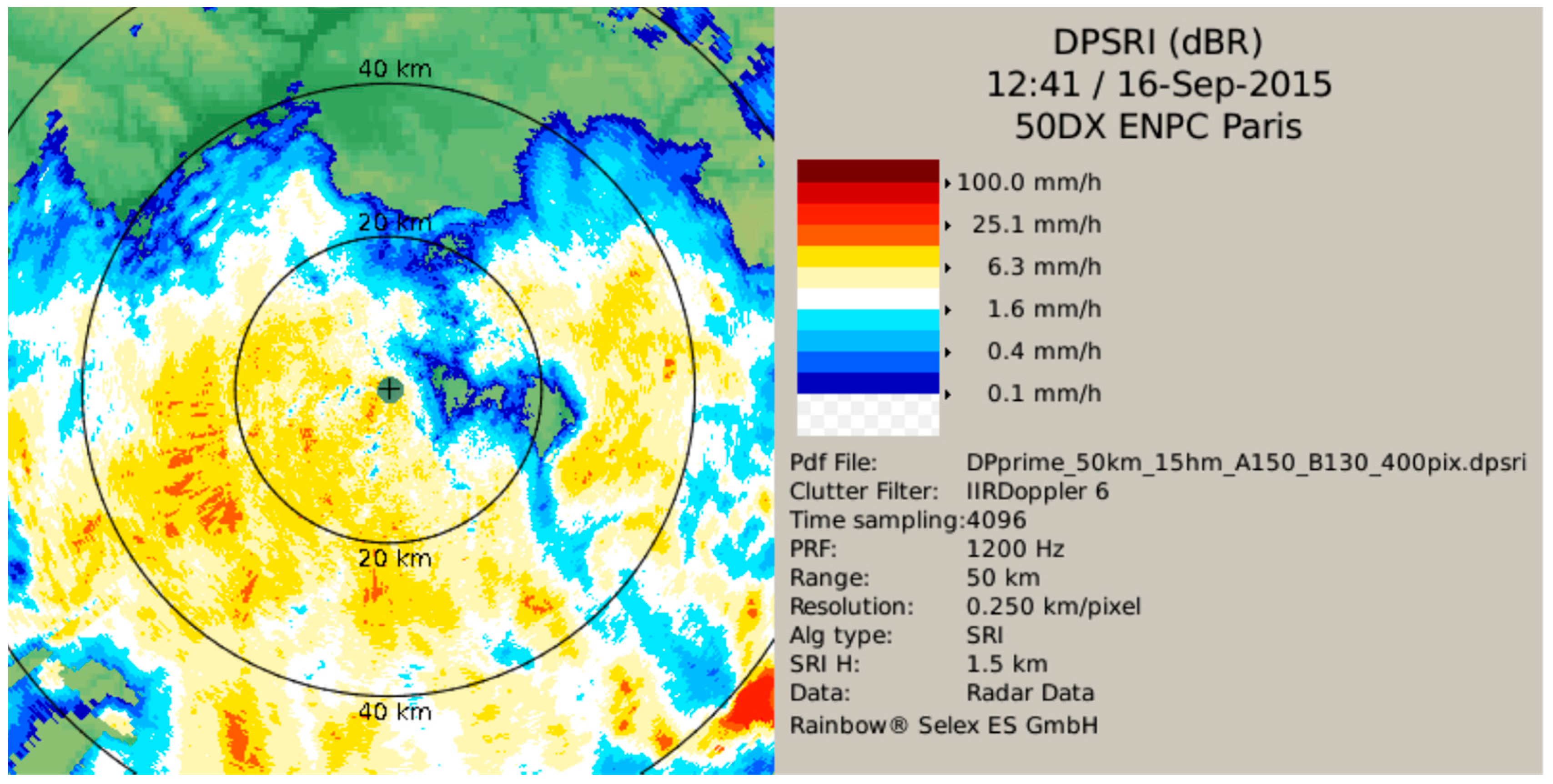
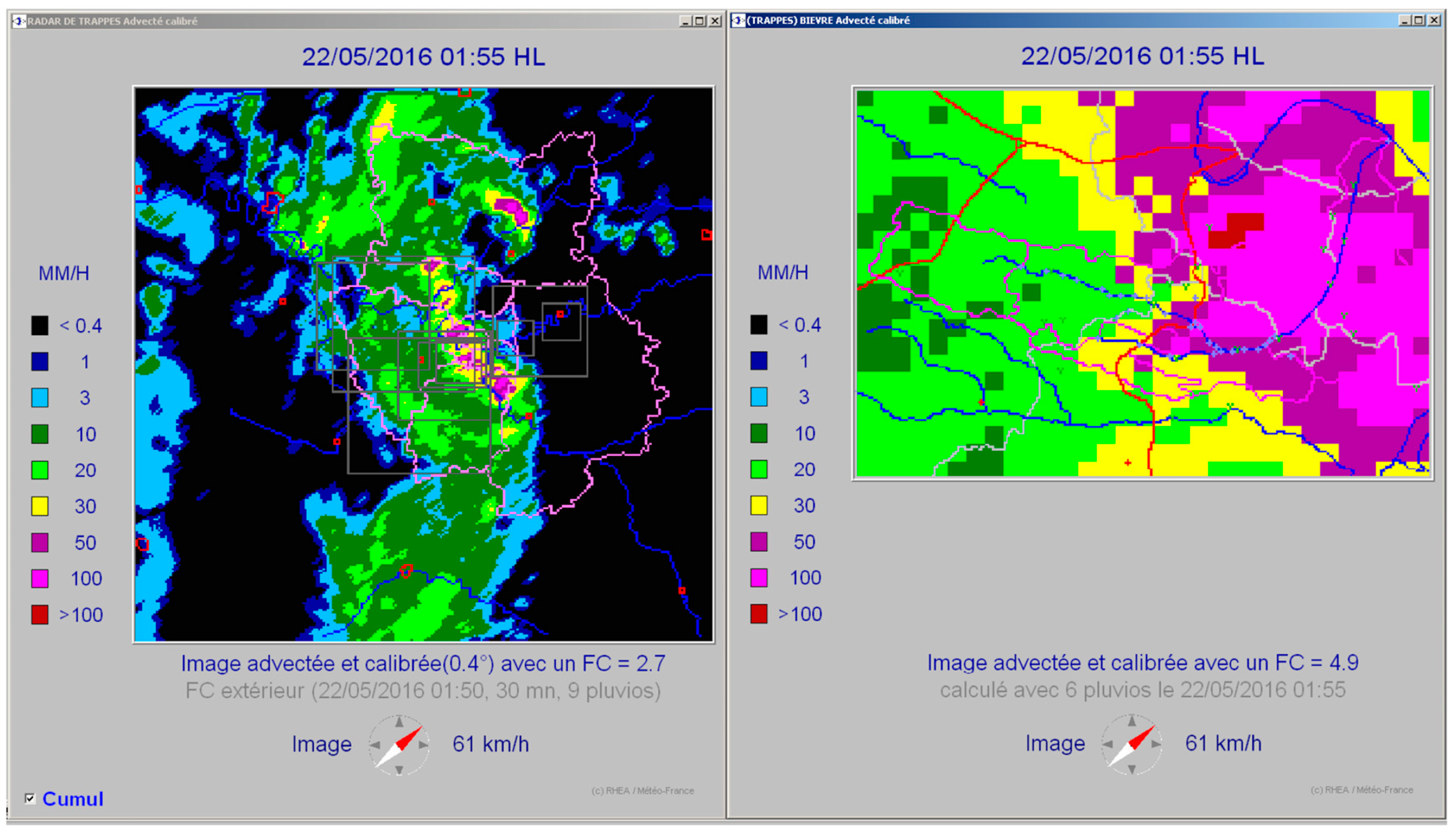
2.2. Storm Events and Rainfall Data
2.3. Multifractal Analysis
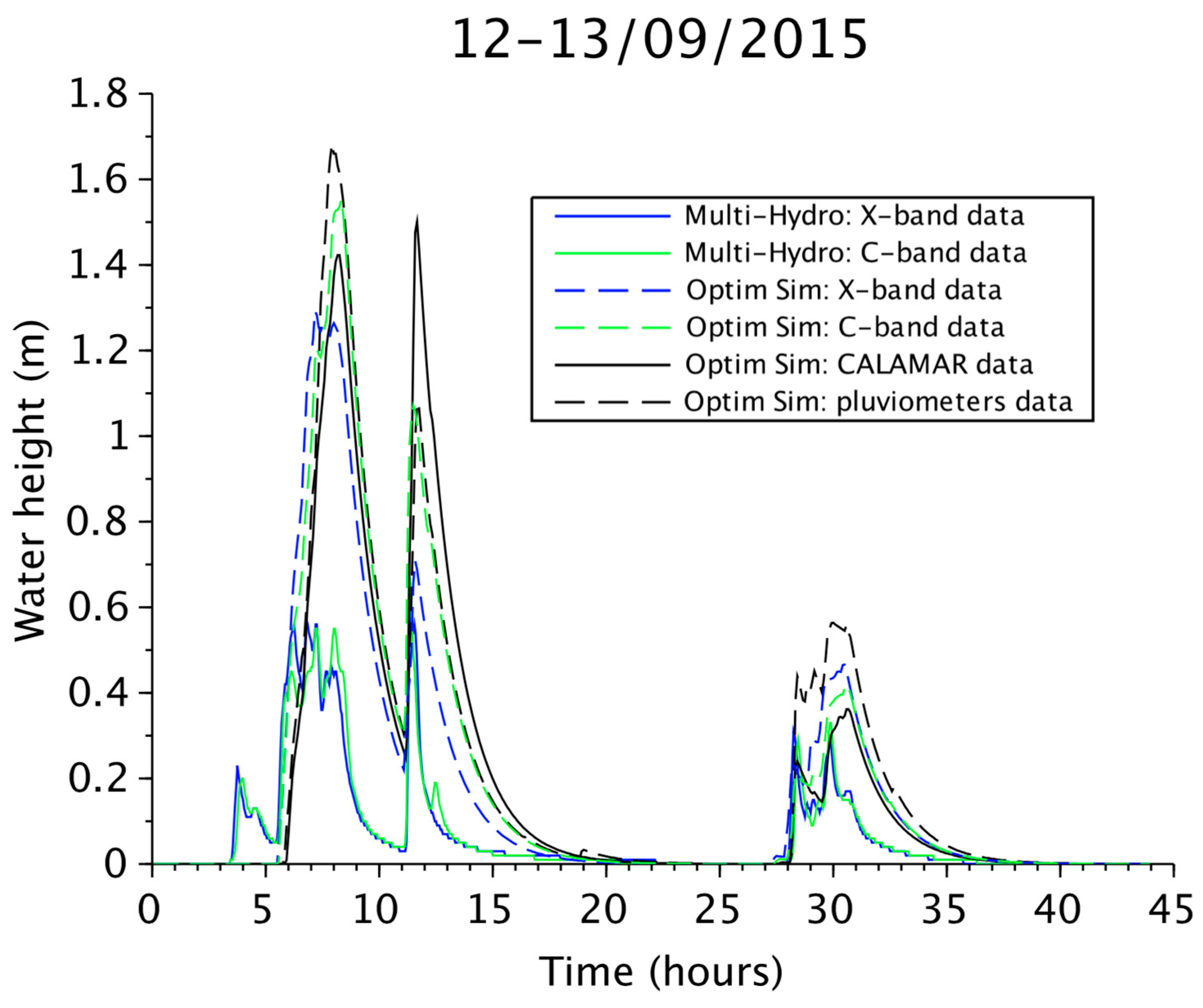
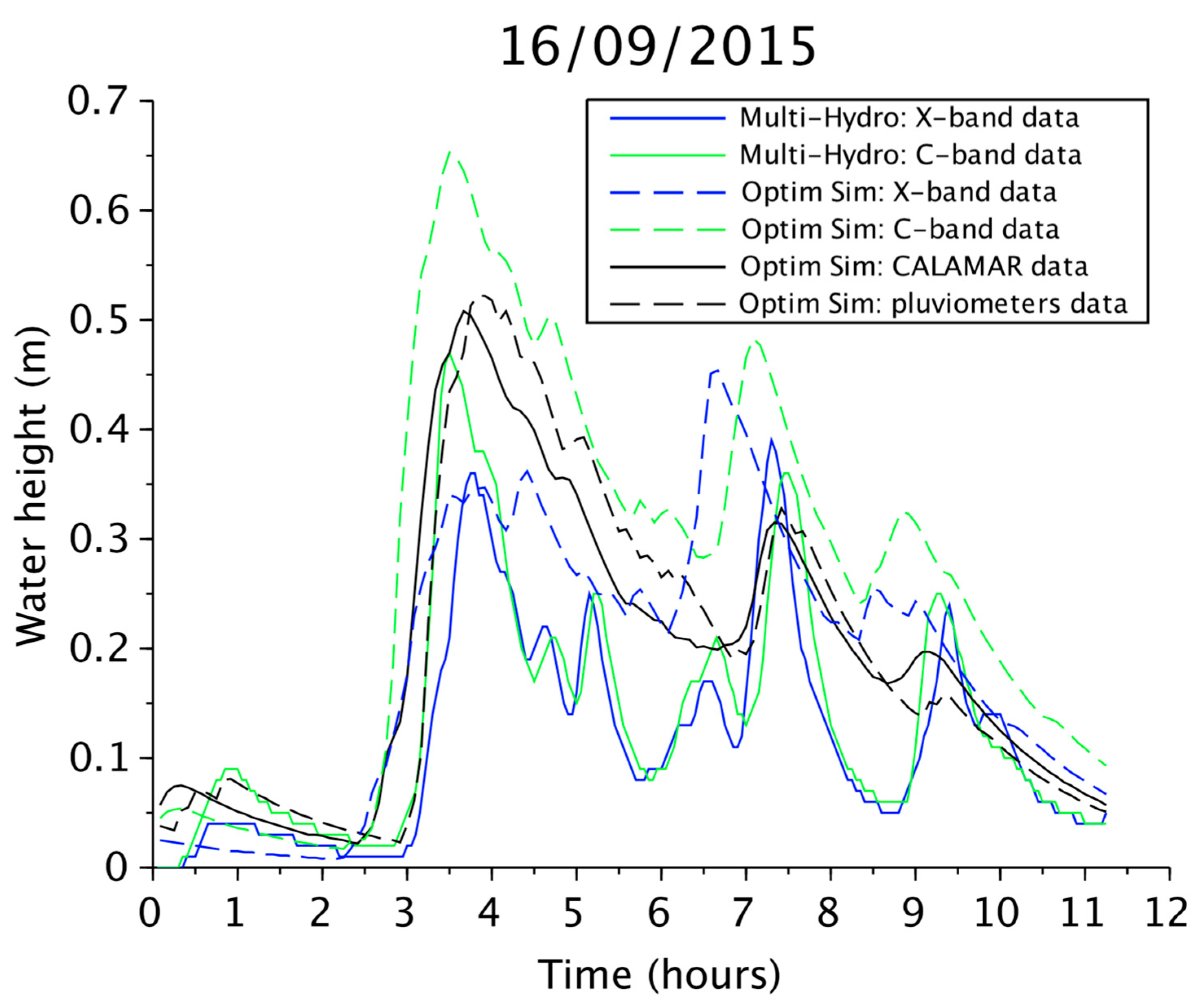
3. Results
3.1. Hydrological Modelling
3.1.1. Multi-Hydro Description and Implementation
3.1.2. Optim Sim/InfoWorks and the Bièvre Catchment
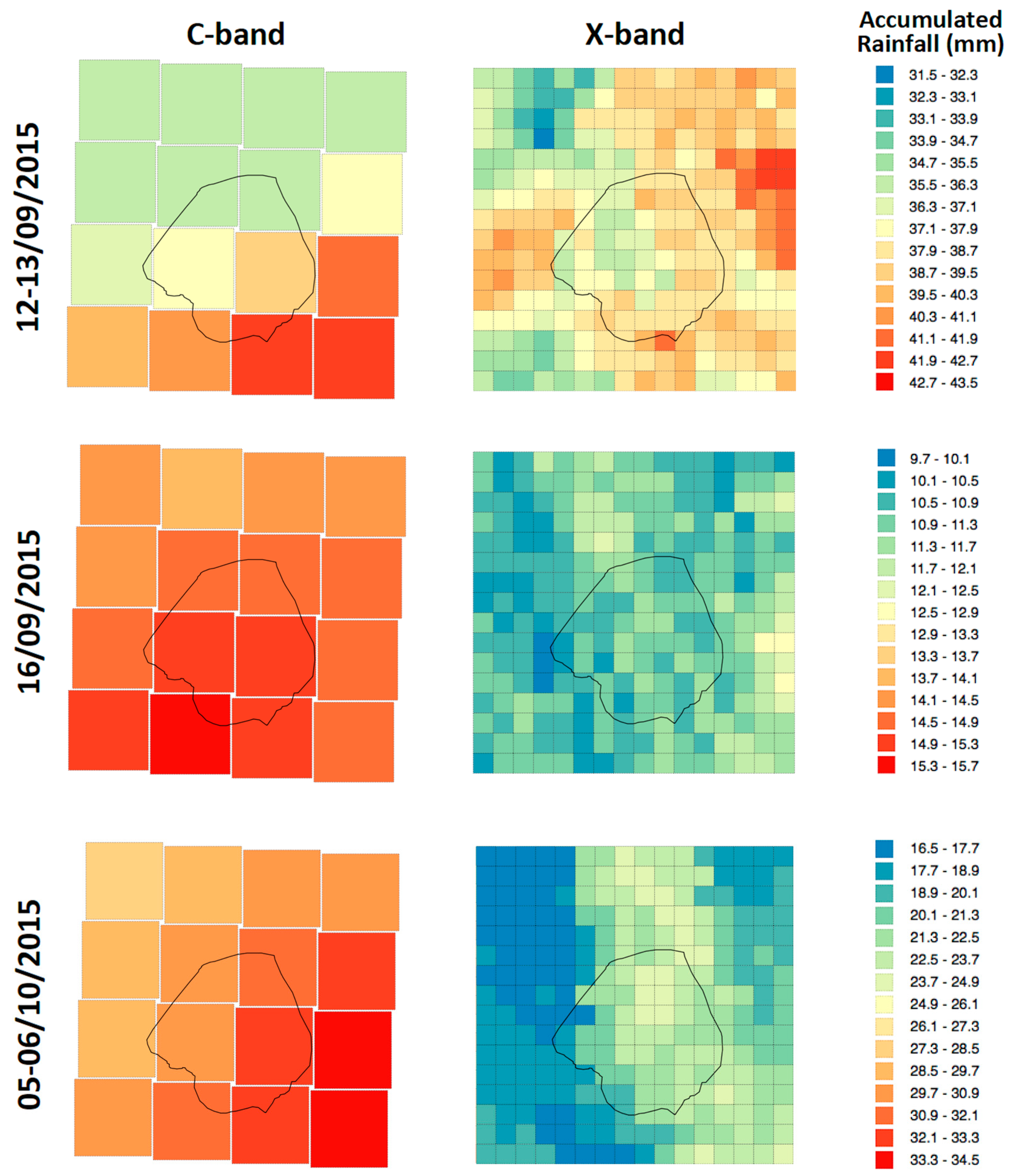
3.2. Hydrological Simulations
4. Discussions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- United Nations, Department of Economic and Social Affairs. Population Division, World Urbanization Prospects: The 2014 Revision, CD-ROM Edition; United Nations, Department of Economic and Social Affairs: New York, NY, USA, 2014. [Google Scholar]
- Sustainable Development Goals. Available online: https://sustainabledevelopment.un.org/?menu=1300 (accessed on 19 May 2016).
- WHO Library Cataloguing-in-Publication Data. Global Report on Urban Health: Equitable, Healthier Cities for Sustainable Development; WHO: Geneva, Switzerland; UN-Habitat: Nairobi, Kenya, 2016; ISBN 978-92-4-156527-1. [Google Scholar]
- IPCC. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- Burns, M.; Fletcher, T.D.; Hatt, B.E.; Ladson, A.; Walsh, C.J. Hydrologic shortcomings of conventional urban stormwater management and opportunities for reform. Landsc. Urban Plan. 2012, 105, 230–240. [Google Scholar] [CrossRef]
- Furusho, C.; Andrieu, H.; Chancibault, K. Analysis of the hydrological behaviour of an urbanizing basin. Hydrol. Process. 2014, 28, 1809–1819. [Google Scholar] [CrossRef]
- Schmitt, T.G.; Thomas, M.; Ettrich, N. Analysis and modeling of flooding in urban drainage systems. J. Hydrol. 2004, 299, 300–311. [Google Scholar] [CrossRef]
- Huang, H.J.; Cheng, S.J.; Wen, J.C. Effect of growing watershed imperviousness on hydrograph parameters and peak discharge. Hydrol. Process. 2008, 22, 2075–2085. [Google Scholar] [CrossRef]
- Chen, J.; Arleen, A.H.; Lensyl, D.U. A GIS-based model for flood inundation. J. Hydrol. 2009, 373, 184–192. [Google Scholar] [CrossRef]
- Olang, L.O.; Furst, J. Effects of land cover change on flood peak discharges and runoff volumes: Model estimates for the Nyando River Basin, Kenya. Hydrol. Process. 2010, 25, 80–89. [Google Scholar] [CrossRef]
- Salvadore, E.; Bronders, J.; Batelaan, O. Hydrological modelling of urbanized catchemnts: A review and future directions. J. Hydrol. 2015, 529, 62–81. [Google Scholar] [CrossRef]
- Braud, I.; Fletcher, T.D.; Andrieu, H. Hydrology of peri-urban catchments: Processes and modelling. J. Hydrol. 2013, 485, 1–4. [Google Scholar] [CrossRef]
- Fletcher, T.D.; Andrieu, H.; Hamel, P. Understanding, management and modelling of urban hydrology and its consequences for receiving waters; a state of the art. Adv. Water Resour. 2013, 51, 261–279. [Google Scholar] [CrossRef]
- Niemczynowicz, J. Urban hydrology and water management – present and future challenges. Urban Water 1999, 1, 1–14. [Google Scholar] [CrossRef]
- Price, R.K.; Vojinović, Z. Urban Hydroinformatics: Data, Models and Decision support for Integrated Urban Water Management; IWA Publishing: London, UK, 2011. [Google Scholar]
- Schirmer, M.; Leschik, S.; Musolff, A. Current research in urban hydrogeology—A review. Adv. Water Resour. 2012, 51, 280–291. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.-P.; Gires, A.; Pina, R.; Reinoso-Rondinel, R.; Bruni, G.; Ichiba, A.; Gaitan, S.; Cristiano, E.; van Assel, J.; et al. Impact of spatial and temporal resolution of rainfall inputs on urban hydrodynamic modelling outputs: A multi-catchment investigation. J. Hydrol. 2015, 531, 389–407. [Google Scholar] [CrossRef]
- Fabry, F.; Bellon, A.; Duncan, M.R.; Austin, G.L. High resolution rainfall measurements by radar for very small basins: The sampling problem reexamined. J. Hydrol. 1994, 161, 415–428. [Google Scholar] [CrossRef]
- Berne, A.; Delrieu, G.; Creutin, J.-D.; Obled, C. Temporal and spatial resolution of rainfall measurements required for urban hydrology. J. Hydrol. 2004, 299, 166–179. [Google Scholar] [CrossRef]
- Bringi, V.N.; Chandrasekar, V. Polarimetric Doppler Weather Radar: Principles and Applications; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Illingworth, A.J.; Blackman, T.M. The need to represent raindrop size spectra as normalized gamma distributions for the interpretation of polarization radar observations. J. Appl. Meteorol. 2002, 41, 286–297. [Google Scholar] [CrossRef]
- Figueras i Ventura, J.; Boumahmoud, A.-A.; Fradon, B.; Dupuy, P.; Tabary, P. Long-term monitoring of French polarimetric radar data quality and evaluation of several polarimetric quantitative precipitation estimators in ideal conditions for operational implementation at C-band. Q. J. R. Meteorol. Soc. 2012, 138, 2212–2228. [Google Scholar] [CrossRef]
- Pina, R.; Ochoa-Rodríguez, S.; Simões, N.; Mijic, A.; Sa Marques, A.; Maksimovič, C. Semi-distributed or fully distributed rainfall-runoff models for urban pluvial flood modelling? Water 2016, 8, 58. [Google Scholar] [CrossRef]
- Ichiba, A. X-Band Radar Data and Predictive Management in Urban Hydrology. Ph.D. Thesis, Earth Sciences, Université Paris-Est, Champs-sur-Marne, France, 2016. [Google Scholar]
- Gires, A.; Abbes, J.-B.; Paz, I.S.R.; Tchiguirinskaia, I.; Schertzer, D. Multifractal characterisation of simulated surface flow: A case study with Multi-Hydro in Jouy-en-Josas, France. J. Hydrol. 2018, 558, 482–495. [Google Scholar] [CrossRef]
- El-Tabach, E.; Tchiguirinskaia, I.; Mahmood, O.; Schertzer, D. Multi-Hydro: A Spatially Distributed Numerical Model to Assess and Manage Runoff Processes in Peri-Urban Watersheds. In Proceedings of the Road Map Towards a Flood Resilient Urban Environment, Paris, France, 26–27 November 2009; Pascheet, E., Evelpidou, N., Zevenbergen, C., Ashley, R., Garvin, S., Eds.; Hamburger Wasserbau-Schriftien: Hamburg, Germany, 2009. [Google Scholar]
- Giangola-Murzyn, A. Modélisation et Paramétrisation Hydrologique de la ville, Résilience aux Inondations. Ph.D. Thesis, Earth Sciences, Université Paris-Est, Champs-sur-Marne, France, 2013. [Google Scholar]
- Schertzer, D.; Lovejoy, S. Physical modelling and analysis of rain and clouds by anisotropic scaling multiplicative processes. J. Geophys. Res. 1987, D8, 9693–9714. [Google Scholar] [CrossRef]
- Mellot, P. Paris inondé: Photographies JANVIER 1910; Éditions de Lodi: Midi Pyrénées, France, 2003; 208p. [Google Scholar]
- RainGain Final Conference. Available online: http://www.raingain.eu/en/8-9-june-2015-raingain-final-conference-paris (accessed on 20 May 2016).
- Paz, I.; Willinger, B.; Gires, A.; Ichiba, A.; Monier, L.; Zobrist, C.; Tisserand, B.; Tchiguirinskaia, I.; Schertzer, D. Multifractal Comparison of Reflectivity and Polarimetric Rainfall Data from C-and X-Band Radars and Respective Hydrological Responses of a Complex Catchment Model. Water 2018, 10, 269. [Google Scholar] [CrossRef]
- Parent du Châtelet, J. ARAMIS, le réseau Français de radars pour la surveillance des précipitations. La Météorologie 2003, 40, 44–52. [Google Scholar] [CrossRef][Green Version]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Tabary, P.; Boumahmoud, A.-A.; Andrieu, H.; Thompson, R.J.; Illingworth, A.J.; Le Bouar, E.; Testud, J. Evaluation of two “integrated” polarimetric Quantitative Precipitation Estimation (QPE) algorithms at C-band. J. Hydrol. 2011, 405, 248–260. [Google Scholar] [CrossRef]
- Figueras i Ventura, J.; Tabary, P. The new French operational polarimetric radar rainfall rate product. J. Appl. Meteorol. Climatol. 2013, 52, 1817–1835. [Google Scholar] [CrossRef]
- Selex. Selex METEOR Manual; Selex: Roman, Italy, 2015. [Google Scholar]
- Keefe, P.; Stevens, P. CALAMAR and NEXRAD Dramatically Increase Accuracy of Urban Hydrology. In Proceedings of the WEF Annual Conference, Anaheim, CA, USA, 3–7 October 1993. [Google Scholar]
- Stevens, P.; Lopez, M.; Jacquet, G. Evaluation of Gauge Adjusted Radar for Rainfall Measurement in RDII Programs. Glob. Solut. Urban Drain. 2002, 1–14. [Google Scholar] [CrossRef]
- RHEA. Available online: http://www.rhea.tm.fr (accessed on 3 June 2016).
- Ladoy, P.; Schmitt, F.; Schertzer, D.; Lovejoy, S. Variabilité temporelle multifractale des observations pluviométriques à Nîmes. C. R. Acad. Sci. II 1993, 317, 775–782. [Google Scholar]
- Tessier, Y.; Lovejoy, S.; Schertzer, D. Universal multifractals in rain and clouds: Theory and observations. J. Appl. Meteorol. 1993, 32, 223–250. [Google Scholar] [CrossRef]
- Tessier, Y.; Lovejoy, S.; Hubert, P.; Schertzer, D.; Pecknold, S. Multifractal analysis and modelling of rainfall and river flows and scaling, causal transfer functions. J. Geophys. Res. 1996, 101, 26427–26440. [Google Scholar] [CrossRef]
- Olsson, J.; Niemczynowicz, J. Multifractal analysis of daily spatial rainfall distributions. J. Hydrol. 1996, 187, 29–43. [Google Scholar] [CrossRef]
- de Lima, M.I.P.; Grasman, J. Multifractal analysis of 15-min and daily rainfall from a semi-arid region in Portugal. J. Hydrol. 1999, 220, 1–11. [Google Scholar] [CrossRef]
- Deidda, R. Rainfall downscaling in a space-time multifractal framework. Water Resour. Res. 2000, 36, 1779–1794. [Google Scholar] [CrossRef]
- Veneziano, D.; Langousis, A.; Furcolo, P. Multifractality and rainfall extremes: A review. Water Resour. Res. 2006, 42, W06D15. [Google Scholar] [CrossRef]
- García-Marín, A.P.; Jiménez-Hornero, F.J.; Ayuso-Muñoz, J.L. Universal multifractal description of an hourly rainfall time series from a location in southern Spain. Atmósfera 2008, 21, 347–355. [Google Scholar]
- Serinaldi, F. Multifractality, imperfect scaling and hydrological properties of rainfall time series simulated by continuous universal multifractal and discrete random cascade models. Nonlin. Process. Geophys. 2010, 17, 697–714. [Google Scholar] [CrossRef]
- Gires, A.; Schertzer, D.; Tchiguirinskaia, I.; Lovejoy, S.; Onof, C.; Maksimovic, C.; Simoes, N. Impact of small scale rainfall uncertainty on urban discharge forecasts. In Proceedings of the Weather Radar and Hydrology, Exeter, UK, 27 April 2011; Moore, J., Cole, S., Illingworth, A., Eds.; IAHS Publ.: Exeter, UK, 2011; pp. 351, 400–406. [Google Scholar]
- Tchiguirinskaia, I.; Schertzer, D.; Hoang, C.T.; Lovejoy, S. Multifractal study of three storms with different dynamics over the Paris region. In Proceedings of the Weather Radar and Hydrology, Exeter, UK, 27 April 2011; Moore, J., Cole, S., Illingworth, A., Eds.; IAHS Publ.: Exeter, UK, 2011; pp. 351, 421–426. [Google Scholar]
- Rodríguez, R.; Casas, M.; Redaño, A. Multifractal analysis of the rainfall time distribution on the metropolitan area of Barcelona (Spain). Meteorol. Atmos. Phys. 2013, 121, 181–187. [Google Scholar] [CrossRef]
- Hoang, C.-T.; Tchiguirinskaia, I.; Schertzer, D.; Lovejoy, S. Caractéristiques multifractales et extrêmes de la précipitation à haute resolution, application à la détection du changement climatique. Revue des Sciences de l’Eau—J. Water Sci. 2014, 27, 205–216. [Google Scholar] [CrossRef][Green Version]
- Paz, I.S.R. Quantifying the Rain Heterogeneity by X-Band Radar Measurements for Improving Flood Forecasting. Ph.D. Thesis, Université Paris-Est, Champs-sur-Marne, France, 2018. [Google Scholar]
- Parisi, G.; Frisch, U. A multifractal model of intermittency. In Turbulence and Predictability in Geophysical Fluid Dynamics and Climate Dynamics; Ghil, M., Benzi, R., Parisi, G., Eds.; North-Holland: Amsterdam, The Netherlands, 1985; pp. 84–88. [Google Scholar]
- Lavallée, D.; Lovejoy, S.; Schertzer, D.; Ladoy, P. Nonlinear variability and landscape topography: Analysis and simulation. In Fractals in Geography; De Cola, L., Lam, N., Eds.; Prentice-Hall: Upper Saddle River, NJ, USA, 1993; pp. 171–205. [Google Scholar]
- Alves de Souza, B.; da Silva Rocha Paz, I.; Ichiba, A.; Willinger, B.; Gires, A.; Amorim, J.C.C.; de Miranda Reis, M.; Tisserand, B.; Tchiguirinskaia, I.; Schertzer, D. Multi-hydro hydrological modelling of a complex peri-urban catchment with storage basins comparing C-band and X-band radar rainfall data. Hydrol. Sci. J. 2018, 63, 1619–1635. [Google Scholar] [CrossRef]
- Velleux, M.L.; England, J.F.; Julien, P.Y. TREX Watershed Modelling Framework User’s Manual: Model Theory and Description; Department of Civil Engineering, Colorado State University: Fort Collins, CO, USA, 2011; 106p. [Google Scholar]
- Lappala, E.G.; Healy, R.W.; Weeks, E.P. Documentation of Computer Program VS2D to Solve the Equations of Fluid Flow in Variably Saturated Porous Media; Water-Resources Investigations Report 83-4099; U.S. Geological Survey: Reston, VA, USA, 1987; 184p.
- Rossman, L.A. Storm Water Management Model, User’s Manual, Version 5.0; EPA/600/R-05/040; U.S. Environmental Protection Agency: Washington, DC, USA, 2010.
- Tabary, P. The new French operational radar rainfall product. Part I: Methodology. Weather Forecast. 2007, 22, 393–408. [Google Scholar] [CrossRef]



| Events | Radar | Space Resolution | Time Resolution | Space Grid Dimension | Time Duration | Time Steps |
|---|---|---|---|---|---|---|
| 12/13-09-2015 | C-band | 1 km | 5 min | 64 × 64 | 44 h | 528 |
| 12/13-09-2015 | X-band | 250 m | 3.41 min | 256 × 256 | 44 h | 773 |
| 16-09-2015 | C-band | 1 km | 5 min | 64 × 64 | 11.3 h | 136 |
| 16-09-2015 | X-band | 250 m | 3.41 min | 256 × 256 | 11.3 h | 199 |
| 5/6-10-2015 | C-band | 1 km | 5 min | 64 × 64 | 31 h | 372 |
| 5/6-10-2015 | X-band | 250 m | 3.41 min | 256 × 256 | 31 h | 545 |
| Events | Radar | α | C1 |
|---|---|---|---|
| 12/13-09-2015 | C-band | 1.249 | 0.217 |
| 12/13-09-2015 | X-band | 1.536 | 0.184 |
| 16-09-2015 | C-band | 1.022 | 0.116 |
| 16-09-2015 | X-band | 1.431 | 0.108 |
| 5/6-10-2015 | C-band | 1.577 | 0.152 |
| 5/6-10-2015 | X-band | 1.787 | 0.153 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paz, I.; Willinger, B.; Gires, A.; Alves de Souza, B.; Monier, L.; Cardinal, H.; Tisserand, B.; Tchiguirinskaia, I.; Schertzer, D. Small-Scale Rainfall Variability Impacts Analyzed by Fully-Distributed Model Using C-Band and X-Band Radar Data. Water 2019, 11, 1273. https://doi.org/10.3390/w11061273
Paz I, Willinger B, Gires A, Alves de Souza B, Monier L, Cardinal H, Tisserand B, Tchiguirinskaia I, Schertzer D. Small-Scale Rainfall Variability Impacts Analyzed by Fully-Distributed Model Using C-Band and X-Band Radar Data. Water. 2019; 11(6):1273. https://doi.org/10.3390/w11061273
Chicago/Turabian StylePaz, Igor, Bernard Willinger, Auguste Gires, Bianca Alves de Souza, Laurent Monier, Hervé Cardinal, Bruno Tisserand, Ioulia Tchiguirinskaia, and Daniel Schertzer. 2019. "Small-Scale Rainfall Variability Impacts Analyzed by Fully-Distributed Model Using C-Band and X-Band Radar Data" Water 11, no. 6: 1273. https://doi.org/10.3390/w11061273
APA StylePaz, I., Willinger, B., Gires, A., Alves de Souza, B., Monier, L., Cardinal, H., Tisserand, B., Tchiguirinskaia, I., & Schertzer, D. (2019). Small-Scale Rainfall Variability Impacts Analyzed by Fully-Distributed Model Using C-Band and X-Band Radar Data. Water, 11(6), 1273. https://doi.org/10.3390/w11061273






