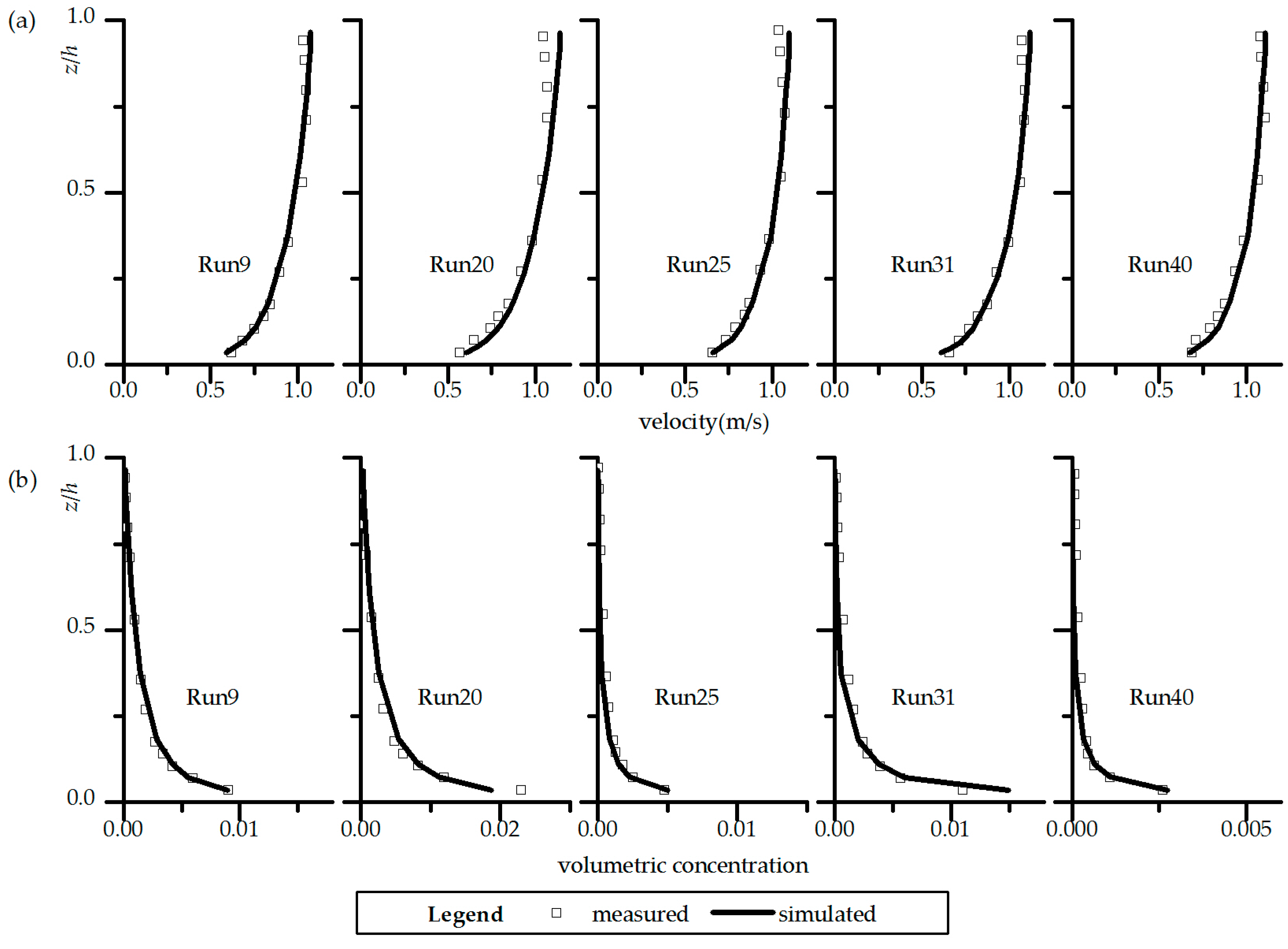
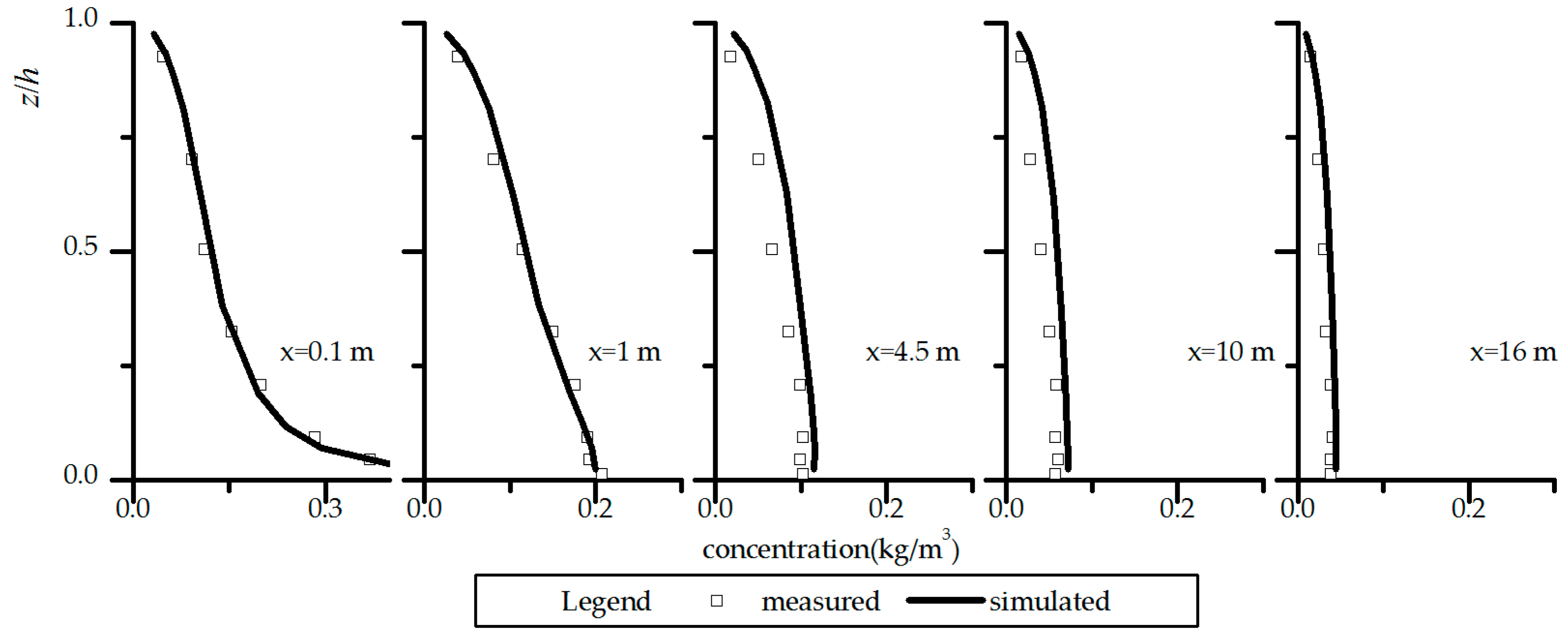
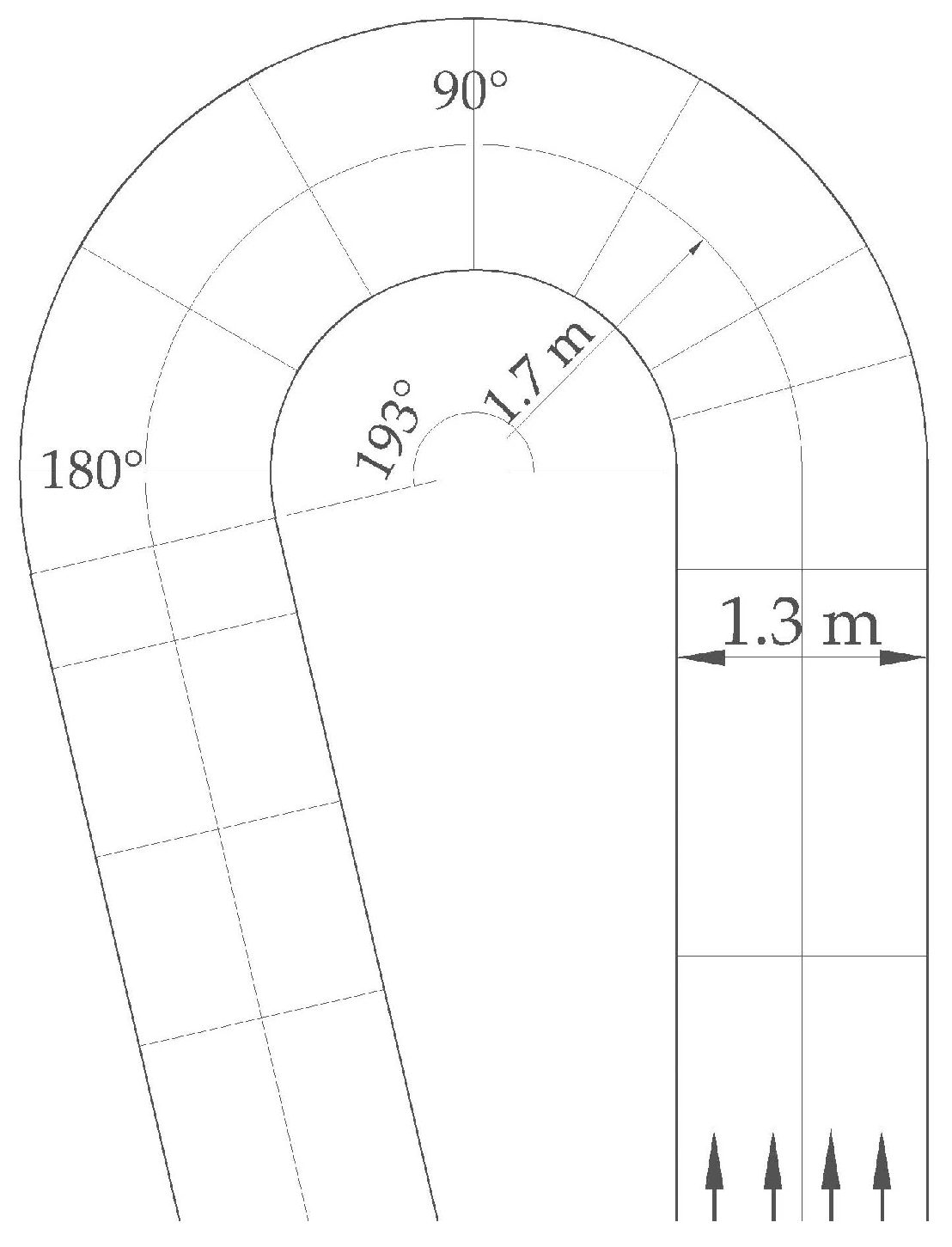
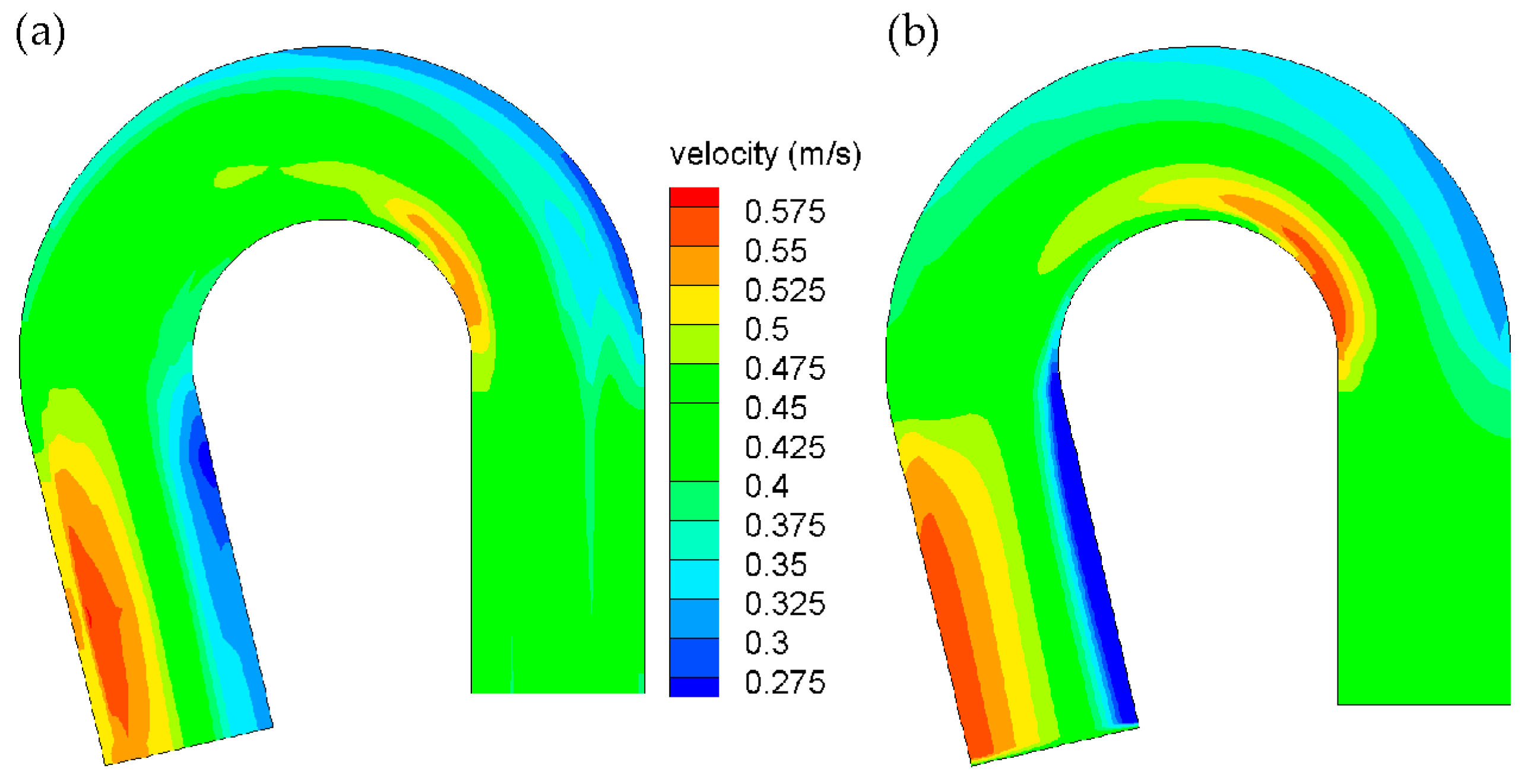
1. Introduction
In fluvial process studies, suspension has always been known to have a fundamental role in defining the preferential bend migration, since the stratification brought by suspended load modifies the turbulence, flow structure and sediment entrainment. Early works relate sediment stratification effect on flow velocity to concentration profiles. Vanoni [
1] and Einsterin and Chien [
2] classically documented the sediment stratification effect on the velocity profile in turbulent open channel flows. Vanoni showed that the von Karman constant κ reduces at high sediment concentration. This was based on the hypothesis that the suspended sediment dampens turbulence and increases velocity gradient near the wall. Later, many laboratory investigations [
3,
4,
5] confirmed this finding. Castro-Orgaz et al. [
6] analytically indicated that the reduction of κ in the high concentration condition is a physically coherent approximation. Suspension stratification effect modulates the turbulence intensity which in turn reduces the vertical sediment diffusivity. A few attempts referred the suspension effect to heat or salinity induced stratification effect [
7]. By analogy with thermally stratified boundary layers, the Flux Richardson number or the gradient Richardson number for sediment-laden flow is defined as a measure of stratification effect or turbulence damping [
8,
9] and the Monin-Obukhov length scale is introduced to establish damping functions for the eddy viscosity [
10]. Herrmann and Madsen [
11] obtained the optimal parameters for damping eddy diffusivity from observations. Nezu and Azuma [
12] presented simultaneous measurements of both sediment and fluid in dilute flows. They pointed out that flow turbulence intensity is slightly dampened far from the bed while it rises in the near-wall region owing to the velocity difference between fluid and sediment. The ratio of concentration to slope is a primary indicator of stratification effect (which is greater in low slope rivers) according to Wright and Parker [
13]. For high suspension concentration, Lamb et al. [
9] experimentally observed that the Richardson number critical value of ~1/4 for completely damped turbulence [
7] is not applicable where the major source of suspension is transported turbulence; and Muste et al. [
14] provided the priority of two-phase over traditional mixed-flow perspective on sediment laden flows from image velocimetry experiments.
Although sediment laden flows have been widely studied by using various numerical models, most studies concern low suspension concentration using the advection-diffusion equation. The fundamental assumptions of these models limit their applicability. The advection-diffusion theory regulates the upward transfer of suspension due to turbulent diffusion with the downward settlement. Winterverp [
15,
16] numerically explained the sediment stratification effect by a buoyancy destruction term in the standard k-ε turbulence model at low concentration. Later, concerning hindered settling, van Maren et al. [
17] extended this explanation to hyperconcentrated flows. Byun and Wang [
18] coupled the sediment transport model and the 3D tidal hydrodynamics model to examine the reduction of turbulence and bottom shear stress due to the sediment stratification effect. Amoudry and Souza [
19] performed 3D simulations and showed that sediment stratification effect leads to non-negligible modifications for bed evolution. Cantero et al. [
20] exploited Direct Numerical Simulation (DNS)s of sediment laden flows under the dilute flow assumption and Boussinesq approximation. For higher settling velocity, the vertical Reynolds fluxes could be completely suppressed locally and relaminarization occurs [
20,
21]. For the condition of complete turbulence suppression, the critical product of the Richardson number and sediment settling velocity has a logarithmic dependence on the Reynolds number [
22]. Dutta et al. [
23] further investigated the sediment stratification effect on the vertical sediment diffusivity by DNSs. Dallali and Armenio [
24] used Large Eddy Simulation (LES) to investigate suspension transport, supporting that the buoyancy effect on flow momentum is not neglectable for small particles. Alternatively, two-phase flow theory addresses water and sediment phases separately [
25]. Recently, several models based the two-phase flow theory have been developed to include small scale mechanics [
26,
27,
28]. The drift velocity shows that the inertia of fluid, particle turbulence and collisions effect contribute to sediment dispersion [
26].
The Boussinesq approximation [
29] is the basis for mathematical formulation of various flow problems. According to Kundu and Cohen [
30], after subtracting a static reference state, i.e.,
(
, where
ρ0 and
p0 = reference mixture density and pressure, and
= acceleration of gravity), the momentum equation can be expressed as
where
t = time;
p′ and
ρ′ = local deviations of pressure and mixture density from static reference state;
= flow velocity vector; and
ν = kinematic viscosity.
Both the inertia and buoyancy terms (the term on the left-hand side and the second term on the right-hand side of the above equation, respectively) contain the density ratio. With the Boussinesq approximation, the sediment stratification effect is shown as the buoyancy term while the inertia effect (the density ratio in the inertia term) is neglected. One then has
Sediment concentration near the water surface is always much lower than that near the bed for the condition of heavy particles. A large vertical density gradient which has obvious inertia effect on flow can be a result of high bulk sediment concentration. The vertical concentration gradient is often very large with significant inertia variations. Therefore, the applicability of the Boussinesq approximation needs to be assessed in such a case. To the best of our knowledge, there have been no reported documents on the numerical comparison of sediment laden open-channel flows with and without considering the Boussinesq approximation.
Because the role of fluid inertia is highly important in the acceleration/deceleration processes of fluid flow, a 3D modelling method is adopted to thoroughly analyze the inertia effects of suspended sediment under complicated flow boundary conditions. The 3D model is substantially different from traditional hydrodynamic models under Boussinesq approximation which only consider the stratification effect of suspensions as the buoyance term. In the following sections, first, model setup is provided; second, a few cases are selected for model verification; third, numerical experiments with and without Boussinesq approximation are presented for comparison; and finally, discussions and suggestions with regards to the sediment inertia effect are given.
2. Model Setup
2.1. Hydrodynamic Model
The governing hydrodynamic equations are 3D shallow water equations based on the hydrostatic pressure. The mass and momentum equations are written as follows:
where
x,
y and
z = Cartesian coordinates;
u,
v and
w = components of velocity in the
x,
y and
z directions;
p = pressure;
ρ = density of mixture; and
νh and
νz = eddy viscosity in the horizontal (
x and
y) and vertical (
z) directions. The density of the mixture is determined by
where
c = volumetric concentration of sediment;
ρw = water density; and
ρs = sediment density.
Similar to layer-integrated models [
31,
32], the vertical velocity is calculated from the integrated continuity equation as follows
where
zb = bed elevation; and
wzb is the vertical velocity at the bed. At the water surface,
where
H = water surface elevation.
The pressure in the horizontal momentum equations is given by integration of vertical momentum equation as
where
pa = pressure at the water surface which is set to zero in the present simulations. The pressure gradient is obtained as follows
Eddy diffusivity and viscosity are obtained from a two-equation
k-ω turbulence closure model [
33]. Complete extinction of local turbulence is unsustainable according to Cantero et al. [
22]. To prevent the turbulence to be totally damped by the sediment stratification effect, a prescribed upper threshold 0.2 is set on the flux Richardson number. As the Reynolds-Averaged Navier–Stokes (RANS) model is incapable of modeling flow under conditions of strong stratification [
34], an empirical distribution [
25] for viscosity is reserved here as follows.
where
h = water depth; and
U* = friction velocity.
2.2. Sediment Transport Model
Sediment transport is represented by the advection-diffusion equation,
where
wf = sediment settling velocity; and
εh and
εz = eddy diffusivity in the horizontal (
x and
y) and vertical (
z) directions.
2.3. Boundary Condition
There are two thin layers of δ at the water surface and the bed boundaries, thus the thickness of the calculation domain is
h − 2δ. Vertical boundary conditions are implemented at these two interfaces. Normal gradients of horizontal velocities as well as the net vertical flux of sediment are zero at the upper interface. At the bottom one, we enforce the bottom frictional stress for momentum equations as
where
ub and
vb = near-bed components of horizontal velocity; and
CD = drag coefficient to be calibrated. Besides, the near-bed net flux of sediment is
where
qsu = sediment entrainment rate; and
cb = near-bed volumetric concentration.
Flow condition at the inlet is given by flow discharge. In other words, the flow velocity profile at the inlet can be estimated through the transport equation for turbulent components and momentum equations with the assumption that flow is locally uniform at this boundary. Similarly, the suspended sediment concentration profile at the inlet is determined by assuming local equilibrium in the inlet sediment entrainment. At the outlet, the water level is set to prescribed values as the flow is assumed to be subcritical.
2.4. Domain Discretization
For discretization of the computational domain, a Spectral Element Method (SEM) is used in the vertical direction (due to the importance of the vertical variations in the present work) and the finite difference method is employed in the horizontal directions. Besides, for ease of implementation of the boundary conditions, vertical domain is discretized into three layers (due to the existence of two thin layers adjacent to water surface and bed) with unstretched z-coordinates. First, vertical space is divided into a number of sublayers with evenly thickness of h0. The top/bottom sublayer is combined with its adjacent sublayer, producing a layer with a thickness between h0 and 2h0. Then, all the rest inner sublayers are combined to form an inner layer with its thickness being multiple of h0. Therefore, there will be three vertical layers throughout the whole calculation domain. All these three layers are variable according to water surface and bed changes during calculation process. Thickness thresholds zmin and zmax are imposed over top and bottom layers. When the thickness of the top/bottom layer is out of range (>zmax or <zmin), after the calculation of water surface/bed elevation at a certain time step, the layer interface will move a distance of h0 inward or outward to ensure the thickness stays in the range. Let h0 = (zmax − zmin)/2, after adjustment, its thickness will be close to (zmax − zmin)/2. Then, there is no need to readjust the thickness for small surface/bed changes. Every thickness adjustment is accompanied by local redistribution of physical quantities.
This kind of vertical discretization allows us to conveniently employ the finite dimensional space/polynomial of relatively higher degree for inner layer and lower degree for top/bottom layers. For the horizontal diffusion/viscosity calculations at the inner layer, if the horizontally adjacent inner layers are consistent, the calculations will be straight-forward as in the z-coordinates method, otherwise, additional interpolations need to be carried out separately for each calculation. For the calculations at the top/bottom layer, the horizontally adjacent layers are always inconsistent, and interpolations are required.
Horizontal domain is discretized using curvilinear coordinates into staggered grids. The governing equations need to be converted accordingly for implementation. Here, we present only the framework in the Cartesian coordinates for simplicity.
2.5. Solution of Generalized Equation by SEM
The horizontal momentum, sediment and turbulence transport equations can be generalized as
where
ϕ = the physical quantity to be solved;
wf is set only for sediment transport; σ = the Prandtl–Schmidt number for
ϕ; and
f = other terms. The top and bottom boundaries are chosen according to the specific equation to be solved. At each vertical layer
i with thickness
Li =
zi+1 −
zi, generalized equation is conducted under local vertical coordinate
ζ = 2 (
z −
zi)/
Li − 1. We set an approximation such that
ϕ belongs to the finite dimensional space of degree
N. Choosing the Legendre polynomials as the local basis functions, the approximate solution is defined by
where
ϕk and
hk(ζ) = the coefficients and the Lagrange form of Legendre polynomials, respectively; interpolation point
ζk = Legendre–Gauss–Lobatto point with its weight
ωk; and
and
= the Legendre polynomials and their derivatives. Generalized equation is multiplied by the test function and integrated over
ζ (between [–1, 1]) and time step. We choose the local basis function as the test function. Then, the weak formulation after including boundary condition, can be derived as
The integral coefficients are given as
where
= the weighting function of Gaussian quadrature for
ζj. The depth integrated continuity and horizontal momentum equations are solved in the coupled way.
Depth integrated continuity equation is discretized with a semi-implicit approach in curvilinear coordinates as
where
ξ and
η = horizontal curvilinear coordinates;
and
= depth-averaged values of
u and
v;
θ = the implicitness factor for temporal discretization; and
= Jacobi determinant. Substituting the discretized continuity equation into the horizontal momentum equations,
where
=
;
ν =
νh for simplification;
σ = Schmidt number; and
um*n = the backtracked value of
um at time step
n. Momentum equation for
v has a similar form. Underlined terms are zero at the outlet for imposing water level condition for subcritical flows. In the momentum and sediment transport equations, advection terms are incorporated in the total derivatives. By backtracking characteristic lines accurately under Eulerian–Lagrangian context [
35], the backtracked value at the foot of the characteristic lines at time step
n can be approximated by interpolation. The final set of momentum equations can be solved by Conjugate Gradient. Equation (21) is semi-implicit with respect to
v. Hence,
v is firstly taken as an explicit quantity in the horizontal momentum for
u, and then one more iteration is applied after the solution of the horizontal momentum equations. Once the horizontal velocities are known, water surface level and vertical velocity can be computed using the depth integrated continuity equation.
4. Conclusions
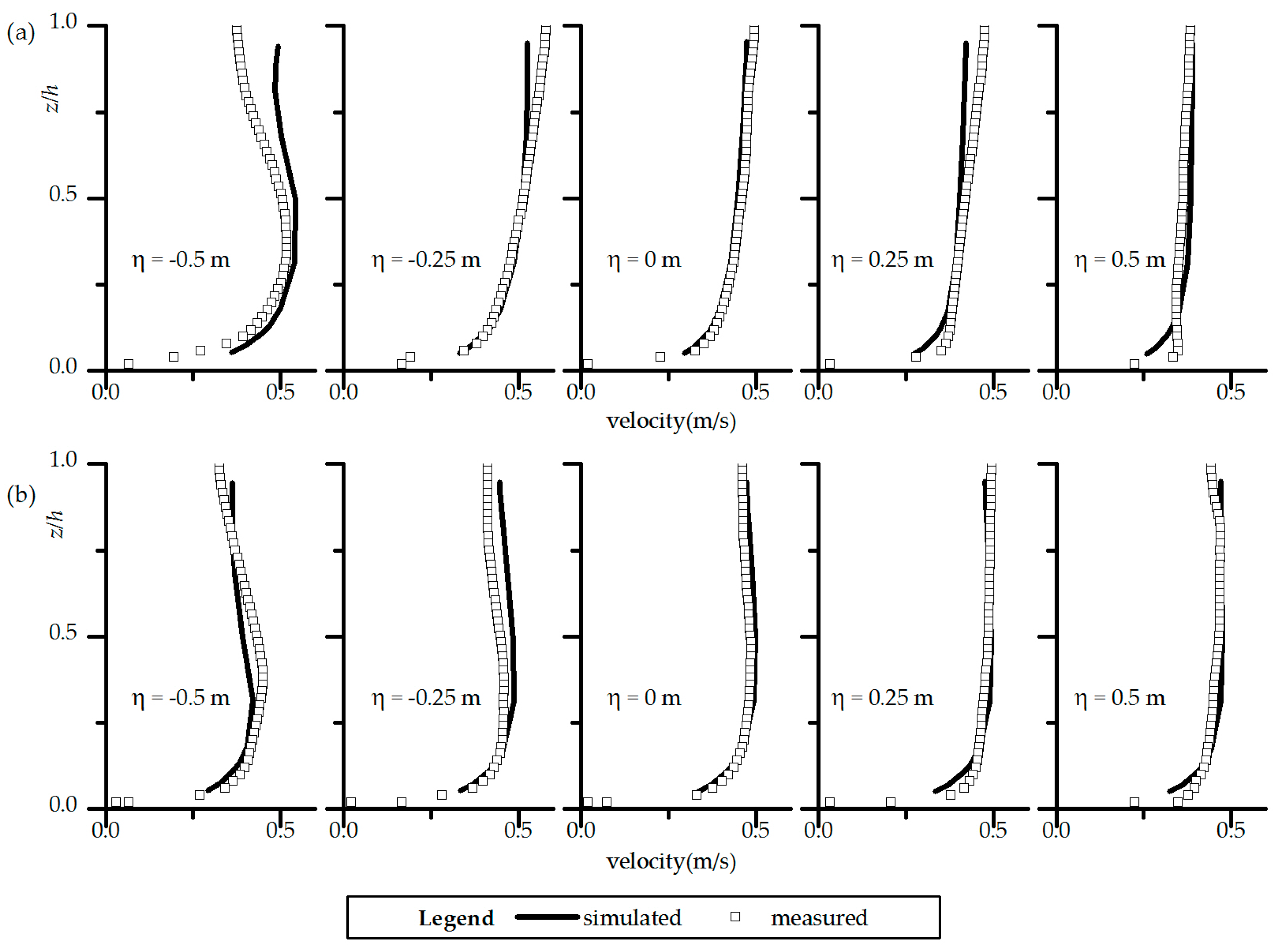
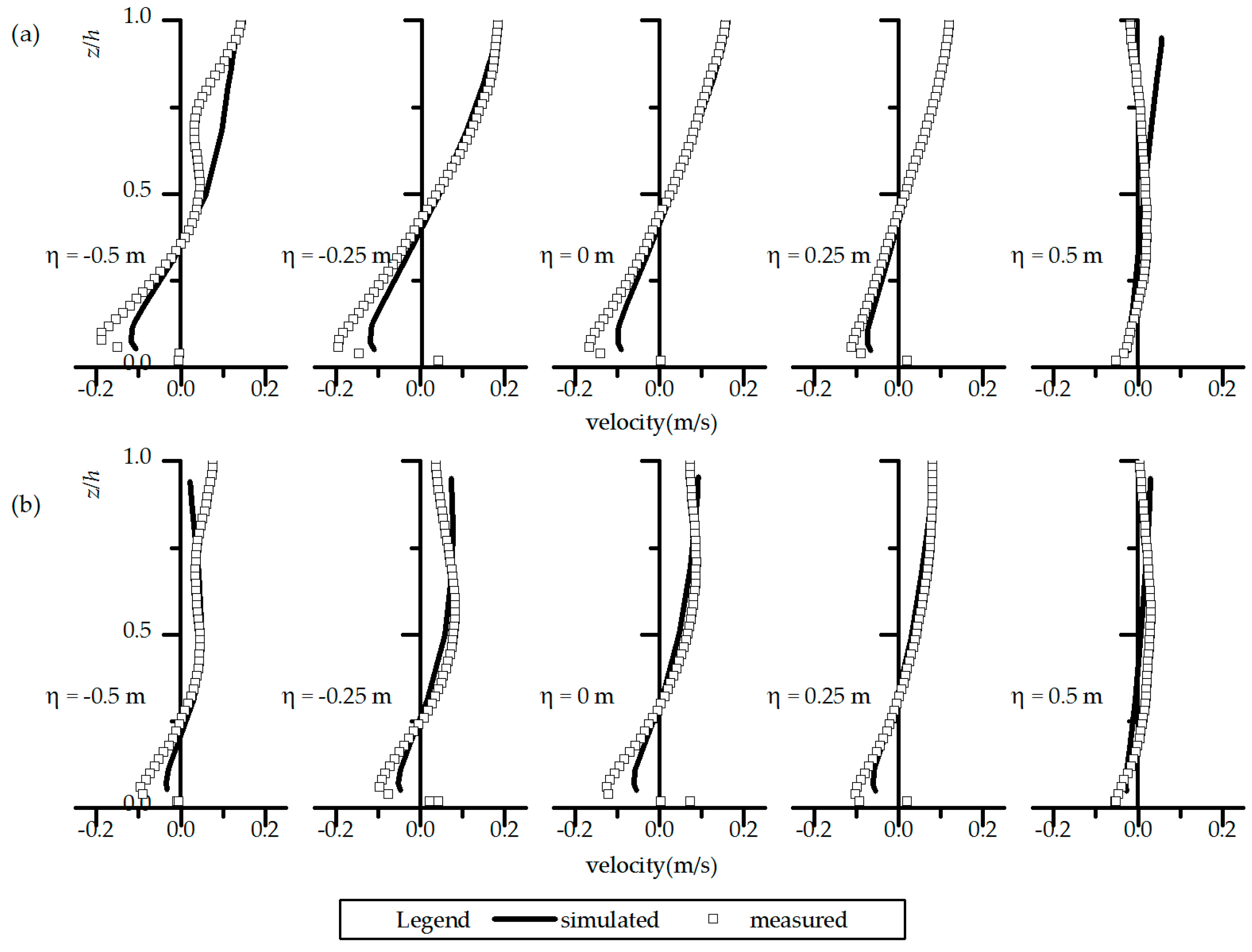
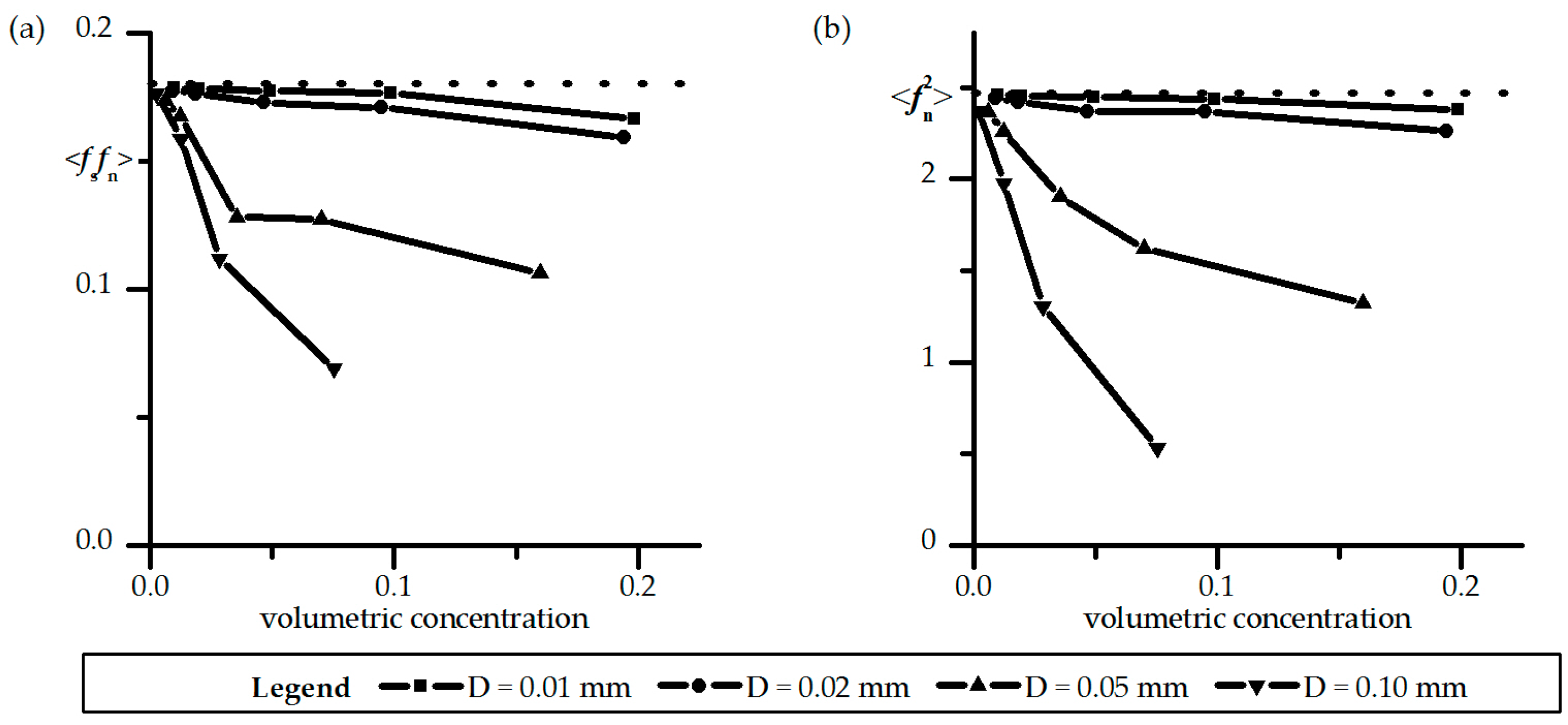
This paper presents 3D numerical simulations of sediment laden flows in open channel meanders concerning suspension inertia effect on the flow structure. The 3D governing equations without the Boussinesq approximation were used here and both the inertia and buoyant effects were considered. The velocity and concentration calculations performed in bend channels with comparison between the cases with and without Boussinesq approximation. Sediment size and specific density of sediment were studied to demonstrate the integrated effect. Although the additional turbulence transport produced by the presence of sediment could not be simulated by the present model due to the limitations with the employed turbulence closure model, the modifications in the vertical profiles of concentration and velocity due to the sediment were still estimated successfully, similar to the previous studies.
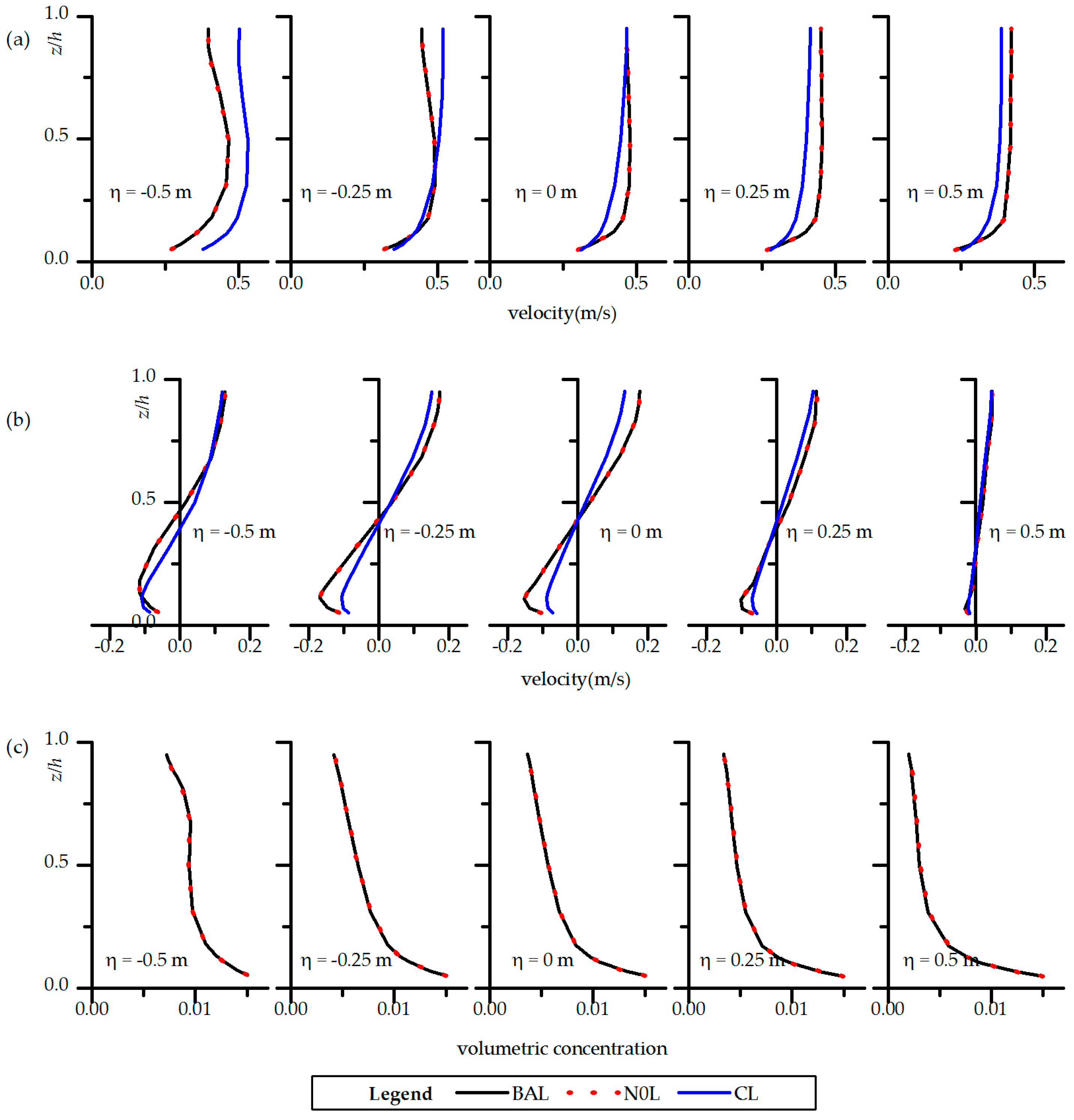
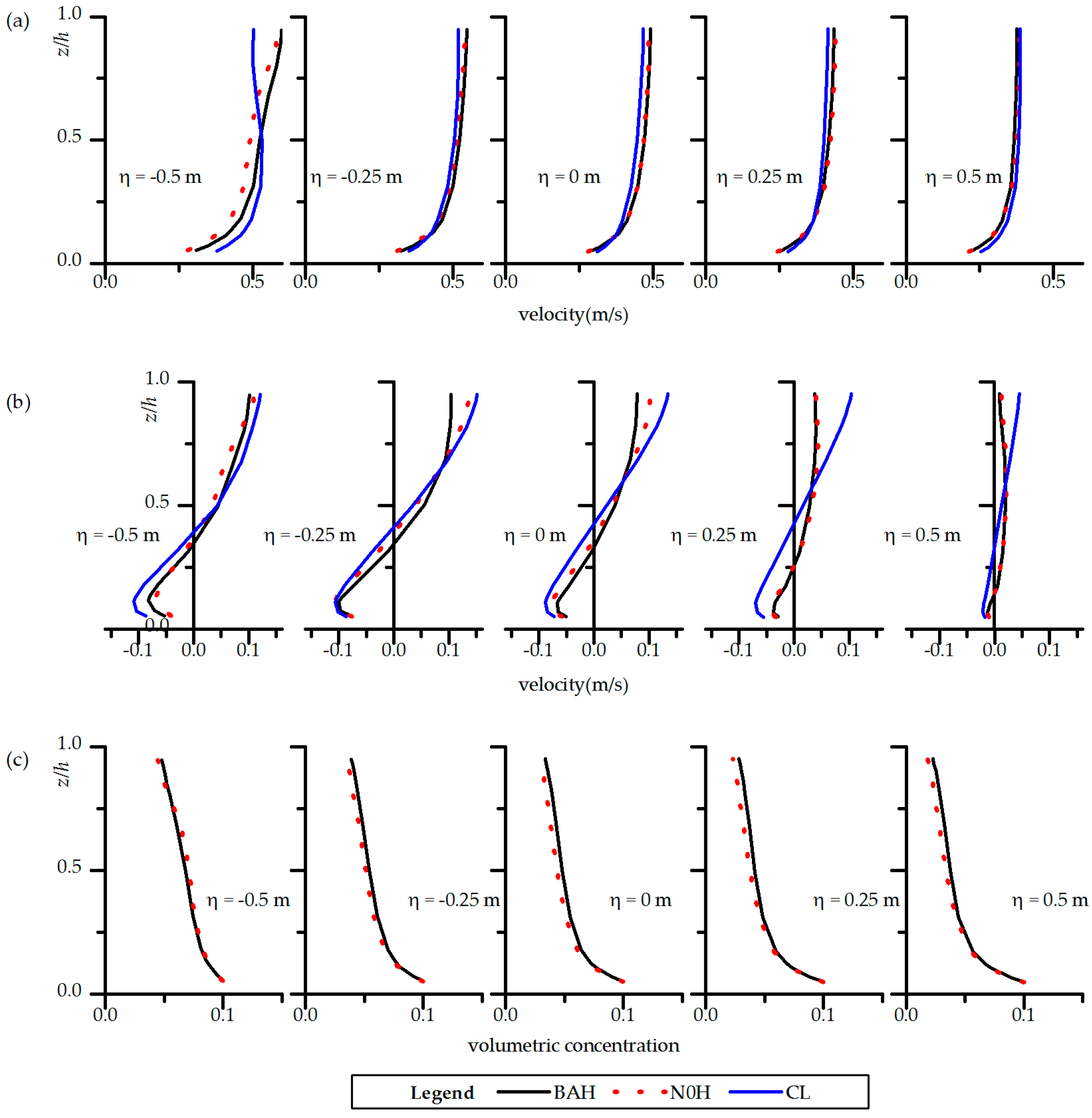
The Boussinesq approximation that neglects all other density effects except buoyancy for dilute flows results in obvious discrepancy in flow structure and sediment transport for high sediment concentration in meandering channels. Both the inertia and stratification effects of sediment play important roles in river meandering processes. The stratification effect promotes secondary flow at lower concentration by reducing eddy viscosity and suppresses secondary flow at higher concentration by the buoyance force acting on transversal pressure. The inertia effect suppresses secondary flow which is important at higher concentration. Depending on the sediment concentration and diameter, the integrated effect results in an increase and a decrease of the secondary flow at lower and higher concentrations, respectively. This suggests that the dominance of the sediment effect depends on the concentration. With the increase of concentration under a specific sediment size, secondary flow increases to reach a maximum and then declines. Moreover, as the sediment concentration rises, an exponentially decaying rate has been found for the secondary flow subject to inertia effect (
Figure 9). It is concluded that numerical simulations without considering the Boussinesq approximation is necessary when concentration is high in meandering channels.
The present qualitative predictions based on the 3D numerical simulations provide a new perspective on sediment laden flow. A quantitative analysis of the inertia and stratification performance in meandering channels provides a comprehensive understanding of the water-sediment interactions. The lower Yellow River carries a heavy sediment load with bed material mainly composed of fine sand and silt. The main stream channel migrates very fast during the occurrence of hyperconcentrated flows while the meandering mechanics is still an open question. Extensive research efforts, including numerical modelling, have been continuously carried out on meandering mechanisms. Highly efficient 2D models are still the main tools for river engineering and perform quite satisfactorily in straight or mild meandering rivers [
40]. This study would give some cues to 2D and 3D modelling of fluvial process for sediment laden flows.