A New Flash Flood Warning Scheme Based on Hydrodynamic Modelling
Abstract
1. Introduction
2. Hydrodynamic Model
3. Materials and Methods
3.1. Hazard Index
3.2. Building Database of Critical Threshold Rainfalls
3.2.1. Modelling Scenarios
3.2.2. Calculation of Critical Rainfall
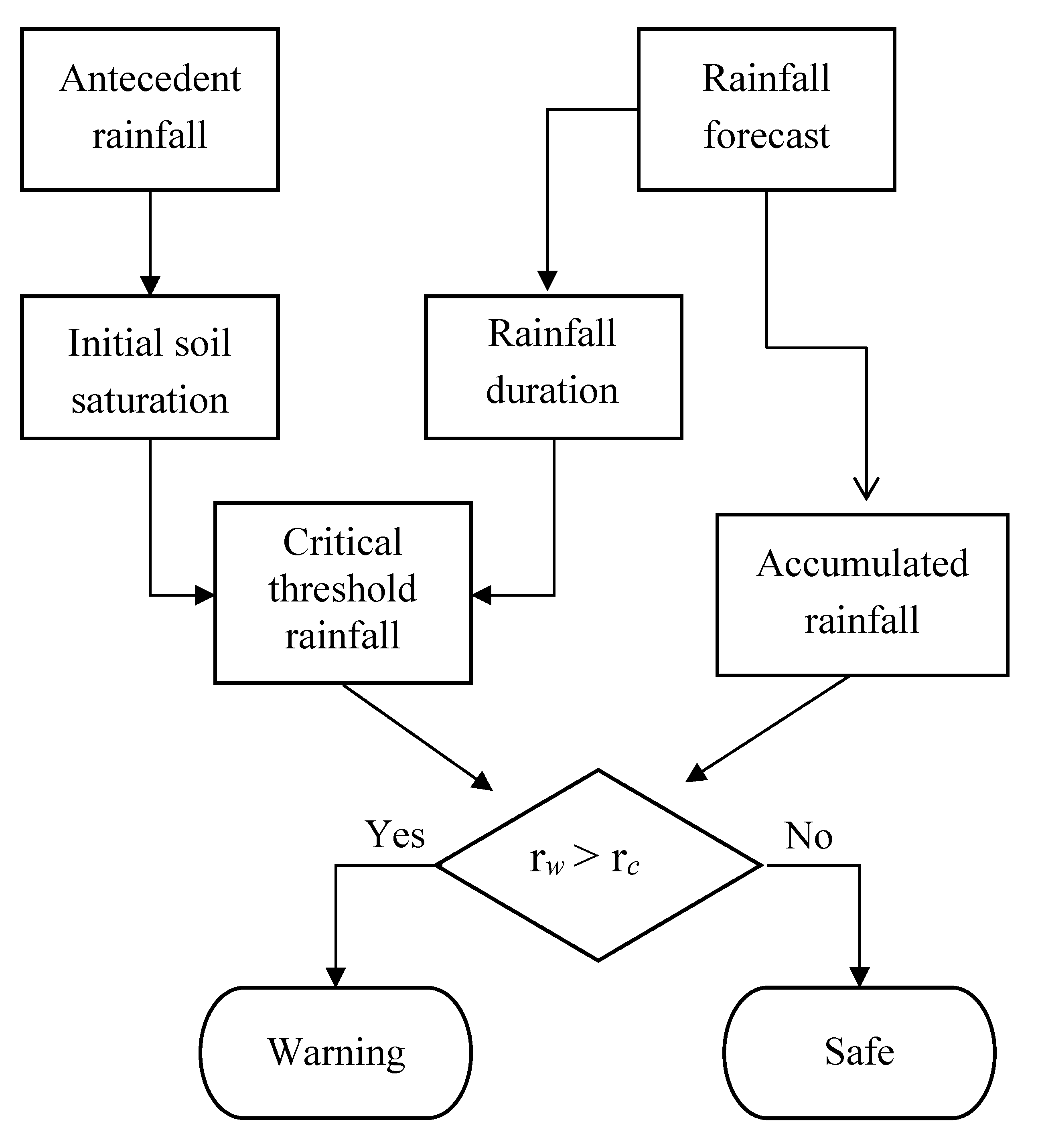
3.3. Flood Warning Operation Flow
- (1)
- Determine the rainfall duration time according to the rainfall forecast.
- (2)
- Determine the antecedent soil moisture type according to the 5-day accumulated rainfall (Table 2).
- (3)
- Based on the rainfall duration and antecedent soil type determination, determine the corresponding critical rainfall from the database.
- (4)
- Calculate the accumulated rainfall at the decision moment, . Calculate the accumulated rainfall at the warning moment, . The calculation time steps for both and are 15 min for a 1-h rainfall duration, while they are 30 min for both 3-h and 6-h rainfall durations.
- (5)
- Compare the rainfall at the warning time, , and the critical rainfall, ; if > , send the warning information to the target community.
3.4. Comparison with Existing Systems and Limitations
4. Case Study
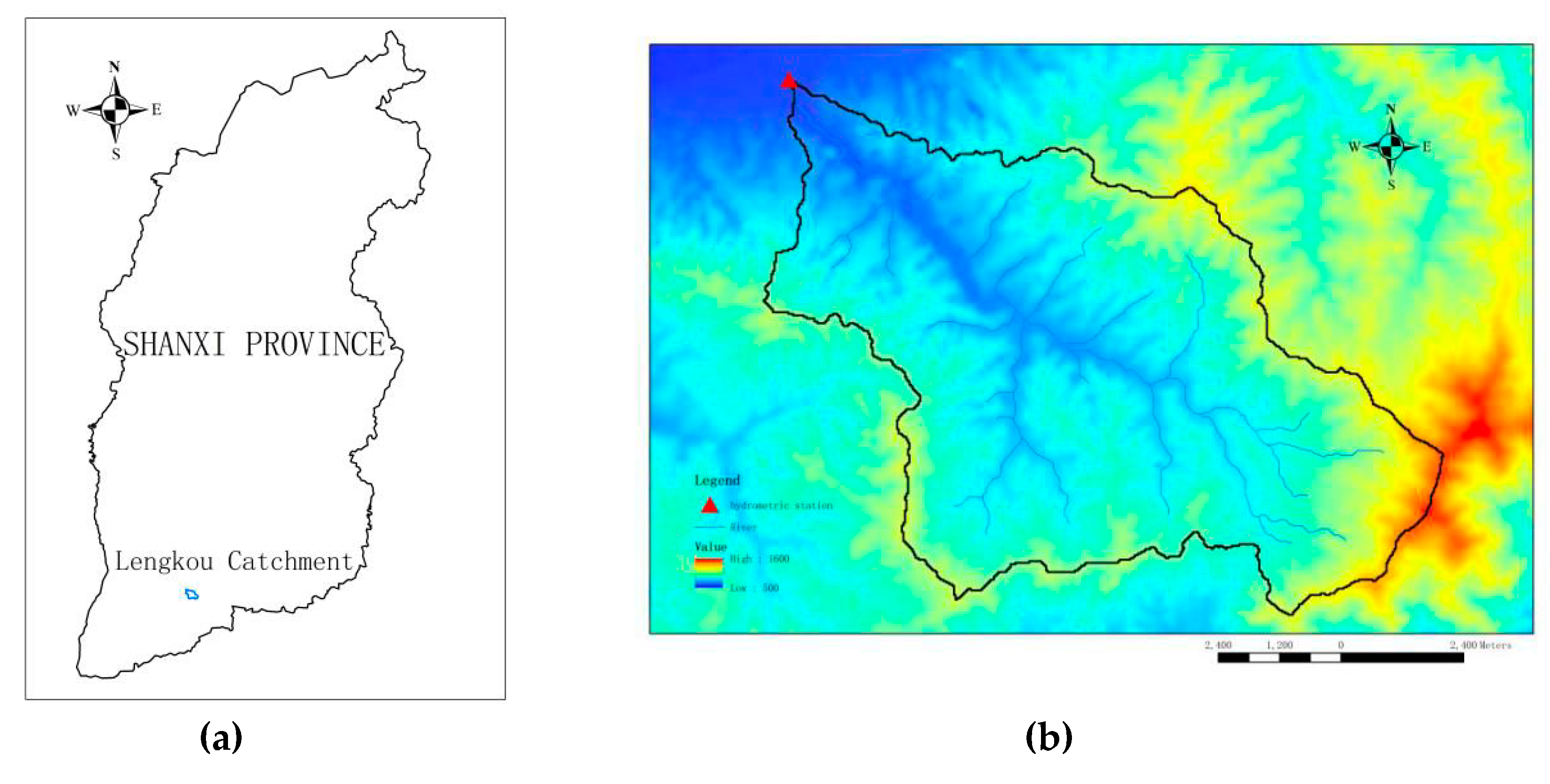
4.1. Introduction of Lengkou Catchment
4.2. Results
4.2.1. Impact of Critical Hazard Index
4.2.2. Impact of Rainfall Duration
4.2.3. Impact of Antecedent Rainfall
4.3. Example of Flood Warning Operation
- (1)
- According to the rainfall forecast (Table 3), the rainfall duration can be determined to be 3 h.
- (2)
- As the flood season of the Lengkou catchment occurs in the growing season and the antecedent rainfall is 30 mm, the initial soil saturation is classified as dry (Table 2).
- (3)
- Choose the critical rainfall for the catchment in relation to a 3-h rainfall duration and initial dry soil conditions from the critical rainfall database.
- (4)
- Compute the accumulative rainfall at the warning moment, such as the last row of Table 3.
- (5)
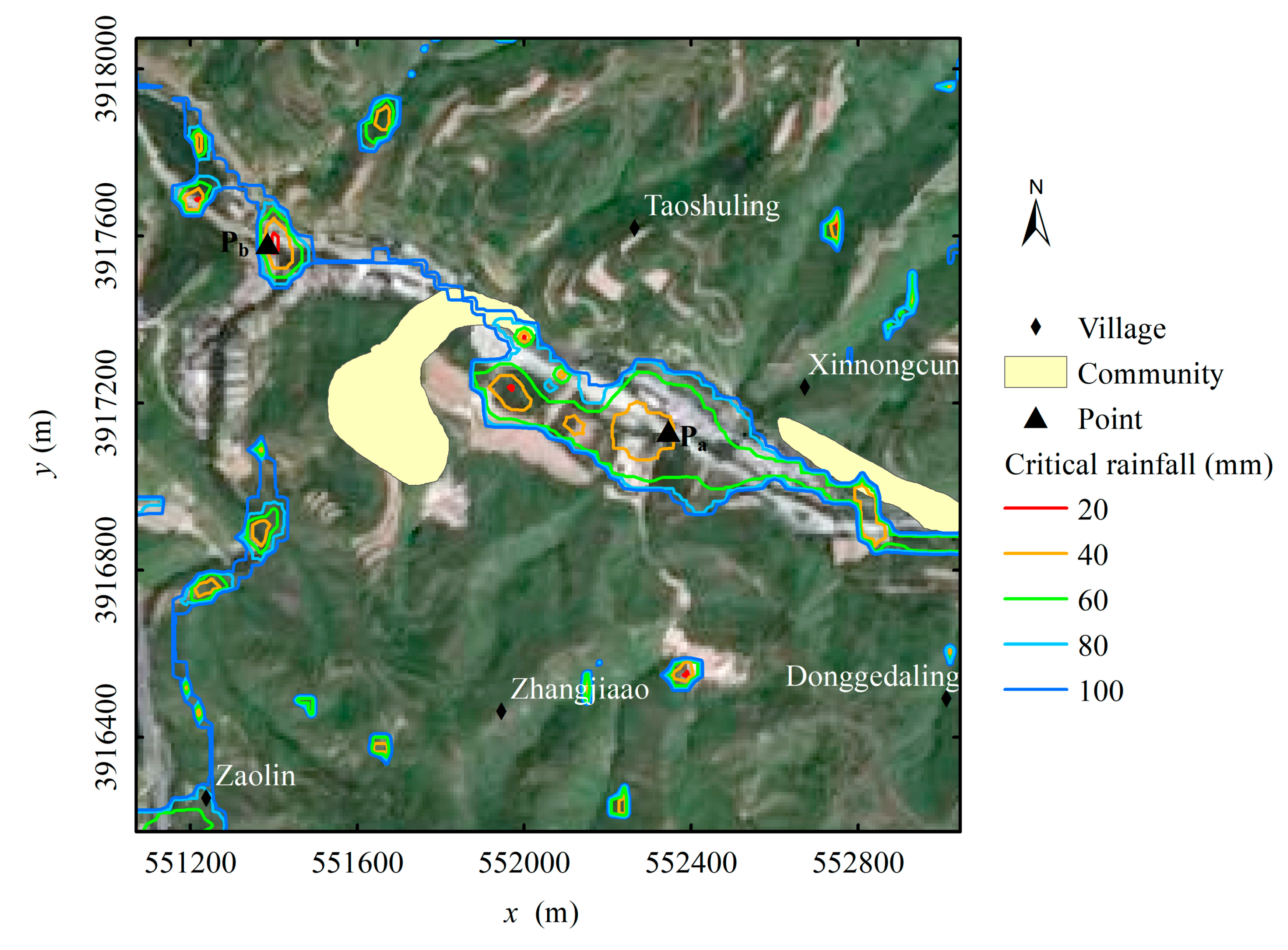
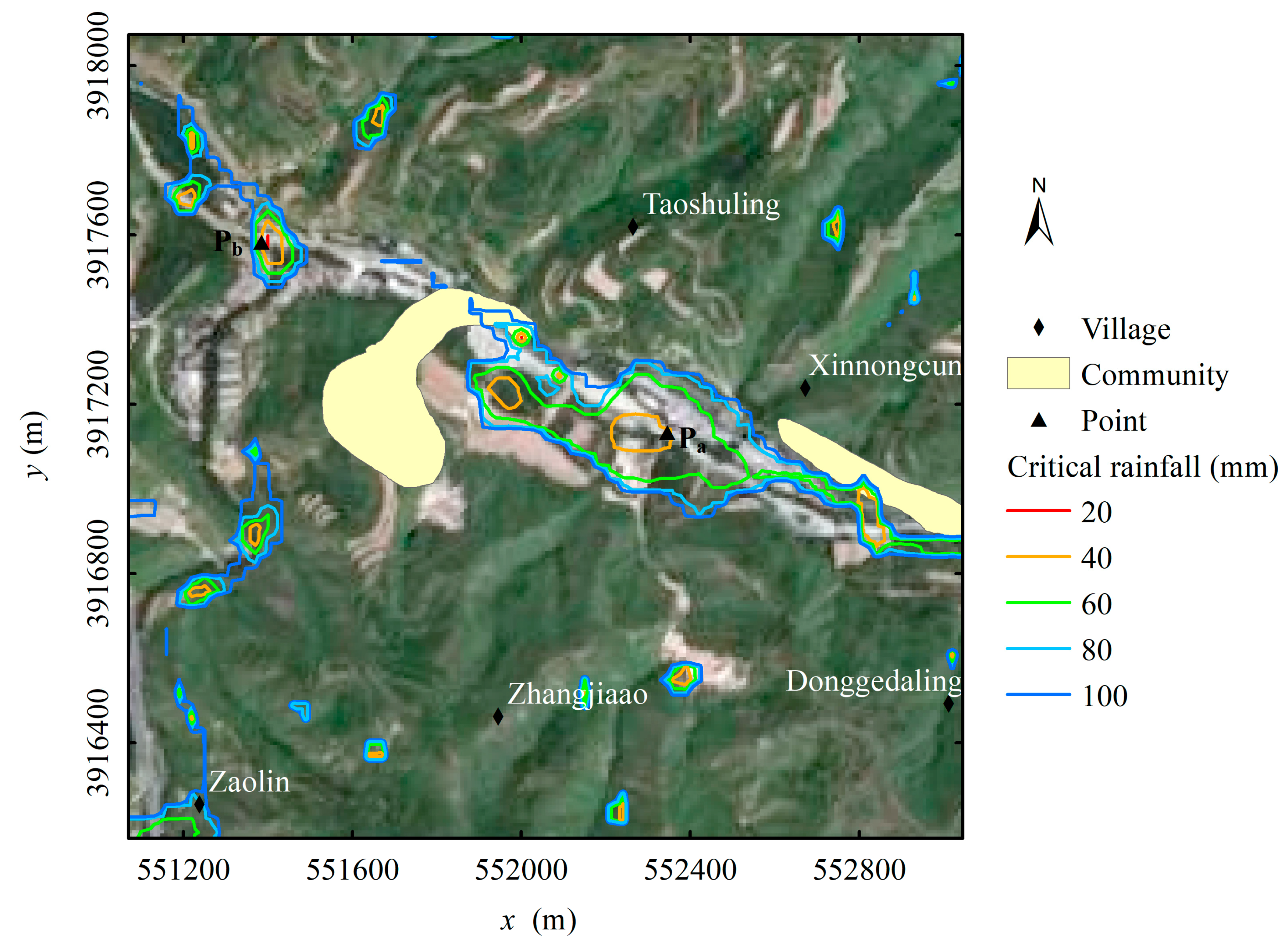
- Taking location Pa as an example, the critical rainfalls are 35 mm and 40 mm for PE and IE, respectively. At decision time = 1.0 h, the cumulative rainfall is 25 mm, and the rainfall forecasted for the next 30 min is 15 mm. Therefore, the cumulative rainfall at the warning time is 40 mm. If the rainfall intensity is assumed to be uniform during the next 30 min (i.e., from t = 1.0 to 1.5 h), the cumulative rainfall will reach 35 mm at t = 1.17 h (as shown in Figure 11). Thus, a PE warning will be sent to the people at Pa. The cumulative rainfall will reach 40 mm at = 1.5 h (as shown in Figure 12). Therefore, an IE warning should be sent to people at both locations Pa and Pb.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kleinen, T.; Petschel-Held, G. Integrated assessment of changes in flooding probabilities due to climate change. Clim. Chang. 2007, 81, 283–312. [Google Scholar] [CrossRef]
- Beniston, M.; Stoffel, M.; Hill, M. Impacts of climatic change on water and natural hazards in the Alps: Can current water governance cope with future challenges? Examples from the European “ACQWA” project. Environ. Sci. Policy 2011, 14, 734–743. [Google Scholar] [CrossRef]
- Liu, C.J.; Guo, L.; Ye, L.; Zhang, S.F.; Zhao, Y.Z.; Song, T.Y. A review of advances in China’s flash flood early-warning system. Nat. Hazards 2018, 92, 619–634. [Google Scholar] [CrossRef]
- Golian, S.; Saghafian, B.; Maknoon, R. Derivation of Probabilistic Thresholds of Spatially Distributed Rainfall for Flood Forecasting. Water Resour. Manag. 2010, 24, 3547–3559. [Google Scholar] [CrossRef]
- Martina, M.L.V.; Todini, E.; Libralon, A. Hydrological Modelling and the Water Cycle; Sorooshian, S., Hsu, K.-L., Coppola, E., Tomassetti, B., Verdecchia, M., Visconti, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 203–227. [Google Scholar]
- Montesarchio, V.; Lombardo, F.; Napolitano, F. Rainfall thresholds and flood warning: An operative case study. Nat. Hazards Earth Syst. Sci. 2009, 9, 135–144. [Google Scholar] [CrossRef]
- Ma, M.H.; Zhang, J.N.; Su, H.D.; Wang, D.C.; Wang, Z.L. Update of Early Warning Indicators of Flash Floods: A Case Study of Hunjiang District, Northeastern China. Water 2019, 11, 314. [Google Scholar] [CrossRef]
- Cao, Z.; Wang, X.; Zhang, S.; Pender, G. Hydrodynamic modelling in support of flash flood warning. Proc. ICE Water Manag. 2010, 163, 327–340. [Google Scholar] [CrossRef]
- Defra and Environment Agency (DEA). Flood and Coastal Defence R&D Programme, R&D Outputs: Flood Risks to People. (Phase 2 Project Record, FD2321/PR); DEA: London, UK, 2006.
- Bracken, L.J.; Cox, N.J.; Shannon, J. The relationship between rainfall inputs and flood generation in south-east Spain. Hydrol. Process. 2008, 22, 683–696. [Google Scholar] [CrossRef]
- Norbiato, D.; Borga, M.; Degli Esposti, S.; Gaume, E.; Anquetin, S. Flash flood warning based on rainfall thresholds and soil moisture conditions: An assessment for gauged and ungauged basins. J. Hydrol. 2008, 362, 274–290. [Google Scholar] [CrossRef]
- Martina, M.L.V.; Todini, E.; Libralon, A. A Bayesian decision approach to rainfall thresholds based flood warning. Hydrol. Earth Syst. Sci. 2006, 10, 413–426. [Google Scholar] [CrossRef]
- Amadio, P.; Mancini, M.; Menduni, G.; Rabuffetti, D.; Ravazzani, G. A real time flood forecasting system based on rainfall thresholds working on the Arno watershed: Definition and reliability analysis. In Proceedings of the 5th EGS Plinius Conference, Corsica, France, 1–3 October 2003. [Google Scholar]
- Hapuarachchi, H.A.P.; Wang, Q.J.; Pagano, T.C. A review of advances in flash flood forecasting. Hydrol. Process. 2011, 25, 2771–2784. [Google Scholar] [CrossRef]
- Carpenter, T.; Sperfslage, J.; Georgakakos, K.; Sweeney, T.; Fread, D. National threshold runoff estimation utilizing GIS in support of operational flash flood warning systems. J. Hydrol. 1999, 224, 21–44. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Horritt, M.S.; Wilson, M.D. Simple spatially-distributed models for predicting flood inundation: A review. Geomorphology 2007, 90, 208–225. [Google Scholar] [CrossRef]
- Reed, S.; Schaake, J.; Zhang, Z. A distributed hydrologic model and threshold frequency-based method for flash flood forecasting at ungauged locations. J. Hydrol. 2007, 337, 402–420. [Google Scholar] [CrossRef]
- Javelle, P.; Fouchier, C.; Arnaud, P.; Lavabre, J. Flash flood warning at ungauged locations using radar rainfall and antecedent soil moisture estimations. J. Hydrol. 2010, 394, 267–274. [Google Scholar] [CrossRef]
- Cools, J.; Vanderkimpen, P.; El Afandi, G.; Abdelkhalek, A.; Fockedey, S.; El Sammany, M.; Abdallah, G.; El Bihery, M.; Bauwens, W.; Huygens, M. An early warning system for flash floods in hyper-arid Egypt. Nat. Hazards Earth Syst. Sci. 2012, 12, 443–457. [Google Scholar] [CrossRef]
- Biondi, D.; De Luca, D.L. Performance assessment of a Bayesian Forecasting System (BFS) for real-time flood forecasting. J. Hydrol. 2013, 479, 51–63. [Google Scholar] [CrossRef]
- Woolhiser, D.A.; Liggett, J.A. Unsteady, one-dimensional flow over a plane--the rising hydrograph. Water Resour. Res. 1967, 3, 753–771. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Singh, V.P. Effect of microtopography, slope length and gradient, and vegetative cover on overland flow through simulation. J. Hydrol. Eng. 2004, 9, 375–382. [Google Scholar] [CrossRef]
- Ogden, F.L.; Julien, P.Y. Runoff sensitivity to temporal and spatial rainfall variability at runoff plane and small basin scales. Water Resour. Res. 1993, 29, 2589–2597. [Google Scholar] [CrossRef]
- Philipp, A.; Grundmann, J. Integrated modeling system for flash flood routing in ephemeral rivers under the influence of groundwater recharge dams. J. Hydraul. Eng. 2013, 139, 1234–1246. [Google Scholar] [CrossRef]
- Warnock, A.; Kim, J.; Ivanov, V.; Katopodes, N.D. Self-Adaptive Kinematic-Dynamic Model for Overland Flow. J. Hydraul. Eng. 2014, 140, 169–181. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J.; Suarez, J. Overland flow computations in urban and industrial catchments from direct precipitation data using a two-dimensional shallow water model. Water Sci. Technol. 2010, 62, 1998–2008. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Warnock, A.; Ivanov, V.Y.; Katopodes, N.D. Coupled modeling of hydrologic and hydrodynamic processes including overland and channel flow. Adv. Water Resour. 2012, 37, 104–126. [Google Scholar] [CrossRef]
- Rousseau, M.; Cerdan, O.; Delestre, O.; Dupros, F.; James, F.; Cordier, S. Overland Flow Modelling with the Shallow Water Equation using a Well Balanced Numerical Scheme: Adding Efficiency or just More Complexity? 2012. Available online: https://hal.archives-ouvertes.fr/hal-00664535/ (accessed on 12 May 2019).
- Berardi, L.; Laucelli, D.; Simeone, V.; Giustolisi, O. Simulating floods in ephemeral streams in Southern Italy by full-2D hydraulic models. Int. J. River Basin Manag. 2013, 11, 1–17. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Macchione, F. A storm event watershed model for surface runoff based on 2D fully dynamic wave equations. Hydrol. Process. 2013, 27, 554–569. [Google Scholar] [CrossRef]
- Pan, J.J.; Cao, Z.X.; Wang, X.K.; Cao, S.Y. Comparative study of simplified and full hydrodynamic models for flash floods. J. Sichuan Univ. (Eng. Sci. Ed.) 2012, 44, 1–6. (In Chinese) [Google Scholar]
- Oreskes, N.; Shrader-Frechette, K.; Belitz, K. Verification, validation, and confirmation of numerical models in the earth sciences. Science 1994, 263, 641–646. [Google Scholar] [CrossRef]
- Huang, W.; Cao, Z.X.; Qi, W.J.; Pender, G.; Zhao, K. Full 2D hydrodynamic modelling of rainfall-induced flash floods. J. Mt. Sci. 2015, 12, 1203–1218. [Google Scholar] [CrossRef]
- Green, W.H.; Ampt, G. Studies on soil physics, part 1: The flow of air and water through soils. J. Agric. Sci. 1911, 4, 1–24. [Google Scholar]
- Toro, E. Shock-Capturing Methods for Free-Surface Shallow Flows; John Wiley: London, UK, 2001. [Google Scholar]
- Iwagaki, Y. Fundamental Studies on the Runoff by Characteristics; Bulletins—Disaster Prevention Research Institute, Kyoto University: Kyoto, Japan, 1955; Volume 10, pp. 1–25. [Google Scholar]
- De Lima, J.L.M.P. Model KININF for overland flow on pervious surfaces. In Overland Flow: Hydraulics and Erosion Mechanics; Parson, T., Abrahams, A., Eds.; UCL Press: London, UK, 1992; pp. 69–88. [Google Scholar]
- Xia, J.; Falconer, R.A.; Lin, B.; Tan, G. Numerical assessment of flood hazard risk to people and vehicles in flash floods. Environ. Model. Softw. 2011, 26, 987–998. [Google Scholar] [CrossRef]
- Fowler, A.M.; Hennessy, K.J. Potential impacts of global warming on the frequency and magnitude of heavy precipitation. Nat. Hazards 1995, 11, 283–303. [Google Scholar] [CrossRef]
- Cannon, S.H.; Gartner, J.E.; Wilson, R.C.; Bowers, J.C.; Laber, J.L. Storm rainfall conditions for floods and debris flows from recently burned areas in southwestern Colorado and southern California. Geomorphology 2008, 96, 250–269. [Google Scholar] [CrossRef]
- Zhai, X.; Guo, L.; Liu, R.; Zhang, Y. Rainfall threshold determination for flash flood warning in mountainous catchments with consideration of antecedent soil moisture and rainfall pattern. Nat. Hazards 2018, 94, 605–625. [Google Scholar] [CrossRef]
- NWS Manual 10-950. 2002. Available online: http://www.nws.noaa.gov/directives/010/pd01009050a.pdf (accessed on 12 May 2019).
- NWS Manual 10-950. 2017. Available online: https://www.nws.noaa.gov/directives/sym/pd01009050curr.pdf (accessed on 12 May 2019).
- DWRSP (Department of Water Resources of Shanxi Province). Handbook of Hydrological Calculation of Shanxi Province; Yellow River Conservancy Press: Zhengzhou, China, 2010. (In Chinese) [Google Scholar]
- SCS. National Engineering Handbook, Section 4: Hydrology; US Government Printing Office: Washington, DC, USA, 1972.

| Rainfall Duration (h) | Total Rainfall (mm) | Modelling Duration (h) | Number of Scenarios | Notes |
|---|---|---|---|---|
| 1 | 10, 20, 30, 40, 50, 60, 70, 80 | 3 | 8 | Initial soil moistures are dry, medium, and saturated. |
| 3 | 10, 25, 40, 55, 70, 85, 100 | 6 | 7 | |
| 6 | 10, 30, 50, 70, 90, 110, 130, 150, 170 | 12 | 9 |
| Antecedent Moisture Classes (AMC) | Total 5-day Antecedent Accumulated Rainfall (mm) | Ratio | |
|---|---|---|---|
| Dormant Season | Growing Season | ||
| Dry | <12.7 | <35.5 | 1.0/3.0 |
| Medium | 12.7~28.0 | 35.5~53.3 | 2.0/3.0 |
| Saturated | >28 | >53.3 | 1.0 |
| Time | |||||||
|---|---|---|---|---|---|---|---|
| (h) | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| (h) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 |
| ) | 10 | 10 | 15 | 10 | 15 | 5 | 0 |
| ) | 0 | 15 | 10 | 10 | 15 | 8 | 2 |
| (mm) | 0 | 15 | 25 | 35 | 50 | 58 | 60 |
| Cumulative rainfall at warning time: | 10 | 25 | 40 | 45 | 65 | 63 | 60 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, W.; Cao, Z.; Huang, M.; Duan, W.; Ni, Y.; Yang, W. A New Flash Flood Warning Scheme Based on Hydrodynamic Modelling. Water 2019, 11, 1221. https://doi.org/10.3390/w11061221
Huang W, Cao Z, Huang M, Duan W, Ni Y, Yang W. A New Flash Flood Warning Scheme Based on Hydrodynamic Modelling. Water. 2019; 11(6):1221. https://doi.org/10.3390/w11061221
Chicago/Turabian StyleHuang, Wei, Zhixian Cao, Minghai Huang, Wengang Duan, Yufang Ni, and Wenjun Yang. 2019. "A New Flash Flood Warning Scheme Based on Hydrodynamic Modelling" Water 11, no. 6: 1221. https://doi.org/10.3390/w11061221
APA StyleHuang, W., Cao, Z., Huang, M., Duan, W., Ni, Y., & Yang, W. (2019). A New Flash Flood Warning Scheme Based on Hydrodynamic Modelling. Water, 11(6), 1221. https://doi.org/10.3390/w11061221





