Abstract
The resilience of a water distribution system (WDS) is defined as its ability to prepare, respond to, and recover from a catastrophic failure event such as an earthquake or intentional contamination. Robustness (ROB), one of the components of resilience, is the ability to maintain functionality to meet customer demands. Recently, the traditional probability-based system performance perspective has begun to shift toward the ROB and system performance variation point of view. This paper provides a state-of-the-art review of WDS ROB-based approaches proposed in three research categories: Design, operation, and management. While few pioneering works have been published in the latter two areas, an ROB indicator was proposed and thoroughly investigated for WDS design. Then, some future works are recommended in each of the three domains to promote developments in WDS ROB. Finally, a brief summary of this paper is presented, from which the final conclusions of the state-of-the-art review and recommendations are drawn. The new paradigm of WDS ROB-based design, operation, and management is in its infant stage and should be carved out in future studies.
1. Introduction
The resilience of a water distribution system (WDS) is defined as its ability to prepare, respond to, and recover from a catastrophic failure event such as an earthquake or intentional contamination [1,2]. Therefore, resilience considers the following system performance characteristics before, during, and after the failure: Robustness (ROB), redundancy (REDU), rapidity (RAP), and resourcefulness (RES) (the so-called 4Rs) [1,3]. While the first two are related to pre-failure system performance characteristics, the latter two are related to post-failure ones.
ROB is generally defined as the ability of the system to maintain its functionality (system performance level) to supply the required quantity of water to customers at the acceptable pressure and quality [4,5,6]. A group of researchers have defined ROB as the ability to reduce the impact of component failures and used the optimum connectively level of a network to measure the system ROB [7]. WDS ROB can be improved by installing bigger pipes and pumps, which can help maintain the service pressure above the minimum requirement [1]. REDU is related to the system’s alternative ways and paths of supplying water to customers. Parallel pipes and/or dense grid network configurations are considered for WDS REDU. Therefore, ROB and REDU are improved by pre-failure actions on the system (physical measures).
RAP and RES are related to the post-failure system performance. RAP is the speed of responding to (and recovering from) a failure event [1], and is generally measured by the time to recover (TTR) to normal conditions [8]. For example, the early detection of pipe burst/leakage and cyberattack reduces the TTR and improves system RAP [9,10,11,12]. To repair the failed components of a WDS, and resume normal operations, human and material resources should be prepared and dispatched effectively. Securing emergency water volume in tanks and bottled water can help mitigate the impact of service interruptions from pipe breaks and segment isolation [1,13,14,15]. A WDS with a large number of human resources for failure detection and repair (e.g., inspectors, engineers, and laborers) [16] has a higher RES than one that lacks resources, because the simultaneous repair of multiple failures is possible.
The four resilience components are interdependent: Improving one can lead to the enhancement of the others. Redundant network connectivity (e.g., emergency pipe connection among district metering areas (DMAs)) provides access to available water volume in tanks located in neighboring DMAs. Water resources/supply during seismic events can be preserved by the robust physical strength of tanks and associated pipelines. Moreover, rapid response to pipe and pump failures can be achieved with a sufficient number of emergency response staff and teams for dispatch.
This paper conducts a state-of-the-art literature review of WDS ROB studies and recommends potential research topics in the ROB context. Before the advent of the ROB concept [5,17], reliability (REL) was long considered as the measure of system performance in the WDS domain [18,19,20,21,22]. System REL is defined as the ability to supply the required quantity of water to customers at the appropriate pressure and quality, and is generally quantified according to service success probability [4]. Jung et al. [4] confirmed that using an ROB measure, i.e., the coefficient of variation of stochastic pressures, resulted in networks that performed consistently under uncertain failure conditions (i.e., pipe burst and fire flow) that were not considered in the design phase, compared with traditional REL-based design. Details on the mathematical comparisons between REL and ROB will be described in the following section.
ROB is related to the persistence of system performance; hence, it is clearly distinguished from other traditional system performance characteristics (such as REL, availability, and connectivity). Jung et al. [15] proved from their two correlation analyses of eight system performance metrics using 16 real WDSs that ROB has a weak correlation with traditional reliability and availability measures. A non-robust WDS shows significantly reduced functionality from disturbances and high pressure fluctuations owing to normal demand variations; in terms of water quality, stable chlorine concentration should be maintained in a robust system. Therefore, proper methodologies and indicators should be used to secure and improve WDS ROB effectively.
First, this paper summarizes previous studies on WDS ROB with respect to three research categories: Design, operation, and management (Section 2). Then, some future works are recommended for each of the three domains in Section 3 to promote the development of the field of WDS ROB. Finally, Section 4 provide a brief summary of the whole paper from which final conclusions on the state-of-the-art review and recommendations are drawn.
2. Robustness-Based Approaches
This section provides a detailed review of recent ROB-based methodologies proposed for the following: (1) WDS design and planning, (2) operation, and (3) management. Note that the review mainly focuses on methodologies that rigorously fit the definition of ROB (see the previous section) although some papers do not explicitly use the term “robustness.” On the other hand, there are many studies that use the term “robustness” that deal with other system performance characteristics such as reliability.
Recent ROB studies can be classified into two groups: (1) Studies in the first category propose a ROB indicator that quantifies the level of system ROB for WDS design, operation, and management; (2) those in the second category develop a ROB-based framework/model with which robust planning and management solutions are derived. The following subsections provide details on the two groups of studies.
2.1. Design and Planning
2.1.1. Hydraulic Robustness
The term “robustness” was first used in Kapelan, et al. [23] in the context of WDS design and planning. They proposed a multi-objective optimal WDS design model that minimized total system cost and maximized system robustness, and investigated the tradeoff between the two objectives for a range of uncertainty levels of nodal demand and pipe roughness. The ROB in [23] was quantified with the traditional REL formulation, meaning the probability that the stochastic nodal pressure is greater than or equal to the minimum pressure requirement.
where RELi is the reliability at node i, Prob() is a probability function of a given condition defined in the parenthesis, Pi and Pmin are the random and minimum required pressure at node i, respectively, and n is the number of nodes.
Giustolisi et al. [17] were the first to develop the ROB indicator () that explicitly incorporates the variations in stochastic pressure, which was maximized while minimizing the total system cost in their robustness-based WDS design model. The ROB indicator was calculated by the residual between the average pressure head and minimum pressure head divided by the standard deviation of stochastic pressure heads. Therefore, the proposed multi-objective WDS design seeks a design solution with high average pressure and low pressure variations to maximize . In [17], another robustness concept was introduced in formulating the system’s representative ROB value given the nodal ROB values: The system ROB value was calculated by the ROB value at the worst-performing node (the critical node). The Apulian network design problem was solved by the robustness-based design model in which the impact of uncertain demand and roughness and the type of probability density functions used were investigated from the resulting optimal cost and layout.
Puccini et al. [24] also proposed an ROB indicator for WDS design, which was computed from the average ratio of the number of nodes (Nw) with deficit pressure (node with pressure lower than the allowable minimum pressure) under single pipe failure conditions. The ROB indicator is calculated by 1 minus Nw as follows:
where is the total number of pipes, and is the number of nodes with deficit pressure under the kth pipe’s break condition (k = 1, …, np). However, the proposed index does not indicate the severity of failure and variation.
The coefficient of variation (COV) obtained given uncertain independent variables (in WDS, with varying nodal demand and pipe roughness from disturbances) can indicate the average-normalized level of variation of dependent variables (pressure and pipe flow). Therefore, the COV is the critical statistic that can be used in quantifying the ROB of a system. Inspired by this fact, Jung et al. [4] proposed a ROB indicator calculated based on the COV of stochastic pressures as
where ROBi is the robustness at node i, and and are the average and standard deviations of stochastic pressure, respectively (COV = ). With regard to the proposed ROB scheme, a network yielding pressures in the range 23–33 m is preferred over that with pressures in the range 18–38 m given the same average pressure of 28 m (40 psi) (Figure 1). The system ROB was defined as the minimum nodal ROB value (=). Therefore, increasing the system ROB decreases the variations in stochastic pressure while maximizing the average pressure at the critical node.
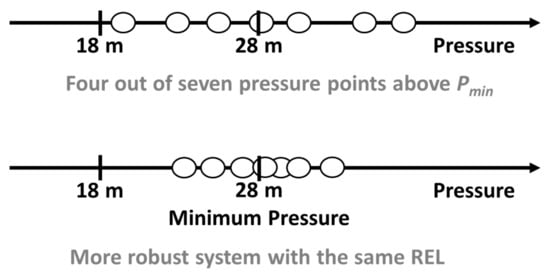
Figure 1.
Pressure variations in a robust water distribution system.
They incorporated the proposed ROB indicator into a multi-objective WDS design model to minimize the total system cost and maximize the ROB. Two types of the Anytown network design problems [25], i.e., pipe-only design and pipe and pump design problems, were solved using the proposed ROB-based and traditional REL-based design models. They were the first to quantitatively verify that the ROB-based design performs better than the REL-based design under pipe break and fire flow conditions not considered in the design phase. It was also confirmed that considering the ROB maximization objective resulted in engineeringly sound pipe configurations in which transmission lines are installed across the center of each pressure zone that small pipes either tap into or branch out from.
In their follow-up study [15], they investigated correlation between the ROB indicator and other reliability measures based on values obtained from 16 real networks with diverse characteristics (including network size and density, number of reservoirs, and average pipe size). It was mathematically proved that the ROB indicator has a weak correlation with the traditional REL measure (service success probability measured by Equation (1)), but it can be used as a surrogate measure of (1) system availability [25] quantified under single pipe failure conditions with 100% valve installation (N rule), and (2) seismic reliability [26] quantified under multiple pipe failure conditions during an earthquake. For example, the Pearson correlation coefficient of −0.06 was obtained between the minimum nodal ROB and minimum nodal REL. The minimum and demand-weighted averaged nodal ROBs have a correlation coefficient of 0.82 and 0.85, respectively, with the system availability metric. The seismic reliability indicator has a Spearman’s rank correlation coefficient of 0.89 with the minimum nodal ROB. Therefore, it was again confirmed that the ROB indicator, which does not take into account mechanical failure conditions in quantification but considers only hydraulic failure, can accurately reflect the system performance consistency under various disturbance conditions, and thus effectively constrain failure severity when used in WDS design optimization [1,4].
While Jung et al. [4] identified the effect of using the ROB indicator in pipe sizing given a fixed network layout, their follow-up study [27] investigated the use of the ROB indicator in the simultaneous determination of pipe sizes and layout (Table 1). They compared the Pareto optimal pipe design solutions of a large water grid network obtained by two types of design approaches: (1) The ROB- and REL-based approaches (hydraulic) and (2) two topological-metric-based approaches to minimize the total system cost and maximize the average node degree or meshedness coefficient ratios [7]. Jung and Kim [27] tried to derive a generalized conclusion on the features of ROB-based design and the indicator based on optimized network pipe sizes and layouts. Note that Jung et al. [15] tried to do the same based on the results of the correlation analysis between different indicator values of a number of networks (Table 1).

Table 1.
Summary of a group of consequential ROB studies in the context of WDS design.
Comparison of the two studies confirmed that using the ROB-based approach resulted in the most engineeringly sound layout and pipe hierarchy (smooth decrease in pipe sizes from the upstream to the downstream) among the four design approaches. In the ROB-based designs, as the total system cost increased, the Pareto optimal design added small distribution pipes to the two transmission pipelines passing through the center of the grid network. Note that the smallest pipe (50 mm) was added without a hydraulic purpose but simply to increase the number of pipes in the system in the topological-metric-based design.
The planning of the water system, consisting of water supply and distribution systems, generally considers temporally longer and spatially larger scales than the design: (1) A long time period (e.g., 50 years) is considered, and (2) not only WDS components (pipe, pump, valve, etc.) but also those of the water supply system (WSS) (water treatment plants, bulk water supply pipes, etc.) are determined. Therefore, a number of uncertainties are associated with water system planning. For example, decisions are made with the imperfect knowledge and information on the future development of the area and changes in public sentiment on water reuse [29,30].
An ROB concept has been applied to solve the planning problem and provide a compromise solution that performs well for all potential future scenarios [29,30,31,32,33,34,35,36,37,38,39] (“robust planning” or “robust optimization”). In robust planning, the planning/design period is often discretized into two to three periods over which adaptive decisions are made based on the information available over time. Therefore, the multiperiod-based robust planning approach can reduce system regret cost (i.e., overpayment and supplementary cost) by reducing the gap between what is implemented and what is actually needed. Another way to maintain the performance of the resultant solution is to minimize the variations in total system cost across potential future scenarios (second objective), in addition to minimizing the average total system cost (first objective) [29,30]. Note that the regret cost is computed by the absolute residual between the cost of the compromise (overall) solution and that of the scenario-optimal solution.
2.1.2. Structural Robustness
Compared with hydraulic ROB, structural ROB gives more weight to considering WDS connectivity than to hydraulic performance and its variations, which helps reduce the risk of water service outage [7,40]. Therefore, graph theory methodologies, which take into account network topological characteristics, are often used as the underlying analytical tool to investigate structural ROB [28].
Table 2 summarizes several representative structural ROB measures based on graph theory, which can be divided into two groups: Statistical and spectral [40]. Statistical indicators, such as average node-degree, average path length, and central-point dominance, quantify the organizational properties of the network based on the most frequent motifs and structural patterns, and relate them to network ROB and dynamics [40]. Spectral indicators (e.g., algebraic connectivity, spectral gap, and spectral radius), derived from the spectrum of a network adjacency matrix, quantify the network invariants that reveal useful information on the well-connectedness of the network, connectivity strength, and failure tolerance (e.g., link- and node-connectivity) [40].

Table 2.
Summary of structural ROB indicators based on graph theory.
The higher the algebraic connectivity, the more difficult it is to split the network into independent components [47]. A high average node degree indicates numerous possible connections (detours) in the network. The shorter the average path length, the greater the network water supply efficiency [48]. A network with high central-point dominance is a more centralized network [43]. The lower the spectral gap, the easier it is to split into sub regions by small failures [47]. A robust network has a low spectral radius value [47].
Few efforts have been made to apply structural ROB metrics to WDS design. Yazdani and Jeffrey [7] investigated the structural ROB of benchmark WDSs to identify vulnerable nodes or links under random failure of components. The results showed that algebraic connectivity and spectral gap are the important factors in determining structural ROB. Yazdani et al. [28] explored a WDS expansion problem using structural ROB analysis. The method was applied to the WDS of a developing country with a different expansion strategy, i.e., branched to looped (reflected by meshedness coefficient). The study concluded that the looped system has greater ROB as well as REDU.
In this section, we reviewed the state-of-the-art studies on WDS ROB for design and planning. In the context of WDS design, the ROB indicator has evolved in a way to incorporate the characteristics of system ROB more effectively, i.e., the persistence of system performance, by using the coefficient of variation of stochastic pressure. Consequential follow-up studies investigated the relationship between ROB and other traditional REL measures and the impact of considering the metric on layout and pipe size design. Robustness planning frameworks have also been proposed as an alternative that performs well over a set of future scenarios. We summarized structural ROB indicators and studies used them for WDS design.
2.2. Operation
WDS consists of various control components, such as pump, valve, and tank, which alter their state dynamically. Variable speed pumps change their speed to increase water head gain while additional pumps are turned on to deliver increased flow. The opening area of the flow control valve is altered in response to varying system conditions. From a hydraulic point of view, the purpose of WDS operation is to provide the required quantity of water at the required consistent pressure under disturbances. Therefore, the ROB concept should be applied to WDS operation problems to investigate its various aspects. However, little success has been achieved in incorporating the ROB concept in these problems, mainly because of the lack of ROB awareness in the domain.
Jung et al. [5] proposed a robustness-constrained WDS pump design and operation model to minimize total pump construction and operation costs with a constraint on the level of operational ROB. In their study, the system operational ROB index was defined as the maximum value of nodal daily maximum pressure differences in the system. This was the first study that converted dynamic system performance under unsteady conditions into a single ROB measure. The study confirmed that constraining the pressure variations in a day led to the installation of a greater number of small pumps than the least-cost approach, in which a few large pumps were constructed. A nonlinear tradeoff relationship was identified between the daily maximum pressure difference and the total pump construction and operation costs.
Di Nardo et al. [49] applied various graph theory measures (algebraic connectivity, spectral gap, and spectral radius) to divide WDS into subsections for operation and management purposes. They proved that ROB analysis based on graph theory provides useful metrics for continuity checks and network partitioning.
2.3. Management
In this study, WDS management is defined as the organization and coordination of system monitoring and failure response activities to achieve the system’s water supply goal. Over the last decade, few efforts have been made to introduce ROB in management activities such as pipe burst detection and segment isolation [2,50]. A pipe burst is the rupture caused by pipe deterioration, excessive pressure, and earthquakes, which should be promptly detected and located to repair or replace with a new pipe to avoid further collateral damage [8]. Numerous data-driven methods have been proposed to detect abnormal patterns in system hydraulic data (pressure and pipe flow) measured in a meter network (a group of meters installed over the system) [51,52]. Once a pipe burst is located, adjacent valves are shut down for recovery actions, which can cause water service interruptions in the area bounded by the valves (i.e., segment) [2,13,14].
Although pipe burst detectability increases with the increase in the number of meters [8], the total number of meters that can be installed in a system is generally constrained by budget and potential meter installation sites. Therefore, a limited number of meters are placed at their optimal location to provide informative data for system management and surveillance purposes. Little effort has been made to consider meter failure conditions (e.g., from mechanical issues or cyberattack) in optimal meter placement, which significantly reduces the quality/amount of system information in data acquired from the meter network. Jung and Kim [50] proposed a measure for the mechanical ROB of a meter network calculated by the coefficient of variation of detection probabilities (DPs) under single meter failure conditions, which was incorporated in a multi-objective meter placement model for WDS pipe burst detection to minimize the total meter cost, rate of false alarms, and mechanical ROB measure, and maximize DP. It was confirmed that the proposed ROB-based model can determine the optimal meter location and best combination of meters (among pressure and pipe flow meters) to maintain high detectability under meter failure conditions.
Having large segments with many nodes and pipes within the system increases the risk of extensive service interruptions. To avoid such collateral service failures and improve system ROB, large segments should be divided into multiple smaller segments of manageable size by installing additional valves; this decreases the potential maximum undelivered demand under pipe break conditions. Given budget constraints and limited spatial availability, the optimal number and location of valves should be determined for the installation problem. Choi et al. [2] were the first to introduce the concept of ROB in WDS optimal valve installation. They developed a ROB-based valve installation method that (1) prioritizes segments based on segment total demand and the existence of important public facilities (e.g., hospital, elderly center, fire station), and (2) selects the segments where valves should be installed to minimize the maximum undelivered segment demand under pipe break conditions.
3. Recommendations
This section raises some research issues and provides recommendations for future studies. More efforts should be made to better understand WDS ROB and its effects on system performance and operational/management efficiency.
One should be always note that ROB is one of the components of resilience (along with REDU, RAP, and RES). Therefore, the relationship between ROB and the other components should be investigated for successful response to (and recovery from) WDS failure events. To the best of the authors’ knowledge, no study has been performed to investigate the effects of pre-failure system performance measures (ROB and REDU) on post-failure performance measures (RAP and RES). Constructing a pipe network with low failure severity (i.e., a robust network) would help the system rapidly resume normal operations (high rapidity). To investigate the aforementioned issues, proper quantification methods and measures should be developed for REDU, RAP, and RES. For example, how can we comprehensively measure the RES of a WDS? Addressing this question is not as simple as just counting the number of response team members or the number of available emergency water supply vehicles.
3.1. Design and Planning
Although the ROB measure proposed in [4] considers the persistence of WDS performance, it is not as intuitive as the traditional probability-based reliability measure (Equation (1)) which indicates service success probability. For example, the ROB value of 0.8 does not accurately reflect the system’s water supply capacity but it could be used to compare different system designs. On the other hand, a reliability of 0.8 indicates 80% satisfaction of the minimum pressure requirement constraint. Therefore, rigorous analysis should be conducted to provide guidance on selecting the threshold ROB value to support engineering decision-making. This can be achieved with a large number of networks with various layouts and characteristics to derive a generalized conclusion on the selection.
The relationship between ROB and other existing reliability/resilience measures can be further examined. While Jung et al. [15] investigated the relationship between ROB and the traditional reliability measures (e.g., single-pipe failure availability and seismic reliability), other types of system performance measures (e.g., Todini’s resilience [53], its modified versions, and entropy-based reliability [54]) can also be used. Network topological indicators and a combined measure [55] can be used to identify the association between ROB and network topological characteristics (e.g., degree of looping [7], loop diameter uniformity). One can either (1) identify the relationship from a scatter plot of each of the two performance measures quantified in various networks [15], or (2) determine the Pareto relationship from the Pareto optimal design solutions obtained by minimizing the total cost and maximizing the two measures in a single network [55,56].
Finally, a novel robust planning approach should be developed to obtain a cost-effective compromise solution that performs well across potential future scenarios (e.g., high demand-low supply, low demand-high supply conditions). While most previous planning approaches have been applied to simple or simplified planning problems, it is more likely to have a redundant planning solution in a large real-world planning problem, if the average and variations in total system costs (the sum of total construction and regret costs) are minimized, just to decrease the gap between costs in different scenarios. In this case, the regret cost should be maintained within a reasonable range.
3.2. Operation and Management
The adoption of ROB in WDS operation and management (O&M) is at a relatively early stage compared with the domain of design and planning. First, the existing ROB index should be extended for quantifying the persistence of system performance under various unsteady conditions, in which system components such as pumps, valves, and tanks change their state simultaneously (e.g., ON/OFF, degree of opening) in response to disturbances (e.g., demand fluctuations, hydraulic and mechanical failure conditions). For example, Jung et al. [5]’s ROB indicator for pump operation could be improved to take into account varying undelivered total demand from segment isolation caused by neighboring valve closures for the recovery of a failed pipe.
Another research field to be pioneered is the development of ROB-based operational and management frameworks from which optimal O&M solutions are produced. Given that the level of uncertainties is still high even in the time-scale generally considered in WDS operation (e.g., minutes, hours, days), an optimal operational decision could be no longer optimal in an hour in which unanticipated system condition unfolds. As in WDS robust planning, minimizing the system’s failure severity under uncertain future condition (shorter time horizon for operation than planning) helps improve system ROB and the interesting research question is on how we can produce operational strategies to guarantee such performance characteristics. Some examples are by Zhuang et al. [9] and Jung et al. [57]. Zhuang et al. proposed an adaptive pump operation approach to provide usable pressure under pipe break and system repair/recovery conditions. Jung et al. developed a real-time pump operation model based on a dynamic process that rolls forward with each update of the supervisory control and data acquisition (SCADA) system monitoring information and demand forecast.
While Jung and Kim [50] proposed an ROB indicator to quantify the consistency of burst detectability of a meter network under meter failure conditions, the meter network’s ROB should also be considered in other meter-data-driven management activities and problems. ROB can be incorporated in state estimation network design where the optimal measurement locations, intervals, and type of measurements are determined to estimate state variables of interest that cannot be directly measured (e.g., nodal demands) [58]. Nodal demands are estimated using pressure and pipe flow measurements in WDS demand estimation problems, in which variations in estimation accuracy measures (e.g., root-mean-square-error) can be minimized to maintain the level of information in data under meter failure conditions.
4. Summary and Conclusions
This review first described the general definition and characteristics of WDS ROB. ROB is the system’s ability to maintain its functionality to supply water under disturbances, and should be understood as one of the four components of resilience (along with REDU, RAP, RES). Therefore, ROB is distinguished from traditional REL measures that are often quantified based on service success probability. Then, the state-of-the-art of ROB-based approaches were reviewed in three research areas of WDS: (1) Design and planning, (2) operation, and (3) management. These studies can be classified into two groups: (1) Development of ROB indicators and (2) proposing ROB-based frameworks from which a robust solution (for design, planning, and O&M) is derived. WDS ROB is a new research field pioneered during the last decade; hence, the majority of previous ROB studies focus on developing a ROB indicator for WDS design and planning.
Most ROB measures are incorporated into the variations of system performance of interest. Jung et al. [4]’s ROB indicator for design was computed from the coefficient of variation of stochastic pressure, whereas Jung and Kim [50]’s measure was calculated by the coefficient of variation of DPs under single meter failure conditions. While pressure was considered a WDS performance indicator in the former study, DP was used to quantify a meter network’s performance in the latter. The difference and uniqueness of the proposed ROB indicator were confirmed in subsequent studies [15,27]. A few robust planning approaches/frameworks have been proposed to obtain a robust water and wastewater infrastructure under uncertain future scenarios.
While little effort has been devoted to introducing ROB in the O&M domain, a few pioneering works have been published. First, a ROB-based pump design and scheduling model was proposed to smoothen the pressure trajectory during the day. The proposed ROB indicator is the first attempt to incorporate dynamic system performance under unsteady conditions into a single ROB measure. In the domain of WDS management, a ROB-based optimal valve installation method was introduced to minimize the potential total undelivered demand under segment isolation (i.e., failure severity).
This paper was then finalized by delivering some recommendations for future studies. Understanding the various aspects of WDS performance helps pave the way for a resilient system that can efficiently prepare, respond to, and recover from catastrophic failure events. Traditional probability-based system performance point of view is being shifted toward the system performance variation, ROB, and other resilience-based point of view. The new paradigm of WDS ROB-based design and O&M has just begun and should be carved out in subsequent studies.
Author Contributions
J.H.K. and D.J. have equivalently contributed to the literature review and summary, manuscript writing, and the recommendations of potential research topics. S.L. performed a thorough literature review on structural robustness.
Funding
This research was supported by the Keimyung University Research Grant of 2018.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lansey, K. Sustainable, robust, resilient, water distribution systems. In Proceedings of the WDSA 2012: 14th Water Distribution Systems Analysis Conference, Adelaide, South Australia, 24–27 September 2012; p. 1. [Google Scholar]
- Choi, Y.H.; Jung, D.; Jun, H.; Kim, J.H. Improving Water Distribution Systems Robustness through Optimal Valve Installation. Water 2018, 10, 1223. [Google Scholar] [CrossRef]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthquake spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Jung, D.; Kang, D.; Kim, J.H.; Lansey, K. Robustness-based design of water distribution systems. J. Water Resour. Plann. Manage. 2013, 140, 04014033. [Google Scholar] [CrossRef]
- Jung, D.; Lansey, K.E.; Choi, Y.; Kim, J.H. Robustness-based optimal pump design and scheduling for water distribution systems. J. Hydroinf. 2015, 18, 500–513. [Google Scholar] [CrossRef]
- Jung, D.; Kim, J. Robust Meter Network for Water Distribution Pipe Burst Detection. Water 2017, 9, 820. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. Applying network theory to quantify the redundancy and structural robustness of water distribution systems. J. Water Resour. Plann. Manage. 2011, 138, 153–161. [Google Scholar] [CrossRef]
- Jung, D.; Kang, D.; Liu, J.; Lansey, K. Improving the rapidity of responses to pipe burst in water distribution systems: a comparison of statistical process control methods. J. Hydroinf. 2015, 17, 307–328. [Google Scholar] [CrossRef]
- Zhuang, B.; Lansey, K.; Kang, D. Resilience/availability analysis of municipal water distribution system incorporating adaptive pump operation. J. Hydraul. Eng. 2012, 139, 527–537. [Google Scholar] [CrossRef]
- Taormina, R.; Galelli, S.; Tippenhauer, N.O.; Salomons, E.; Ostfeld, A. Characterizing Cyber-Physical Attacks on Water Distribution Systems. J. Water Resour. Plann. Manage. 2017, 143, 04017009. [Google Scholar] [CrossRef]
- Henry, D.; Ramirez-Marquez, J.E. Generic metrics and quantitative approaches for system resilience as a function of time. Reliab. Eng. Syst. Saf. 2012, 99, 114–122. [Google Scholar] [CrossRef]
- Ostfeld, A.; Salomons, E. Optimal layout of early warning detection stations for water distribution systems security. J. Water Resour. Plann. Manage. 2004, 130, 377–385. [Google Scholar] [CrossRef]
- Jun, H.; Loganathan, G. Valve-controlled segments in water distribution systems. J. Water Resour. Plann. Manage. 2007, 133, 145–155. [Google Scholar] [CrossRef]
- Jun, H.; Loganathan, G.; Deb, A.; Grayman, W.; Snyder, J. Valve distribution and impact analysis in water distribution systems. J. Environ. Eng. 2007, 133, 790–799. [Google Scholar] [CrossRef]
- Jung, D.; Yoo, D.G.; Kang, D.; Kim, J.H. Linear Model for Estimating Water Distribution System Reliability. J. Water Resour. Plann. Manage. 2016, 142, 04016022. [Google Scholar] [CrossRef]
- Nayak, M.A.; Turnquist, M.A. Optimal Recovery from Disruptions in Water Distribution Networks. Comput.-Aided Civ. Infrastruct. Eng. 2016, 31, 566–579. [Google Scholar] [CrossRef]
- Giustolisi, O.; Laucelli, D.; Colombo, A.F. Deterministic versus stochastic design of water distribution networks. J. Water Resour. Plann. Manage. 2009, 135, 117–127. [Google Scholar] [CrossRef]
- Lansey, K.E.; Mays, L.W. Optimization model for water distribution system design. J. Hydraul. Eng. 1989, 115, 1401–1418. [Google Scholar] [CrossRef]
- Duan, N.; Mays, L.W.; Lansey, K.E. Optimal reliability-based design of pumping and distribution systems. J. Hydraul. Eng. 1990, 116, 249–268. [Google Scholar] [CrossRef]
- Tolson, B.A.; Maier, H.R.; Simpson, A.R.; Lence, B.J. Genetic algorithms for reliability-based optimization of water distribution systems. J. Water Resour. Plann. Manage. 2004, 130, 63–72. [Google Scholar] [CrossRef]
- Xu, C.; Goulter, I.C. Reliability-based optimal design of water distribution networks. J. Water Resour. Plann. Manage. 1999, 125, 352–362. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water distribution reliability: analytical methods. J. Water Resour. Plann. Manage. 1988, 114, 253–275. [Google Scholar] [CrossRef]
- Kapelan, Z.S.; Savic, D.A.; Walters, G.A. Multiobjective design of water distribution systems under uncertainty. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Puccini, G.; Blaser, L.; Bonetti, C.; Butarelli, A. Robustness-based design of water distribution networks. Water Util. J. 2016, 13, 13–28. [Google Scholar]
- Cullinane, M.J.; Lansey, K.E.; Mays, L.W. Optimization-availability-based design of water-distribution networks. J. Hydraul. Eng. 1992, 118, 420–441. [Google Scholar] [CrossRef]
- Yoo, D.G.; Jung, D.; Kang, D.; Kim, J.H.; Lansey, K. Seismic hazard assessment model for urban water supply networks. J. Water Resour. Plann. Manage. 2015, 142, 04015055. [Google Scholar] [CrossRef]
- Jung, D.; Kim, J.H. Water Distribution System Design to Minimize Costs and Maximize Topological and Hydraulic Reliability. J. Water Resour. Plann. Manage. 2018, 144, 06018005. [Google Scholar] [CrossRef]
- Yazdani, A.; Otoo, R.A.; Jeffrey, P. Resilience enhancing expansion strategies for water distribution systems: A network theory approach. Environ. Modell. Softw. 2011, 26, 1574–1582. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Scenario-based robust optimization of regional water and wastewater infrastructure. J. Water Resour. Plann. Manage. 2012, 139, 325–338. [Google Scholar] [CrossRef]
- Kang, D.; Lansey, K. Multiperiod planning of water supply infrastructure based on scenario analysis. J. Water Resour. Plann. Manage. 2012, 140, 40–54. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Finance 1952, 7, 77–91. [Google Scholar]
- Mulvey, J.M.; Vanderbei, R.J.; Zenios, S.A. Robust optimization of large-scale systems. Oper. Res. 1995, 43, 264–281. [Google Scholar] [CrossRef]
- Watkins, D.W., Jr.; McKinney, D.C. Finding robust solutions to water resources problems. J. Water Resour. Plann. Manage. 1997, 123, 49–58. [Google Scholar] [CrossRef]
- Walski, T. Long-term water distribution design. In Proceedings of the World Environmental and Water Resources Congress 2013, Cincinnati, OH, USA, 19–23 May 2013; pp. 830–844. [Google Scholar]
- Basupi, I.; Kapelan, Z. Flexible water distribution system design under future demand uncertainty. J. Water Resour. Plann. Manage. 2013, 141, 04014067. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Walski, T.M. Accounting for Phasing of Construction within the Design of Water Distribution Networks. J. Water Resour. Plann. Manage. 2014, 140, 598–606. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Walski, T.M. Taking Account of Uncertainty in Demand Growth When Phasing the Construction of a Water Distribution Network. J. Water Resour. Plann. Manage. 2015, 141, 04014049. [Google Scholar] [CrossRef]
- Watkins, D.W., Jr.; McKinney, D.C. Screening Water Supply Options for the Edwards Aquifer Region in Central Texas. J. Water Resour. Plann. Manage. 1999, 125, 14–24. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Walski, T.M. Comparison of various phased approaches for the constrained minimum-cost design of water distribution networks. Urban Water J. 2016, 13, 270–283. [Google Scholar] [CrossRef]
- Yazdani, A.; Jeffrey, P. A complex network approach to robustness and vulnerability of spatially organized water distribution networks. In Proceedings of the 12th annual Water Distribution Systems Analysis conference WDSA2010, Tucson, AZ, USA, 12–15 September 2010; pp. 129–130. [Google Scholar]
- Newman, M. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Costa, L.d.F.; Rodrigues, F.A.; Travieso, G.; Villas Boas, P.R. Characterization of complex networks: A survey of measurements. Adv. Phys. 2007, 56, 167–242. [Google Scholar] [CrossRef]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 35–41. [Google Scholar] [CrossRef]
- Fiedler, M. Algebraic connectivity of graphs. Czech. Math. J. 1973, 23, 298–305. [Google Scholar]
- Estrada, E. Network robustness to targeted attacks. The interplay of expansibility and degree distribution. Eur. Phys. J. B-Condens. Matter and Complex Syst. 2006, 52, 563–574. [Google Scholar] [CrossRef]
- Bonacich, P. Power and Centrality: A Family of Measures. Am. J. Sociology 1987, 92, 1170–1182. [Google Scholar] [CrossRef]
- Giudicianni, C.; Di Nardo, A.; Di Natale, M.; Greco, R.; Santonastaso, G.F.; Scala, A. Topological Taxonomy of Water Distribution Networks. Water 2018, 10, 444. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Di Nardo, A.; Giudicianni, C.; Greco, R.; Herrera, M.; Santonastaso, G.F. Applications of Graph Spectral Techniques to Water Distribution Network Management. Water 2018, 10, 45. [Google Scholar] [CrossRef]
- Jung, D.; Kim, J.H. Using Mechanical Reliability in Multiobjective Optimal Meter Placement for Pipe Burst Detection. J. Water Resour. Plann. Manage. 2018, 144, 04018031. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, S. A review of data-driven approaches for burst detection in water distribution systems. Urban Water J. 2017, 14, 972–983. [Google Scholar] [CrossRef]
- Jung, D.; Lansey, K. Water distribution system burst detection using a nonlinear Kalman filter. J. Water Resour. Plann. Manage. 2014, 141. [Google Scholar] [CrossRef]
- Todini, E. A More Realistic Approach to the “Extended Period Simulation” of Water Distribution Networks. In Advances in Water Supply Management, Proceedings of the CCWI ’03 Conference, London, UK, 15–17 September 2003; Maksimovic, C., Butler, D., Memon, F., Eds.; CRC Press: London, UK, 2003. [Google Scholar] [CrossRef]
- Tanyimboh, T.T.; Templeman, A.B. A quantified assessment of the relationship between the reliability and entropy of water distribution systems. Eng. Optim. 2000, 33, 179–199. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Todini, E. The combined use of resilience and loop diameter uniformity as a good indirect measure of network reliability. Urban Water J. 2016, 13, 167–181. [Google Scholar] [CrossRef]
- Creaco, E.; Fortunato, A.; Franchini, M.; Mazzola, M. Comparison between entropy and resilience as indirect measures of reliability in the framework of water distribution network design. Procedia Eng. 2014, 70, 379–388. [Google Scholar] [CrossRef]
- Jung, D.; Kang, D.; Kang, M.; Kim, B. Real-time pump scheduling for water transmission systems: Case study. KSCE J. Civ. Eng. 2015, 19, 1987–1993. [Google Scholar] [CrossRef]
- Jung, D.; Kim, J.H. State Estimation Network Design for Water Distribution Systems. J. Water Resour. Plann. Manage. 2018, 144, 06017006. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).