Abstract
With reference to a classical wet tank equipped with a wastewater submersible pump, in this research, an advanced numerical model has been used in order to obtain the optimal pump scheduling of on/off operation and variable pump speed. Then, in order to evaluate the time decay of pump performances, the mechanical wear has been artificially simulated and the performance curves have been experimentally obtained for different rotational speeds. Finally, the benefits, as well as the feasibility, of pump scheduling have been evaluated for differing operating conditions. According to the results, the optimal pump scheduling achieves large energy savings up to 43%, for soft mechanical wear. If the mechanical wear is considered, the energy savings are large as well, between 35.60% and 26.70%, for medium and hard mechanical wear, respectively. On the other hand, the limitation of such a strategy has been highlighted: the feasibility of pump scheduling is limited by the elevation of the downstream tank. According to the results, energy savings can be achieved until the elevation of the downstream tank is 67% of the pressure head at the best efficiency point, whereas such percentage decreases to 50% for hard mechanical wear. Finally, the results show that plant efficiency is strongly affected by the mechanical wear: an accurate maintenance of the pumping system is therefore recommended in order to attenuate the time decay of pump performances.
1. Introduction
Nowadays one of the main challenges in international community policies consist of increasing the efficiency of systems consuming energy [1]. As an example, in the European Union, the Directive 2009/125/EC [2] fosters some technical changes in the industrial design of water pumps [3].
According to the basics of the eco-design, a pumping system, made by a pump, motor, speed driver and regulation devices, is considered as a single part of the water transport system. In order to assess the real energy consumption, a pumping system should be therefore analyzed in its own entirety.
Management techniques, aimed at increasing the energy efficiency in water systems, are deeply investigated in literature. With regard to water supply systems, different strategies have been proposed to both reduce energy consumption [4,5,6] and water leakage [7], such as pressure control by pressure reducing valves (PRVs) [8,9], energy recovery by micro-turbines or pumps as turbines (PATs) [10,11,12,13,14,15] and optimal location of PRVs or PATs within a water network [16,17,18,19]. Optimal pump scheduling [20,21] is a further strategy of considerable interest within the management of water supply and drainage networks. Indeed, due to the possible variations in the operating conditions (such as variable flow and level oscillation within the wet tank), the pump (or multiple pumps) cannot operate at its own best efficiency point (BEP) [22]. Thus, a pump scheduling is required in order to optimize the system performances. This strategy can be performed by the use of a variable frequency driver (VFD) in order to vary the impeller rotation speed, according to the variation of operating conditions.
A pump scheduling optimization consists of finding, for each time step, the set of values describing whether each pump is working or not (on/off scheduling) and what the rotational speed is [22]. Several studies exist in literature dealing with pump scheduling by different sophisticated optimization tools and algorithms. The first several studies were focused on the use of linear programming [23], integer linear programming [24] and non-linear programming [25]. The latter are unlikely to allow the obtained results to be extended to any systems different from those analyzed. More recently, heuristic algorithms [26,27,28,29] were employed in couple with artificial neural networks to reproduce results of previous hydraulic simulations.
With regard to drainage pumping systems, the topic of pump scheduling has been investigated by very few studies [22,30], due to the non-linear behavior of stormwater flow rates. Since the drainage pumping systems are equipped with storage tanks, the pump scheduling therefore consists of optimizing the instantaneous rotational speed of the pump and the on/off sequence, depending on the water level within the tank.
In drainage systems, a further aspect that should be considered is the time decay of pump performances. Indeed, due to the effect of solid transport, the pump is affected by significant mechanical wear. In case of really high sediment concentration, mechanical wear is likely to be responsible for pump failure, otherwise a progressive reduction of pump performances is observed. Thus, it should be worth investigating if the optimal scheduling changes due to the time decay, as well as assessing any differences in energy reduction between new and used pumps.
In this research, several experiments have been performed on a submersible pump. In addition, the mechanical wear has been reproduced artificially in order to investigate the behavior of an aged machine as well. Two different scenarios have been compared from a strictly energetic point of view. In the first scenario, the pump is assumed to be working in constant speed and in the on/off mode, according to the water level in the tank. The optimized pump scheduling is instead performed in the second scenario, finding the on/off sequence, as well as the instantaneous rotational speed of the pump. Then, a comparison of energy savings between the two scenarios has been carried out with the aid of efficiency indices. Finally, boundary conditions, that is, the stage of mechanical wear, the size of the pump and elevation of the downstream tank, have been modified to make the comparison under differing operating conditions.
2. Materials and Methods
2.1. Tank Design
The design of the pumping system has been performed by best practice criteria, assuming a constant speed pump and an on/off control based on the water level within the wet well. The sketch of the wet tank containing the submersible pump is shown in Figure 1 [22].
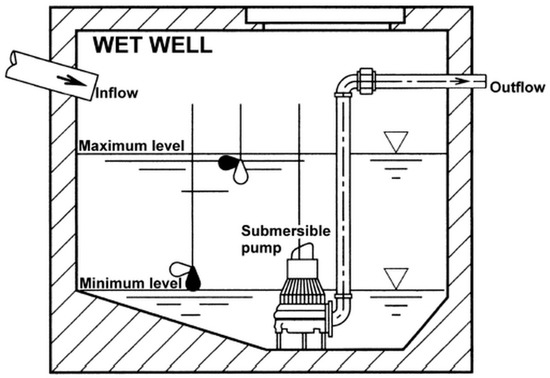
Figure 1.
Sketch of the wet well of the pumping station with a single submersible pump [22].
The pumping time required to pass from the maximum to the minimum water level in the wet well is expressed by Equation (1):
where is the storage capacity of the tank, is the input flow rate (variable in time) and is the pumped flow rate. Obviously, the pumped flow rate depends both on the pumping head, which is variable due to the variability of both the water level inside the wet well and the head loss, which in turn depends on the pumped discharge. Nevertheless, only for the purpose of designing the wet well, if the pumping head is high, its variability can be neglected, along with the variability of , which can be definitively considered constant. Thus, if the pump unit is correctly chosen, the output discharge that appears in Equation (1) can be considered equal to (i.e., the discharge at the best efficiency point (BEP) of the pump). Then, for the energy assessment and the case study, the complete hydraulic momentum equation will be used, to consider the variability of the output discharge during the day.
The time required by the inflow stream to fill the storage tank when the pump is off is:
The duration of a pump cycle (i.e., the required time between two starts of the pump) can be therefore expressed as:
Furthermore, the number of starts in one hour can be obtained by Equation (4).
If, as explained before, is considered constant, by deriving Equation (4) with respect to , the maximum number of starts occurs when is the half of . Therefore, the storage volume can be obtained by replacing, in Equation (4), the value of . It only depends on the characteristics of the machine (i.e., and the maximum allowed number of starts per hour, ), usually suggested by the pump manufacturer:
2.2. Optimization Model
If the pump speed is varied with a speed driver, then its performance can be modified instantly to reduce its power absorption. Nevertheless, during the day, the input flow rate is variable, and the problem of reducing the daily energy must consider the whole flow pattern. Thus, a complete and complex optimization model must be used, as shown by [22]. The objective function and hydraulic constraints of the model are shown in Equations (6) and (7), respectively.
where , , , are the optimization variables, representing the pumped discharge, the rotational speed of the pump, the water level into the well tank and the switch of the pump, respectively, at the time instant . is a binary variable which is equal to 1, if the pump is on at the i-th interval, and 0 otherwise. The objective function in Equation (6) is the energy spent by the pump, calculated as the sum within the time window of the power () requested by the pump in the time instant , whose length is . Moreover, in the first equation of the system (Equation (7)), the pressure head requested by the plant, namely , has been set, for each time instant , equal to the head ensured by the pump—if it is switched on (i.e., is 1)—calculated by a second order interpolating polynomial curve of experimental points. The second equation of the system (Equation (7)) expresses the water level in the wet well at the time instant by means of a centered finite difference scheme of the continuity equation, considering the difference between the input () and output () discharge. Furthermore, according to the continuity equation, represents the cross-section area of the well, whereas and represent, respectively, the pumped and inflow discharge. The first two equations, namely the momentum and the continuity equation, consider the variability of the operating point of the pump, depending on the rotating speed and the water level inside the wet well. Moreover, the pumped discharge of each time step can be set between a maximum and a minimum value. In particular, the minimum value has been set equal to 0, whereas the maximum value, namely , has been assumed as three times . Such constraint is an identity if the pump is switched off (i.e., is 0). Concerning the instant rotation pump speed , it can be varied within the allowable motor speed range. Furthermore, a minimum and a maximum bond have been fixed for the water level . Finally, a maximum bond has been fixed also for the number of starts per hour, namely .
The optimization problem is classified as mixed integer non-linear (MINLP) since it involves both linear and non-linear constraints, continuous and integer variables and a non-linear objective function. The Basic Open-Source Nonlinear Mixed INteger Programming (BONMIN) [31] has been chosen to solve the optimization. Further details on model equations and on the resolution of the optimization problem can be found in [22].
3. Case Study
3.1. Experimental Investigation of Pump Performances and Aging of the Pump
A submersible sewage pump (K series—Caprari S.p.A., Modena, Italy) has been tested in the hydro energy laboratory (HELab) of the CESMA—University of Naples Federico II. The pump best efficiency point occurs when the discharge is equal to 4 litres per second, with a pumping head equal to 25.5 m and a maximum efficiency equal to 0.24.
A detailed section of the hydraulic components of the tested pump is shown in Figure 2.
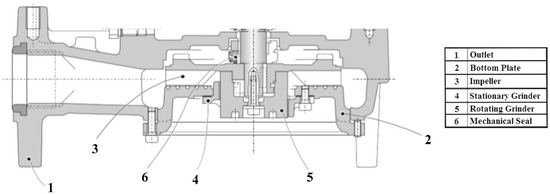
Figure 2.
A detailed section of the tested Caprari K series pump.
The pump test was carried out according the ISO9906 standard regulation [32] which describes the methodology to lead a lab test for the measurement of the steady performances of a pump. The submersible pump was fed by an underground storage reservoir, characterized by a 110 m3 volume and a 3 m water height. The hydraulic scheme of the test line is presented in Figure 3.
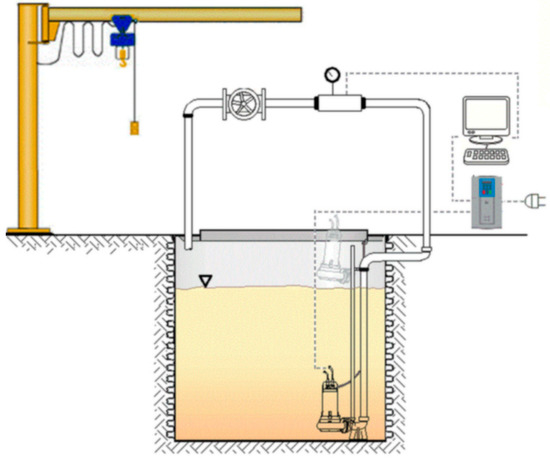
Figure 3.
Sketch of the experimental test line.
According to Figure 3, the pump is located on the bottom of the tank and conveys the water into a 2” steel pipe (internal diameter 54 mm). A piezoelectric transducer (accuracy < 0.5%) was employed to measure the pressure downstream the pump. The measurement section was located 2 diameters from the pump exit. Another piezometric transducer was used to measure the water level within the tank. Since the tank is very large compared to the pump and its discharge, the velocity inside the tank can be considered equal to zero. Thus, the pump head could be calculated as the difference between the pressure head downstream the pump and the water level in the tank. A regulation valve was used to set the discharge value, which was measured by an electro-magnetic discharge meter (accuracy < 0.5%). The input power was measured by a wattmeter (accuracy < 0.5%). In addition, a SCADA system ensured the automatic acquisition of the data. The test line is closed and the water is therefore conveyed back to the tank, as shown in Figure 3. For the sake of generality and standardization, all the tests were carried out with fresh water, even if the pump was designed to work with sewage water.
The automatic measuring system acquires additional parameters, including temperature (considered constant in the whole tank) and the waveform of the electric signal. The wave frequency of the electric supply was varied by a VFD (Santerno, IRIS BLUE, 11 kW, Poggio Piccolo (BO), Italy) whose efficiency was preliminarily assessed at full speed condition (50 Hz). According to such a preliminary test, the average efficiency of the VFD was 98%, whereas the efficiency at the best efficiency point amounted to 98% as well. Then, six different values of frequency (from 50 Hz to 25 Hz with a pace of 5 Hz) were tested to modify the rotational speed of the motor from 1500 to 3000 rpm. For each value of frequency, different discharges were set by a gate valve. For each discharge, five sets of measurements composed of 200 samples each (acquisition rate 0.01 s, averaging time 2 s) were acquired. The test started after a warm-up time, during which the pump was operating at its BEP and its maximum speed (50 Hz), as requested by the ISO9906 standard [32].
Characteristic and efficiency curves of the tested pump are shown in Figure 4 for different values of rotational speed (i.e., six different values of induction frequency of the motor), ranging between 25 and 50 Hz. In Figure 4, , , and η represent, respectively, pressure head, discharge and efficiency of the pump. The efficiency is comprehensive of both the hydraulic efficiency of the hydraulic part and the electric efficiency of the motor. The efficiency values decreased along with the rotational speed. This behavior occurs due to two reasons: the electrical efficiency of the motor reduces when the induction frequency was reduced, and the hydraulic efficiency of the pump reduces when the angular velocity of the impeller was reduced. This last behavior is in contrast with the affinity law theory but experimentally demonstrated by many studies [33,34,35]. Of course, the performance curves of Figure 4 are representative of steady conditions, while the pump usually operates in a tank whose water level is variable. Nevertheless, the water level variability inside the wet well can be considered slow, and unsteady behavior of the system can be neglected in the equations of the system (Equation (7)) without any considerable error, as demonstrated by [25]. Any further information about the pump test can be found in the ISO9906 regulation [32].
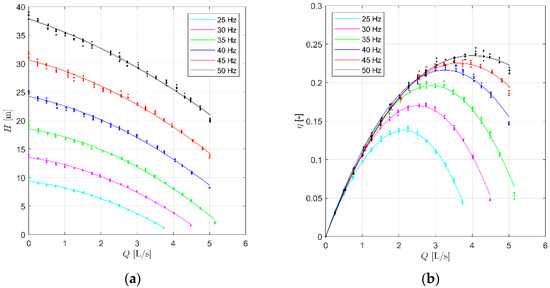
Figure 4.
Characteristic (a) and efficiency (b) curves of the tested pump.
Due to sediment motion, the pump was affected by progressive wear. In order to avoid the clog of solid particles between the open impeller and the bottom, the inner part of the bottom plate is generally equipped with concentric circular slots characterized by a depth of some millimeters (2 mm for the tested pump). As an effect of the wear, the crests between the circular slots are subject to a significant reduction, until a complete abrasion in the presence of high wear. As the bottom plate is abraded, the clearance between the impeller and the plate increases and the performance of the machine decreases. The effect of the erosion has been simulated. This effect has been reproduced by introducing calibrated thick elements under the fixing screws of the plate, preventing the complete tightening, imposing the distance between the plate and the impeller clearance. A sketch of the pump section with the impeller and the bottom plate is shown in Figure 5, as well as the effect of the erosion on the bottom plate and its simulation.
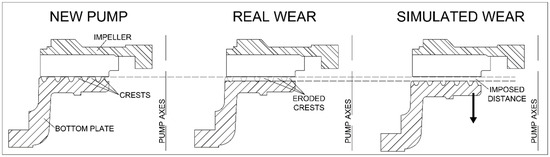
Figure 5.
Sketch of the pump section and effect and simulation of the erosion.
Two different stages of mechanical wear were simulated by using elements characterized by a thickness of 1 mm and 2 mm, as representative of an intermediate and high wear, respectively. Characteristic and efficiency curves of the artificially aged pump have been therefore obtained. Of course, according to this procedure, the wear of the electric motor is neglected. The aging of an electric motor has been considered much slower than the aging of both the impeller and the bottom plate which operate with sewage water. Figure 6 and Figure 7 show the characteristic curves of a pump affected by medium and hard mechanical wear, respectively.
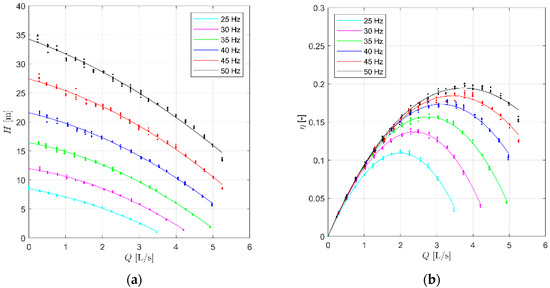
Figure 6.
Characteristic (a) and efficiency (b) curves of a pump affected by a medium wear.
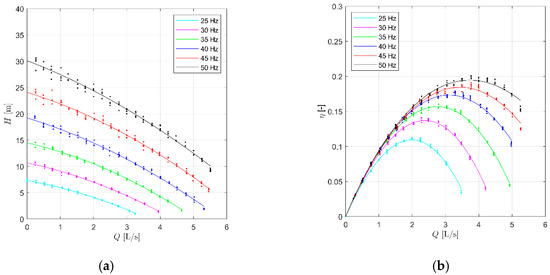
Figure 7.
Characteristic (a) and efficiency (b) curves of a pump affected by hard wear.
According to Figure 6 and Figure 7, the increase of mechanical wear results in a reduction of both pressure head and efficiency. If the maximum speed (50 Hz) performance is compared for a pump with medium wear, the maximum head for 50 Hz is 35 m (versus 37.5 m for the new pump), with a 3.7 L/s BEP discharge and a BEP efficiency equal to 0.22. For the pump with hard wear, the maximum head further decreases to 30 meters, with a maximum efficiency lower than 0.17 and a 3.6 L/s BEP discharge. In Figure 8, the efficiency and characteristic curves of the aged pumps are compared with the performance of the new pump. The differences in pump efficiency between a new and an aged pump are smaller for the lower pump speeds. This behavior probably occurs because the erosion of the bottom plate slightly affects the pump performance when the rotating speed is low.
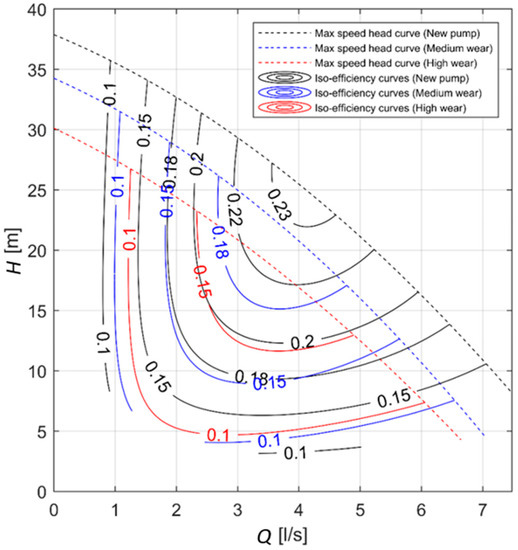
Figure 8.
Comparison of characteristic and efficiency curves for different stages of wear.
3.2. Sewage Flow Pattern and Wet Well Design
As a daily pattern of the wet tank inflow, the hydrograph measured in Arena Sant’Antonio pumping station (Naples, IT) was used. The shape of the hydrograph is shown in Figure 9.
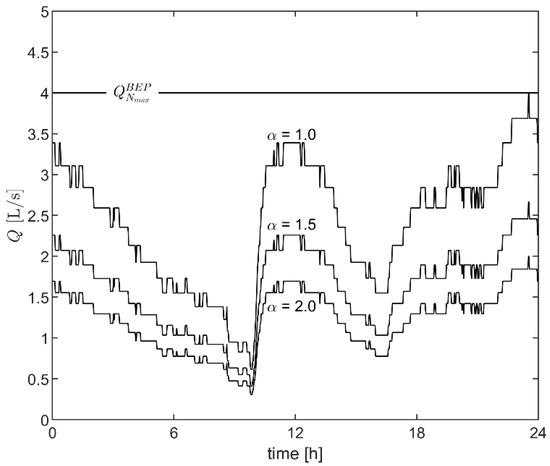
Figure 9.
Design hydrographs for different values of α.
For the tested pump the storage volume of the wet well resulted in about 0.45 m3, as calculated by Equation (5). A circular wet well with a diameter of 1.13 meters (1 m2 surface) was chosen. The experimental daily pattern was scaled by dividing the measured discharge by the maximum measured discharge, as shown in Equation (8).
Then, in order to analyze different design conditions, a maximum discharge was considered as a fraction of the discharge at the BEP condition for the maximum impeller speed (i.e., 2900 rpm–50 Hz), namely .
where the coefficient α has been set equal to 1, 1.5 and 2, corresponding to an undersized, slightly oversized and oversized pump, respectively. The resulting values of correspond respectively, to a high, medium and small fraction of the maximum flow rate . Thus, according to Equation (8), the inlet discharge pattern was obtained as follows:
In Figure 9, the pattern is presented for different values of fraction rate α. When α is equal to 1, the flow hydrograph exhibits the highest values of the input discharge and its maximum value corresponds to the BEP discharge of the pump operating at its maximum speed (50 Hz). Higher values of α correspond to lower input discharge (i.e., the higher α is, the more the pump is oversized with respect to the inflow discharge).
Then, the pumping head is calculated for each time instant by the following quadratic head-loss formula:
where is the static head when the wet well is empty; is the water level in the wet well at the time ; is the pumped flowrate; is a coefficient depending on both the material and the diameter of the outlet pipe, whose expression is shown as follows:
where represents the pressure head at BEP condition for the maximum impeller speed; is a coefficient equal to:
The coefficient has been set equal to 0.25, 0.5 and 0.75, being representative of pumping systems characterized, respectively, by a small, medium and high elevation of the downstream tank (). The effect of on the plant curves is shown in Figure 10.
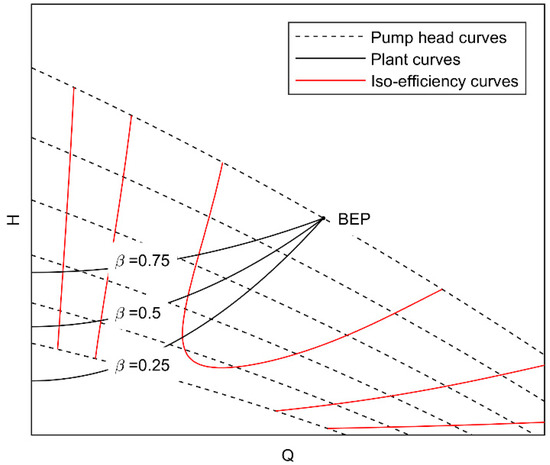
Figure 10.
Pump head curves and plant curve depending on β.
According to Figure 10, the quantity is the ratio between the friction losses and the total pumping head at the BEP. As the output discharge reduces (due to a rotational speed reduction), the needed pumping head reduces, and this reduction is higher for lower values. Furthermore, for lower values, the efficiency reduction with the discharge is lower when compared with larger values. Thus, an output discharge reduction is expected to be more convenient for lower values.
4. Results and Discussion
The optimization model has been applied to different scenarios, corresponding to different pump size, elevation of the downstream tank and pump mechanical wear. For each case, a codified name has been assigned, based on three letters—S, M and H. According to the codified name, the first letter is representative of the stage of mechanical wear (i.e., soft (S), medium (M), or hard (H)); the second and third letter refer, respectively, to the fraction of pumped discharge (at BEP point and full speed) with respect to the maximum inflow discharge, and the entity of downstream tank elevation (i.e., small (S), medium (M) or high (H).)
4.1. Energy Indexes
In order to compare the two control strategies (constant speed and optimized speed), three energy indexes have been defined. Such indexes are based on three values of energy: (i) a reference value of daily requested energy, , that can be calculated for each scenario as follows,
(ii) the daily energy required by the pumping station operating at its maximum speed, with starts and stops controlled by the water level bonds () and (iii) the daily energy required by the pumping station operating with the optimal pump scheduling (). The latter was calculated by the application of the optimization model with a 1 min timestep, while the former was calculated considering the variability of the output flow due to the variation of the water level inside the wet well and the performance of the pump operating at its maximum speed with a 1 s timestep.
Then, two efficiencies are obtained, such as, and , as shown in Equations (15) and (16).
Finally, the reduction of energy use by variable speed control is calculated as follows:
4.2. Results of the Energy Assessment and Discussion
The main figures of the energetic comparison are shown in Table 1. Without any optimal pump scheduling, considering a new pump operating at a constant speed in on/off mode, the efficiency of the pumping system amounts to between 0.20 (case S_S_H) and 0.08 (case S_H_S). In particular, the largest value corresponds to a small BEP flow rate and a high downstream tank elevation, whereas the lowest value refers to a high BEP flow rate and small downstream tank elevation. For the intermediate pump BEP flow rate (case S_M_H), the maximum efficiency of the pumping system was found to be 0.19. By accounting for mechanical wear, the efficiency of the constant speed pumping system decreases, ranging between 0.15 (case H_M_H) and 0.07 (case H_H_S). The effect of the reduction in BEP efficiency due to the time decay (from 0.23 for a new pump to 0.17 for hard mechanical wear) is partially balanced by the reduction of the pumping head, thus, the hydraulic power required for pumping at BEP condition. Moreover, with regard to an undersized pump (α = 1), no solution is obtained, since the highest inflow exceeds the outflow discharge.

Table 1.
Main figures of the energetic comparison and savings achieved by the optimal pump scheduling.
When the pump scheduling is optimized, the efficiency of the pumping system significantly increases, ranging between 0.21 (case S_S_H) and 0.14 (case S_H_S), if the static head is low. The benefit of the optimization decreases as the static head increases. Furthermore, the reduction in the energy use is very large for β equal to 0.25, since varies between −43.10% (case S_H_S) and −31.60% (case S_S_S). The benefit of pump scheduling decreases for β equal to 0.5, varying between −8.80% (case S_H_M) and −17.90% (case S_S_M). No reduction in the energy use is observed for β equal to 0.75, except a small reduction (i.e., −3.40%) for the undersized pump (α = 1). Among all the working conditions, the use of an oversized pump (α = 2) in variable speed pump scheduling represents the solution saving the most energy.
In the presence of mechanical wear, the pump scheduling allows a significant energy reduction, that is, −35.60% for medium mechanical wear (case M_H_S) and −26.70% for hard mechanical wear (case H_H_S), but only for the low static head cases. For a fixed value of mechanical wear (δ), the use of an oversized pump (α = 2) is proven to be the best choice again.
With reference to the efficiency (both and ), the best operating conditions seem to occur with α equal to 1 (i.e., for an undersized pump). Indeed, the efficiency of the system is the highest for each erosion level and each static head. Nevertheless, when the system is designed with α equal to 1, its reliability is low, since the pump is not able to convey a discharge higher than the maximum predicted discharge. On the other hand, when α is equal to 2, the probability that the input discharge overcomes the pumping discharge significantly decreases, but, both in constant speed regulation and in optimized regulation, the system efficiency decreases too. The choice of α, during the design of the pumping system, should be then related both to the reliability of the system (i.e., its capacity to convey high discharges) and its efficiency.
In order to deeply investigate the effect of mechanical wear on the system efficiency, new calculations have been performed by refining the steps in the β values. The calculations were carried out by assuming a slightly undersized pump (α = 1.5), which is a compromise between reliability and efficiency. The results have been obtained for different mechanical wear conditions, as shown in Figure 11. The figure shows the system efficiency in the on/off mode (dashed line) and optimal scheduling (continuous line) for different β values and mechanical wear. The effect of the optimization on the efficiency seems to be not affected by the static head; thus, the benefit decreases as β increases. For soft mechanical wear, an optimal pump scheduling ensures energy savings until β = 0.67. This value decreases as the mechanical wear increases, with a minimum value β = 0.5 for the hardest wear.
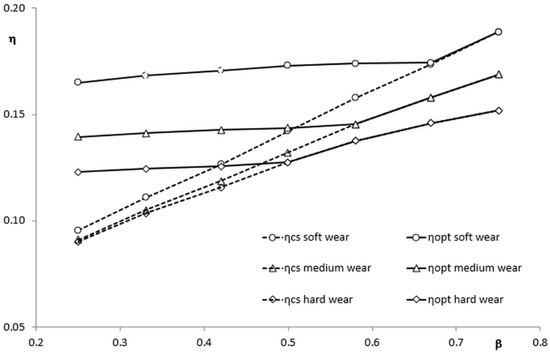
Figure 11.
System efficiency in both constant and variable speeds for different wear conditions.
5. Conclusions
In this research, experimental tests have been performed on a grinder pump and mechanical wear has been reproduced artificially in order to evaluate the time decay of pump performances. Characteristic curves have been therefore obtained for different stages of mechanical wear.
For the sake of generality, several parameters have been introduced, thus different working conditions have been evaluated. Such parameters, α and β, have been varied in order to consider, respectively, different pump sizes and elevations of the downstream tank.
An optimal pump scheduling has been performed and the mathematical model [22] has been solved by the Basic Open-Source Nonlinear Mixed INteger Programming (BONMIN) [31]. Furthermore, the optimization problem has been performed for each stage of mechanical wear, as well as for all the working conditions.
The obtained results show that optimal pump scheduling represents a powerful strategy to reduce energy consumption in wastewater pumping systems, if compared with an on/off operation at constant speed. The maximum energy savings were about 43% for soft mechanical wear, oversized pump and small elevation tank (case S_H_S). In the presence of mechanical wear, the maximum energy reduction amounts were between −35.60% and −26.70% for medium and hard mechanical wear, respectively. Furthermore, the benefit of pumping scheduling decreases as the elevation of the downstream tank (i.e., β) increases. Indeed, for soft mechanical wear, an optimal pump scheduling allows energy savings until β = 0.67 whereas, for the hardest mechanical wear, the cut-off value of β decreases to 0.5. Furthermore, in the presence of mechanical wear, no solution has been obtained with reference to an undersized pump (α = 1), since the highest inflow exceeds the outflow discharge.
With regard to the efficiency (both and ), the best operating conditions seem to occur for an undersized pump (α = 1). Nevertheless, if the system is equipped with such an undersized pump, its reliability is low, since the pump is not able to convey a discharge higher than the maximum predicted discharge. On the other hand, in case of an oversized pump (α = 2), system efficiency is very low. Therefore, the choice of α should consider both the reliability and efficiency of the system.
Finally, the results show that plant efficiency is strongly affected by mechanical wear. An accurate pump maintenance is therefore recommended in order to prevent the reduction of machine efficiency, thus reducing energy consumption.
Author Contributions
Conceptualization, O.F., R.M. and M.C.M.; methodology, O.F., R.M. and M.C.M.; software, O.F., R.M. and M.C.M.; validation, O.F., R.M. and M.C.M.; formal analysis, O.F., R.M. and M.C.M.; investigation, O.F., R.M. and M.C.M.; resources, O.F., R.M. and M.C.M.; data curation, O.F., R.M. and M.C.M.; writing—original draft preparation, O.F., R.M. and M.C.M.; writing—review and editing, O.F., R.M. and M.C.M.; visualization, O.F., R.M. and M.C.M.; supervision, O.F., R.M. and M.C.M.; project administration, O.F., R.M. and M.C.M.; funding acquisition, O.F., R.M. and M.C.M.
Funding
This paper was partly funded by the ERDF (European Regional Development Fund) Interreg Atlantic Area Programme 2014–2020, through the REDAWN (Reduction Energy Dependency in Atlantic area Water Networks) project EAPA 198/2016.
Acknowledgments
The authors thank Caprari S.p.A for having provided the pump used during the test.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Smith, A.; Chewpreecha, U.; Mercure, J.-F.; Pollitt, H. EU Climate and Energy Policy Beyond 2020: Is a Single Target for GHG Reduction Sufficient? In The European Dimension of Germany’s Energy Transition; Springer: Cham, Switzerland, 2019; ISBN 978-3-030-03373-6. [Google Scholar]
- European Council. Directive 2009/125/EC of the European Parliament and of the Council of 21 October 2009 establishing a framework for the setting of ecodesign requirements for energy-related products (recast). Off. J. Eur. Union 2009, 13, 10–35. [Google Scholar]
- Gallagher, J.; Basu, B.; Browne, M.; Kenna, A.; McCormack, S.; Pilla, F.; Styles, D. Adapting Stand-Alone Renewable Energy Technologies for the Circular Economy through Eco-Design and Recycling. J. Ind. Ecol. 2017, 23, 133–140. [Google Scholar] [CrossRef]
- Xue, X.; Hawkins, T.; Schoen, M.; Garland, J.; Ashbolt, N. Comparing the Life Cycle Energy Consumption, Global Warming and Eutrophication Potentials of Several Water and Waste Service Options. Water 2016, 8, 154. [Google Scholar] [CrossRef]
- Fecarotta, O.; Ramos, H.M.; Derakhshan, S.; Del Giudice, G.; Carravetta, A. Fine Tuning a PAT Hydropower Plant in a Water Supply Network to Improve System Effectiveness. J. Water Resour. Plan. Manag. 2018, 144, 04018038. [Google Scholar] [CrossRef]
- Morani, M.C.; Carravetta, A.; Del Giudice, G.; McNabola, A.; Fecarotta, O. A Comparison of Energy Recovery by PATs against Direct Variable Speed Pumping in Water Distribution Networks. Fluids 2018, 3, 41. [Google Scholar] [CrossRef]
- Olsson, G. Water and Energy: Threats and Opportunities—Second Edition. Water Intell. Online 2015. [Google Scholar] [CrossRef]
- Karadirek, I.E.; Kara, S.; Yilmaz, G.; Muhammetoglu, A.; Muhammetoglu, H. Implementation of Hydraulic Modelling for Water-Loss Reduction Through Pressure Management. Water Resour. Manag. 2012, 26, 2555–2568. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.M.; López-Jiménez, P.A. Energy recovery in existing water networks: Towards greater sustainability. Water 2017, 9, 97. [Google Scholar] [CrossRef]
- Carravetta, A.; Derakhshan Houreh, S.; Ramos, H.M. Pumps as Turbines: Fundamentals and Applications; Springer: Cham, Switzerland, 2018; ISBN 978-3-319-67506-0. [Google Scholar]
- Ramos, H.M.; Mello, M.; De, P.K. Clean power in water supply systems as a sustainable solution: From planning to practical implementation. Water Sci. Technol. Water Supply 2010, 10, 39. [Google Scholar] [CrossRef]
- Arriaga, M. Pump as turbine—A pico-hydro alternative in Lao People’s Democratic Republic. Renew. Energy 2010, 35, 1109–1115. [Google Scholar] [CrossRef]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. Pump as turbine (PAT) design in water distribution network by system effectiveness. Water 2013, 5, 1211–1225. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Ramos, H.M. A new low-cost installation scheme of PATs for pico-hydropower to recover energy in residential areas. Renew. Energy 2018, 125, 1003–1014. [Google Scholar] [CrossRef]
- Pugliese, F.; De Paola, F.; Fontana, N.; Giugni, M.; Marini, G. Performance of vertical-axis pumps as turbines. J. Hydraul. Res. 2018, 56, 482–493. [Google Scholar] [CrossRef]
- Fecarotta, O.; Aricò, C.; Carravetta, A.; Martino, R.; Ramos, H.M. Hydropower Potential in Water Distribution Networks: Pressure Control by PATs. Water Resour. Manag. 2015, 29, 699–714. [Google Scholar] [CrossRef]
- Corcoran, L.; Mcnabola, A.; Coughlan, P. Optimization of Water Distribution Networks for Combined Hydropower Energy Recovery and Leakage Reduction. J. Water Resour. Plan. Manag. 2015, 142, 1–8. [Google Scholar] [CrossRef]
- Giugni, M.; Fontana, N.; Ranucci, A. Optimal Location of PRVs and Turbines in Water Distribution Systems. J. Water Resour. Plan. Manag. 2014, 140, 6014004. [Google Scholar] [CrossRef]
- Fecarotta, O.; McNabola, A. Optimal Location of Pump as Turbines (PATs) in Water Distribution Networks to Recover Energy and Reduce Leakage. Water Resour. Manag. 2017, 31, 5043–5059. [Google Scholar] [CrossRef]
- McCormick, G.; Powell, R.S. Optimal Pump Scheduling in Water Supply Systems with Maximum Demand Charges. J. Water Resour. Plan. Manag. 2003, 129, 372–379. [Google Scholar] [CrossRef]
- Castro-Gama, M.; Pan, Q.; Lanfranchi, E.A.; Jonoski, A.; Solomatine, D.P. Pump Scheduling for a Large Water Distribution Network; Elsevier: Milan, Italy, 2017; pp. 436–443. [Google Scholar]
- Fecarotta, O.; Carravetta, A.; Morani, M.C.; Padulano, R. Optimal Pump Scheduling for Urban Drainage under Variable Flow Conditions. Resources 2018, 7, 73. [Google Scholar] [CrossRef]
- Jowitt, P.W.; Germanopoulos, G. Optimal Pump Scheduling inWater? Supply Networks. J. Water Resour. Plan. Manag. 1992, 118, 406–422. [Google Scholar] [CrossRef]
- Little, K.W.; McCrodden, B.J. Minimization of Raw Water Pumping Costs Using MILP. J. Water Resour. Plan. Manag. 1989, 115, 511–522. [Google Scholar] [CrossRef]
- Tabesh, M. Scheduling and operating costs in water distribution networks. Proc. Inst. Civ. Eng. 2013, 166, 432–442. [Google Scholar]
- López-Ibáñez, M.; Prasad, T.D.; Paechter, B. Ant Colony Optimization for Optimal Control of Pumps in Water Distribution Networks. J. Water Resour. Plan. Manag. 2008, 134, 337–346. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Tabesh, M.; Ataeekia, B. Ant-colony optimization of pumping schedule to minimize the energy cost using variable-speed pumps in water distribution networks. Urban Water J. 2014, 11, 335–347. [Google Scholar] [CrossRef]
- De Paola Fontana, N.; Giugni, M.; Marini, G.; Pugliese, F. An Application of the Harmony-Search Multi-Objective (HSMO) Optimization Algorithm for the Solution of Pump Scheduling Problem. Procedia Eng. 2016, 162, 494–502. [Google Scholar] [CrossRef]
- De Paola, F.; Fontana, N.; Giugni, M.; Marini, G.; Pugliese, F. Optimal solving of the pump scheduling problem by using a Harmony Search optimization algorithm. Hydroinformatics 2017, 19, 879–889. [Google Scholar] [CrossRef]
- Gorjian Jolfaei, N.; Jin, B.; Chow, C.; Bressan, F.; Gorjian, N. An Optimised Energy Saving Model for Pump Scheduling in Wastewater Networks. In Asset Intelligence through Integration and Interoperability and Contemporary Vibration Engineering Technologies; Springer: Cham, Switzerland, 2018; pp. 197–208. ISBN 978-3-319-95711-1. [Google Scholar]
- Belotti, P.; Kirches, C.; Leyffer, S.; Linderoth, J.; Luedtke, J.; Mahajan, A. Mixed-integer nonlinear optimization. Acta Numer. 2013, 22, 1–131. [Google Scholar] [CrossRef]
- Rotodynamic pumps. Hydraulic performance acceptance tests. Grades 1, 2 and 3; BS EN ISO 9906:2012; British Standards Institution (BSI): London, England, 2012. [Google Scholar]
- Carravetta, A.; Conte, M.C.; Fecarotta, O.; Ramos, H.M. Evaluation of PAT performances by modified affinity law. Proc. Procedia Eng. 2014, 89, 581–587. [Google Scholar] [CrossRef]
- Carravetta, A.; Antipodi, L.; Golia, U.; Fecarotta, O. Energy saving in a water supply network by coupling a pump and a Pump As Turbine (PAT) in a turbopump. Water 2017, 9, 62. [Google Scholar] [CrossRef]
- Simpson, A.R.; Marchi, A. Evaluating the Approximation of the Affinity Laws and Improving the Efficiency Estimate for Variable Speed Pumps. J. Hydraul. Eng. 2013, 139, 1314–1317. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).