1. Introduction
Weirs of different shapes are extensively used as measuring devices and control structures in laboratories, irrigation projects, and hydraulic engineering. Determining the discharge coefficient in open channels is one of the primary issues in hydraulic engineering. According to the weir width, weirs can generally be classified into two categories: finite crest length weirs and sharp-crested weirs (or thin-plate weirs).
A rectangular thin-plate weir is characterized by having no effect on a free-falling nappe and a good relationship between the head over the weir and flow. The upstream water level is headed up by the control structure, and the flow is formed under the action of gravity. The centrifugal inertial force has a certain influence on the pressure distribution on the surface of the building and the discharge capacity of the building. When a sharp-crested weir is used in irrigation projects and hydraulic engineering, there are sediments and sundries in the water, which will damage the crest. Therefore, the flow rate cannot be accurately measured. A weir with a rounded upstream corner can increase the discharge capacity and improve the above situation, especially when the weir height is small.
Azimi and Rajaratnam [
1] studied weirs of a finite crest length and classified them into four groups: long-crested weirs, broad-crested weirs, short-crested weirs, and sharp-crested weirs, defined by the range of
h/
L > 2, where
h is the upstream, and
L is the crest length. For a rectangular thin-plate weir, the classical discharge equation derived from energy consideration [
2] can be written as follows:
where
Q is the discharge,
w is the width of the open channel,
h is the upstream measured head,
g is the acceleration of gravity, and
Cd is the discharge coefficient in connection with the upstream head, assuming that the velocity head and surface tension are not taken into consideration.
Many researchers have conducted extensive experiments on the determination of the discharge coefficient and derived different calculation formulas. When processing hydraulic problems involving heuristic engineering reasoning in the face of model testing and actual prototype implementation, James [
3] proposed that it is best handled by physical models. For the round-crested weir used in this experiment, based on dimensional analysis, the equation for the discharge coefficient and other parameters can be written as follows:
where
h is the upstream measured head,
P is the height of the thin-plate weir,
b is the half weir width in the direction of the channel, and
r is the radius of the upstream corner of the weir.
For the broad-crested weir with round upstream edges, Harrison [
4] proposed an expression based on an application of critical flow theory and took account of the boundary-layer development in order to calculate the discharge coefficient. Smith [
5] studied the discharge characteristics and the effects of rounded upstream corners by conducting an investigation with two models, and Tracy [
6] provided a comprehensive summary of previous studies on flow regime over rectangular broad-crested weirs with upstream corners of three shapes.
For the square-edged broad-crested weir, Hall [
7] proposed an equation for the free flow characteristics based on boundary-layer theory, and utilized the experimental data of Bazin [
8] to verify this equation. Applying the momentum relationship, Doeringsfeld and Baker [
9] derived a theoretical formula for the flow rate over a squared-edged, rectangular, and broad-crested weir. Surya Rao [
10] analyzed the characteristics of flow over broad-crested weirs with square and elliptical upstream corners in order to study the effect of finite crest length. For the rounded-crested weir, Ruschak and Weinstein [
11] analyzed the viscous flow of the gravity-driven flow over a round-crested weir, and proposed an empirical equation between the head and the velocity. Honar [
12] found that under subcritical flow conditions, the side enthalpy exit occurred 10% more frequently with a rounded edge inlet than a squared edge entrance.
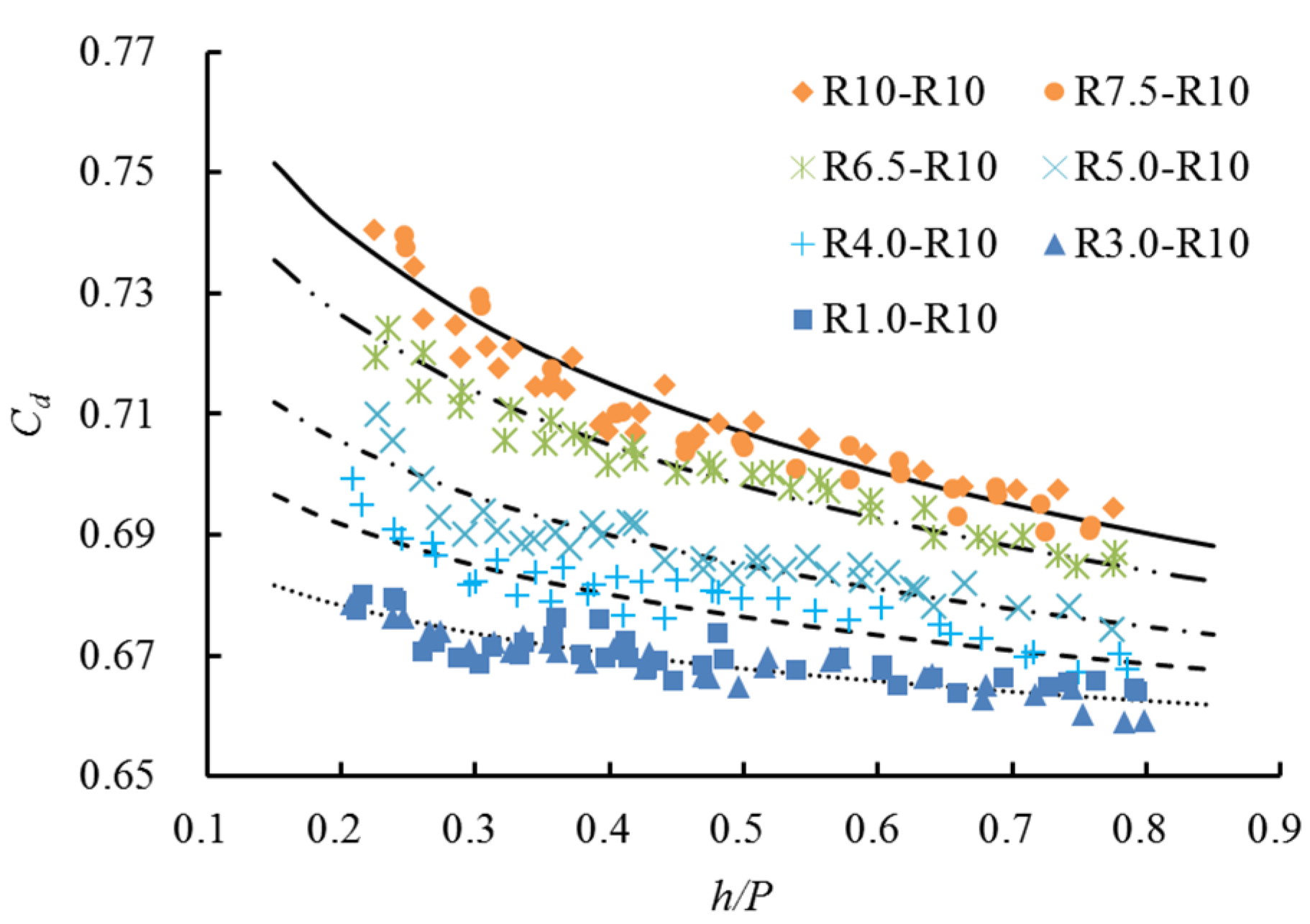
Ramamurthy et al. [
13] found that the discharge coefficient of round-nosed broad-crested weirs can be calculated based on the upstream head, due to its relationship with the radius of the upstream crested corner, and that the flow characteristic depends on the ratios of
H/
L and
R/
P, where
H is upstream head,
R is the radius of the upstream top corner,
L is length of weir, and
P is height of weir. When
R/
P is between 0.000 and 0.094, the presence of a rounded upstream corner has no effect on the natural outflow over the weir. As
R/
P increases from 0.094 to 0.250, the discharge coefficient increases gradually. Formulation of the discharge coefficient for free flow based on momentum relationships was proposed.
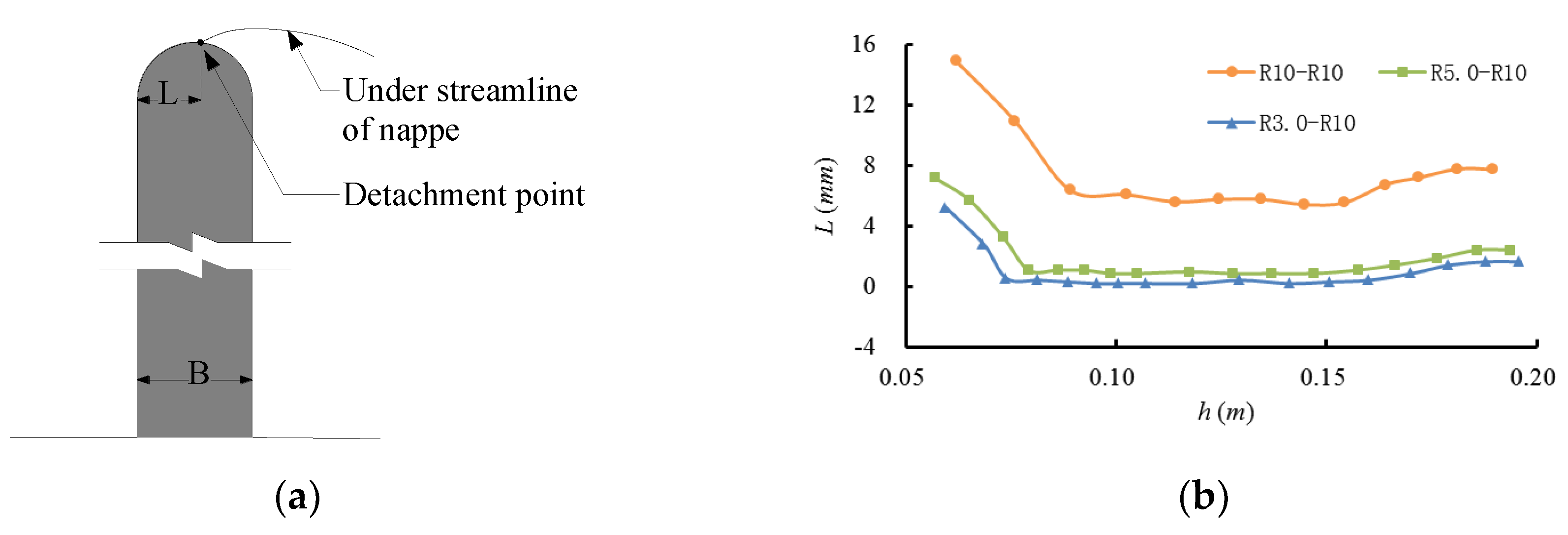
Abou-seide and Quraishi [
14] conducted eight sets of experiments with upstream edge rounding, and found that the maximum value of the discharge coefficient was obtained when the ratio between the radius of the rounded upstream corner to the weir breadth in the direction of flow was greater than or equal to 0.75. Harrison [
4] and Woodburn [
15] suggested that the discharge coefficient of a broad-crested weir increased by reducing flow separation as
R/
Hmax was increased up to 0.11, where
R is the rounded upstream corner and
Hmax is the maximum value of the upstream total head, and stated that the discharge coefficient did not increase distinctly when
R/
Hmax was increased beyond 0.11.
Previous studies on weirs with rounded upstream corners were mostly based on broad-crested weirs. Hager [
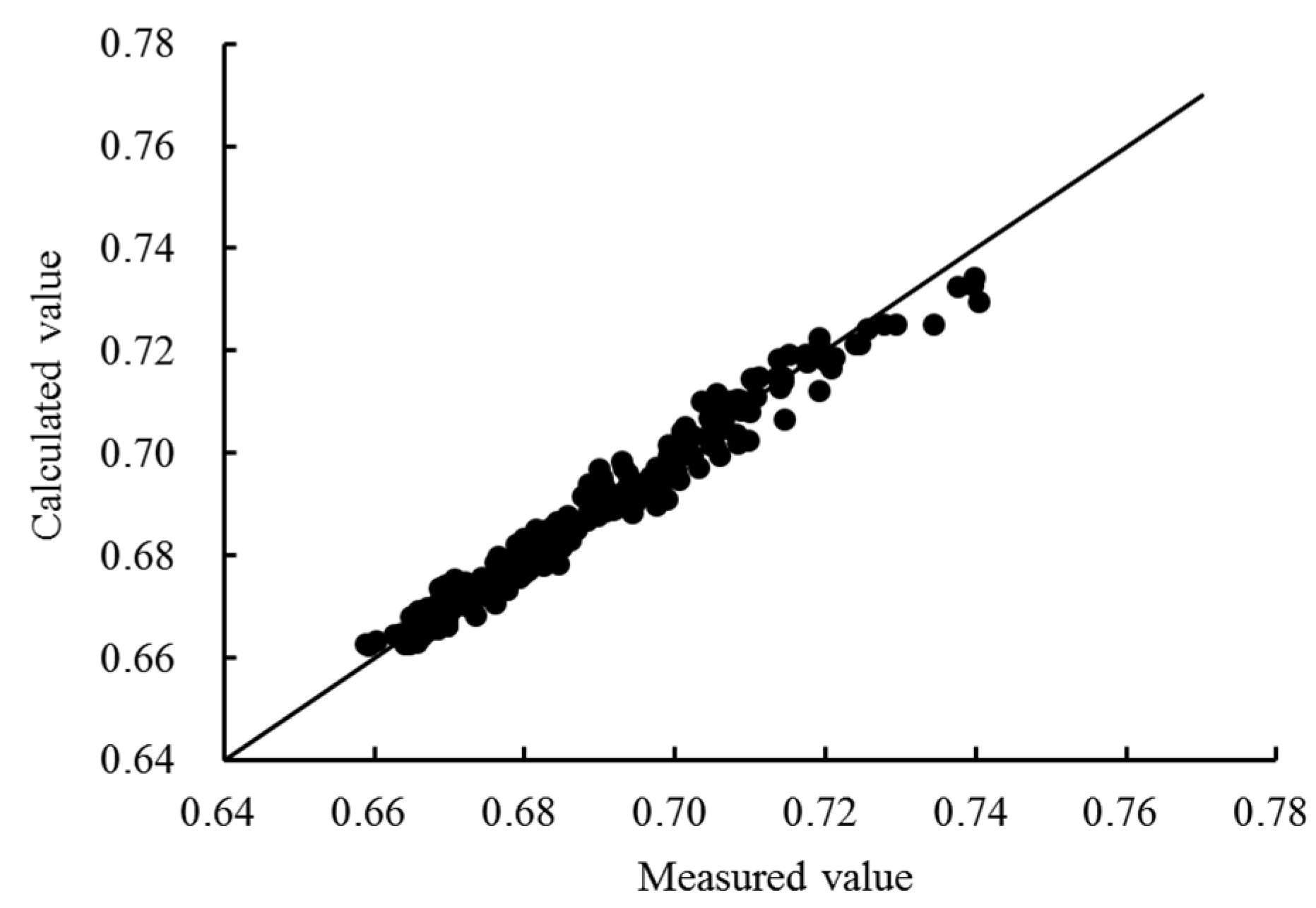
16] considered the measurement accuracy of the broad-crested weir to be relatively low and stated that the hydraulic characteristics are too poor as an overflow structure. In this article, a series of comprehensive experiments are investigated to study the hydraulic characteristics of flow over a round-crested weir with a thickness of 0.02 m. An experiential formula for the discharge coefficient based on the experimental data collected is developed.
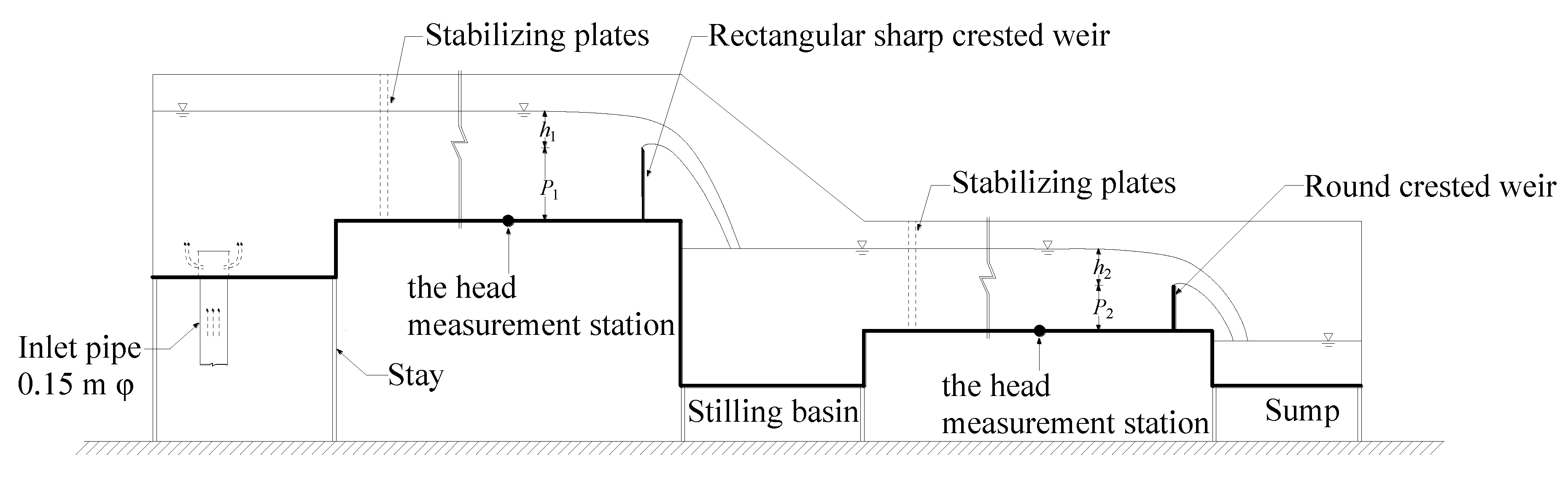
2. Experimental Setup
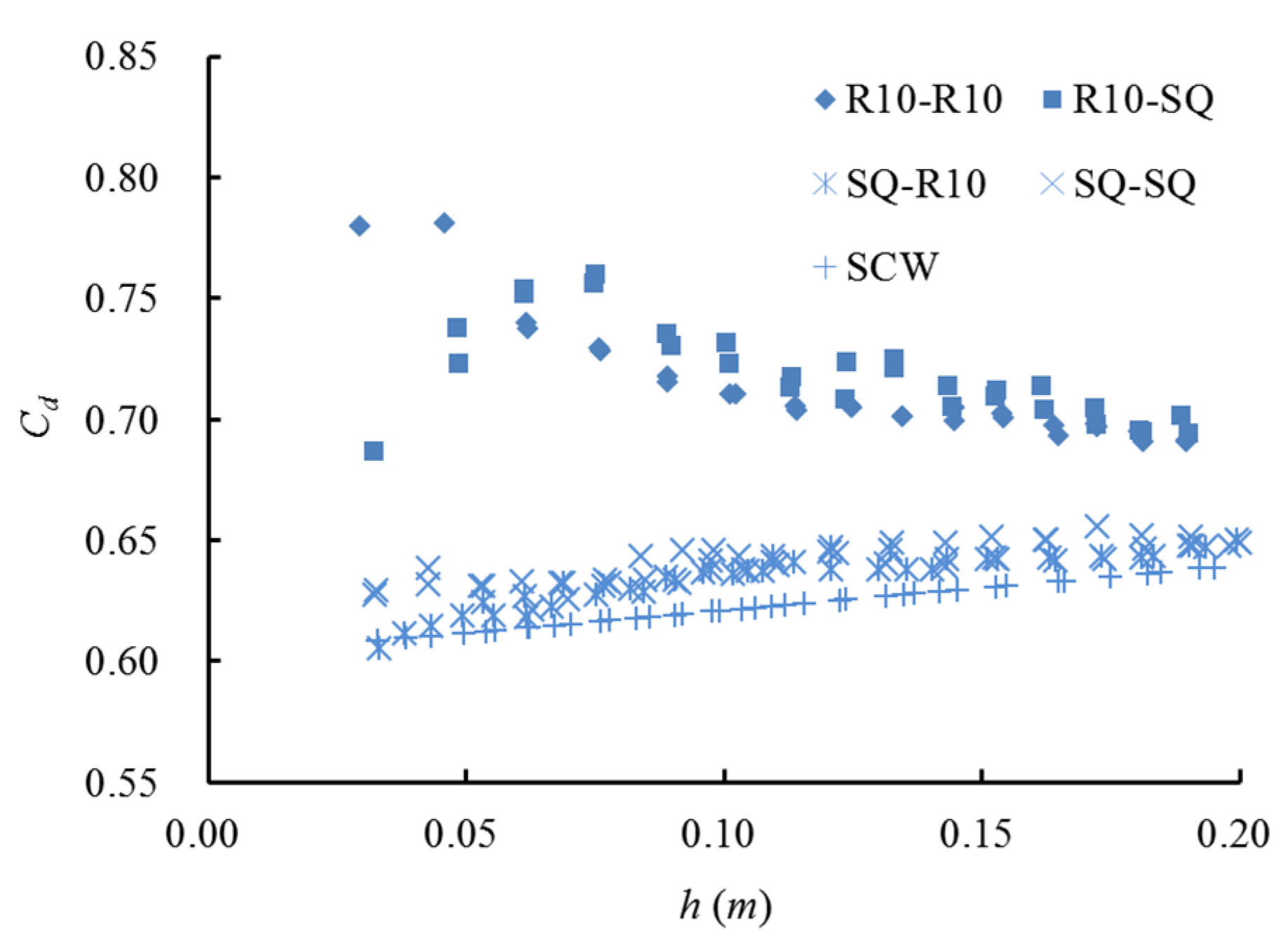
The experimental procedure consisted of measuring the flow rate of the open-horizontal channel and determining the discharge coefficient of the round-crested weir, shown in
Figure 1. According to the water flow path, the first rectangular channel, which was 7.00 m long, 0.52 m wide, and 0.80 m deep, and the next one, which was 7.00 m long, 0.52 m wide, and 0.70 m deep, were used for the tests.
After the flow came out of the inlet pipe, there was a holding sheet above the entrance to decrease the flow velocity and thus stop surface waves caused by fluctuation in the entrance. The floor and side walls of the channel were made of transparent 0.01 m thick tempered glass. The stilling basin, which was 1.00 m long, was 0.30 m lower than the downstream floor to eliminate the kinetic energy of the flow passing through the rectangular sharp-crested weir.
James [
17] proposed that model construction quality and flow measurement method can cause differences in discharge capability of models and prototypes. The flow rate of a rectangular sharp-crested weir (scw) can be measured with an electronic flow-meter with a precision of ±0.5%. The weir was made of 0.01 m thick and 0.40 m high plexiglass, with a 60° downstream incline at the crest. Bos [
2] proposed a discharge coefficient calculation formula of a sharp-crested weir in a full-width channel, as shown in Equation (3). The flow calculated by Equations (1) and (3) was compared with the electronic flow meter reading.
Aydin et al. [
18] pointed out that the head discharge relationship is related to the weir’s height for a larger flow rate if
P ≤ 0.04 m. Based on Kindsvater and Carter’s [
19] data, the minimum height of the sharp-crested weir was suggested to be 0.10 m by Bos [
2]. The round-crested weirs, as shown in
Figure 2 and
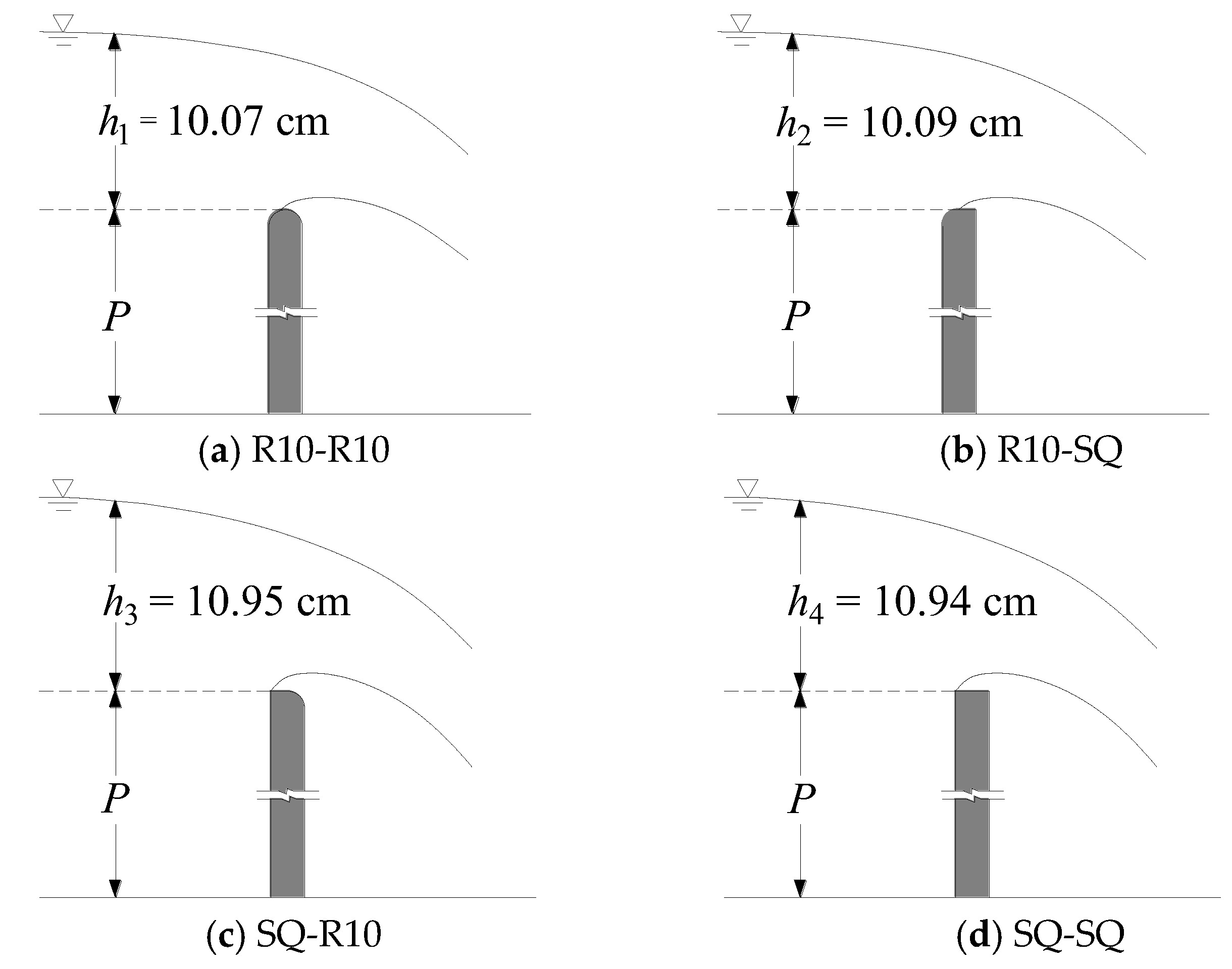
Table 1, were made of 0.02 m thickness and 0.25 m high plexiglass in order to ensure that the discharge and the weir’s height were independent of measured heads.
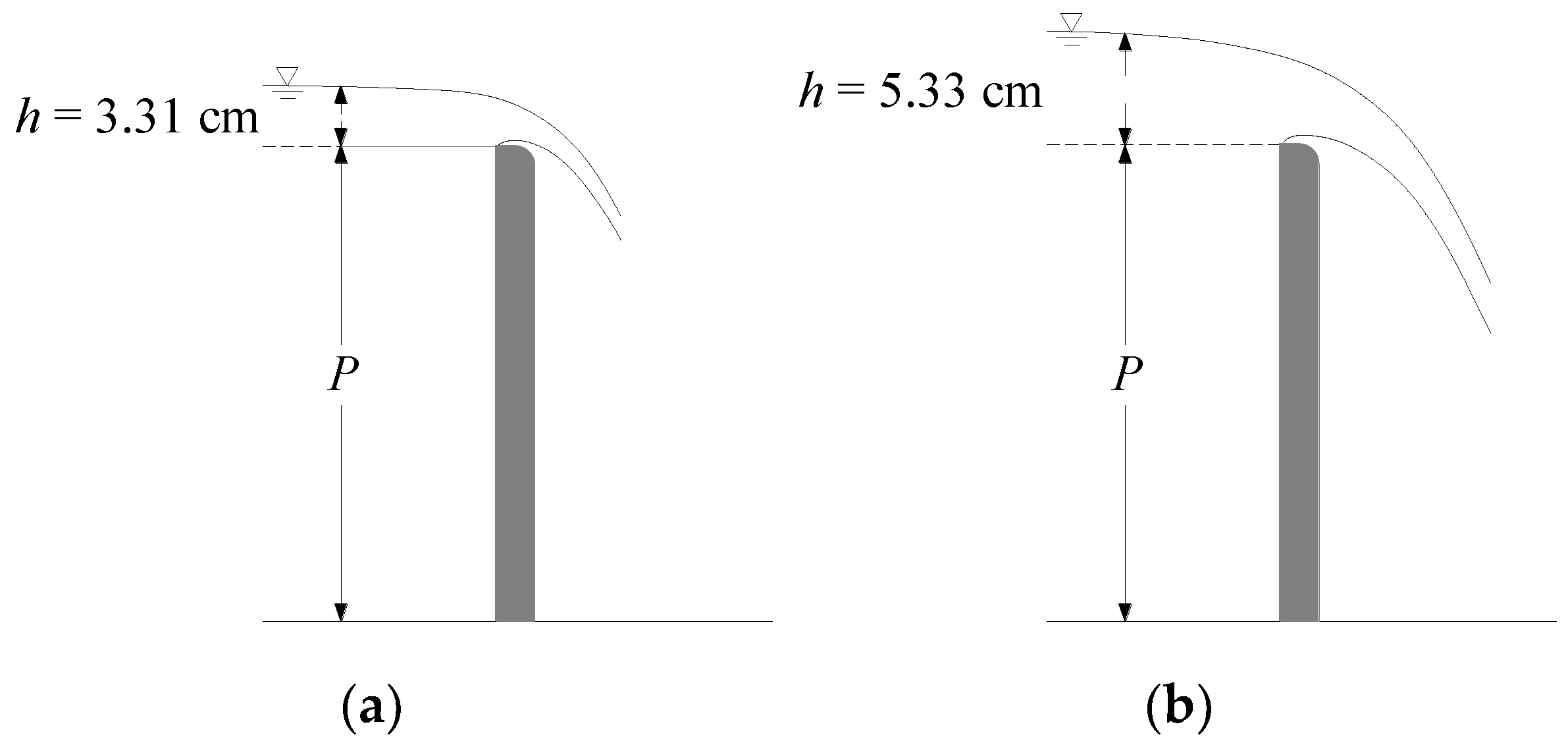
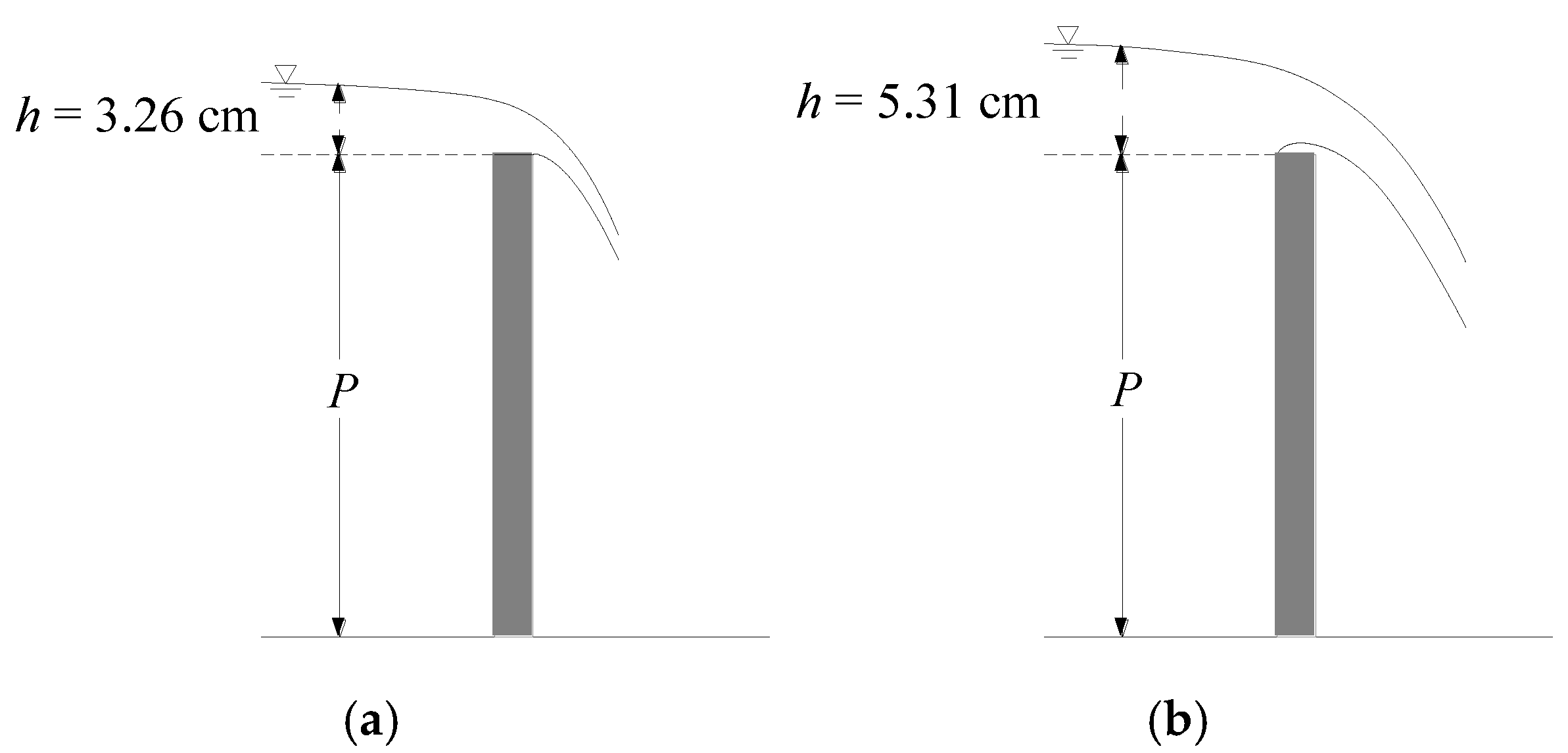
In order to determine the head discharge relationship of a round-crested weir with round upstream corners of different radii, accurate measurement of the head was required, and each geometry was investigated twice. A vent should be provided downstream of the weir in order to prevent negative pressure and form a free-falling nappe. A camera (Nikon D5300 AF-P 18-55, Nikon Optical Instruments (China) Co., Ltd, Wuxi City, China) was used to take pictures of the form of the nappe during the experiment. Measurements were made by the SDA1000 sensor data acquisition system (Chengdu Yufan Technology Co., Ltd, Chengdu City, China) and the point gages (Beijing Zhecheng Technology Co., Ltd, Beijing City, China), and the average value was taken as the water head. The accuracy of the point gages was 0.1 mm, and the accuracy of SDA1000 sensor data acquisition system was 0.01 mm. Bos [
2] suggested that the head measurement station should be fixed at an appropriate upstream distance equal to between three and four times the maximum head over the weir in order to avoid the area of the surface being drawn down. The point for measuring the water head was set at a distance of 1.00 m from the round-crested weir.