A Comparative Study of Water and Bromide Transport in a Bare Loam Soil Using Lysimeters and Field Plots
Abstract
1. Introduction
2. Materials and Methods
2.1. Location, Climate, and Characteristics of the Soil
2.2. Field plots
2.3. Lysimeters
2.4. Climate Data
2.5. Modelling
2.5.1. Presentation of the Model
2.5.2. Representation of the Soil Profiles in HYDRUS-1D
2.5.3. Initial and Boundary Conditions
2.5.4. Parameter Optimization Based on the Data Acquired from the Field Plots
- Initial values were obtained by using the Rosetta software [38] based on the particle size distribution measured for each soil material of each plot, its bulk density as well as its water content measured in the laboratory at −330 and −15,000 cm matric heads.
- These initial values were then used as input for the RetC software [39], which was used to fit the van Genuchten retention curve θ(h) to the measured water retention data. As recommended by Wösten and van Genuchten (1988) [40], the parameter was not optimized. The simulations based on these RetC parameters will be identified as RP165.
- The values and confidence intervals for parameters , α and n calculated by the RetC software were then used as input in inverse simulations with HYDRUS-1D. Saturated hydraulic conductivity () values obtained from laboratory measurements on Field Plot 3 were used to calculate initial values and confidence intervals for all field plots. The simulations based on these HYDRUS-1D inversed parameters will be identified as P165.
2.5.5. Parameter Optimization Based on the Data Acquired from the Lysimeters
2.5.6. Cross Simulations
2.6. Evaluation of Simulation Quality
3. Results and Discussion
3.1. Measurements
3.1.1. Soil Physical Characteristics
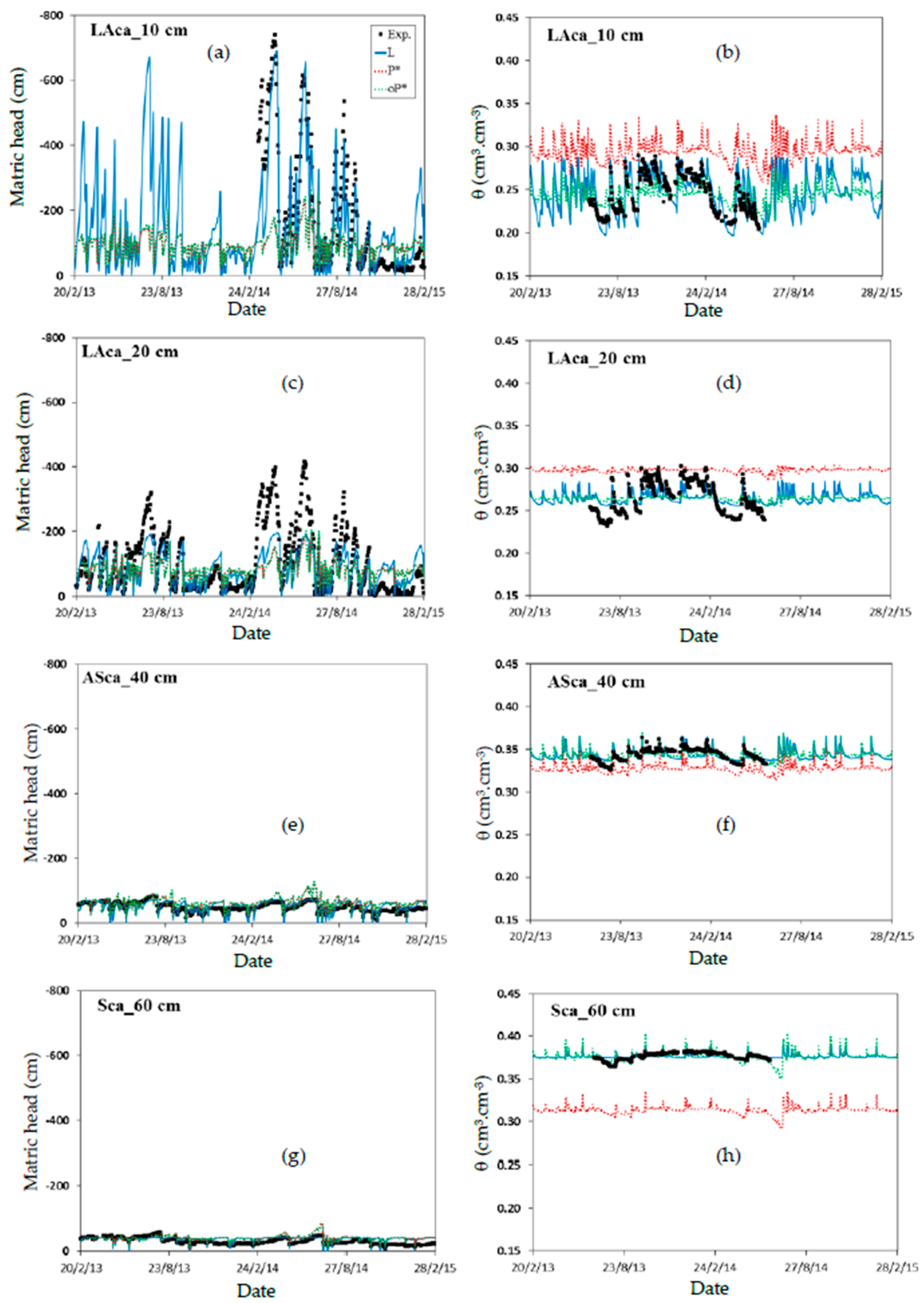
3.1.2. Water Dynamics
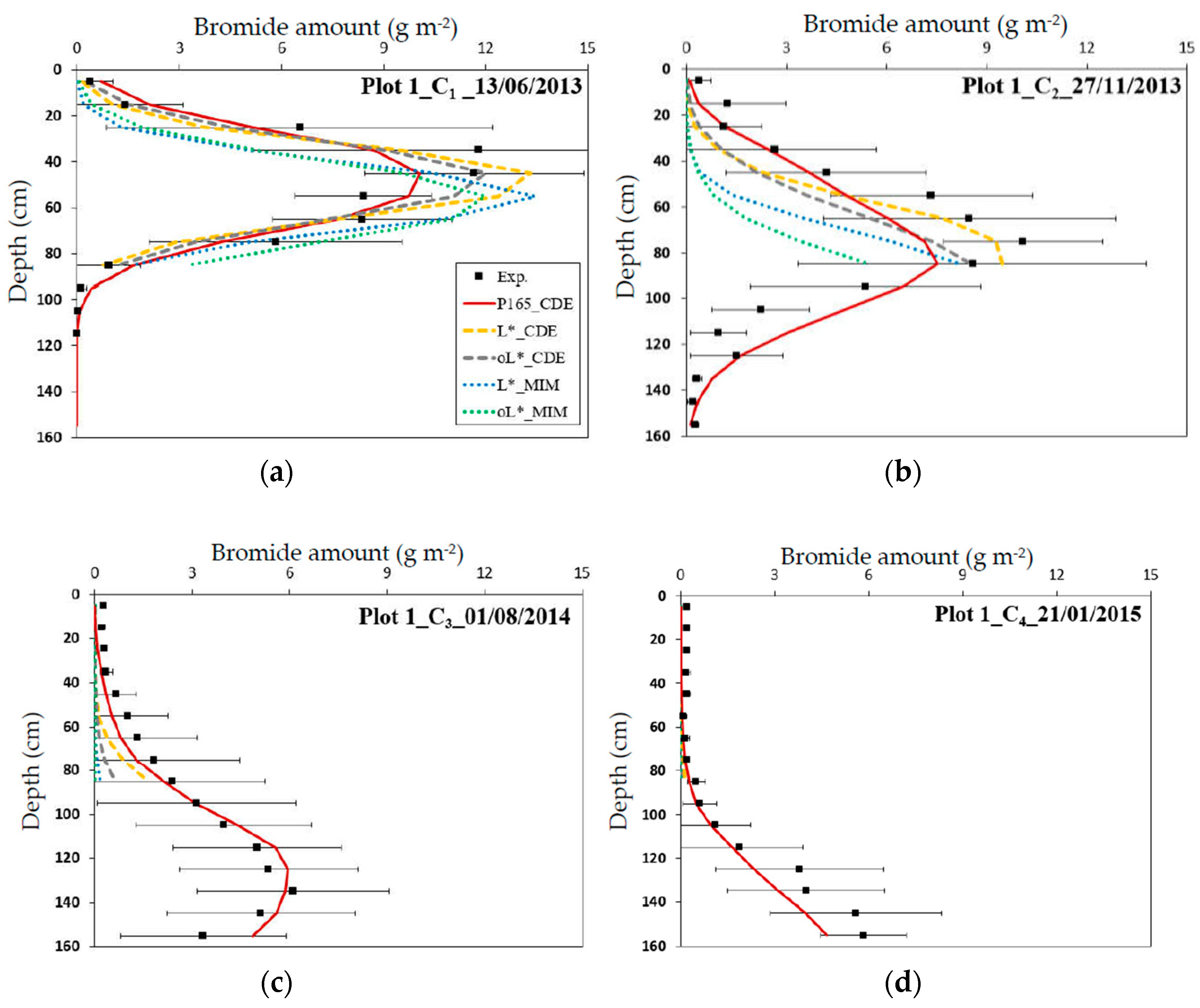
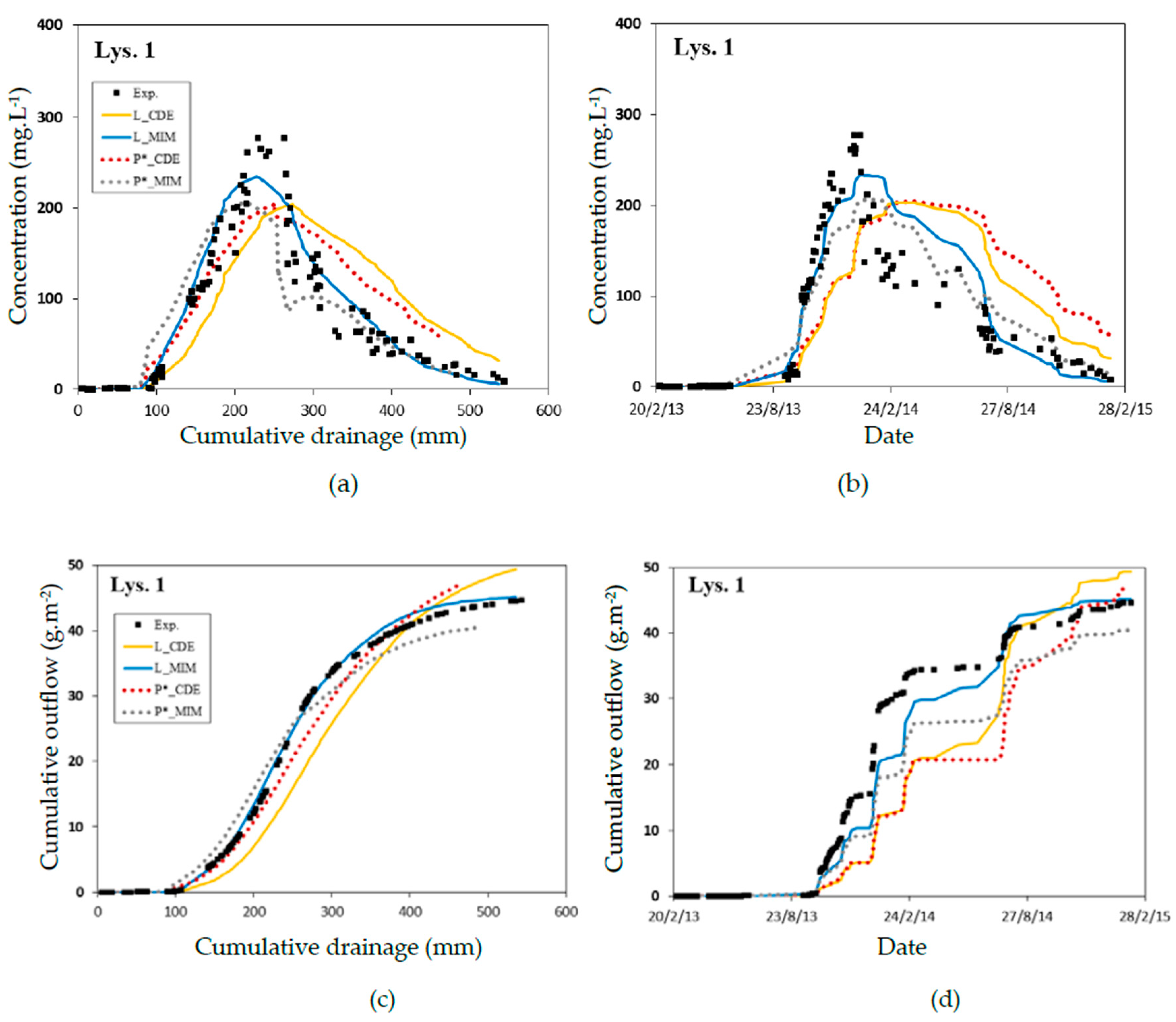
3.1.3. Bromide Transport
3.2. Modelling
3.2.1. Field Plots
3.2.2. Lysimeters
3.2.3. Cross Simulations
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ngo, V.V.; Latifi, M.A.; Simonnot, M.-O. Estimability analysis and optimisation of soil hydraulic parameters from field lysimeter data. Transp. Porous Media 2013, 98, 485–504. [Google Scholar] [CrossRef]
- Pütz, T.; Brumhard, B.; Dressel, J.; Kaiser, R.; Wüstemeyer, A.; Scholz, K.; Schäfer, H.; König, T.; Führ, F. FELS: A Comprehensive Approach to Studying the Fate of Pesticides in Soil at the Laboratory, Lysimeter and Field Scales. In The Lysimeter Concept; Führ, F., Hance, R.J., Plimmer, J.R., Nelson, J.O., Eds.; American Chemical Society: Washington, DC, USA, 1998; Volume 699, pp. 152–162. ISBN 978-0-8412-3568-7. [Google Scholar]
- Singh, G.; Kaur, G.; Williard, K.; Schoonover, J.; Kang, J. Monitoring of water and solute transport in the vadose zone: A review. Vadose Zone J. 2018, 17. [Google Scholar] [CrossRef]
- Kohnke, H.; Dreibelbis, F.R.; Davidson, J.M. A Survey and Discussion of Lysimeters and a Bibliography on Their Construction and Performance; USDA: Washington, DC, USA, 1940.
- Aboukhaled, A.; Alfaro, A.; Smith, M. Lysimeters; FAO Irrigation and Drainage Paper; 2nd Print; Food and Agriculture Organization of the United Nations: Rome, Italy, 1982; ISBN 978-92-5-101186-7. [Google Scholar]
- Meissner, R.; Seeger, J.; Rupp, H.; Seyfarth, M.; Borg, H. Measurement of dew, fog, and rime with a high-precision gravitation lysimeter. J. Plant Nutr. Soil Sci. 2007, 170, 335–344. [Google Scholar] [CrossRef]
- von Unold, G.; Fank, J. Modular design of field lysimeters for specific application needs. Water Air Soil Pollut. 2008, 8, 233–242. [Google Scholar] [CrossRef]
- Bergström, L. Use of lysimeters to estimate leaching of pesticides in agricultural soils. Environ. Pollut. 1990, 67, 325–347. [Google Scholar] [CrossRef]
- Colman, E.A. A laboratory study of lysimeter drainage under controlled soil moisture tension. Soil Sci. 1946, 62, 365–382. [Google Scholar] [CrossRef]
- Dowdell, R.J.; Webster, C.P. A Lysimeter study using nitrogen-15 on the uptake of fertilizer nitrogen by perennial ryegrass swards and losses by leaching. J. Soil Sci. 1980, 31, 65–75. [Google Scholar] [CrossRef]
- Vereecken, H.; Dust, M. Modeling Water Flow and Pesticide Transport at Lysimeter and Field Scale. In The Lysimeter Concept; Führ, F., Hance, R.J., Plimmer, J.R., Nelson, J.O., Eds.; American Chemical Society: Washington, DC, USA, 1998; Volume 699, pp. 189–202. ISBN 978-0-8412-3568-7. [Google Scholar]
- Flury, M.; Yates, M.V.; Jury, W.A. Numerical analysis of the effect of the lower boundary condition on solute transport in lysimeters. Soil Sci. Soc. Am. J. 1999, 63, 1493–1499. [Google Scholar] [CrossRef]
- Winton, K.; Weber, J.B. A Review of field lysimeter studies to describe the environmental fate of pesticides. Weed Technol. 1996, 10, 202–209. [Google Scholar] [CrossRef]
- Baroni, G.; Facchi, A.; Gandolfi, C.; Ortuani, B.; Horeschi, D.; Van Dam, J.C. Uncertainty in the determination of soil hydraulic parameters and its influence on the performance of two hydrological models of different complexity. Hydrol. Earth Syst. Sci. 2010, 14, 251–270. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Sonnleitner, M.A.; Schulin, R. Uncertainty in estimation of soil hydraulic parameters by inverse modeling: Example lysimeter experiments. Soil Sci. Soc. Am. J. 1999, 63, 501–509. [Google Scholar] [CrossRef]
- Durner, W.; Jansen, U.; Iden, S.C. Effective hydraulic properties of layered soils at the lysimeter scale determined by inverse modelling. Eur. J. Soil Sci. 2008, 59, 114–124. [Google Scholar] [CrossRef]
- Schelle, H.; Durner, W.; Iden, S.C.; Fank, J. Simultaneous estimation of soil hydraulic and root distribution parameters from lysimeter data by inverse modeling. Procedia Environ. Sci. 2013, 19, 564–573. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Stauffer, P.H.; Wöhling, T.; Robinson, B.A.; Vesselinov, V.V. Inverse modeling of subsurface flow and transport properties: A review with new developments. Vadose Zone J. 2008, 7, 843–864. [Google Scholar] [CrossRef]
- Jene, B.; Fent, G.; Kubiak, R. Transport of [14C] benazolin and bromide in large zero-tension outdoor lysimeters and the undisturbed field in a sandy soil. Pestic. Sci. 1999, 55, 500–501. [Google Scholar] [CrossRef]
- Kubiak, R.; Führ, F.; Mittelstaedt, W.; Hansper, M.; Steffens, W. Transferability of lysimeter results to actual field situations. Weed Sci. 1988, 36, 514–518. [Google Scholar] [CrossRef]
- Abdou, H.M.; Flury, M. Simulation of water flow and solute transport in free-drainage lysimeters and field soils with heterogeneous structures. Eur. J. Soil Sci. 2004, 55, 229–241. [Google Scholar] [CrossRef]
- FAO. World Reference Base for Soil Resources 2014; World Soil Resources Reports; FAO: Rome, Italy, 2015; ISBN 978-92-5-108369-7. [Google Scholar]
- Baize, D.; Girard, M.C. Référentiel Pédologique 2008; Savoir Faire; Quae: Versailles, France, 2009; ISBN 978-978-2759-20-7. [Google Scholar]
- Klute, A.; Gardner, W.H. Water Content. In SSSA Book Series; Soil Science Society of America, American Society of Agronomy: Madison, WI, USA, 1986; pp. 493–544. ISBN 978-0-89118-864-3. [Google Scholar]
- Richards, L.A. Porous plate apparatus for measuring moisture retention and transmission by soil. Soil Sci. 1948, 66, 105–110. [Google Scholar] [CrossRef]
- Amoozegar, A. A compact constant-head permeameter for measuring saturated hydraulic conductivity of the vadose zone. Soil Sci. Soc. Am. J. 1989, 53, 1356–1361. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. FAO-56 dual crop coefficient method for estimating evaporation from soil and application extensions. J. Irrig. Drain. Eng. 2005, 131, 2–13. [Google Scholar] [CrossRef]
- Mutziger, A.J.; Burt, C.M.; Howes, D.J.; Allen, R.G. Comparison of measured and FAO-56 modeled evaporation from bare soil. J. Irrig. Drain. Eng. 2005, 131, 59–72. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software packages. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Publishing Company: New York, NY, USA, 1972; ISBN 978-0-444-00114-6. [Google Scholar]
- Millington, R.J.; Quirk, J.P. Permeability of porous solids. Trans. Faraday Soc. 1961, 57, 1200–1207. [Google Scholar] [CrossRef]
- van Genuchten, M.T.; Wierenga, P.J. Mass transfer studies in sorbing porous media I. Analytical solutions. Soil Sci. Soc. Am. J. 1976, 40, 473–480. [Google Scholar] [CrossRef]
- Jacques, D.; Šimŭnek, J.; Timmerman, A.; Feyen, J. Calibration of Richards’ and convection–dispersion equations to field-scale water flow and solute transport under rainfall conditions. J. Hydrol. 2002, 259, 15–31. [Google Scholar] [CrossRef]
- Schaap, M.; Leij, F.J.; Genuchten, M.T.V. Rosetta: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- van Genuchten, M.T.; Leij, F.J.; Yates, S.R. The RETC Code for Quantifying Hydraulic Functions of Unsaturated Soils; US Department of Agriculture: Riverside, CA, USA, 1991.
- Wösten, J.H.M.; van Genuchten, M.T. Using texture and other soil properties to predict the unsaturated soil hydraulic functions. Soil Sci. Soc. Am. J. 1988, 52, 1762–1770. [Google Scholar] [CrossRef]
- van Dam, J.C.; Stricker, J.N.M.; Droogers, P. Inverse method to determine soil hydraulic functions from multistep outflow experiments. Soil Sci. Soc. Am. J. 1994, 58, 647–652. [Google Scholar] [CrossRef]
- Whalley, W.R.; Ober, E.S.; Jenkins, M. Measurement of the matric potential of soil water in the rhizosphere. J. Exp. Bot. 2013, 64, 3951–3963. [Google Scholar] [CrossRef] [PubMed]
- Warrick, A.W.; Wierenga, P.J.; Young, M.H.; Musil, S.A. Diurnal fluctuations of tensiometric readings due to surface temperature changes. Water Resour. Res. 1998, 34, 2863–2869. [Google Scholar] [CrossRef]
- Harris, C.; Davies, M.C.R. Pressures Recorded During Laboratory Freezing and Thawing of a Natural Silt-Rich Soil. In Proceedings of the Seventh International Conference, Yellowknife, NT, Canada, 23–27 June 1998; pp. 23–27. [Google Scholar]
- Isch, A. Caractérisation de la Dynamique Hydrique et du Transport de Solutés en Sol nu Soumis à des Apports Répétés de Produits Residuaires Organiques: Application au Risque de Lixiviation des Nitrates. Ph.D. Thesis, Université de Strasbourg, Strasbourg, France, 2016. [Google Scholar]
- Eching, S.O.; Hopmans, J.W. Optimization of hydraulic functions from transient outflow and soil water pressure data. Soil Sci. Soc. Am. J. 1993, 57, 1167–1175. [Google Scholar] [CrossRef]
- Hupet, F.; Lambot, S.; Javaux, M.; Vanclooster, M. On the identification of macroscopic root water uptake parameters from soil water content observations. Water Resour. Res. 2002, 38, 1–14. [Google Scholar] [CrossRef]
- Bohne, K.; Roth, C.; Leij, F.J.; Van Genuchten, M.T. Rapid method for estimating the unsaturated hydraulic conductivity from infiltration measurement. Soil Sci. 1993, 155, 237–244. [Google Scholar] [CrossRef]
- van Dam, J.C.; Stricker, J.N.M.; Droogers, P. Inverse method for determining soil hydraulic functions from one-step outflow experiments. Soil Sci. Soc. Am. J. 1992, 56, 1042–1050. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Hopmans, J.W.; Šimůnek, J.; Romano, N.; Durner, W. Inverse Methods. In Methods of Soil Analysis: Part 4 Physical Methods; Soil Science Society of America: Madison, WI, USA, 2002; pp. 963–1008. [Google Scholar]
- Šimůnek, J.; Hopmans, J.W. Parameter optimization and Nonlinear Fitting. In Methods of Soil Analysis: Part 4 Physical Methods; Soil Science Society of America: Madison, WI, USA, 2002; pp. 139–157. [Google Scholar]
- Phogat, V.; Skewes, M.A.; Cox, J.W.; Alam, J.; Grigson, G.; Šimůnek, J. Evaluation of water movement and nitrate dynamics in a lysimeter planted with an orange tree. Agric. Water Manag. 2013, 127, 74–84. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Iqbal, J.; Thomasson, J.A.; Jenkins, J.N.; Owens, P.R.; Whisler, F.D. Spatial variability analysis of soil physical properties of alluvial soils. Soil Sci. Soc. Am. J. 2005, 69, 1338–1351. [Google Scholar] [CrossRef]
- Dobriyal, P.; Qureshi, A.; Badola, R.; Hussain, S.A. A review of the methods available for estimating soil moisture and its implications for water resource management. J. Hydrol. 2012, 458, 110–117. [Google Scholar] [CrossRef]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil moisture measurement for ecological and hydrological watershed-scale observatories: A review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Stephens, D.B. Vadose Zone Hydrology; CRC Press: Boca Raton, FL, USA, 1996; ISBN 978-0-87371-432-7. [Google Scholar]
- Audry, P.; Combeau, A.; Humbel, F.-X.; Roose, E.; Vizier, J.-F. Essai Sur Les Etudes de Dynamique Actuelle des Sols: Définition, Méthodologie, Techniques, Limitations Actuelles, Quelques Voies de Recherches Possibles; ORSTOM: Paris, France, 1972; 254p. [Google Scholar]
- Webster, C.P.; Shepherd, M.A.; Goulding, K.W.T.; Lord, E. Comparisons of methods for measuring the leaching of mineral nitrogen from arable land. J. Soil Sci. 1993, 44, 49–62. [Google Scholar] [CrossRef]
- Clothier, B.E.; Green, S.R.; Deurer, M. Preferential flow and transport in soil: Progress and prognosis. Eur. J. Soil Sci. 2008, 59, 2–13. [Google Scholar] [CrossRef]
- Jarvis, N.; Koestel, J.; Larsbo, M. Understanding preferential flow in the vadose zone: Recent advances and future prospects. Vadose Zone J. 2016, 15. [Google Scholar] [CrossRef]
- Ghodrati, M.; Jury, W.A. A field study of the effects of soil structure and irrigation method on preferential flow of pesticides in unsaturated soil. J. Cont. Hydrol. 1992, 11, 101–125. [Google Scholar] [CrossRef]
- Kung, K.-J.S.; Steenhuis, T.S.; Kladivko, E.J.; Gish, T.J.; Bubenzer, G.; Helling, C.S. Impact of preferential flow on the transport of adsorbing and non-adsorbing tracers. Soil Sci. Soc. Am. J. 2000, 64, 1290–1296. [Google Scholar] [CrossRef]
- Alletto, L.; Pot, V.; Giuliano, S.; Costes, M.; Perdrieux, F.; Justes, E. Temporal variation in soil physical properties improves the water dynamics modeling in a conventionally-tilled soil. Geoderma 2015, 243, 18–28. [Google Scholar] [CrossRef]
- Kumar, S.; Sekhar, M.; Reddy, D.V.; Kumar, M.S.M. Estimation of soil hydraulic properties and their uncertainty: Comparison between laboratory and field experiment. Hydrol. Process. 2010, 24, 3426–3435. [Google Scholar] [CrossRef]
- Mermoud, A.; Xu, D. Comparative analysis of three methods to generate soil hydraulic functions. Soil Tillage Res. 2006, 87, 89–100. [Google Scholar] [CrossRef]
- Mertens, J.; Madsen, H.; Kristensen, M.; Jacques, D.; Feyen, J. Sensitivity of soil parameters in unsaturated zone modelling and the relation between effective, laboratory andin situ estimates. Hydrol. Process. 2005, 19, 1611–1633. [Google Scholar] [CrossRef]
- Wöhling, T.; Vrugt, J.A.; Barkle, G.F. Comparison of three multiobjective optimization algorithms for inverse modeling of vadose zone hydraulic properties. Soil Sci. Soc. Am. J. 2008, 72, 305–319. [Google Scholar] [CrossRef]
- Vanderborght, J.; Vereecken, H. Review of dispersivities for transport modeling in soils. Vadose Zone J. 2007, 6, 29–52. [Google Scholar] [CrossRef]
- Konukcu, F. Modification of the Penman method for computing bare soil evaporation. Hydrol. Process. 2007, 21, 3627–3634. [Google Scholar] [CrossRef]
- Snyder, R.L.; Bali, K.; Ventura, F.; Gomez-MacPherson, H. Estimating evaporation from bare or nearly bare soil. J. Irrig. Drain. Eng. 2000, 126, 399–403. [Google Scholar] [CrossRef]
- McMahon, T.A.; Peel, M.C.; Lowe, L.; Srikanthan, R.; McVicar, T.R. Estimating actual, potential, reference crop and pan evaporation using standard meteorological data: A pragmatic synthesis. Hydrol. Earth Syst. Sci. 2013, 17, 1331–1363. [Google Scholar] [CrossRef]
- Howell, T.A.; Schneider, A.D.; Jensen, M.E. History of Lysimeter Design and Use for Evapotranspiration Measurements; ASCE: Honolulu, HI, USA, 1991; pp. 1–9. [Google Scholar]
- van Bavel, C.H.M. Lysimetric measurements of evapotranspiration rates in the Eastern United States1. Soil Sci. Soc. Am. J. 1961, 25, 138–141. [Google Scholar] [CrossRef]
- Prasuhn, V. Tracerversuche Mit Bromid auf Verschiedenen Lysimetern in der Schweiz; Höhere Bundeslehr- und Forschungszentrum für Landwirtschaft Raumberg-Gumpenstein: Irdning-Stainach, Austria, 2015; pp. 21–28. [Google Scholar]
- Köhne, S.; Lennartz, B.; Köhne, J.M.; Šimůnek, J. Bromide transport at a tile-drained field site: Experiment, and one- and two-dimensional equilibrium and non-equilibrium numerical modeling. J. Hydrol. 2006, 321, 390–408. [Google Scholar] [CrossRef]
- Snow, V.O.; Clothier, B.E.; Scotter, D.R.; White, R.E. Solute transport in a layered field soil: Experiments and modelling using the convection-dispersion approach. J. Cont. Hydrol. 1994, 16, 339–358. [Google Scholar] [CrossRef]
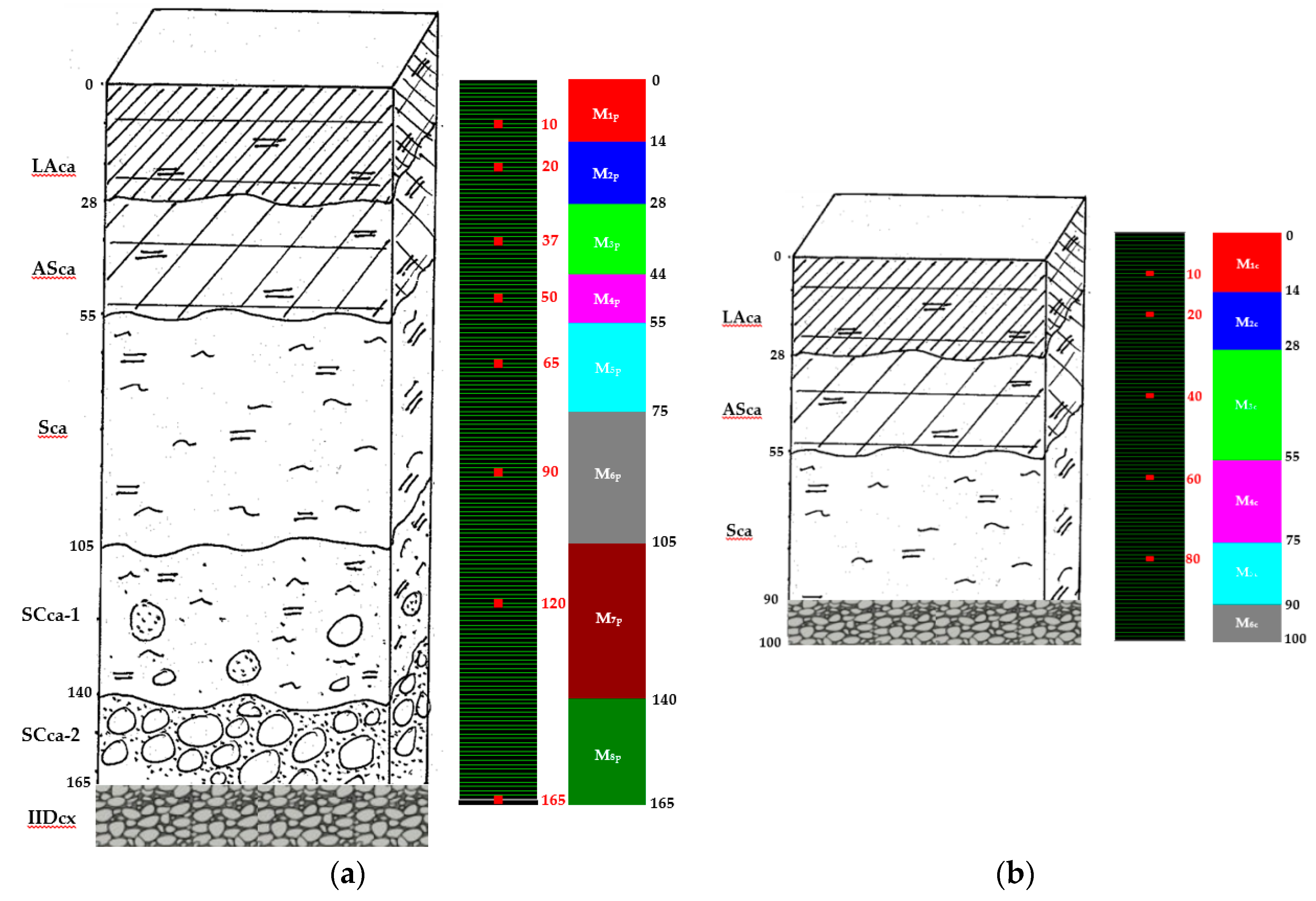
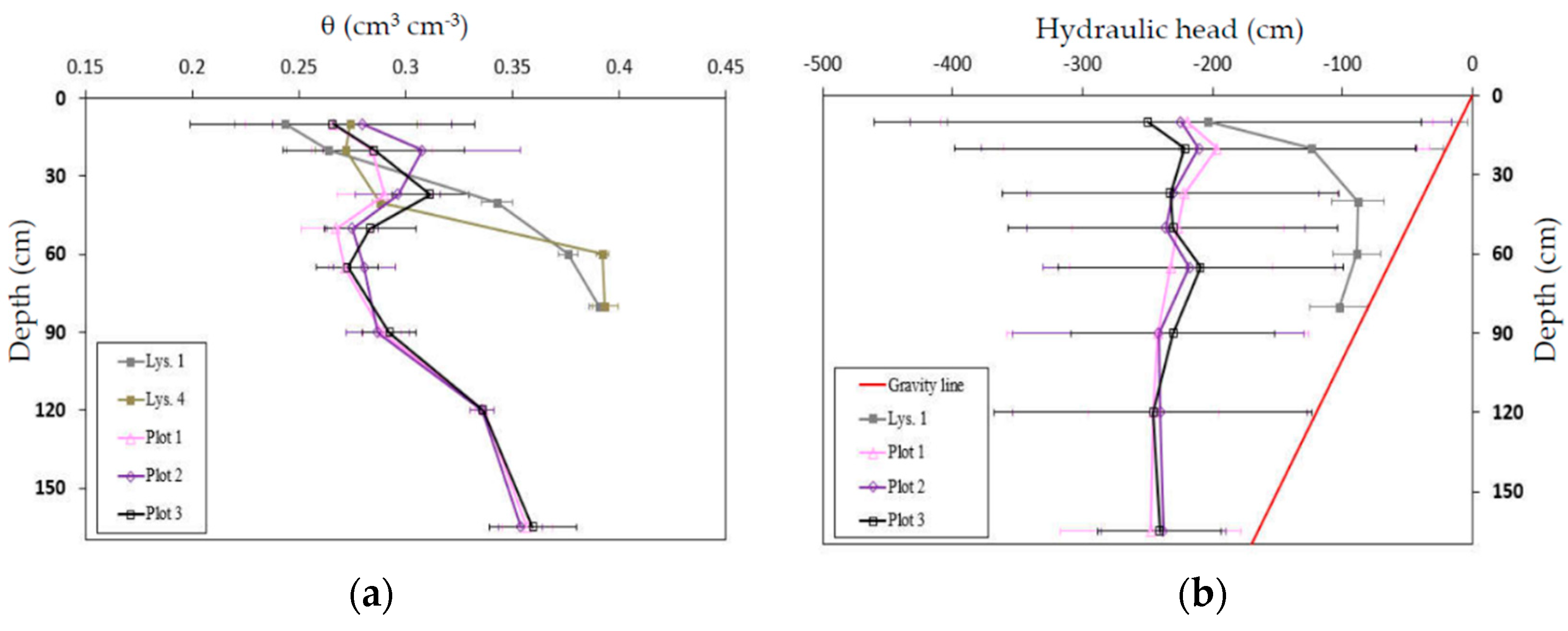
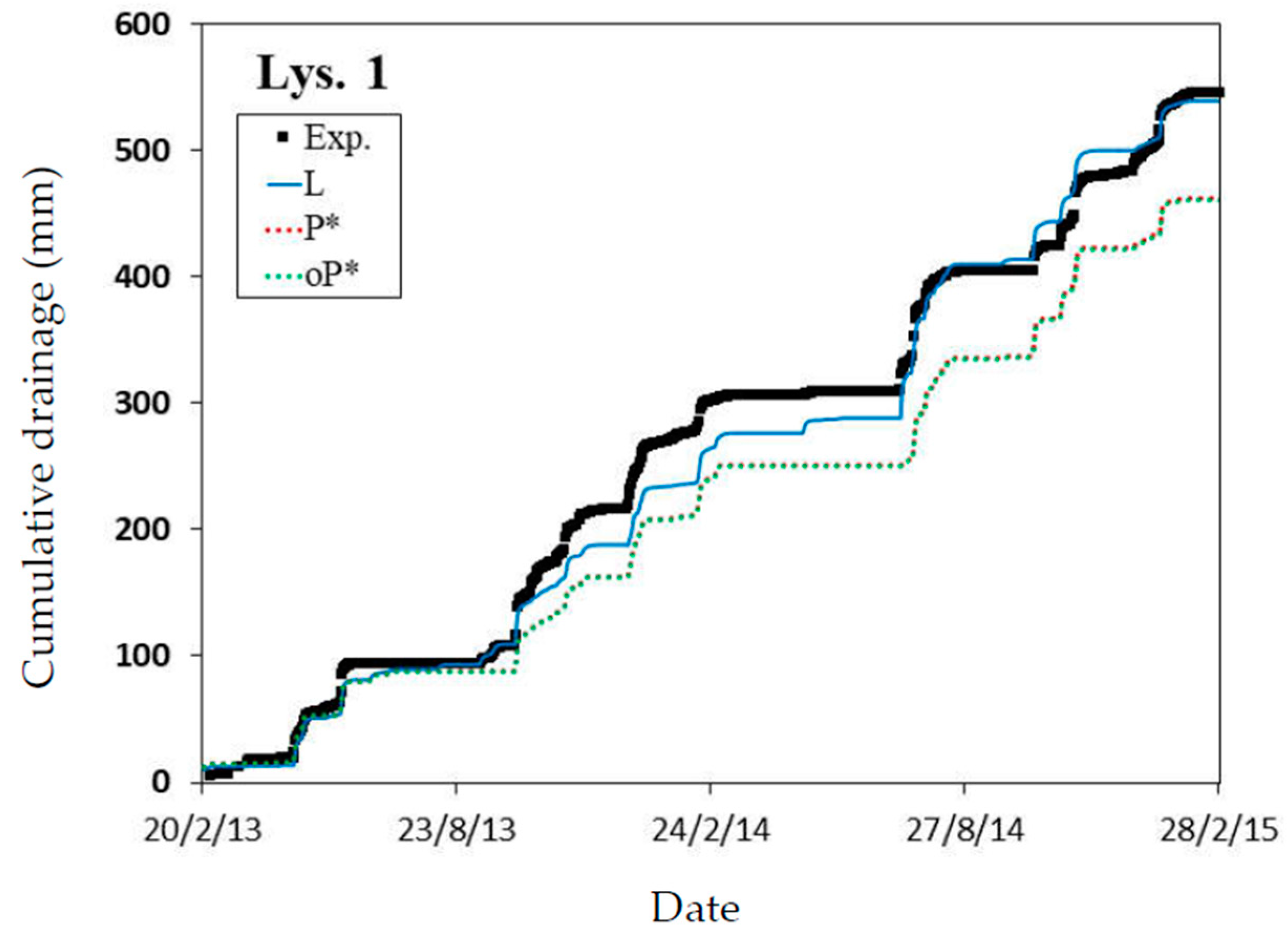
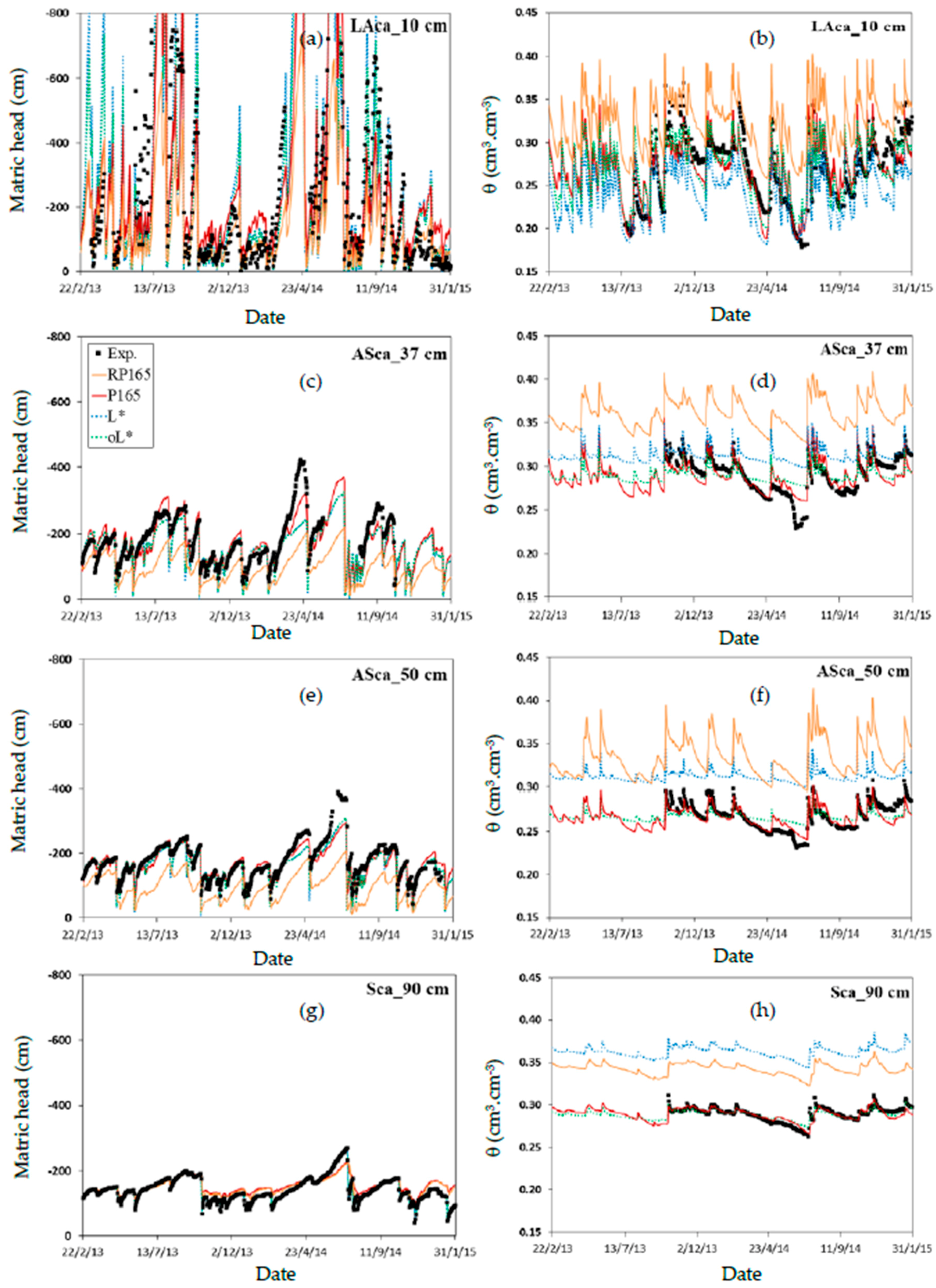
| Layer (cm) | Field Plots (2012) | Lysimeters (1983) | ||||||
|---|---|---|---|---|---|---|---|---|
| Clay | Silt | Sand | ρb | Clay | Silt | Sand | ρb | |
| (%) | (g cm−3) | (%) | (g cm−3) | |||||
| 0–30 | 23.6 (0.7) | 65.9 (0.8) | 10.5 (0.9) | 1.38 (0.11) | 23.9 | 69.2 | 6.9 | 1.34 |
| 30–60 | 23.7 (1.7) | 66.0 (0.9) | 10.3 (1.2) | 1.25 (0.07) | 23.3 | 70.4 | 6.4 | 1.22 |
| 60–90 | 16.4 (1.7) | 68.6 (1.5) | 15.0 (1.3) | 1.41 (0.08) | 17.5 | 72.3 | 10.3 | 1.37 |
| Soil Material | α | n | λ | ||||
|---|---|---|---|---|---|---|---|
| cm3 cm−3 | cm−1 | - | cm d−1 | cm | cm3 cm−3 | ||
| M1p | 0.066 (0.073) [0.066–0.076] | 0.364 (0.411) [0.359–0.368] | 0.021 (0.054) [0.020–0.023] | 1.252 (1.162) [1.240–1.264] | 101.2 | 4.0 | 0.329 [0.327–0.330] |
| M2p | 0.076 (0.077) [0.076–0.079] | 0.381 (0.439) [0.370–0.391] | 0.077 (0.196) [0.067–0.087] | 1.144 (1.139) [1.133–1.155] | 776.8 [571.4–982.2] | 4.0 | 0.317 [0.316–0.319] |
| M3p | 0.075 (0.076) [0.075–0.080] | 0.373 (0.420) [0.370–0.376] | 0.036 (0.028) [0.034–0.038] | 1.181 (1.162) [1.161–1.200] | 45.6 | 4.0 | 0.325 [0.323–0.327] |
| M4p | 0.065 (0.068) [0.065–0.070] | 0.313 (0.448) [0.295–0.330] | 0.007 (0.076) [0.001–0.012] | 1.364 (1.183) [1.343–1.384] | 76.9 | 4.0 | 0.299 [0.297–0.301] |
| M5p | 0.046 (0.048) [0.046–0.051] | 0.320 (0.412) [0.306–0.335] | 0.017 (0.043) [0.012–0.021] | 1.158 (1.204) [1.116–1.200] | 27.1 [7.9–46.3] | 1.5 | 0.302 [0.300–0.304] |
| M6p | 0.050 (0.051) [0.050–0.055] | 0.327 (0.395) [0.322–0.332] | 0.004 (0.007) [0.002–0.006] | 1.654 (1.279) [1.442–1.867] | 16.7 | 1.5 | 0.315 [0.313–0.317] |
| M7p | 0.041 (0.044) [0.041–0.047] | 0.351 (0.394) [0.342–0.360] | 0.002 (0.005) [0.002–0.002] | 1.452 (1.452) | 16.1 | 3.0 | / |
| M8p | 0.040 (0.037) [0.036–0.040] | 0.390 (0.311) [0.382–0.398] | 0.006 (0.002) [0.006–0.006] | 1.463 (1.463) | 19.8 | 3.0 | / |
| Simulation | M1p_10 | M2p_20 | M3p_37 | M4p_50 | M5p_65 | M6p_90 | M7p_120 | M8p_165 |
|---|---|---|---|---|---|---|---|---|
| h_RP165 | 0.21 | 0.06 | −0.71 | −1.26 | −0.81 | 0.86 | 0.86 | 1.00 |
| h_P165 | 0.48 | 0.47 | 0.72 | 0.78 | 0.79 | 0.88 | 0.87 | 1.00 |
| h_P90 | 0.49 | 0.46 | 0.69 | 0.83 | 0.78 | 1.00 | / | / |
| h_L* | 0.41 | 0.43 | 0.48 | 0.63 | 0.76 | 1.00 | / | / |
| h_oL* | 0.48 | 0.44 | 0.51 | 0.66 | 0.76 | 1.00 | / | / |
| θ_RP165 | −1.39 | −1.76 | −9.92 | −17.73 | −22.48 | −35.59 | −13.52 | −19.88 |
| θ_P165 | 0.65 | 0.58 | 0.64 | 0.71 | 0.84 | 0.73 | 0.67 | 0.83 |
| θ_P90 | 0.67 | 0.61 | 0.71 | 0.81 | 0.80 | 0.44 | / | / |
| θ_L* | 0.21 | −0.31 | −0.76 | −7.35 | −133.53 | −69.30 | / | / |
| θ_oL* | 0.62 | 0.30 | 0.38 | 0.39 | 0.84 | 0.80 | / | / |
| Simulation | C1 (13 June 2013) | C2 (27 November 2013) | C3 (1 August 2014) | C4 (21 January 2015) |
|---|---|---|---|---|
| P165_CDE | 0.93 | 0.80 | 0.93 | 0.89 |
| P90_CDE | 0.87 | 0.82 | 0.80 | / |
| L*_CDE | 0.74 | 0.84 | 0.20 | / |
| oL*_CDE | 0.84 | 0.65 | −0.73 | / |
| L*_MIM | 0.30 | 0.11 | −1.37 | / |
| oL*_MIM | 0.38 | −0.47 | −1.57 | / |
| Simulation | M1c_10 | M2c_20 | M3c_40 | M4c_60 | M5c_80 |
|---|---|---|---|---|---|
| h_L | 0.74 | 0.54 | −0.14 | −0.93 | −0.07 |
| h_P* | −0.06 | 0.17 | −0.72 | −1.59 | 0.53 |
| h_oP* | −0.06 | 0.17 | −0.80 | −1.60 | 0.54 |
| θ_L | 0.62 | 0.41 | 0.43 | 0.07 | 0.05 |
| θ_P* | −5.69 | −1.59 | −9.97 | −142.89 | −165.11 |
| θ_oP* | 0.33 | 0.36 | 0.36 | 0.37 | 0.43 |
| Simulation | Lys. 1 |
|---|---|
| d_L | 0.81 |
| CV | −1.2 |
| d_P* | 0.79 |
| CV | −14.7 |
| d_oP* | 0.79 |
| CV | −14.9 |
| Soil Material | α | n | ||||
|---|---|---|---|---|---|---|
| cm3 cm−3 | cm−1 | - | cm d−1 | cm3 cm−3 | ||
| M1c | 0.062 (0.072) [0.062–0.108] | 0.289 (0.402) [0.287–0.291] | 0.020 (0.047) [0.020–0.020] | 1.194 (1.168) [1.189–1.200] | 10.0 (110.2) | 0.286 [0.282–0.290] |
| M2c | 0.097 (0.078) [0.069–0.097] | 0.288 (0.394) [0.286–0.290] | 0.200 (0.084) | 1.050 (1.168) | 1000.0 (575.2) | 0.324 [0.320–0.329] |
| M3c | 0.109 (0.080) [0.065–0.109] | 0.366 (0.423) [0.364–0.368] | 0.035 (0.055) | 1.100 (1.174) | 30.0 (73.9) | 0.384 [0.380–0.388] |
| M4c | 0.065 (0.075) [0.065–0.095] | 0.389 (0.431) [0.387–0.391] | 0.012 (0.068) | 1.140 (1.181) | 15.0 (76.9) | 0.410 |
| M5c | 0.058 (0.049) [0.043–0.058] | 0.396 (0.394) [0.394–0.398] | 0.009 (0.021) | 1.150 (1.252) | 25.0 (22.9) | 0.397 |
| M6c | 0.010 | 0.450 | 0.150 | 3.000 | 3000.0 | / |
| Parameter | Lys. 1 |
|---|---|
| λ [cm] | 2.00 |
| [cm3 cm−3] | 0.060 |
| C0* [g m−2] | 59.2 |
| [d−1] | 10−6 |
| Variable | Simulation | Lys. 1 |
|---|---|---|
| Concentration | L_CDE | 0.37 (0.61) |
| L_MIM | 0.83 (0.93) | |
| P*_CDE | 0.34 (0.80) | |
| P*_MIM | 0.84 (0.67) | |
| Cumulated Outflow | L_CDE | 0.08 (0.32) |
| L_MIM | 0.60 (0.63) | |
| P*_CDE | 0.41 (0.39) | |
| P*_MIM | 0.90 (0.18) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isch, A.; Montenach, D.; Hammel, F.; Ackerer, P.; Coquet, Y. A Comparative Study of Water and Bromide Transport in a Bare Loam Soil Using Lysimeters and Field Plots. Water 2019, 11, 1199. https://doi.org/10.3390/w11061199
Isch A, Montenach D, Hammel F, Ackerer P, Coquet Y. A Comparative Study of Water and Bromide Transport in a Bare Loam Soil Using Lysimeters and Field Plots. Water. 2019; 11(6):1199. https://doi.org/10.3390/w11061199
Chicago/Turabian StyleIsch, Arnaud, Denis Montenach, Frederic Hammel, Philippe Ackerer, and Yves Coquet. 2019. "A Comparative Study of Water and Bromide Transport in a Bare Loam Soil Using Lysimeters and Field Plots" Water 11, no. 6: 1199. https://doi.org/10.3390/w11061199
APA StyleIsch, A., Montenach, D., Hammel, F., Ackerer, P., & Coquet, Y. (2019). A Comparative Study of Water and Bromide Transport in a Bare Loam Soil Using Lysimeters and Field Plots. Water, 11(6), 1199. https://doi.org/10.3390/w11061199






