Risks Analysis and Response of Forecast-Based Operation for Ankang Reservoir Flood Control
Abstract
1. Introduction
2. Materials and Methods
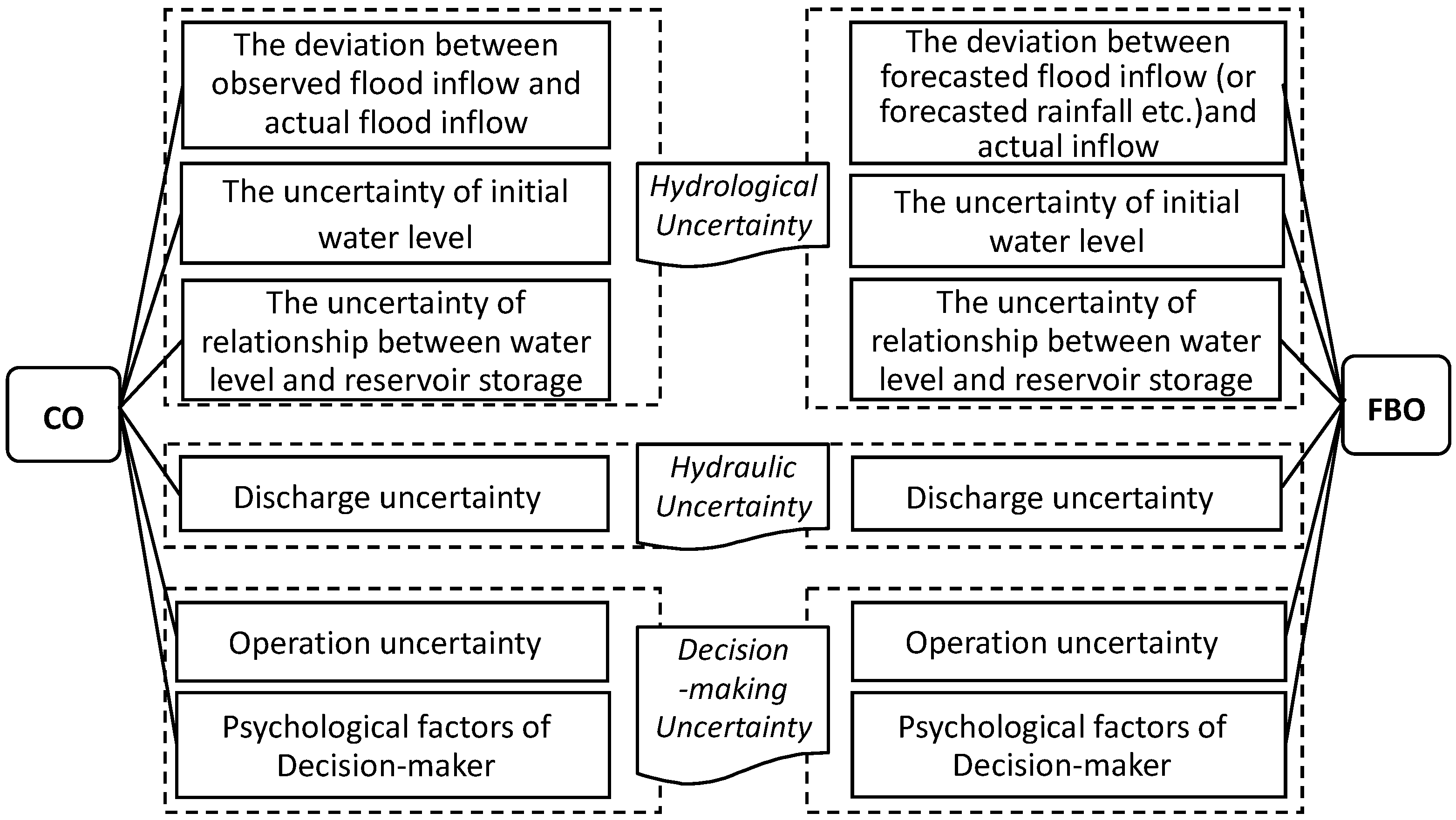
2.1. The Contrast of Risk Factors for Two Operation Modes
- The flood inflow is actually an instantaneous value, which changes from time to time, thus it is difficult to measure along with the rise and the drop of the flood wave. Even if it can be calculated as the average inflow in a certain period of time, there are still deviations. In practice, the flood inflow is usually estimated according to the observation of the adjacent upstream hydrometric station, or the change of water level in the period by back calculation. Therefore, the so-called “observed inflow” is actually an estimated value, which largely based on the upstream river flow and the experience of dispatcher; the value, in fact, has a large deviation sometimes from “the true inflow”.
- What is “inflow”? Where is the cross section once the stream flow passes? Can it be thought of as in the reservoir? All these concepts are actually vague. In view of dynamic change of the water surface curve under different storage conditions of reservoirs and the impact of different flood waves, there is no a constant cross section to define “inflow” and the inflow itself is a concept with fuzzy characteristics, which cannot be accurately determined.
- The flood wave and real-time inflow are under the effects of boundary conditions. Even if the dynamic change of storage capacity is considered, it is not possible to fully describe the inflow process and its effects. Although they theoretically comply with the Saint-Venant equations for the unsteady flow, they are difficult to solve due to various complicated conditions. Conversely, even if the flood flow is the same, for different water levels or different operation stages of the reservoir, the evolution and the hydraulic effects of the flood wave in the reservoir are different.
2.2. The Main Risk Sources and Factors
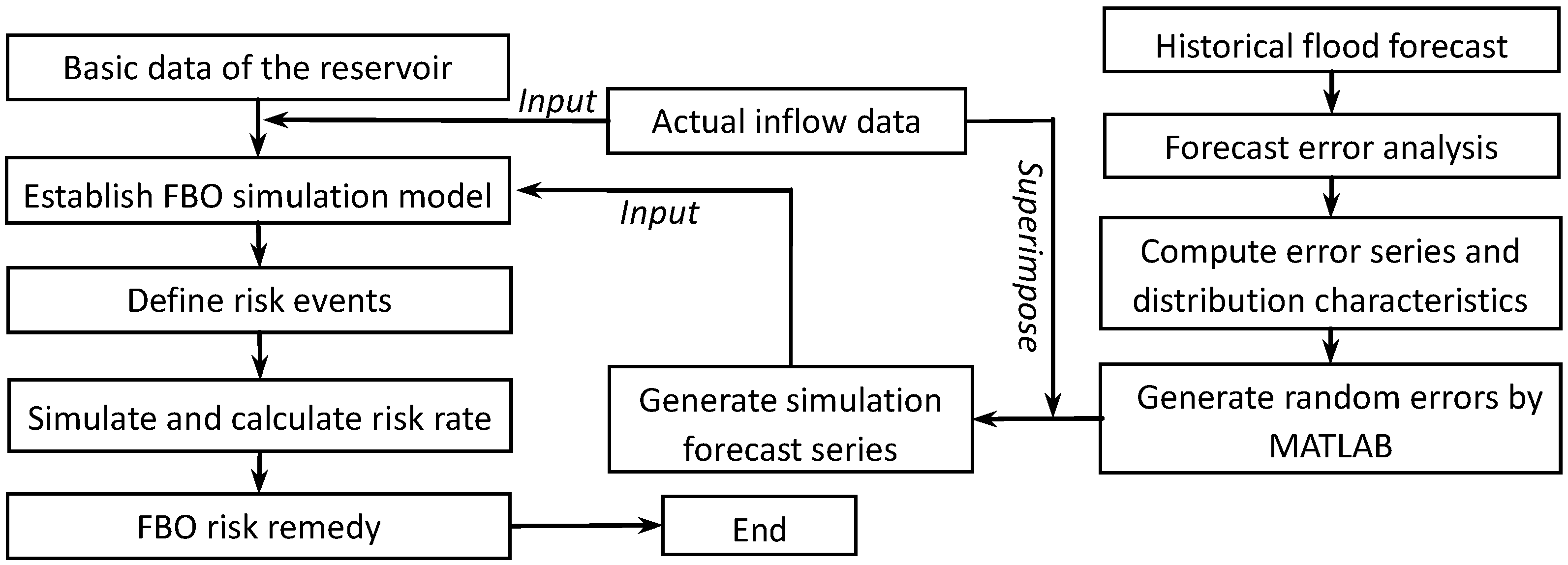
2.3. Forecasted Accuracy and Flood Regulation Risk
2.3.1. The Distribution and Evaluation of Forecast Error
2.3.2. Flood Regulation Risk Based on Monte-Carlo
3. Case Study
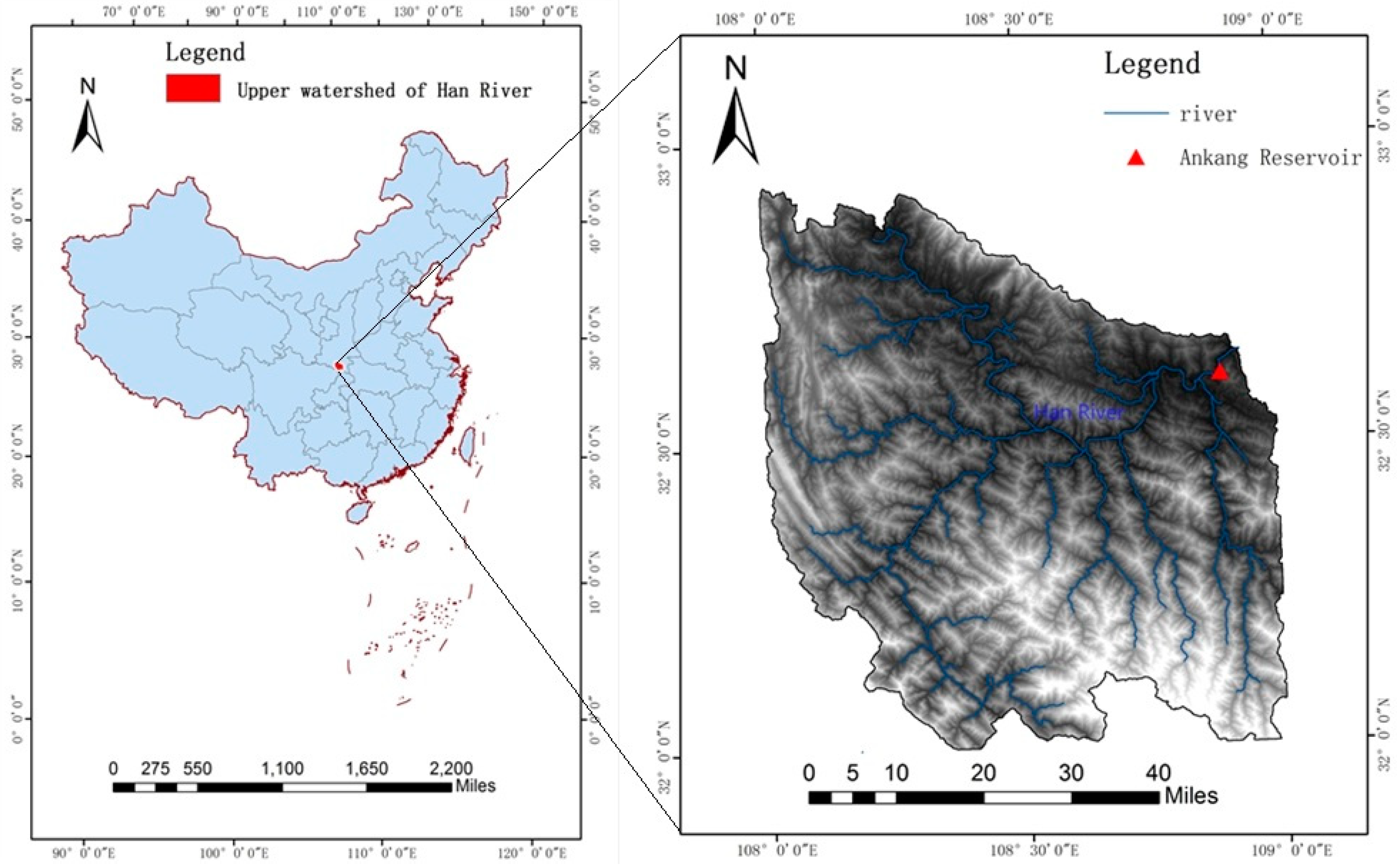
3.1. Overview of Ankang Reservoir
3.2. The Formulated FBO Rules for Ankang Reservoir
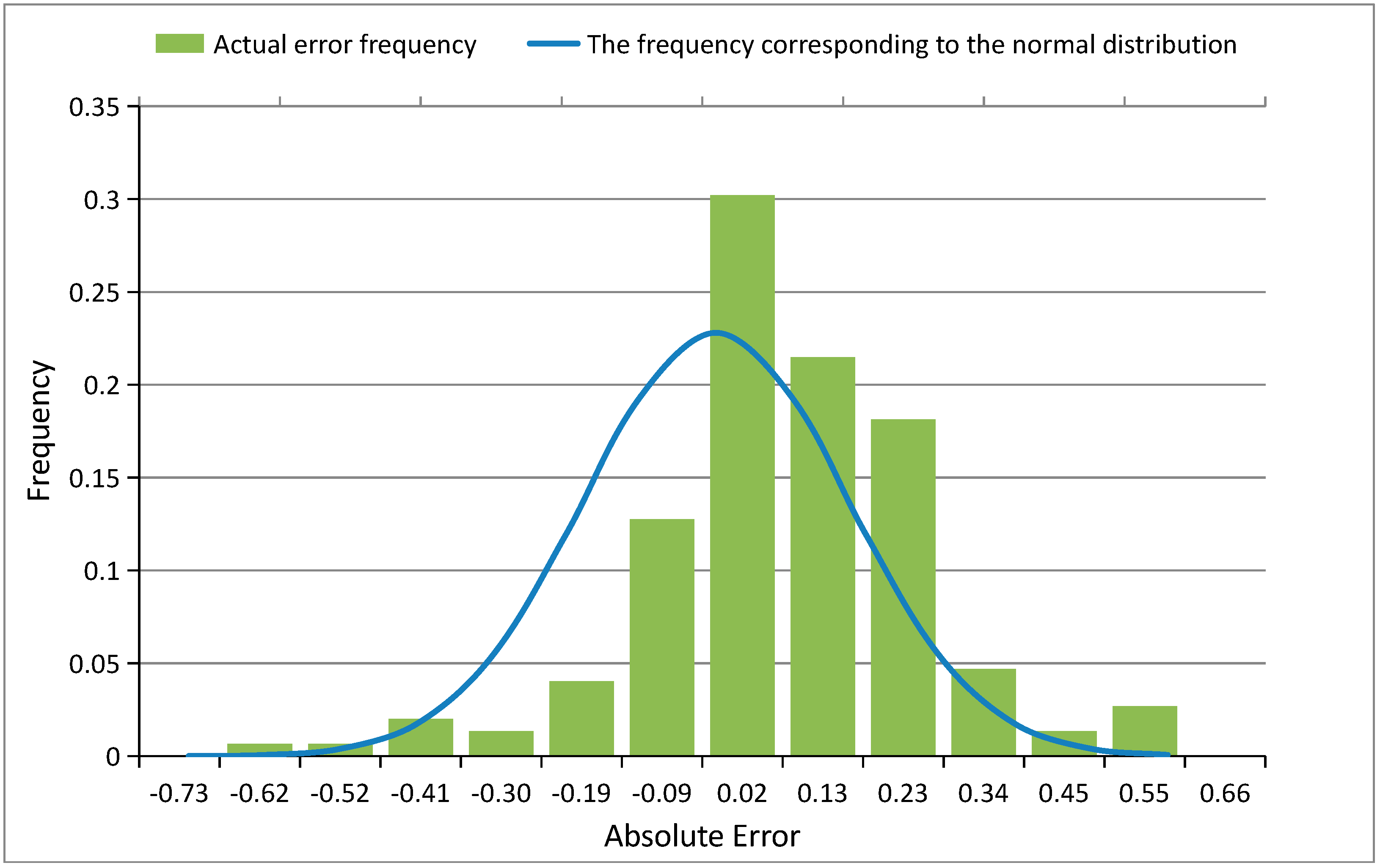
3.3. Error Analysis on Forecasted Net Rainfall
3.4. Risk Analysis of Ankang Reservoir Forecast-Based Operation
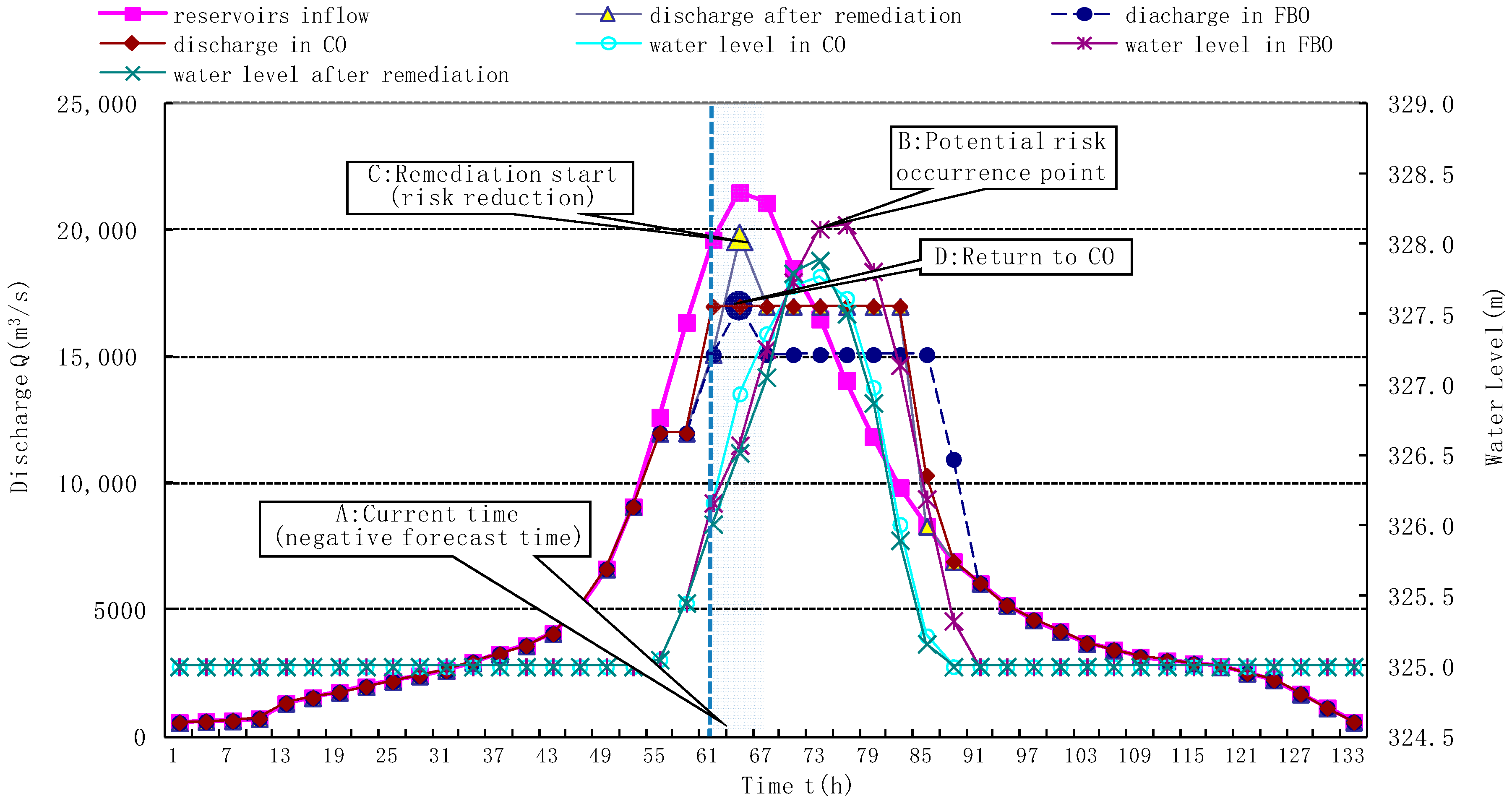
3.5. Preliminary Probing on the Remedies of Significant Forecast Error
4. Conclusions
- (1)
- Qualitative analysis showed that, among different types of uncertainties, the hydrological uncertainty should be considered as the significant risk source in reservoir flood control. Therefore, the forecast factor accuracy and its availability are crucial to determine the feasibility of FBO. As an illustration, the distribution of forecasted net rainfall errors for the Ankang hydrological monitoring and forecasting system obeyed approximately normal distribution based on the hypothesis test.
- (2)
- The Monte Carlo simulation is more appropriate for risk evaluation of FBO in view of its multiple factors and complexity. In contrast to CO, there are obvious advantages for FBO in risk control during real time flood regulation: for 20-year floods, the possible risk rate was reduced to approximately a quarter of CO. For five-year floods, the possible risk rate was reduced by more than half of CO.
- (3)
- The risk remedial measures for FBO were discussed conceptually. The basic assumption on remedies of significant forecast bias in FBO was put forward according to the different classifications of the forecast errors, false-negative and false-positive. Theoretically, there are two types of risk reduction techniques: single-step operation and multi-step operation. Taking the single-step risk reduction as an example, the main idea of the technique is presented with a schematic diagram, while, in view of the complexity of this problem, especially the intrinsic uncertainties in hydrologic process and forecast products, we believe that it is hard to find a quantitative and fixed model for various situations. All of these issues are subject to further study.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vechpanich, E.; Ruangrassamee, P.; Putthividhya, A.; Tanaka, K. Applications of Land Surface Model to Assess Impacts of Climate Change of Rainfall Pattern and Surface Runoff in the Chao Phraya River Basin of Thailand. In Proceedings of the World Environmental & Water Resources Congress, Austin, TX, USA, 17 May 2015. [Google Scholar]
- Etkin, D. Utilizing Seasonal Forecasts to Improve Reservoir Operations in the Comoe River Basin. Ph.D. Thesis, Tufts University, Medford, MA, USA, 2009. [Google Scholar]
- Mo, C.; Mo, G.; Peng, L.; Zhong, H.; Wang, D.; Huang, Y.; Jin, J. Reservoir operation by staging due to climate variability. Hydrol. Sci. J./J. Des. Sci. Hydrol. 2018, 63, 1–12. [Google Scholar] [CrossRef]
- Karami, H.; Mousavi, S.F.; Farzin, S.; Ehteram, M.; Singh, V.P.; Kisi, O. Improved Krill Algorithm for Reservoir Operation. Water Resour. Manag. 2018, 32, 3353–3372. [Google Scholar] [CrossRef]
- Ehteram, M.; Mousavi, S.F.; Karami, H.; Farzin, S.; Singh, V.P.; Chau, K.W.; El-Shafie, A. Reservoir operation based on evolutionary algorithms and multi-criteria decision-making under climate change and uncertainty. J. Hydroinform. 2018, 20, jh2018094. [Google Scholar] [CrossRef]
- Nohara, D.; Hori, T.; Sato, Y. Real-Time Reservoir Operation for Drought Management Considering Operational Ensemble Predictions of Precipitation in Japan. Adv. Hydroinform. 2018. [Google Scholar] [CrossRef]
- Guo, S.; Zhang, H.; Chen, H.; Peng, D.; Liu, P.; Pang, B.O. A reservoir flood forecasting and control system for China. Hydrol. Sci. J. 2004, 49, 972. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef]
- Arunkumar, R.; Jothiprakash, V. Optimal Reservoir Operation for Hydropower Generation using Non-linear Programming Model. J. Inst. Eng. 2012, 93, 111–120. [Google Scholar] [CrossRef]
- Reznicek, K.; Cheng, T.C.E. Stochastic modelling of reservoir operations. Eur. J. Oper. Res. 1991, 50, 235–248. [Google Scholar] [CrossRef]
- Tao, B.; Kan, Y.B.; Chang, J.X.; Qiang, H.; Chang, F.J. Fusing feasible search space into PSO for multi-objective cascade reservoir optimization. Appl. Soft Comput. 2017, 51, 328–340. [Google Scholar]
- Haddad, O.B.; Afshar, A.; Mariño, M.A. Honey-Bees Mating Optimization (HBMO) Algorithm: A New Heuristic Approach for Water Resources Optimization. Water Resour. Manag. 2006, 20, 661–680. [Google Scholar] [CrossRef]
- Yeh, W.W.G. Reservoir Management and Operations Models: A State-of-the-Art Review. Water Resour. Res. 1985, 21, 1797–1818. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multi-reservoir systems: State-of-the-art review. J Water Resour Plan Manage ASCE. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- LINDASEE; STANOPENSHAW. Applying soft computing approaches to river level forecasting. Int. Assoc. Sci. Hydrol. Bull. 1999, 44, 16. [Google Scholar]
- Young, P.C. Advances in real-time flood forecasting. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2002, 360, 1433–1450. [Google Scholar] [CrossRef]
- Koussis, A.D.; Lagouvardos, K.; Mazi, K.; Kotroni, V.; Sitzmann, D.; Lang, J.R.; Zaiss, H.; Buzzi, A.; Malguzzi, P. Flood Forecasts for Urban Basin with Integrated HydroMeteorological Model. J. Hydrol. Eng. 2003, 8, 1–11. [Google Scholar] [CrossRef]
- Krstanovic, P.F.; Singh, V.P. A univariate model for long-term streamflow forecasting. Stoch. Hydrol. Hydraul. 1991, 5, 189–205. [Google Scholar] [CrossRef]
- Thornes, J.E.; Stephenson, D.B. How to judge the quality and value of weather forecast products. Meteorol. Appl. 2010, 8, 307–314. [Google Scholar] [CrossRef]
- Dalezios, N.R.; Tyraskis, P.A. Maximum entropy spectra for regional precipitation analysis and forecasting. J. Hydrol. 1989, 109, 25–42. [Google Scholar] [CrossRef]
- Bai, T.; Wei, J.; Yang, W.; Huang, Q. Multi-Objective Parameter Estimation of Improved Muskingum Model by Wolf Pack Algorithm and Its Application in Upper Hanjiang River, China. Water 2018, 10, 1415. [Google Scholar] [CrossRef]
- Bolouri-Yazdeli, Y.; Haddad, O.B.; Fallah-Mehdipour, E.; Mariño, M.A. Evaluation of real-time operation rules in reservoir systems operation. Water Resour. Manag. 2014, 28, 715–729. [Google Scholar] [CrossRef]
- Mosavi, A.; Ozturk, P.; Chau, K.W. Flood Prediction Using Machine Learning Models: Literature Review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Apel, H.; Thieken, A.H.; Merz, B.; Blöschl, G. A Probabilistic Modelling System for Assessing Flood Risks. Nat. Hazards 2006, 38, 79–100. [Google Scholar] [CrossRef]
- Xu, Z.X.; Ito, K.; Liao, S.; Wang, L. Incorporating inflow uncertainty into risk assessment for reservoir operation. Stoch. Hydrol. Hydraul. 1997, 11, 433–448. [Google Scholar] [CrossRef]
- Yazicigil, H.; Houck, M.H. The effects of risk and reliability on optimal reservoir design1. Jawra J. Am. Water Resour. Assoc. 2010, 20, 417–424. [Google Scholar] [CrossRef]
- Paik, K. Analytical derivation of reservoir routing and hydrological risk evaluation of detention basins. J. Hydrol. 2008, 352, 191–201. [Google Scholar] [CrossRef]
- Plate, E.J. Flood risk and flood management. J. Hydrol. 2005, 267, 2–11. [Google Scholar] [CrossRef]
- Zhang, Y.K. Theories and Methods of Risk Analysis for Multipurpose Reservoir Operation. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2012. [Google Scholar]
- Burn, D.H.; Venema, H.D.; Simonovic, S.P. Risk-based performance criteria for real-time reservoir operation. Can. J. Civ. Eng. 1991, 18, 36–42. [Google Scholar] [CrossRef]
- Pan, L.; Lin, K.; Wei, X. A two-stage method of quantitative flood risk analysis for reservoir real-time operation using ensemble-based hydrologic forecasts. Stoch. Environ. Res. Risk Assess. 2015, 29, 803–813. [Google Scholar]
- Zhong, P.; Zeng, J. Research on Risk Analysis of Reservoir Real- time Flood Control Operation. Water Power 2008, 34, 8–9. [Google Scholar]
- Apel, H.; Thieken, A.H.; Merz, B.; Blöschl, G. Flood risk assessment and associated uncertainty. Nat. Hazards Earth Syst. Sci. 2004, 4, 295–308. [Google Scholar] [CrossRef]
- Cheng, C.T.; Chau, K.W. Flood control management system for reservoirs. Environ. Model. Softw. 2004, 19, 1141–1150. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, Q.; Yan, A.; Lin, L. Reduction of Risks in Hydro Engineering Stage Construction Using Discharge Control of Upriver Reservoir. In Proceedings of the International Conference on Risk Analysis & Crisis Response, Shanghai, China, 25 September 2007. [Google Scholar]
| Number | Inflow (m3/s) | Water Level Z (m) | Release (m3/s) | Notes |
|---|---|---|---|---|
| 1 | Qin and Qout represent flood inflow and discharge | |||
| 2 | , flood rising | |||
| 3 | ||||
| 4 | ||||
| 5 | Free overflow |
| No. | Cumulative Net Rainfall (mm) | Water Level Z (m) | Release (m3/s) | Remarks |
|---|---|---|---|---|
| 1 | Qin and Qout represent flood inflow and discharge | |||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | Free overflow |
| Frequency(%) | 0.01 | 0.1 | 1 | 5 | 10 | 20 |
| The Absolute Error of the Net Rain(mm) | 0.7182 | 0.6 | 0.4564 | 0.3282 | 0.2599 | 0.1772 |
| Return Period (year) | Za_max(m) | Qa_max (m3/s) | Simulation Times | Counts (Z > Za_max or Q > Qa_max) | Frequency P (%) | Risk Rate Ψ (%) |
|---|---|---|---|---|---|---|
| 10,000 | 337.05 | —— | 10,000 | 0 | 0 | 0 |
| 1000 | 333.1 | —— | 10,000 | 0 | 0 | 0 |
| 100 | 330.0 | —— | 10,000 | 0 | 0 | 0 |
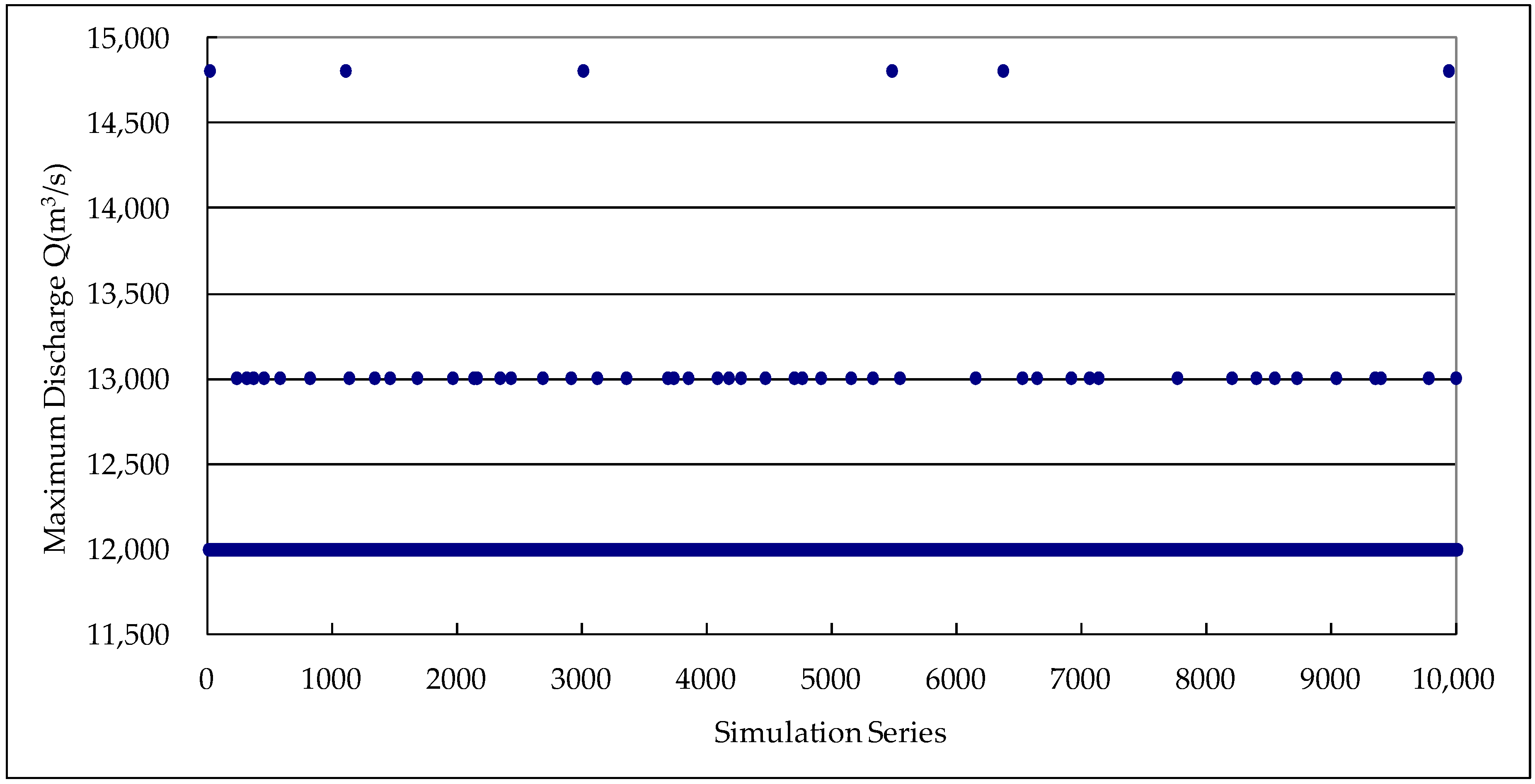
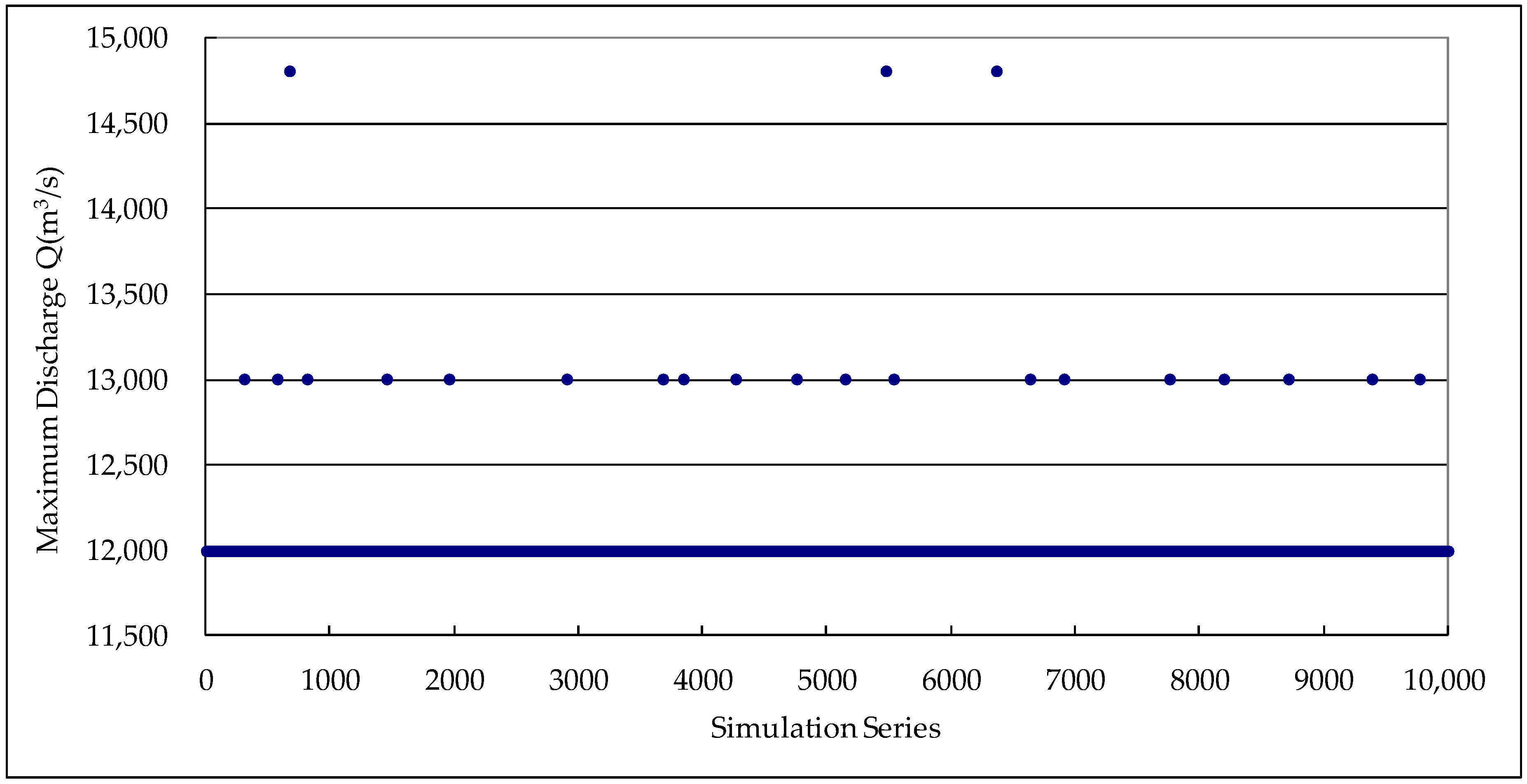
| 20 | 328.6 | 17,000 | 10,000 | 5 | 0.05 | 0.0025 |
| 5 | 326.7 | 12,000 | 10,000 | 54 | 0.54 | 0.108 |
| Return Period (year) | Za_max(m) | Qa_max (m3/s) | Simulation Times | Counts (Z > Za_max or Q > Qa_max) | Frequency P (%) | Risk Rate Ψ (%) |
|---|---|---|---|---|---|---|
| 10,000 | 337.05 | —— | 10,000 | 0 | 0 | 0 |
| 1000 | 333.1 | —— | 10,000 | 0 | 0 | 0 |
| 100 | 330.0 | —— | 10,000 | 0 | 0 | 0 |
| 20 | 328.6 | 17,000 | 10,000 | 1 | 0.01 | 0.0005 |
| 5 | 326.7 | 12,000 | 10,000 | 22 | 0.22 | 0.044 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Lyu, J.; Jia, Z.; Wang, L.; Xu, B. Risks Analysis and Response of Forecast-Based Operation for Ankang Reservoir Flood Control. Water 2019, 11, 1134. https://doi.org/10.3390/w11061134
Liu Z, Lyu J, Jia Z, Wang L, Xu B. Risks Analysis and Response of Forecast-Based Operation for Ankang Reservoir Flood Control. Water. 2019; 11(6):1134. https://doi.org/10.3390/w11061134
Chicago/Turabian StyleLiu, Zhao, Jiawei Lyu, Zhifeng Jia, Lixia Wang, and Bin Xu. 2019. "Risks Analysis and Response of Forecast-Based Operation for Ankang Reservoir Flood Control" Water 11, no. 6: 1134. https://doi.org/10.3390/w11061134
APA StyleLiu, Z., Lyu, J., Jia, Z., Wang, L., & Xu, B. (2019). Risks Analysis and Response of Forecast-Based Operation for Ankang Reservoir Flood Control. Water, 11(6), 1134. https://doi.org/10.3390/w11061134





