Assessing the Predictability of an Improved ANFIS Model for Monthly Streamflow Using Lagged Climate Indices as Predictors
Abstract
1. Introduction
2. Background
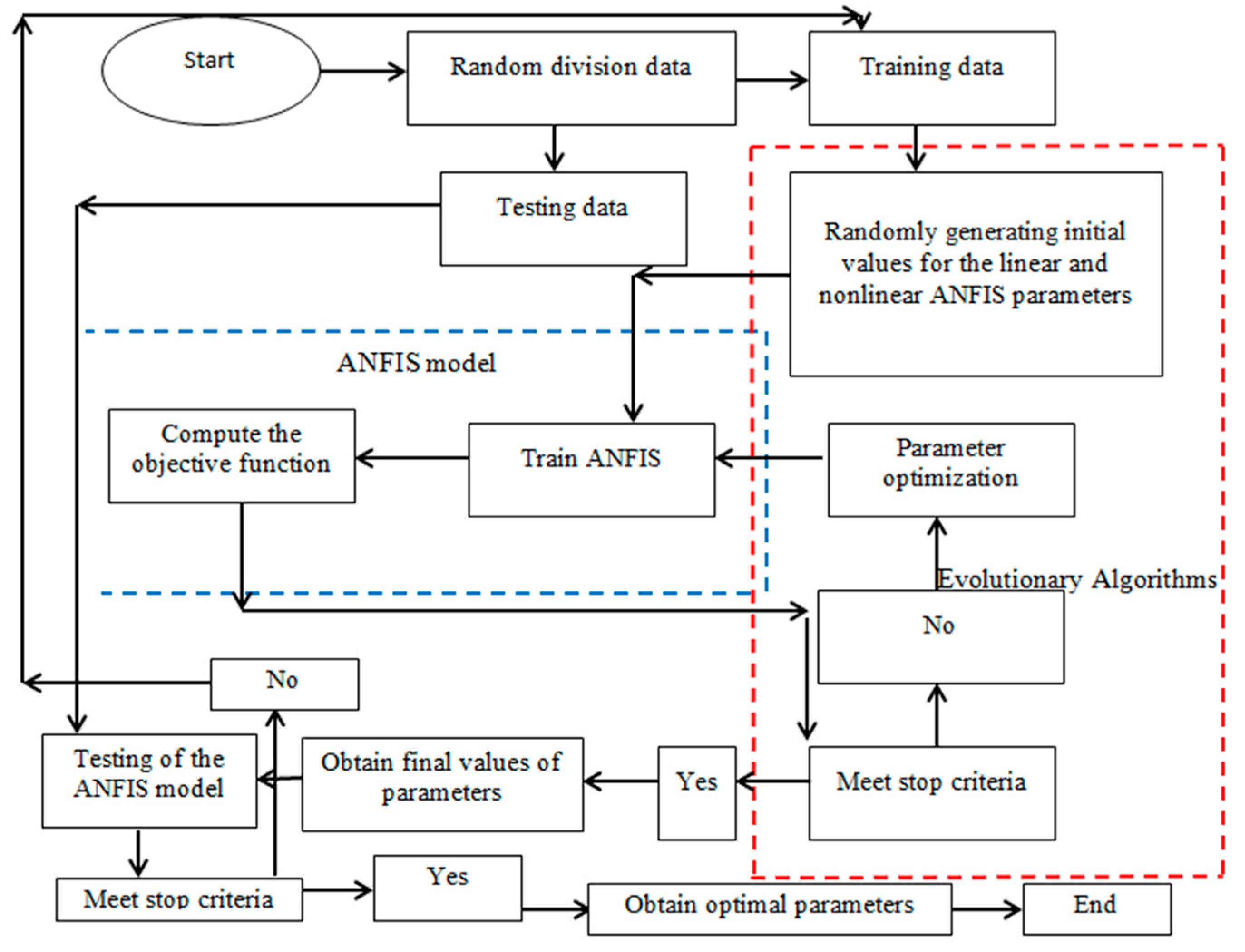
3. Materials and Methods
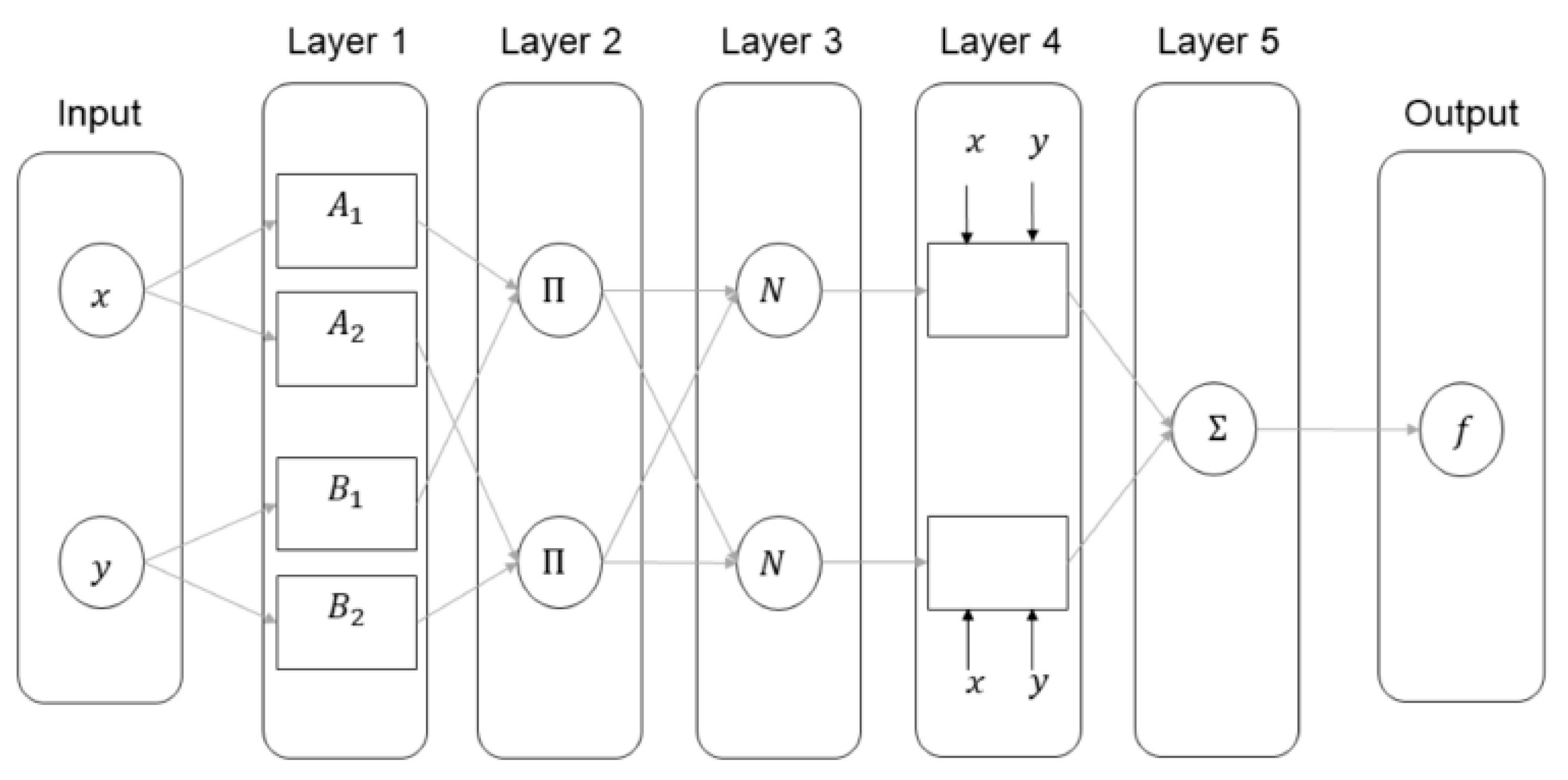
3.1. ANFIS
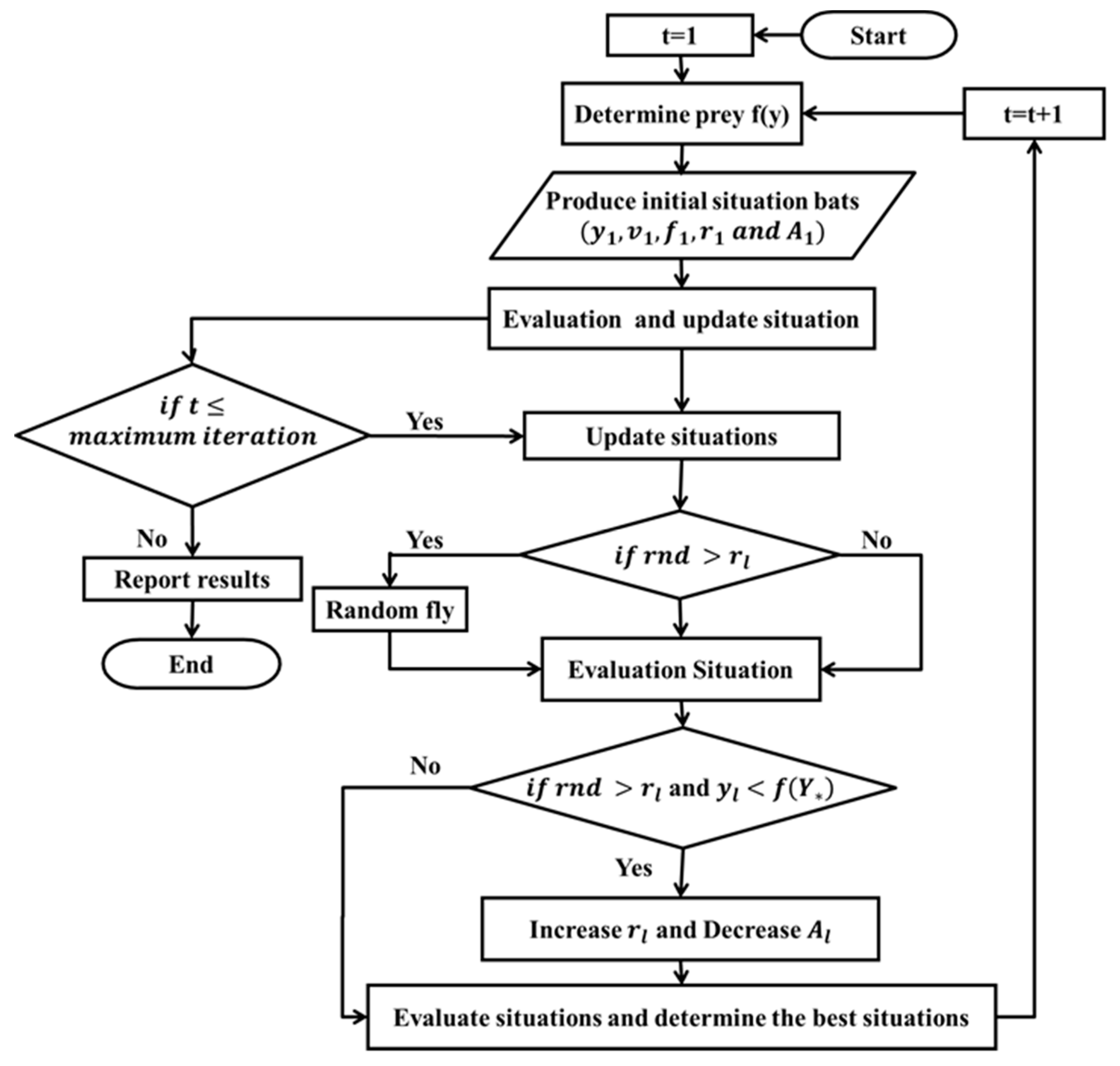
3.2. Bat Algorithm (BA)
- (1)
- All bats use echolocation to identify the food location.
- (2)
- The bats fly at the random velocity (vl) at the location yl with the frequency fmin and the wavelength . The loudness parameter for the bats is given by A0.
- (3)
- The volume can vary from A0 to Amin.
3.3. Particle Swarm Optimization (PSO)
3.4. Genetic Algorithm (GA)
3.5. Principal Component Analysis (PCA)
- (1)
- PCA is considered to be a statistical nonparametric method and thus, it is necessary to evaluate the Kaiser–Meyer–Olkin (KMO) test. This index is computed based on simple and partial correlation coefficients. If the value of the KMO coefficient is more than 0.5, the PCA method can be applied to the data [36,37,38].where and aij are the simple correlation coefficient and partial correlation coefficient, respectively, between variables i,j.
- (2)
- The second level is used for the conversion of data to the standard format:where Z is the standard value for the data, is the average of each variable and is the standard deviation for each variable.
- (3)
- The correlation matrix is computed to show the variations in the samples and the correlations of different variables with each other. The members of the main diagonal of the matrix are considered as variance of the input variables, and other arrays are considered as covariances of the input variables [34].
- (4)
- The Eigen vectors and Eigen values are computed based on the following equation:where R is the correlation matrix, is the Eigen value, and I is the unit matrix. It should be noted that Eigen vectors describe the component characteristics and each component includes a percentage of initial information. A higher Eigen value shows that the generated component of the Eigen value includes a higher percentage of initial data. The selection of some initial components based on the highest value of their variance is considered to be important for the PCA.
3.6. Data Splitting
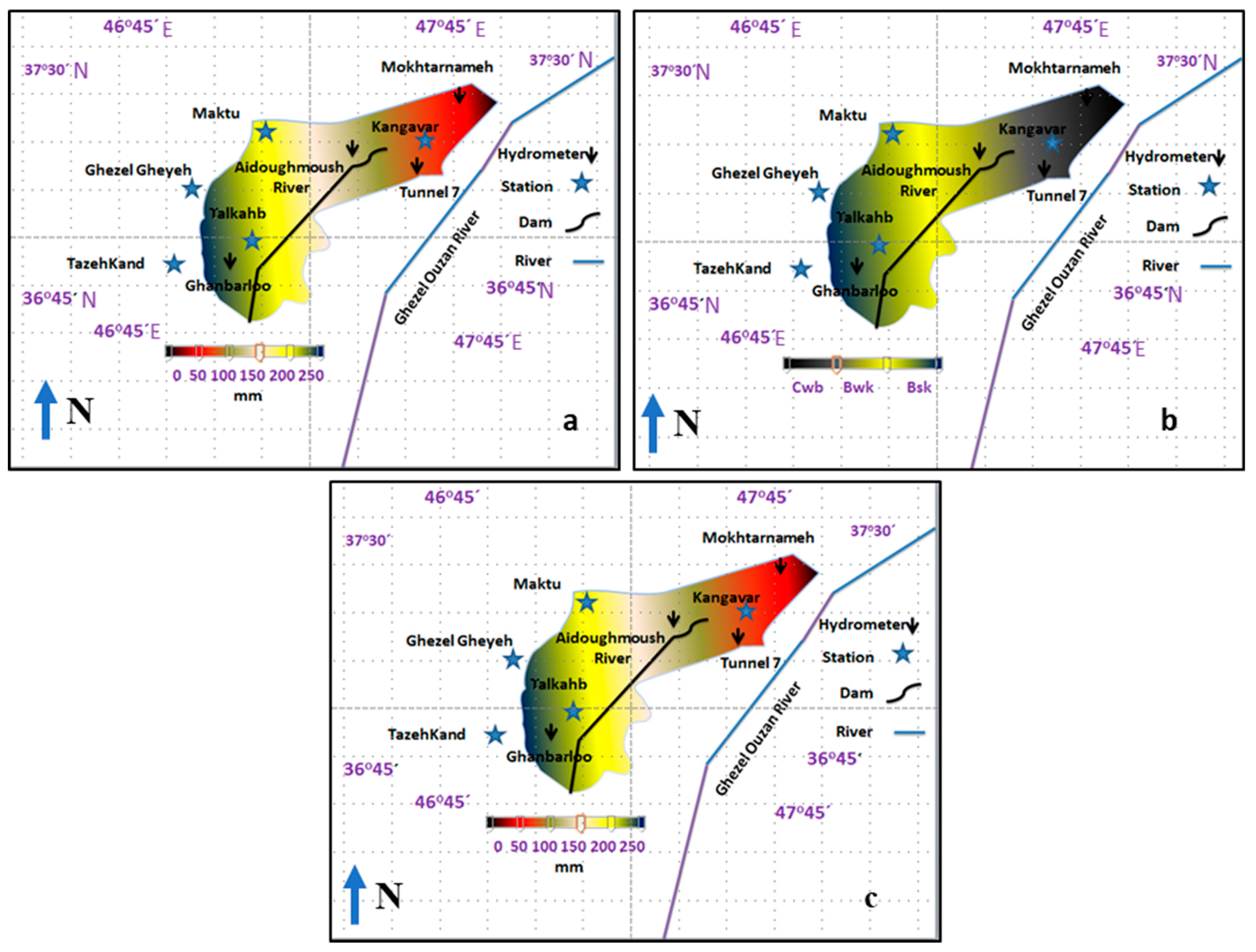
4. Case Study
5. Discussion and Results
5.1. Results of PCA
5.2. Study of Sensitivity Analysis by Vayring Parameter Values
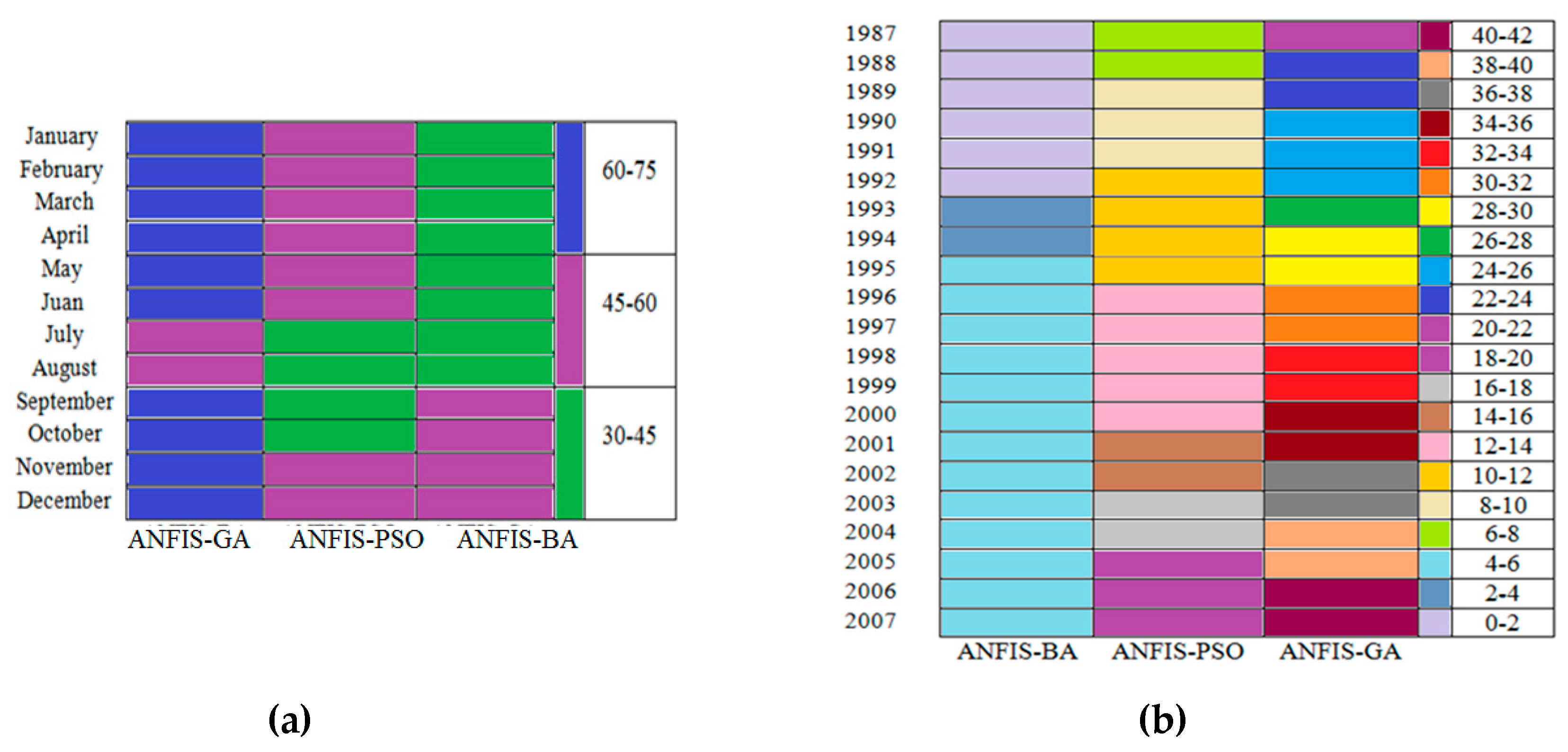
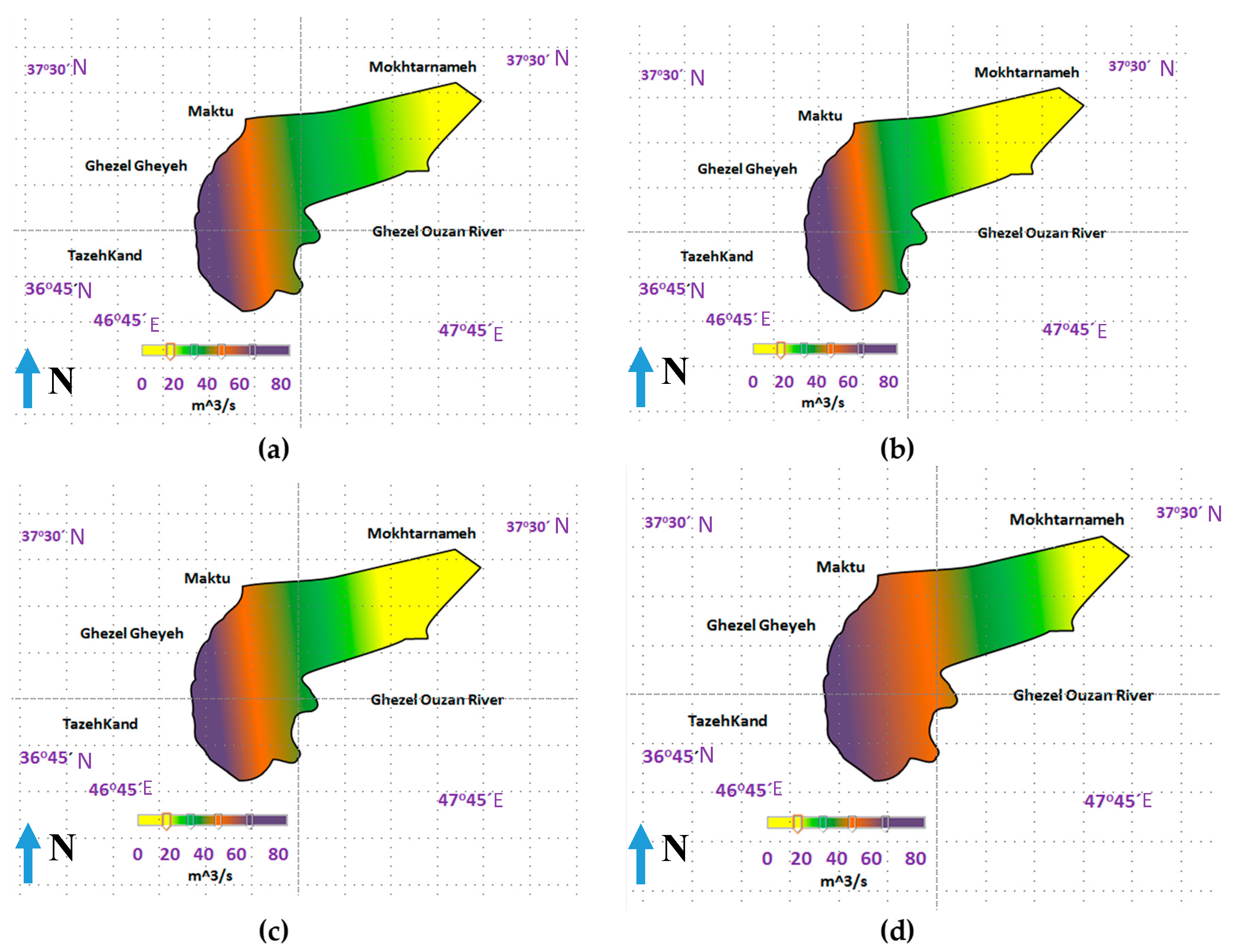
5.3. Results for Comparison of ANFIS-BA, ANFIS, PSO and ANFIS GA
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| First Part | Second Part | Third Part |
| B (arid) | W (desert) | - |
| S (steppe) | - | |
| h (hot) | ||
| k (cold) | ||
| C (temperate) | S (dry summer) | - |
| W (dry winter) | - | |
| F (without dry season) | - | |
| - | a (hot summer) | |
| - | b (warm summer) | |
| - | c (cold summer) |
References
- Goodrich, D.C.; Woolhiser, D.A. Catchment Hydrology. Rev. Geophys. 1991, 29, 202–209. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Salvadori, G.; De Michele, C. Catchment compatibility via copulas: A non-parametric study of the dependence structures of hydrological responses. Adv. Water Resour. 2016, 90, 116–133. [Google Scholar] [CrossRef]
- Scheel, K.; Morrison, R.R.; Annis, A.; Nardi, F. Understanding the Large-Scale Influence of Levees on Floodplain Connectivity Using a Hydrogeomorphic Approach. JAWRA J. Am. Water Resour. Assoc. 2019, 55, 413–429. [Google Scholar] [CrossRef]
- Dariusz, M.; Andrea, P.; Andrzej, W. Flood frequency analysis by an event-based rainfall-runoff model in selected catchments of southern Poland. Soil Water Res. 2018, 13, 170–176. [Google Scholar] [CrossRef]
- Bhandari, S.; Kalra, A.; Tamaddun, K.; Ahmad, S. Relationship between Ocean-Atmospheric Climate Variables and Regional Streamflow of the Conterminous United States. Hydrology 2018, 5, 30. [Google Scholar] [CrossRef]
- Sulca, J.; Takahashi, K.; Espinoza, J.-C.; Vuille, M.; Lavado-Casimiro, W. Impacts of different ENSO flavors and tropical Pacific convection variability (ITCZ, SPCZ) on austral summer rainfall in South America, with a focus on Peru. Int. J. Climtol. 2017, 38, 420–435. [Google Scholar] [CrossRef]
- Caillouet, L.; Rousseau, A.N.; Savary, S.; Foulon, E. Improving operational ensemble streamflow forecasts by selecting past meteorological scenarios according to climate indices. Proceedings of AGU Fall Meeting, Washington, DC, USA, 10–14 December 2018; Available online: file:///C:/Users/MDPI/Downloads/2018_12_AGU_presentation_Final.pdf (accessed on 15 May 2019).
- Tamaddun, K.A.; Kalra, A.; Bernardez, M.; Ahmad, S. Effects of ENSO on Temperature, Precipitation, and Potential Evapotranspiration of North India’s Monsoon: An Analysis of Trend and Entropy. Water 2019, 11, 189. [Google Scholar] [CrossRef]
- Gomez, F.A.; Lee, S.-K.; Hernandez, F.J.; Chiaverano, L.M.; Muller-Karger, F.E.; Liu, Y.; Lamkin, J.T. ENSO-induced co-variability of Salinity, Plankton Biomass and Coastal Currents in the Northern Gulf of Mexico. Sci. Rep. 2019, 9, 178. [Google Scholar] [CrossRef]
- Tamaddun, K.A.; Kalra, A.; Ahmad, S. Spatiotemporal Variation in the Continental US Streamflow in Association with Large-Scale Climate Signals Across Multiple Spectral Bands. Water Resour. Manag. 2019, 23, 1947–1968. [Google Scholar] [CrossRef]
- Kalra, A.; Sagarika, S.; Ahmad, S. Long-Term Changes in the Continental United States Streamflow and Teleconnections with Oceanic-Atmospheric Indices. World Environ. Water Resour. Congr. 2016, 2016, 498. [Google Scholar]
- Tamaddun, K.A.; Kalra, A.; Ahmad, S. Wavelet analyses of western US streamflow with ENSO and PDO. J. Water Clim. Chang. 2016, 8, 26–39. [Google Scholar] [CrossRef]
- Kashid, S.S.; Ghosh, S.; Maity, R. Streamflow prediction using multi-site rainfall obtained from hydroclimatic teleconnection. J. Hydrol. 2010, 395, 23–38. [Google Scholar] [CrossRef]
- Maity, R.; Kashid, S.S. Short-Term Basin-Scale Streamflow Forecasting Using Large-Scale Coupled Atmospheric–Oceanic Circulation and Local Outgoing Longwave Radiation. J. Hydrometeorol. 2010, 11, 370–387. [Google Scholar] [CrossRef]
- Wei, W.; Watkins, D.W. Data mining methods for hydroclimatic forecasting. Adv. Water Resour. 2011, 34, 1390–1400. [Google Scholar] [CrossRef]
- Thakur, B.; Pathak, P.; Kalra, A.; Ahmad, S. Changing characteristics of streamflow in the Midwest and its relation to oceanic-atmospheric oscillations. Proceedings of AGU Fall Meeting, San Francisco, CA, USA, 12–16 December 2016; Available online: http://adsabs.harvard.edu/abs/2016AGUFM.H33C1549T (accessed on 15 May 2019).
- Gimenez, J.C.; Lentini, E.J.; Fernández Cirelli, A. Forecasting Streamflows in the San Juan River Basin in Argentina. In Water and Sustainability in Arid Regions; Springer: Dordrecht, The Netherlands, 2010; pp. 261–274. [Google Scholar]
- Lima, C.H.R.; Lall, U. Climate informed monthly streamflow forecasts for the Brazilian hydropower network using a periodic ridge regression model. J. Hydrol. 2010, 380, 438–449. [Google Scholar] [CrossRef]
- Kalra, A.; Li, L.; Li, X.; Ahmad, S. Improving Streamflow Forecast Lead Time Using Oceanic-Atmospheric Oscillations for Kaidu River Basin, Xinjiang, China. J. Hydrol. Eng. 2013, 18, 1031–1040. [Google Scholar] [CrossRef]
- Rasouli, K.; Hsieh, W.W.; Cannon, A.J. Daily streamflow forecasting by machine learning methods with weather and climate inputs. J. Hydrol. 2012, 414–415, 284–293. [Google Scholar] [CrossRef]
- Kalra, A.; Ahmad, S.; Nayak, A. Increasing streamflow forecast lead time for snowmelt-driven catchment based on large-scale climate patterns. Adv. Water Resour. 2013, 53, 150–162. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, P.; Zhang, Y. A Probabilistic Wavelet–Support Vector Regression Model for Streamflow Forecasting with Rainfall and Climate Information Input*. J. Hydrometeorol. 2015, 16, 2209–2229. [Google Scholar] [CrossRef]
- Deo, R.C.; Şahin, M. Erratum to: An extreme learning machine model for the simulation of monthly mean streamflow water level in eastern Queensland. Environ. Monit. Assess. 2016, 188, 90. [Google Scholar] [CrossRef]
- Liang, Z.; Li, Y.; Hu, Y.; Li, B.; Wang, J. A data-driven SVR model for long-term runoff prediction and uncertainty analysis based on the Bayesian framework. Theor. Appl. Climtol. 2017, 133, 137–149. [Google Scholar] [CrossRef]
- Esha, R.I.; Imteaz, M.A. Assessing the predictability of MLR models for long-term streamflow using lagged climate indices as predictors: A case study of NSW (Australia). Hydrol. Res. 2018, 50, 262–281. [Google Scholar] [CrossRef]
- Kim, T.; Shin, J.-Y.; Kim, H.; Kim, S.; Heo, J.-H. The Use of Large-Scale Climate Indices in Monthly Reservoir Inflow Forecasting and Its Application on Time Series and Artificial Intelligence Models. Water 2019, 11, 374. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, Q.J.; Schepen, A.; Griffiths, M. Ensemble forecasting of monthly and seasonal reference crop evapotranspiration based on global climate model outputs. Agric. For. Meteorol. 2019, 264, 114–124. [Google Scholar] [CrossRef]
- Reed, E.V.; Cole, J.E.; Lough, J.M.; Thompson, D.; Cantin, N.E. Linking climate variability and growth in coral skeletal records from the Great Barrier Reef. Coral Reefs 2018, 38, 29–43. [Google Scholar] [CrossRef]
- Neves, M.C.; Jerez, S.; Trigo, R.M. The response of piezometric levels in Portugal to NAO, EA, and SCAND climate patterns. J. Hydrol. 2019, 568, 1105–1117. [Google Scholar] [CrossRef]
- Chiri, H.; Abascal, A.J.; Castanedo, S.; Antolínez, J.A.A.; Liu, Y.; Weisberg, R.H.; Medina, R. Statistical simulation of ocean current patterns using autoregressive logistic regression models: A case study in the Gulf of Mexico. Ocean Model. 2019, 136, 1–12. [Google Scholar] [CrossRef]
- Zare, M.; Koch, M. Groundwater level fluctuations simulation and prediction by ANFIS- and hybrid Wavelet-ANFIS/Fuzzy C-Means (FCM) clustering models: Application to the Miandarband plain. J. Hydro-Environ. Res. 2018, 18, 63–76. [Google Scholar] [CrossRef]
- Ali, M.; Deo, R.C.; Downs, N.J.; Maraseni, T. Multi-stage hybridized online sequential extreme learning machine integrated with Markov Chain Monte Carlo copula-Bat algorithm for rainfall forecasting. Atmos. Res. 2018, 213, 450–464. [Google Scholar] [CrossRef]
- Farzin, S.; Singh, V.; Karami, H.; Farahani, N.; Ehteram, M.; Kisi, O.; Allawi, M.; Mohd, N.; El-Shafie, A. Flood Routing in River Reaches Using a Three-Parameter Muskingum Model Coupled with an Improved Bat Algorithm. Water 2018, 10, 1130. [Google Scholar] [CrossRef]
- Chi, S.; Ni, S.; Liu, Z. Back Analysis of the Permeability Coefficient of a High Core Rockfill Dam Based on a RBF Neural Network Optimized Using the PSO Algorithm. Math. Probl. Eng. 2015, 2015, 1–15. [Google Scholar] [CrossRef]
- Montaseri, M.; Hesami Afshar, M.; Bozorg-Haddad, O. Development of Simulation-Optimization Model (MUSIC-GA) for Urban Stormwater Management. Water Resour. Manag. 2015, 29, 4649–4665. [Google Scholar] [CrossRef]
- Solgi, A.; Pourhaghi, A.; Bahmani, R.; Zarei, H. Pre-processing data using wavelet transform and PCA based on support vector regression and gene expression programming for river flow simulation. J. Earth Syst. Sci. 2017, 126, 65. [Google Scholar] [CrossRef]
- Kalra, A.; Ahmad, S. Estimating annual precipitation for the Colorado River Basin using oceanic-atmospheric oscillations. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Jiang, Z.; Qi, J.; Su, S.; Zhang, Z.; Wu, J. Water body delineation using index composition and HIS transformation. Int. J. Remote Sens. 2011, 33, 3402–3421. [Google Scholar] [CrossRef]
- Dubreuil, V.; Fante, K.P.; Planchon, O.; Sant’Anna Neto, J.L. Climate change evidence in Brazil from Köppen’s climate annual types frequency. Int. J. Climatol. 2018, 39, 1446–1456. [Google Scholar] [CrossRef]
- Tong, W.; Franklin, J.; Zhou, X.; Li, L.; Besenyi, G. Machine Learning on Spark for the Optimal IDW-based Spatiotemporal Interpolation. Int. Conf. Gisci. Short Pap. Proc. 2016. [Google Scholar] [CrossRef]
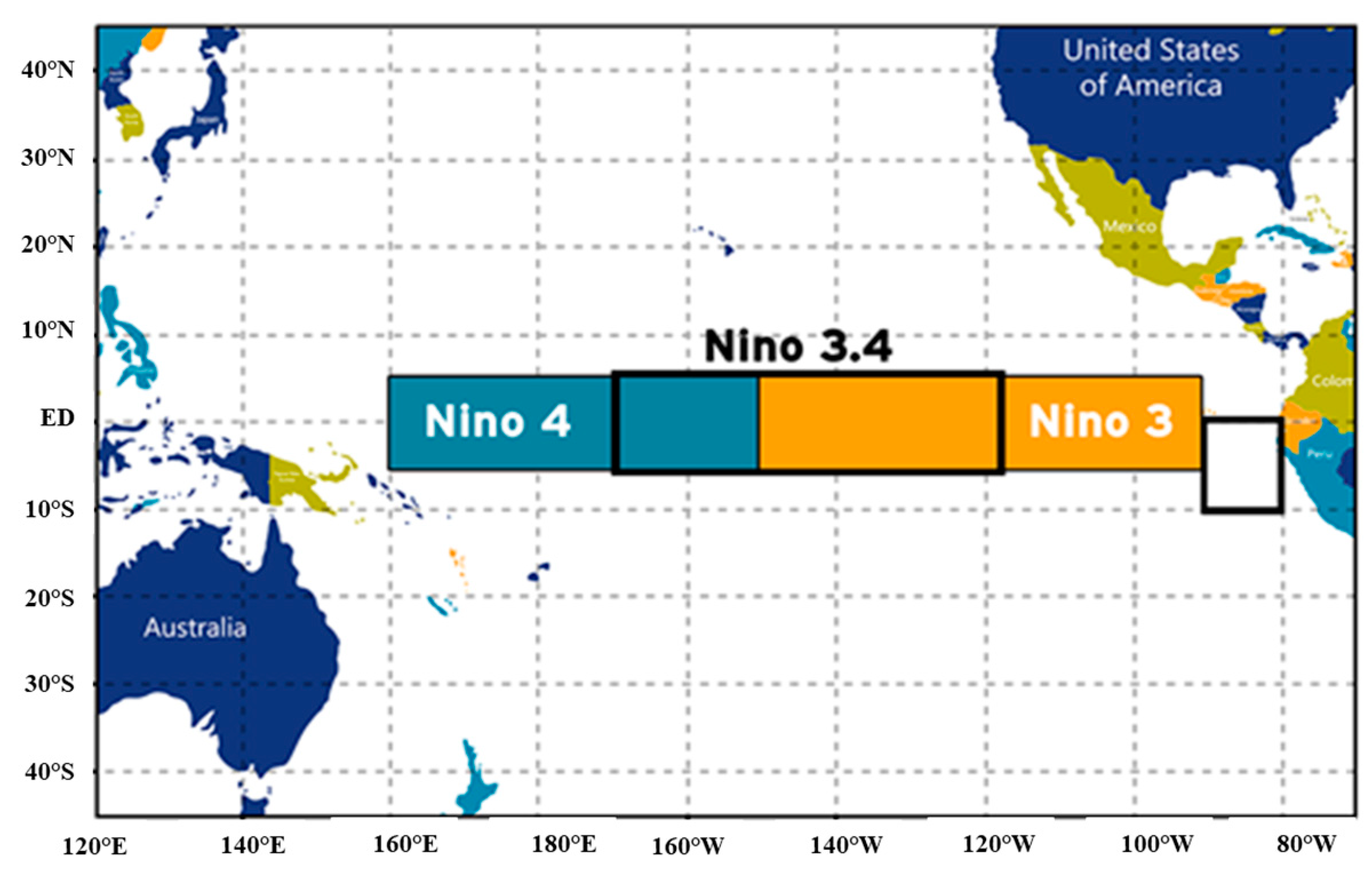


| Predicators | Predicator Definition | Origin | Data Period | Data Source |
|---|---|---|---|---|
| NINO4 | Average SST anomaly over centre Pacific Ocean | Pacific Ocean | 1987–2007 | https://library.noaa.gov http://sdwebx.worldbank.org/climateporta |
| NINO3 | Average SST anomaly over centre Pacific Ocean | Pacific Ocean | 1987–2007 | https://library.noaa.gov http://sdwebx.worldbank.org/climateporta |
| NINO3.4 | Average SST anomaly over centre Pacific Ocean | Pacific Ocean | 1987–2007 | https://library.noaa.gov http://sdwebx.worldbank.org/climateporta |
| PDO | Average SST anomaly over centre Pacific Ocean | Pacific Ocean | 1987–2007 | http://research.jisao.washington.edu/pdo/PDO.latest.txt |
| Components | Value of Each Component from 16 | Varince Prenatage of Data | Comulative Variantagece Prenatage |
|---|---|---|---|
| PCA1 | 6.72 | 42.000 | 42.000 |
| PCA2 | 3.68 | 23.000 | 65.000 |
| PCA3 | 2.08 | 13.000 | 78.000 |
| PCA4 | 1.12 | 7.000 | 85.000 |
| PCA5 | 0.88 | 5.500 | 90.500 |
| PCA6 | 0.80 | 5.000 | 95.500 |
| PCA7 | 0.496 | 3.100 | 98.600 |
| PCA8 | 0.179 | 1.12 | 99.720 |
| PCA9 | 0.0128 | 0.08 | 99.80 |
| PCA10 | 0.0128 | 0.08 | 99.88 |
| PCA11 | 0.0064 | 0.04 | 99.92 |
| PCA12 | 0.0064 | 0.04 | 99.96 |
| PCA13 | 0.0016 | 0.01 | 99.97 |
| PCA14 | 0.0016 | 0.01 | 99.98 |
| PCA15 | 0.0016 | 0.01 | 99.99 |
| PCA16 | 0.0016 | 0.01 | 100 |
| Components | PCA1 | PCA2 | PCA3 | PCA4 | PCA5 |
|---|---|---|---|---|---|
| NINO3 (t) | 0.12 | 0.11 | 0.09 | 0.07 | 0.06 |
| NINO3 (t − 3) | 0.67 | 0.64 | 0.61 | 0.55 | 0.53 |
| NINO3 (t − 6) | 0.94 | 0.92 | 0.91 | 0.90 | 0.87 |
| NINO3 (t − 9) | 0.61 | 0.60 | 0.59 | 0.52 | 0.50 |
| NINO4 (t) | 0.11 | 0.10 | 0.08 | 0.05 | 0.03 |
| NINO4 (t − 3) | 0.62 | 0.60 | 0.57 | 0.55 | 0.51 |
| NINO4 (t − 6) | 0.91 | 0.90 | 0.88 | 0.86 | 0.85 |
| NINO4 (t − 9) | 0.60 | 0.55 | 0.52 | 0.50 | 0.49 |
| NINO3.4 (t) | 0.10 | 0.09 | 0.08 | 0.07 | 0.05 |
| NINO3.4 (t − 3) | 0.61 | 0.56 | 0.51 | 0.49 | 0.42 |
| NINO3.4 (t − 6) | 0.89 | 0.82 | 0.80 | 0.79 | 0.77 |
| NINO3.4 (t − 9) | 0.60 | 0.52 | 0.49 | 0.45 | 0.40 |
| PDO (t) | 0.11 | 0.10 | 0.09 | 0.08 | 0.07 |
| PDO (t − 3) | 0.59 | 0.57 | 0.55 | 0.51 | 0.45 |
| PDO (t − 6) | 0.90 | 0.89 | 0.82 | 0.80 | 0.79 |
| PDO (t − 9) | 0.62 | 0.60 | 0.57 | 0.44 | 0.42 |
| Components | PCA1 | PCA2 | PCA3 | PCA4 | PCA5 |
|---|---|---|---|---|---|
| NINO3 (t) | 0.12 | 0.10 | 0.08 | 0.06 | 0.05 |
| NINO3 (t − 3) | 0.56 | 0.55 | 0.52 | 0.49 | 0.48 |
| NINO3 (t − 6) | 0.91 | 0.89 | 0.87 | 0.86 | 0.83 |
| NINO3 (t − 9) | 0.55 | 0.53 | 0.50 | 0.49 | 0.48 |
| NINO4 (t) | 0.11 | 0.12 | 0.10 | 0.09 | 0.08 |
| NINO4 (t − 3) | 0.52 | 0.49 | 0.47 | 0.45 | 0.44 |
| NINO4 (t − 6) | 0.90 | 0.88 | 0.85 | 0.83 | 0.82 |
| NINO4 (t − 9) | 0.50 | 0.45 | 0.45 | 0.42 | 0.41 |
| NINO3.4 (t) | 0.09 | 0.08 | 0.06 | 0.05 | 0.05 |
| NINO3.4 (t − 3) | 0.51 | 0.50 | 0.49 | 0.47 | 0.45 |
| NINO3.4 (t − 6) | 0.30 | 0.29 | 0.27 | 0.26 | 0.24 |
| NINO3.4 (t − 9) | 0.50 | 0.44 | 0.47 | 0.45 | 0.43 |
| PDO (t) | 0.08 | 0.07 | 0.06 | 0.06 | 0.05 |
| PDO (t − 3) | 0.50 | 0.47 | 0.46 | 0.44 | 0.42 |
| PDO (t − 6) | 0.29 | 0.27 | 0.25 | 0.22 | 0.21 |
| PDO (t − 9) | 0.49 | 0.45 | 0.44 | 0.40 | 0.38 |
| BA | |||||||
| Objective Function | Maximum Load Ness | Objective Function | Minimum Frequency | Objective Function | Maximum Frequency | Objective Function | Population Size |
| 2.6 | 0.3 | 2.9 | 1 | 3.1 | 3 | 2.7 | 20 |
| 2.5 | 0.5 | 2.7 | 2 | 2.9 | 5 | 2.3 | 40 |
| 2.2 | 0.7 | 2.2 | 3 | 2.2 | 7 | 2.2 | 60 |
| 2.7 | 0.90 | 2.8 | 4 | 3.2 | 9 | 2.4 | 80 |
| PSO | |||||||
| Objective Function | w | Objective Function | C2 | Objective Function | C1 | Objective Function | Population Size |
| 3.5 | 0.3 | 4.4 | 1.6 | 4.1 | 1.6 | 4.12 | 20 |
| 2.89 | 0.5 | 3.1 | 1.8 | 3.90 | 1.8 | 3.89 | 40 |
| 2.93 | 0.7 | 2.2 | 2.0 | 3.82 | 2.0 | 3.82 | 60 |
| 3.23 | 0.90 | 2.8 | 2.2 | 3.89 | 2.2 | 3.94 | 80 |
| GA | |||||||
| Objective Function | Crossover Rate | Objective Function | Mutation Probability | Objective Function | Population Size | ||
| 7.01 | 0.30 | 7.12 | 0.20 | 7.25 | 20 | ||
| 6.14 | 0.50 | 6.91 | 0.40 | 6.92 | 40 | ||
| 6.34 | 0.70 | 6.14 | 0.60 | 6.12 | 60 | ||
| 6.52 | 0.90 | 6.45 | 0.80 | 6.25 | 80 | ||
| Model | Train | Test | ||||||
|---|---|---|---|---|---|---|---|---|
| RMSE | MAE | WI | NSE | RMSE | MAE | WI | NSE | |
| ANFIS-GA | 3.22 | 2.89 | 0.87 | 0.88 | 4.25 | 4.02 | 0.85 | 0.84 |
| ANFIS-PSO | 3.02 | 2.85 | 0.89 | 0.90 | 4.01 | 3.85 | 0.88 | 0.86 |
| ANFIS-BA | 2.10 | 1.76 | 0.95 | 0.94 | 2.98 | 2.78 | 0.92 | 0.92 |
| Model | p Value | d Factor |
|---|---|---|
| ANFIS-BA | 90% | 0.52 |
| ANFIS-PSO | 86% | 0.72 |
| ANFIS-GA | 83% | 0.75 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ehteram, M.; Afan, H.A.; Dianatikhah, M.; Ahmed, A.N.; Ming Fai, C.; Hossain, M.S.; Allawi, M.F.; Elshafie, A. Assessing the Predictability of an Improved ANFIS Model for Monthly Streamflow Using Lagged Climate Indices as Predictors. Water 2019, 11, 1130. https://doi.org/10.3390/w11061130
Ehteram M, Afan HA, Dianatikhah M, Ahmed AN, Ming Fai C, Hossain MS, Allawi MF, Elshafie A. Assessing the Predictability of an Improved ANFIS Model for Monthly Streamflow Using Lagged Climate Indices as Predictors. Water. 2019; 11(6):1130. https://doi.org/10.3390/w11061130
Chicago/Turabian StyleEhteram, Mohammad, Haitham Abdulmohsin Afan, Mojgan Dianatikhah, Ali Najah Ahmed, Chow Ming Fai, Md Shabbir Hossain, Mohammed Falah Allawi, and Ahmed Elshafie. 2019. "Assessing the Predictability of an Improved ANFIS Model for Monthly Streamflow Using Lagged Climate Indices as Predictors" Water 11, no. 6: 1130. https://doi.org/10.3390/w11061130
APA StyleEhteram, M., Afan, H. A., Dianatikhah, M., Ahmed, A. N., Ming Fai, C., Hossain, M. S., Allawi, M. F., & Elshafie, A. (2019). Assessing the Predictability of an Improved ANFIS Model for Monthly Streamflow Using Lagged Climate Indices as Predictors. Water, 11(6), 1130. https://doi.org/10.3390/w11061130









