Spatial Pattern Analysis and Prediction of Gully Erosion Using Novel Hybrid Model of Entropy-Weight of Evidence
Abstract
1. Introduction
2. Materials and Methods
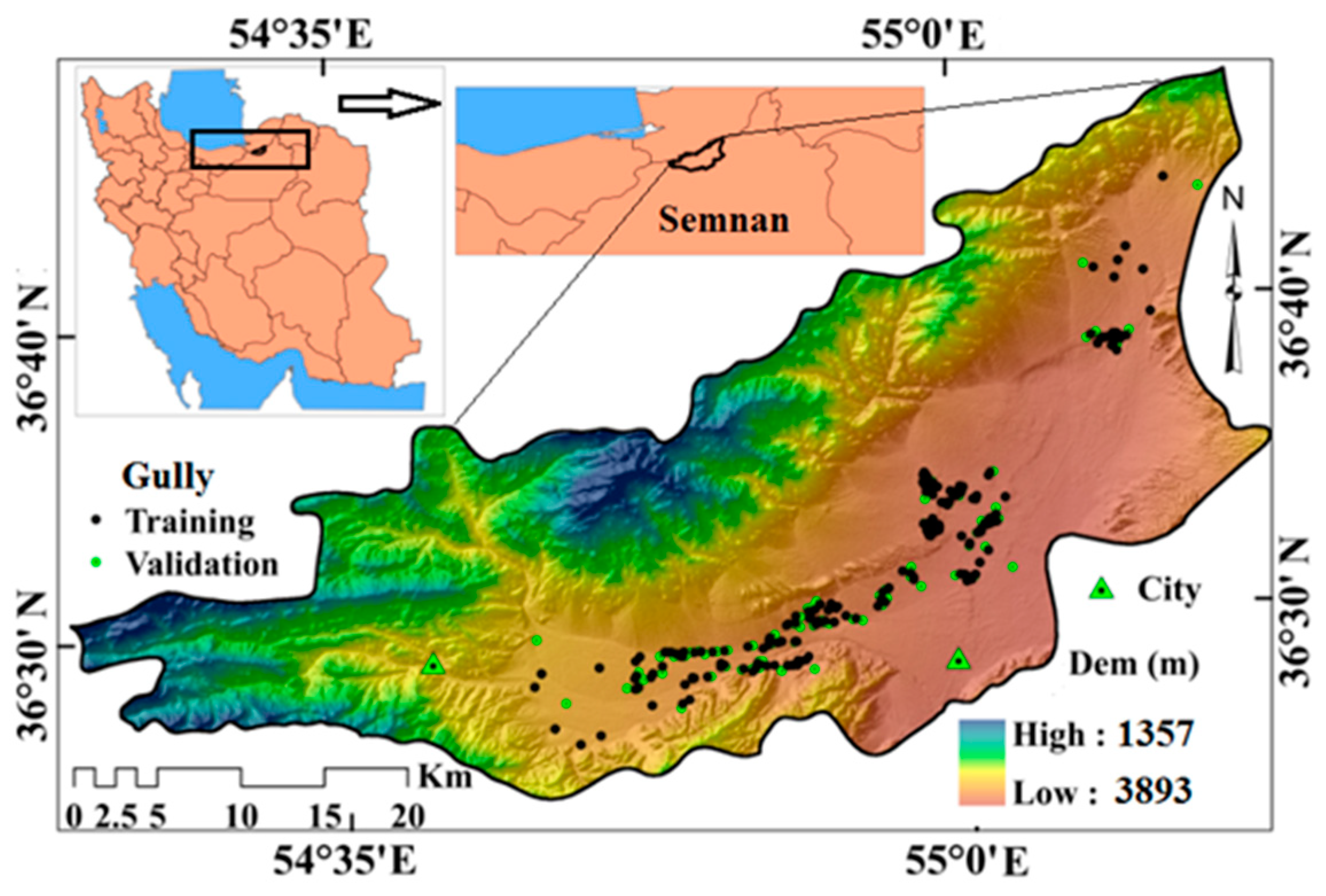
2.1. Study Area
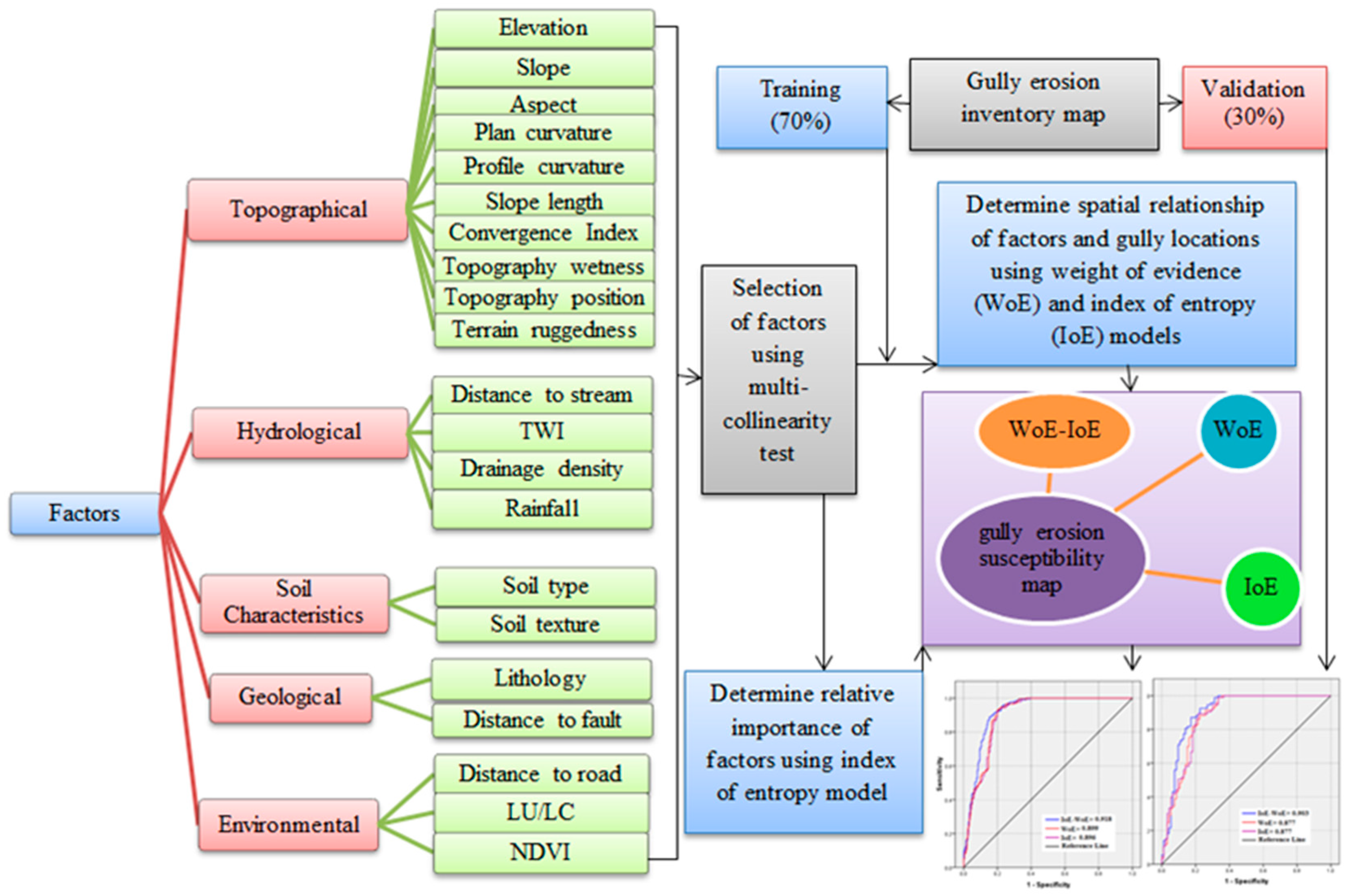
2.2. Methodology
2.2.1. Gully-erosion Inventory Map (GEIM)
2.2.2. Gully Erosion Conditioning Factors (GECFs)
2.3. Multi-collinearity Analysis
2.4. Models
2.4.1. Index of Entropy (IoE)
2.4.2. Weight of Evidence (WoE) Model
2.5. Validation Method
3. Results
3.1. Multi-collinearity Analysis Among GECFs
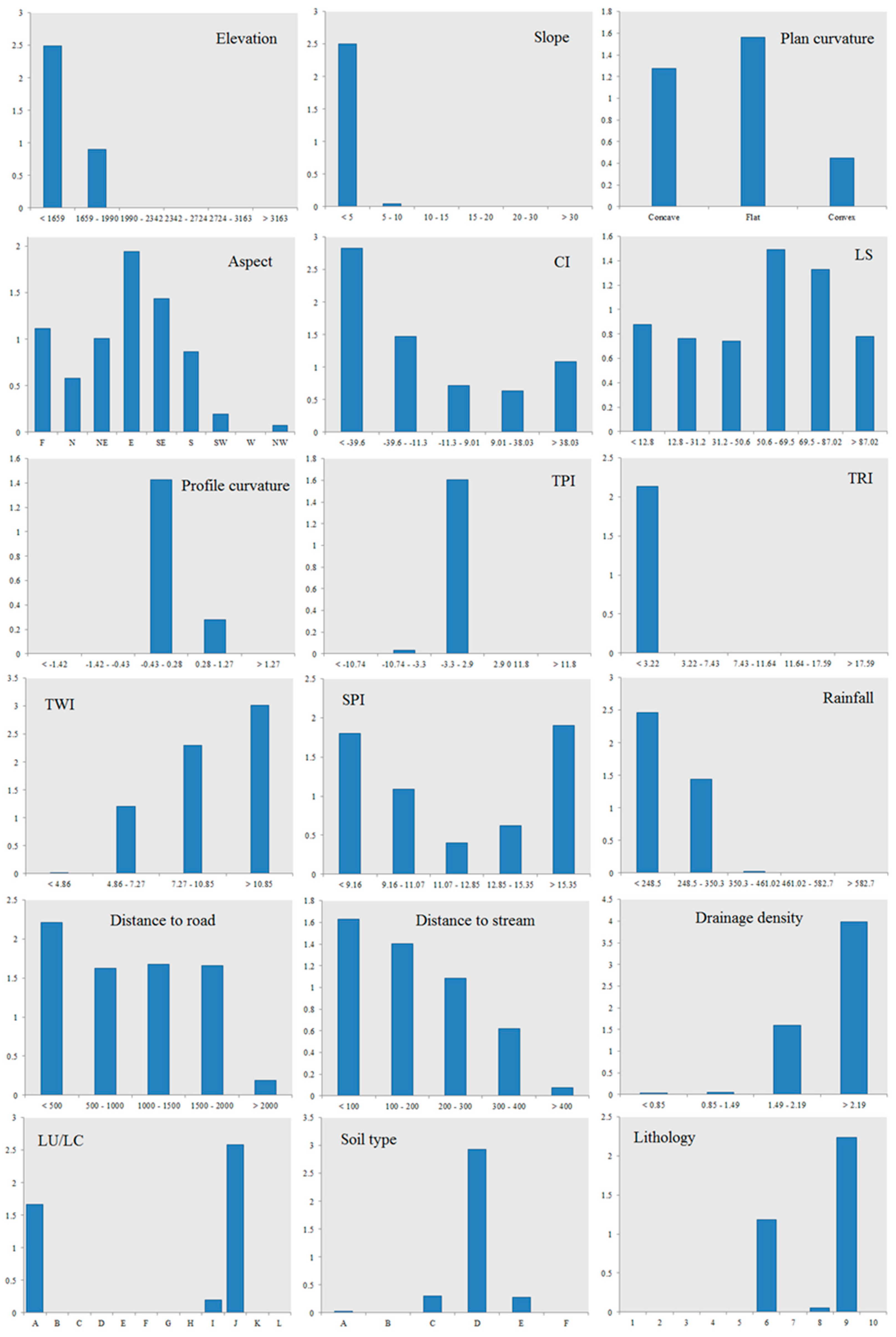
3.2. Determine the Spatial Relationship between GECFs and Occurred Gullies
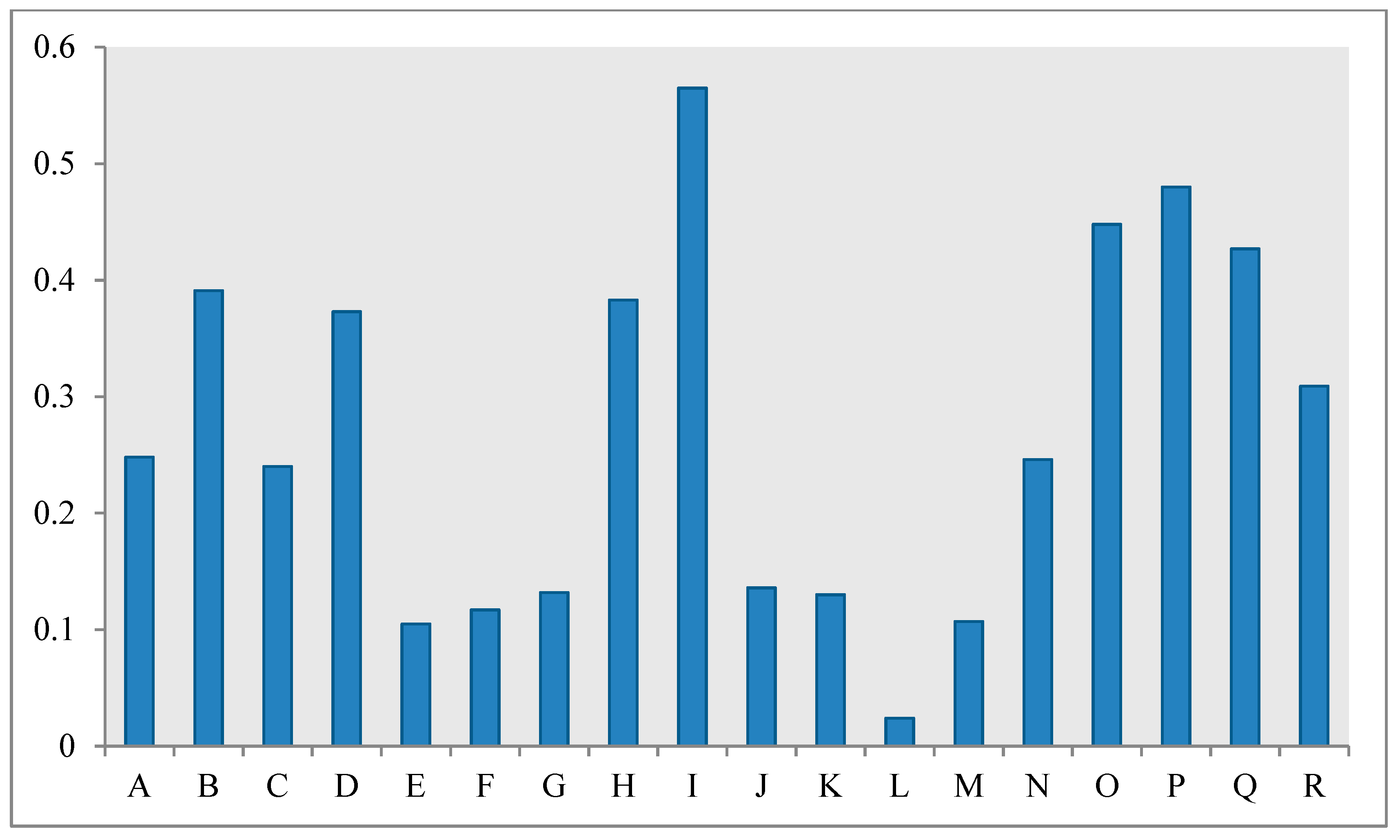
3.3. Determining the Relative Importance of GECFs in the IoE Model
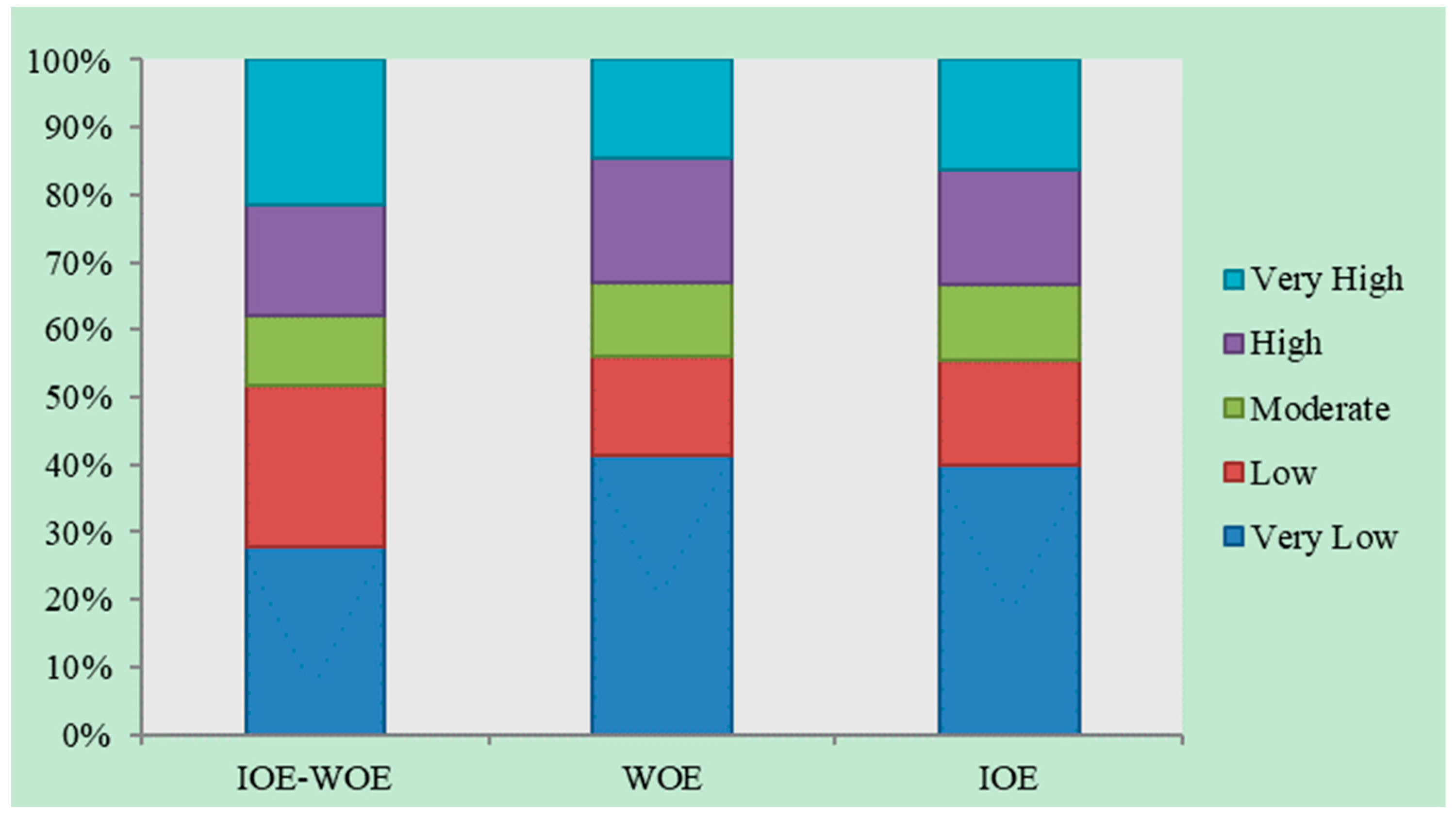
3.4. Gully Erosion Susceptibility Mapping (GESM)
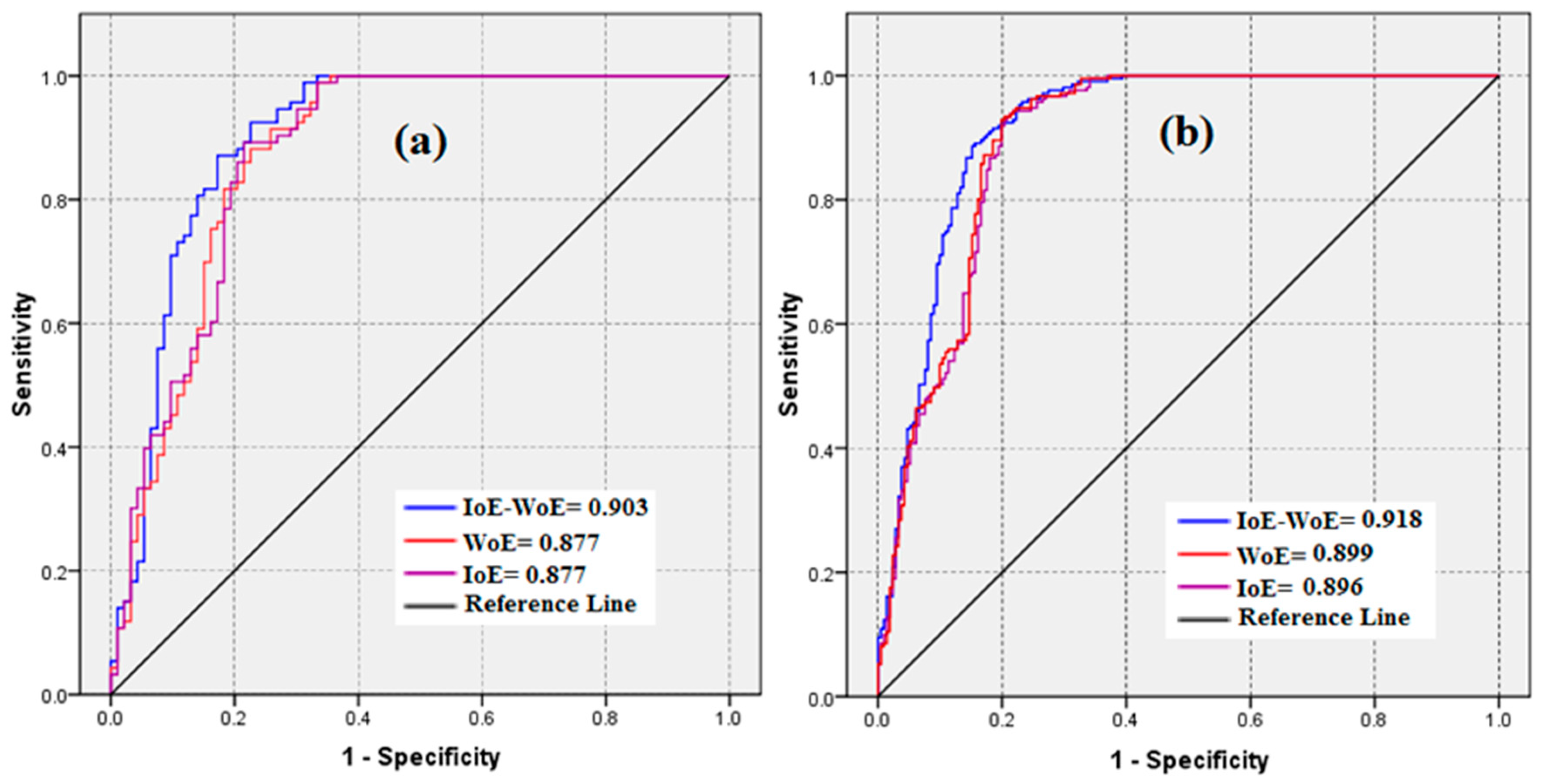
3.5. Validation of Results
4. Discussion
5. Conclusions
- Based on extensive field surveys and multicollinearity tests, topographical, hydrological, geological, soil characteristics, and environmental factors are significant factors that influence gullying in the study area.
- Spatial comparisons of GECFs and gullies using IoE and WoE models show that areas with low elevations, low slopes, and flat topography concentrate surface runoff, and areas near streams and roads, having sparse vegetation, and higher drainage densities have greater potential for gully occurrence.
- By using the IoE model to determine the relative importance of GECFs, we have revealed that drainage density, slope degree, and rainfall are key conditional factors for gully erosion in the study area.
- Validation showed that integration of the WoE and IoE models improves the performance of either of them individually, but also decreases the disadvantages inherent in each. The WoE-IoE integrated model had higher prediction accuracy than the WoE and IoE models.
- Integration of the WoE and IoE models and use of remote sensing data and GIS technique be a powerful tool for GESM and have excellent accuracy.
- The novel method introduced in this research is adaptable and can be used in other areas.
- Our approach can be used to control the growth of the gullies when human-induced.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peugeot, S.; Cappelare, B.; Vieux, B.E.; Seguis, L.; Maia, A. Hydrologic process simulation of a semiarid endoreic catchment in Sahelan west, model-aided data analysis and screening. J. Hydrol. 2003, 279, 224–243. [Google Scholar] [CrossRef]
- Boardman, J.; Parsons, A.J.; Holland, R.; Holmes, P.J. Development of Badlands and Gullies in the Sneeuberg; Catena: Great Karoo, South Africa, 2003; Volume 50, pp. 165–184. [Google Scholar]
- McIntosh, P.; Mike, L. Soil erodibility and erosion hazard: Extending these cornerstone soil conservation oncepts to headwater streams in the forestry estate in Tasmania. For. Ecol. Manag. 2005, 220, 128–139. [Google Scholar] [CrossRef]
- Amsler, L.M.; Ramonell, C.G.; Toniolo, H.A. Morphologic changes in the Parana river channel in the li ght of the climate variability during the 20the century. Geomorphology 2005, 65, 56–70. [Google Scholar]
- Marker, M.; Angeli, L.; Bottai, L.; Costantini, R. Assessment of land degradation susceptibility by scenario analysis. Geomorphology 2008, 93, 120–129. [Google Scholar] [CrossRef]
- Zhou, P. Effect of vegetation cover on soil erosion in a mountainous watershed. Catena 2008, 75, 319–325. [Google Scholar] [CrossRef]
- Battagli, S.A.; Leoni, L.; Sartori, F. Mineralogical and grain size composition of clays developing calanchi and biancane erosional landforms. Geomorphology 2002, 49, 153–170. [Google Scholar] [CrossRef]
- Borrelli, P.; Märker, M.; Panagos, P.; Schütt, B. Modeling soil erosion and river sediment yield for an intermountain drainage basin of the Central Apennines, Italy. Catena 2014, 114, 45–58. [Google Scholar]
- Luffman, I.E.; Nandi, A.; Spiegel, T. Gully morphology, hillslope erosion, and precipitation characteristics in the Appalachian Valley and Ridge province, southeastern USA. Catena 2015, 133, 221–232. [Google Scholar] [CrossRef]
- Rafaello, B.; Reis, E. Controlling factors of the size and location of large gully systems: A regression based exploration using reconstructed pre-erosion topography. Catena 2016, 147, 621–631. [Google Scholar]
- Poesen, J.; Nachtergaele, J.; Verstraeten, G.; Valentin, C. Gully Erosion and Environment Change: Importance and Research Needs. Catena 2003, 50, 91–133. [Google Scholar] [CrossRef]
- Frankl, A.; Deckers, J.; Moulaert, L.; Van Damme, A.; Haile, M.; Poesen, J.; Nyssen, J. Integrated solutions for combating gully erosion in areas prone to soil piping: Innovations from the drylands of Northern Ethiopia. Land Degrad. Dev. 2014, 27, 1797–1804. [Google Scholar] [CrossRef]
- Meliho, M.; Khattabi, A.; Mhammdi, N. A GIS-based approach for gully erosion susceptibility modeling using bivariate statistics methods in the Ourika watershed, Morocco. Environ. Earth Sci. 2018, 77, 655. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Yamani, M.; Pourghasemi, H.R.; Lombardo, L. Spatial modeling of gully erosion using Evidential Belief Function, Logistic Regression and a new ensemble EBF–LR algorithm. Land Degrad. Dev. 2018, 29, 4035–4049. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Pourghasemi, H.R.; Rezaei, K.; Kerle, N. Spatial Modeling of Gully Erosion Using GIS and R Programing: A Comparison among Three Data Mining Algorithms. Appl. Sci. 2018, 8, 1369. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Pourghasemi, H.R.; Lee, S.; Yamani, M. GIS-based gully erosion susceptibility mapping: A comparison among three data-driven models and AHP knowledge-based technique. Environ. Earth Sci. 2018, 77, 628. [Google Scholar] [CrossRef]
- Arabameri, A.; Pourghasemi, H.R. Spatial Modeling of Gully Erosion Using Linear and Quadratic Discriminant Analyses in GIS and R. In Spatial Modeling in GIS and R for Earth and Environmental Sciences, 1st ed.; Pourghasemi, H.R., Gokceoglu, C., Eds.; Elsevier Publication: Amsterdam, The Netherlands, 2019; p. 796. [Google Scholar]
- Nwankwo, C.; Nwankwoala, H.O. Gully Erosion Susceptibility Mapping in Ikwuano Local Government Area of Abia State, Nigeria Using GIS Techniques. Earth Sci. Malaysis 2018, 2, 08–15. [Google Scholar]
- Azareh, A.; Rahmati, O.; Rafiei-Sardooi, E.; Sankey, J.B.; Lee, S.; Shahabi, H.; BinAhmad, B. Modeling gully-erosion susceptibility in a semi-arid region, Iran: Investigation of applicability of certainty factor and maximum entropy models. Sci. Total Environ. 2019, 655, 684–696. [Google Scholar] [CrossRef] [PubMed]
- Nachtergaele, J.; Poesen, J.; Sidorchuk, A.; Torri, D. Prediction of concentrated flow width in ephemeral gully channels. Hydrol. Process. 2002, 16, 1935–1953. [Google Scholar] [CrossRef]
- Saynor, M.J.; Erskine, W.D.; Evans, K.G.; Eliot, I. Gully ignition and implication for management of scour holes in the vicinity of the jabiluka mine, Australia. Geogr. Ann. 2004, 86, 19–201. [Google Scholar] [CrossRef]
- Campo-Bescós, M.; Flores-Cervantes, J.; Bras, R.; Casalí, J.; Giráldez, J. Evaluation of a gully headcut retreat model using multitemporal aerial photographs and digital elevation models. J. Geophys. Res. Earth Surf. 2013, 118, 2159–2173. [Google Scholar] [CrossRef]
- Conoscenti, C.; Angileri, S.; Cappadonia, C.; Rotigliano, E.; Agnesi, V.; Märker, M. Gully erosion susceptibility assessment by means of GIS-based logistic regression: A case of Sicily (Italy). Geomorphology 2014, 204, 399–411. [Google Scholar] [CrossRef]
- Chaplot, V.; Giborie, G.; Marchand, P.; Valentin, C. Dynamic modeling for linear erosion intiation and development under climate and land-use changes in northen Laos. Catena 2005, 63, 318–328. [Google Scholar] [CrossRef]
- Dotter weich, M. High resolution reconstruction of a 1300 year old gully system in northern Bararian. Holocene 2005, 15, 997–1005. [Google Scholar]
- Rescher, N. The Stochastic revolution and the nature of scientific explanation. Synthese 1962, 14, 200–215. [Google Scholar] [CrossRef]
- Derose, R.C.; Gomez, B.; Marden, M.; Trustrum, N.A. Gully erosion in Mangatu Forest, New Zealand, estimated from digital elevation models. Earth Surf. Process. Landf. 1998, 23, 1045–1053. [Google Scholar] [CrossRef]
- Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluating the influence of geo-environmental factors on gully erosion in a semi-arid region of Iran: An integrated framework. Sci. Total Environ. 2017, 579, 913–927. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K. Spatial prediction of gully erosion using ALOS PALSAR data and ensemble bivariate and data mining models. Geosci. J. 2019, 1–18. [Google Scholar] [CrossRef]
- Zabihi, M.; Mirchooli, F.; Motevalli, A.; Darvishan, A.K.; Pourghasemi, H.R.; Zakeri, M.A.; Sadighi, F. Spatial modeling of gully erosion in Mazandaran Province, northern Iran. Catena 2018, 161, 1–13. [Google Scholar] [CrossRef]
- Dube, F.; Nhapi, I.; Murwira, A.; Gumindoga, W.; Goldin, J.; Mashauri, D.A. Potential of weight of evidence modeling for gully erosion hazard assessment in Mbire District—Zimbabwe. Phys. Chem. Earth 2014, 67, 145–152. [Google Scholar] [CrossRef]
- Hosseinalizadeh, M.; Kariminejad, N.; Chen, W.; Pourghasemi, H.R.; Alinejad, M.; Behbahani, A.M.; Tiefenbacher, J.P. Gully headcut susceptibility modeling using functional trees, naïve Bayes tree, and random forest models. Geoderma 2019, 342, 1–11. [Google Scholar] [CrossRef]
- Kornejady, A.; Heidari, K.; Nakhavali, M. Assessment of landslide susceptibility, semi-quantitative risk and management in the Ilam dam basin, Ilam. Iran. Environ. Resour. Res. 2015, 3, 85–109. [Google Scholar]
- Rahmati, O.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Feizizadeh, B. Evaluation of different machine learning models for predicting and mapping the susceptibility of gully erosion. Geomorphology 2017, 298, 118–137. [Google Scholar] [CrossRef]
- Amiri, M.; Pourghasemi, H.R.; Ghanbarian, G.A.; Afzali, S.F. Assessment of the importance of gully erosion effective factors using Boruta algorithm and its spatial modeling and mapping using three machine learning algorithms. Geoderma 2019, 340, 55–69. [Google Scholar] [CrossRef]
- Hosseinalizadeh, M.; Kariminejad, N.; Chen, W.; Pourghasemi, H.R.; Alinejad, M.; Behbahani, A.M.; Tiefenbacher, J.P. Spatial modeling of gully headcuts using UAV data and four best-first decision classifier ensembles (BFTree, Bag-BFTree, RS-BFTree, and RF-BFTree). Geomorphology 2019, 329, 184–193. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K. Gully erosion zonation mapping using integrated geographically weighted regression with certainty factor and random forest models in GIS. J. Environ. Manag. 2019, 232, 928–942. [Google Scholar] [CrossRef]
- Hosseinalizadeh, M.; Kariminejad, N.; Rahmati, O.; Keesstra, S.; Alinejad, M.; Behbahani, A.M. How can statistical and artificial intelligence approaches predict piping erosion susceptibiIIlity? Sci. Total Environ. 2019, 646, 1554–1566. [Google Scholar] [CrossRef] [PubMed]
- Pourghasemi, H.R.; Yousefi, S.; Kornejady, A.; Cerdà, A. Performance assessment of individual and ensemble data-mining techniques for gully erosion modeling. Sci. Total Environ. 2017, 609, 764–775. [Google Scholar] [CrossRef]
- Shirani, K.; Pasandi, M.; Arabameri, A. Landslide susceptibility assessment by Dempster–Shafer and Index of Entropy models, Sarkhoun basin, Southwestern Iran. Nat. Hazards 2018, 93, 1379–1418. [Google Scholar] [CrossRef]
- Xie, Z.; Chen, G.; Meng, X.; Zhang, Y.; Qiao, L.; Tan, L. A comparative study of landslide susceptibility mapping using weight of evidence, logistic regression and support vector machine and evaluated by sbas-insar monitoring: Zhouqu to wudu segment in Bailong River Basin, China. Environ. Earth Sci. 2017, 76, 313. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Ahmad, B.; Panahi, M.; Hong, H. Landslide detection and susceptibility mapping by airsar data using support vector machine and index of entropy models in Cameron highlands, Malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef]
- Haghizadeh, A.; Siahkamari, S.; Haghiabi, A.H.; Rahmati, O. Forecasting flood-prone areas using Shannon’s entropy model. J. Earth Syst. Sci. 2017, 126, 39. [Google Scholar] [CrossRef]
- Al-Abadi, A.M.; Pourghasemi, H.R.; Shahid, S.; Ghalib, H.B. Spatial Mapping of Groundwater Potential Using Entropy Weighted Linear Aggregate Novel Approach and GIS. Arabian J. Sci. Eng. 2017, 42, 1185–1199. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Cerda, A.; Lombardo, L.; Rodrigo-Comino, J. GIS-based groundwater potential mapping in Shahroud plain, Iran. A comparison among statistical (bivariate and multivariate), data mining and MCDM approaches. Sci. Total Environ. 2019, 658, 160–177. [Google Scholar] [CrossRef]
- I.R. of Iran Meteorological Organization (IRIMO). 2012. Available online: http://www.mazan daranmet.ir (accessed on 12 August 2018).
- Geology Survey of Iran (GSI). 1997. Available online: http://www.gsi.ir/Main/Lang_en/index.html (accessed on 12 August 2018).
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014; World Soil Resources Report; FAO: Rome, Italy, 2014. [Google Scholar]
- Cama, M.; Conoscenti, C.; Lombardo, L.; Rotigliano, E. Exploring relationships between grid cell size and accuracy for debris-flow susceptibility models: A test in the Giampilieri catchment (Sicily, Italy). Environ. Earth Sci. 2016, 75, 1–21. [Google Scholar] [CrossRef]
- Parras-Alcántara, L.; Lozano-García, B.; Keesstra, S.; Cerdà, A.; Brevik, E.C. Long-term effects of soil management on ecosystem services and soil loss estimation in olive grove top soils. Sci. Total Environ. 2016, 571, 498–506. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Conoscenti, C. Gully erosion susceptibility mapping using GIS-based multi-criteria decision analysis techniques. Catena 2019, 180, 282–297. [Google Scholar] [CrossRef]
- Boreggio, M.; Bernard, M.; Gregoretti, C. Evaluating the influence of gridding techniques for Digital Elevation Models generation on the debris flow routing modeling: A case study from Rovina di Cancia basin (North-eastern Italian Alps). Front. Earth Sci. 2018, 6, 89. [Google Scholar] [CrossRef]
- Wu, C.Y.; Mossa, J.; Mao, L.; Almulla, M. Comparison of different spatial interpolation methods for historical hydrographic data of the lowermost Mississipi River. Ann. GIS 2019, in press. [Google Scholar] [CrossRef]
- Gesch, D.; Oimoen, M.; Zhang, Z.; Meyer, D.; Danielson, J. Validation of the ASTER global digital elevation model version 2 over the conterminous United States. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, B4, 281–286. [Google Scholar] [CrossRef]
- Zhou, C.; Ge, L.E.D.; Chang, H.C. A case study of using external DEM in InSAR DEM generation. Geo-Spat. Inf. Sci. 2005, 8, 14–18. [Google Scholar]
- Zhang, W.; Wang, W.; Chen, L. Constructing DEM based on InSAR and the relationship between InSAR DEM’s precision and terrain factors. Energy Procedia 2012, 16, 184–189. [Google Scholar] [CrossRef]
- Arabameri, A.; Pourghasemi, H.R.; Yamani, M. Applying different scenarios for landslide spatial modeling using computational intelligence methods. Environ. Earth Sci. 2017, 76, 832. [Google Scholar] [CrossRef]
- Arabameri, A.; Pourghasemi, H.R.; Cerda, A. Erodibility prioritization of sub-watersheds using morphometric parameters analysis and its mapping: A comparison among TOPSIS, VIKOR, SAW, and CF multi-criteria decision making models. Sci. Total Environ. 2017, 613–614, 1385–1400. [Google Scholar]
- Arabameri, A.; Pradhan, B.; Pourghasemi, H.R.; Rezaei, K. Identification of erosion-prone areas using different multi-criteria decision-making techniques and GIS. Geomat. Nat. Hazards Risk 2018, 9, 1129–1155. [Google Scholar] [CrossRef]
- Arabameri, A.; Rezaei, K.; Cerda, A.; Conoscenti, C.; Kalantari, Z. A comparison of statistical methods and multi-criteria decision making to map flood hazard susceptibility in Northern Iran. Sci. Total Environ. 2019, 660, 443–458. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Sohrabi, M.; Kalantari, Z. GIS-based landslide susceptibility mapping using numerical risk factor bivariate model and its ensemble with linear multivariate regression and boosted regression tree algorithms. J. Mt. Sci. 2019, 16, 595–618. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Saro, L.; Sohrabi, M. An Ensemble Model for Landslide Susceptibility Mapping in a Forested Area. Geocarto Int. 2019. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Mohammady, M.; Pradhan, B. Landslide susceptibility mapping using index of entropy and conditional probability models in GIS: Safarood Basin, Iran. Catena 2012, 97, 71–84. [Google Scholar] [CrossRef]
- Rahmati, O.; Haghizadeh, A.; Pourghasemi, H.R.; Noormohamadi, F. Gully erosion susceptibility mapping: The role of GISbased bivariate statistical models and their comparison. Nat. Hazards 2016, 82, 1231–1258. [Google Scholar] [CrossRef]
- Conforti, M.; Aucelli, P.P.; Robustelli, G.; Scarciglia, F. Geomorphology and GIS analysis formapping gully erosion susceptibility in the Turbolo streamcatchment (Northern Calabria, Italy). Nat. Hazards 2011, 56, 881–898. [Google Scholar] [CrossRef]
- Conoscenti, C.; Agnesi, V.; Cama, M.; Alamaru Caraballo-Arias, N.; Rotigliano, E. Assessment of Gully Erosion Susceptibility Using Multivariate Adaptive Regression Splines and Accounting for Terrain Connectivity. Land Degrad. Dev. 2018, 29, 724–736. [Google Scholar] [CrossRef]
- Romer, C.; Ferentinou, M. Shallow landslide susceptibility assessment in a semiarid environment A Quaternary catchment of KwaZulu-Natal, South Africa. Eng. Geol. 2016, 201, 29–44. [Google Scholar] [CrossRef]
- Hong, H.; Tsangaratos, P.; Ilia, I. Application of fuzzy weight of evidence and data mining techniques in construction of flood susceptibility map of Poyang County, China. Sci. Total Environ. 2018, 625, 575–588. [Google Scholar] [CrossRef] [PubMed]
- Yesilnacar, E.K. The Application of Computational Intelligence to Landslide Susceptibility Mapping in Turkey. Ph.D. Thesis, Department of Geomatics the University of Melbourne, Melbourne, Australia, 2005. [Google Scholar]
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling susceptibility to landslides using the weight of evidence approach: Western Colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Brice, J.B. Erosion and Deposition in Loess-Mantled Great Plains, Medecine Creek Drainage Basin, Nebraska. Geol. Surv. Prof. Pap. 1966, 235–339. [Google Scholar]
- Heed, B.H. Morphology of gullies in the colorado rocky mountains. Bulletin of the International Association of Scientific Hydrology. Hydrol. Sci. J. 1970, 2, 79–89. [Google Scholar]
- Ireland, H.A.; Sharpe, C.F.; Eargle, D.H. Principles of Gully Erosion in the Piedmont of South Carolina; Tech. Bull. 633.; USDA: Washington, DC, USA, 1939.
- Hongchun, Z.H.U.; Guoan, T.; Kejian, Q.; Haiying, L. Extraction and analysis of gully head of loess plateau in china based on digital elevation model. Chin. Geogr. Sci. 2014, 24, 328–338. [Google Scholar]
- Le Roux, J.J.; Sumner, P.D. Factors controlling gully development: Comparing continuous and discontinuous gullies. Land Degrad. Dev. 2012, 23, 440–449. [Google Scholar] [CrossRef]
- Nyssen, J.; Poesen, J.; Moeyersons, J.; Luyten, E.; Veyret-Picot, M.; Deckers, J.; Haile, M.; Govers, G. Impact of road building on gully erosion risk: A case study from the northern Ethiopian highlands. Earth Surf. Process. Landf. 2002, 27, 1267–1283. [Google Scholar] [CrossRef]
- Gessesse, B.; Bewket, W.; Bräuning, A. Model-based characterization and monitoring of runoff and soil erosion in response to land use/land cover changes in the Modjo watershed, Ethiopia. Land Degrad. Dev. 2015, 26, 711–724. [Google Scholar] [CrossRef]
- Gellis, A.C.; Cheama, A.; Laahty, V.; Lalio, S. Assessment of gully control structure in the rio Nutria Watershed, New Mexico. J. Am. Water Res. Assoc. 1995, 31, 633–646. [Google Scholar] [CrossRef]
- Golestani, G.; Issazadeh, L.; Serajamani, R. Lithology effects on gully erosion in Ghoori chay Watershed using RS & GIS. Int. J. Biosci. 2014, 4, 71–76. [Google Scholar]
- Wang, Q.; Li, W.; Chen, W.; Bai, H. GIS-based assessment of landslide susceptibility using certainty factor and index of entropy models for the Qianyang County of Baoji city, China. J. Earth Syst. Sci. 2015, 124, 1399–1415. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Pourtaghie, Z.S.; Rezaei, A. Groundwater qanat potential mapping using frequency ratio and Shannon’s entropy models in the Moghan Watershed, Iran. Earth Sci. Inf. 2015, 8, 171–186. [Google Scholar] [CrossRef]
- Umar, Z.; Pradhan, B.; Ahmad, A.; Neamah Jebur, M.; Shafapour Tehrani, M. Earthquake induced landslide susceptibility mapping using an integrated ensemble frequency ratio and logistic regression models in West Sumatera Province, Indonesia. Catena 2014, 118, 124–135. [Google Scholar] [CrossRef]
- ThaiPham, B.; Prakash, I.; Tien Bui, D. Spatial prediction of landslides using a hybrid machine learning approach based on Random Subspace and Classification and Regression Trees. Geomorphology 2018, 303, 256–270. [Google Scholar]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Lee, C.-W. Assessment of Landslide Susceptibility Using Statistical-and Artificial Intelligence-Based FR–RF Integrated Model and Multiresolution DEMs. Remote Sens. 2019, 11, 999. [Google Scholar] [CrossRef]
- Du, G.; Zhang, Y.; Iqbal, J. Landslide susceptibility mapping using an integrated model of information value method and logistic regression in the Bailongjiang watershed, Gansu Province, China. J. Mount. Sci. 2017, 14, 249. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Hoang, N.D.; Thanh, N.Q.; Nguyen, D.B.; Van Liem, N.; Pradhan, B. Spatial prediction of rainfall-induced landslides for the Lao Cai area (Vietnam) using a hybrid intelligssent approach of least squares support vector machines inference model and artificial bee colony optimization. Landslides 2017, 14, 447–458. [Google Scholar] [CrossRef]
- Dehnavi, A.; Aghdam, I.N.; Pradhan, B.; Morshed, V.M.H. A new hybrid model using step-wise weight assessment ratio analysis (SWARA) technique and adaptive neuro-fuzzy inference system (ANFIS) for regional landslide hazard assessment in Iran. Catena 2015, 135, 122–148. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kerle, N. Random forests and evidential belief function-based landslide susceptibility assessment in Western Mazandaran Province, Iran. Environ. Earth Sci. 2016, 75, 1–17. [Google Scholar] [CrossRef]
- Keesstra, S.; Mol, G.; de Leeuw, J.; Okx, J.; de Cleen, M.; Visser, S. Soil-related sustainable development goals: Four concepts to make land degradation neutrality and restoration work. Land 2018, 7, 133. [Google Scholar] [CrossRef]
- Keesstra, S.D.; Bouma, J.; Wallinga, J.; Tittonell, P.; Smith, P.; Cerdà, A.; Montanarella, L.; Quinton, J.N.; Pachepsky, Y.; van der Putten, W.H.; et al. The significance of soils and soil science towards realization of the United Nations Sustainable Development Goals. Soil 2016, 2, 111–128. [Google Scholar] [CrossRef]
- Keesstra, S.; Nunes, J.; Novara, A.; Finger, D.; Avelar, D.; Kalantari, Z.; Cerdà, A. The superior effect of nature based solutions in land management for enhancing ecosystem services. Sci. Total Environ. 2018, 610, 997–1009. [Google Scholar] [CrossRef] [PubMed]
- Keesstra, S.; Nunes, J.P.; Saco, P.; Parsons, T.; Poeppl, R.; Masselink, R.; Cerdà, A. The way forward: Can connectivity be useful to design better measuring and modeling schemes for water and sediment dynamics? Sci. Total Environ. 2018, 644, 1557–1572. [Google Scholar] [CrossRef]


| Group | Unit | Description | Age |
|---|---|---|---|
| 1 | Cm | Dark grey to black fossiliferous limestone with subordinate black shale ( MOBARAK FM ) | Carboniferous |
| 2 | DCkh | Yellowish, thin to thick-bedded, fossileferous argillaceous limestone, dark grey limestone, greenish marl and shale, locally including gypsum | Devonian |
| 3 | Ea.bvs | Andesitic to basaltic volcano sediment | Eocene |
| Ek | Well bedded green tuff and tuffaceous shale (KARAJ FM) | Eocene | |
| Ea.bv | Andesitic and basaltic volcanic | Eocene | |
| 4 | Jl | Light grey, thin-bedded to massive limestone (LAR FM) | Jurassic-Cretaceous |
| Jd | Well-bedded to thin-bedded, greenish-grey argillaceous limestone with intercalations of calcareous shale (DALICHAI FM) | Jurassic | |
| 5 | Ku | Upper cretaceous, undifferentiated rocks | Late.Cretaceous |
| K2m | Marl, shale and dendritic limestone | Late.Cretaceous | |
| 6 | Murc | Red conglomerate and sandstone | Miocene |
| Murmg | Gypsiferous marl | Miocene | |
| Mc | Red conglomerate and sandstone | Miocene | |
| 7 | Osh | Greenish-grey siltstone and shale with intercalations of flaggy limestone (SHIRGESHT FM) | Ordovician |
| 8 | Pd | Red sandstone and shale with subordinate sandy limestone (DORUD FM) | Permian |
| Plc | Polymictic conglomerate and sandstone | Pliocene | |
| Pz1a.bv | Andesitic basaltic volcanic | Paleozoic | |
| P | Undifferentiated Permian rocks | Permian | |
| PeEz | Reef-type limestone and gypsiferous marl (ZIARAT FM) | Paleocene-Eocene | |
| PlQc | Fluvial conglomerate, piedmont conglomerate and sandstone. | Pliocene-Quaternary | |
| 9 | Qft1 | High-level piedmont fan and valley terrace deposits | Quaternary |
| Qal | Stream channel, braided channel and flood plain deposits | Quaternary | |
| Qft2 | Low-level piedmont fan and valley terrace deposits | Quaternary | |
| 10 | TRe2 | Thick bedded dolomite | Early-Middle.Triassic |
| TRJs | Dark grey shale and sandstone (SHEMSHAK FM) | Triassic-Jurassic |
| Factors | Collinearity Statistics | Factors | Collinearity Statistics | ||
|---|---|---|---|---|---|
| Tolerance | VIF | Tolerance | VIF | ||
| Aspect | 0.902 | 1.109 | SPI | 0.584 | 1.919 |
| CI | 0.635 | 1.574 | Soil texture | 0.030 | 33.769 |
| NDVI | 0.095 | 10.479 | TPI | 0.392 | 2.553 |
| Drainage density | 0.322 | 3.107 | TWI | 0.374 | 3.509 |
| Distance to road | 0.685 | 1.460 | Lithology | 0.271 | 3.688 |
| Distance to stream | 0.604 | 1.655 | SOIL | 0.471 | 2.124 |
| LS | 0.975 | 1.025 | LU | 0.265 | 3.778 |
| Plan curvature | 0.494 | 2.025 | Elevation | 0.643 | 1.276 |
| Profile curvature | 0.508 | 1.968 | TRI | 0.426 | 2.265 |
| Rainfall | 0.289 | 4.179 | Slope | 0.543 | 1.498 |
| Distance to fault | 0.022 | 45.046 | SPI | 0.584 | 1.919 |
| Factor | Value | Total Pixels | Total Gullies | Weight of Evidence | ||||
|---|---|---|---|---|---|---|---|---|
| No | % | No | % | C | S© | C/S© | ||
| Elevation (m) | <1659 | 479814 | 32.482 | 171 | 81.043 | 2.185 | 0.176 | 12.439 |
| 1659–1990 | 309671 | 20.964 | 40 | 18.957 | −0.126 | 0.176 | −0.716 | |
| 1990–2342 | 239854 | 16.238 | 0 | 0.000 | −0.177 | 0.069 | −2.574 | |
| 2342–2724 | 209109 | 14.156 | 0 | 0.000 | −0.153 | 0.069 | −2.218 | |
| 2724–3163 | 146912 | 9.946 | 0 | 0.000 | −0.105 | 0.069 | −1.522 | |
| >3163 | 91792 | 6.214 | 0 | 0.000 | −0.064 | 0.069 | −0.932 | |
| Slope (°) | <5 | 588363 | 39.831 | 210 | 99.526 | 5.760 | 1.002 | 5.746 |
| 5–10 | 149259 | 10.105 | 1 | 0.474 | −3.162 | 1.002 | −3.154 | |
| 10–15 | 124159 | 8.405 | 0 | 0.000 | −0.088 | 0.069 | −1.276 | |
| 15–20 | 143874 | 9.740 | 0 | 0.000 | −0.102 | 0.069 | −1.489 | |
| 20–30 | 280859 | 19.014 | 0 | 0.000 | −0.211 | 0.069 | −3.064 | |
| >30 | 190637 | 12.906 | 0 | 0.000 | −0.138 | 0.069 | −2.007 | |
| PC | Concave | 571885 | 38.715 | 104 | 49.289 | 0.431 | 0.138 | 3.129 |
| Flat | 308591 | 20.891 | 69 | 32.701 | 0.610 | 0.147 | 4.156 | |
| Convex | 596675 | 40.394 | 38 | 18.009 | −1.127 | 0.179 | −6.289 | |
| Aspect | F | 6262 | 0.424 | 1 | 0.474 | 0.112 | 1.002 | 0.112 |
| N | 132304 | 8.957 | 11 | 5.213 | −0.311 | 0.360 | −0.862 | |
| NE | 152509 | 10.325 | 22 | 10.427 | 0.011 | 0.225 | 0.049 | |
| E | 245198 | 16.599 | 68 | 32.227 | 0.871 | 0.147 | 5.914 | |
| SE | 341071 | 23.090 | 70 | 33.175 | 0.503 | 0.146 | 3.441 | |
| S | 273880 | 18.541 | 34 | 16.114 | −0.170 | 0.187 | −0.906 | |
| SW | 144941 | 9.812 | 4 | 1.896 | −1.728 | 0.505 | −3.424 | |
| W | 89718 | 6.074 | 0 | 0.000 | −0.063 | 0.069 | −0.910 | |
| NW | 91269 | 6.179 | 1 | 0.474 | −2.627 | 1.002 | −2.621 | |
| CI | <−39.6 | 91462 | 6.223 | 37 | 17.619 | 1.171 | 0.181 | 6.463 |
| −39.6–−11.3 | 289807 | 19.717 | 61 | 29.048 | 0.511 | 0.152 | 3.362 | |
| −11.3–9.01 | 663255 | 45.125 | 68 | 32.381 | −0.541 | 0.147 | −3.667 | |
| 9.01–38.03 | 341553 | 23.238 | 31 | 14.762 | −0.559 | 0.195 | −2.871 | |
| >38.03 | 83751 | 5.698 | 13 | 6.190 | 0.088 | 0.286 | 0.308 | |
| LS (m) | <12.8 | 352071 | 23.834 | 44 | 20.853 | −0.172 | 0.169 | −1.015 |
| 12.8–31.2 | 220640 | 14.937 | 24 | 11.374 | −0.314 | 0.217 | −1.446 | |
| 31.2–50.6 | 197564 | 13.375 | 21 | 9.953 | −0.334 | 0.230 | −1.454 | |
| 50.6–69.5 | 211467 | 14.316 | 45 | 21.327 | 0.484 | 0.168 | 2.880 | |
| 69.5–87.02 | 279653 | 18.932 | 53 | 25.118 | 0.362 | 0.159 | 2.282 | |
| >87.02 | 215757 | 14.606 | 24 | 11.374 | −0.287 | 0.217 | −1.325 | |
| Profile curvature | <−1.42 | 39576 | 2.679 | 0 | 0.000 | −0.027 | 0.069 | −0.395 |
| −1.42–−0.43 | 150920 | 10.217 | 0 | 0.000 | −0.108 | 0.069 | −1.566 | |
| −0.43–0.28 | 987589 | 66.858 | 201 | 95.261 | 2.299 | 0.324 | 7.096 | |
| 0.28–1.27 | 249999 | 16.924 | 10 | 4.739 | −1.410 | 0.324 | −4.351 | |
| >1.27 | 49067 | 3.322 | 0 | 0.000 | −0.034 | 0.069 | −0.491 | |
| TPI | <−10.74 | 69120 | 4.679 | 0 | 0.000 | −0.048 | 0.069 | −0.696 |
| −10.74–−3.3 | 233435 | 15.803 | 1 | 0.474 | −3.674 | 1.002 | −3.666 | |
| −3.3–2.9 | 914956 | 61.941 | 210 | 99.526 | 4.860 | 1.002 | 4.849 | |
| 2.9–11.8 | 201144 | 13.617 | 0 | 0.000 | −0.146 | 0.069 | −2.127 | |
| >11.8 | 58497 | 3.960 | 0 | 0.000 | −0.040 | 0.069 | −0.587 | |
| TRI | <3.22 | 692266 | 46.865 | 211 | 100 | 0.758 | 0.069 | 11.011 |
| 3.22–7.43 | 286708 | 19.410 | 0 | 0.000 | −0.216 | 0.069 | −3.135 | |
| 7.43–11.64 | 285453 | 19.325 | 0 | 0.000 | −0.215 | 0.069 | −3.120 | |
| 11.64–17.59 | 174864 | 11.838 | 0 | 0.000 | −0.126 | 0.069 | −1.830 | |
| >17.59 | 37860 | 2.563 | 0 | 0.000 | −0.026 | 0.069 | −0.377 | |
| TWI | <4.86 | 582464 | 39.432 | 1 | 0.474 | −4.918 | 1.002 | −4.906 |
| 4.86–7.27 | 585130 | 39.612 | 101 | 47.867 | 0.336 | 0.138 | 2.441 | |
| 7.27–10.85 | 237436 | 16.074 | 78 | 36.967 | 1.119 | 0.143 | 7.848 | |
| >10.85 | 72122 | 4.883 | 31 | 14.692 | 1.211 | 0.194 | 6.226 | |
| SPI | <9.16 | 322599 | 21.839 | 83 | 39.336 | 0.842 | 0.141 | 5.975 |
| 9.16–11.07 | 437271 | 29.602 | 68 | 32.227 | 0.123 | 0.147 | 0.835 | |
| 11.07–12.85 | 455113 | 30.810 | 26 | 12.322 | −1.153 | 0.209 | −5.507 | |
| 12.85–15.35 | 203521 | 13.778 | 18 | 8.531 | −0.539 | 0.246 | −2.185 | |
| >15.35 | 58648 | 3.970 | 16 | 7.583 | 0.686 | 0.260 | 2.636 | |
| Rainfall (mm) | <248.5 | 284466 | 19.258 | 100 | 47.393 | 1.329 | 0.138 | 9.641 |
| 248.5–350.3 | 535319 | 36.240 | 110 | 52.133 | 0.650 | 0.138 | 4.720 | |
| 350.3–461.02 | 321491 | 21.764 | 1 | 0.474 | −4.068 | 1.002 | −4.058 | |
| 461.02–582.7 | 208018 | 14.082 | 0 | 0.000 | −0.152 | 0.069 | −2.205 | |
| >582.7 | 127857 | 8.656 | 0 | 0.000 | −0.091 | 0.069 | −1.315 | |
| Dis to road (m) | <500 | 224545 | 15.201 | 71 | 33.649 | 1.040 | 0.146 | 7.139 |
| 500–1000 | 193768 | 13.118 | 45 | 21.327 | 0.585 | 0.168 | 3.483 | |
| 1000–1500 | 166957 | 11.303 | 40 | 18.957 | 0.608 | 0.176 | 3.459 | |
| 1500–2000 | 147431 | 9.981 | 35 | 16.588 | 0.584 | 0.185 | 3.157 | |
| >2000 | 744451 | 50.398 | 20 | 9.479 | −2.273 | 0.235 | −9.670 | |
| Dis to stream (m) | <100 | 408797 | 27.675 | 95 | 45.024 | 0.761 | 0.138 | 5.500 |
| 100–200 | 298966 | 20.239 | 60 | 28.436 | 0.449 | 0.153 | 2.939 | |
| 200–300 | 245504 | 16.620 | 38 | 18.009 | 0.097 | 0.179 | 0.542 | |
| 300–400 | 157383 | 10.654 | 14 | 6.635 | −0.518 | 0.277 | −1.872 | |
| >400 | 366502 | 24.811 | 4 | 1.896 | −2.838 | 0.505 | −5.622 | |
| Drainage density (km/km2) | <0.85 | 398195 | 26.957 | 2 | 0.939 | −3.662 | 0.710 | −5.155 |
| 0.85–1.49 | 497684 | 33.692 | 4 | 1.878 | −3.279 | 0.505 | −6.497 | |
| 1.49–2.19 | 368973 | 24.979 | 85 | 39.906 | 0.690 | 0.140 | 4.935 | |
| >2.19 | 212300 | 14.372 | 122 | 57.277 | 2.078 | 0.139 | 15.005 | |
| LU/LC | Agriculture (A) | 281159 | 19.034 | 67 | 31.754 | 0.683 | 0.148 | 4.617 |
| Dense-forest (B) | 155 | 0.010 | 0 | 0.000 | 0.000 | 0.069 | −0.002 | |
| Good-range (C) | 8660 | 0.586 | 0 | 0.000 | −0.006 | 0.069 | −0.085 | |
| Agri-dryfarming (D) | 243 | 0.016 | 0 | 0.000 | 0.000 | 0.069 | −0.002 | |
| Dryfarming (E) | 16235 | 1.099 | 0 | 0.000 | −0.011 | 0.069 | −0.161 | |
| Low-forest (F) | 337471 | 22.846 | 0 | 0.000 | −0.259 | 0.069 | −3.768 | |
| Woodland (G) | 233619 | 15.816 | 0 | 0.000 | −0.172 | 0.069 | −2.501 | |
| Mod-forest (H) | 83527 | 5.655 | 0 | 0.000 | −0.058 | 0.069 | −0.846 | |
| Mod-range (I) | 105592 | 7.148 | 3 | 1.422 | −1.675 | 0.581 | −2.880 | |
| Poor-range (J) | 382114 | 25.868 | 141 | 66.825 | 1.753 | 0.146 | 11.992 | |
| Rock (K) | 23154 | 1.567 | 0 | 0.000 | −0.016 | 0.069 | −0.230 | |
| Urban (L) | 5220 | 0.353 | 0 | 0.000 | −0.004 | 0.069 | −0.051 | |
| Soil type | Rock Outcrop/Entisols (A) | 486282 | 32.920 | 2 | 0.948 | −3.938 | 0.710 | −5.542 |
| Alfisols (B) | 7086 | 0.480 | 0 | 0.000 | −0.005 | 0.069 | −0.070 | |
| Aridisols (C) | 161526 | 10.935 | 7 | 3.318 | −1.275 | 0.384 | −3.317 | |
| Entisols/Inceptisols (D) | 479698 | 32.475 | 201 | 95.261 | 3.733 | 0.324 | 11.522 | |
| Inceptisols (E) | 24777 | 1.677 | 1 | 0.474 | −1.276 | 1.002 | −1.273 | |
| Mollisols (F) | 317783 | 21.513 | 0 | 0.000 | −0.242 | 0.069 | −3.519 | |
| Lithology | Group 1 | 76475 | 5.177 | 0 | 0.000 | −0.053 | 0.069 | −0.772 |
| Group 2 | 131673 | 8.914 | 0 | 0.000 | −0.093 | 0.069 | −1.356 | |
| Group 3 | 114748 | 7.768 | 0 | 0.000 | −0.081 | 0.069 | −1.175 | |
| Group 4 | 94149 | 6.374 | 0 | 0.000 | −0.066 | 0.069 | −0.957 | |
| Group 5 | 33722 | 2.283 | 0 | 0.000 | −0.023 | 0.069 | −0.336 | |
| Group 6 | 117907 | 7.982 | 20 | 9.479 | 0.188 | 0.235 | 0.801 | |
| Group 7 | 31564 | 2.137 | 0 | 0.000 | −0.022 | 0.069 | −0.314 | |
| Group 8 | 134059 | 9.076 | 1 | 0.474 | −3.043 | 1.002 | −3.036 | |
| Group 9 | 594531 | 40.248 | 190 | 90.047 | 2.598 | 0.230 | 11.297 | |
| Group 10 | 148324 | 10.041 | 0 | 0.000 | −0.106 | 0.069 | −1.537 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arabameri, A.; Cerda, A.; Tiefenbacher, J.P. Spatial Pattern Analysis and Prediction of Gully Erosion Using Novel Hybrid Model of Entropy-Weight of Evidence. Water 2019, 11, 1129. https://doi.org/10.3390/w11061129
Arabameri A, Cerda A, Tiefenbacher JP. Spatial Pattern Analysis and Prediction of Gully Erosion Using Novel Hybrid Model of Entropy-Weight of Evidence. Water. 2019; 11(6):1129. https://doi.org/10.3390/w11061129
Chicago/Turabian StyleArabameri, Alireza, Artemi Cerda, and John P. Tiefenbacher. 2019. "Spatial Pattern Analysis and Prediction of Gully Erosion Using Novel Hybrid Model of Entropy-Weight of Evidence" Water 11, no. 6: 1129. https://doi.org/10.3390/w11061129
APA StyleArabameri, A., Cerda, A., & Tiefenbacher, J. P. (2019). Spatial Pattern Analysis and Prediction of Gully Erosion Using Novel Hybrid Model of Entropy-Weight of Evidence. Water, 11(6), 1129. https://doi.org/10.3390/w11061129







