Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.2. Correction for Pixel Scale Error
2.3. Method Development
3. Application and Results
- (1)
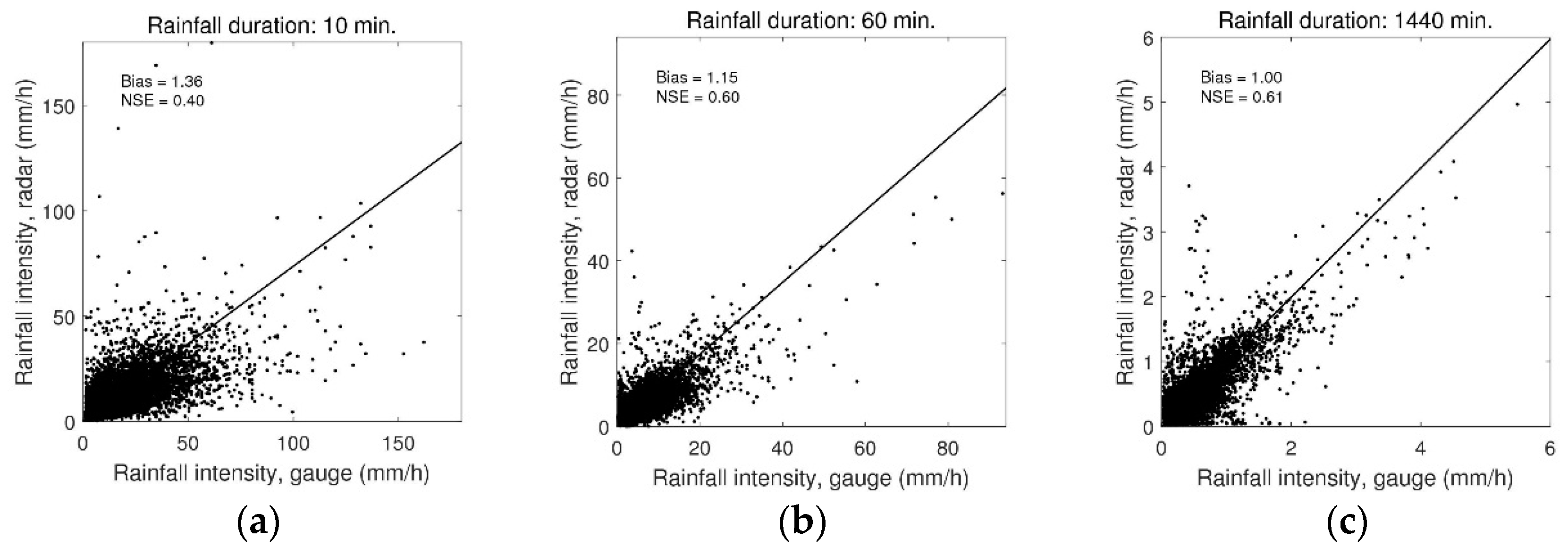
- Applying Equation (1), a correction of the pixel scale error is performed. Results are shown for selected durations in Figure 3 and Table 1. It is evident that the error between rain gauge intensities and radar intensities are significantly larger for short rainfall durations. This is a result of the daily mean-field bias adjustment and leads to a bias factor of 1 for the 1440 min durations (1 day). As shown in Figure 3, there is a considerable scatter between maximum rain gauge intensities and the corresponding radar intensities, which is also explained by the Nash–Sutcliffe Efficiency (NSE)-values in Table 1 and Figure 3. Furthermore, the scatter is larger for the shorter durations indicating high uncertainties. However, as the study aims for a mean pixel scale error, the dispersion of the pixel scale error is not considered any further.
- (2)
- (3)
- The correlation lengths, λ are fitted (Equation (6)) as a function of duration (Figure 6). From Figure 6, it is evident that there is a large variability from storm to storm, but that the mean fit well to the power function with r2 of 0.98. It shows that the power-law function in Equation (6) can be further used to derive a relationship of the storm-centred ARF as a function of area and duration. In addition to the mean relationship, the uncertainty corresponding to mean plus/minus one standard deviation (assuming a Gaussian distribution) is investigated. This uncertainty will provide insight into the variability from storm to storm.
- (4)
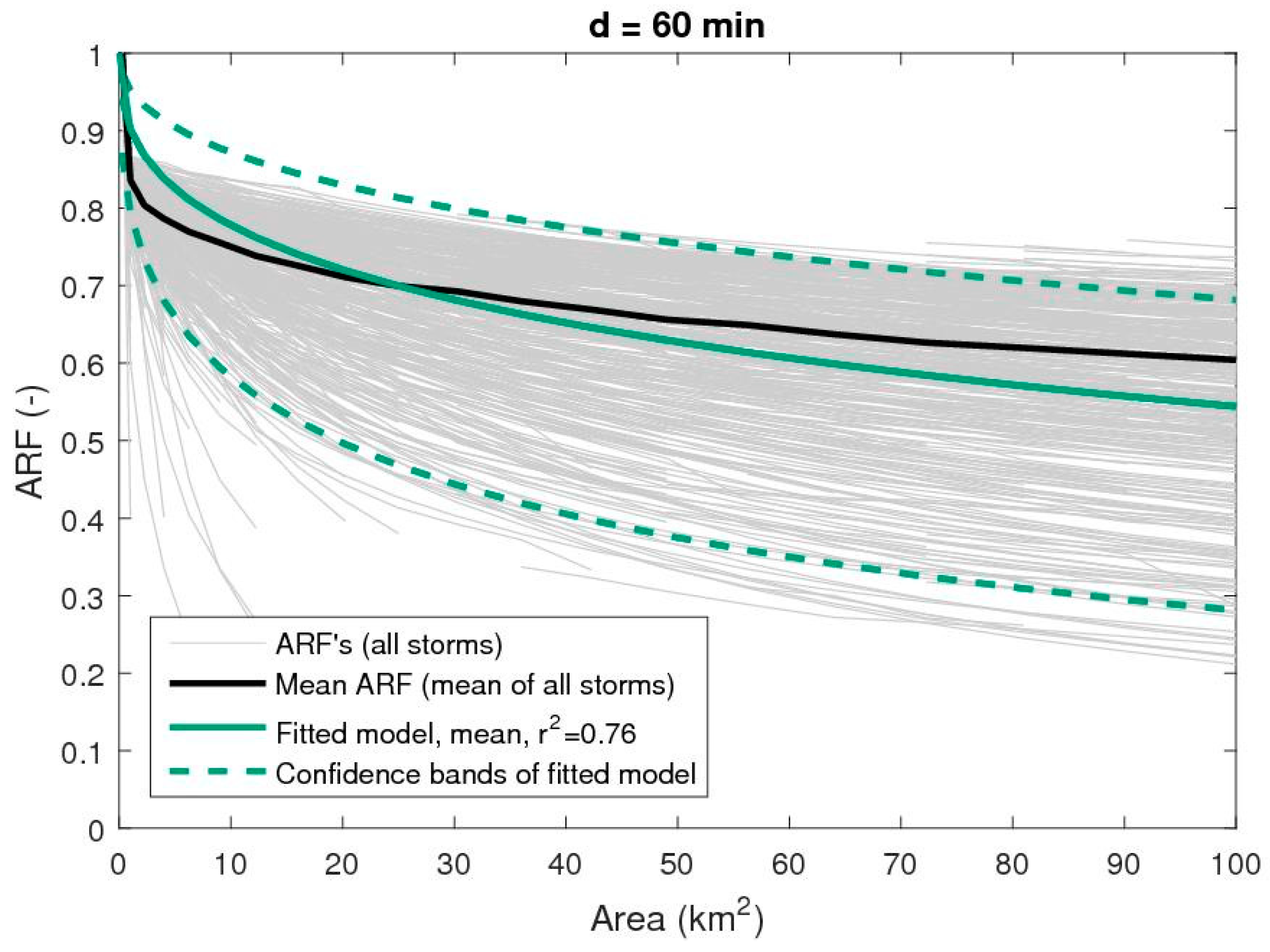
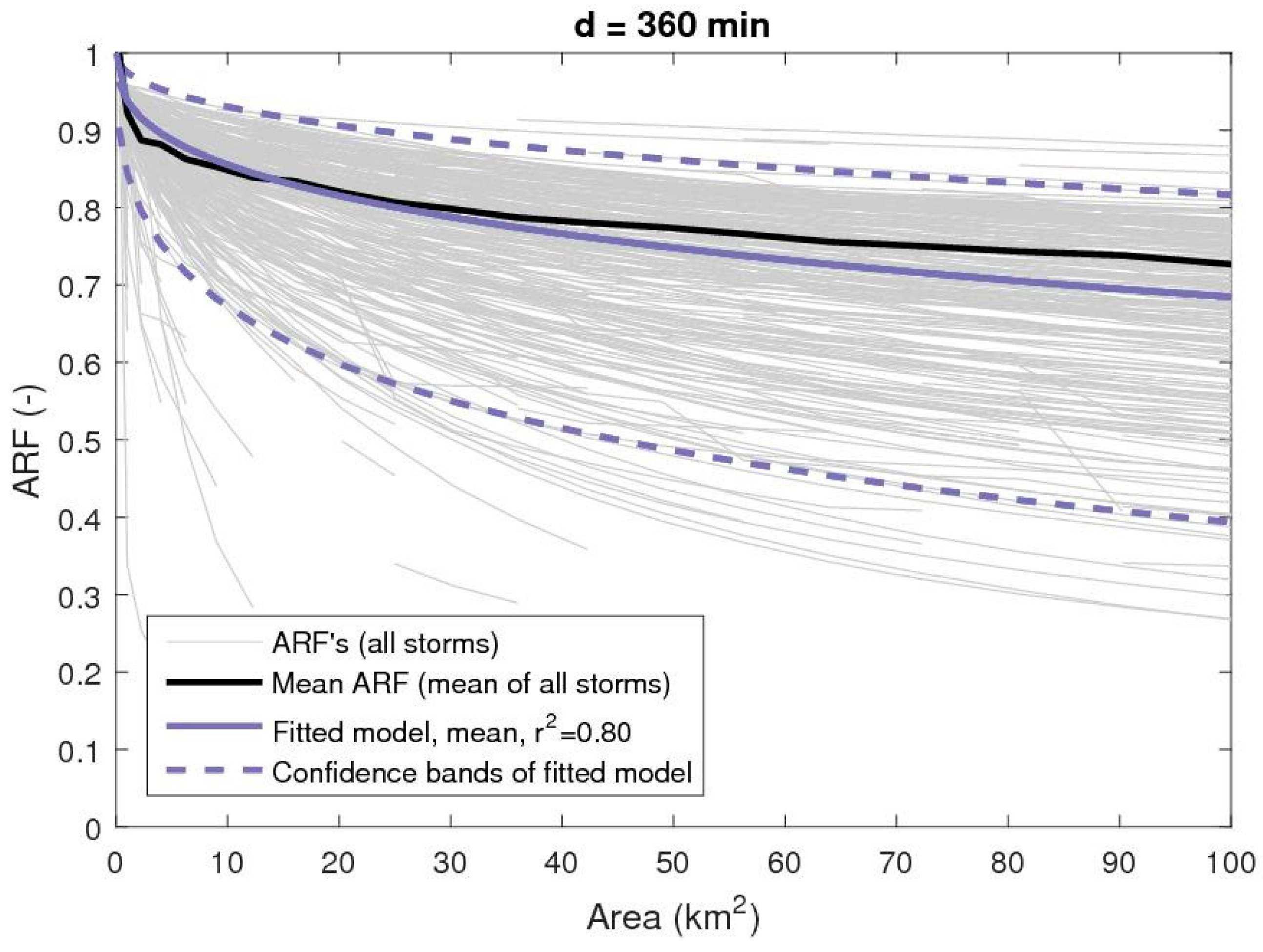
- Applying the obtained function of correlation length and duration, each storm is re-fitted by the relationship in Equation (7) to derive an ARF function. Examples of this fit are shown in Figure 4 and Figure 5 for durations of 60 and 360 min, respectively. Comparing with the mean ARF functions, the fitted relationships show a slight overestimation for the small areas and correspondingly an underestimation for large areas. For some durations, the opposite case occurs (not shown). This uncertainty is a trade-off of fitting a fixed parameter relationship to all durations.
- (5)
4. Discussion
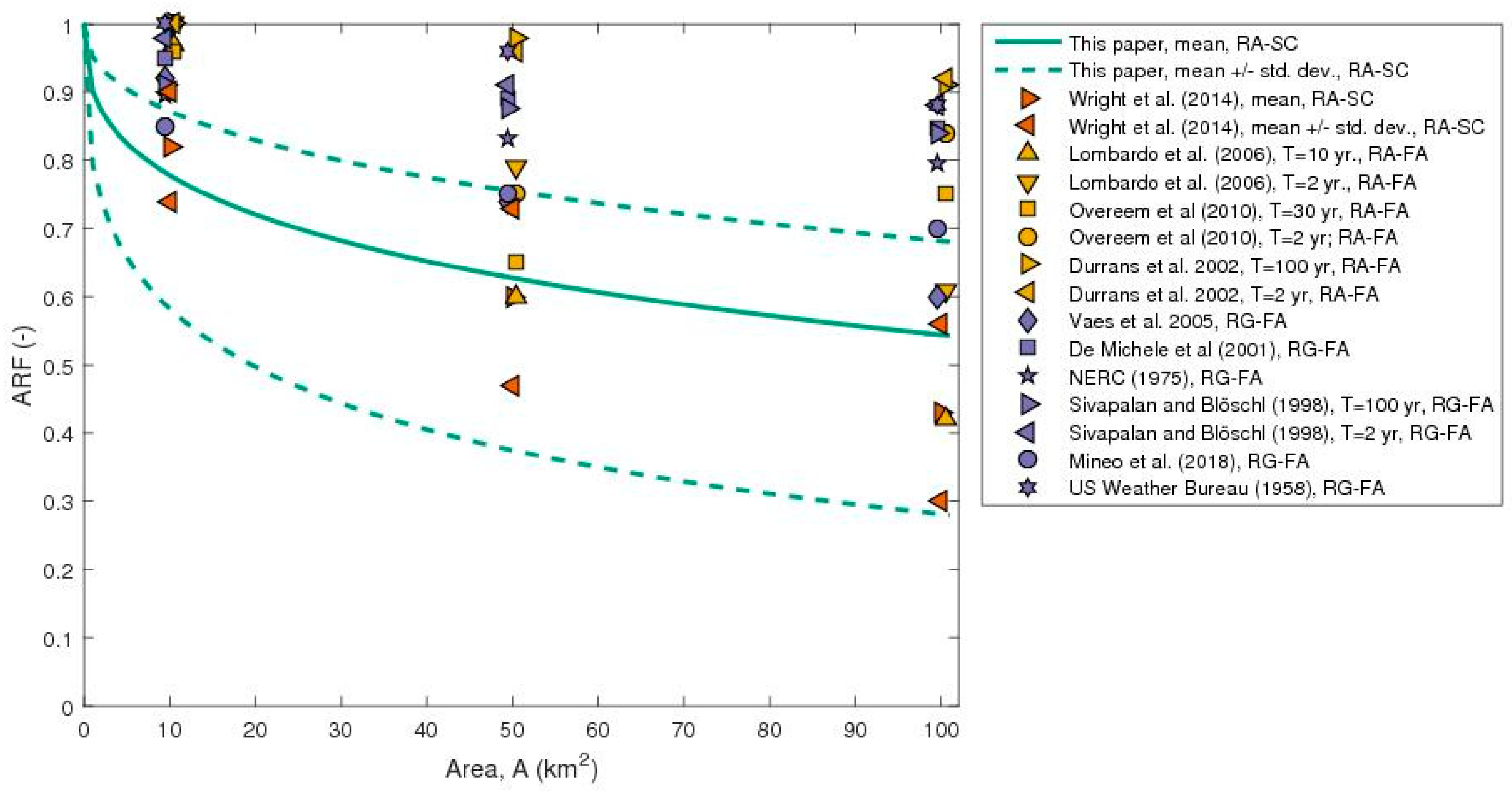
4.1. Comparison with Previous Studies
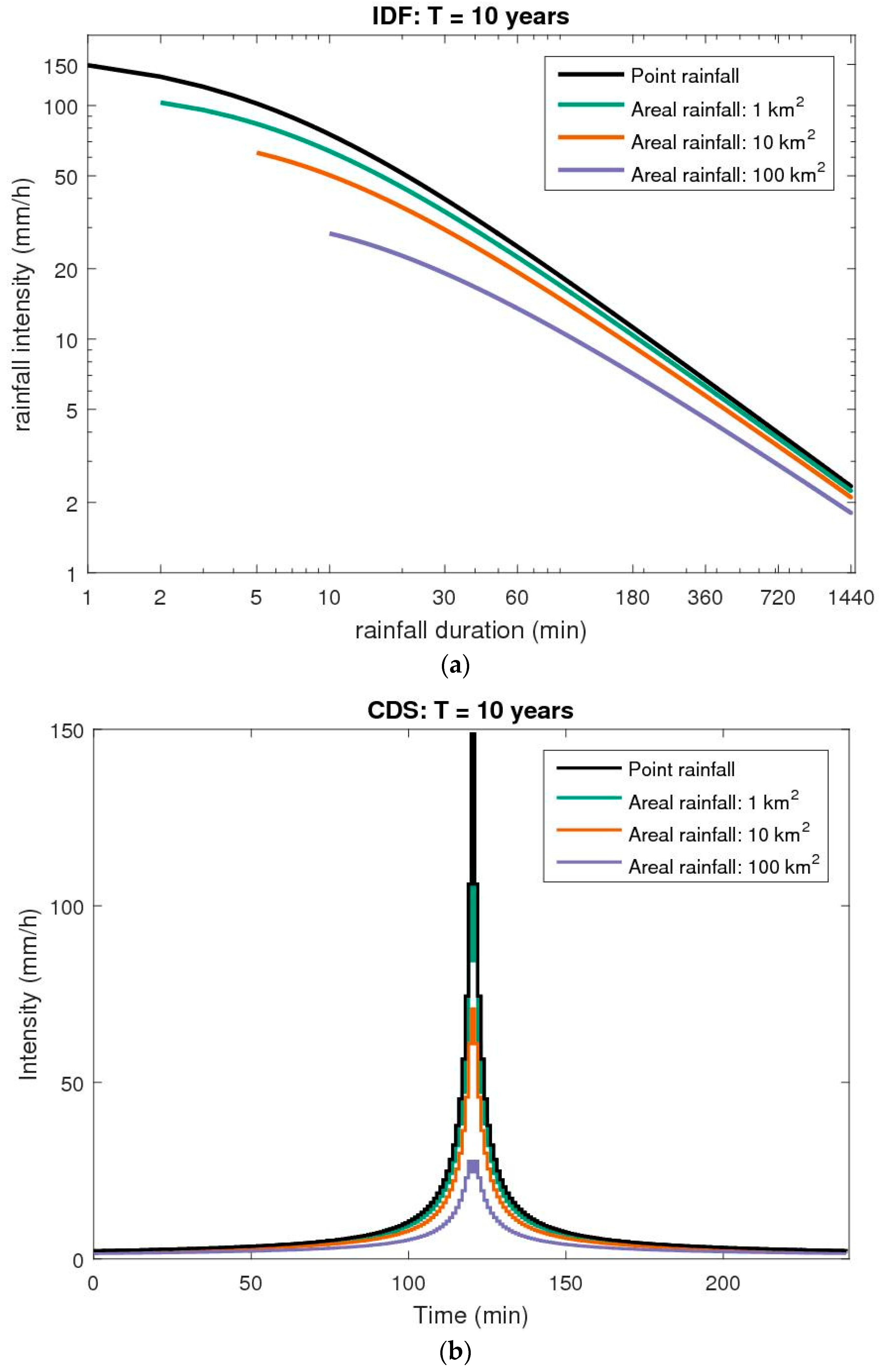
4.2. Implementation in Urban Drainage Design
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Willems, P. Compound intensity/duration/frequency-relationships of extreme precipitation for two seasons and two storm types. J. Hydrol. 2000, 233, 189–205. [Google Scholar] [CrossRef]
- Madsen, H.; Arnbjerg-Nielsen, K.; Mikkelsen, P.S. Update of regional intensity-duration-frequency curves in Denmark: Tendency towards increased storm intensities. Atmos. Res. 2009, 92, 343–349. [Google Scholar] [CrossRef]
- WPC Funktionspraksis for afløbssystemer under regn, skrift nr. 27 (Practice for drainage systems during rain, Guideline no. 27); The Water Pollution Committee of the Society of Danish Engineers; IDA: Copenhagen, Denmark, 2007. [Google Scholar]
- Rodriguez-Iturbe, I.; Mejía, J.M. On the transformation of point rainfall to areal rainfall. Water Resour. Res. 1974, 10, 729–735. [Google Scholar] [CrossRef]
- Sivapalan, M.; Blöschl, G. Transformation of point rainfall to areal rainfall: Intensity-duration-frequency curves. J. Hydrol. 1998, 204, 150–167. [Google Scholar] [CrossRef]
- Villarini, G.; Serinaldi, F.; Krajewski, W.F. Modeling radar-rainfall estimation uncertainties using parametric and non-parametric approaches. Adv. Water Resour. 2008, 31, 1674–1686. [Google Scholar] [CrossRef]
- U.S. Weather Bureau. Rainfall Intensity-Frequency Regime Part 2-Southeastern United States, Technical Paper No. 29; Department of Commerce: Washington, DC, USA, 1958.
- NERC (Natural Environment Research Council, UK). Flood Studies Report; Natural Environment Research Council: Swindon, UK, 1975; Volume II. [Google Scholar]
- Asquith, W.H.; Famiglietti, J.S. Precipitation areal-reduction factor estimation using an annual-maxima centered approach. J. Hydrol. 2000, 230, 55–69. [Google Scholar] [CrossRef]
- De Michele, C.; Kottegoda, N.T.; Rosso, R. The derivation of areal reduction factor of storm rainfall from its scaling properties. Water Resour. Res. 2001, 37, 3247–3252. [Google Scholar] [CrossRef]
- Vaes, G.; Willems, P.; Berlamont, J. Areal rainfall correction coefficients for small urban catchments. Atmos. Res. 2005, 77, 48–59. [Google Scholar] [CrossRef]
- Veneziano, D.; Langousis, A. The areal reduction factor: A multifractal analysis. Water Resour. Res. 2005, 41, 1–15. [Google Scholar] [CrossRef]
- Mineo, C.; Ridolfi, E.; Napolitano, F.; Russo, F. The areal reduction factor: A new analytical expression for the Lazio Region in central Italy. J. Hydrol. 2018, 560, 471–479. [Google Scholar] [CrossRef]
- Durrans, S.R.; Julian, L.T.; Yekta, M. Estimation of Depth-Area Relationships using Radar-Rainfall Data. J. Hydrol. Eng. 2007, 7, 356–367. [Google Scholar] [CrossRef]
- Allen, R.J.; DeGaetano, A.T. Considerations for the use of radar-derived precipitation estimates in determining return intervals for extreme areal precipitation amounts. J. Hydrol. 2005, 315, 203–219. [Google Scholar] [CrossRef]
- Lombardo, F.; Napolitano, F.; Russo, F. On the use of radar reflectivity for estimation of the areal reduction factor. Nat. Hazards Earth Syst. Sci. 2006, 6, 377–386. [Google Scholar] [CrossRef][Green Version]
- Overeem, A.; Buishand, T.A.; Holleman, I.; Uijlenhoet, R. Extreme value modeling of areal rainfall from weather radar. Water Resour. Res. 2010, 46, 1–10. [Google Scholar] [CrossRef]
- Wright, D.B.; Smith, J.A.; Baeck, M.L. Critical Examination of Area Reduction Factors. J. Hydrol. Eng. 2014, 19, 769–776. [Google Scholar] [CrossRef]
- Pavlovic, S.; Perica, S.; St Laurent, M.; Mejía, A. Intercomparison of selected fixed-area areal reduction factor methods. J. Hydrol. 2016, 537, 419–430. [Google Scholar] [CrossRef]
- Svensson, C.; Jones, D.A. Review of methods for deriving areal reduction factors. J. Flood Risk Manag. 2010, 3, 232–245. [Google Scholar] [CrossRef]
- Omolayo, A.S. On the transposition of areal reduction factors for rainfall frequency estimation. J. Hydrol. 1993, 145, 191–205. [Google Scholar] [CrossRef]
- Schilling, W. Rainfall data for urban hydrology: what do we need? Atmos. Res. 1991, 27, 5–21. [Google Scholar] [CrossRef]
- Einfalt, T.; Arnbjerg-Nielsen, K.; Golz, C.; Jensen, N.-E.; Quirmbach, M.; Vaes, G.; Vieux, B. Towards a roadmap for use of radar rainfall data in urban drainage. J. Hydrol. 2004, 299, 186–202. [Google Scholar] [CrossRef]
- Thorndahl, S.; Einfalt, T.; Willems, P.; Nielsen, J.E.; ten Veldhuis, M.-C.; Arnbjerg-Nielsen, K.; Rasmussen, M.R.; Molnar, P. Weather radar rainfall data in urban hydrology. Hydrol. Earth Syst. Sci. 2017, 21, 1359–1380. [Google Scholar] [CrossRef]
- Bengtsson, L.; Niemczynowicz, J. Areal reduction factors from rain movement. Nord. Hydrol. 1986, 17, 65–82. [Google Scholar] [CrossRef]
- Thorndahl, S.; Beven, K.J.; Jensen, J.B.; Schaarup-Jensen, K. Event based uncertainty assessment in urban drainage modelling, applying the GLUE methodology. J. Hydrol. 2008, 357, 421–437. [Google Scholar] [CrossRef]
- Thorndahl, S.; Willems, P. Probabilistic modelling of overflow, surcharge and flooding in urban drainage using the first-order reliability method and parameterization of local rain series. Water Res. 2008, 42, 455–466. [Google Scholar] [CrossRef]
- Thorndahl, S.; Schaarup-Jensen, K.; Rasmussen, M.R. On hydraulic and pollution effects of converting combined sewer catchments to separate sewer catchments. Urban Water J. 2013, 12, 120–130. [Google Scholar] [CrossRef]
- Thorndahl, S.; Nielsen, J.E.; Rasmussen, M.R. Bias adjustment and advection interpolation of long-term high resolution radar rainfall series. J. Hydrol. 2014, 508, 214–226. [Google Scholar] [CrossRef]
- Nielsen, J.E.; Thorndahl, S.; Rasmussen, M.R. A numerical method to generate high temporal resolution precipitation time series by combining weather radar measurements with a nowcast model. Atmos. Res. 2014, 138, 1–12. [Google Scholar] [CrossRef]
- Marshall, J.S.; Palmer, W.M. The distribution of raindrops with size. J. Meteor 1945, 5, 165–166. [Google Scholar] [CrossRef]
- Smith, J.A.; Krajewski, W.F. Estimation of the Mean Field Bias of Radar Rainfall Estimates. J. Appl. Meteorol. 2002, 30, 397–412. [Google Scholar] [CrossRef]
- Kitchen, M.; Blackall, R.M. Representativeness errors in comparisons between radar and gauge measurements of rainfall. J. Hydrol. 1992, 134, 13–33. [Google Scholar] [CrossRef]
- Habib, E.; Ciach, G.J.; Krajewski, W.F. A method for filtering out raingauge representativeness errors from the verification distributions of radar and raingauge rainfall. Adv. Water Resour. 2004, 27, 967–980. [Google Scholar] [CrossRef]
- Krajewski, W.F.; Villarini, G.; Smith, J.A. Radar-Rainfall Uncertainties: Where are We after Thirty Years of Effort? Bull. Am. Meteorol. Soc. 2010, 91, 87–94. [Google Scholar] [CrossRef]
- Peleg, N.; Ben-Asher, M.; Morin, E. Radar subpixel-scale rainfall variability and uncertainty: Lessons learned from observations of a dense rain-gauge network. Hydrol. Earth Syst. Sci. 2013, 17, 2195–2208. [Google Scholar] [CrossRef]
- Peleg, N.; Marra, F.; Fatichi, S.; Paschalis, A.; Molnar, P.; Burlando, P. Spatial variability of extreme rainfall at radar subpixel scale. J. Hydrol. 2018, 556, 922–933. [Google Scholar] [CrossRef]
- Villarini, G.; Mandapaka, P.V.; Krajewski, W.F.; Moore, R.J. Rainfall and sampling uncertainties: A rain gauge perspective. J. Geophys. Res. Atmos. 2008, 113, 1–12. [Google Scholar] [CrossRef]
- Madsen, H.; Gregersen, I.B.; Rosbjerg, D.; Arnbjerg-Nielsen, K. Regional frequency analysis of short duration rainfall extremes using gridded daily rainfall data as co-variate. Water Sci. Technol. 2017, 75, 1971–1981. [Google Scholar] [CrossRef] [PubMed]
- Keifer, C.J.; Chu, H.H. Synthetic Storm Pattern for Drainage Design. J. Hydraul. Div. 1957, 83, 1–25. [Google Scholar]


| Duration, d (min) | 1 | 10 | 30 | 60 | 180 | 360 | 720 | 1440 |
| Bias, B (-) | 1.63 | 1.36 | 1.21 | 1.15 | 1.07 | 1.04 | 1.03 | 1.00 |
| Nash–Sutcliffe Efficiency, NSE (-) | 0.21 | 0.40 | 0.52 | 0.60 | 0.63 | 0.62 | 0.62 | 0.61 |
| Root mean square error, RMSE (mm/h) | 22.47 | 9.82 | 4.61 | 2.65 | 1.12 | 0.66 | 0.38 | 0.21 |
| b1 | b2 | b3 | |
|---|---|---|---|
| mean | 0.31 | 0.38 | 0.26 |
| mean – 1 × std. dev. | 0.21 | 0.45 | 0.36 |
| mean + 1 × std. dev. | 0.47 | 0.37 | 0.17 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thorndahl, S.; Nielsen, J.E.; Rasmussen, M.R. Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology. Water 2019, 11, 1120. https://doi.org/10.3390/w11061120
Thorndahl S, Nielsen JE, Rasmussen MR. Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology. Water. 2019; 11(6):1120. https://doi.org/10.3390/w11061120
Chicago/Turabian StyleThorndahl, Søren, Jesper Ellerbæk Nielsen, and Michael R. Rasmussen. 2019. "Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology" Water 11, no. 6: 1120. https://doi.org/10.3390/w11061120
APA StyleThorndahl, S., Nielsen, J. E., & Rasmussen, M. R. (2019). Estimation of Storm-Centred Areal Reduction Factors from Radar Rainfall for Design in Urban Hydrology. Water, 11(6), 1120. https://doi.org/10.3390/w11061120






