Assess Effectiveness of Salt Removal by a Subsurface Drainage with Bundled Crop Straws in Coastal Saline Soil Using HYDRUS-3D
Abstract
:1. Introduction
2. Materials and Methods
2.1. Field Experiment
2.2. Model Development
2.2.1. Mathematical Model
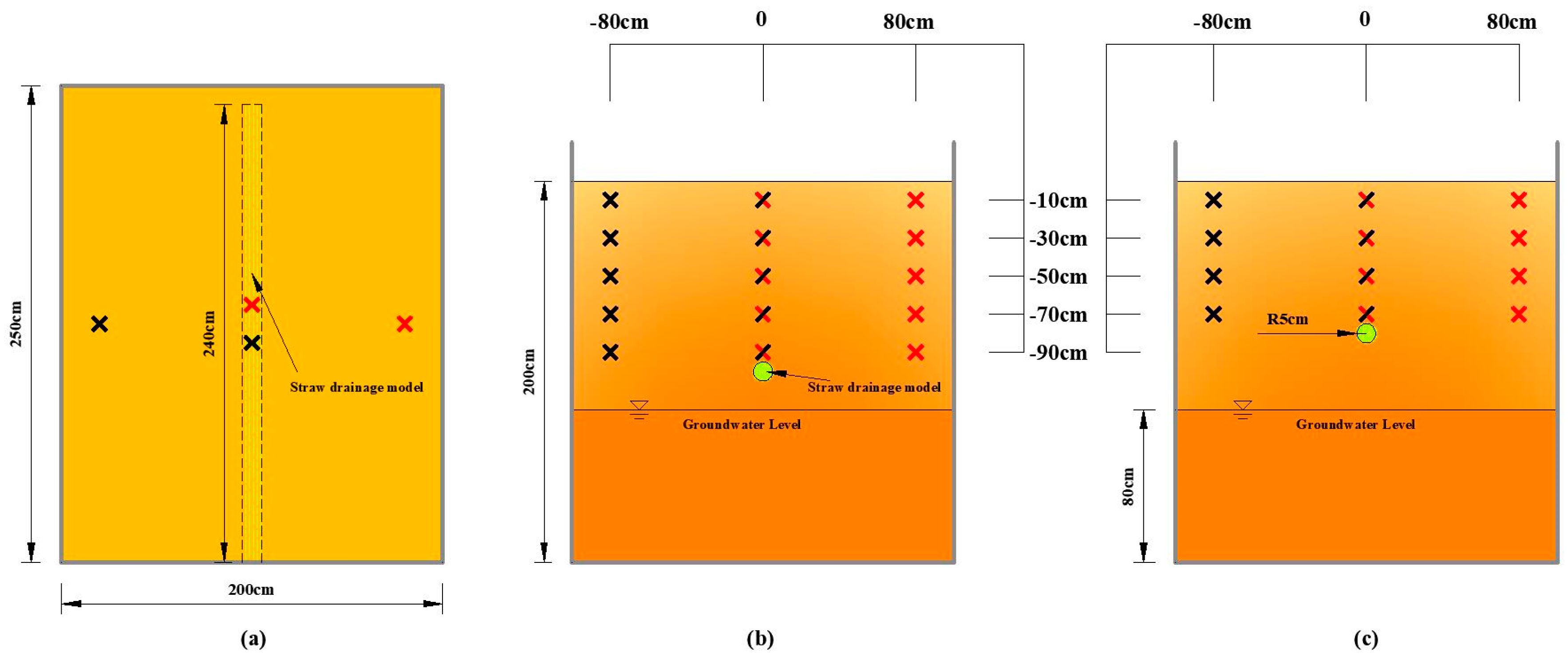
2.2.2. Modeling Domain and Initial and Boundary Conditions
2.3. Statistical Analysis
3. Result and Discussion
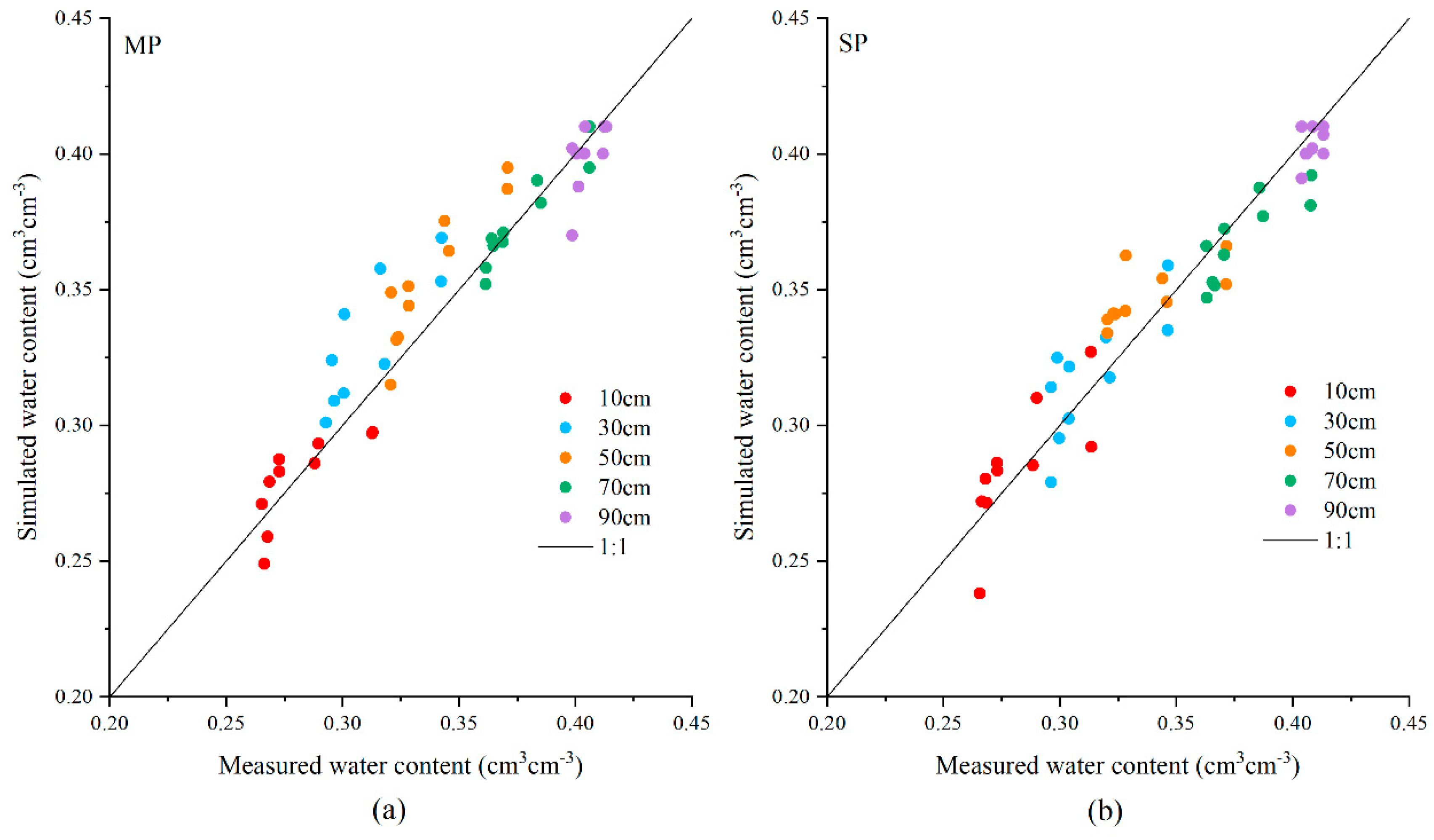
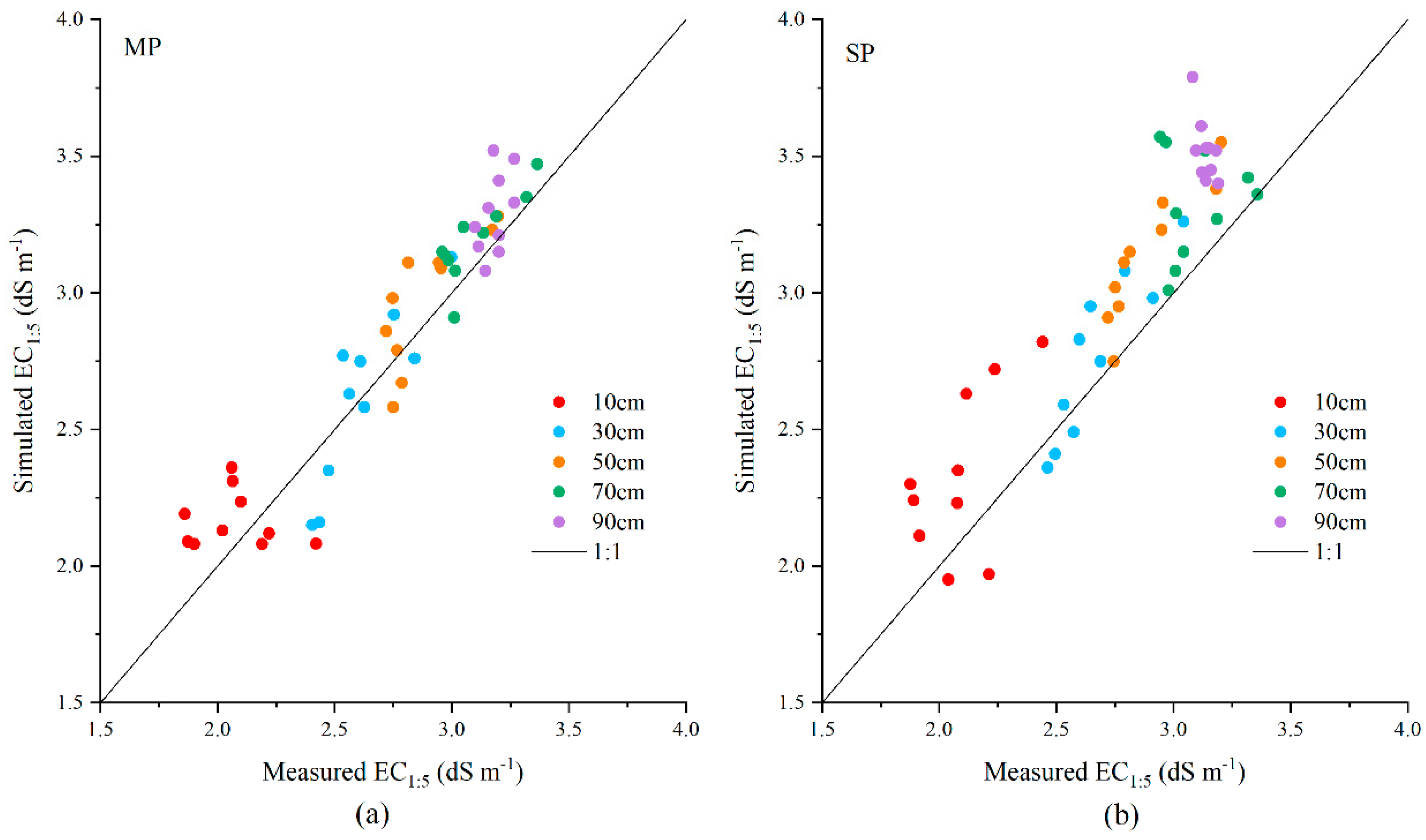
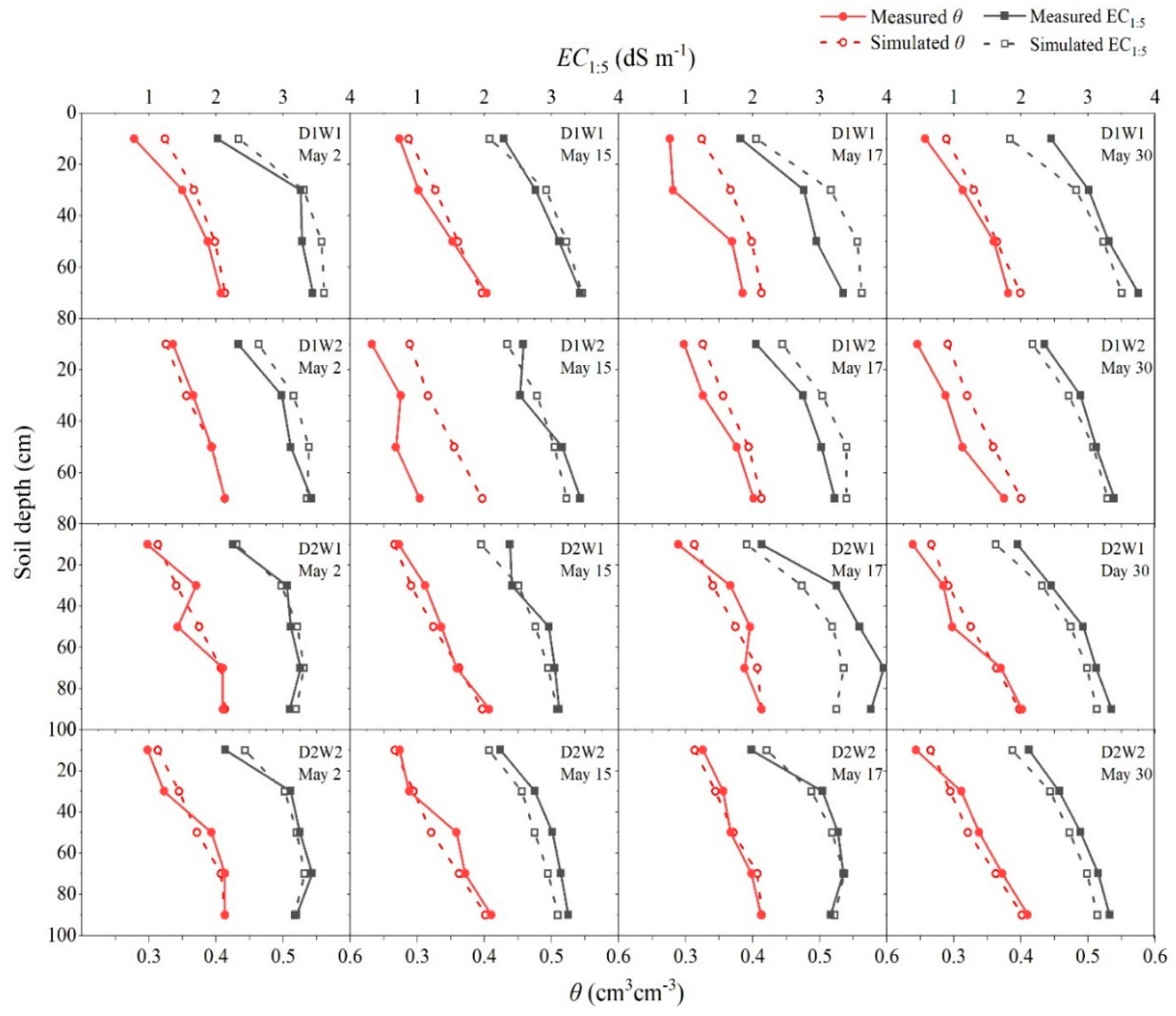
3.1. Model Calibration and Validation
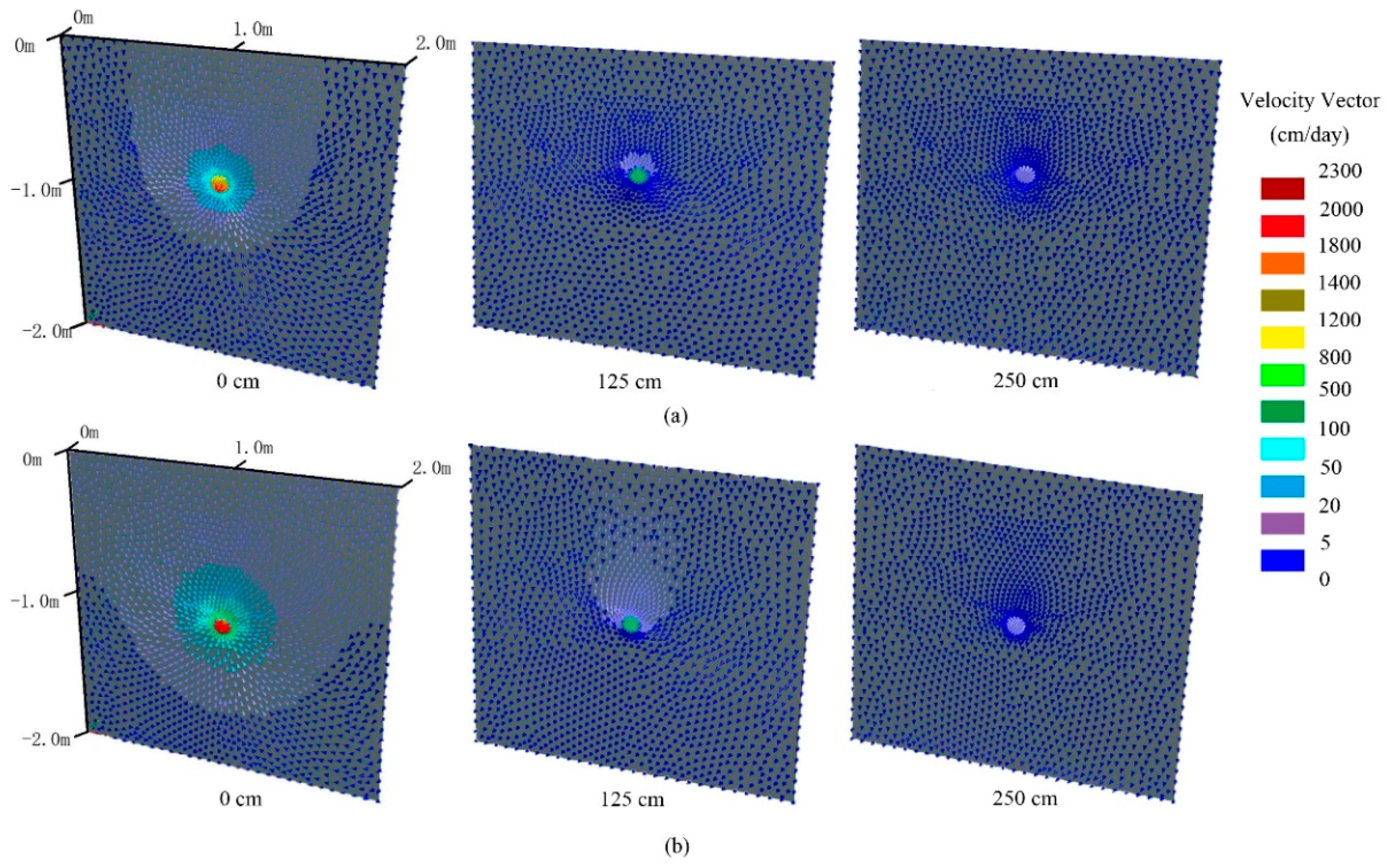
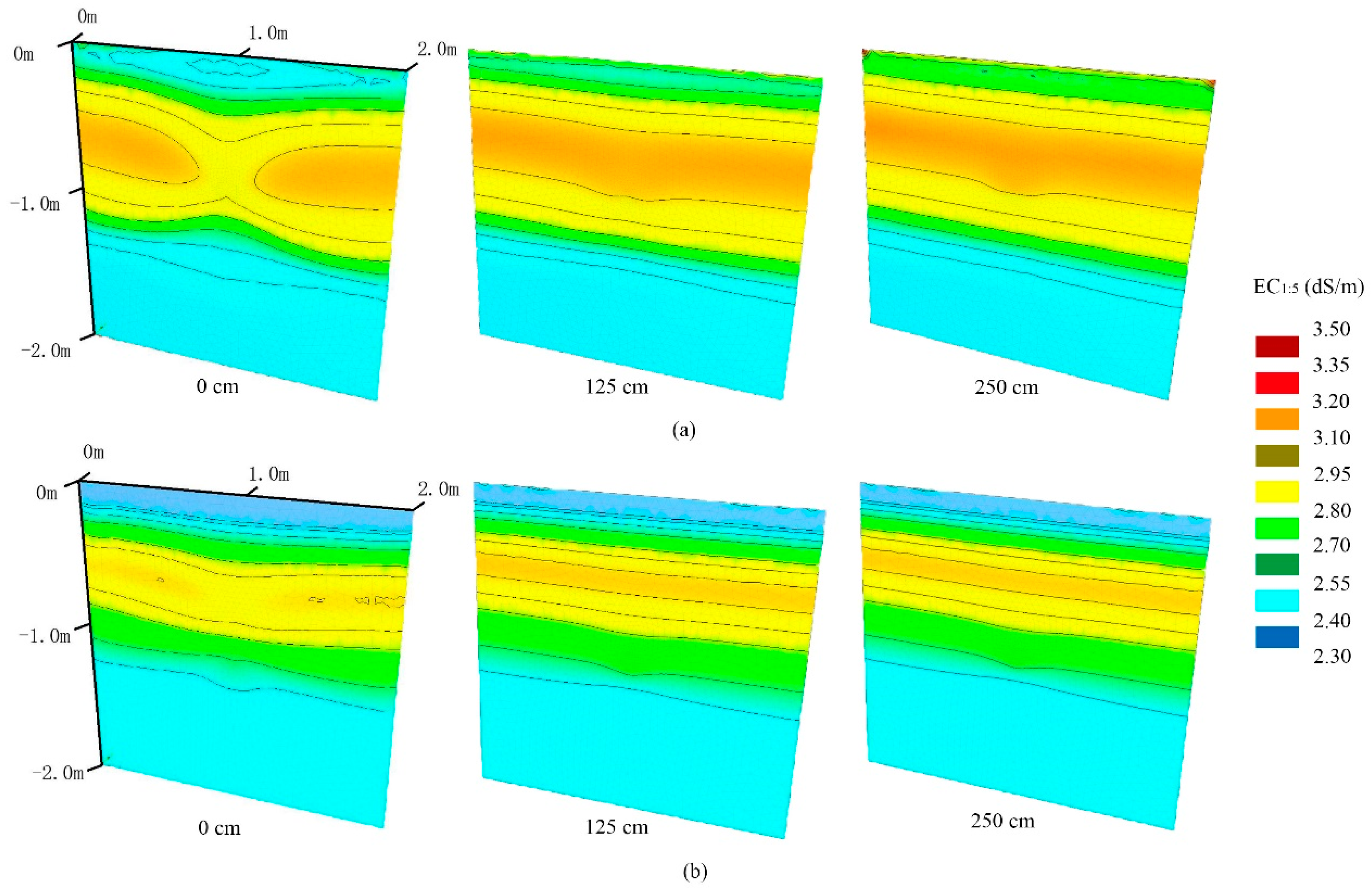
3.2. Water Movement and Salt Distribution.
3.3. Mass Balance of Soil Water and Salt
3.4. Evaluation of the Leaching Capacity of Straw Drainage Modules
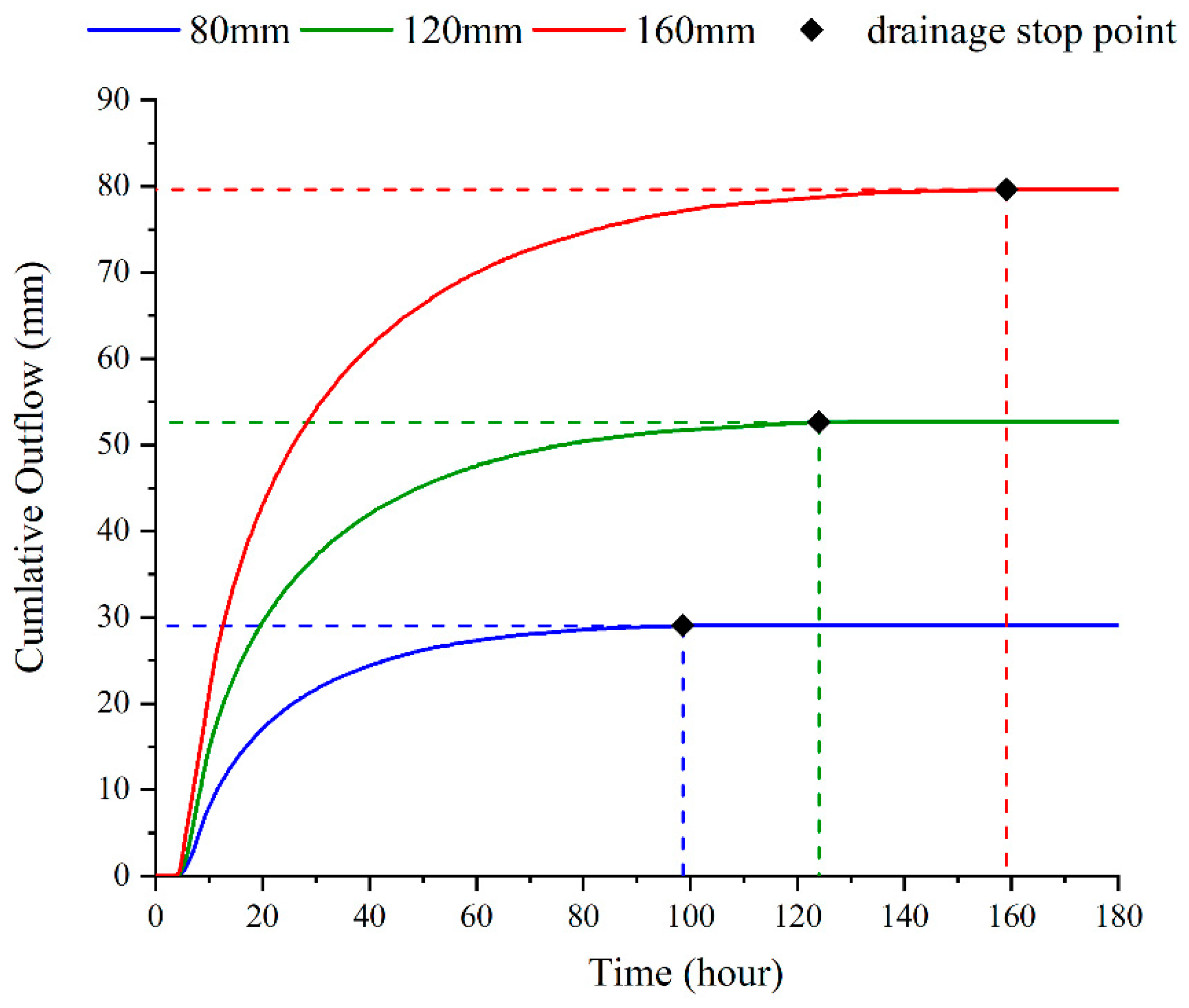
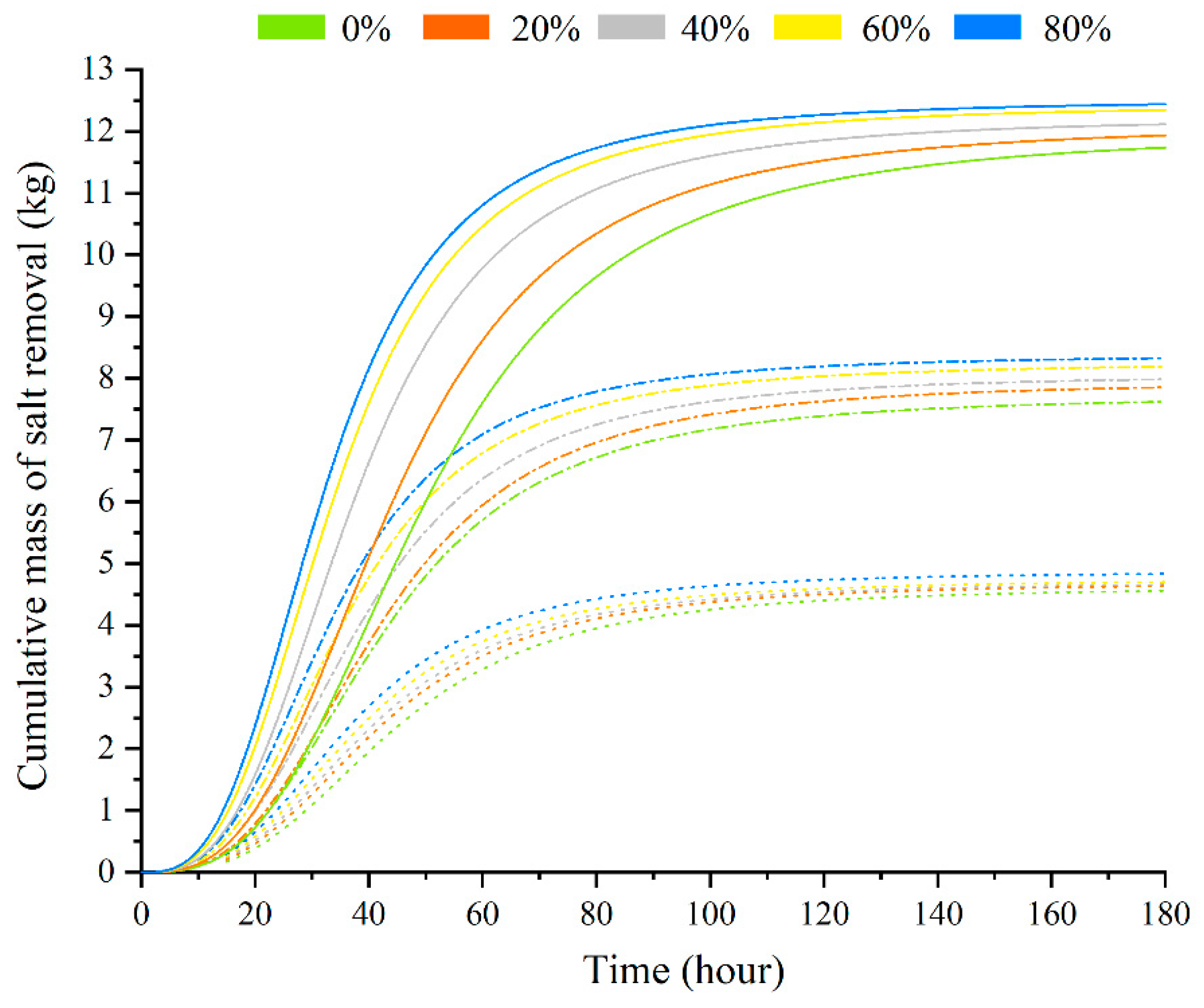
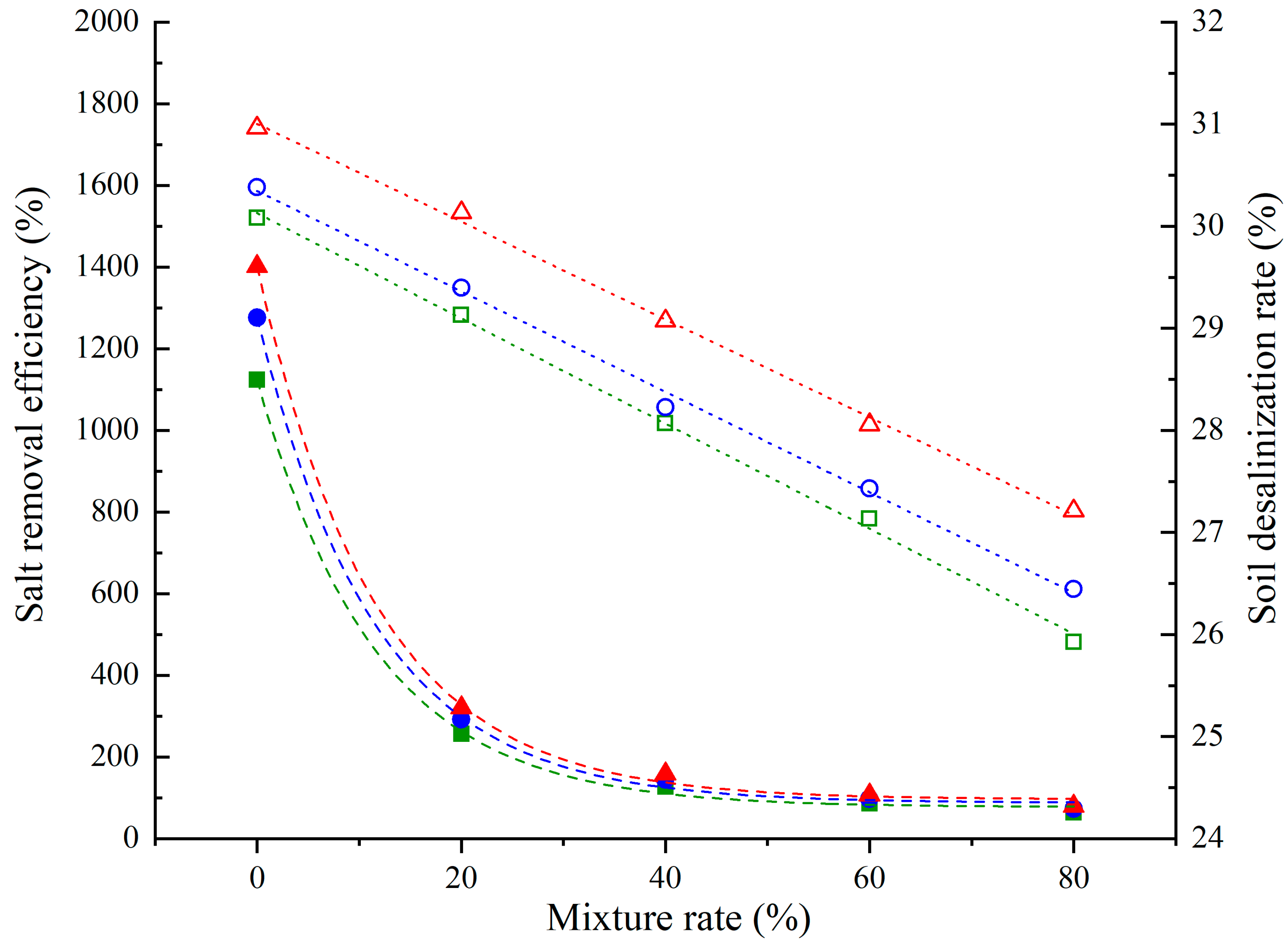
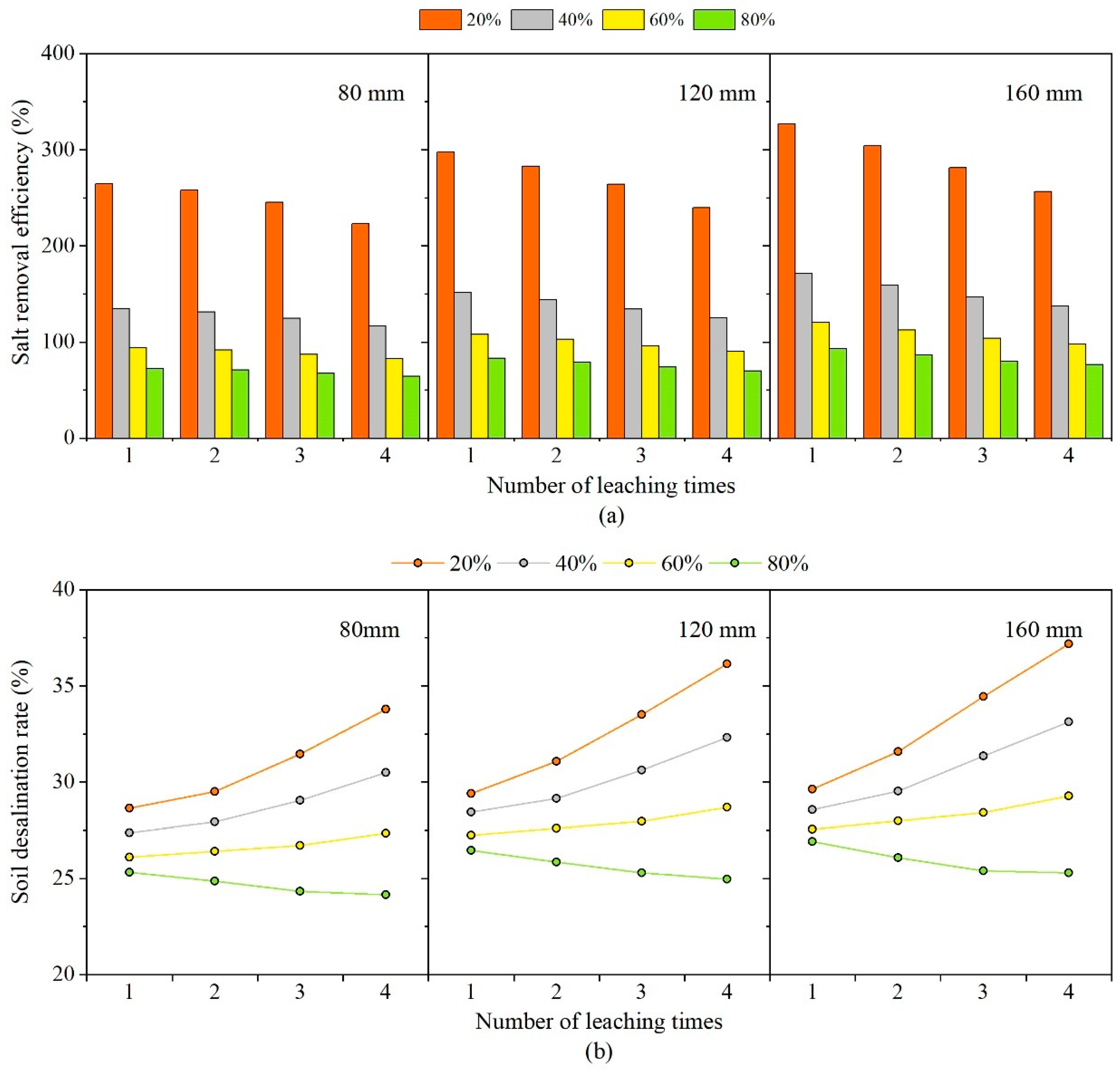
3.4.1. Cumulative Outflow and Salt Removal
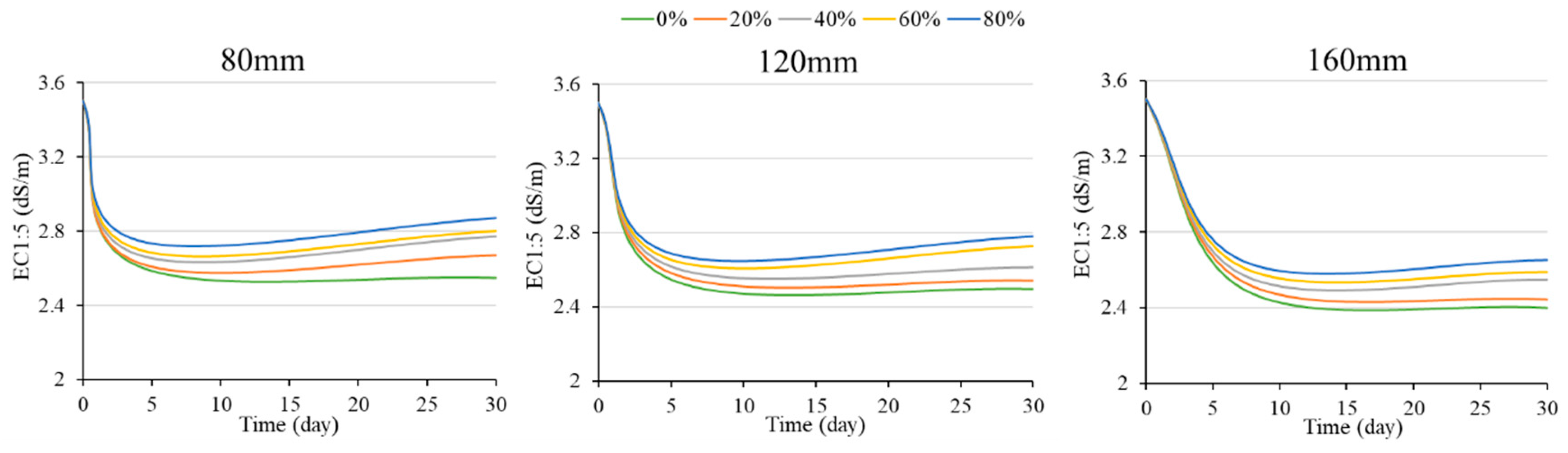
3.4.2. Variation of Soil Salt Content
3.4.3. Desalination Performance
4. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Wang, F.; Wall, G. Mudflat development in Jiangsu Province, China: Practices and experiences. Ocean Coast. Manag. 2010, 53, 691–699. [Google Scholar] [CrossRef]
- Long, X.H.; Liu, L.P.; Shao, T.Y.; Shao, H.B.; Liu, Z.P. Developing and sustainably utilize the coastal mudflat areas in China. Sci. Total Environ. 2016, 569, 1077–1086. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, S.; Qu, X. Dynamic control of drainage and calculation method of drainage spacing based on the idea of combining the control of salinization with subsurface waterlogging. J. Hydraul. Eng. 2008, 11, 1204–1210. (In Chinese) [Google Scholar]
- Shao, X.H.; Chang, T.T.; Cai, F.; Wang, Z.Y.; Huang, M.Y. Effects of subsurface drainage design on soil desalination in coastal resort of China. J. Food Agric. Environ. 2012, 10, 935–938. [Google Scholar]
- Qadir, M.; Ghafoor, A.; Murtaza, G. Amelioration strategies for saline soils: A review. Land Degrad. Dev. 2000, 11, 501–521. [Google Scholar] [CrossRef]
- Pereira, C.S.; Lopes, I.; Abrantes, I.; Sousa, J.P.; Chelinho, S. Salinization effects on coastal ecosystems: A terrestrial model ecosystem approach. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2019, 374. [Google Scholar] [CrossRef]
- Martínez-Alvarez, V.; González-Ortega, M.J.; Martin-Gorriz, B.; Soto-García, M.; Maestre-Valero, J.F. Seawater desalination for crop irrigation—Current status and perspectives. In Emerging Technologies for Sustainable Desalination Handbook; Elsevier: Amsterdam, The Netherlands, 2018; pp. 461–492. [Google Scholar]
- Guo, S.H.; Liu, Z.L.; Li, Q.S.; Yang, P.; Wang, L.L.; He, B.Y.; Xu, Z.M.; Ye, J.S.; Zeng, E.Y. Leaching heavy metals from the surface soil of reclaimed tidal flat by alternating seawater inundation and air drying. Chemosphere 2016, 157, 262–270. [Google Scholar] [CrossRef]
- Hu, Y.H.; Lindo-Atichati, D. Experimental equations of seawater salinity and desalination capacity to assess seawater irrigation. Sci. Total Environ. 2019, 651, 807–812. [Google Scholar] [CrossRef]
- Hornbuckle, J.W.; Christen, E.W.; Faulkner, R.D. Analytical Solution for Drainflows from Bilevel Multiple-Drain Subsurface Drainage Systems. J. Irrig. Drain. Eng. 2012, 138, 642–650. [Google Scholar] [CrossRef]
- Christen, E.; Skehan, D. Design and management of subsurface horizontal drainage to reduce salt loads. J. Irrig. Drain. Eng. 2001, 127, 148–155. [Google Scholar] [CrossRef]
- Bahceci, I.; Dinc, N.; Tari, A.F.; Agar, A.I.; Sonmez, B. Water and salt balance studies, using SaltMod, to improve subsurface drainage design in the Konya-Cumra Plain, Turkey. Agric. Water Manag. 2006, 85, 261–271. [Google Scholar] [CrossRef]
- Luo, W.; Sands, G.R.; Youssef, M.; Strock, J.S.; Song, I.; Canelon, D. Modeling the impact of alternative drainage practices in the northern Corn-belt with DRAINMOD-NII. Agric. Water Manag. 2010, 97, 389–398. [Google Scholar] [CrossRef]
- Lu, P.; Zhang, Z.; Feng, G.; Wan, C.; Shi, X. Effect of straw draining piece depth in soil on soil water-salt distribution in saline soil and its drainage-salt inhibiting performance. Trans. CSAE 2017, 33, 115–121. (In Chinese) [Google Scholar]
- Lu, P.R.; Zhang, Z.Y.; Feng, G.X.; Huang, M.Y.; Shi, X.F. Experimental Study on the Potential Use of Bundled Crop Straws as Subsurface Drainage Material in the Newly Reclaimed Coastal Land in Eastern China. Water 2018, 10, 31. [Google Scholar] [CrossRef]
- Montagne, D.; Cornu, S.; Le Forestier, L.; Cousin, I. Soil Drainage as an Active Agent of Recent Soil Evolution: A Review. Pedosphere 2009, 19, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Allen, D.; Arthur, S.; Haynes, H.; Wallis, G.S.; Wallerstein, N. Influences and drivers of woody debris movement in urban watercourses. Sci. China Technol. Sci. 2014, 57, 1512–1521. [Google Scholar] [CrossRef] [Green Version]
- Siyal, A.A.; van Genuchten, M.T.; Skaggs, T.H. Solute transport in a loamy soil under subsurface porous clay pipe irrigation. Agric. Water Manag. 2013, 121, 73–80. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. The HYDRUS Software Package for Simulating the Two- and Three-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably-Saturated Porous Media; PC-Progress: Prague, Czech Republic, 2018. [Google Scholar]
- Boivin, A.; Simunek, J.; Schiavon, M.; van Genuchten, M.T. Comparison of pesticide transport processes in three tile-drained field soils using HYDRUS-2D. Vadose Zone J. 2006, 5, 838–849. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Noory, H. Modeling paddy field subsurface drainage using HYDRUS-2D. Paddy Water Environ. 2015, 13, 477–485. [Google Scholar] [CrossRef]
- De Vos, J.A.; Raats, P.A.C.; Feddes, R.A. Chloride transport in a recently reclaimed Dutch polder. J. Hydrol. 2002, 257, 59–77. [Google Scholar] [CrossRef]
- Tao, Y.; Wang, S.; Xu, D.; Yuan, H.; Chen, H.J.A.W.M. Field and numerical experiment of an improved subsurface drainage system in Huaibei plain. Agric. Water Manag. 2017, 194, 24–32. [Google Scholar] [CrossRef]
- Filipovic, V.; Mallmann, F.J.K.; Coquet, Y.; Simunek, J. Numerical simulation of water flow in tile and mole drainage systems. Agric. Water Manag. 2014, 146, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Li, S.H.; Zhou, D.M.; Luan, Z.Q.; Pan, Y.; Jiao, C.C. Quantitative simulation on soil moisture contents of two typical vegetation communities in Sanjiang Plain, China. Chin. Geogr. Sci. 2011, 21, 723–733. [Google Scholar] [CrossRef]
- Honari, M.; Ashrafzadeh, A.; Khaledian, M.; Vazifedoust, M.; Mailhol, J.C. Comparison of HYDRUS-3D Soil Moisture Simulations of Subsurface Drip Irrigation with Experimental Observations in the South of France. J. Irrig. Drain. Eng. 2017, 143. [Google Scholar] [CrossRef]
- Liu, G.; Yang, J.; Jiang, Y. Salinity characters of soils and groundwater in typical coastal area in Jiangsu Province. Soils 2005, 37, 163–168. (In Chinese) [Google Scholar]
- Chen, L.J.; Feng, Q.; Li, F.R.; Li, C.S. A bidirectional model for simulating soil water flow and salt transport under mulched drip irrigation with saline water. Agric. Water Manag. 2014, 146, 24–33. [Google Scholar] [CrossRef]
- Slavich, P.; Petterson, G. Estimating the electrical conductivity of saturated paste extracts from 1: 5 soil, water suspensions and texture. Soil Res. 1993, 31, 73–81. [Google Scholar] [CrossRef]
- Hanson, B.; Hopmans, J.W.; Simunek, J. Leaching with subsurface drip irrigation under saline, shallow groundwater conditions. Vadose Zone J. 2008, 7, 810–818. [Google Scholar] [CrossRef]
- Grattan, S. Irrigation Water Salinity and Crop Production; UCANR Publications: Oakland, CA, USA, 2002; Volume 9. [Google Scholar]
- Eberbach, P.; Humphreys, E.; Kukal, S. The effect of rice straw mulch on evapotranspiration, transpiration and soil evaporation of irrigated wheat in Punjab, India. Agric. Water Manag. 2011, 98, 1847–1855. [Google Scholar]
- Vangenuchten, M.T. A closed form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J.; van Genuchten, M.T. ROSETTA: A computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J. Hydrol. 2001, 251, 163–176. [Google Scholar] [CrossRef]
- Hudan, T.; Sultan. Inverse Estimation for Soil and Straw Hydraulic Parameters from Lysimeters. J. Irrig. Drain. 2009, 28, 68–70. (In Chinese) [Google Scholar]
- Phogat, V.; Mahadevan, M.; Skewes, M.; Cox, J.W. Modelling soil water and salt dynamics under pulsed and continuous surface drip irrigation of almond and implications of system design. Irrig. Sci. 2012, 30, 315–333. [Google Scholar] [CrossRef]
- Zhu, Y.; Shi, L.S.; Yang, J.Z.; Wu, J.W.; Mao, D.Q. Coupling methodology and application of a fully integrated model for contaminant transport in the subsurface system. J. Hydrol. 2013, 501, 56–72. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: Washington, DC, USA, 2013. [Google Scholar]
- Phogat, V.; Pitt, T.; Cox, J.W.; Simunek, J.; Skewes, M.A. Soil water and salinity dynamics under sprinkler irrigated almond exposed to a varied salinity stress at different growth stages. Agric. Water Manag. 2018, 201, 70–82. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Huang, Y.; Long, H.; Hou, S.; Xing, A.; Sun, Z. Simulations of water movement and solute transport through different soil texture configurations under negative-pressure irrigation. Hydrol. Process. 2017, 31, 2599–2612. [Google Scholar] [CrossRef]
- Cote, C.M.; Bristow, K.L.; Charlesworth, P.B.; Cook, F.J.; Thorburn, P.J. Analysis of soil wetting and solute transport in subsurface trickle irrigation. Irrig. Sci. 2003, 22, 143–156. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, Q.A.; Peng, C.; Wu, N.; Wang, Y.; Fang, X.; Jiang, H.; Xiang, W.; Chang, J.; Deng, X. Methane emissions from rice paddies natural wetlands, lakes in China: Synthesis new estimate. Glob. Chang. Biol. 2013, 19, 19–32. [Google Scholar] [CrossRef] [PubMed]
- Phogat, V.; Skewes, M.; Cox, J.; Simunek, J. Statistical assessment of a numerical model simulating agro hydro-chemical processes in soil under drip fertigated mandarin tree. Irrig. Drain. Syst. Eng. 2016, 5, 2. [Google Scholar]
- Wang, C.; Zhang, Z.Y.; Fan, S.M.; Mwiya, R.; Xie, M.X. Effects of straw incorporation on desiccation cracking patterns and horizontal flow in cracked clay loam. Soil Tillage Res. 2018, 182, 130–143. [Google Scholar] [CrossRef]
- Gabiri, G.; Burghof, S.; Diekkrüger, B.; Leemhuis, C.; Steinbach, S.; Näschen, K. Modeling spatial soil water dynamics in a tropical floodplain, East Africa. Water 2018, 10, 191. [Google Scholar] [CrossRef]
- Akay, O.; Fox, G.A.; Simunek, J. Numerical simulation of flow dynamics during macropore-subsurface drain interactions using HYDRUS. Vadose Zone J. 2008, 7, 909–918. [Google Scholar] [CrossRef]
- Mirjat, M.; Mughal, A.; Chandio, A. Simulating water flow and salt leaching under sequential flooding between subsurface drains. Irrig. Drain. 2014, 63, 112–122. [Google Scholar] [CrossRef]
- Mirjat, M.; Rose, D.; Adey, M. Desalinisation by zone leaching: Laboratory investigations in a model sand-tank. Soil Res. 2008, 46, 91–100. [Google Scholar] [CrossRef]
- Sands, G.; Song, I.; Busman, L.; Hansen, B. The effects of subsurface drainage depth and intensity on nitrate loads in the northern cornbelt. Trans. ASABE 2008, 51, 937–946. [Google Scholar] [CrossRef]
- Ghumman, A.R.; Ghazaw, Y.M.; Niazi, M.F.; Hashmi, H.N. Impact assessment of subsurface drainage on waterlogged and saline lands. Environ. Monit. Assess. 2011, 172, 189–197. [Google Scholar] [CrossRef]
- Feng, G.X.; Zhang, Z.Y.; Wan, C.Y.; Lu, P.R.; Bakour, A. Effects of saline water irrigation on soil salinity and yield of summer maize (Zea mays L.) in subsurface drainage system. Agric. Water Manag. 2017, 193, 205–213. [Google Scholar] [CrossRef]
- Ayers, R.; Westcot, D. Water Quality for Irrigation; FAO Irrigation and Drainage Paper; FAO: Rome, Italy, 1985; Volume 20. [Google Scholar]
- Christen, E.W.; Ayars, J.E.; Hornbuckle, J.W. Subsurface drainage design and management in irrigated areas of Australia. Irrig. Sci. 2001, 21, 35–43. [Google Scholar] [CrossRef]
- Sharma, D.P.; Tyagi, N.K. On-farm management of saline drainage water in arid and semi-arid regions. Irrig. Drain. 2004, 53, 87–103. [Google Scholar] [CrossRef]
- Tedeschi, A.; Dell’Aquila, R. Effects of irrigation with saline waters, at different concentrations, on soil physical and chemical characteristics. Agric. Water Manag. 2005, 77, 308–322. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Fan, Q.; Wang, T. Study on Relationship between pH Value of Protected Field Soil and Its Salinity Content and Composition under Leach Condition. Water Sav. Irrig. 2009, 6, 8–11. (In Chinese) [Google Scholar]
| Factors | Variable Parameters |
|---|---|
| Leaching amount | 80, 120, 160 mm |
| Leaching water salinity | Seawater mixture rate: 0, 20, 40, 60, 80% |
| Number of leaching events | 1, 2, 3, 4 times |
| Soil Water Content | Soil Salt Content | |||||||
|---|---|---|---|---|---|---|---|---|
| ME | RMSE | NSE | R2 | ME | RMSE | NSE | R2 | |
| MP a | 0.004 | 0.015 | 0.905 | 0.906 | 0.130 | 0.157 | 0.807 | 0.872 |
| SP b | 0.006 | 0.018 | 0.799 | 0.882 | 0.235 | 0.416 | −0.073 | 0.449 |
| MP b | 0.004 | 0.017 | 0.857 | 0.877 | 0.225 | 0.289 | 0.602 | 0.799 |
| SP a | 0.002 | 0.024 | 0.781 | 0.819 | 0.146 | 0.209 | 0.735 | 0.856 |
| Treatments | Soil Water Content | Soil Salt Content | ||||||
|---|---|---|---|---|---|---|---|---|
| ME | RMSE | NSE | R2 | ME | RMSE | NSE | R2 | |
| D1W1 | −0.024 | 0.028 | 0.595 | 0.829 | −0.081 | 0.283 | 0.681 | 0.763 |
| D1W2 | −0.031 | 0.035 | 0.395 | 0.724 | −0.069 | 0.222 | 0.677 | 0.720 |
| D2W1 | 0.003 | 0.018 | 0.881 | 0.882 | 0.175 | 0.210 | 0.709 | 0.835 |
| D2W2 | 0.006 | 0.014 | 0.912 | 0.919 | 0.113 | 0.131 | 0.862 | 0.901 |
| Treatment | Components | Water Balance (mm) | Salt Balance (kg) | ||
|---|---|---|---|---|---|
| 1st Leaching | 2nd Leaching | 1st Leaching | 2nd Leaching | ||
| D1W1 | Input amount | 160 | 160 | 4.3 | 4.3 |
| Soil evaporation | 25.5 | 30.8 | 0 | 0 | |
| Drainage amount | 67.4 | 76.8 | 8.8 | 7.8 | |
| Soil storage | 67.1 | 52.4 | −4.5 | −3.5 | |
| D1W2 | Input amount | 160 | 160 | 9.2 | 9.2 |
| Soil evaporation | 25.5 | 30.8 | 0 | 0 | |
| Drainage amount | 68.2 | 77 | 8.3 | 7.9 | |
| Soil storage | 66.3 | 52.2 | 0.9 | 1.3 | |
| D2W1 | Input amount | 160 | 160 | 4.3 | 4.3 |
| Soil evaporation | 25.5 | 30.8 | 0 | 0 | |
| Drainage amount | 100.4 | 105.6 | 11.6 | 10.8 | |
| Soil storage | 34.1 | 23.6 | −7.3 | −6.5 | |
| D2W2 | Input amount | 160 | 160 | 9.2 | 9.2 |
| Soil evaporation | 25.5 | 30.8 | 0 | 0 | |
| Drainage amount | 99.5 | 99.8 | 10.3 | 9.9 | |
| Soil storage | 35 | 29.4 | −1.1 | −0.7 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, P.; Zhang, Z.; Sheng, Z.; Huang, M.; Zhang, Z. Assess Effectiveness of Salt Removal by a Subsurface Drainage with Bundled Crop Straws in Coastal Saline Soil Using HYDRUS-3D. Water 2019, 11, 943. https://doi.org/10.3390/w11050943
Lu P, Zhang Z, Sheng Z, Huang M, Zhang Z. Assess Effectiveness of Salt Removal by a Subsurface Drainage with Bundled Crop Straws in Coastal Saline Soil Using HYDRUS-3D. Water. 2019; 11(5):943. https://doi.org/10.3390/w11050943
Chicago/Turabian StyleLu, Peirong, Zhanyu Zhang, Zhuping Sheng, Mingyi Huang, and Zemin Zhang. 2019. "Assess Effectiveness of Salt Removal by a Subsurface Drainage with Bundled Crop Straws in Coastal Saline Soil Using HYDRUS-3D" Water 11, no. 5: 943. https://doi.org/10.3390/w11050943
APA StyleLu, P., Zhang, Z., Sheng, Z., Huang, M., & Zhang, Z. (2019). Assess Effectiveness of Salt Removal by a Subsurface Drainage with Bundled Crop Straws in Coastal Saline Soil Using HYDRUS-3D. Water, 11(5), 943. https://doi.org/10.3390/w11050943





