Recent and Future Changes in Rainfall Erosivity and Implications for the Soil Erosion Risk in Brandenburg, NE Germany
Abstract
1. Introduction
- Which aggregated rainfall index is best to estimate current R factors and their recent change in NE Germany?
- How does climate change affect regional R factors and the risk of soil erosion?
- How does the rainfall index affect future trends and how does the impact compare to other sources of uncertainty such as the choice of climate model, bias correction, and RCP scenario?
2. Materials and Methods
2.1. Study Area
2.2. Rainfall Indices and the Variability of Calculated R Factors
2.3. Climate Scenarios
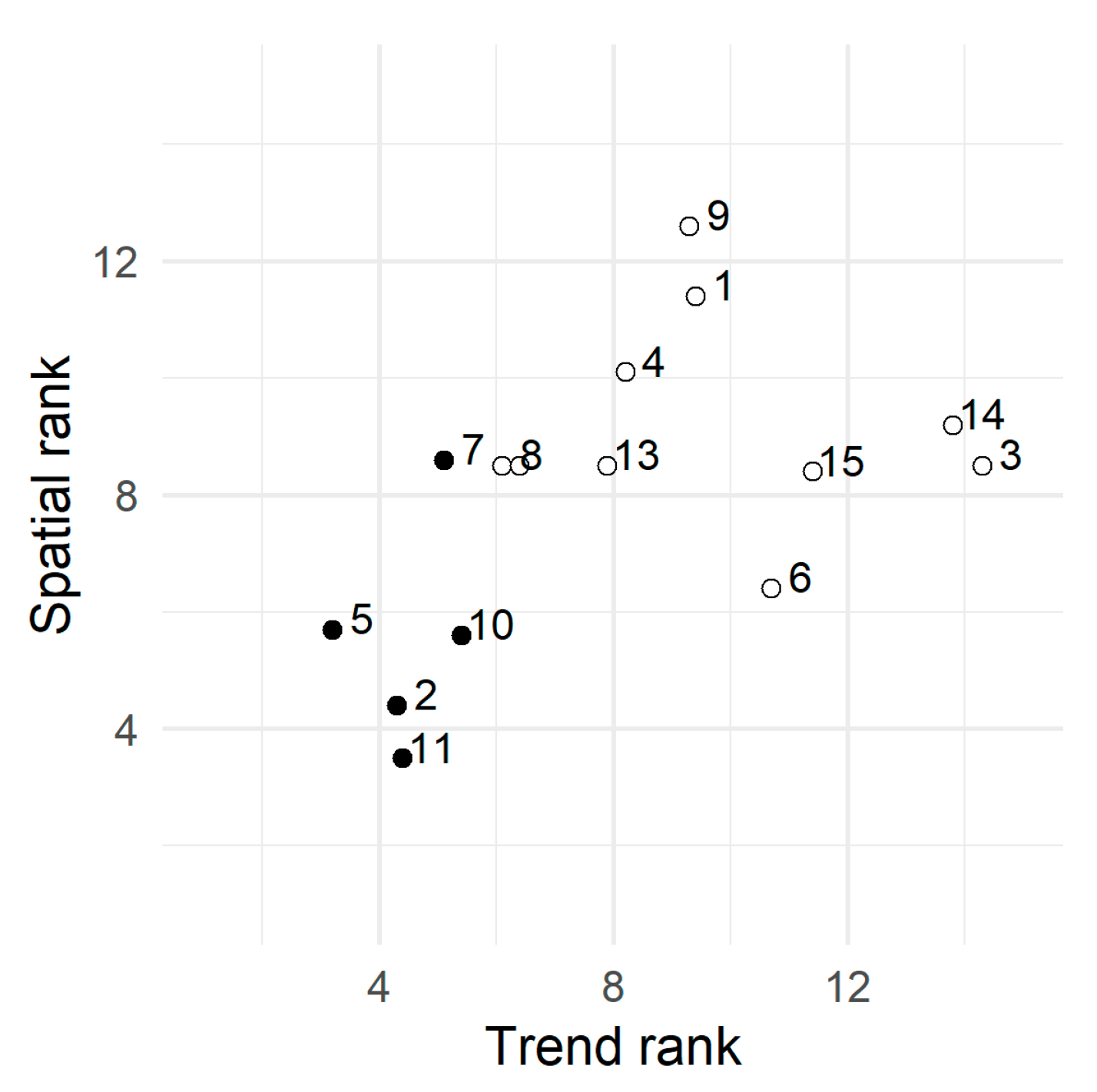
- Spatial rank: For each station, the long-term average rainfall indices were calculated. KGE, APB and RMSE were obtained for each climate model.
- Trend rank: For each station, we calculated the annual indices from REGNIE and the climate models and determined KGE, APB and RMSE from the linear trend. For each climate model, we averaged KGE, APB, and RMSE for the ranking.
2.4. Impact of Climate Change on R Factors, Uncertainties, Consequences for the Extent of Erosion-Risk Areas
3. Results
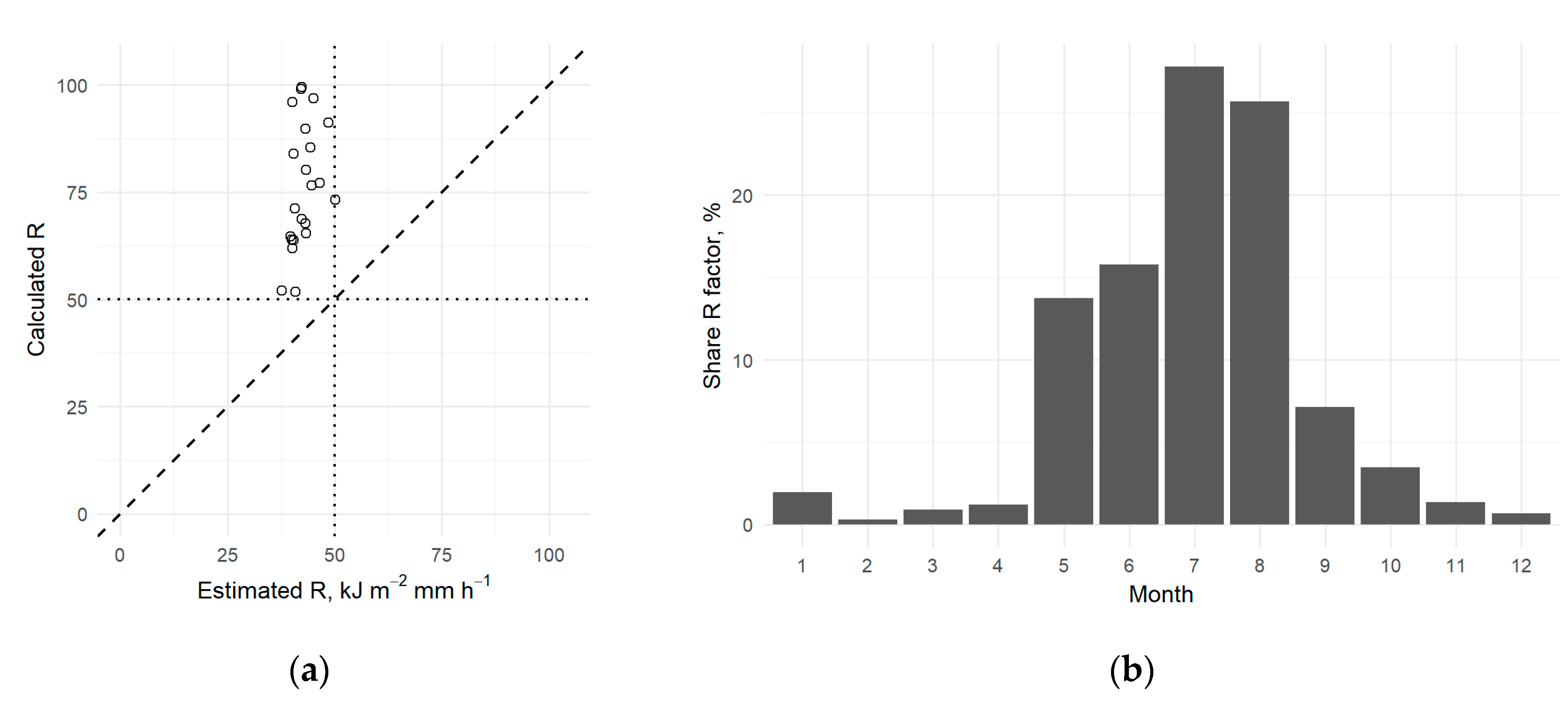
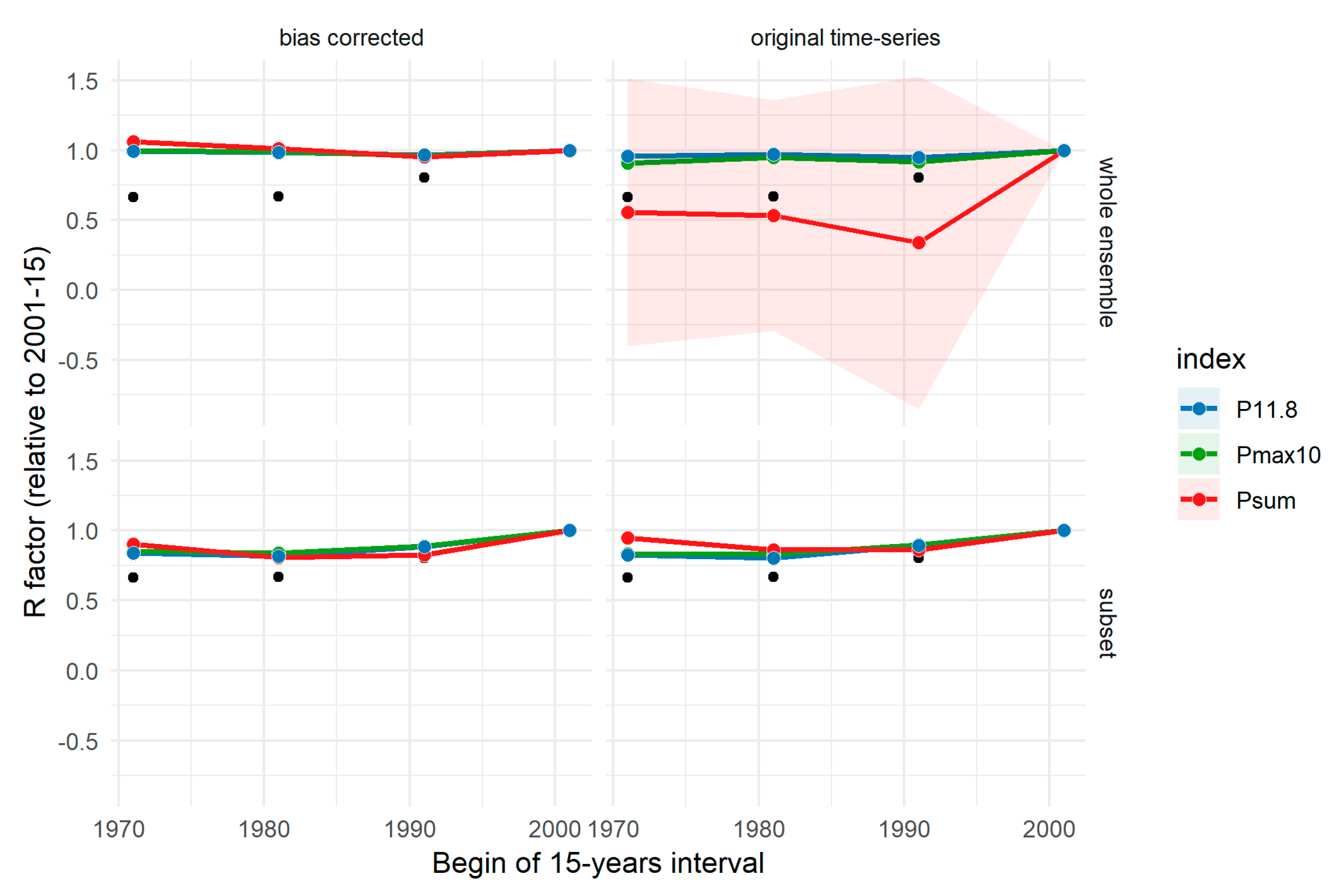
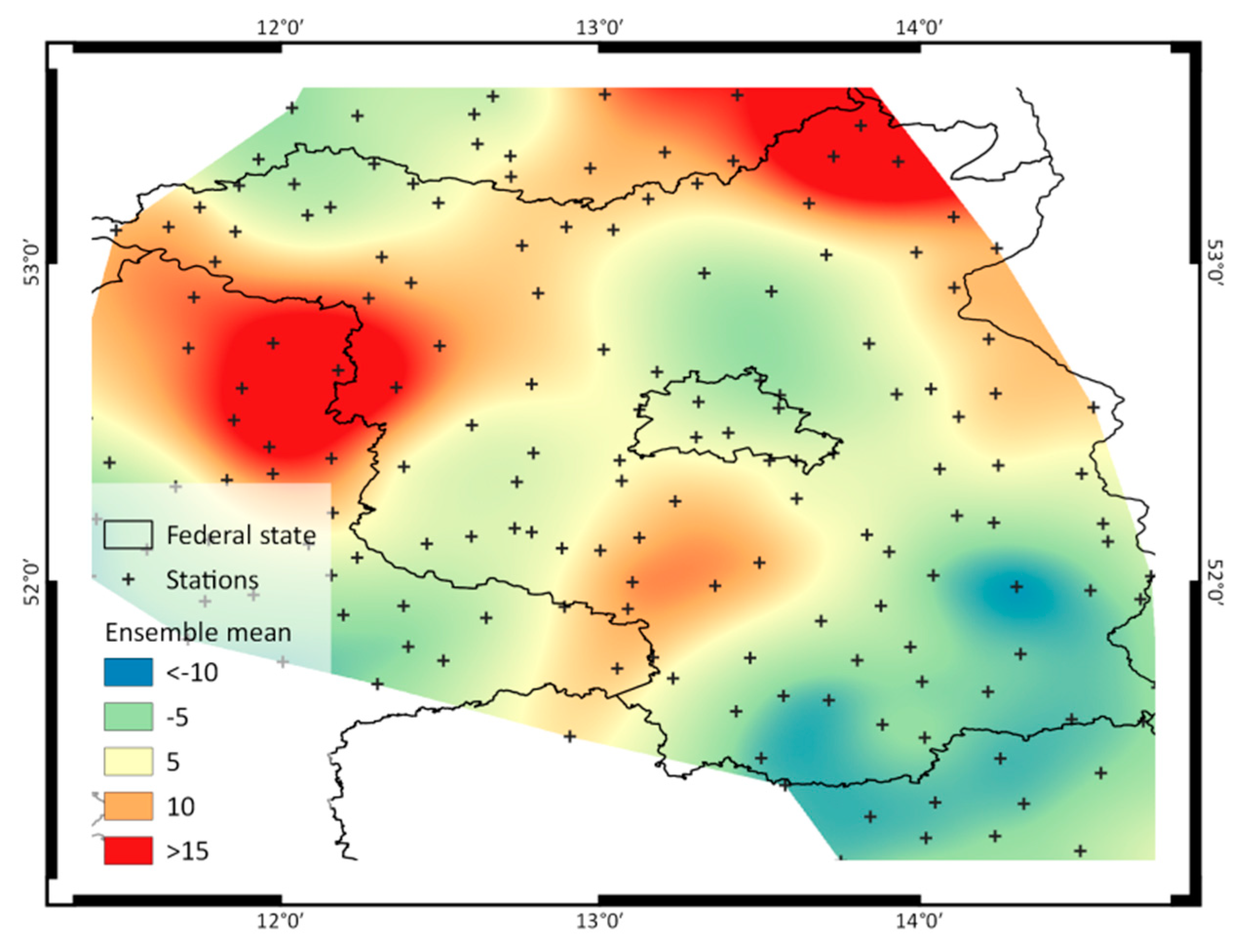
3.1. Rainfall Indices and the Spatial Variability of Current R Factors
3.2. Ranking of Climate Models
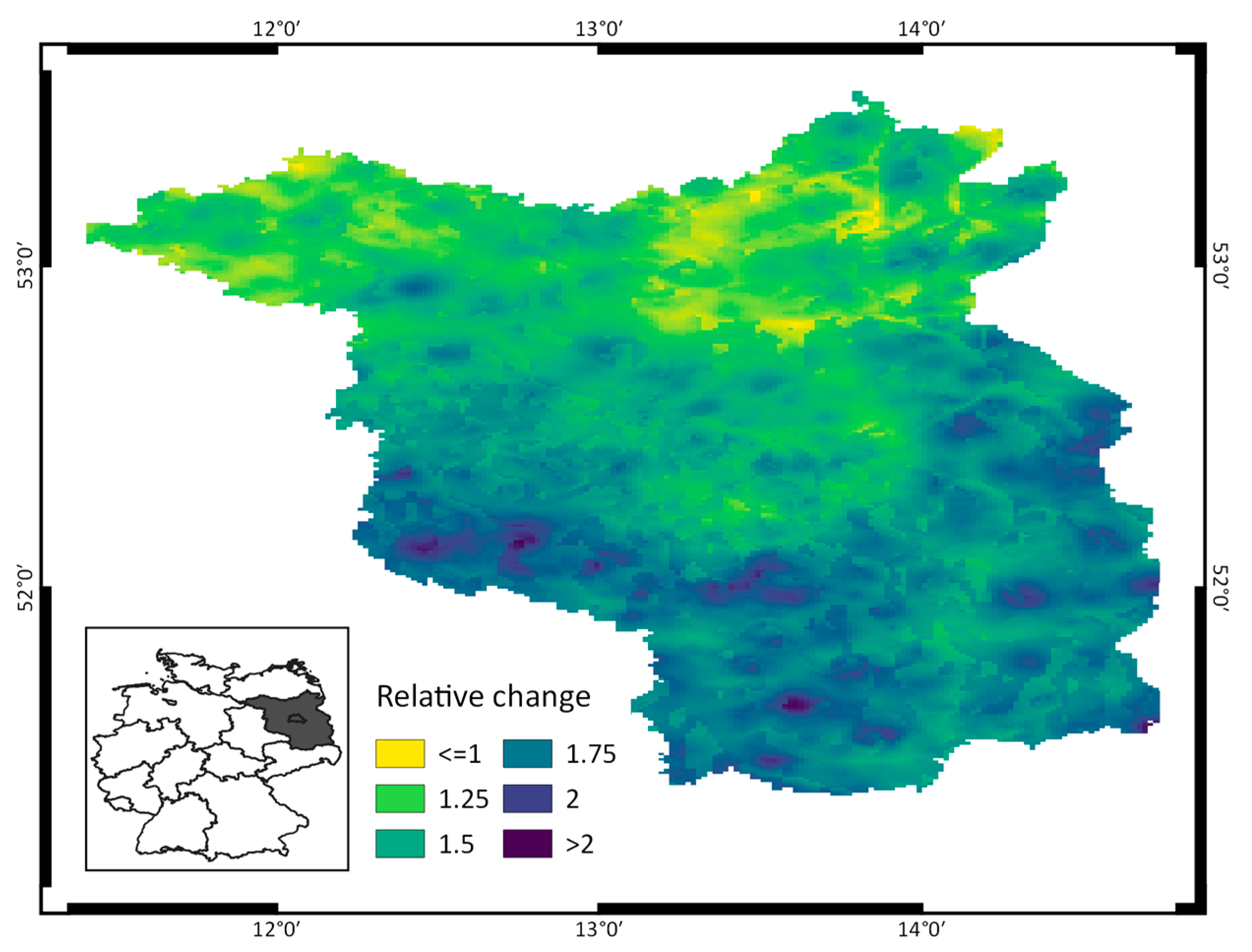
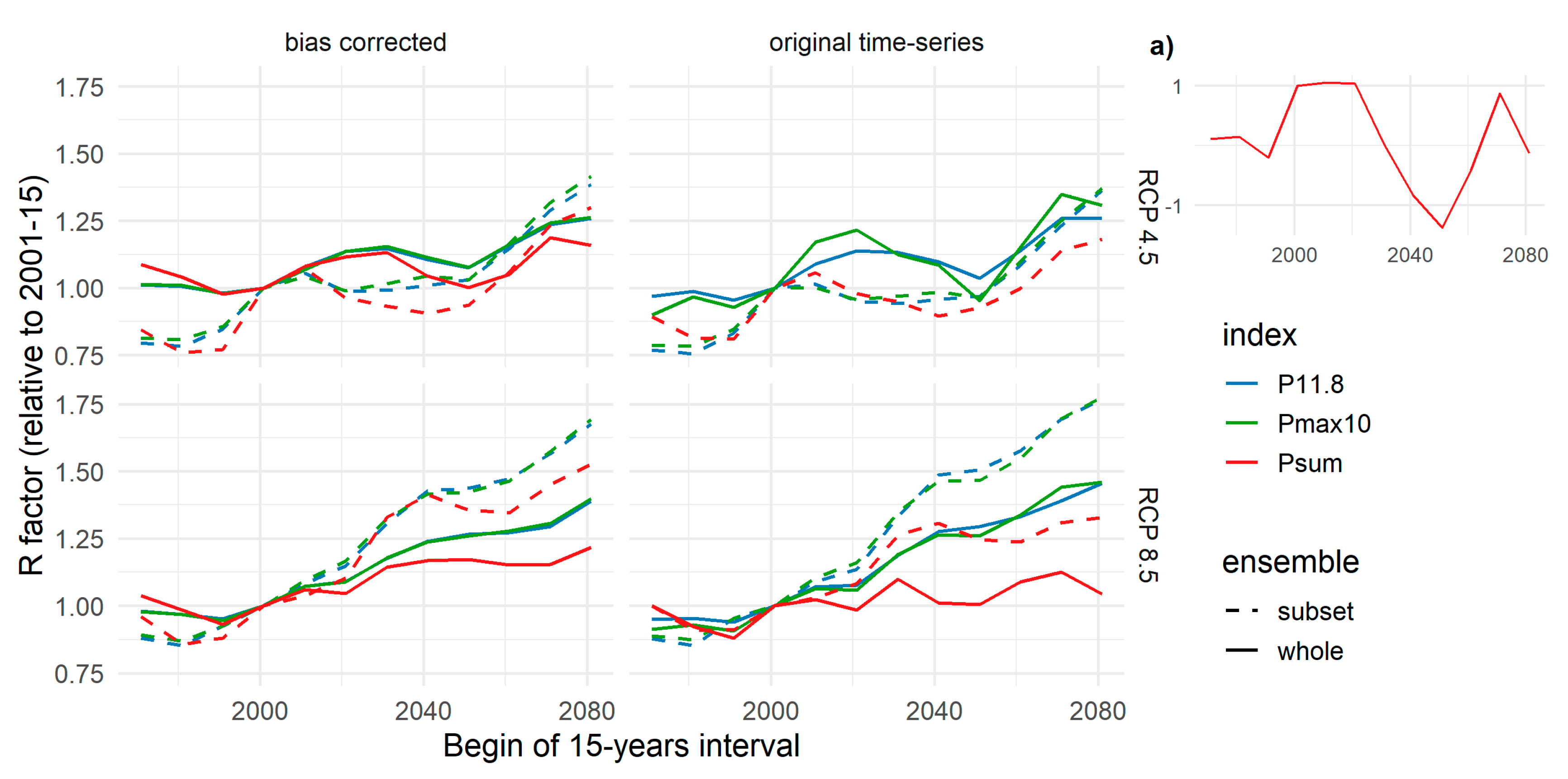
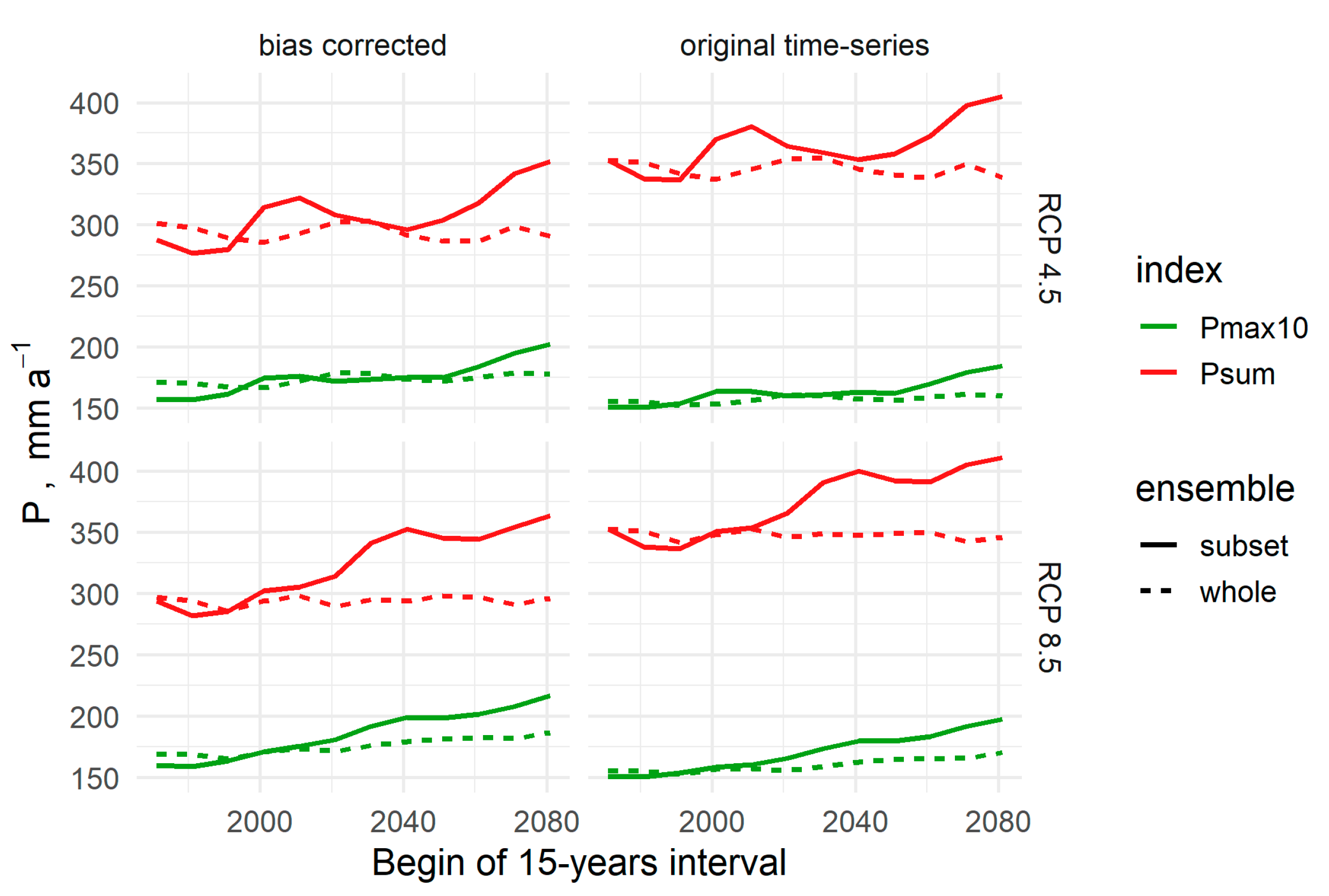
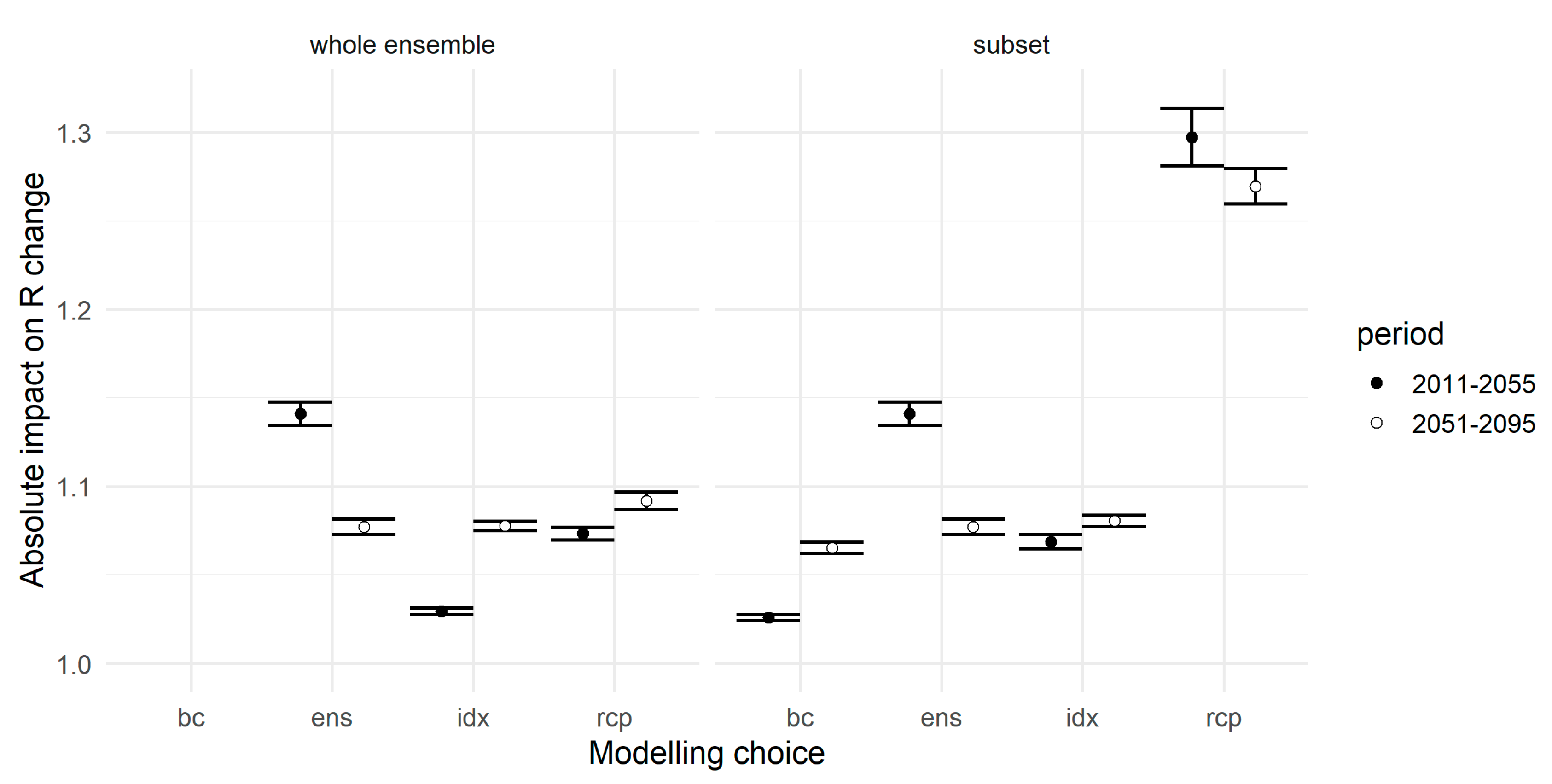
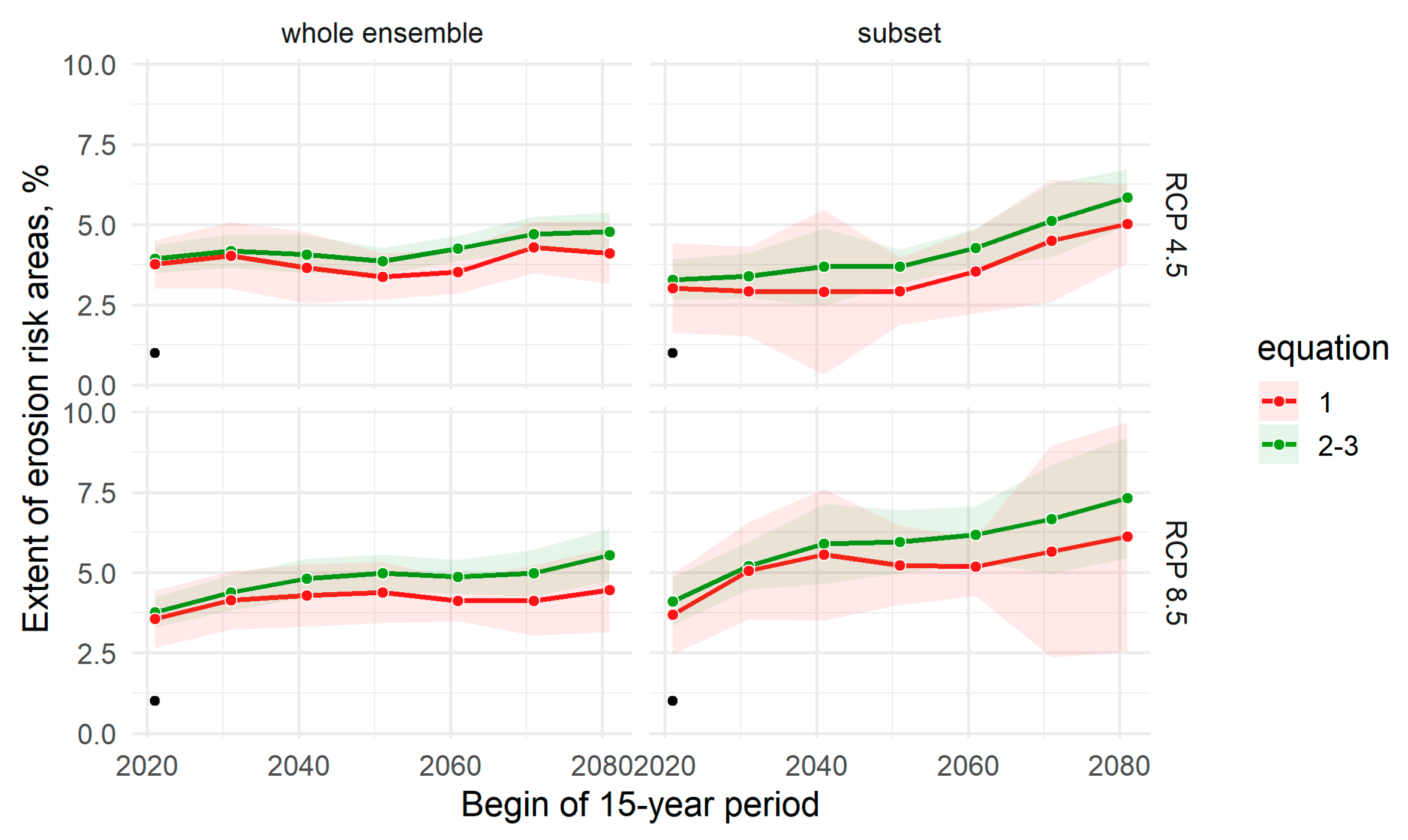
3.3. Climate Scenarios and Soil Erosion Risk
4. Discussion
4.1. Indices to Estimate Current R Factors
4.2. Climate Change Impacts on R Factors and the Soil Erosion Risk
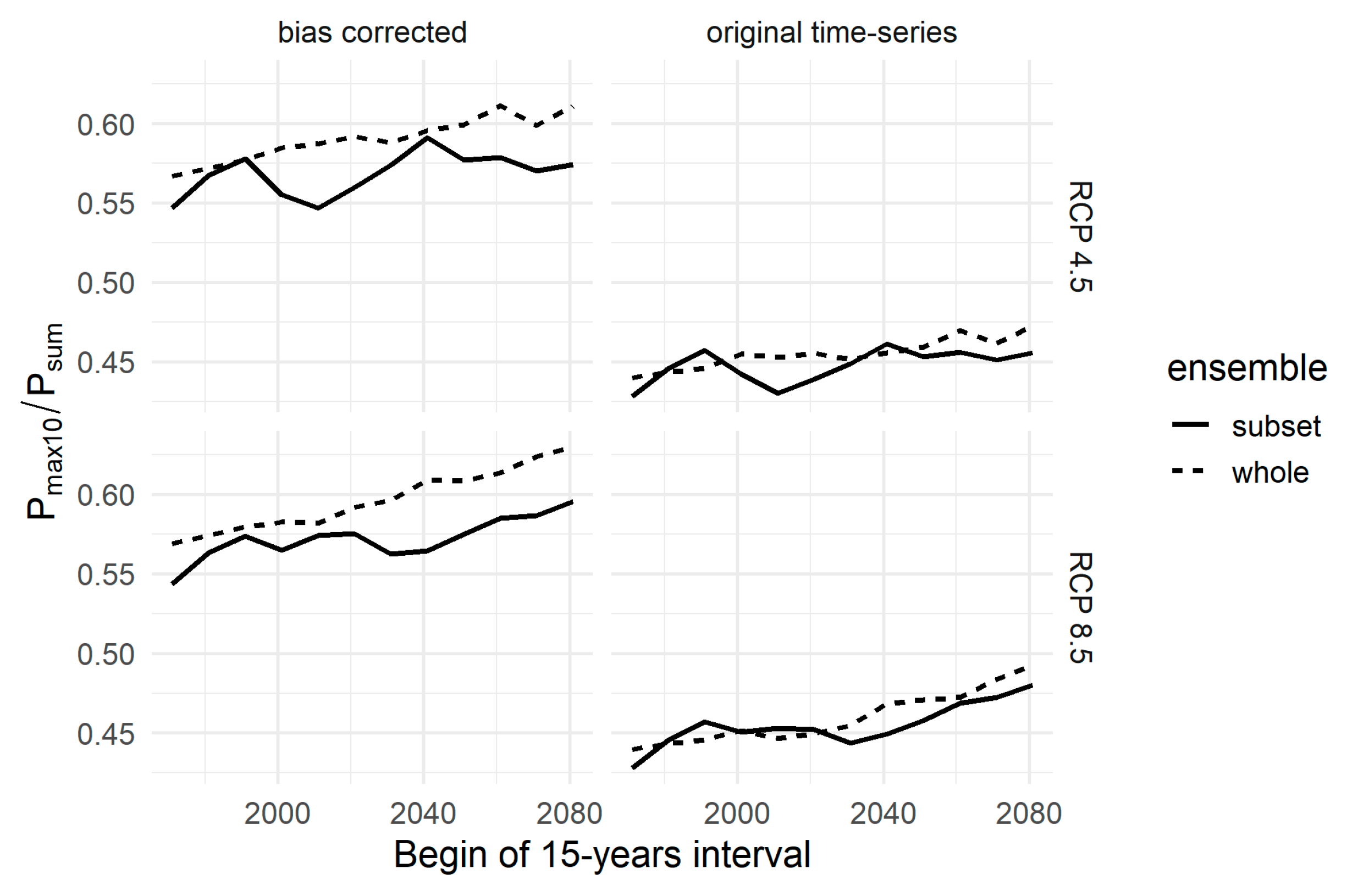
4.3. Impact of Index Choice on Future R Factors and other Sources of Uncertainty
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| Station ID | Date | Value (mm d−1) | Update |
|---|---|---|---|
| 880 | 1999-08-03 | 134.7 | 0 |
| 880 | 2014-08-04 | 16.9 | 101.9 1 |
| 430 | 2003-01-08 | 76.1 | 0 |
| 430 | 2006-08-25 | 130 | - |
| 6170 | 2009-06-30 | 43.6 | - 2 |
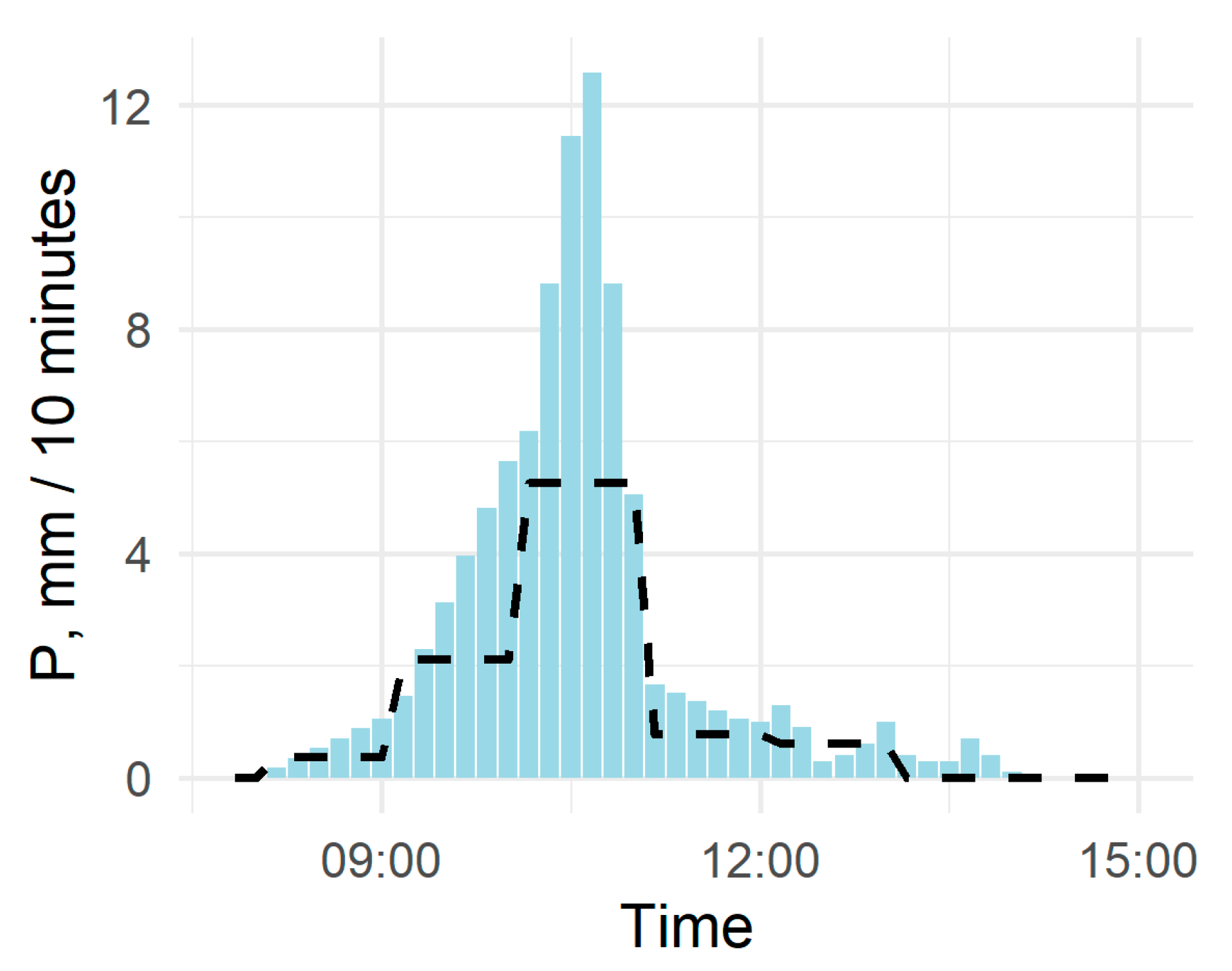
Appendix C


Appendix D
| ID | Trend (KGE) | Trend (APB) | Trend (RMSE) | Trend (Mean) | Spatial (KGE) | Spatial (APB) | Spatial (RMSE) | Spatial (Mean) | Mean | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 7 | 10.6 | 10.6 | 9.4 | 10.8 | 11.8 | 11.7 | 11.4 | 10.4 | |
| 2 1 | 4.1 | 4.5 | 4.4 | 4.3 | 5.1 | 4.1 | 4.1 | 4.4 | 4.35 | |
| 3 | 14.3 | 14 | 14.4 | 14.3 | 8.1 | 8.8 | 8.6 | 8.5 | 11.4 | |
| 4 | 7.1 | 9.1 | 8.5 | 8.2 | 8.1 | 11.1 | 11.3 | 10.1 | 9.15 | |
| 5 1 | 5.7 | 1.8 | 2.1 | 3.2 | 6.2 | 5.8 | 5.3 | 5.7 | 4.45 | |
| 6 | 11.2 | 10.3 | 10.7 | 10.7 | 7.2 | 5.8 | 6.3 | 6.4 | 8.55 | |
| 7 1 | 4.2 | 5.5 | 5.6 | 5.1 | 9.9 | 8 | 7.8 | 8.6 | 6.85 | |
| 8 | 5.4 | 6.6 | 6.3 | 6.1 | 8.1 | 8.8 | 8.8 | 8.5 | 7.3 | |
| 9 | 7.7 | 10.4 | 9.8 | 9.3 | 12.4 | 12.7 | 12.7 | 12.6 | 10.95 | |
| 10 1 | 8 | 4.2 | 4.2 | 5.4 | 6.2 | 5.3 | 5.4 | 5.6 | 5.5 | |
| 11 1 | 5.9 | 3.7 | 3.7 | 4.4 | 3.8 | 3.3 | 3.3 | 3.5 | 3.95 | |
| 12 | 6.4 | 6.5 | 6.3 | 6.4 | 9.2 | 8.3 | 8 | 8.5 | 7.45 | |
| 13 | 7.3 | 8.2 | 8.3 | 7.9 | 8.1 | 8.3 | 9.3 | 8.5 | 8.2 | |
| 14 | 14.2 | 13.4 | 13.9 | 13.8 | 8.1 | 9.8 | 9.8 | 9.2 | 11.5 | |
| 15 | 11.7 | 11.3 | 11.3 | 11.4 | 8.8 | 8.3 | 8 | 8.4 | 9.9 | |
| Bias Correction | Variable | Trend (KGE) | Trend (APB) | Trend (RMSE) | Spatial (KGE) | Spatial (APB) | Spatial (RMSE) |
|---|---|---|---|---|---|---|---|
| Pmax10 | −1.3 | 10.0 | 17.7 | 0.9 | 8.1 | 13.0 | |
| Yes | P11.8 | −0.8 | 18.5 | 24.7 | 0.8 | 12.8 | 16.0 |
| Psum | −0.5 | 6.9 | 23.1 | 1.0 | 0.0 | 0.1 | |
| Pmax10 | −1.2 | 15.8 | 26.1 | 0.4 | 14.5 | 25.1 | |
| No | P11.8 | −0.9 | 34.3 | 42.9 | 0.4 | 30.9 | 41.3 |
| Psum | −0.6 | 29.0 | 87.5 | 0.4 | 27.7 | 86.0 |
References
- FAO; ITPS. Status of the World’s Soil Resources; Food and Agriculture Organization of the United Nations and Intergovernmental Technical Panel on Soils: Rome, Italy, 2015; p. 607. [Google Scholar]
- Pimentel, D. Soil Erosion: A Food and Environmental Threat. Environ. Dev. Sustain. 2006, 8, 119–137. [Google Scholar] [CrossRef]
- Panagos, P.; Imeson, A.; Meusburger, K.; Borrelli, P.; Poesen, J.; Alewell, C. Soil Conservation in Europe: Wish or Reality? LDD 2016, 27, 1547–1551. [Google Scholar] [CrossRef]
- Verheijen, F.G.A.; Jones, R.J.A.; Rickson, R.J.; Smith, C.J. Tolerable versus actual soil erosion rates in Europe. Earth-Sci. Rev. 2009, 94, 23–38. [Google Scholar] [CrossRef]
- Panagos, P.; Standardi, G.; Borrelli, P.; Lugato, E.; Montanarella, L.; Bosello, F. Cost of agricultural productivity loss due to soil erosion in the European Union: From direct cost evaluation approaches to the use of macroeconomic models. LDD 2018, 29, 471–484. [Google Scholar] [CrossRef]
- Rickson, R.J. Can control of soil erosion mitigate water pollution by sediments? Sci. Total Environ. 2014, 468–469, 1187–1197. [Google Scholar] [CrossRef]
- Zessner, M.; Zoboli, O.; Hepp, G.; Kuderna, M.; Weinberger, C.; Gabriel, O. Shedding Light on Increasing Trends of Phosphorus Concentration in Upper Austrian Rivers. Water 2016, 8, 404. [Google Scholar] [CrossRef]
- Einsele, G.; Hinderer, M. Terrestrial sediment yield and the lifetimes of reservoirs, lakes, and larger basins. Geol. Rundsch. 1997, 86, 288–310. [Google Scholar] [CrossRef]
- Vanmaercke, M.; Poesen, J.; Govers, G.; Verstraeten, G. Quantifying human impacts on catchment sediment yield: A continental approach. Glob. Planet. Chang. 2015, 130, 22–36. [Google Scholar] [CrossRef]
- Borrelli, P.; Robinson, D.A.; Fleischer, L.R.; Lugato, E.; Ballabio, C.; Alewell, C.; Meusburger, K.; Modugno, S.; Schütt, B.; Ferro, V.; et al. An assessment of the global impact of 21st century land use change on soil erosion. Nat. Commun. 2017, 8, 2013. [Google Scholar] [CrossRef]
- Deutsches Institut für Normung. Bodenbeschaffenheit—Ermittlung der Erosionsgefährdung von Böden durch Wasser mit Hilfe der ABAG; Norm DIN 19708:2005-02; Beuth: Berlin, Germany, 2005. [Google Scholar]
- Schwertmann, U.; Vogl, W.; Kainz, M. Bodenerosion durch Wasser: Vorhersage des Abtrags und Bewertung von Gegenmahahmen; Ulmer: Stuttgart, Germany, 1987. [Google Scholar]
- Diodato, N.; Borrelli, P.; Fiener, P.; Bellocchi, G.; Romano, N. Discovering historical rainfall erosivity with a parsimonious approach: A case study in Western Germany. J. Hydrol. 2017, 544, 1–9. [Google Scholar] [CrossRef]
- Meusburger, K.; Steel, A.; Panagos, P.; Montanarella, L.; Alewell, C. Spatial and temporal variability of rainfall erosivity factor for Switzerland. Hydrol. Earth Syst. Sci. 2012, 16, 167–177. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Borrelli, P.; Meusburger, K.; Klik, A.; Rousseva, S.; Tadić, M.P.; Michaelides, S.; Hrabalíková, M.; Olsen, P.; et al. Rainfall erosivity in Europe. Sci. Total Environ. 2015, 511, 801–814. [Google Scholar] [CrossRef]
- Deumlich, D. Beitrag zur Erarbeitung einer Isoerodentkarte Deutschlands. Arch. Acker- Pfl. Boden. 1993, 37, 17–24. [Google Scholar]
- Li, Z.; Fang, H. Impacts of climate change on water erosion: A review. Earth-Sci. Rev. 2016, 163, 94–117. [Google Scholar] [CrossRef]
- Zolina, O. Change in intense precipitation in Europe. In Changes in Flood Risk in Europe; Kundzewicz, Z.W., Ed.; IAHS Press: Wallingford, UK, 2012; pp. 97–120. [Google Scholar]
- Zolina, O.; Simmer, C.; Belyaev, K.; Gulev, S.K.; Koltermann, P. Changes in the Duration of European Wet and Dry Spells during the Last 60 Years. J. Clim. 2013, 26, 2022–2047. [Google Scholar] [CrossRef]
- Łupikasza, E.B. Seasonal patterns and consistency of extreme precipitation trends in Europe, December 1950 to February 2008. Clim. Res. 2017, 72, 217–237. [Google Scholar] [CrossRef][Green Version]
- van den Besselaar, E.J.M.; Klein Tank, A.M.G.; Buishand, T.A. Trends in European precipitation extremes over 1951–2010. Int. J. Climatol. 2013, 33, 2682–2689. [Google Scholar] [CrossRef]
- Hänsel, S.; Petzold, S.; Matschullat, J. Precipitation Trend Analysis for Central Eastern Germany 1851–2006. In Bioclimatology and Natural Hazards; Střelcová, K., Mátyás, C., Kleidon, A., Lapin, M., Matejka, F., Blaženec, M., Škvarenina, J., Holécy, J., Eds.; Springer: Dordrecht, The Netherlands, 2009; pp. 29–38. [Google Scholar]
- Łupikasza, E.B.; Hänsel, S.; Matschullat, J. Regional and seasonal variability of extreme precipitation trends in southern Poland and central-eastern Germany 1951–2006. Int. J. Climatol. 2011, 31, 2249–2271. [Google Scholar] [CrossRef]
- Murawski, A.; Zimmer, J.; Merz, B. High spatial and temporal organization of changes in precipitation over Germany for 1951–2006. Int. J. Climatol. 2016, 36, 2582–2597. [Google Scholar] [CrossRef]
- Zolina, O. Multidecadal trends in the duration of wet spells and associated intensity of precipitation as revealed by a very dense observational German network. Environ. Res. Lett. 2014, 9, 025003. [Google Scholar] [CrossRef]
- Pińskwar, I.; Choryński, A.; Graczyk, D.; Kundzewicz, Z.W. Observed changes in extreme precipitation in Poland: 1991–2015 versus 1961–1990. Theor. Appl. Climatol. 2018. [Google Scholar] [CrossRef]
- Beranová, R.; Kyselý, J. Trends of precipitation characteristics in the Czech Republic over 1961–2012, their spatial patterns and links to temperature and the North Atlantic Oscillation. Int. J. Climatol. 2018, 38, e596–e606. [Google Scholar] [CrossRef]
- Fiener, P.; Neuhaus, P.; Botschek, J. Long-term trends in rainfall erosivity-analysis of high resolution precipitation time series (1937–2007) from Western Germany. Agric. For. Meteorol. 2013, 171–172, 115–123. [Google Scholar] [CrossRef]
- Verstraeten, G.; Poesen, J.; Demarée, G.; Salles, C. Long-term (105 years) variability in rain erosivity as derived from 10-min rainfall depth data for Ukkel (Brussels, Belgium): Implications for assessing soil erosion rates. J. Geophys. Res. Atmos. 2006, 111, 1–11. [Google Scholar] [CrossRef]
- Hanel, M.; Pavlásková, A.; Kyselý, J. Trends in characteristics of sub-daily heavy precipitation and rainfall erosivity in the Czech Republic. Int. J. Climatol. 2016, 36, 1833–1845. [Google Scholar] [CrossRef]
- Panagos, P.; Ballabio, C.; Meusburger, K.; Spinoni, J.; Alewell, C.; Borrelli, P. Towards estimates of future rainfall erosivity in Europe based on REDES and WorldClim datasets. J. Hydrol. 2017, 548, 251–262. [Google Scholar] [CrossRef]
- Wurbs, D.; Steininger, M. Wirkungen der Klimaänderungen auf die Böden—Untersuchungen zu Auswirkungen des Klimawandels auf die Bodenerosion durch Wasser; UBA: Dessau-Roßlau, Germany, March 2011; p. 225. [Google Scholar]
- Hübener, H.; Bülow, K.; Fooken, C.; Früh, B.; Hoffmann, P.; Höpp, S.; Keuler, K.; Menz, C.; Mohr, V.; Radtke, K.; et al. ReKliEs-De Ergebnisbericht; World Data Center for Climate (WDCC) at DKRZ: Hamburg, Germany, December 2017; p. 56. [Google Scholar]
- Schwarzak, S.; Hänsel, S.; Matschullat, J. Projected changes in extreme precipitation characteristics for Central Eastern Germany (21st century, model-based analysis). Int. J. Climatol. 2015, 35, 2724–2734. [Google Scholar] [CrossRef]
- European Environment Agency. Ecoregions for Rivers and Lakes. Available online: https://www.eea.europa.eu/ds_resolveuid/2C5D9354-5FC8-4EB3-BD7A-299D95EBAF (accessed on 13 March 2019).
- Deutscher Wetterdienst. Available online: ftp://ftp-cdc.dwd.de (accessed on 12 May 2016).
- ECA&D. Website of the European Climate Assessment & Dataset Project. Available online: https://eca.knmi.nl/ (accessed on 22 February 2019).
- Deumlich, D.; Völker, L. Bodenabtragskarte für Brandenburg in 25m-Auflösung; Leibniz Centre for Agricultural Landscape Research: Müncheberg, Germany, 2012. [Google Scholar]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Rathjens, H.; Bieger, K.; Srinivasan, R.; Chaubey, I.; Arnold, J.G. CMhyd User Manual—Documentation for Preparing Simulated Climate Change Data for Hydrologic Impact Studies. 2016, p. 16. Available online: https://swat.tamu.edu/media/115265/bias_cor_man.pdf (accessed on 21 December 2018).
- Kiesel, J.; Gericke, A.; Rathjens, H.; Wetzig, A.; Kakouei, K.; Jähnig, S.C.; Fohrer, N. Climate change impacts on ecologically relevant hydrological indicators in three catchments in three European ecoregions. Ecol. Eng. 2019, 127, 404–416. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424–425, 264–277. [Google Scholar] [CrossRef]
- Nychka, D.; Furrer, R.; Paige, J.; Sain, S. Fields: Tools for Spatial Data, R package version 9.6; University Corporation for Atmospheric Research: Boulder, CO, USA, 2017. [Google Scholar]
- Ministry of Rural Development, Environment and Agriculture of the Federal State of Brandenburg. Digitales Feldblockkataster des Landes Brandenburg 2019. Available online: http://geobroker.geobasis-bb.de/index.php (accessed on 22 October 2018).
- Fiener, P.; Auerswald, K. Spatial variability of rainfall on a sub-kilometre scale. Earth Surf. Process. Landf. 2009, 34, 848–859. [Google Scholar] [CrossRef]
- Fischer, F.K.; Winterrath, T.; Auerswald, K. Temporal- and spatial-scale and positional effects on rain erosivity derived from point-scale and contiguous rain data. Hydrol. Earth Syst. Sci. 2018, 22, 6505–6518. [Google Scholar] [CrossRef]
- Fischer, F.K.; Kistler, M.; Brandhuber, R.; Maier, H.; Treisch, M.; Auerswald, K. Validation of official erosion modelling based on high-resolution radar rain data by aerial photo erosion classification. Earth Surf. Process. Landf. 2018, 43, 187–194. [Google Scholar] [CrossRef]
- Auerswald, K.; Fischer, F.K.; Winterrath, T.; Brandhuber, R. Rain erosivity map for Germany derived from contiguous radar rain data. Hydrol. Earth Syst. Sci. 2019, 32, 1819–1832. [Google Scholar] [CrossRef]
- Ehret, U.; Zehe, E.; Wulfmeyer, V.; Warrach-Sagi, K.; Liebert, J. HESS Opinions “Should we apply bias correction to global and regional climate model data?”. Hydrol. Earth Syst. Sci. 2012, 16, 3391–3404. [Google Scholar] [CrossRef]
- Vogel, E.; Deumlich, D.; Kaupenjohann, M. Bioenergy maize and soil erosion—Risk assessment and erosion control concepts. Geoderma 2016, 261, 80–92. [Google Scholar] [CrossRef]
- Köcher, A. (DWD, Offenbach, Hessen, Germany). Personal communication, 2016.
- Heil, U. (DWD, Offenbach, Hessen, Germany). Personal communication, 2016.
- Karlsruhe Institute of Technology. Wettergefahren-Frühwarnung. Available online: http://www.wettergefahren-fruehwarnung.de/Ereignis/20060830_e.html (accessed on 20 March 2019).
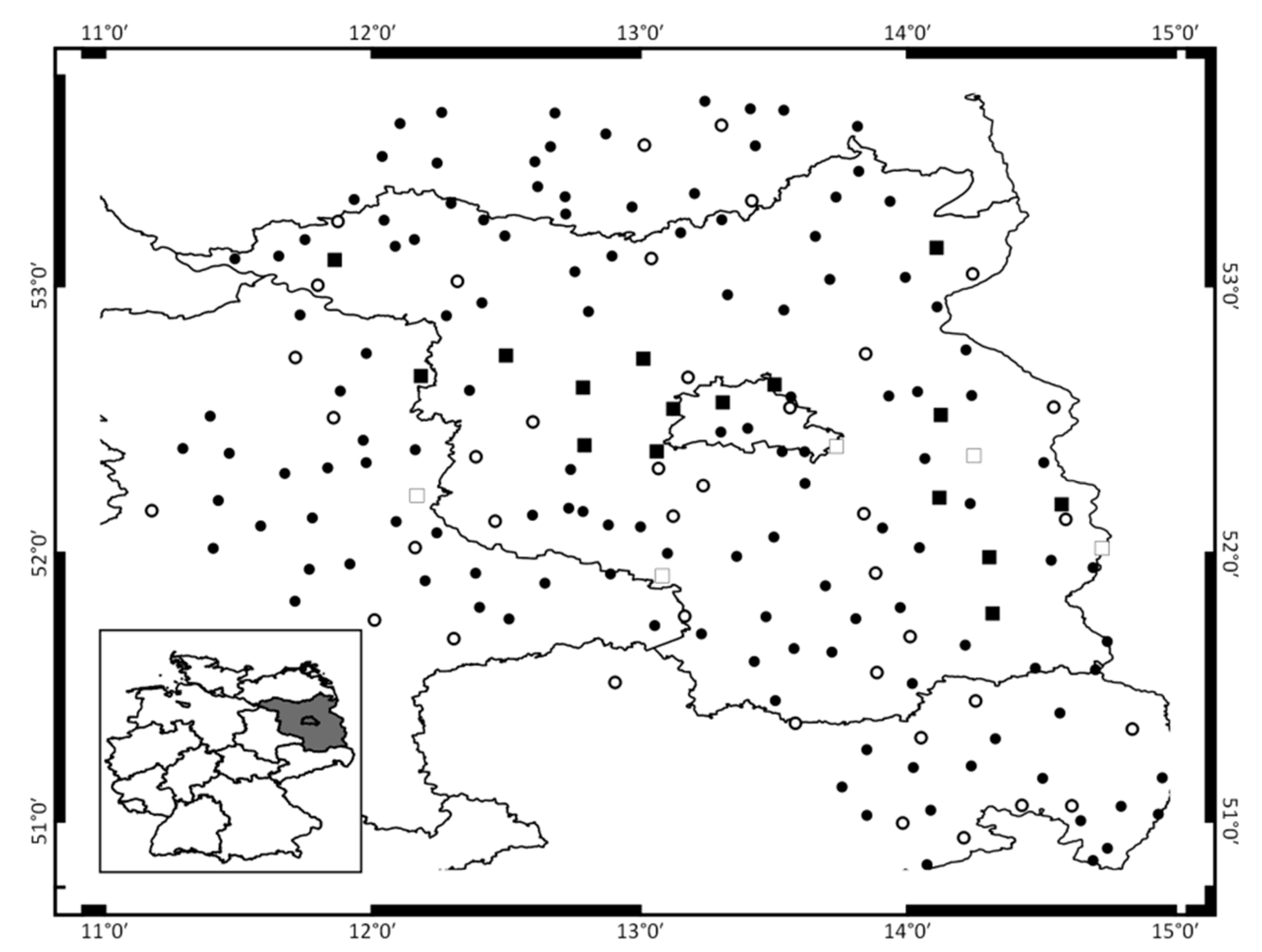
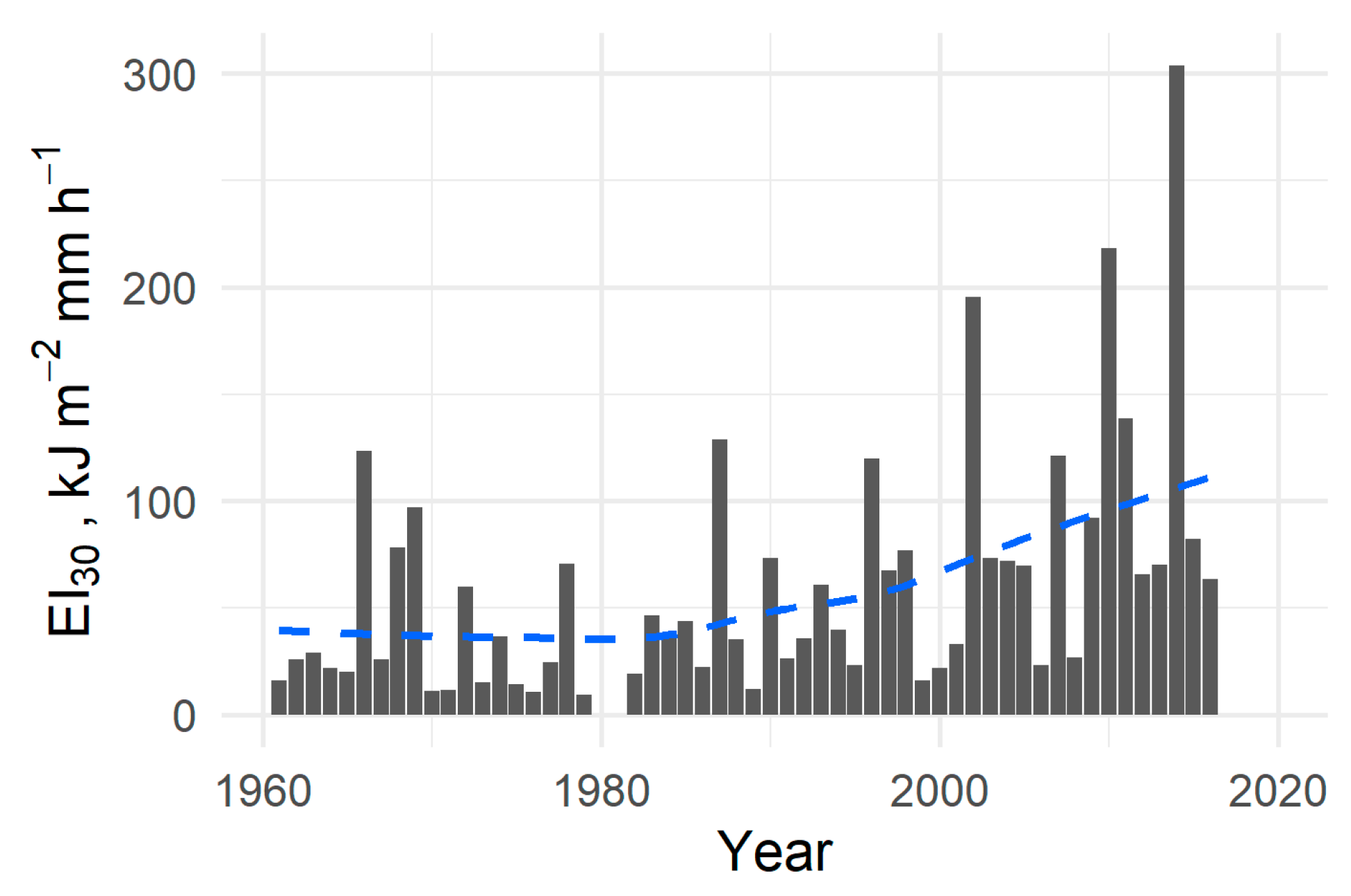
| ID | Name | Longitude | Latitude | Start Year | Calculated R kJ m−2 mm h−1 | Data Gaps |
|---|---|---|---|---|---|---|
| 400 | Berlin Buch | 13.500 | 52.633 | 2004 | 77.2 | |
| 410 | Berlin Kaniswall | 13.733 | 52.400 | 2004 | 68.7 | |
| 430 | Berlin Tegel 3 | 13.317 | 52.567 | 2000 1 | 61.9 2 | |
| 714 | Neu Madlitz | 14.250 | 52.367 | 2005 | 96.9 | |
| 880 | Cottbus 3 | 14.317 | 51.783 | 2000 1 | 83.9 | |
| 1052 | Drewitz | 12.167 | 52.217 | 2003 | 85.4 | Jan–Mar 2003 |
| 1801 | Groß Kreutz | 12.800 | 52.400 | 2003 | 63.8 | |
| 2625 | Kleßen | 12.500 | 52.733 | 2003 | 80.2 | Jan–Mar 2003 3 Nov–4 Apr |
| 2733 | Kremmen | 13.017 | 52.733 | 2005 | 89.8 | |
| 2856 | Langenlipsdorf | 13.083 | 51.917 | 2004 | 71.2 | |
| 2997 | Lieberose | 14.300 | 51.983 | 2003 | 99.4 | Jan–Apr 2003 |
| 3015 | Lindenberg 3 | 14.117 | 52.217 | 2000 | 63.9 | |
| 3376 | Müncheberg | 14.117 | 52.517 | 2004 | 99.1 | Dec 2005 |
| 3881 | Passow | 14.100 | 53.150 | 2005 | 52.0 | |
| 3906 | Perleberg | 11.867 | 53.100 | 2004 | 67.7 | |
| 3967 | Pohlitz | 14.567 | 52.183 | 2005 | 91.2 | Jan–Mar 2005 |
| 3987 | Potsdam 3 | 13.067 | 52.383 | 2000 | 76.6 | Nov–Dec 2000 |
| 4555 | Schollene | 12.183 | 52.667 | 2007 | 73.2 | |
| 4637 | Staaken | 13.117 | 52.533 | 2009 | 51.8 | |
| 5614 | Winterfeld-Sallenthin | 11.250 | 52.750 | 2004 | 65.4 | Jan–Mar 2004 |
| 5825 | Berge | 12.783 | 52.617 | 2003 | 64.7 | |
| 6170 | Coschen | 14.733 | 52.017 | 2003 | 95.9 | Jan–Mar 2003 |
| Purpose | Data Source | Resolution | Data Set | Period | Chapter |
|---|---|---|---|---|---|
| R calculation | Station data | 10 min | 22 | ≥2000–2015 | 2.2 |
| Regression analyses | REGNIE | Daily | 22 | ≥2000–2015 | 2.2 |
| Bias correction, ranking | REGNIE, climate models | Daily | 188 | 1971–2015 | 2.3 |
| R scenarios | Climate models | Daily | 188 | 1971–2100 | 2.3 |
| Erosion risk areas | REGNIE | Daily | (grid) | 2001–2015 | 2.2 |
| ” | Climate models | Daily | 188 | 2021–2100 | 2.4 |
| ID | Institute | GCM | RCM | Ensemble | Version |
|---|---|---|---|---|---|
| 1 | CLMcom | CNRM-CERFACS-CNRM-CM5 | CCLM4-8-17 | r1i1p1 | v1 |
| 2 | SMHI | CNRM-CERFACS-CNRM-CM5 | RCA4 | r1i1p1 | v1 |
| 3 | CLMcom | ICHEC-EC-EARTH | CCLM4-8-17 | r12i1p1 | v1 |
| 4 | DMI | ICHEC-EC-EARTH | HIRHAM5 | r3i1p1 | v1 |
| 5 | KNMI | ICHEC-EC-EARTH | RACMO22E | r1i1p1 | v1 |
| 6 | SMHI | ICHEC-EC-EARTH | RCA4 | r12i1p1 | v1 |
| 7 | IPSL-INERIS | IPSL-IPSL-CM5A-MR | WRF331F | r1i1p1 | v1 |
| 8 | SMHI | IPSL-IPSL-CM5A-MR | RCA4 | r1i1p1 | v1 |
| 9 | CLMcom | MOHC-HadGEM2-ES | CCLM4-8-17 | r1i1p1 | v1 |
| 10 | KNMI | MOHC-HadGEM2-ES | RACMO22E | r1i1p1 | v2 |
| 11 | SMHI | MOHC-HadGEM2-ES | RCA4 | r1i1p1 | v1 |
| 12 | CLMcom | MPI-M-MPI-ESM-LR | CCLM4-8-17 | r1i1p1 | v1 |
| 13 | MPI-CSC | MPI-M-MPI-ESM-LR | REMO2009 | r1i1p1 | v1 |
| 14 | MPI-CSC | MPI-M-MPI-ESM-LR | REMO2009 | r2i1p1 | v1 |
| 15 | SMHI | MPI-M-MPI-ESM-LR | RCA4 | r1i1p1 | v1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gericke, A.; Kiesel, J.; Deumlich, D.; Venohr, M. Recent and Future Changes in Rainfall Erosivity and Implications for the Soil Erosion Risk in Brandenburg, NE Germany. Water 2019, 11, 904. https://doi.org/10.3390/w11050904
Gericke A, Kiesel J, Deumlich D, Venohr M. Recent and Future Changes in Rainfall Erosivity and Implications for the Soil Erosion Risk in Brandenburg, NE Germany. Water. 2019; 11(5):904. https://doi.org/10.3390/w11050904
Chicago/Turabian StyleGericke, Andreas, Jens Kiesel, Detlef Deumlich, and Markus Venohr. 2019. "Recent and Future Changes in Rainfall Erosivity and Implications for the Soil Erosion Risk in Brandenburg, NE Germany" Water 11, no. 5: 904. https://doi.org/10.3390/w11050904
APA StyleGericke, A., Kiesel, J., Deumlich, D., & Venohr, M. (2019). Recent and Future Changes in Rainfall Erosivity and Implications for the Soil Erosion Risk in Brandenburg, NE Germany. Water, 11(5), 904. https://doi.org/10.3390/w11050904





