Global Surface Soil Moisture Dynamics in 1979–2016 Observed from ESA CCI SM Dataset
Abstract
:1. Introduction
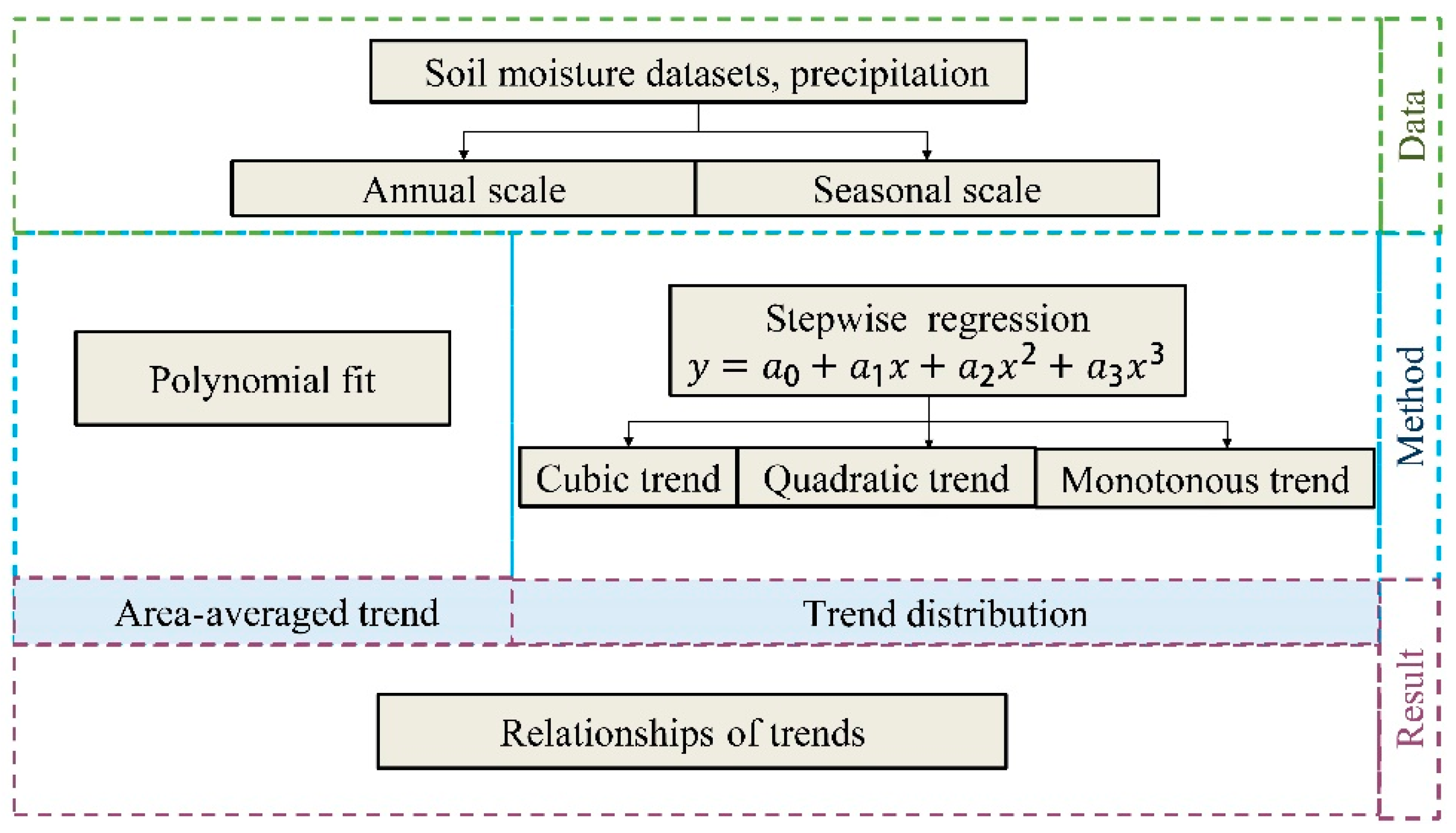
2. Data and Methods
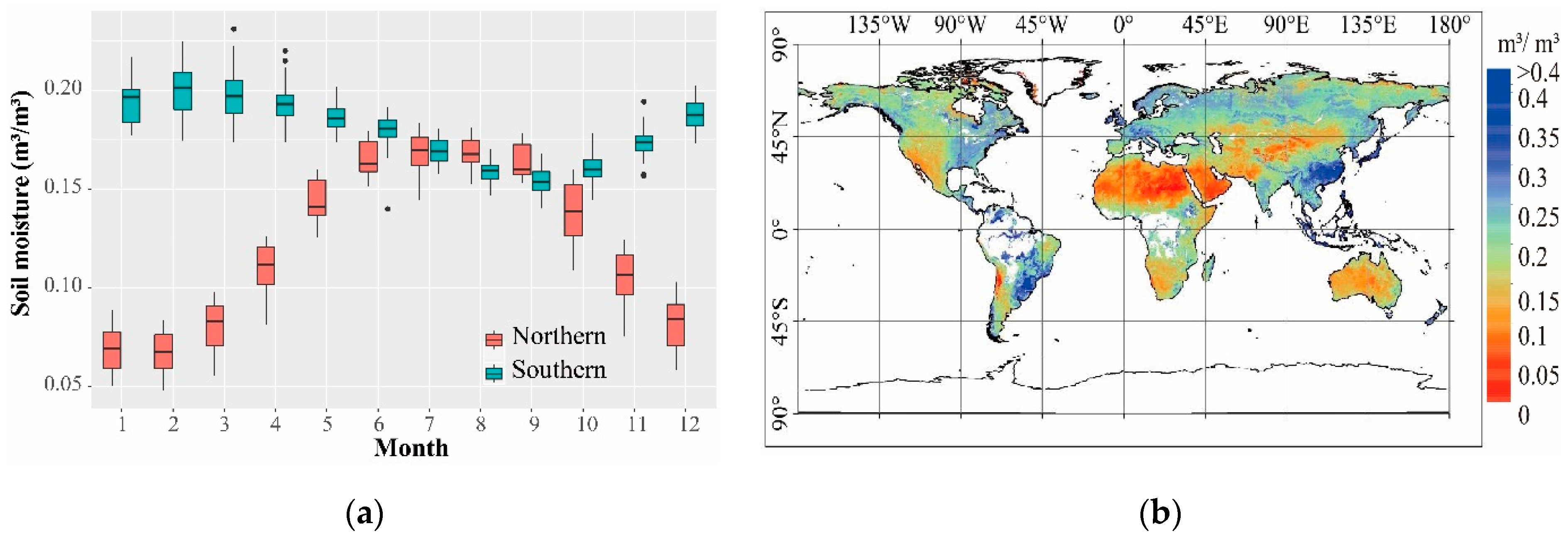
2.1. Data
2.2. Methodology
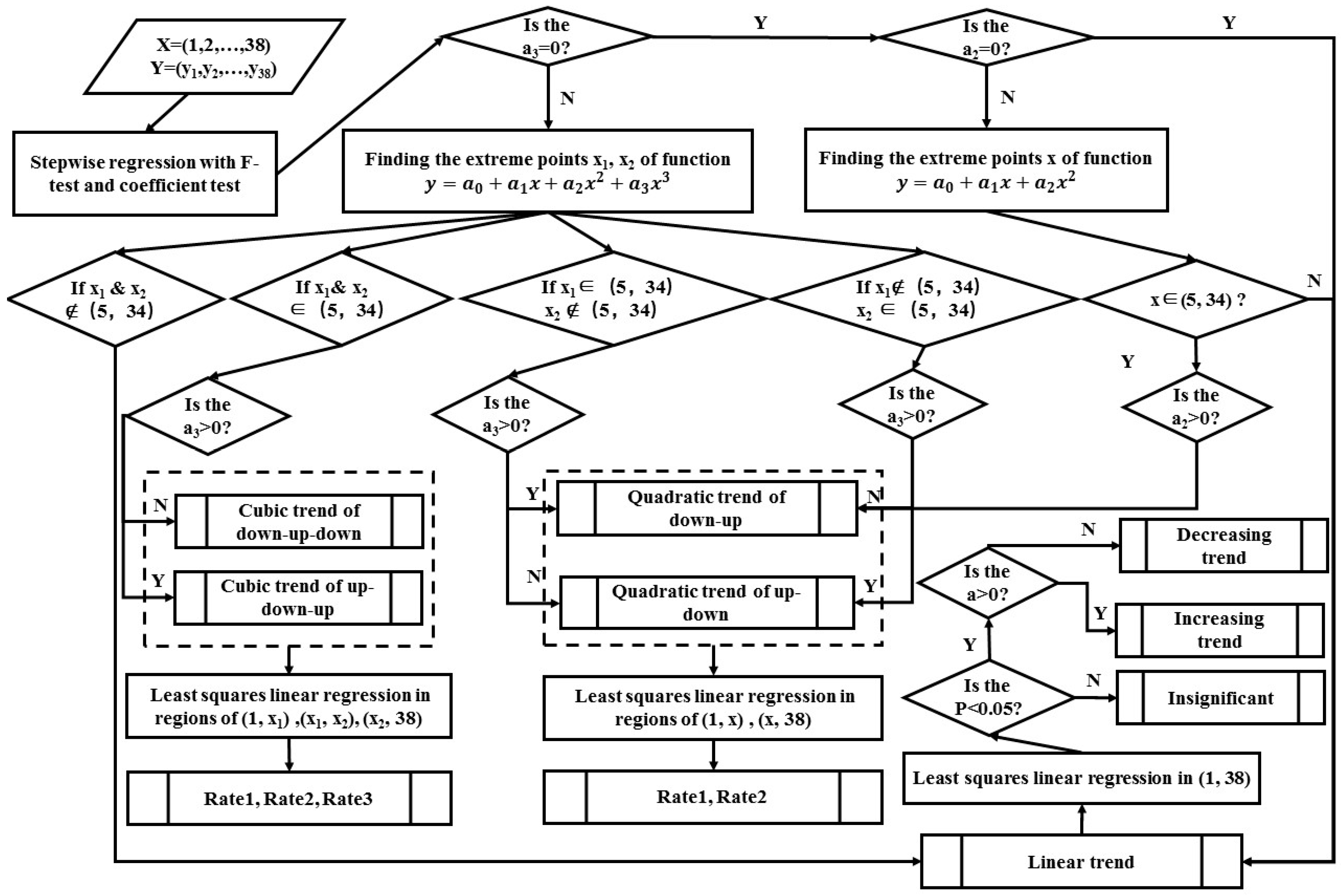
2.2.1. Trend Analysis
2.2.2. Trend Recognition
3. Results
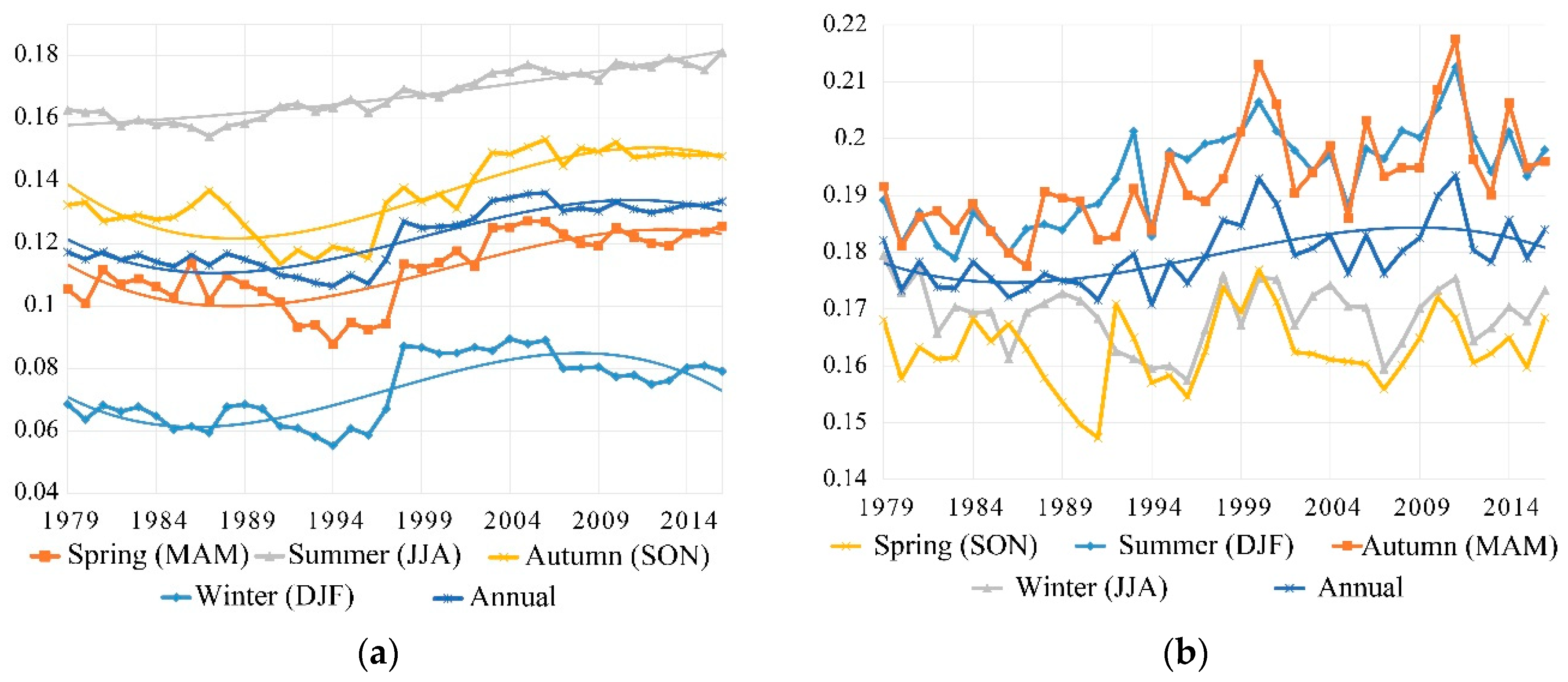
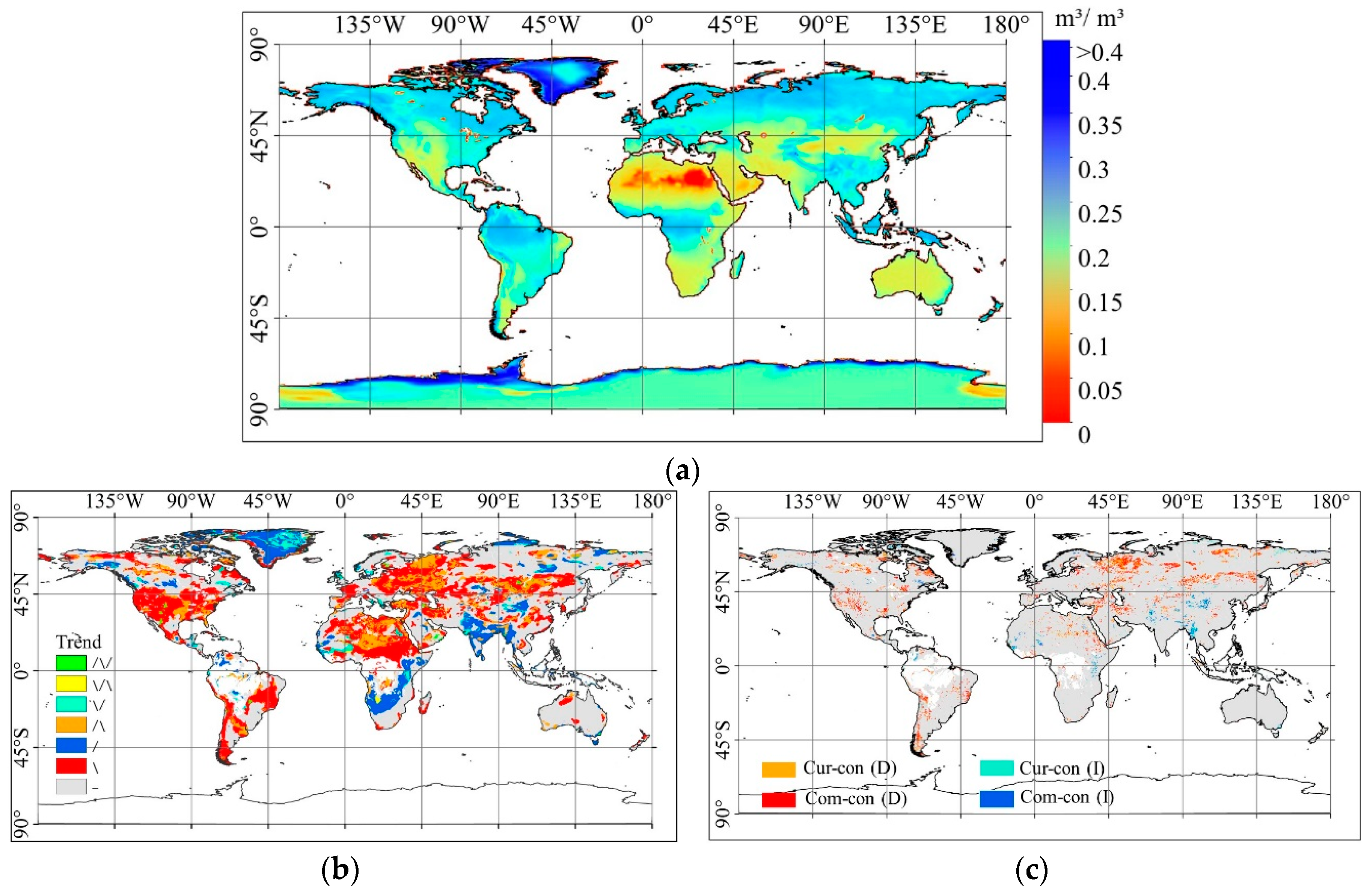
3.1. Area-Averaged Soil Moisture (SM)
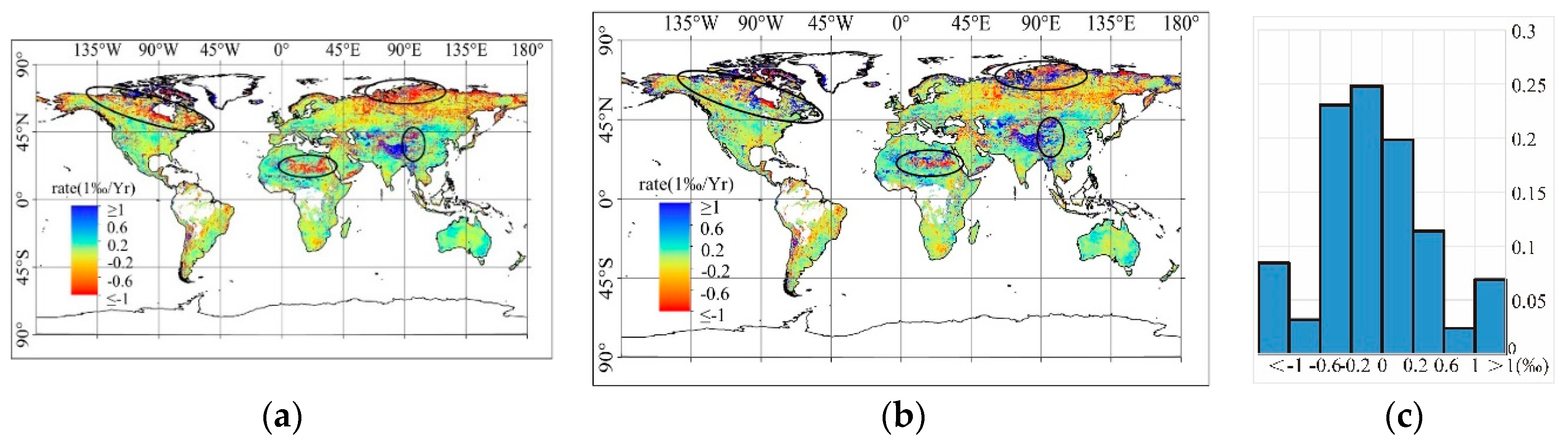
3.2. Annual Trend Distribution
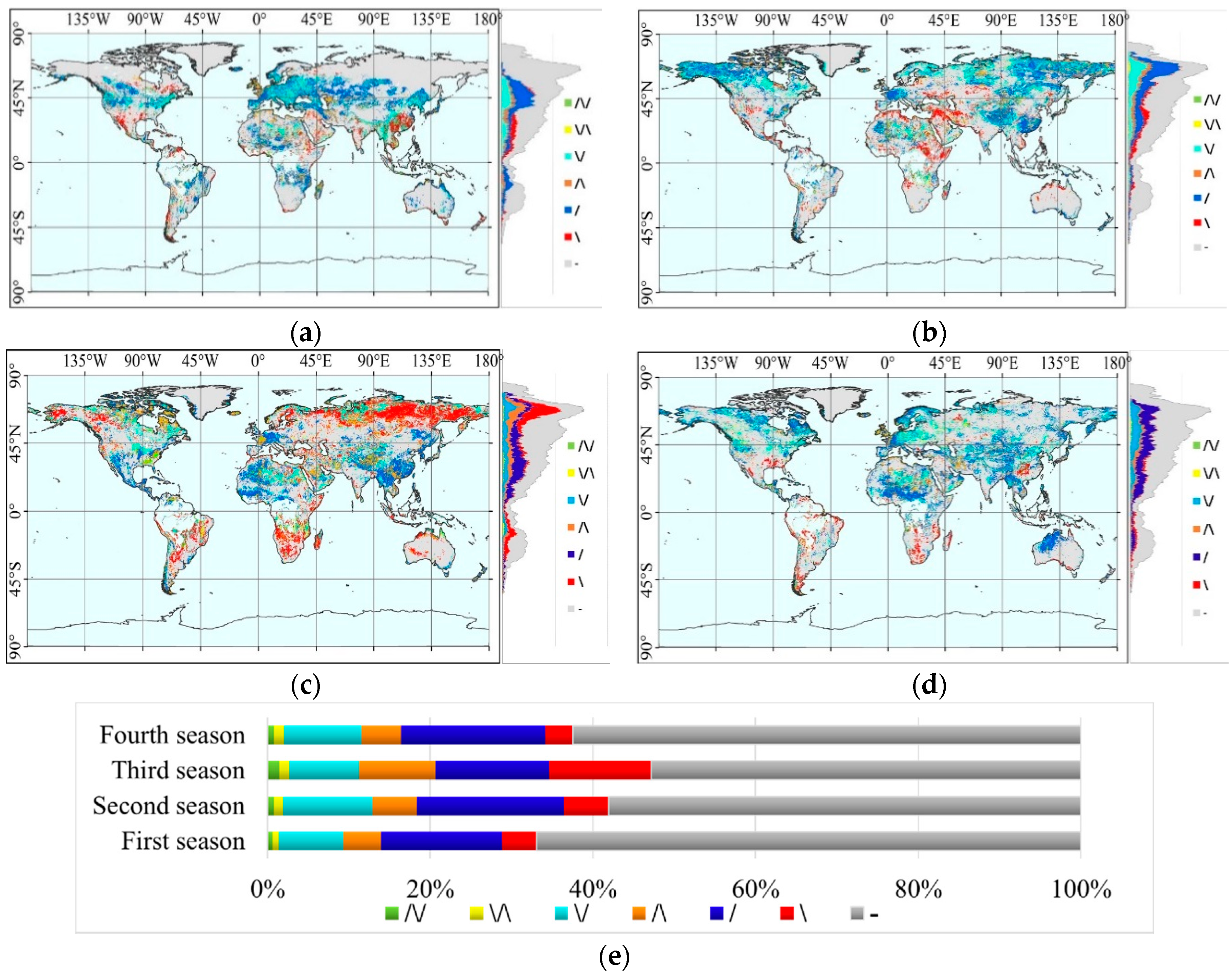
3.3. Seasonal Trend Distributions
4. Discussion
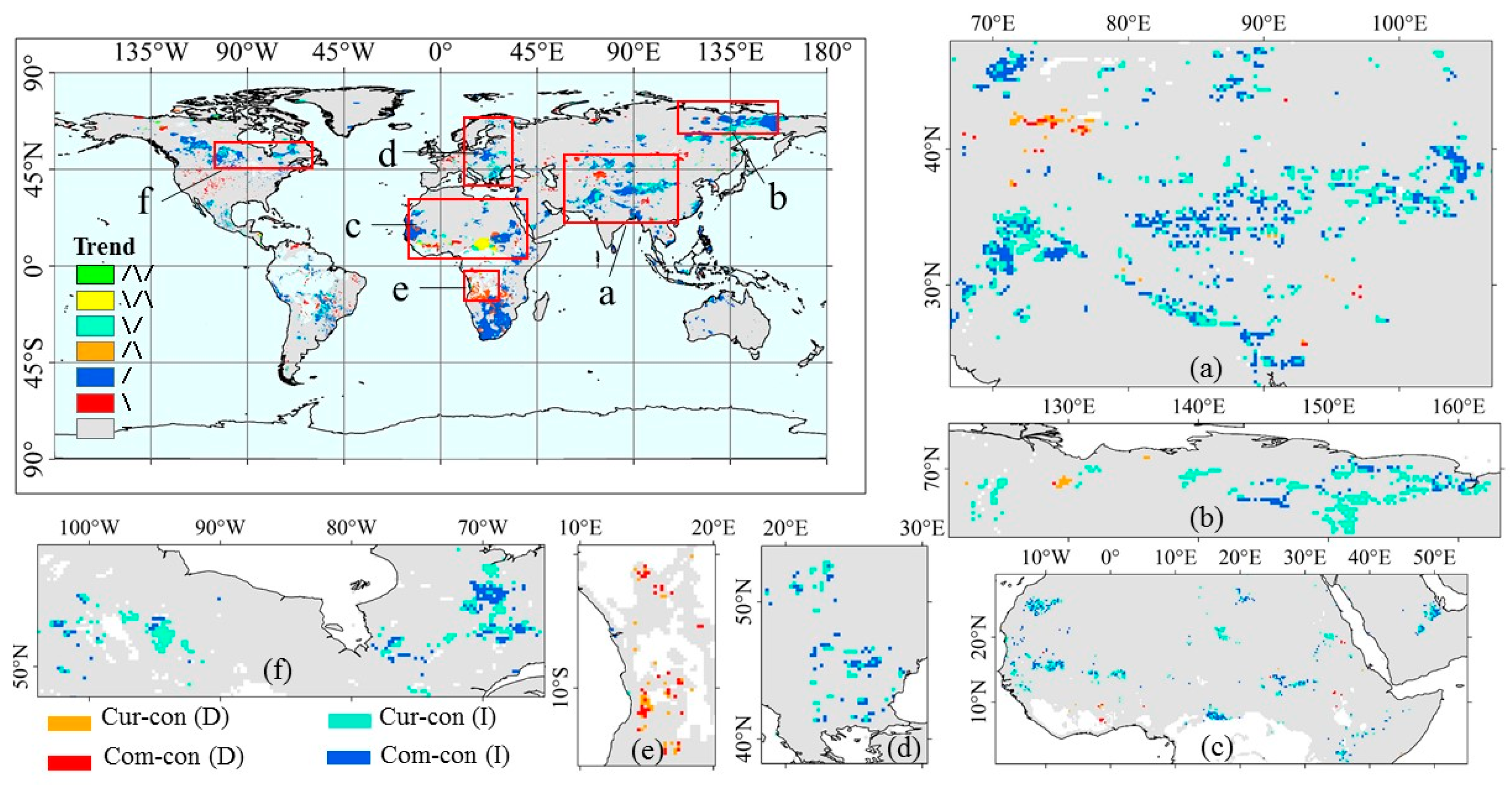
4.1. Evaluation of Results
4.2. Comparisons with Previous Research
4.3. Influence of Precipitation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Gaur, N.; Mohanty, B.P. Land-surface controls on near-surface soil moisture dynamics: Traversing remote sensing footprints. Water Resour. Res. 2016, 52, 6365–6385. [Google Scholar] [CrossRef]
- Dorigo, W.; De Jeu, R.; Chung, D.; Parinussa, R.; Liu, Y.; Wagner, W.; Fernandez-Prieto, D. Evaluating global trends (1988–2010) in homogenized remotely sensed surface soil moisture. Geophys. Res. Lett. 2012, 39, L18405. [Google Scholar] [CrossRef]
- Feng, H.; Zhang, M. Global land moisture trends: drier in dry and wetter in wet overland. Sci. Rep. 2015, 5, 18018. [Google Scholar] [CrossRef] [PubMed]
- An, R.; Zhang, L.; Wang, Z.; Quaye-Ballard, J.A.; You, J.; Shen, X.; Gao, W.; Huang, L.; Zhao, Y.; Ke, Z. Validation of the ESA CCI soil moisture product in China. Int. J. Appl. Earth Obs. Geoinf. 2016, 8, 28–36. [Google Scholar] [CrossRef]
- Li, X.; Gao, X.; Wang, J.; Guo, H. Microwave soil moisture dynamics and response to climate change in Central Asia and Xinjiang Province, China, over the last 30 years. J. Appl. Remote. Sens. 2015, 9, 096012. [Google Scholar] [CrossRef]
- Rahmani, A.; Golian, S.; Brocca, L. Multiyear monitoring of soil moisture over Iran through satellite and reanalysis soil moisture products. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 85–95. [Google Scholar] [CrossRef]
- Wang, S.; Mo, X.; Liu, S.; Lin, Z.; Hu, S. Validation and trend analysis of ECV soil moisture data on cropland in North China Plain during 1981–2010. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 110–121. [Google Scholar] [CrossRef]
- Zheng, X.; Zhao, K.; Ding, Y.; Jiang, T.; Zhang, S.; Jin, M. The spatiotemporal patterns of surface soil moisture in Northeast China based on remote sensing products. J. Water Clim. Change 2016, 7, 708–720. [Google Scholar] [CrossRef]
- Zhan, M.; Wang, Y.; Wang, G.; Hartmann, H.; Cao, L.; Li, X.; Su, B. Long-term changes in soil moisture conditions and their relation to atmospheric circulation in the Poyang Lake basin, China. Quatern. Int. 2017, 440, 23–29. [Google Scholar] [CrossRef]
- Pan, N.Q.; Feng, X.M.; Fu, B.J.; Wang, S.; Ji, F.; Pan, S.F. Increasing global vegetation browning hidden in overall vegetation greening: insights from time-varying trends. Remote Sens. Environ. 2018, 214, 59–72. [Google Scholar] [CrossRef]
- Cho, E.; Zhang, A.; Choi, M. The seasonal difference in soil moisture patterns considering the meteorological variables throughout the Korean peninsula. Terr. Atmos. Ocean. Sci. 2016, 27, 907–920. [Google Scholar] [CrossRef]
- Nie, S.; Luo, Y.; Zhu, J. Trends and scales of observed soil moisture variations in China. Adv. Atmos. Sci. 2008, 25, 43–58. [Google Scholar] [CrossRef]
- Liu, Q.; Du, J.; Shi, J.C.; Jiang, L.M. Analysis of spatial distribution and multi-year trend of the remotely sensed soil moisture on the Tibetan Plateau. Sci. China Earth Sci. 2013, 56, 2173–2185. [Google Scholar] [CrossRef]
- Yin, J.; Porporato, A.; Albertson, J. Interplay of climate seasonality and soil moisture-rainfall feedback. Water Resour. Res. 2014, 50, 6053–6066. [Google Scholar] [CrossRef]
- Zhang, H.; Chang, J.; Zhang, L.; Wang, Y.; Li, Y.; Wang, X. NDVI dynamic changes and their relationship with meteorological factors and soil moisture. Environ. Earth Sci. 2018, 77, 582. [Google Scholar] [CrossRef]
- Bai, W.K.; Gu, X.L.; Li, S.L.; Tang, Y.H.; He, Y.H.; Gu, X.H.; Bai, X.Y. The performance of multiple model-simulated soil moisture datasets relative to ECV satellite data in China. Water 2018, 10, 1384. [Google Scholar] [CrossRef]
- Qiu, J.; Gao, Q.; Wang, S.; Su, Z. Comparison of temporal trends from multiple soil moisture data sets and precipitation: The implication of irrigation on regional soil moisture trend. Int. J. Appl. Earth Obs. 2016, 48, 17–27. [Google Scholar] [CrossRef]
- Chen, X.; Su, Y.; Liao, J.; Shang, J.; Dong, T.; Wang, C.; Liu, W.; Zhou, G.; Liu, L. Detecting significant decreasing trends of land surface soil moisture in eastern China during the past three decades (1979–2010). J. Geophys. Res. Atmos. 2016, 121, 5177–5192. [Google Scholar] [CrossRef]
- Teuling, A.J.; Hupet, F.; Uijlenhoet, R.; Troch, P.A. Climate variability effects on spatial soil moisture dynamics. Geophys. Res. Lett. 2007, 34, L06406. [Google Scholar] [CrossRef]
- Gabiri, G.; Burghof, S.; Diekkrüger, B.; Leemhuis, C.; Steinbach, S.; Näschen, K. Modeling spatial soil water dynamics in a tropical floodplain, East Africa. Water 2018, 10, 191. [Google Scholar] [CrossRef]
- Lekshmi, S.U.S.; Singh, D.N.; Baghini, M.S. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar]
- Petropoulos, G.P.; Ireland, G.; Barrett, B. Surface soil moisture retrievals from remote sensing: Current status, products & future trends. Phys. Chem. Earth. 2015, 3, 36–56. [Google Scholar]
- Catalano, F.; Alessandri, A.; de Felice, M.; Zhu, Z.; Myneni, R.B. Observationally based analysis of land–atmosphere coupling. Earth Syst. Dynam. 2016, 7, 251–266. [Google Scholar] [CrossRef]
- Knist, S.; Goergen, K.; Buonomo, E.; Christensen, O.B.; Colette, A.; Cardoso, R.M.; Fealy, R.; Fernández, J.; García-Díez, M.; Jacob, D.; Kartsios, S.; et al. Land-atmosphere coupling in EURO-CORDEX evaluation experiments. J. Geophys. Res. 2017, 122, 79–103. [Google Scholar] [CrossRef]
- Li, M.; Ma, Z.; Gu, H.; Yang, Q.; Zheng, Z. Production of a combined land surface data set and its use to assess land-atmosphere coupling in China. J. Geophys. Res. 2017, 122, 948–965. [Google Scholar] [CrossRef]
- Carvalhais, N.; Forkel, M.; Khomik, M.; Bellarby, J.; Jung, M.; Migliavacca, M.; Μu, M.Q.; Saatchi, S.; Santoro, M.; Thurner, M.; et al. Global covariation of carbon turnover times with climate in terrestrial ecosystems. Nature 2014, 514, 213–217. [Google Scholar] [CrossRef]
- Richardson, A.D.; Keenan, T.F.; Migliavacca, M.; Ryu, Y.; Sonnentag, O.; Toomey, M. Climate change, phenology, and phenological control of vegetation feedbacks to the climate system. Agric. For. Meteorol. 2013, 169, 156–173. [Google Scholar] [CrossRef]
- Dobriyal, P.; Qureshi, A.; Badola, R.; Hussain, S.A. A review of the methods available for estimating soil moisture and its implications for water resource management. J. Hydrol. 2012, 458, 110–117. [Google Scholar] [CrossRef]
- Wanders, N.; Karssenberg, D.; de Roo, A.; de Jong, S.M.; Bierkens, M.F.P. The suitability of remotely sensed soil moisture for improving operational flood forecasting. Hydrol. Earth Syst. Sci. 2014, 18, 2343–2357. [Google Scholar] [CrossRef]
- Asoka, A.; Gleeson, T.; Wada, Y.; Mishra, V. Relative contribution of monsoon precipitation and pumping to changes in groundwater storage in India. Nat. Geosci. 2017, 10, 109–117. [Google Scholar] [CrossRef]
- Park, S.; Im, J.; Park, S.; Rhee, J. Drought monitoring using high resolution soil moisture through multi-sensor satellite data fusion over the Korean peninsula. Agric. For. Meteorol. 2017, 237, 257–269. [Google Scholar] [CrossRef]
- Nicolai-Shaw, N.; Zscheischler, J.; Hirschi, M.; Gudmundsson, L.; Seneviratne, S.I. A drought event composite analysis using satellite remote-sensing based soil moisture. Remote Sens. Environ. 2017, 203, 216–225. [Google Scholar] [CrossRef]
- Mishra, A.; Vu, T.; Valiya, V.A.; Entekhabi, D. Drought monitoring with soil moisture active passive (SMAP) measurements. J. Hydrol. 2017, 552, 620–632. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A. ESA CCI Soil moisture for improved earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Liu, Y.X.; Wang, Y.L.; Du, Y.Y.; Zhao, M.Y.; Peng, J. The application of polynomial analyses to detect global vegetation dynamics during 1982–2012. Int. J. Remote. Sens. 2016, 37, 1568–1584. [Google Scholar] [CrossRef]
- Tian, L.F.; Collins, C. An effective robot trajectory planning method using a genetic algorithm. Mechatronics 2004, 14, 455–470. [Google Scholar] [CrossRef]
- Feng, H.H. Individual contributions of climate and vegetation change to soil moisture trends across multiple spatial scales. Sci. Rep. 2016, 6, 32782. [Google Scholar] [CrossRef]
- Piao, S.; Yin, L.; Wang, X.; Ciais, P.; Peng, S.; Shen, Z.; Seneviratne, S.I. Summer soil moisture regulated by precipitation frequency in China. Environ. Res. Lett. 2009, 4, 044012. [Google Scholar] [CrossRef]
- Chen, X.; Liu, X.; Liu, Z.; Zhou, P.; Zhou, G.; Liao, J.; Liu, L. Spatial clusters and temporal trends of seasonal surface soil moisture across China in responses to regional cli-mate and land cover changes. Ecohydrology 2017, 10, 1–12. [Google Scholar]
- Meng, X.; Li, R.; Luan, L.; Lyu, S.; Zhang, T.; Ao, Y.; Han, B.; Zhao, L.; Ma, Y. Detecting hydrological consistency between soil moisture and precipitation and changes of soil moisture in summer over the Tibetan Plateau. Clim. Dyn. 2017, 2, 1–12. [Google Scholar] [CrossRef]
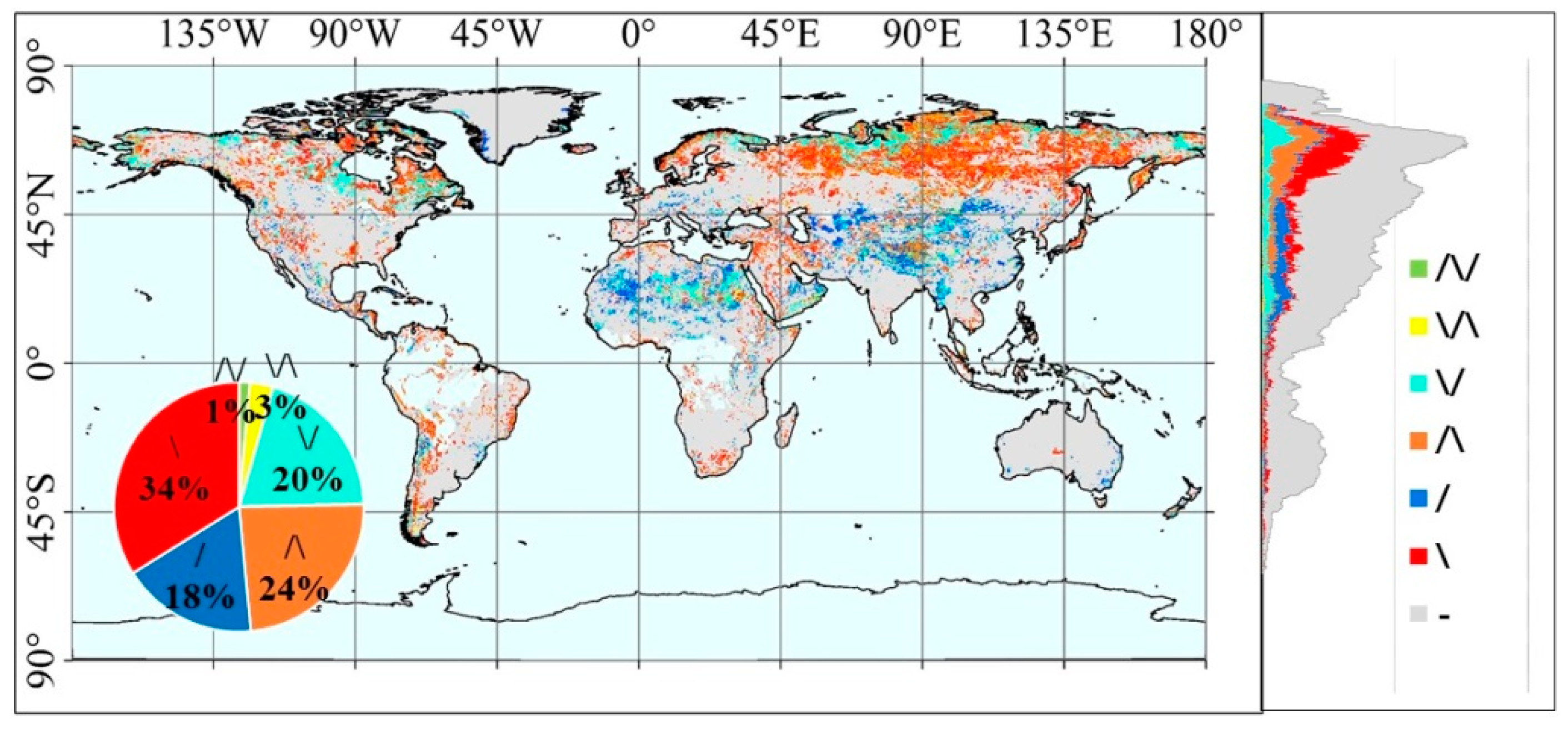
| Significant Change (%) | Proportion of Significant Change (%) | ||||||
|---|---|---|---|---|---|---|---|
| /\/ | \/\ | \/ | /\ | / | \ | ||
| South America | 25.04 | 1.55 | 4.94 | 9.16 | 29.24 | 12.57 | 42.54 |
| Asia | 43.41 | 1.65 | 2.57 | 18.52 | 25.53 | 16.15 | 35.58 |
| Africa | 25.18 | 1.07 | 5.90 | 30.11 | 7.18 | 34.21 | 21.53 |
| North America | 28.41 | 1.26 | 2.37 | 23.25 | 24.92 | 15.68 | 32.52 |
| Europe | 29.68 | 0.82 | 1.93 | 16.33 | 30.40 | 9.29 | 41.23 |
| Oceania | 6.31 | 1.35 | 2.56 | 19.68 | 17.65 | 36.79 | 21.97 |
| Annual | First Seasonal | Third Seasonal | Fourth Seasonal | |||||
|---|---|---|---|---|---|---|---|---|
| Pixels | Percent | Pixels | Percent | Pixels | Percent | Pixels | Percent | |
| /\/ | 1040 | 0.45 | 1471 | 0.64 | 3415 | 1.49 | 1756 | 0.77 |
| \/\ | 2217 | 0.97 | 1664 | 0.73 | 2770 | 1.21 | 2772 | 1.21 |
| \/ | 14,975 | 6.53 | 18,252 | 7.96 | 19,587 | 8.54 | 21,958 | 9.57 |
| /\ | 17,576 | 7.66 | 10,579 | 4.61 | 21,577 | 9.41 | 11,221 | 4.89 |
| / | 13,011 | 5.67 | 34,176 | 14.90 | 32,009 | 13.95 | 40,569 | 17.69 |
| \ | 25,031 | 10.91 | 9719 | 4.24 | 28,891 | 12.59 | 7868 | 3.43 |
| - | 155,543 | 67.81 | 153,532 | 66.93 | 121,144 | 52.81 | 143,249 | 62.45 |
| SUM | 229,393 | 100 | 229,393 | 100 | 229,393 | 100 | 229,393 | 100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, N.; Wang, S.; Liu, Y.; Zhao, W.; Fu, B. Global Surface Soil Moisture Dynamics in 1979–2016 Observed from ESA CCI SM Dataset. Water 2019, 11, 883. https://doi.org/10.3390/w11050883
Pan N, Wang S, Liu Y, Zhao W, Fu B. Global Surface Soil Moisture Dynamics in 1979–2016 Observed from ESA CCI SM Dataset. Water. 2019; 11(5):883. https://doi.org/10.3390/w11050883
Chicago/Turabian StylePan, Ning, Shuai Wang, Yanxu Liu, Wenwu Zhao, and Bojie Fu. 2019. "Global Surface Soil Moisture Dynamics in 1979–2016 Observed from ESA CCI SM Dataset" Water 11, no. 5: 883. https://doi.org/10.3390/w11050883
APA StylePan, N., Wang, S., Liu, Y., Zhao, W., & Fu, B. (2019). Global Surface Soil Moisture Dynamics in 1979–2016 Observed from ESA CCI SM Dataset. Water, 11(5), 883. https://doi.org/10.3390/w11050883







