Large-Scale Hydrological Modelling of the Upper Paraná River Basin
Abstract
1. Introduction
2. Materials and Methods
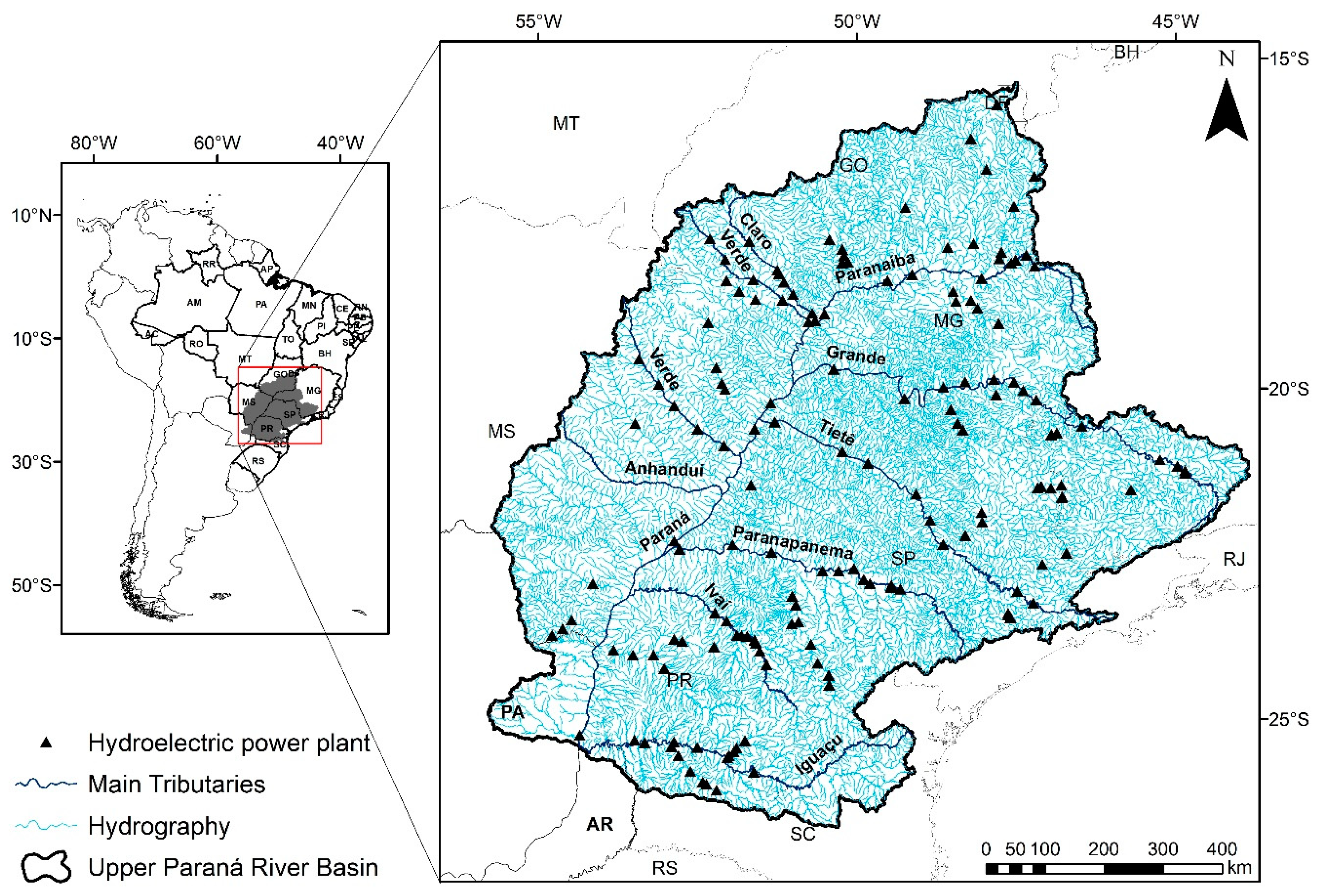
2.1. Study Area
2.2. SWAT Model
2.2.1. Data Description and Model Set Up
Meteorological Data
Topography
Soil Data
Land Use and Land Cover Data
Model Set Up
River Discharge Data
2.3. SUFI-2 and Parameters Calibration
2.4. Objective Function
2.5. Modelling Protocol
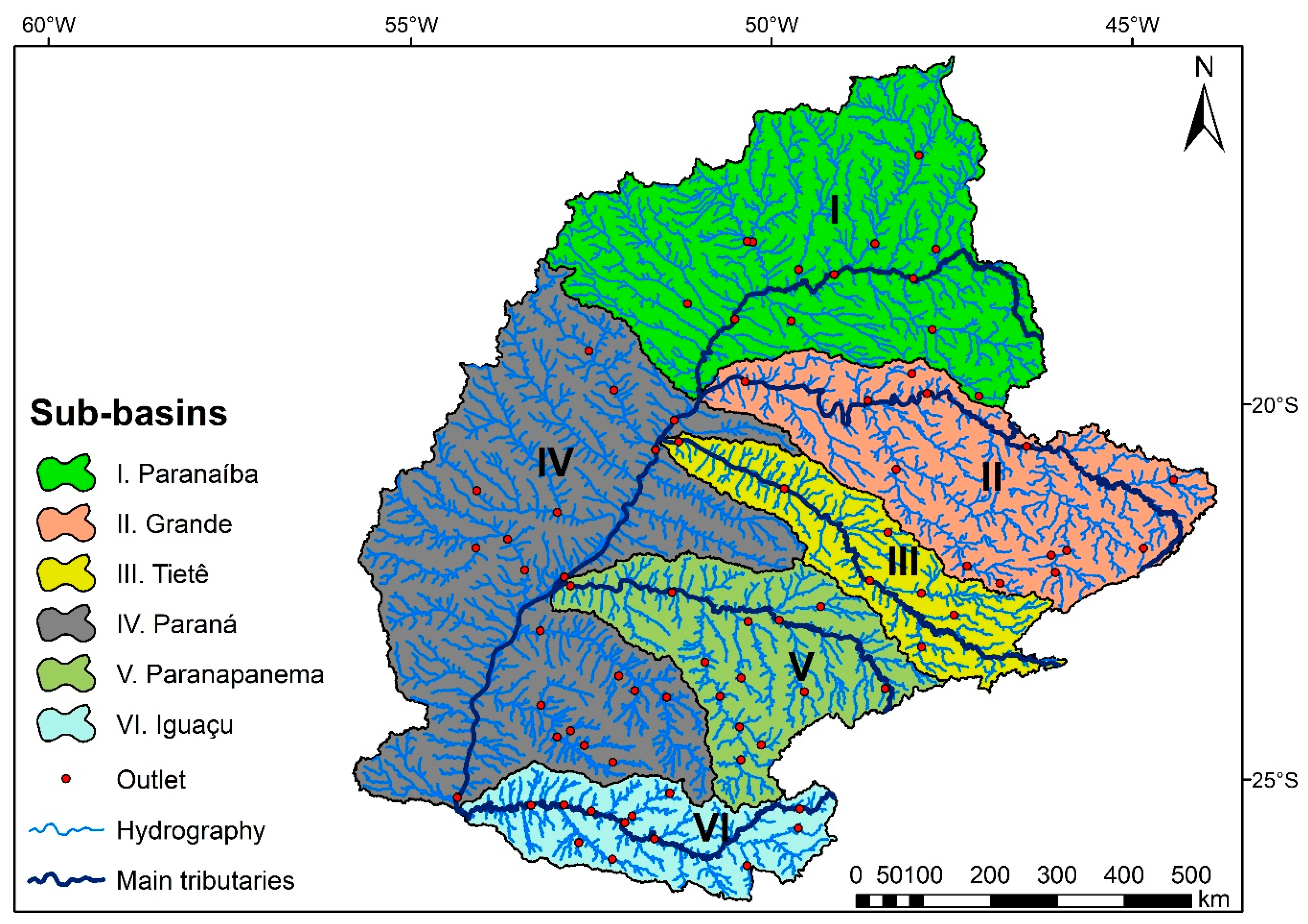
- In order to run the simulation with parallel processing, due to memory limitations as a result of the project size, the basin area was divided into 9 watersheds for calibration and the fitted values in each sub-basin were used for the initial project.
- A multi-objective calibration, which consists of simultaneous multi-site calibration from upstream to downstream outlets, was performed. This technique was recommended by Leta et al. [49] for a heterogeneous basin and presented better results compared to other methods such as single-site calibration (SSC).
- The discharge outlets which performed satisfactory or better in all objective functions that are presented in Table 2 were not considered in the calibration process.
- The initial parameter ranges followed the calibration protocol presented by Abbaspour et al. [48] for large-scale basins. For example, if the simulation presented base flow too low (high), the GWQMN, GW_REVAP, and REVAMPM parameters should increase (decrease). Therefore, before each calibration, the temporal evolution of the discharge simulation was evaluated as to whether it underestimated or overestimated the observation.
- SUFI-2 provides several objective functions for calibration. The objective function selected in the calibration process was NSE. This index has been used in several studies and provided satisfactory results [50].
- Once the sub-project was built for the sub-basin, and the ranges of parameters were defined, the model simulations were run between 150 and 500 times, with a maximum of 3 iterations. The numbers of simulations, as well as of iterations, were based on the size of the sub-project and performance of the initial simulation.
3. Results and Discussion
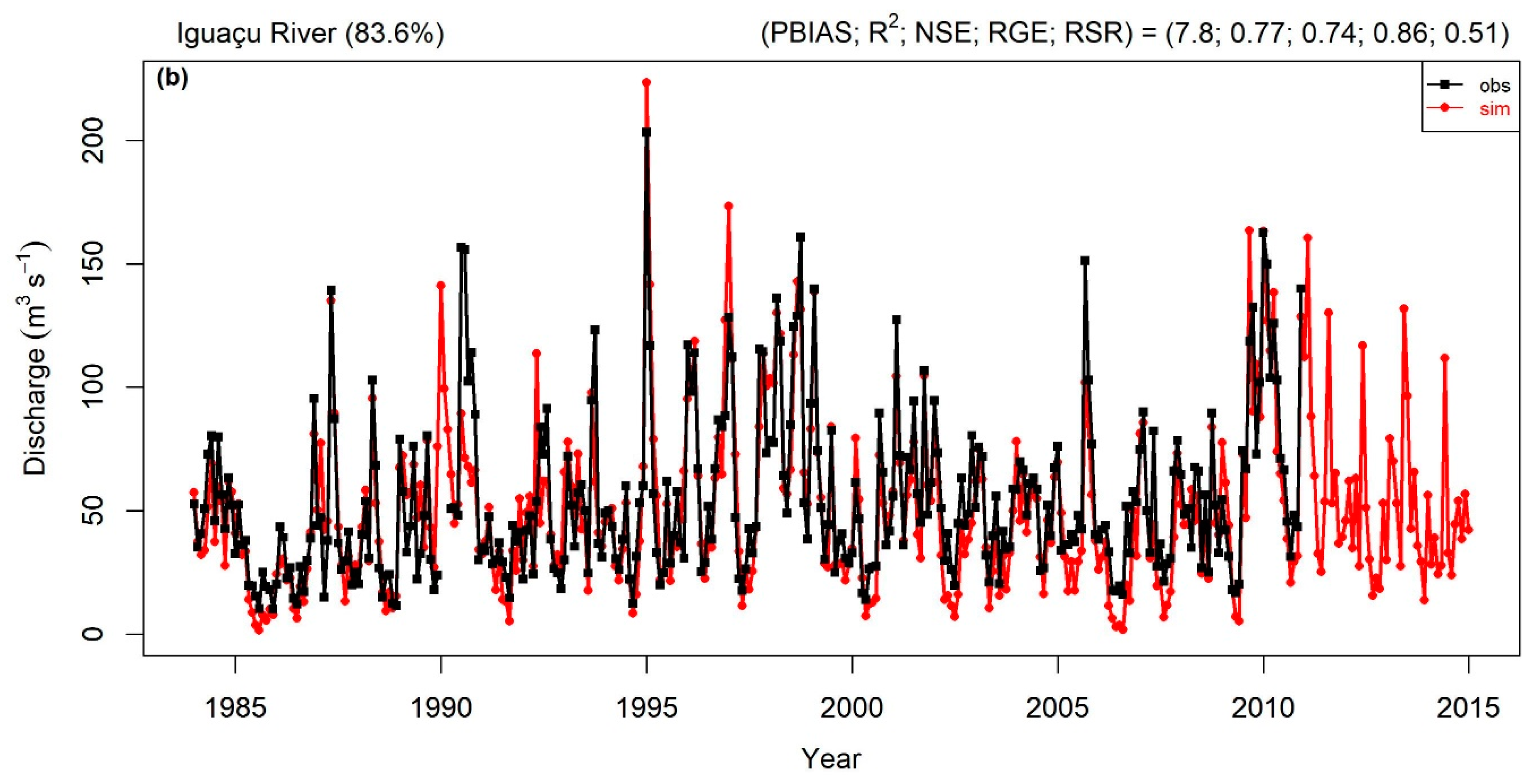
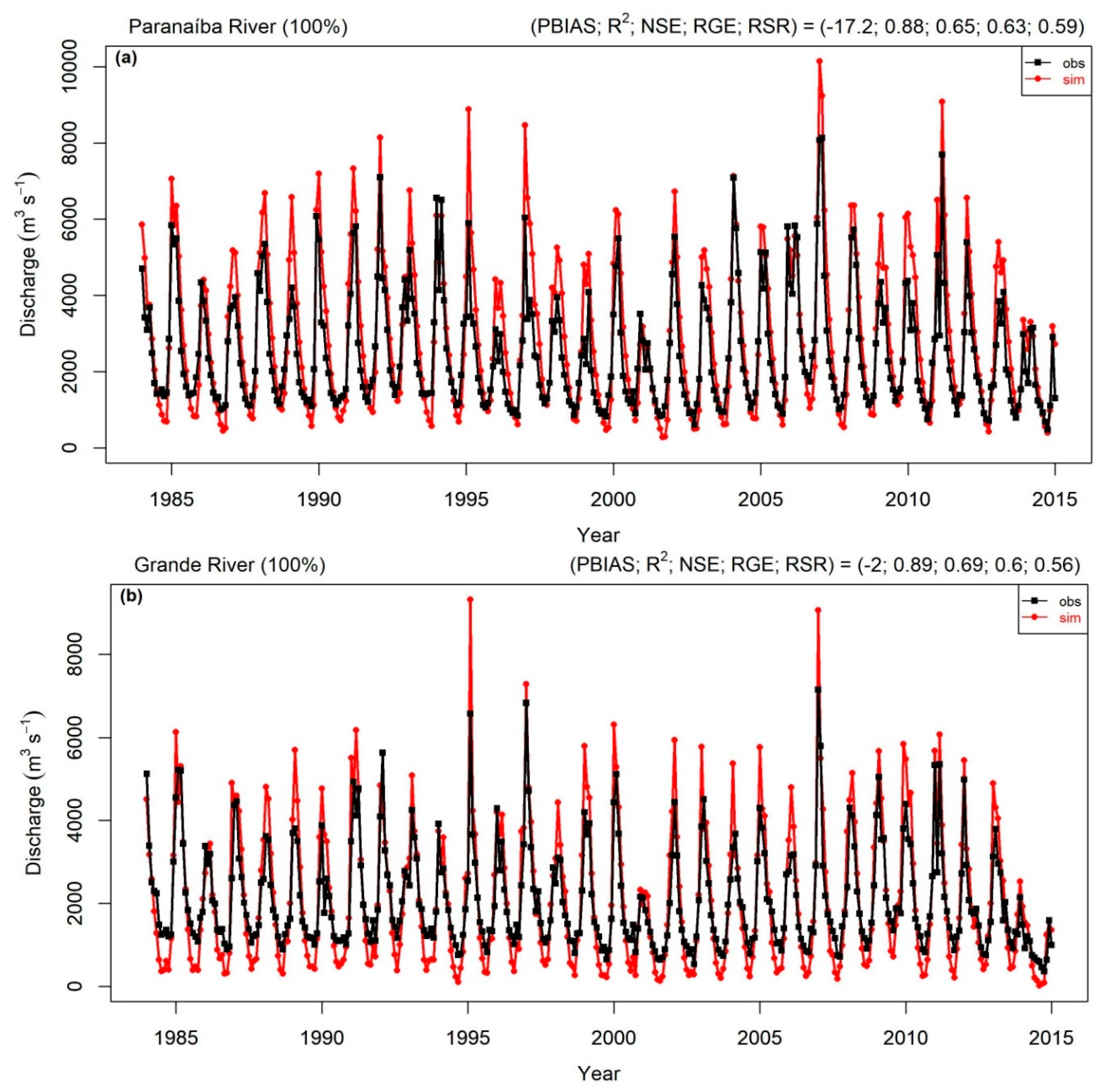
3.1. Sub-Basins Selected for Calibration
3.2. Calibration and Validation Performance
4. Summary and Conclusions
- The methodology used in this work regarding data preparation, model setup, and strategies for calibration and validation, as well as evaluation can be used for other large scale basins, especially in South America.
- Due to the high spatial resolution and the good quality of most datasets collected in both meteorological, and physical variables, 23 outlets over the basin performed satisfactory or better in all the objective functions evaluated without the calibration process. Most of these outlets were found in the Iguaçu sub-basin (VI).
- After the calibration process, most of the outlets analyzed (≥74%) presented better or equally satisfactory in all objective functions, mainly in the southern basin, which is the region with the highest density of stations.
- Although there are outlets with some errors in the simulated discharge, most of the evaluated outlets in the basin are in agreement with the observation especially those located at the final outlet of the main rivers of UPRB, which have the most significant contribution for the final discharge of the basin project.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ficklin, D.L.; Luo, Y.; Luedeling, E.; Zhang, M. Climate change sensitivity assessment of a highly agricultural watershed using SWAT. J. Hydrol. 2009, 374, 16–29. [Google Scholar] [CrossRef]
- Narsimlu, B.; Gosain, A.K.; Chahar, B.R. Assessment of Future Climate Change Impacts on Water Resources of Upper Sind River Basin, India Using SWAT Model. Water Resour. Manag. 2013, 27, 3647–3662. [Google Scholar] [CrossRef]
- Ghaffari, G.; Keesstra, S.; Ghodousi, J.; Ahmadi, H. SWAT-simulated hydrological impact of land-use change in the Zanjanrood Basin, Northwest Iran. Hydrol. Process. 2010, 24, 892–903. [Google Scholar] [CrossRef]
- Wang, G.; Yang, H.; Wang, L.; Xu, Z.; Xue, B. Using the SWAT model to assess impacts of land use changes on runoff generation in headwaters. Hydrol. Process. 2014, 28, 1032–1042. [Google Scholar] [CrossRef]
- Yang, S.; Dong, G.; Zheng, D.; Xiao, H.; Gao, Y.; Lang, Y. Coupling Xinanjiang model and SWAT to simulate agricultural non-point source pollution in Songtao watershed of Hainan, China. Ecol. Modell. 2011, 222, 3701–3717. [Google Scholar] [CrossRef]
- Rouholahnejad, E.; Abbaspour, K.C.; Srinivasan, R.; Bacu, V.; Lehmann, A. Water resources of the Black Sea Basin at high spatial and temporal resolution. Water Resour. Res. 2014, 50, 5866–5885. [Google Scholar] [CrossRef]
- ANEEL. BIG—Banco de Informações de Geração—Capacidade de Geração do Brasil—Usinas hidrelétricas; 2018. Available online: www2.aneel.gov.br/aplicacoes/capacidadebrasil/GeracaoTipoFase.asp (accessed on 15 January 2019).
- Martins, J.A.; Brand, V.S.; Capucim, M.N.; Machado, C.B.; Piccilli, D.G.A.; Martins, L.D. The Impact of Rainfall and Land Cover Changes on the Flow of a Medium-sized River in the South of Brazil. Energy Procedia 2016, 95, 272–278. [Google Scholar] [CrossRef][Green Version]
- Capucim, M.N.; Brand, V.S.; Machado, C.B.; Martins, L.D.; Allasia, D.G.; Homann, C.T.; De Freitas, E.D.; Da Silva Dias, M.A.F.; Andrade, M.F.; Martins, J.A. South America land use and land cover assessment and preliminary analysis of their impacts on regional atmospheric modeling studies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1185–1198. [Google Scholar] [CrossRef]
- Strömbäck, L.; Arheimer, B.; Lindström, G.; Donnelly, C.; Gustafsson, D. The Importance of Open Data and Software for Large Scale Hydrological Modelling. Open Water J. 2013, 2, 32. [Google Scholar]
- Tucci, C.E. Impactos da Variabilidade Climática e do Uso do Solo Nos Recursos Hídricos; Câmara Temática de Recursos Hídricos, Agência Nacional de Águas (ANA): Brasilia, Brazil, 2002; p. 150.
- Antico, A.; Torres, M.E.; Diaz, H.F. Contributions of different time scales to extreme Paraná floods. Clim. Dyn. 2016, 46, 3785–3792. [Google Scholar] [CrossRef]
- Camilloni, I.A.; Barros, V.R. Extreme discharge events in the Paraná River and their climate forcing. J. Hydrol. 2003, 278, 94–106. [Google Scholar] [CrossRef]
- IBGE. Available online: http://www.ibge.gov.br/apps/populacao/projecao/ (accessed on 20 January 2019).
- ANA—Agência Nacional de Águas. 2018. Available online: http://www3.ana.gov.br/ (accessed on 10 January 2019).
- Brea, M.; Zucol, A.F. The Paraná-Paraguay Basin: Geology and Paleoenvironments. In Historical Biogeography of Neotropical Freshwater Fishes; Albert, J.S., Reis, R., Eds.; University of California Press: Berkeley, CA, USA, 2012; pp. 69–88. [Google Scholar]
- Menegazzo, M.C.; Catuneanu, O.; Chang, H.K. The South American retroarc foreland system: The development of the Bauru Basin in the back-bulge province. Mar. Pet. Geol. 2016, 73, 131–156. [Google Scholar] [CrossRef]
- De Paula e Silva, F.; Kiang, C.H.; Caetano-Chang, M.R. Sedimentation of the Cretaceous Bauru Group in São Paulo, Paraná Basin, Brazil. J. S. Am. Earth Sci. 2009, 28, 25–39. [Google Scholar] [CrossRef]
- Carvalho, L.M.V.; Jones, C.; Silva, A.E.; Liebmann, B.; Silva Dias, P.L. The South American Monsoon System and the 1970s climate transition. Int. J. Climatol. 2011, 31, 1248–1256. [Google Scholar] [CrossRef]
- Grimm, A.M. Interannual climate variability in South America: Impacts on seasonal precipitation, extreme events, and possible effects of climate change. Stoch. Environ. Res. Risk Assess. 2011, 25, 537–554. [Google Scholar] [CrossRef]
- Velasco, I.; Fritsch, J.M. Mesoscale convective complexes in the Americas. J. Geophys. Res. 1987, 92, 9591–9613. [Google Scholar] [CrossRef]
- Salio, P.; Nicolini, M.; Zipser, E.J. Mesoscale Convective Systems over Southeastern South America and Their Relationship with the South American Low-Level Jet. Mon. Weather Rev. 2007, 135, 1290–1309. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large Area Hydrologic Modelling and Assessment Part I: Model Development. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical Development, Applications, and Future Research Directions. Trans. ASABE 2007, 50, 1211–1250. [Google Scholar] [CrossRef]
- Douglas-Mankin, K.R.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) Model: Current Developments and Applications. Trans. ASABE 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- Neitsch, S.; Arnold, J.; Kiniry, J.; Williams, J. Soil & Water Assessment Tool: Theoretical Documentation Version 2009; Texas Water Resource Institute: College Station, TX, USA, 2011. [Google Scholar]
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Ruelland, D.; Ardoin-Bardin, S.; Billen, G.; Servat, E. Sensitivity of a lumped and semi-distributed hydrological model to several methods of rainfall interpolation on a large basin in West Africa. J. Hydrol. 2008, 361, 96–117. [Google Scholar] [CrossRef]
- Fauconnier, Y. Evaluation de La Ressource Dans Le Bassin Versant de l’Ibicuí Grâce à La Modélisation Hydrologique: Application de l’outil SWAT. Master´s Thesis, University of Le Mans, Le Mans, France, 2017. [Google Scholar]
- Mercuri, E.G.F.; Deppe, F.; Lohmann, M.; Simões, K. Metodologia da geração de dados de entrada e aplicação do modelo SWAT para bacias hidrográficas brasileiras. In Proceedings of the XIV Simpósio Brasileiro de Sensoriamento Remoto, Natal, Brazil, 25–30 April 2009; pp. 4773–4780. [Google Scholar]
- Pereira, D.R. Simulação hidrológica na bacia hidrográfica do rio Pomba usando o modelo SWAT. Ph.D. Thesis, Universidade Federal de Viçosa, Viçaso, MG, Brazil, 2013. [Google Scholar]
- Rudke, A.P. Dinâmica da cobertura do solo para a bacia hidrográfica do alto rio Paraná. Master´s Thesis, Federal University of Techonology Parana, Londrina, Brazil, 2018. [Google Scholar]
- Winchell, M.; Srinivasan, R.; Di Luzio, M.; Arnold, J. ArcSWAT Interface For SWAT2012: User’s Guide; Blackland Research and Extension Center TEXAS Agrilife Research: Temple, TX, USA, 2013.
- Embrapa. Sistema brasileiro de classificação de solos; Centro Nacional de Pesquisa de Solos: Rio de Janeiro, Brazil, 2006; ISBN 85-85864-19-2. [Google Scholar]
- Monteith, J.L. Evaporation and envrionment. Symp. Soc. Exp. Biol. 1965, 19, 205–235. [Google Scholar] [PubMed]
- USDA Soil Conservation Service. National Engineering Handbook; Section 4, Hydrology, Chapter 21; USDA Soil Conservation Service: Washington, DC, USA, 1972.
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating Uncertain Flow and Transport Parameters Using a Sequential Uncertainty Fitting Procedure. Vadose Zone J. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual; Eawag: Duebendorf, Switzerland, 2015. [Google Scholar]
- Rouholahnejad, E.; Abbaspour, K.C.; Vejdani, M.; Srinivasan, R.; Schulin, R.; Lehmann, A. A parallelization framework for calibration of hydrological models. Environ. Modell. Softw. 2012, 31, 28–36. [Google Scholar] [CrossRef]
- Piniewski, M.; Szcześniak, M.; Kardel, I.; Berezowski, T.; Okruszko, T.; Srinivasan, R.; Vikhamar Schuler, D.; Kundzewicz, Z.W. Hydrological modelling of the Vistula and Odra river basins using SWAT. Hydrol. Sci. J. 2017, 62, 1266–1289. [Google Scholar] [CrossRef]
- Kouchi, D.H.; Esmaili, K.; Faridhosseini, A.; Sanaeinejad, S.H.; Khalili, D.; Abbaspour, K.C. Sensitivity of calibrated parameters and water resource estimates on different objective functions and optimization algorithms. Water 2017, 9, 384. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Liew, M. Van Multi-site calibration of the SWAT model for hydrologic modeling. Trans. ASABE 2008, 51, 2039–2049. [Google Scholar] [CrossRef]
- Yapo, P.O.; Gupta, H.V.; Sorooshian, S. Automatic calibration of conceptual rainfall-runoff models: Sensitivity to calibration data. J. Hydrol. 1996, 181, 23–48. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; De Roo, A. Hydrological evaluation of satellite-based rainfall estimates over the Volta and Baro-Akobo Basin. J. Hydrol. 2013, 499, 324–338. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Leta, O.T.; van Griensven, A.; Bauwens, W. Effect of Single and Multisite Calibration Techniques on the Parameter Estimation, Performance, and Output of a SWAT Model of a Spatially Heterogeneous Catchment. J. Hydrol. Eng. 2016, 22, 05016036. [Google Scholar] [CrossRef]
- Meng, H.; Sexton, A.M.; Maddox, M.C.; Sood, A.; Brown, C.W.; Ferraro, R.R.; Murtugudde, R. Modeling rappahannock river basin using swat—Pilot for chesapeake bay watershed. Appl. Eng. Agric. 2010, 26, 795–805. [Google Scholar] [CrossRef]
- Peterson, J.R.; Hamlett, J.M. Hydrologic Calibration of the Swat Model in a Watershed Containing Fragipan Soils. J. Am. Water Resour. Assoc. 1998, 34, 531–544. [Google Scholar] [CrossRef]
- Srivastava, P.; McNair, J.N.; Johnson, T.E. Comparison of process-based and artificial neural network approaches for streamflow modeling in an agricultural watershed. J. Am. Water Resour. Assoc. 2006, 42, 545–563. [Google Scholar] [CrossRef]
- Wu, K.; Johnston, C.A. Hydrologic response to climatic variability in a Great Lakes Watershed: A case study with the SWAT model. J. Hydrol. 2007, 337, 187–199. [Google Scholar] [CrossRef]
- Creech, C.T.; Siqueira, R.B.; Selegean, J.P.; Miller, C. Anthropogenic impacts to the sediment budget of São Francisco River navigation channel using SWAT. Int. J. Agric. Biol. Eng. 2015, 8, 1–20. [Google Scholar]
- Rocha, E.O.; Calijuri, M.L.; Santiago, A.F.; de Assis, L.C.; Alves, L.G.S. The Contribution of Conservation Practices in Reducing Runoff, Soil Loss, and Transport of Nutrients at the Watershed Level. Water Resour. Manag. 2012, 26, 3831–3852. [Google Scholar] [CrossRef]
- Pagliero, L.; Bouraoui, F.; Willems, P.; Diels, J. Large-Scale Hydrological Simulations Using the Soil Water Assessment Tool, Protocol Development, and Application in the Danube Basin. J. Environ. Qual. 2014, 43, 145–154. [Google Scholar] [CrossRef] [PubMed]
- Easton, Z.M.; Fuka, D.R.; White, E.D.; Collick, A.S.; Biruk Ashagre, B.; McCartney, M.; Awulachew, S.B.; Ahmed, A.A.; Steenhuis, T.S. A multi basin SWAT model analysis of runoff and sedimentation in the Blue Nile, Ethiopia. Hydrol. Earth Syst. Sci. 2010, 14, 1827–1841. [Google Scholar] [CrossRef]
- Jha, M.; Arnold, J.G.; Gassman, P.W.; Giorgi, F.; Gu, R.R. Climate Chhange Sensitivity Assessment on Upper Mississippi River Basin Streamflows Using Swat. J. Am. Water Resour. Assoc. 2006, 42, 997–1015. [Google Scholar] [CrossRef]

| Parameter * | Description | Initial Range | |
|---|---|---|---|
| Min | Max | ||
| From Soil | |||
| r_CN2.mgt | SCS runoff curve number | −0.4 | 0.4 |
| r_SOL_AWC.sol | Soil available water storage Capacity (mm H2O mm soil−1) | −0.4 | 0.4 |
| r_SOL_K.sol | Saturated hydraulic conductivity (mm h−1) | −0.8 | 0.8 |
| r_ESCO.hru | Soil evaporation compensation factor | −0.4 | 0.4 |
| r_OV_N.hru | Manning´s n value for overland flow | −0.4 | 0.4 |
| Groundwater | |||
| r_GWQMIN.gw | Threshold depth of water in the shallow aquifer for return flow (mm) | −0.8 | 0.8 |
| r_GW_DELAY.gw | Groundwater delay (days) | −0.8 | 0.8 |
| r_REVAPMN.gw | Threshold depth of water in the shallow aquifer for “revap” (mm) | −0.5 | 0.5 |
| r_RCHRG_DP.gw | Deep aquifer percolation fraction | −0.5 | 0.5 |
| r_GW_REVAP.gw | Groundwater “revap” coefficient | −0.4 | 0.4 |
| r_ALPHA_BF.gw | Base flow alpha factor (days) | −0.8 | 0.8 |
| r_ALPHA_BNK.rte | Base flow alpha factor for bank storage | −0.5 | 0.5 |
| Channel | |||
| r_CH_K2.rte | Effective hydraulic conductivity in channel (mm h−1) | −0.8 | 0.8 |
| r_CH_N2.rte | Manning´s value for main channel | −0.8 | 0.8 |
| Land use and land cover factor | |||
| r_EPCO.bsn | Plant uptake compensation factor | −0.5 | 0.5 |
| r_CANMX.hru | Maximum canopy storage (mm H2O) | −0.4 | 0.4 |
| Sub-basin | |||
| r_SURLAG.bsn | Surface runoff lag time | −0.5 | 0.5 |
| r_SLSUBBSN.hru | Average slope length (m) | −0.4 | 0.5 |
| r_ LAT_TTIME.hru | Lateral flow travel time (days) | −0.5 | 0.5 |
| r_HRU_SLP.hru | Average slope steepness (m m−1) | −0.4 | 0.4 |
| Objective Function | Equation * | Performance Rating | |||
|---|---|---|---|---|---|
| Very Good | Good | Satisfactory | Unsatisfactory | ||
| Percent bias (PBIAS) | |||||
| Coefficient of determination (R2) | |||||
| Nash-Sutcliffe efficiency (NSE) | |||||
| Kling-Gupta efficiency (KGE) | |||||
| Ratio of standard deviation of observations to root mean square error (RSR) | |||||
| River Name | Calibration | Validation |
|---|---|---|
| PBIAS | ||
| Paranaíba | −16.1 | −19.4 |
| Grande | −0.1 | −5.8 |
| Tietê | −1.3 | −10.7 |
| Paranapanema | −12 | −23.1 |
| Paraná | −9.8 | −18.5 |
| R2 | ||
| Paranaíba | 0.86 | 0.9 |
| Grande | 0.88 | 0.92 |
| Tietê | 0.88 | 0.88 |
| Paranapanema | 0.81 | 0.86 |
| Paraná | 0.88 | 0.91 |
| NSE | ||
| Paranaíba | 0.61 | 0.71 |
| Grande | 0.66 | 0.73 |
| Tietê | 0.73 | 0.66 |
| Paranapanema | 0.68 | 0.53 |
| Paraná | 0.56 | 0.51 |
| KGE | ||
| Paranaíba | 0.6 | 0.67 |
| Grande | 0.59 | 0.62 |
| Tietê | 0.67 | 0.61 |
| Paranapanema | 0.77 | 0.64 |
| Paraná | 0.55 | 0.55 |
| RSR | ||
| Paranaíba | 0.63 | 0.53 |
| Grande | 0.58 | 0.52 |
| Tietê | 0.52 | 0.58 |
| Paranapanema | 0.56 | 0.68 |
| Paraná | 0.66 | 0.71 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abou Rafee, S.A.; Uvo, C.B.; Martins, J.A.; Domingues, L.M.; Rudke, A.P.; Fujita, T.; Freitas, E.D. Large-Scale Hydrological Modelling of the Upper Paraná River Basin. Water 2019, 11, 882. https://doi.org/10.3390/w11050882
Abou Rafee SA, Uvo CB, Martins JA, Domingues LM, Rudke AP, Fujita T, Freitas ED. Large-Scale Hydrological Modelling of the Upper Paraná River Basin. Water. 2019; 11(5):882. https://doi.org/10.3390/w11050882
Chicago/Turabian StyleAbou Rafee, Sameh A., Cintia B. Uvo, Jorge A. Martins, Leonardo M. Domingues, Anderson P. Rudke, Thais Fujita, and Edmilson D. Freitas. 2019. "Large-Scale Hydrological Modelling of the Upper Paraná River Basin" Water 11, no. 5: 882. https://doi.org/10.3390/w11050882
APA StyleAbou Rafee, S. A., Uvo, C. B., Martins, J. A., Domingues, L. M., Rudke, A. P., Fujita, T., & Freitas, E. D. (2019). Large-Scale Hydrological Modelling of the Upper Paraná River Basin. Water, 11(5), 882. https://doi.org/10.3390/w11050882









