1. Introduction
Continuous runoff data is prerequisite for hydrological forecasting and water resource management. The reliability of hydrological decision-making increases as the accuracy of the runoff time series increases. However, because of the limitations of monitoring technology and the cost of monitoring, continuous runoff data is not always available, and frequently there are inadequate or no measurements for river basins [
1]. In China, a single hydrological station may control an area of more than 3000 km
2, so although there are monitoring stations on most large rivers, the number of stations is small relative to the size of the watershed. Monitoring stations are generally unevenly distributed, and many small catchments remain ungauged. Therefore, the estimation of continuous runoff is important.
There are many different methods that have been developed to estimate continuous runoffs in ungauged catchments or catchments with limited data. Regionalization is the most common way to address unmonitored catchments by transferring the information from donors to receivers [
2,
3,
4,
5]. The regionalization methods usually can fall into two categories, including model parameter-based methods and flow-based methods, these two categories can be achieved through regression and distance measurement or other methods [
6,
7].
The model parameter-based methods, which assume that the model parameter sets reflect the rainfall-runoff behavior, mean the model parameters are transferred. These methods basically involve the hydrological models [
8,
9,
10,
11,
12]. Among the model parameter-based methods, the parameter transfer (PT) method is the most widely used and give the best simulation [
13]. Both the spatial proximity method and the attribute similarity method are known as the PT method. Applications of the PT method are always influenced by the selection of catchment characteristics [
14,
15]. However, it take a lot of time and energy to achieve reasonable hydrological simulation because of the effort involved in parameter calibration. Also, due to the high heterogeneity in physical properties and complexity of hydrological processes, hydrological model simulation may not be accurate and the physical processes are hard to explain sufficiently well.
In the flow-based methods the runoff is transferred from donor to target. The area ratio (AR) method is the most commonly used flow-based method for transferring flow information. The standard AR method assumes that the runoff per unit area in the donor catchment is equal to that in the target catchment. The application of the AR method requires nothing but the runoff in donor catchment and the drainage area, which make it widely used to estimate daily runoff of catchments that are close [
16]. Many researchers suggested that a multiple-source sites AR method should be used, because the runoff in ungauged catchment is affected by several donor catchments [
16,
17]. On the other hand, different relationships between runoff ratio and area ratio also affect the estimation [
18]. AR methods usually give good simulation of the total runoff deviations [
19]. However, AR methods cannot explain the hydrological processes because the hydrological process is ignored.
Runoff estimation can be improved when different methods are combined rather than used individually [
4,
13,
20]. The estimation of runoff shows a good result when the spatial proximity method and physical similarity method are coupled [
3]. When the AR method is combined with standardizing flows, it performs better than the AR method on 60% of the sites [
19]. Multi-method transfer systems give more accurate simulation and a better explanation of actual hydrological processes than separate transfer methods, because the combined methods exploit the advantages and minimize the disadvantages [
21]. However, transfer methods are usually coupled with the method in the same category, and the transferred information is generally either related to only model parameter or only runoff information [
19]. The combination of the model parameter transfer method and runoff transfer method is seldom studied.
China has plentiful hydrological resources, with hydrological networks covering a large part of the country. Large basins often comprise many small catchments that are frequently hydraulically connected. The sub-watersheds in a basin share similar physical attributes and climatic characteristics, but can be considered separately because of heterogeneity. Due to technical challenges and the constraints on data-sharing policies [
22], it is still difficult to model ungauged catchments [
23]. In this study, therefore, we explored a combined transfer method which could be used to estimate continuous runoff in ungauged catchments. This method used two different categories methods, the PT method and the AR method, to provide estimation of daily and monthly continuous runoff in ungauged catchments. Also the donors’ selection was discussed when different transfer methods were used in this study. The main purpose of this study is to improve the ability to estimate continuous runoff in ungauged basin.
2. Materials and Methods
2.1. Study Area and Data
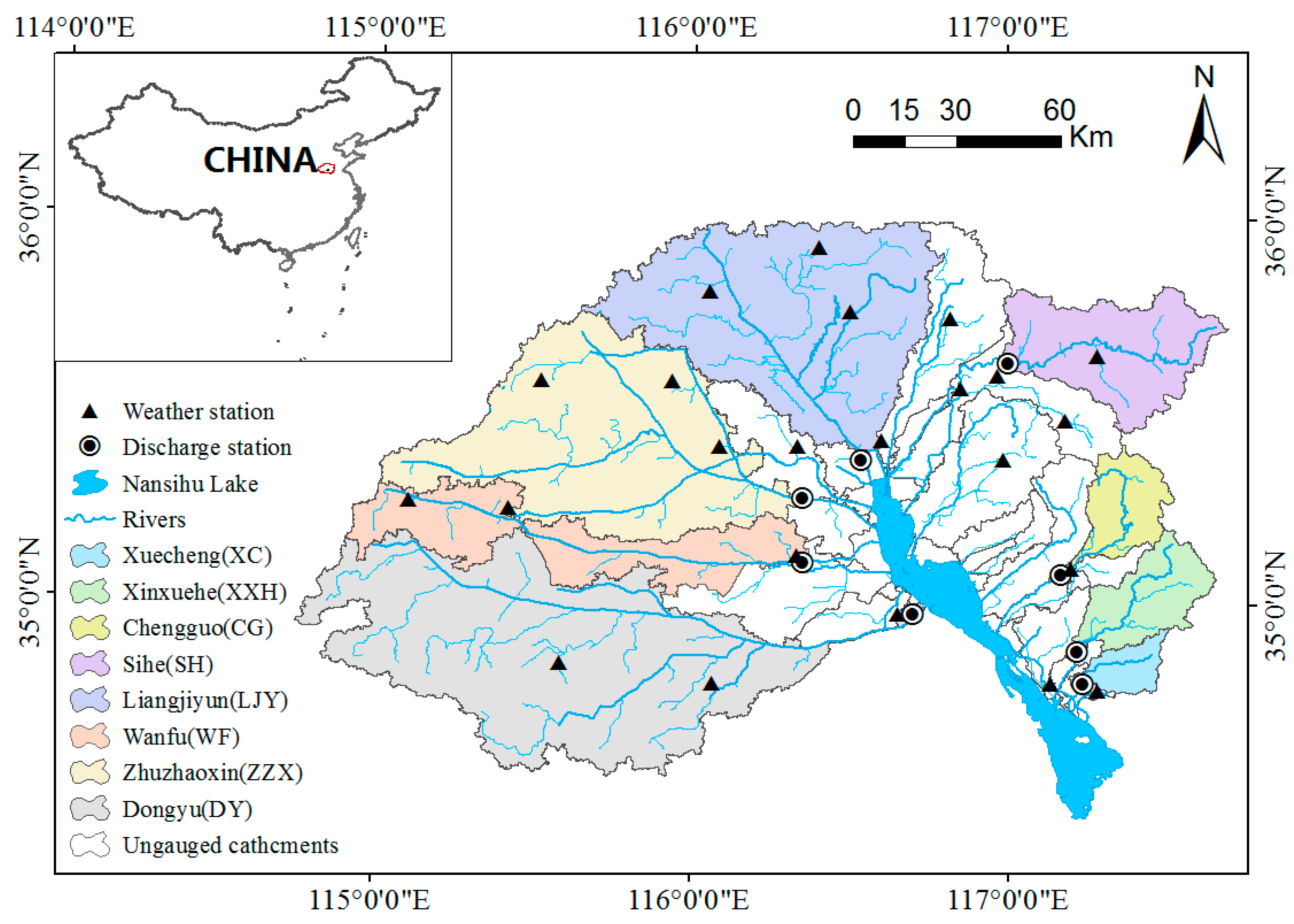
Nansihu Lake is the largest freshwater lake in northern China and also is the main regulating and storage hub for the eastern route of the South-to-North Water Transfer Project. Nansihu Lake Basin, which covers approximately 27,700 km
2, is mainly in Shandong Province but also extends to Jiangsu, Henan, and Anhui Provinces, China (114°47′–117°42′ E, 34°27′–36°0′ N). Seventeen major rivers flow into the lake, of which 11 drain into the eastern part and seven drain into the western part. Nansihu Lake Basin can be divided into two topographically-diverse areas, namely the mountains to the east and the plain to the west. There were eight gauged catchments selected for this study, and they were Xuecheng (XC), Xinxuehe (XXH), Chengguo (CG), Sihe (SH), Liangjiyun (LJY), Wanfu (WF), Zhuzhaoxin (ZZX) and Dongyu (DY), four on both sides respectively. The catchments’ characteristics are detailed in
Table 1.
The main land use types in the mountainous area include agriculture (62.2%), grasslands (16.17%), construction land (12.84%), forest (4.96%), water (3.22%), and barren land (0.61%); in the western plain area, 78.8% of the land is used for agriculture, 16.84% is construction land, 2.44% is water, 1.00% is forest, 0.55% is grassland, and 0.37% is barren. The soil types are quite different in the two parts. Soils in the mountainous area include luvisols (44.84%), fluvisols (19.10%), regosols (18.5%), cambisols (10.97%), vertisols (5.01%), 0.41% gleysols (0.41%), and anthrosols (0.13%); soils in the plain area are mainly fluvisols (85.59%), with cambisols (5.08%), anthrosols (2.06%), luvisols (2.05%), gleysols (1.49%), vertisols (1.41%), solonetz (0.67%), arenosols (0.58%), regosols (0.36%), and solonchaks (0.23%) also present.
The study area has a continental monsoon climate, the monsoon dominates the rainfall and is the main source of runoff. The average annual rainfall ranges from 769 to 816 mm, and more than 85% of the rainfall occurs during the rainy season from July to September. Because most of the rainfall was converted to runoff, we concentrated on the period from July to September in this study. The annual average temperature in the study area ranges from 13.2 °C to 14.0 °C. The national meteorological stations and discharge stations in the study area were showed in
Figure 1.
Data for the study was either downloaded from public domains or collected from local government agencies (
Table 2). Topographic data was provided by Geospatial Data Cloud site, Computer Network information Center, Chinese Academy of Sciences (GDEMDEM 30M); land-use data was downloaded from Data Center for Resource and Environmental Sciences, Chinese Academy of Sciences (2005); soil data was obtained from the Food and Agriculture Organization (2009); meteorological data was obtained from the China surface climate data daily data set (V3.0, China Meteorological Administration, Beijing, China) in the National Meteorological Information Center; the hydrology data was collected from the local water management bureau. Information about the data sources was detailed in
Table 2.
2.2. Description of the Hydrological Model
The United States Environmental Protection Agency (US-EPA) watershed modeling system, Hydrological Simulation Program-FORTRAN (HSPF), was selected for this study. Better Assessment Science Integrating Point and Nonpoint Sources (BASINS) is an integrated environmental simulation and analysis system that includes an open source geographic information system (GIS); watershed and water quality models, e.g., HSPF, SWAT (Soil & Water Assessment Tool), SWMM (Storm Water Management Model), PLOAD (Pollutant Loading Application); meteorological data processing tools, and post-processing data analysis tools [
24]. As a core program in BASINS, the HSPF model can simulate the movement of water, sediment, and point and nonpoint source pollution loads using physical data and empirical equations [
25]. Three main modules are considered in HSPF, including pervious land (PERLND), impervious surface area where little or no infiltration occurs (IMPLND), and stream channels and reservoirs (RCHRES), respectively [
25]. Together, these modules can represent the hydrologic cycle in a watershed. Different modules are activated for various simulation requirements [
26,
27]. In this study, various model parameters were calibrated manually.
2.3. The Parameter Transfer Method Based on Model Parameter Transferred
The PT method, which assumed that the model parameter sets reflect the rainfall-runoff behavior, was used to transfer the model parameters from gauged to ungauged catchments. The physical similarity was often used to identify the model parameter donor and receiver based on the assumption that the physical characteristics of catchment determine the hydrological response behavior [
28]. However, climate characteristics were also important factors affecting runoff, so both climate and physical characteristics should be considered when the donor was selected. Many basic physical and climatic attributes had been shown to influence runoff [
29,
30,
31,
32,
33]. Also, some indices, such as rainfall-area ratio, representing the rainfall and runoff response were also used [
5]. In this study, 10 different indices were considered, including elevation difference, average slope, channel length, drainage density, soil average particle size, pervious area, average annual rainfall, average annual temperature, rainfall-area ratio and the rainfall-runoff ratio. Three groups were set up to verify the effect of different attribute sets on the runoff. The first group (PC), including elevation difference, average slope, channel length, drainage density, soil average particle size, pervious area, average annual rainfall, and average annual temperature, considered both physical attributes and climate characteristics. The second group (RR) focused on the relationship between the rainfall-runoff response, and it consisted of the pervious area, average annual temperature, and the rainfall-runoff ratio. The third group (RA) focused on the correlation between rainfall and the catchment area, and it comprised the average annual rainfall, average annual temperature, and rainfall-area ratio.
It was important how to identify the donors and the receivers both in the model parameter transfer method and the flow transfer method [
34]. Random forest [
35], Cluster analysis [
36,
37] and other methods were used to identify homogeneous regions. In this study, hierarchical clustering was used to group catchments with indices in PC, RR and RA groups respectively. The catchment with the best model simulation performance in each group was considered as donor, and the others in the same group were target catchments. We also made some gauged catchments as target catchments (generally ungauged catchments) for validation purposes. The one that performed best in these three groups was recommended for the following analysis.
2.4. The Drainage Area Ratio Method Based on Flow Transferred
The AR method, which assumed that the runoff per unit drainage area was equal across hydrological-similar basins, was chosen as the runoff transfer method to predict the runoff in ungauged catchments. With cluster analysis, catchments with more similar physical and climate characteristic were grouped together. Therefore, the AR method was applicable to such a watershed with similar physical and climatic characteristics. In the AR method, the daily runoff for a given day was predicted as:
where
Qy,t was the predicted runoff on day t at the target catchment,
Qx,t was the measured runoff on day t at the donor catchment,
Ay was the area of the target catchment, and
Ax was the area of the donor catchment.
Based on the grouping results, the mathematical relationship between the drainage area ratio and the average annual runoff ratio was established for each clustering group. Daily runoff in the target catchment was calculated from the mathematical relationships. As the mathematical relationships differ, the runoff calculations also differ. Both standard and non-standard AR methods were considered when establishing the mathematical relationships, and Equation (1) was expressed as Equations (2) and (3):
2.5. The Improved Method Based on Performance-Weighting
The AR method was generally more reliable for calculating annual runoff as the deviation of annual runoff could be controlled more easily with the AR method than with the PT method. The mathematical relationships in the AR method relied on annual runoff but ignored the accuracy of daily runoff. Therefore, we tried to combine PT method and AR method to explore whether weighted estimation was feasible. Since the combined method aimed to optimize the large deviation of annual runoff caused by the PT method, the weight factor focused on the runoff calculated by the PT method. The formula for the weighted sum was calculated as follows:
where
Q was the final calculated daily runoff,
QPT was the daily runoff calculated with PT method, Q
DAR was the daily runoff calculated with AR method, and w was the weighting factor, which ranged from 0 to 1.
The method used to determine the weighting factor,
w, is important. A major objective of our study was to optimize the deviation in the annual runoff calculated by PT method, so we needed a weighting factor that was inclined to the PT method. The Nash coefficient was used to obtain the weighting factor [
19]. The weighting factor, w, was given by:
where E
NS,DAR was the Nash coefficient obtained with the AR method, E
NS,PT was the Nash coefficient obtained with the PT method, and w ranged from 0 to 1. As
w approached 1, the performance of the PT method improved, and as
w approached 0, the performance of the AR method improved. The weighting factor differed when the Nash coefficients were applied to different time scales. Four sets of weighting factor were calculated to determine the best runoff performance, namely those calculated by daily Nash coefficients (DC), monthly Nash coefficients (MC), the average of the daily and monthly Nash coefficients (DM), and without weighting and using a value of 0.5 for
w (AA).
2.6. Evaluation Methods
Simulation and calculation results were evaluated with the Nash–Sutcliffe efficiency coefficient (E
NS, Equation (7)) [
38] and the coefficient of determination (R
2, Equation (8)). E
NS was used to evaluate the efficiency of the hydrological model and was defined as:
where
Qobs,i was the observed runoff, and
Qsc,i was the simulated or calculated runoff. The values of E
NS ranged from minus infinity to 1, and higher values indicated better agreement. When E
NS was greater than 0.5, the simulation result was considered satisfactory [
39].
The
R2 described the fitting result between the observation and the simulation or calculation and was defined as:
where
Qobs,i was the observed runoff and
Qsc,i was the simulated or calculated runoff. The R
2 ranged from 0 to 1, and a higher value indicated better agreement.
The percent bias (PBIS, Equation (9)) was an indicator of the goodness of fit. It described the magnitude of the average error and was defined as:
where
Qobs,i was the observed runoff and
Qsc,i was the simulated or calculated runoff. As the PBIS approached 0, the deviation between the simulated and the observed data decreased, while, when the PBIS was smaller than 25%, the simulation result was considered satisfactory [
39].
3. Results
3.1. Model Calibration and Validation
To confirm the performance of the PT method, the hydrological model needs to be calibrated and verified to obtain the model parameters that can be transferred. Seven parameters were estimated during the manual calibration, including the lower zone nominal storage, LZSN; the index to infiltration capacity, INFILT; the groundwater recession parameter, AGWRC; the fraction of groundwater inflow that goes to inactive groundwater, DEEPER; the upper zone nominal storage, UZSN; the interflow inflow parameter, INTFW; and the interflow recession parameter, IRC. The model performance during the calibration and validation of the runoff in the gauged catchments was detailed in
Table 3. During the calibration period, daily E
NS and R
2 of each catchment were greater than 0.60, and all the monthly E
NS and R
2 values were greater than 0.76, with most above 0.80; PBIS values were within 10%. The monthly results were better than the daily ones in all catchments during the calibration period. During the validation, the model did not perform well particularly for XXH catchment. While, model performance of SH catchment was good and daily E
NS and R
2 values and monthly ones were greater than 0.61 and 0.85, respectively. Monthly E
NS and R
2 value of LJY, SH, CG, XXH and XC catchment showed better results than daily ones, but the others did not.
In this study, the model performance was reliable if E
NS and R
2 were greater than 0.5 and PBIS was within ±25%; model performance was good when E
NS and R
2 were greater than 0.65 and PBIS was within ±15%. The model calibration and validation results in eight catchments showed that the model generally gave reliable results for this natural basin. The catchment grouping method and the way to identify information donors were described in
Section 2.3, and grouping results are shown in
Table 4. Given the model results, donors in each catchment group were LJY, SH, CG, and XC, respectively. Monthly E
NS in the donor catchments ranged from 0.79 (LJY) to 0.96 (XC) during the calibration, and from 0.45 (LJY) to 0.85 (SH) during the validation. Daily E
NS ranged from 0.68 (LJY) to 0.94 (XC) during the calibration and from 0.32 (XC) to 0.61 (SH) during the validation. Model performance of donors is important for the following transfer methods, and these results are relatively good and can be used in the following analysis.
3.2. Performance of Model Parameter Transfer Method
The clustering results changed as the clustering factors vary, which affected the results of donors and receivers, and also affected the performance of the PT method. To confirm that the PT method was suitable in this study area, three different clustering schemes were set up to determine the donors and receivers (see
Section 2.3), and applied the PT method to each group. Model parameter donors and receivers of each group were shown in
Table 4. The results after model parameter transfer (PC, RR, and RA) were compared with the results from the parameter calibration (CR) (
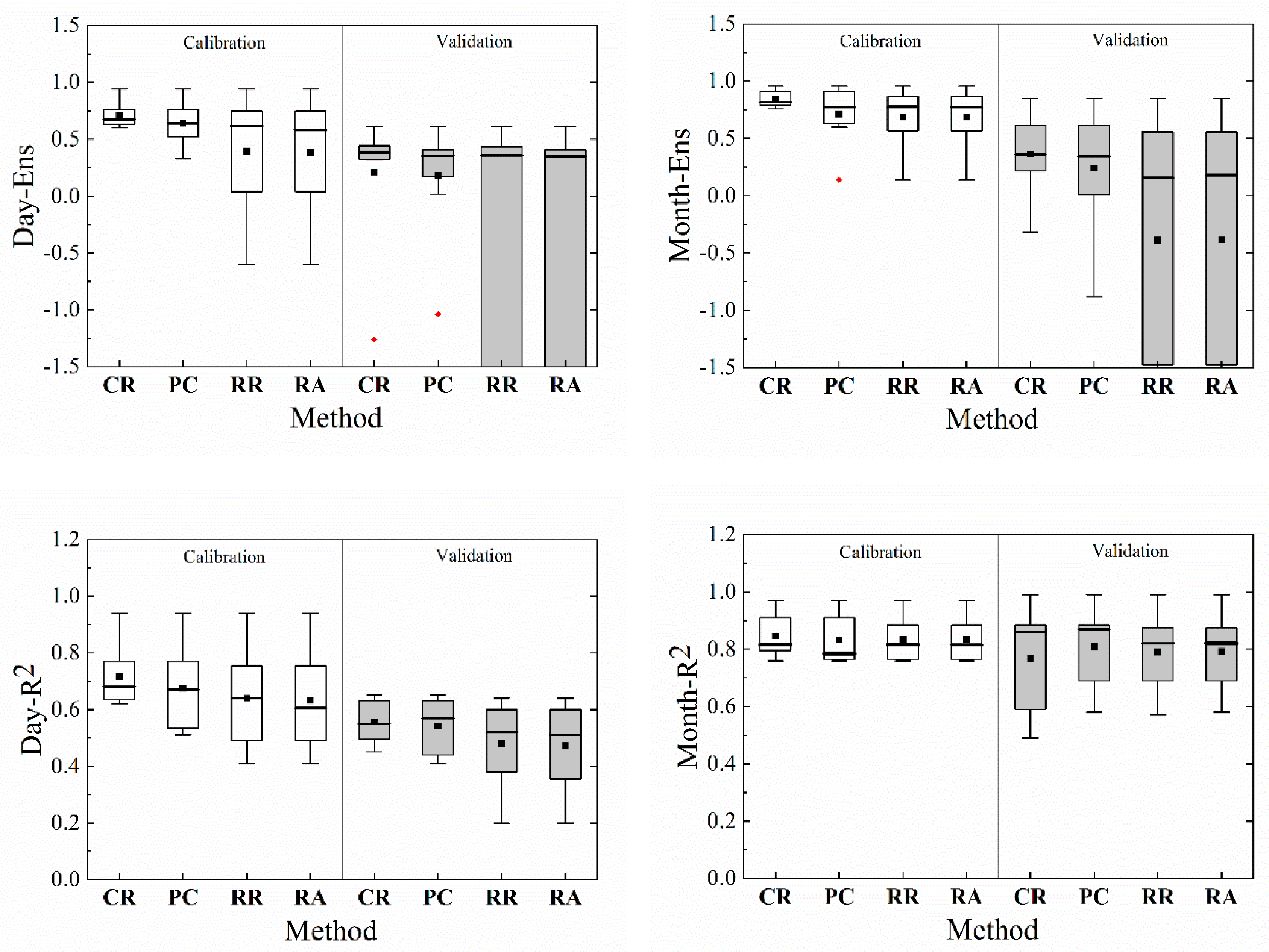
Figure 2).
As shown in
Figure 2, E
NS and R
2 values were lower, and PBIS were also larger, for PT methods than those for the CR. The range of monthly R
2 did not vary much when compared with that of CR, particularly in the validation period. Compared with CR, E
NS value became scattered and PBIS value increased after parameter transfer. Three PT methods tended to underperform relative to CR. The performance of PC for all four indicators except monthly R
2 was significantly better than that of RR and RA and was closer to the range of CR values. The pattern was even more pronounced in E
NS. With the exception of the low monthly E
NS in ZZX (0.14), E
NS values of PC and CR were similar during the calibration period. So the performance of daily and monthly runoff of each indicator deteriorated after parameter transfer. Considering the particularly large values of PBIS, the performance of PC was generally good in three PT methods. Even though the PC group gave the best result, the runoff deviation was still not in the satisfactory range. The PC group was selected as an example in the following study, because it was the best group in the PT methods, namely, eight gauged catchments were clustered into four groups, and LJY, SH, CG, and XC were the parameter donors in each group.
3.3. The Applicability of the Different Area Ratio (AR) Method
In this study, two scenarios were considered in the AR method; the area ratio and runoff ratio were equal in the first (the standard AR method), but were not in the second (the non-standard AR method), and are shown in Equations (2) and (3). Runoff donors and model parameter donors were the same, because the donors’ results were the best in their own groups. Due to the data limitations, AR method was only applied to the PC1 group and LJY was the runoff data donor and DY, WF, and ZZX were the receivers.
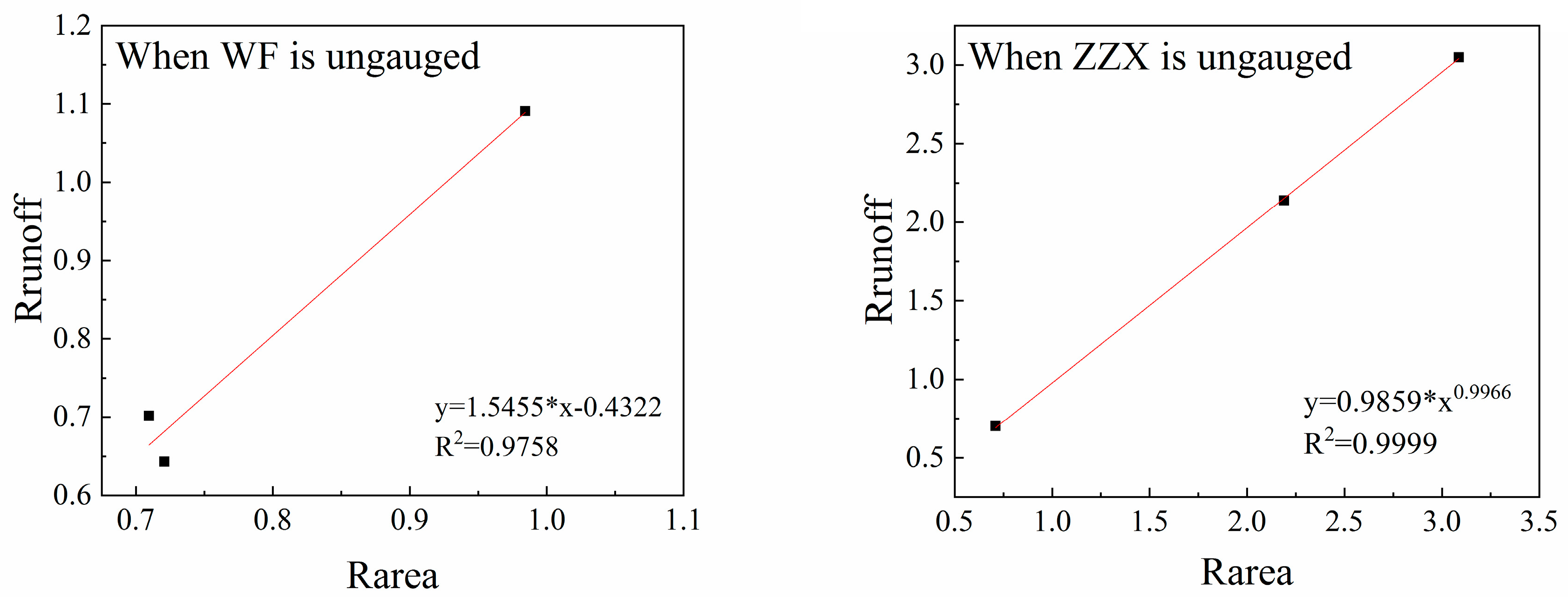
Runoff of the target catchment for the standard AR method was calculated directly with Equation (2), while the formula for calculating the target catchment runoff for the non-standard AR method was developed from the data of the other three catchments. Two catchments were chosen as runoff donors for calculating the runoff in LJY, namely, WF, which had the second best performance in the PC1 group, and ZZX, which was most strongly correlated with the climatic and physical properties of LJY. The equation of the non-standard AR method for each catchment is shown in detail in
Figure 3, and the calculated results were compared with the observed runoff according to Equations (7)–(9).
3.3.1. Comparison of the Standard AR Method and the Non-Standard AR Method
The formula used to calculate runoff in a target catchment affected the runoff transfer results when the AR method was used. Therefore, we compared the standard and non-standard AR methods. The results (
Figure 4) show that, the relationship between the area ratio and the runoff ratio had no obvious influence on R
2 in all considered sites, but did influence E
NS and PBIS. R
2 value and E
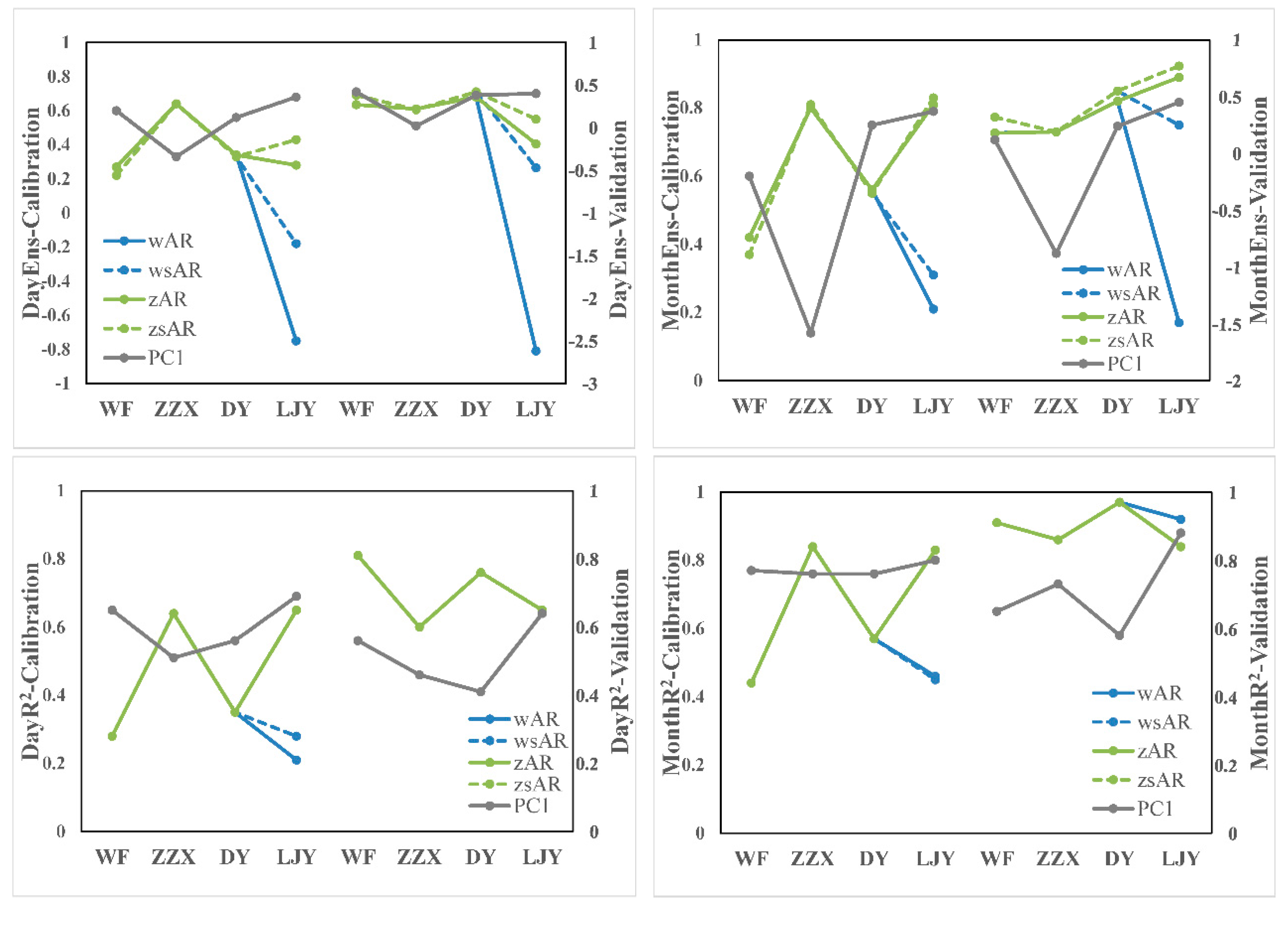
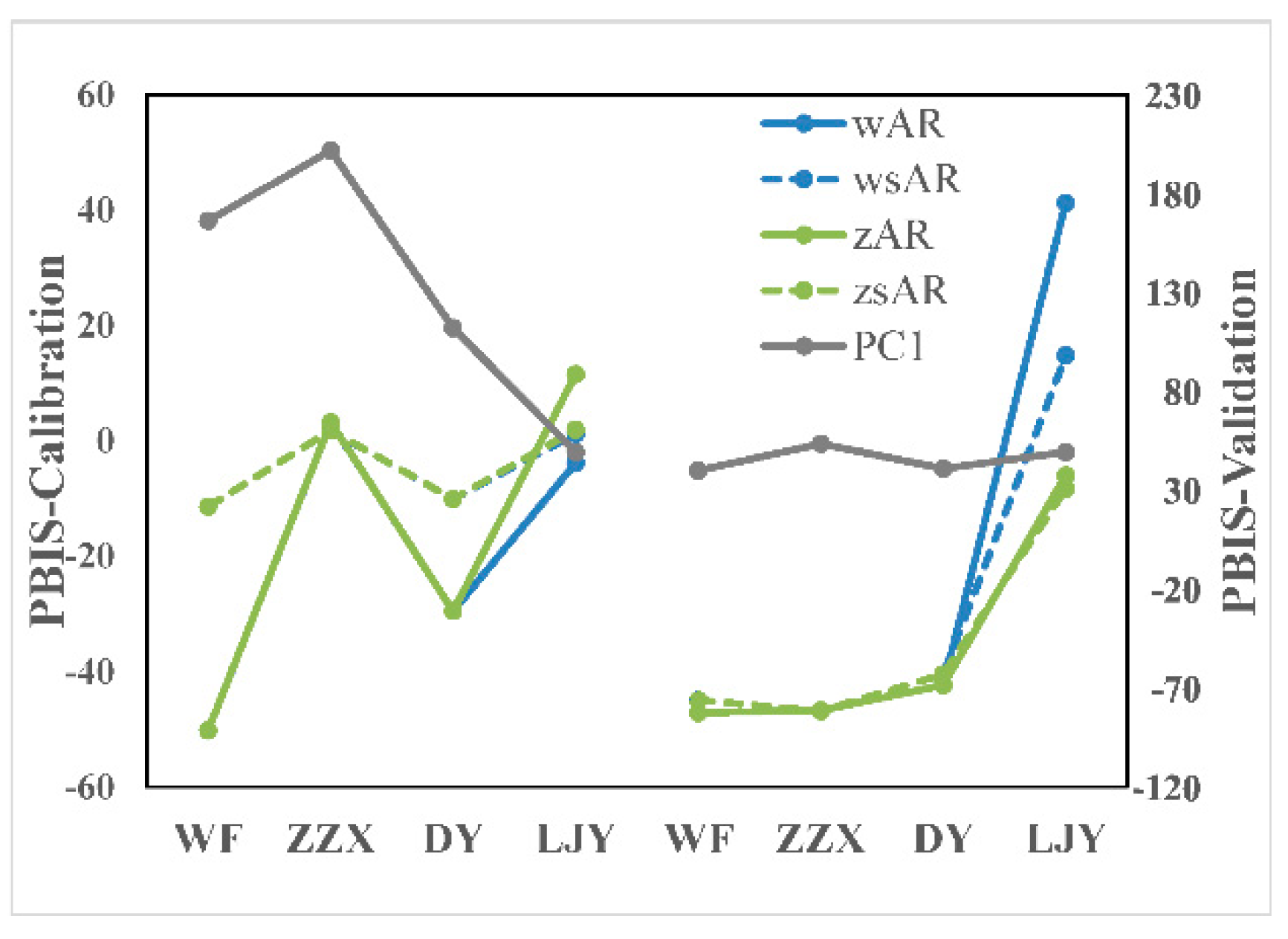
NS value in LJY were slightly higher for the standard AR method than for the non-standard method. PBIS values for the standard AR method ranged from −11.42 to 1.8, and were satisfactory at all sites, while those of the non-standard AR method were only satisfactory for 50% of the considered sites. Even though there were differences, PBIS values for both scenarios were good. Therefore, in this study area, when the area ratio and runoff ratio were considered to be equal, the AR method showed good results.
3.3.2. Performance of AR Method Based on Different Runoff Donors
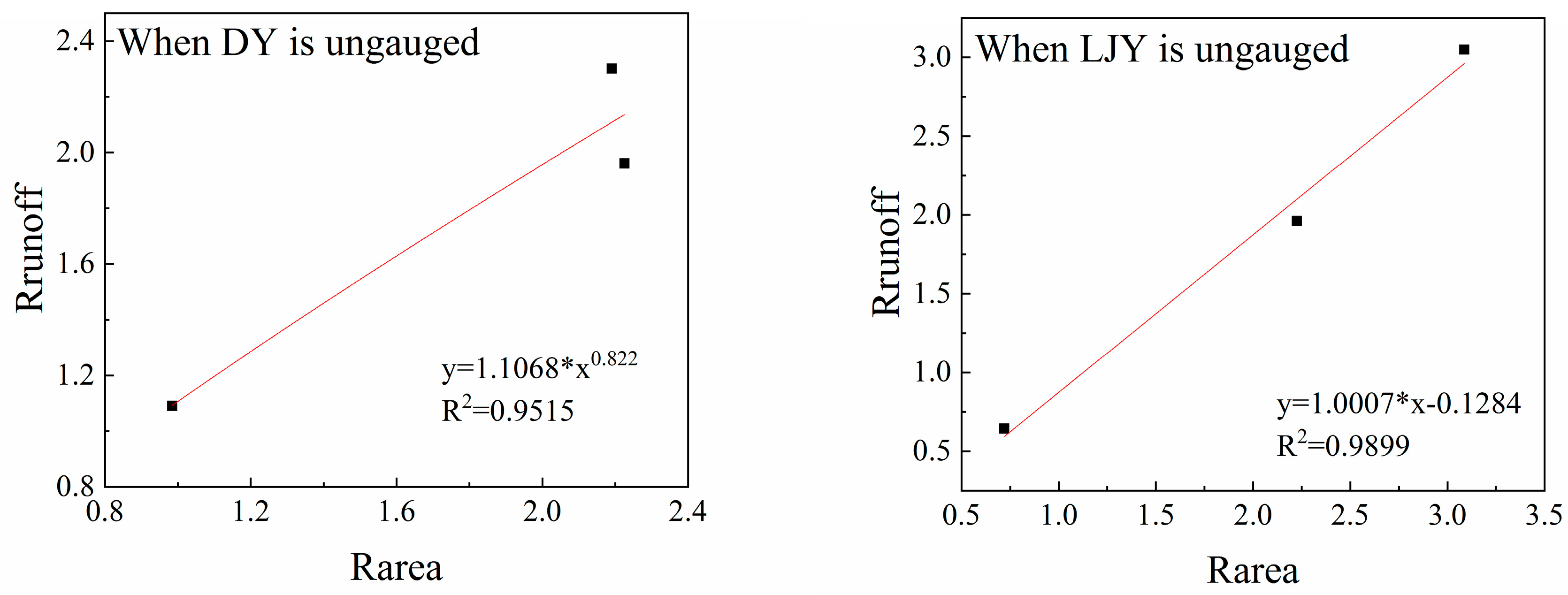
In the AR method, the runoff donors needed to be selected carefully. To calculate the runoff of LJY, which was the donor of the other three catchments in group PC1, we used WF, which performed well in the model parameter calibration period, and ZZX, which had more similar physical attributes with LJY, as the runoff donors for the calculation. These two scenarios were compared. The results (
Figure 4) show that the values of E
NS and R
2 with ZZX as the donor (zAR and zsAR) were higher than those with WF as the donor (wAR and wsAR). During the calibration period, the values of daily E
NS were low (0.28 in zAR and 0.43 in zsAR), and the other indicators performed well. Monthly E
NS was above 0.81, and values of daily and monthly R
2 exceeded 0.65 and 0.83, respectively. PBIS values of both AR methods were −3.84 and 11.54, which were within the satisfactory range. During the validation period, daily E
NS showed a poor performance and PBIS was obviously unsatisfactory. On the whole, when ZZX was used as the runoff donor for LJY, the AR method performed better on all the above indicators in the calibration and validation periods.
3.3.3. Comparison of AR Method and Parameter Transfer (PT) Method
The AR and PT methods were compared by the results of three receiver catchments, WF, ZZX, and DY, using model parameters and runoff from LJY.
Figure 5 shows that PT method (PC1) performed better in all indicators but monthly E
NS than AR method during the calibration period, especially in PBIS, while PBIS was good during the validation period. Although unstable, PBIS value was better than that of AR method at some considered sites. When we focused on the PT method, E
NS of ZZX were outside of the satisfactory range, but daily and monthly E
NS values in WF and DY were above 0.56 and 0.60, respectively. Daily and monthly R
2 values were greater than 0.56 and 0.60, respectively. PBIS values ranged from 19.59 to 38.13, which were not very good. Considering the previous analysis, PBIS results from zsAR were compared with that from PC1, the values for the AR method ranged from −11.42 to −1.95 during the calibration period, while the results of PT method ranged from −1.96 to 50.33, which were much higher than the acceptable range. In the absence of parameter transfer, PBIS values for the validation period tended to be high and ranged from 16.36 to 40.11, which indicates that the high runoff deviation was not only caused by the transfer of model parameters. Both methods gave poor PBIS values during the validation period. Overall, the PT method gave better results in WF and DY, while the AR method performed better in ZZX during the calibration period (
Figure 4), and the PT method showed good performance stability during the validation period.
3.4. Continuous Runoff Estimation by the Different Combination Methods
Based on the results for
Section 3.3, the standard AR method with ZZX was selected as the runoff donor. To ensure that the results could be compared, four catchments in the group PC1 (
Table 4) were chosen as the study area for the combined method. To find the best way to combine the PT method (PC1) and AR method, four weightings were compared, and the most reasonable weighting was used to calculate the runoff in the target catchment. The methods for calculating and setting the weighting were described in detail in
Section 2.5.
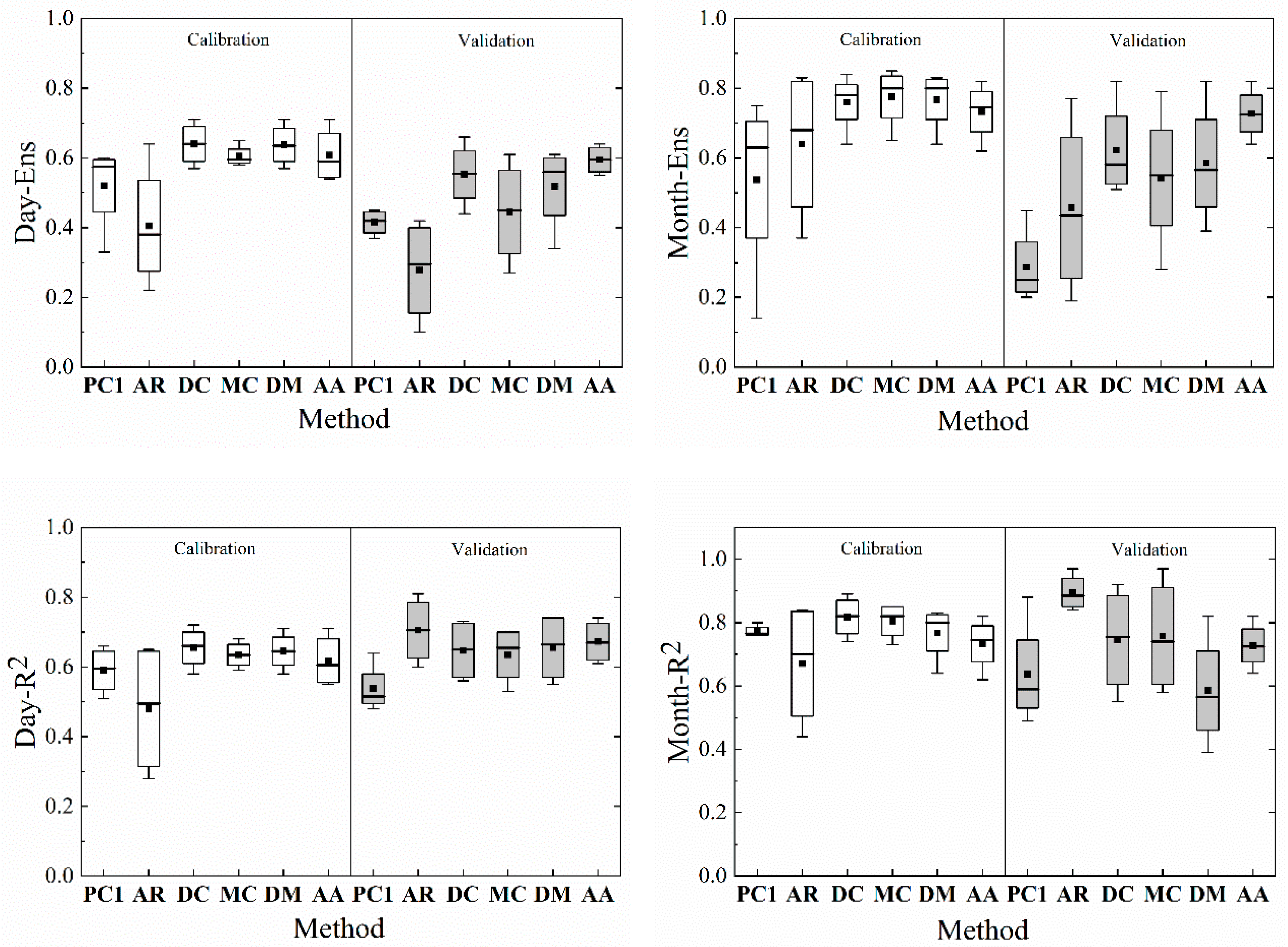
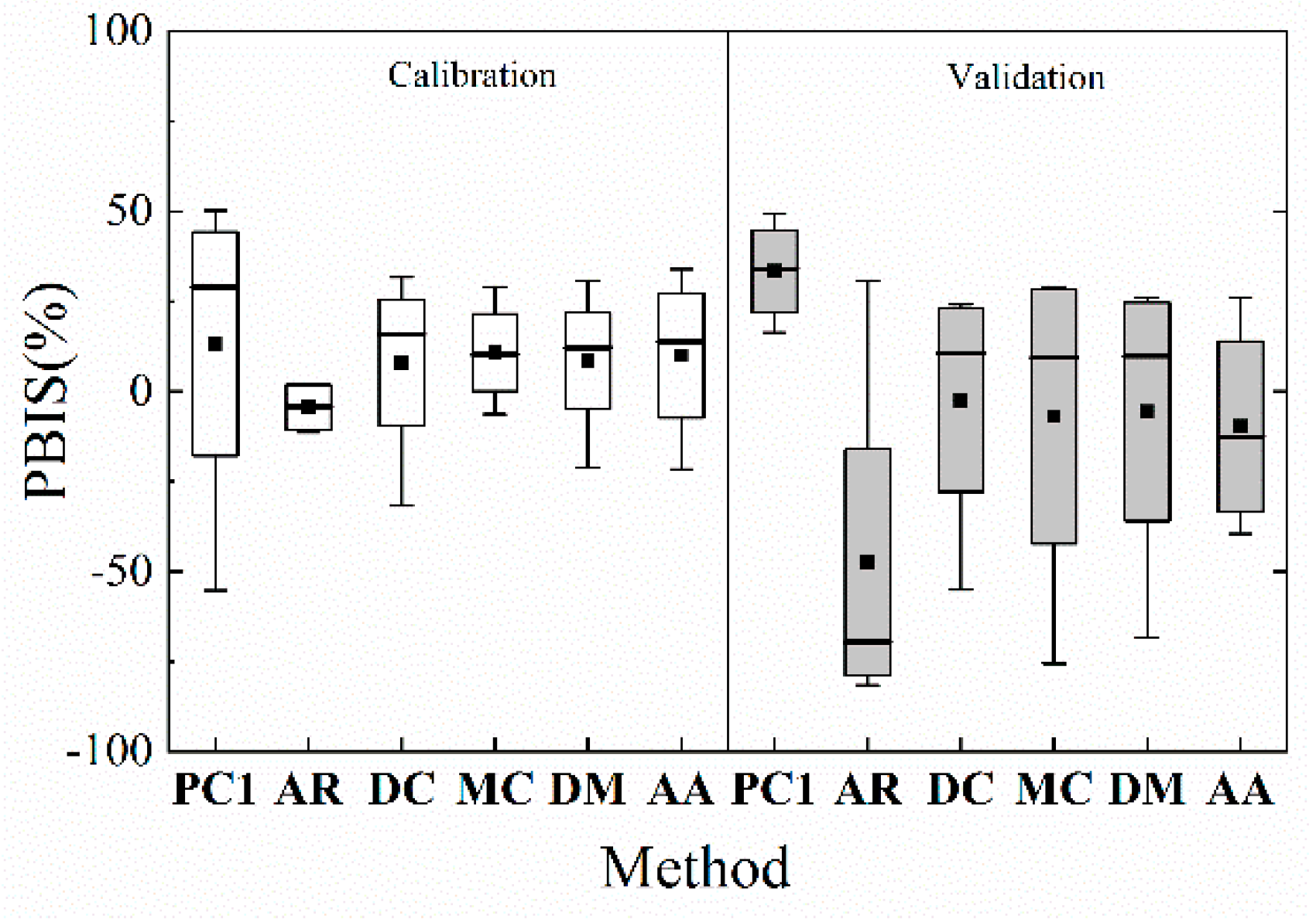
Overall, these four combined methods performed better than either PT or AR methods on their own in the study area (
Figure 5). E
NS values for the calibration period show that the performance of four combined methods was better than that of the PT and AR methods, and the performance was stable in each catchment area. The range of R
2 values for four combined methods was close to that of the PT method, and was much better than that of the AR method. Daily and monthly R
2 values were generally slightly higher and lower than those of the PT method, respectively, but the ranges were still satisfactory. PBIS values were not as good for the four combined methods as for the AR method, but were much better than those for the PT method. During the validation period, E
NS value showed a similar rule with the results in the calibration, and the R
2 value of the AR method was higher than those of four combined methods. Despite this, daily R
2 values of the combined methods were still higher than those of the PT method, and the range of monthly R
2 did not differ significantly from that of the PT method. The performance of four combined methods indicated by PBIS during the validation period was also better than that of two single transfer methods. Even though the range of PBIS was larger than that for the AR method, the mean and median value were closer to 0. So, the results above all showed that the combined methods performed better than the PT and AR methods alone.
While the four combined methods followed similar rules when compared with the PT and AR methods, their performance for each combination was different, and some combinations gave better performance in the study area than others. Therefore, we ranked four combined methods for the calibration and the validation periods by the mean values and the highest values of each indicator. Based on daily ENS value in the calibration period, four methods were ranked as DC = DM > AA > MC, and MC was the most stable. For monthly ENS value in the calibration period, the order was MC > DC > DM > AA. The rankings for daily and monthly ENS values in the validation period were the same, and were ranked AA > DC > DM > MC, and the AA method was the most stable. Therefore, for ENS, the DC and AA methods were ranked highest and had the best performance. Daily and monthly ENS values of the DC method ranged from 0.44 to 0.66, and from 0.51 to 0.82, respectively. Daily and monthly ENS values of the AA method ranged from 0.55 to 0.64, and from 0.64 to 0.82, respectively. Daily R2 values in the calibration and the validation periods were ranked as DC > DM > MC > AA and AA > DM > DC > MC, respectively. Monthly R2 values in the calibration and validation periods were ranked as DC > MC > DM > AA and MC > DC > AA > DM, respectively, and the AA method was the most stable. Even though the results of R2 differed over various time scales, the DC method performed best, and values for daily and monthly R2 ranged from 0.56 to 0.73, and from 0.55 to 0.92, respectively. The AA method was the most stable; daily and monthly ENS values for the AA method ranged from 0.61 to 0.74, and from 0.64 to 0.82, respectively. However, R2 values did not differ much among the combined methods, especially daily R2 values, and daily R2 values of these methods were similar. As PBIS values approached 0, the model results improved. Therefore, we judged the PBIS on the mean and median. The range of PBIS value for each method differed only slightly between the calibration and validation periods. MC was the most stable during the calibration period, and AA was the most stable during the validation period. The deviations in the runoff in each catchment were examined. The large deviation in ZZX, from −27.26 to −75.61, caused the range of PBIS values in the study area to increase. Among four combined methods, the method with the weight calculated by daily ENS (DC) performed best in the study area, while the method where the weight was set at 0.5 (AA) was the most stable.
4. Discussion
The physical characteristics of catchment affect the runoff. The calibration and verification results of model showed that the performance of the model was different in catchments with different characteristics. The model performed better in catchments with large average elevations and small catchment area, such as SH, CG, XXH, and XC than the others (see
Table 1 and
Table 3). The HSPF model usually performed better for simulating runoff in small watersheds than large watersheds [
40]. On the whole, monthly results of the model simulation were better than daily results, and most hydrological models did have better performance on the long-term scale [
40,
41]. The daily rainfall-runoff process was more variable than the longer timescale, and the monthly runoff calculation ignored the influence of daily change, but showed a comprehensive change trend. At the same time, different physical characteristics of catchment also affect the variation of daily scale runoff, because of the hysteresis of runoff response.
The reasons for the poor performance of RR and RA in the study area were examined, and results showed that SH, a parameter donor of CG and XXH, caused E
NS and R
2 to decrease. Groupings in RR and RA were mainly influenced by the rainfall–runoff ratio, the pervious area, and the runoff per unit area. The differences in these factors meant that there were fewer clustering factors, so SH, CG, and XXH were similar when there were only a few influencing factors. In the PC group, which had more clustering factors, CG and XXH were more similar than SH (
Table 1). So, physical attributes combined with the climate characteristics showed a successful recognition of the class of catchment in this study. Therefore, in this study area, the similarity between donor and receiver was determined with considering both physical and climatic characteristics. This deserves some attention, as when only a few factors are used important information may be ignored, which affects the accuracy of the parameter transfer results. The results from the PT methods showed that the performance of XXH were not good for all the PT methods, but the performance of XXH was unsatisfactory for CR, especially during the validation period, which showed that the transfer of the model parameter was not the only reason for the poor results. This also proved that information donors in the transfer method were important, which was also reflected in the application of the AR method. As shown in
Figure 4, when ZZX was donor, AR method performed better on all indicators than when WF was. The physical characteristics of ZZX were closer to the receiver, LJY, while WF was the best-performing catchment in the same group during the parameter calibration period, and the best-performing catchment in the model calibration period was usually the donor in the PT method. Therefore, donors determined from the model calibration results were not suitable for the AR method in this study area, because of the uncertainty introduced during the parameter calibration, especially during the manual calibration. This result also indicated that, in this study area, the AR method supported the hypothesis that physical attributes and climatic characteristics both affected the runoff response. The calculation formula also affected the application of the AR method. When different calculation formulas were tried, the results of the standard AR were better than that of non-standard AR method in this study area (
Figure 4). The standard AR method considered that the runoff per unit area was equal, ignoring the runoff deviation caused by heterogeneity. But this deviation might be related to the degree of difference in physical characteristics. The larger the area difference between the donor and the receiver, the more obvious the deviation caused by heterogeneity would be. However, the area difference between these two in this study area was not large enough to generate the deviation that could be considered. Hortness [
42] and Ries [
43] considered that the standard AR method was more accurate when the ratio of the drainage area between the donor and the target was between 0.5 and 1.5 or between 0.3 and 1.5. The area ratio in this study ranged from 0.46 to 1.41, which was almost consistent with the conclusion of Hortness [
42].
The comparison results showed that, except for monthly R2, the combined method performed better than the AR method and the PT method. In particular for the indicator ENS, the combined method had been significantly improved. The PT method used model parameter described different hydrological processes and did not restrict the total runoff, so the PT method laid more emphasis on runoff results without considering hydrological processes, while ignoring the influence of climate as a driving factor on runoff. The combination of these two methods while weakening the AR method on the total flow deviation, to a great extent optimized the PT method on total flow deviation, and retained the good performance of the PT method in the hydrological process. The results of the four combinations were different because of the weight. When WF, ZZX, DY and LJY runoff were calculated, weight values ranged from 0.50 to 0.79, from 0.05 to 0.5, from 0.5 to 0.76, and from 0.20 to 0.66, respectively. With a wide range of weight changes, the combined methods performed differently, especially in ENS and monthly R2 during the validation period. Among four combined methods, the one with the weight obtained by daily ENS (DC) performed best, and the one with the weight is 0.5 (AA) performed most stable in all considered sites and even better than DC during the validation period. Compared with the simple sum method (AA), complex weight calculation methods such as DC, MC and DM did not bring an obvious improvement. It seemed that it was not worth the added complexity to calculate weight when combined methods offer only small improvements. These results were based on limited data and the conclusions could be verified further in other study areas if more data was available. That said, we believe that these methods and results would be a useful reference for applications in other study areas.
5. Conclusions
An information transfer method provides a useful way to estimate continuous runoff in ungauged catchments. However, most studies focus on the improvement of the same type of transfer method, while the improvement of the combination of different types of transfer methods is often ignored. An improved regionalization method that combined the PT method which was based on model parameter and the AR method based on flow were discussed, and the estimations of daily runoff and monthly runoff from the combined method and the PT and AR methods were compared.
A lake basin in eastern China was chosen as the study area. The results for the PT method using physical attributes and climatic characteristics to determine the donors and receivers were better than those based on either the rainfall runoff ratio or the runoff area ratio. The performance of 40% of the receivers was satisfactory as shown in daily and monthly ENS, and R2 that followed the same pattern as ENS. The deviation of the total runoff was large at most sites and was only satisfactory in one receiver site.
Using the standard AR method, ENS was large in both the calibration and validation periods, and the PBIS value in the calibration period was generally within 11.42%. While the deviation of the runoff in the validation period was relatively large, it was still less than that of the non-standard AR method. In addition, the evaluation results for LJY were better than those for other catchments when the donor was ZZX, which was more physically and climatically similar to LJY than the other catchments.
The performance of the PT and AR methods was compared and results showed that the ENS and R2 of the PT method were better than those of the AR method, but the runoff deviation was lower for AR method than for PT method. We integrated the advantages of the PT method and the AR method, and set four weightings and formed four combined methods (DC, MC, DM, and AA). These four combined methods gave better ENS values than either the PT method or the AR method alone, and the ENS values of DC and AA methods were greater than those of PT and AR methods individually in four catchments. The combined methods made up for the poor performance indicated by ENS and R2 of the AR method and PBIS of the PT method. For the calibration period, R2 and PBIS values of the combined method were good at all the sites. With the exception of the MC and DM methods, which gave slightly worse daily results in DY, R2 values were larger than those for the PT and AR methods, and PBIS of the combined method was better than that of the other two methods at 75% of the sites during the validation period.
The combined method presented in this paper accounts for the shortcomings in PBIS from the PT method and in ENS and R2 from AR method, and gives better estimation of continuous daily and monthly runoff than the individual methods. The results prove that it is possible to improve the efficiency of continuous runoff assessment in ungauged catchments by combining the PT method and AR method, so this idea is also recommended to be widely used.