Extreme Precipitation Spatial Analog: In Search of an Alternative Approach for Future Extreme Precipitation in Urban Hydrological Studies
Abstract
1. Introduction
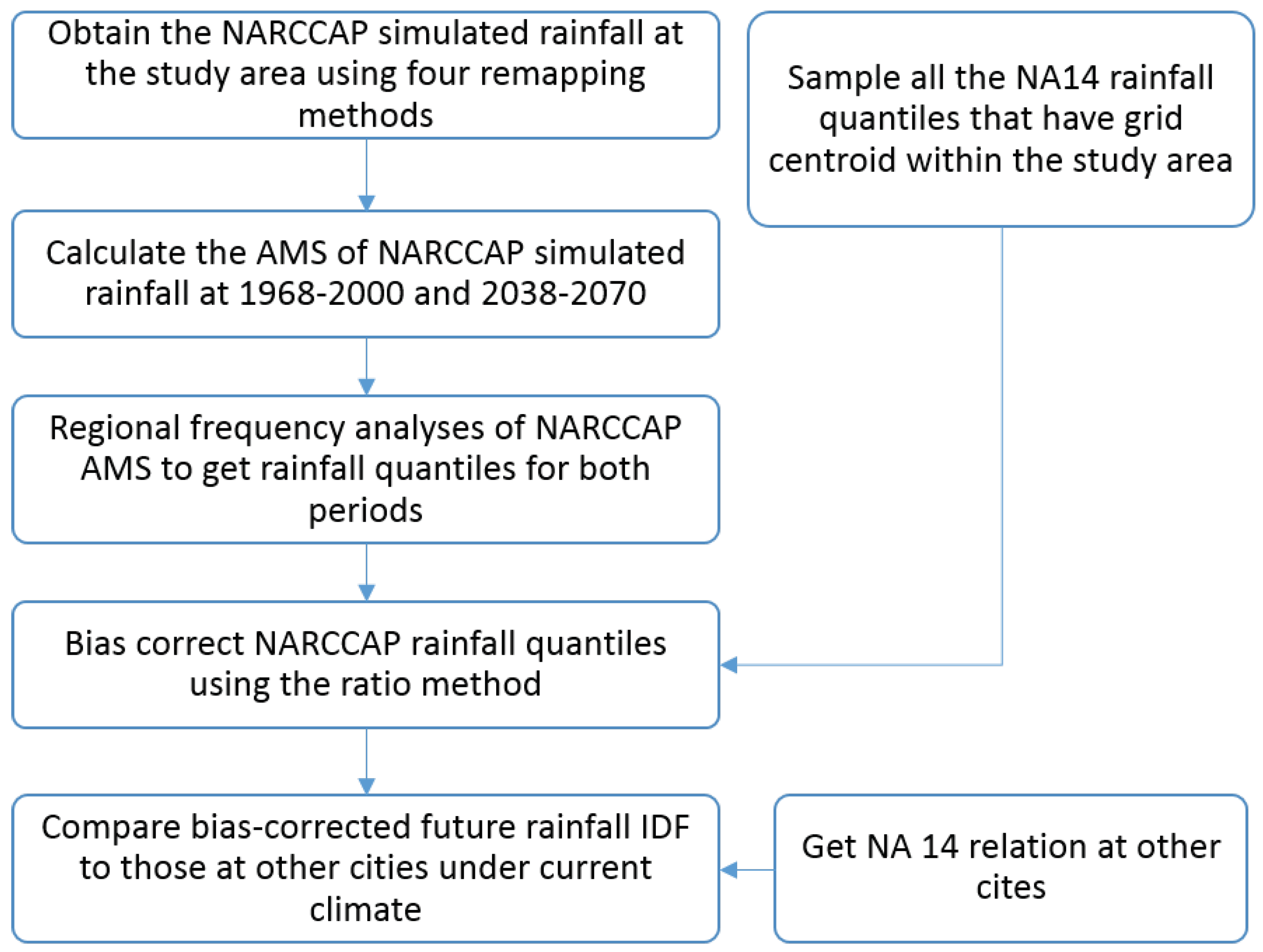
2. Data and Methods
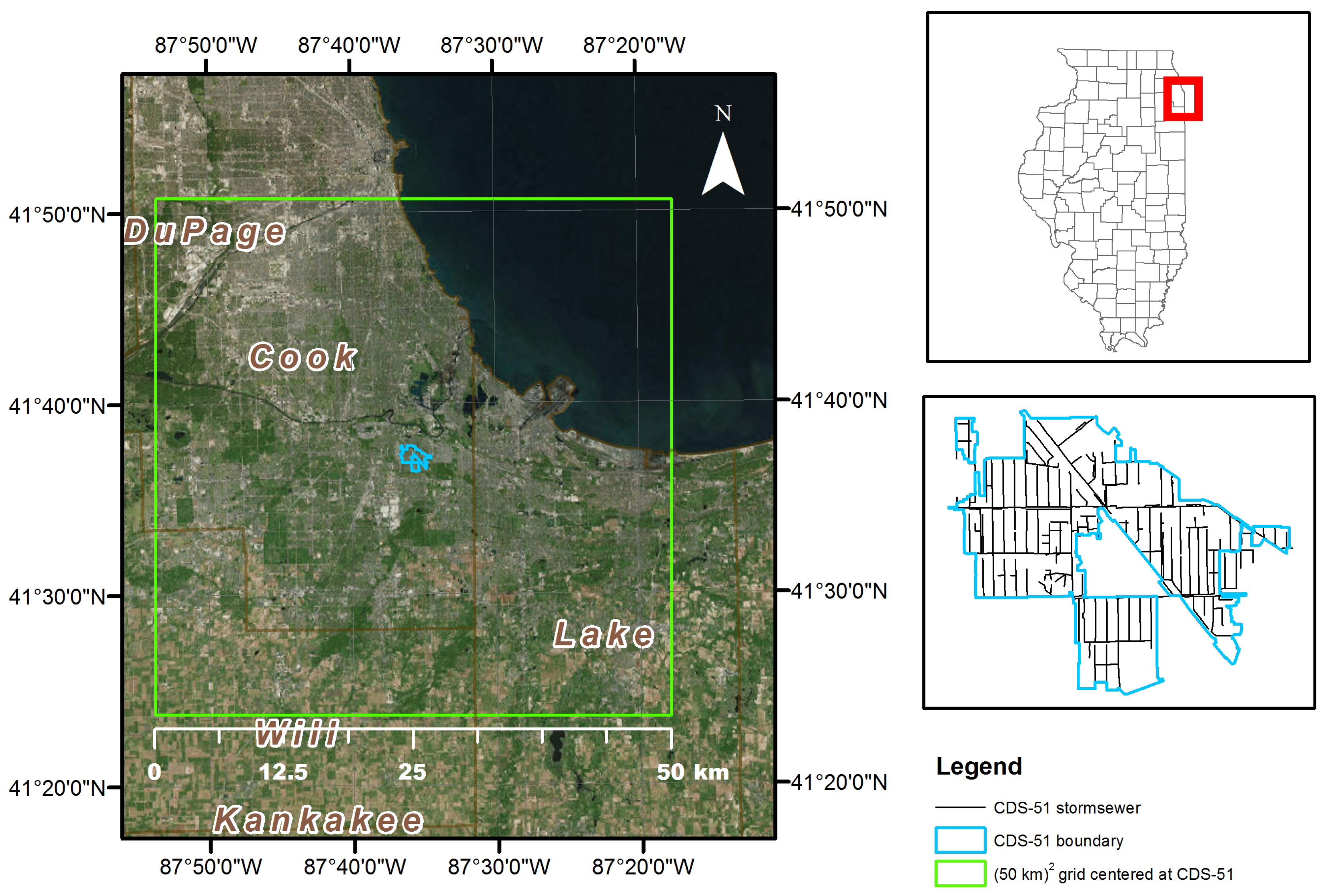
2.1. Study Site
2.2. Precipitation Data
2.3. Regridding and Sampling of Rainfall Data
2.4. Precipitation Frequency Analysis and IDF Relation
2.5. Bias Correction
3. Results
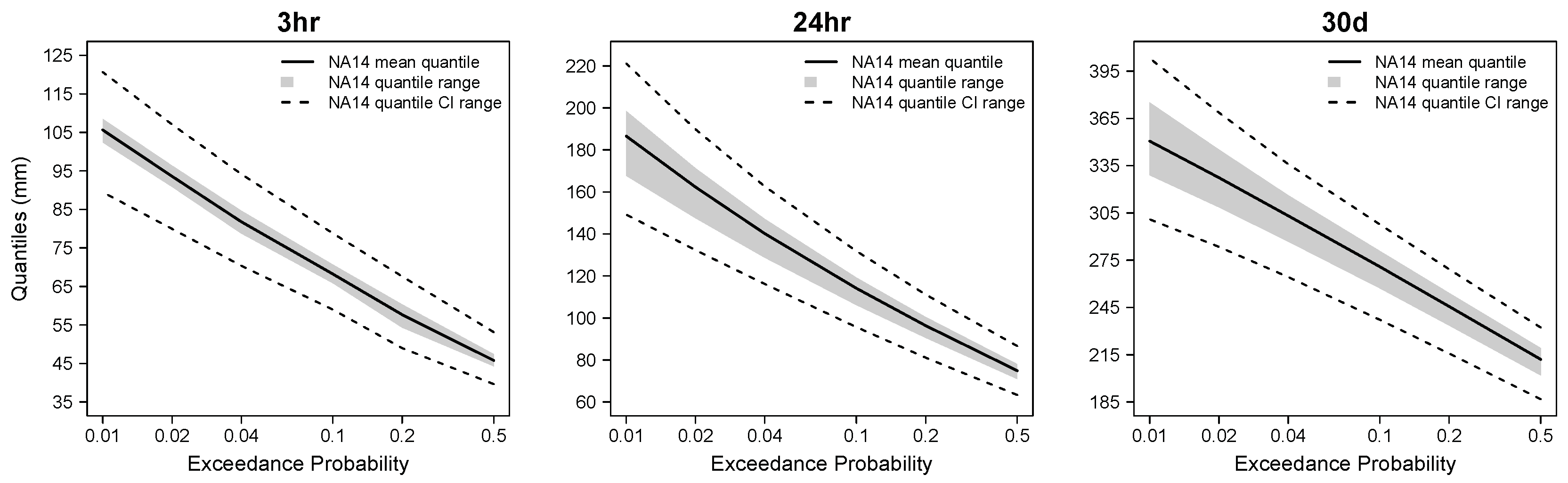
3.1. Rainfall Frequency under Current Climate
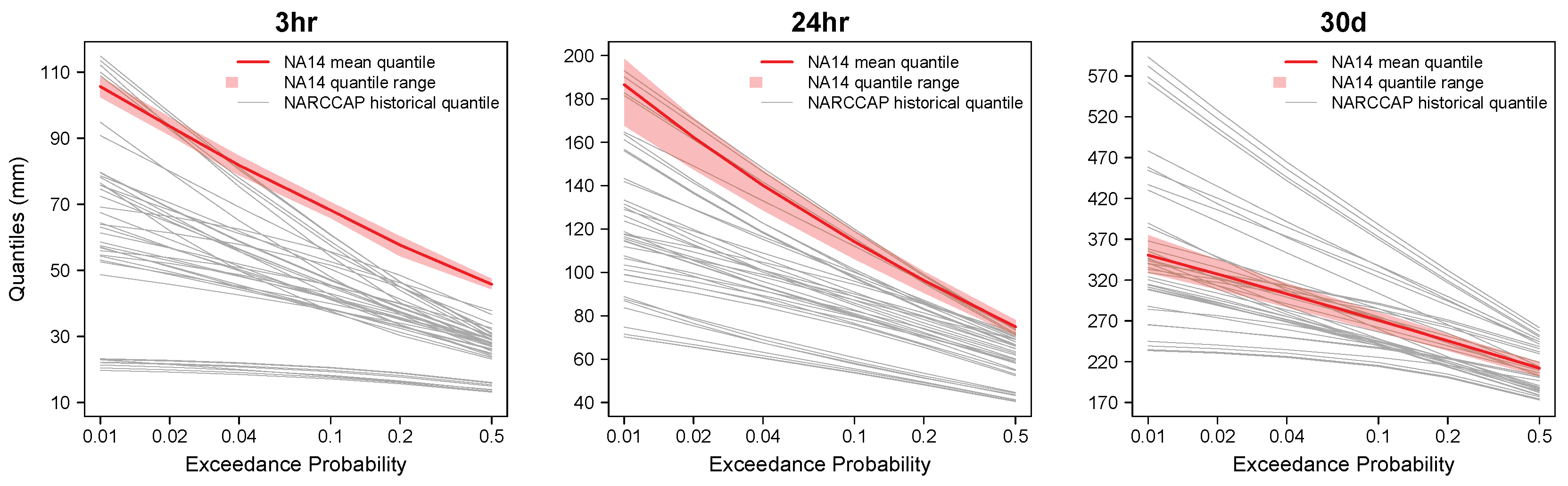
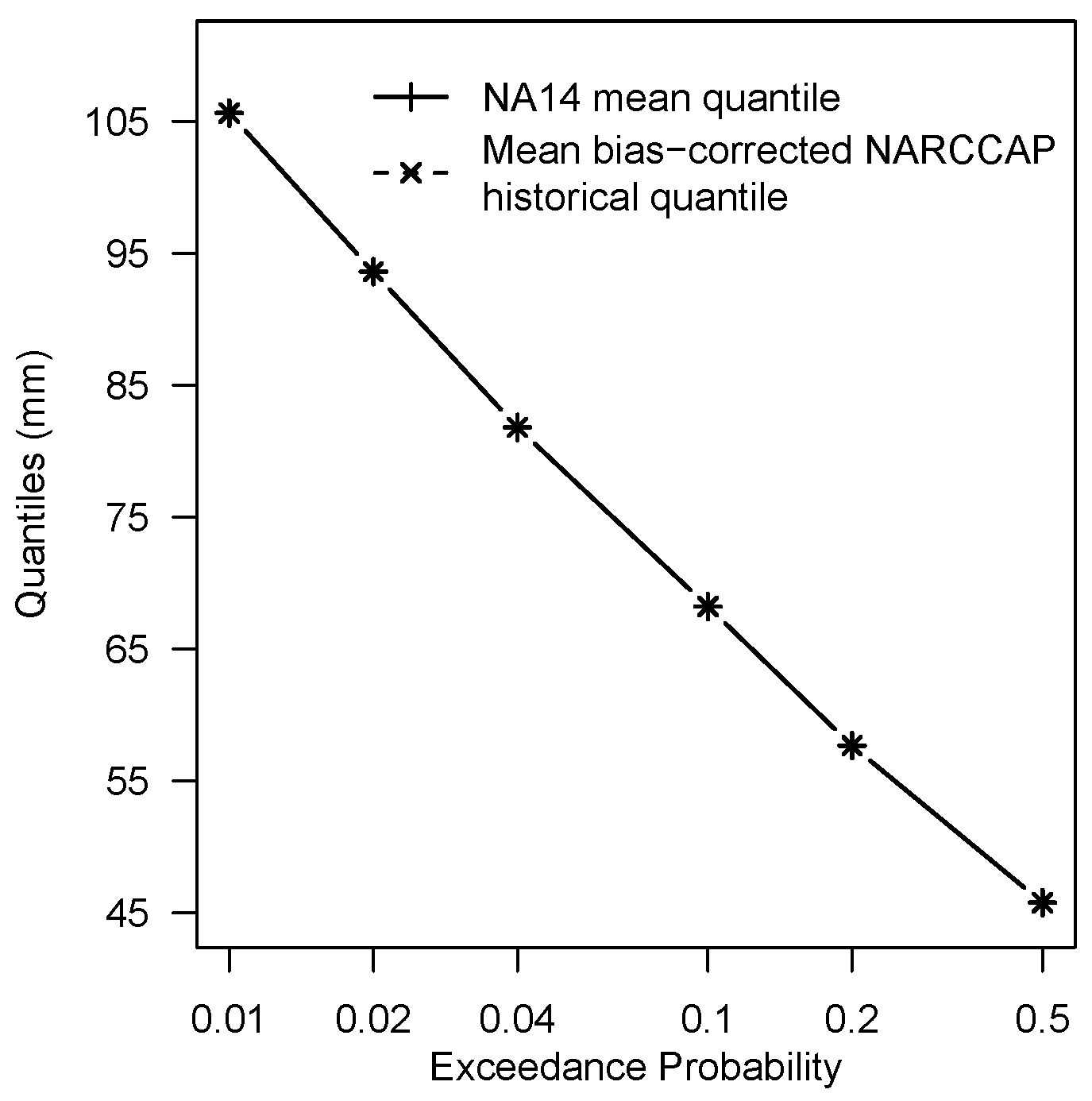
3.2. Modeled Historical Period Rainfall Quantiles vs. Current Rainfall Quantiles
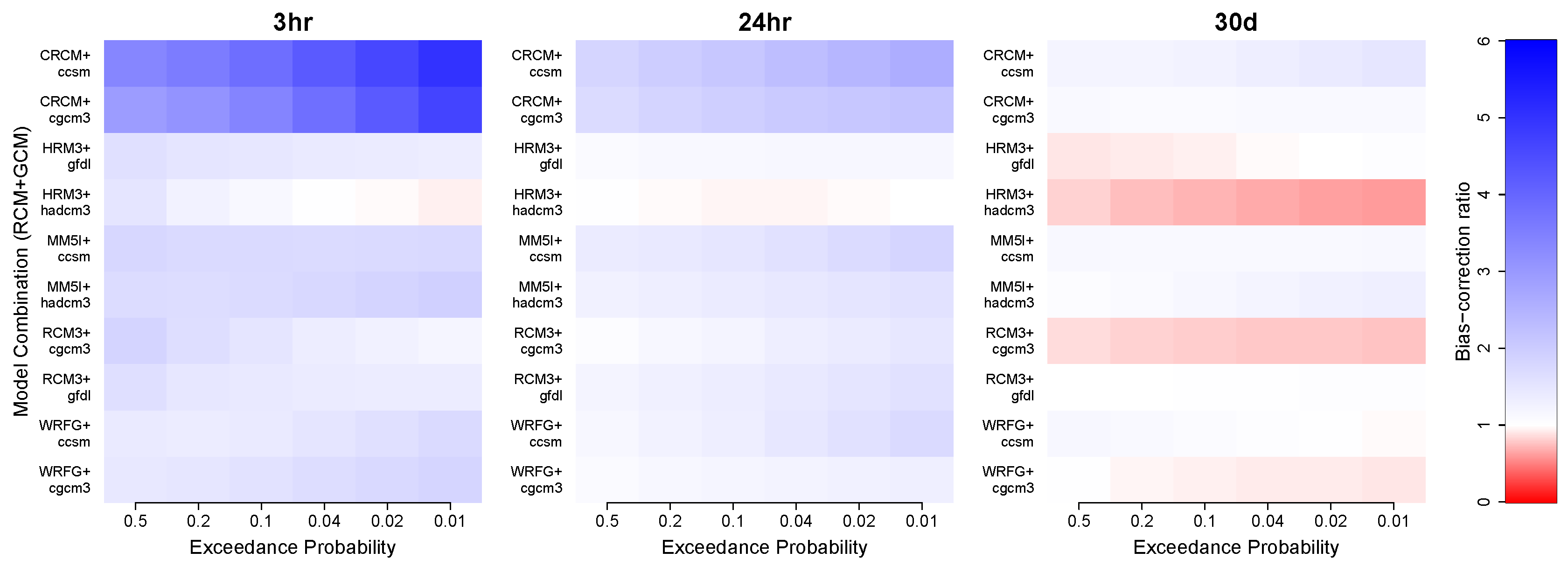
3.3. Bias-Correction of Modeled Frequency Quantiles
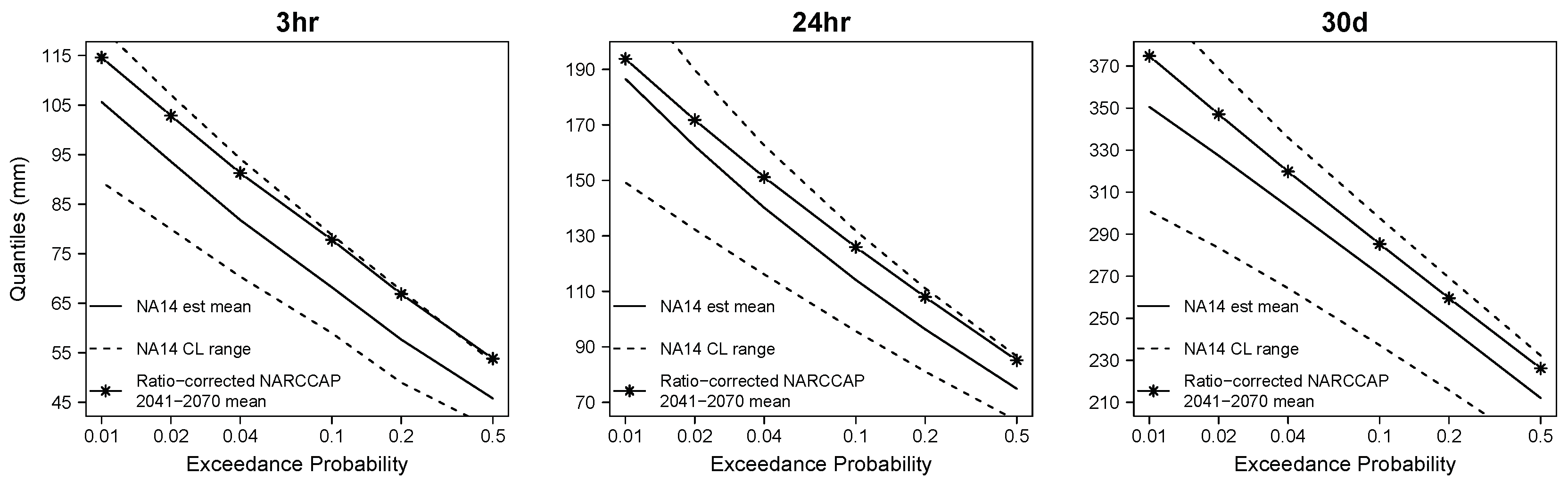
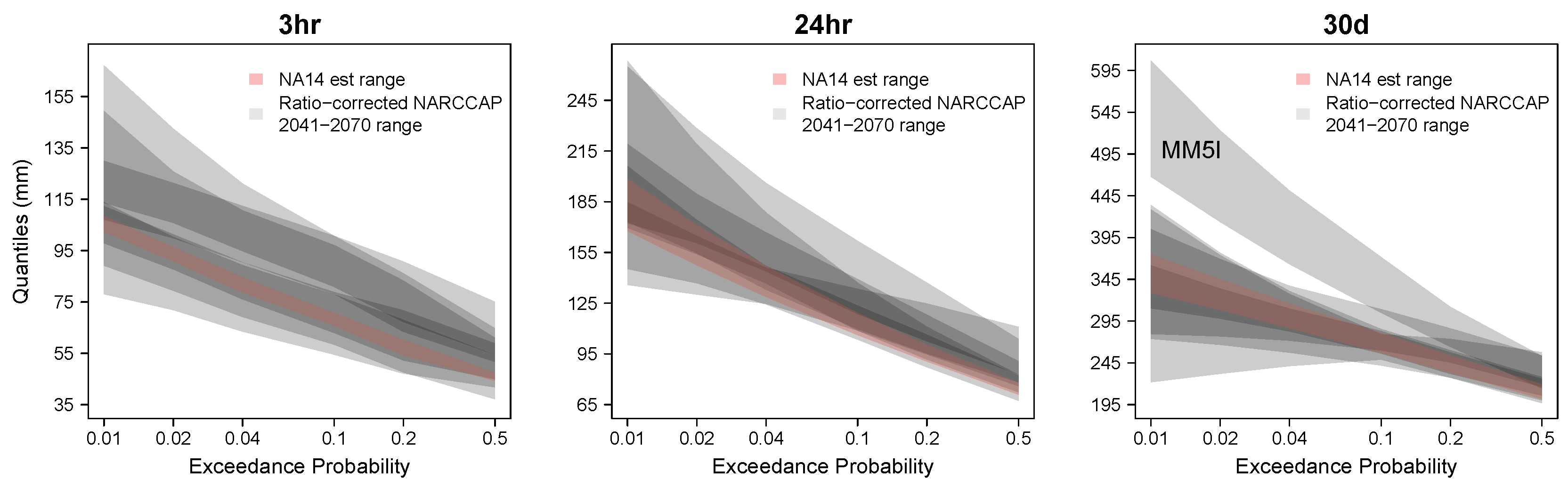
3.4. Bias-Corrected Modeled Future Frequency Quantiles
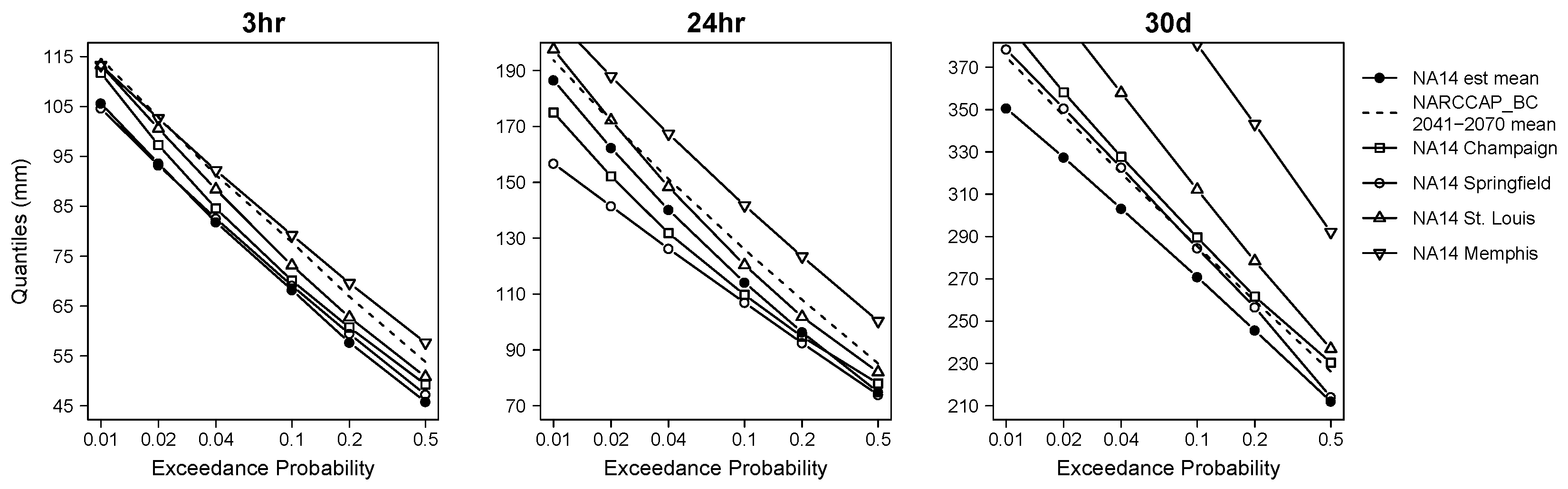
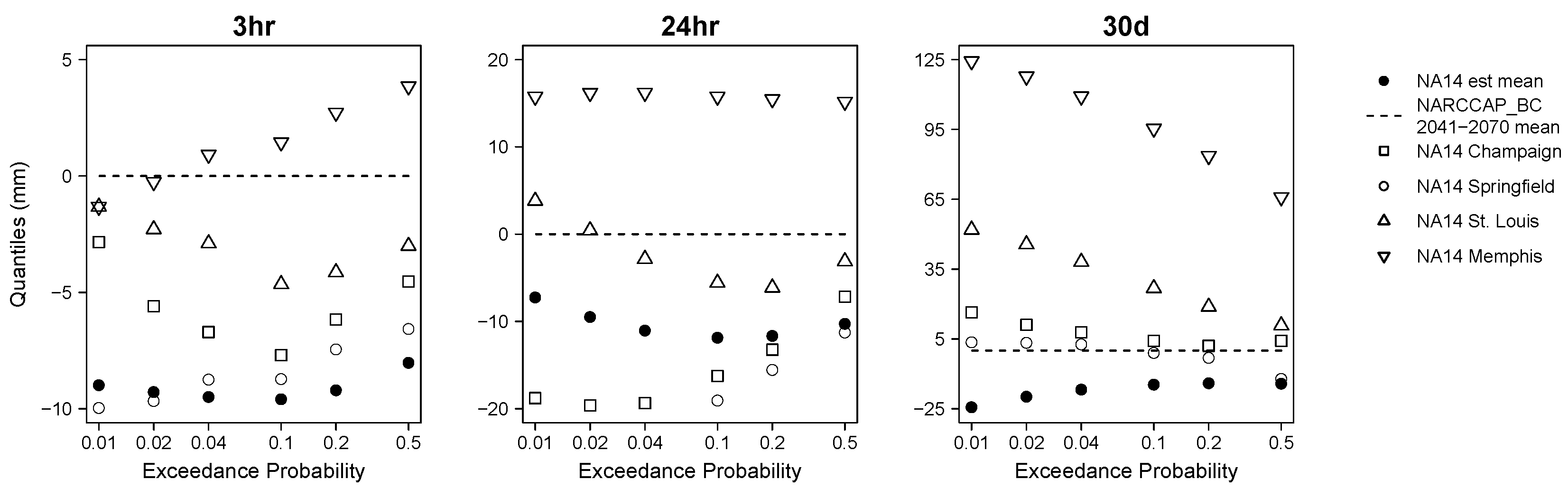
3.5. Rainfall Frequency Quantiles from Other Cities under Current Climate
4. Conclusions and Discussion
- The variances in raw NARCCAP historical frequency quantiles from different combinations of RCM, GCM, and grid remapping methods are much larger than the variance of NA14 quantiles within the study area for all three durations analyzed. Most NARCCAP historical realizations tend to underestimate NA14 quantiles at smaller durations (3-h and 24-h), while at 30-day NA14 quantiles lie within the NARCCAP quantile range. Consequently, bias-correction is required to correct for the NARCCAP biases.
- The bias-correction ratio can serve as a metric for evaluating model performance. There is no individual model combination that best captures the behavior of NA14 rainfall quantiles at all durations and frequencies. The model performance depends on rainfall duration and return period. The correction ratios tend to depend more on the RCM than the GCM, especially at smaller rainfall durations of less than 24 h.
- The projections of future extreme precipitation using bias-corrected NARCCAP 2041–2070 quantiles under A2 scenario have ensemble means and medians that are all statistically higher than the NA14 quantiles, indicating a future intensification of extreme events at all durations and return periods. For individual NARCCAP realizations, most of them are higher than NA14 at all quantiles. The uncertainty in NARCCAP bias-corrected future quantiles is still very large, compared to the variance of NA14 quantiles. This uncertainty increases with return period and rainfall duration.
- We find that future 3-h rainfall in Chicago will be more similar to that of current-day Memphis, while longer-duration 30-day rainfall will be more similar to that of Springfield, IL. This indicates that the spatial analog is potentially a useful method to obtain future extreme precipitation projections, but highlights the fact that the analogs will likely depend on the duration of rainfall of interest.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- World Health Organization & UN-Habitat. Global Report on Urban Health: Equitable Healthier Cities for Sustainable Development; Technical Report; World Health Organization: Geneva, Switzerland, 2016. [Google Scholar]
- United Nations, Department of Economic and Social Affairs, Population Division. World Population Prospects: The 2017 Revision, Key Findings and Advance Tables; ESA/P/WP/248; United Nations, Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2017. [Google Scholar]
- Willems, P.; Olsson, J.; Arnbjerg-Nielsen, K.; Beecham, S.; Pathirana, A.; Gregersen, I.B.; Madsen, H.; Nguyen, V.T.V. Impacts of Climate Change on Rainfall Extremes and Urban Drainage Systems; IWA Publishing: London, UK, 2012. [Google Scholar]
- Winters, B.A.; Angel, J.R.; Ballerine, C.; Byard, J.L.; Flegel, A.; Gambill, D.; Jenkins, E.; McConkey, S.A.; Markus, M.; Bender, B.A.; et al. Report for the Urban Flooding Awareness Act; Technical Report; Illinois Department of Natural Resources: Springfield, IL, USA, 2015. [Google Scholar]
- Illinois Department of Natural Resources Office of Water Resources. Model Stormwater Management Ordinance; Illinois Department of Natural Resources: Springfield, IL, USA, 2015. [Google Scholar]
- Federal Emergency Management Agency (FEMA). Hazus: FEMA’s Methodology for Estimating Potential Losses from Disasters; Federal Emergency Management Agency: Washington, DC, USA, 2018. [Google Scholar]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The Changing Character of Precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1218. [Google Scholar] [CrossRef]
- Field, C.B.; Barros, V.; Stocker, T.F.; Qin, D.; Dokken, D.J.; Ebi, K.L.; Mastrandrea, M.D.; Mach, K.J.; Plattner, G.K.; Allen, S.K.; et al. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- United Nations Framework Convention on Climate Change (UNFCCC). Views and Information on the Effectiveness of the Nairobi Work Programme on Impacts, Vulnerability and Adaptation to Climate Change in Fulfilling Its Objective, Expected Outcome, Scope of Work and Modalities; United Nations Framework Convention on Climate Change: Conn, Germany, 2010. [Google Scholar]
- Sussams, L.; Sheate, W.; Eales, R. Green infrastructure as a climate change adaptation policy intervention: Muddying the waters or clearing a path to a more secure future? J. Environ. Manag. 2015, 147, 184–193. [Google Scholar] [CrossRef]
- Mishra, V.; Lettenmaier, D.P. Climatic trends in major U.S. urban areas, 1950–2009. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on future changes in climate and the hydrologic cycle. Nature 2002, 419, 224–232. [Google Scholar] [CrossRef]
- Karl, T.R.; Meehl, G.A.; Miller, C.D.; Hassol, S.J.; Waple, A.M.; Murray, W.L. Weather and Climate Extremes in a Changing Climate; Technical Report; U.S. Climate Change Science Program: Washington, DC, USA, 2008. [Google Scholar]
- Lenderink, G.; Van Meijgaard, E. Increase in hourly precipitation extremes beyond expectations from temperature changes. Nat. Geosci. 2008, 1, 511–514. [Google Scholar] [CrossRef]
- Mishra, V.; Dominguez, F.; Lettenmaier, D.P. Urban precipitation extremes: How reliable are regional climate models? Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Kunkel, K.E. North American Trends in Extreme Precipitation. Nat. Hazards 2003, 29, 291–305. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar] [CrossRef]
- Cantone, J.; Seo, Y.; Zimmer, A.; Schmidt, A.R.; Garcia, M.H. Hydrologic Modeling of the Calumet TARP System; Technical Report; Ven Te Chow Hydrosystems Laboratory, Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2009. [Google Scholar]
- Cantone, J.; Schmidt, A.R. Improved understanding and prediction of the hydrologic response of highly urbanized catchments through development of the Illinois Urban Hydrologic Model. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Seo, Y.; Schmidt, A.R. Network configuration and hydrograph sensitivity to storm kinematics. Water Resour. Res. 2013, 49, 1812–1827. [Google Scholar] [CrossRef]
- Hohenegger, C.; Brockhaus, P.; Schäer, C. Towards climate simulations at cloud-resolving scales. Meteorol. Z. 2008, 17, 383–394. [Google Scholar] [CrossRef]
- Wakazuki, Y.; Nakamura, M.; Kanada, S.; Muroi, C. Climatological Reproducibility Evaluation and Future Climate Projection of Extreme Precipitation Events in the Baiu Season Using a High-Resolution Non-Hydrostatic RCM in Comparison with an AGCM. J. Meteorol. Soc. Jpn. Ser. II 2008, 86, 951–967. [Google Scholar] [CrossRef]
- Gutowski, W.J.; Decker, S.G.; Donavon, R.A.; Pan, Z.; Arritt, R.W.; Takle, E.S. Temporal-Spatial Scales of Observed and Simulated Precipitation in Central U.S. Climate. J. Clim. 2003, 16, 3841–3847. [Google Scholar] [CrossRef]
- Roberts, N.M.; Lean, H.W. Scale-Selective Verification of Rainfall Accumulations from High-Resolution Forecasts of Convective Events. Mon. Weather Rev. 2008, 136, 78–97. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Markus, M.; Wuebbles, D.J.; Liang, X.Z.; Hayhoe, K.; Kristovich, D.A. Diagnostic analysis of future climate scenarios applied to urban flooding in the Chicago metropolitan area. Clim. Chang. 2012, 111, 879–902. [Google Scholar] [CrossRef]
- Mearns, L.; McGinnis, S.; Arritt, R.; Biner, S.; Duffy, P.; Gutowski, W.; Held, I.; Jones, R.; Leung, R.; Nunes, A.; et al. The North American Regional Climate Change Assessment Program Dataset, 2007, updated 2014. Data downloaded 2016-12-04. Available online: https://www.narccap.ucar.edu/doc/pubs/bams-narccap-overview.pdf (accessed on 4 December 2016).
- Taye, M.T.; Willems, P.; Block, P. Implications of climate change on hydrological extremes in the Blue Nile basin: A review. J. Hydrol. Reg. Stud. 2015, 4, 280–293. [Google Scholar] [CrossRef]
- Wootten, A.; Terando, A.; Reich, B.J.; Boyles, R.P.; Semazzi, F. Characterizing Sources of Uncertainty from Global Climate Models and Downscaling Techniques. J. Appl. Meteorol. Climatol. 2017, 56, 3245–3262. [Google Scholar] [CrossRef]
- Kendon, E.J.; Jones, R.G.; Kjellström, E.; Murphy, J.M. Using and Designing GCM-RCM Ensemble Regional Climate Projections. J. Clim. 2010, 23, 6485–6503. [Google Scholar] [CrossRef]
- Kendon, E.J.; Rowell, D.P.; Jones, R.G. Mechanisms and reliability of future projected changes in daily precipitation. Clim. Dyn. 2010, 35, 489–509. [Google Scholar] [CrossRef]
- Frei, C.; Schöll, R.; Fukutome, S.; Schmidli, J.; Vidale, P.L. Future change of precipitation extremes in Europe: Intercomparison of scenarios from regional climate models. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Gutowski, W.J., Jr.; Giorgi, F.; Timbal, B.; Frigon, A.; Jacob, D.; Kang, H.S.; Raghavan, K.; Lee, B.; Lennard, C.; et al. WCRP COordinated Regional Downscaling EXperiment (CORDEX): A diagnostic MIP for CMIP6. Geosci. Model Dev. 2016, 9, 4087–4095. [Google Scholar] [CrossRef]
- Kling, G.W.; Hayhoe, K.; Johnson, L.B.; Magnuson, J.J.; Polasky, S.; Robinson, S.K.; Shuter, B.J.; Wander, M.M.; Wuebbles, D.J.; Zak, D.R.; et al. Confronting Climate Change in the Great Lakes Region: Impacts on Our Communities and Ecosystems; Technical Report, Union of Concerned Scientists; Ecological Society of America: Washington, DC, USA, 2003. [Google Scholar]
- Grenier, P.; Parent, A.C.; Huard, D.; Anctil, F.; Chaumont, D. An Assessment of Six Dissimilarity Metrics for Climate Analogs. J. Appl. Meteorol. Climatol. 2013, 52, 733–752. [Google Scholar] [CrossRef]
- Retchless, D.P. Communicating climate change: Spatial analog versus color-banded isoline maps with and without accompanying text. Cartogr. Geogr. Inf. Sci. 2014, 41, 55–74. [Google Scholar] [CrossRef]
- Kalkstein, L.S.; Greene, J.S. An evaluation of climate/mortality relationships in large US cities and the possible impacts of a climate change. Environ. Health Perspect. 1997, 105, 84–93. [Google Scholar] [CrossRef]
- Hallegatte, S.; Hourcade, J.C.; Ambrosi, P. Using climate analogues for assessing climate change economic impacts in urban areas. Clim. Chang. 2007, 82, 47–60. [Google Scholar] [CrossRef]
- Kopf, S.; Ha-Duong, M.; Hallegatte, S. Using maps of city analogues to display and interpret climate change scenarios and their uncertainty. Nat. Hazards Earth Syst. Sci. 2008, 8, 905–918. [Google Scholar] [CrossRef]
- Kellett, J.; Hamilton, C.; Ness, D.; Pullen, S. Testing the limits of regional climate analogue studies: An Australian example. Land Use Policy 2015, 44, 54–61. [Google Scholar] [CrossRef]
- Horváth, L.; Solymosi, N.; Gaál, M. Use of the spatial analogy to understand the effects of climate change. In Environmental, Health and Humanity Issues in the Down Danubian Region; World Scientific: Singapore, 2009; pp. 215–222. [Google Scholar] [CrossRef]
- Ramírez-Villegas, J.; Lau, C.; Köhler, A.; Signer, J.; Jarvis, A.; Arnell, N.; Osborne, T.M.; Hooker, J. Climate Analogues: Finding Tomorrow’s Agriculture Today; Technical Report, Working Paper 12; CCAFS: Copenhagen, Denmark, 2011. [Google Scholar]
- Hirschboeck, K.K. Climate and floods. US Geol. Surv. Water-Supply Pap. 1991, 2375, 67–88. [Google Scholar]
- Berne, A.; Delrieu, G.; Creutin, J.D.; Obled, C. Temporal and spatial resolution of rainfall measurements required for urban hydrology. J. Hydrol. 2004, 299, 166–179. [Google Scholar] [CrossRef]
- Cristiano, E.; ten Veldhuis, M.C.; van de Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar] [CrossRef]
- Hayhoe, K.; VanDorn, J.; Croley, T., II; Schlegal, N.; Wuebbles, D. Regional climate change projections for Chicago and the US Great Lakes. J. Great Lakes Res. 2010, 36, 7–21. [Google Scholar] [CrossRef]
- Wuebbles, D.J.; Hayhoe, K.; Parzen, J. Introduction: Assessing the effects of climate change on Chicago and the Great Lakes. J. Great Lakes Res. 2010, 36, 1–6. [Google Scholar] [CrossRef]
- Nakicenovic, N.; Alcamo, J.; Grubler, A.; Riahi, K.; Roehrl, R.; Rogner, H.H.; Victor, N. Special Report on Emissions Scenarios (SRES), A Special Report of Working Group III of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Markus, M.; Angel, J.; Byard, G.; McConkey, S.; Zhang, C.; Cai, X.; Notaro, M.; Ashfaq, M. Communicating the Impacts of Projected Climate Change on Heavy Rainfall Using a Weighted Ensemble Approach. J. Hydrol. Eng. 2018, 23, 04018004. [Google Scholar] [CrossRef]
- Notaro, M.; Lorenz, D.; Hoving, C.; Schummer, M. Twenty-First-Century Projections of Snowfall and Winter Severity across Central-Eastern North America. J. Clim. 2014, 27, 6526–6550. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Mearns, L.; McGinnis, S.; Korytina, D.; Arritt, R.; Biner, S.; Bukovsky, M.; Chang, H.I.; Christensen, O.; Herzmann, D.; Jiao, Y.; et al. The NA-CORDEX Dataset, version 1.0; 2017. Available online: https://doi.org/10.5065/D6SJ1JCH (accessed on 18 March 2019).
- Wuebbles, D.J.; Meehl, G.; Hayhoe, K.; Karl, T.R.; Kunkel, K.; Santer, B.; Wehner, M.; Colle, B.; Fischer, E.M.; Fu, R.; et al. CMIP5 Climate Model Analyses: Climate Extremes in the United States. Bull. Am. Meteorol. Soc. 2014, 95, 571–583. [Google Scholar] [CrossRef]
- Meehl, G.A.; Covey, C.; Delworth, T.; Latif, M.; McAvaney, B.; Mitchell, J.F.B.; Stouffer, R.J.; Taylor, K.E. THE WCRP CMIP3 Multimodel Dataset: A New Era in Climate Change Research. Bull. Am. Meteorol. Soc. 2007, 88, 1383–1394. [Google Scholar] [CrossRef]
- Metropolitan Water Reclamation District of Greater Chicago (MWRDGC). Tunnel and Reservoir Plan (TARP); MWRDGC: Chicago, IL, USA, 1999. [Google Scholar]
- Tang, Y.; Schmidt, A. Probabilistic Hydrologic Model to Simulate Response of Urban Drainage System to Implementation of Low Impact Development Stormwater Practices. In World Environmental and Water Resources Congress 2013: Showcasing the Future; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2013. [Google Scholar] [CrossRef]
- Wang, A.K.; Park, S.Y.; Huang, S.; Schmidt, A.R. Hydrologic Response of Sustainable Urban Drainage to Different Climate Scenarios. In World Environmental and Water Resources Congress 2015: Floods, Droughts, and Ecosystems; ASCE: Reston, VA, USA, 2015. [Google Scholar] [CrossRef]
- Mearns, L.; Gutowski, W.; Jones, R.; Leung, R.; McGinnis, S.; Nunes, A.; Qian, Y. A Regional Climate Change Assessment Program for North America. Eos Trans. Am. Geophys. Union 2009, 90, 311. [Google Scholar] [CrossRef]
- Bonnin, G.M.; Todd, D.; Lin, B.; Parzybok, T.; Yekta, M.; Riley, D. Precipitation-Frequency Atlas of the United States, NOAA Atlas 14, Volume 2, Version 3.0; Technical Report; NOAA, National Weather Service: Silver Spring, MD, USA, 2005. [Google Scholar]
- Räisänen, J.; Ylhäisi, J.S. How Much Should Climate Model Output Be Smoothed in Space? J. Clim. 2011, 24, 867–880. [Google Scholar] [CrossRef]
- Kopparla, P.; Fischer, E.M.; Hannay, C.; Knutti, R. Improved simulation of extreme precipitation in a high-resolution atmosphere model. Geophys. Res. Lett. 2013, 40, 5803–5808. [Google Scholar] [CrossRef]
- CDO. Climate Data Operators. 2018. Available online: https://code.mpimet.mpg.de/projects/cdo (accessed on 16 May 2019).
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Landwehr, J.M.; Matalas, N.C.; Wallis, J.R. Probability weighted moments: Definition and relation to parameters of several distributions expressable in inverse form. Water Resour. Res. 1979, 15, 1049–1054. [Google Scholar] [CrossRef]
- Hosking, J.R.M. Package ‘lmom’, R Package, Version 2.6; 2017. Available online: https://cran.r-project.org/package=lmom (accessed on 18 March 2019).
- Papalexiou, S.M.; Koutsoyiannis, D. Battle of extreme value distributions: A global survey on extreme daily rainfall. Water Resour. Res. 2013, 49, 187–201. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Rainfall extremes: Toward reconciliation after the battle of distributions. Water Resour. Res. 2014, 50, 336–352. [Google Scholar] [CrossRef] [PubMed]
- Zalina, M.; Desa, M.; Nguyen, V.T.A.; Kassim, A. Selecting a probability distribution for extreme rainfall series in Malaysia. Water Sci. Technol. 2002, 45, 63–68. [Google Scholar] [CrossRef]
- Anderson, B.; Siriwardena, L.; Western, A.; Chiew, F.; Seed, A.; Bloschl, G. Which theoretical distribution function best fits measured within day rainfall distributions across Australia? In 30th Hydrology & Water Resources Symposium: Past, Present & Future. Conference Design; Institution of Engineers, Australia: Launceston, Australia, 2006; pp. 498–503. [Google Scholar]
- Alam, M.A.; Emura, K.; Farnham, C.; Yuan, J. Best-Fit Probability Distributions and Return Periods for Maximum Monthly Rainfall in Bangladesh. Climate 2018, 6, 9. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill International Editions: New York, NY, USA, 1988. [Google Scholar]
- Whetton, P.; Macadam, I.; Bathols, J.; O’Grady, J. Assessment of the use of current climate patterns to evaluate regional enhanced greenhouse response patterns of climate models. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Reifen, C.; Toumi, R. Climate projections: Past performance no guarantee of future skill? Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Hayhoe, K.; Edmonds, J.; Kopp, R.; LeGrande, A.; Sanderson, B.; Wehner, M.; Wuebbles, D. Climate models, scenarios, and projections. In Climate Science Special Report: Fourth National Climate Assessment, Volume I; Wuebbles, D., Fahey, D., Hibbard, K., Dokken, D., Stewart, B., Maycock, T., Eds.; U.S. Global Change Research Program: Washington, DC, USA, 2017; Chapter 4; pp. 133–160. [Google Scholar] [CrossRef]
- Anandhi, A.; Frei, A.; Pierson, D.C.; Schneiderman, E.M.; Zion, M.S.; Lounsbury, D.; Matonse, A.H. Examination of change factor methodologies for climate change impact assessment. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Lafon, T.; Dadson, S.; Buys, G.; Prudhomme, C. Bias correction of daily precipitation simulated by a regional climate model: A comparison of methods. Int. J. Climatol. 2013, 33, 1367–1381. [Google Scholar] [CrossRef]
- Monette, A.; Sushama, L.; Khaliq, M.N.; Laprise, R.; Roy, R. Projected changes to precipitation extremes for northeast Canadian watersheds using a multi-RCM ensemble. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Khaliq, M.; Sushama, L.; Monette, A.; Wheater, H. Seasonal and extreme precipitation characteristics for the watersheds of the Canadian Prairie Provinces as simulated by the NARCCAP multi-RCM ensemble. Clim. Dyn. 2015, 44, 255–277. [Google Scholar] [CrossRef]
- Kunkel, K.E.; Easterling, D.R.; Kristovich, D.A.R.; Gleason, B.; Stoecker, L.; Smith, R. Meteorological Causes of the Secular Variations in Observed Extreme Precipitation Events for the Conterminous United States. J. Hydrometeorol. 2012, 13, 1131–1141. [Google Scholar] [CrossRef]
- Feng, Z.; Leung, L.R.; Hagos, S.; Houze, R.A.; Burleyson, C.D.; Balaguru, K. More frequent intense and long-lived storms dominate the springtime trend in central US rainfall. Nat. Commun. 2016, 7, 13429. [Google Scholar] [CrossRef]

| No. | RCM | GCM |
|---|---|---|
| 1 | CRCM | ccsm |
| 2 | CRCM | cgcm3 |
| 3 | HRM3 | gfdl |
| 4 | HRM3 | hadcm3 |
| 5 | MM5I | ccsm |
| 6 | MM5I | hadcm3 |
| 7 | RCM3 | cgcm3 |
| 8 | RCM3 | gfdl |
| 9 | WRFG | ccsm |
| 10 | WRFG | cgcm3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.K.; Dominguez, F.; Schmidt, A.R. Extreme Precipitation Spatial Analog: In Search of an Alternative Approach for Future Extreme Precipitation in Urban Hydrological Studies. Water 2019, 11, 1032. https://doi.org/10.3390/w11051032
Wang AK, Dominguez F, Schmidt AR. Extreme Precipitation Spatial Analog: In Search of an Alternative Approach for Future Extreme Precipitation in Urban Hydrological Studies. Water. 2019; 11(5):1032. https://doi.org/10.3390/w11051032
Chicago/Turabian StyleWang, Ariel Kexuan, Francina Dominguez, and Arthur Robert Schmidt. 2019. "Extreme Precipitation Spatial Analog: In Search of an Alternative Approach for Future Extreme Precipitation in Urban Hydrological Studies" Water 11, no. 5: 1032. https://doi.org/10.3390/w11051032
APA StyleWang, A. K., Dominguez, F., & Schmidt, A. R. (2019). Extreme Precipitation Spatial Analog: In Search of an Alternative Approach for Future Extreme Precipitation in Urban Hydrological Studies. Water, 11(5), 1032. https://doi.org/10.3390/w11051032





