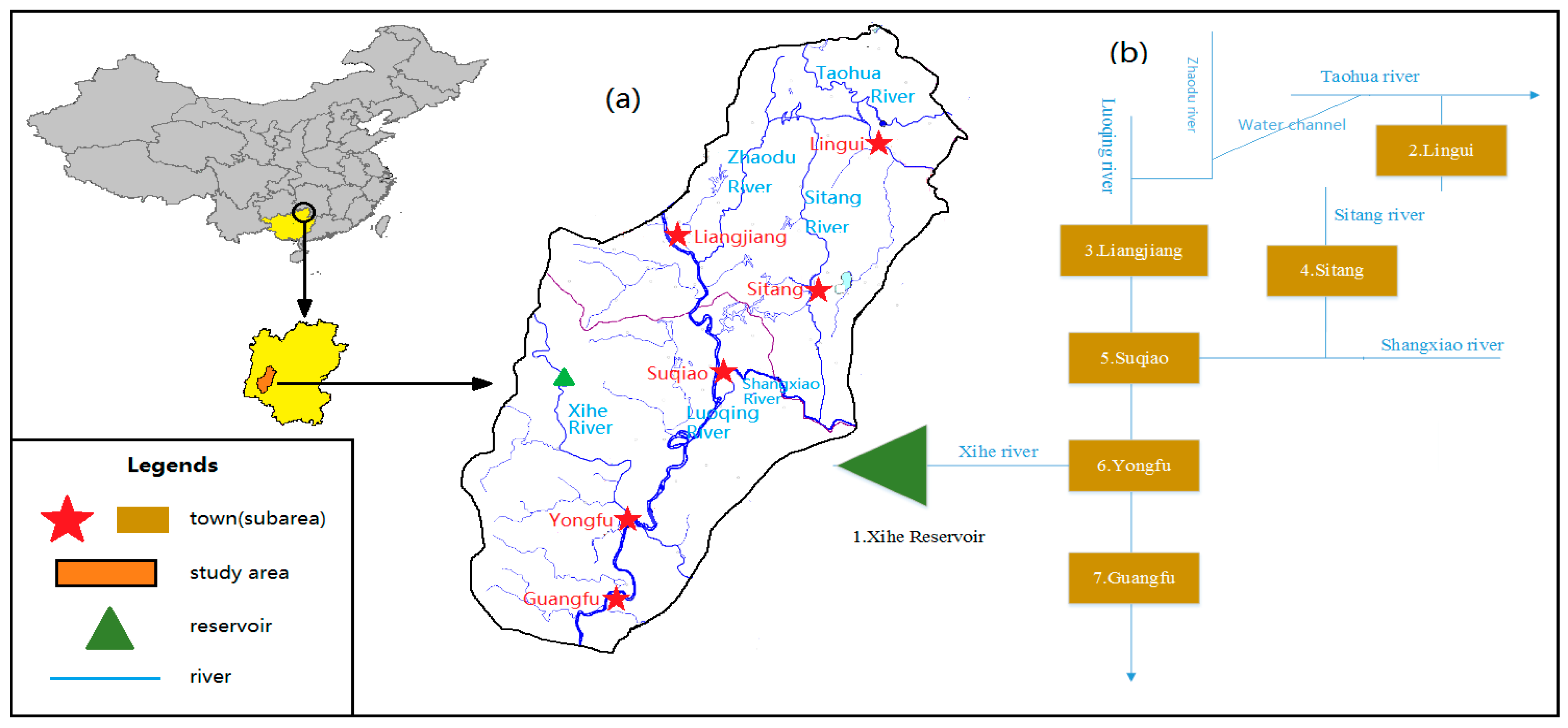
1. Introduction
It is widely known that the continuous increase of the water demand and the limited quantity of water resources are severely restricting the development of the global economy. Constructing reservoirs is one of the crucial manifestations in solving water resources problems. However, socio-economic water supplies from reservoirs are not only changing the natural flow, but also deteriorating the riverine ecosystems by affecting the sediments’ nutrient distribution and degrading the flows of the river downstream [
1,
2]. To reduce the negative impact of reservoirs on ecosystems, a water resource allocation approach is needed that can ensure that the water supply and the protection of the downstream riverine ecosystem can be incorporated into the management of water resources to achieve the goal of sustainable water use [
3]. It is, therefore, of great significance to incorporate the needs of human society and ecological requirements.
Several mathematic programming methods have the ability to satisfy multiple water users in water resource allocation. For example, linear programming is frequently applied in water resources systems due to its easy formulation and simple arithmetic [
4]. To resolve the nonlinear programming, several improved intelligent optimal algorithms have emerged as computer techniques have rapidly been developed [
5,
6], such as non-dominated-sorting genetic algorithm II (NSGA-II) [
7,
8]. Dynamic programming that uses the two-stage method is one of the most popular optimization techniques for water resources issues, such as two-stage stochastic programming (TSP) [
9,
10], and the progressive optimality algorithm (POA) [
11,
12]. These searching methods have been popular among many researchers because of their high efficiency, and they are widely used in water resources management in many regions.
Optimization technologies have been applied to solve the problem of both single-objective and multi-objective optimizations in large complex water resources systems. However, recent studies have focused more on multi-objective programming rather than single-objective programming, because it has to face different aspects of operational targets [
13]. Among all objectives, ecological objectives are of great importance in water resources management. It is necessary for humans to exploit natural resources, especially water resources, in order to meet social and economic needs, but the excessive exploitation of water resources will inevitably affect the ecological environment [
14,
15,
16,
17]. In addition, humans usually take water from rivers that can no longer be considered solely to be natural systems, having rather the double property of being both natural and the result of human-hydrological interaction, resulting in an inexorable trend of social development in recent years [
18]. The artificial intervention in the natural flow regime has become a key factor of severe deterioration of riverine ecosystems [
19]. Therefore, as described at the beginning, environmental factors are being brought to the forefront in reservoir operation [
20,
21], and optimal models of water resources have considered environmental targets in many studies [
22,
23], increasing their integrity and practical applicability. Based on these, studying the development and utilization of water resources by using an integrated and comprehensive method is becoming an inevitable trend [
24].
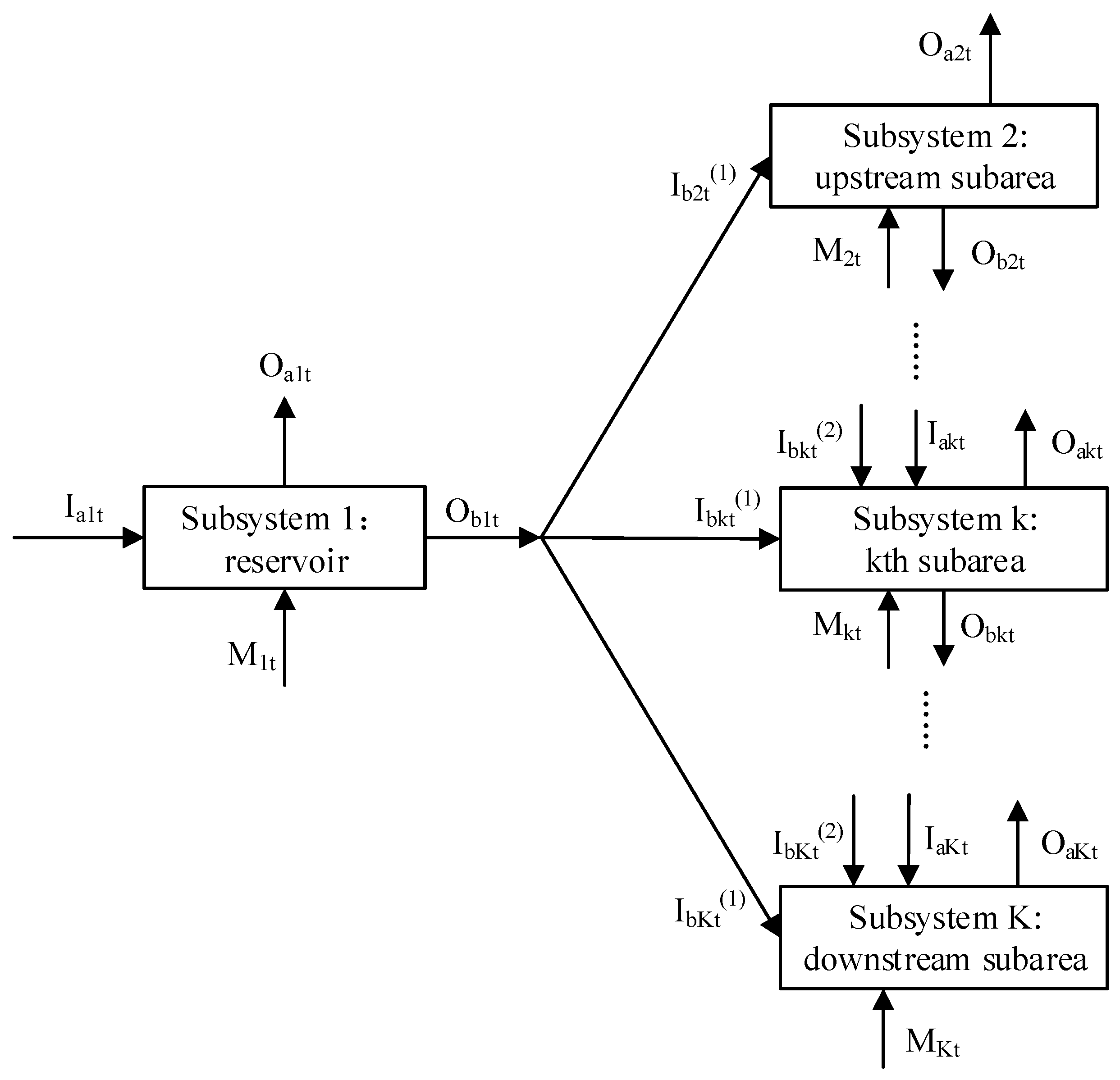
Comprehensive water resources planning for a watershed or region is a large and complicated system in most cases, because it involves how to reasonably utilize an integrated water resources system composed of numerous rivers in a certain region, as well as multiple development goals, restraints and effects [
25]. The complexity of water resources systems is reflected in the scales of both time and space, which constitute a high-dimensioned system. The length of the time is usually divided into multiple time steps that depend on different situations. For example, to analyze the water supply, especially in agricultural settings, the time scale is usually divided into monthly time steps. If flood control during flood seasons aquatic ecology in consideration of flow velocity are studied, the time scale is usually divided into daily or even hourly time steps. However, it is too difficult to collect such high-accuracy data. The complexity in the space scale is reflected by comprehensive water resources planning for a certain river basin or region that is usually divided into several sub-areas or sub-river basins, instead of carrying out planning for the whole area. A sub-area may contain many river channels and water projects. The precision of the sub-areas also depends on the situation. Moreover, water supply is usually divided into several users such as domestic, industrial and agricultural users, and this naturally involves an order or priority among the different water users. The priority should be relatively balanced [
26], but domestic water users should have a higher priority compared with others [
4]. Therefore, time and space scales, coupled with a large number of water users, constitutes a complex water system with high dimensionality.
Due to this high level of complexity, there has also been an upsurge in the number of system analysis methods in recent years, such as aggregation-decomposition (AD) and decomposition-coordination (DC) in water resources management, which are appealing because of their clear hierarchical structure and organic integrated wholeness. For AD, the aggregation method regards the whole system as an integer in accordance with the water balance equation, while the decomposition method allocates water resources to each subsystem to maximize the profit [
27]. To effectively reduce the system dimensions, the DC method has also been popular in many studies [
28,
29]. The decomposition-coordination method of large complex system theory divides a large complex system into its smaller constituent subsystems [
30]. For example, the Dantzig-Wolfe decomposition technique is a typical method for linear programming using a diagonal structure [
31]; Generalized Bender Decomposition (GBD) is a powerful approach for complex non-linear programming [
32]. Its main function is to reduce the system dimensionality and divide it into several hierarchical subsystems with lower dimensionality. This method requires less computing time and is significantly simplified with respect to optimizing each subsystem, because of its lower number of system dimensions. In general, if an optimal solution for each subsystem can be figured out, this will result in the optimal solution for the overall system. Meanwhile, the coordination of each subsystem can also reflect the overall optimal solution of the whole complex system [
33]. Previous studies have typically placed more focus on social objectives, such as complex water supply systems [
34], power generation [
35,
36], flood control [
30], and even irrigation water use [
37] by using system analysis techniques. However, for the sustainable development of a river basin or a region, the AD method is seldom used, since it is not able to entirely lead to a benefit for all parties, especially with respect to ecological needs, and water allocation should respond not only to the pursuit of socioeconomic benefit, such as achieving maximum water supply, but should also provide the maximum benefit for the environmental protection of a river in order to avoid excessive economic tendency decisions.
It is evident that socio-economic and ecological benefit are mutually contradictory. Achieving a balanced status between these two aspects to promote sustainable development in a region is, therefore, a key issue. To achieve this goal, we developed an optimal water allocation model considering social and ecological needs, and these two objectives were embedded in each subsystem by using the system analysis technique. The model was based on a system analysis technique that used the decomposition-coordination method and the discrete differential dynamic programming (DDDP) method. Based on these two methods, these two objectives can be well-coordinated and we can effectively find the optimal solution of both subsystem and overall system. The whole model was applied to a real-world simulation to validate its feasibility and to provide a reference for water resources management.
3. System Analysis Technique for Finding the Optimal Solution
3.1. Decomposition-Coordination (DC) Method
3.1.1. System Decomposition
Obviously, it is quite difficult to optimize such a large and complex system using traditional methods, because of its high number of dimensions and its complicated structure. Thus, we can use the system analysis technique. The decomposition-coordination method is one of the most effective ways of implementing the system analysis technique. According to its basic principle, the key procedure of this method is disaggregating a large system into several subsystems with a hierarchical structure [
33,
35]. The subsystems have their own objectives, and their locally optimal solutions can be figured out.
According to the system model constructed above, the total objective and constraints of the large complex system of water resources can be expressed by the Lagrange function [
29], formulated by:
where
L is the expression of the Lagrange function. The variables
λkt and
μkt are the Lagrange multipliers, which are also called coordinative variables. Equation (12) is the expression of the Lagrange function. Meanwhile, Equation (12) can be separated as follows to make the function additive:
where
F1,kt is the water supply objective and
.
F2,t is the ecological objective and
. The water balance equation is satisfied in this model; thus, the last two items of Equation (13) are equal to 0. Then, Equation (13) is defined as being the total system model Lagrange function, and can be regarded as a summary of all subsystems. In absolute terms, the equation is also the sum of the expression of the objectives for each subsystem. In view of this, the problem of a large complex problem can be decomposed into several sub-problems, expressed as follows:
Constraints: see Equations (3)–(11).
By converting the Lagrange function of the large system, the large-scale water resources allocation problem was divided into relatively small sub-problems. Obviously, the different objectives are reflected by decomposed subproblems. In other words, the objective function of subsystem 1 is the ecological target of the downstream reservoir, and the objective functions of subsystem 2 to subsystem K are the water supply targets for each sub-area. From an overall perspective, the whole model considers an ecological as well as a water supply objective. In this way, if we determine the optimal solution for all small subsystems, the solution of a large system will naturally be solved through the coordination method.
3.1.2. System Coordination
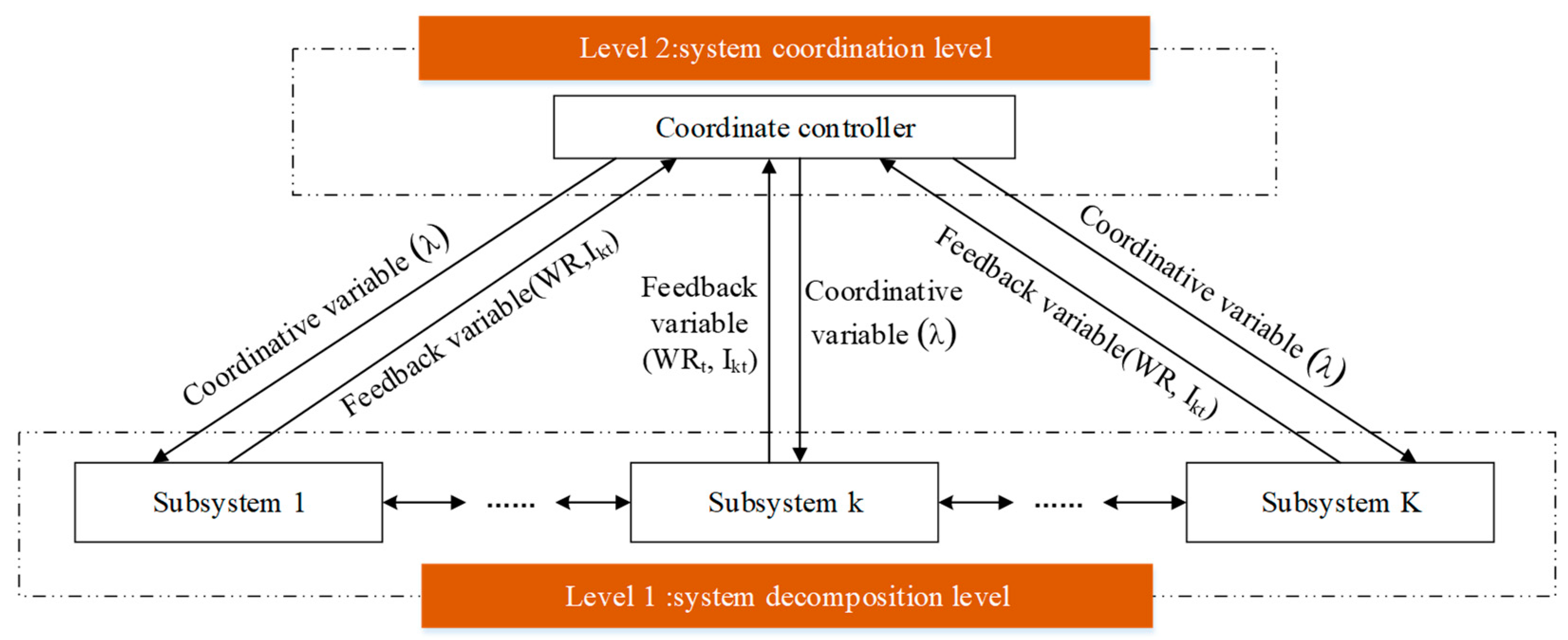
Figure 2 depicts the structure for both decomposition and coordination levels. Based on the optimal solution of each subsystem (Level 1 in
Figure 2), the coordination process is carried out through the Lagrange multiplier
λkt and
μkt to obtain the overall optimal solution. The decomposition and coordination processes are closely related. According to the dual theory, if we consider the Lagrange multiplier as variables, Equation (12) can be translated into a dual function, the maximum value of which can be determined, formulated as follows:
According to the condition of obtaining the extremum value of the function, Equation (16) obtains the maximum value when the following condition is satisfied.
where
m denotes the iteration number. Equation (17) suggests that the optimal outflow of the upper reaches of the
kth subsystem is regarded as the inflow of the
kth subsystem, as well as the new correlation estimate value and constraints. At this level,
WRkt and
Ikt are feedback variables, and they are optimized in each subsystem and used to respond to the coordination level. The following condition should also be satisfied if the Lagrange function achieves its maximum.
The iteration equation of coordination factor λ is obtained by Equation (20).
3.2. Subsystem Solving
If we take each time step as a stage, water allocation can be seen as the sequential allocation at each stage. The total input in a water resources system is usually the historical reservoir inflow over multiple years, which is always given from hydrological statistical yearbooks. Therefore, dynamic programming was formulated to effectively utilize the sequential decision structure of optimization problems [
43]. In addition, this system model satisfies the condition of decision segmentation, with the mathematical model being as presented below:
(1) Stage variables: Select each time step as a stage variable, with t = 1, 2, …, T.
(2) State variables: the initial storage of the reservoir and the initial total water quantity of each sub-area can be selected as state variables, defined by V0,t and W0,t.
(3) Decision variables: WS and Q determine the reservoir storage, while TWS and WR determine the total water quantity of sub-area. It should be stressed that the value of WS is determined by the value of Q, because of the constraint of water balance of reservoir and its storage, and WR has little effect on the accuracy of the model. Therefore, Q and TWS are the main decision variables in this model.
(4) State transition equation: water balance equation of reservoir and sub-areas can be selected as the state transition equation, expressed by Equation (3) and Equation (9)
(5) Recurrence formulation:
where
ft(Vt) and
are the minimum values of an objective function of subsystem 1 and subsystem
k from the beginning of the
tth time step to the
Tth time step, which can indirectly reflect the ecological and water deficit ratio.
ft+1(Vt+1) and
are the minimum values of an objective function of subsystem 1 and subsystem
k for the rest period (from (
t+1)
th time step to
Tth time step).
gt(Vt,Qt) is the minimum ecological water deficit ratio of stage
t with the decision variables
Qt at the state
Vt.
is the minimum water deficit ratio of stage
t with the decision variable
TWSt at state
Wt.
However, when the dimension is too high, it may be impossible to figure out the optimal solution, and this is called the “curse of dimension”. Therefore, an improved DP called Discrete Differential Dynamic Programming (DDDP) was used to solve this problem [
44]. To improve the normal DP method, DDDP is an iteration arithmetic which gradually approximates the predetermined objective. When seeking the optimal solution to a problem, upper and lower boundaries are needed in each stage to generate a corridor in the overall situation. The width of the corridor plays an important role in seeking the optimal results. If the corridor is too wide, it may give lower precision. Otherwise, it may introduce more complexity. The normal DP is used in the corridor to seek the optimal values. The results are not necessarily optimal at the beginning, and only change the allocation of water resources. The corridor width is usually set to be large, and it will gradually converge to a small value for precision as further iterations are executed. The optimal solution will be determined as the corridor width narrows.
3.3. Whole Solving Procedures
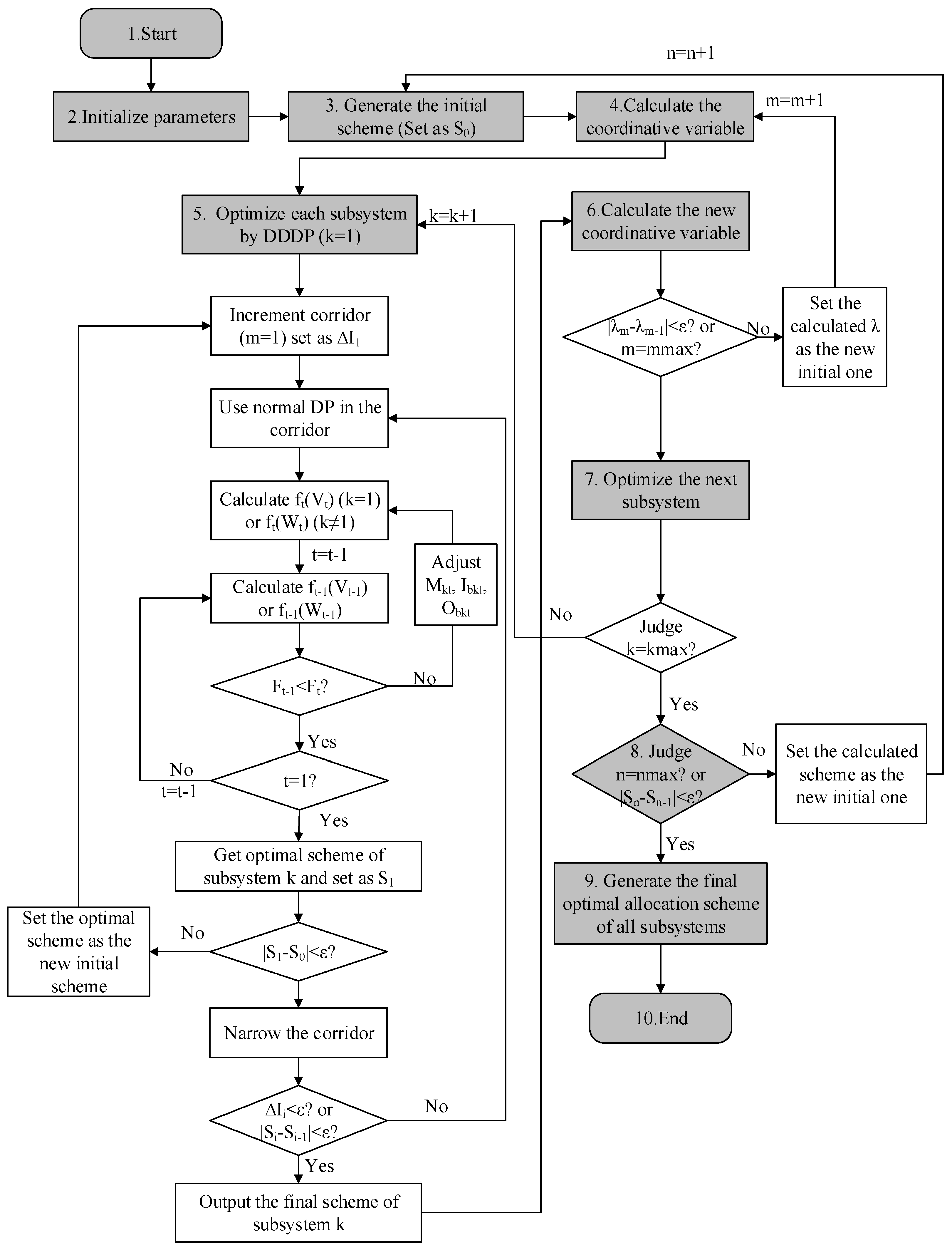
Figure 3 shows the whole procedure for the solution of the large water resources system using the DC and DDDP methods. The DC method was first used to decompose the complex large water resources system into small subsystems and to generate the corresponding sub-problems, and then all of the subsystems were coordinated to figure out their coordinative variables; this is essential to determining the optimal solution to the complex large system. The DDDP method was used to determine the optimal solution for both the subsystems and the whole system. The detailed solution procedure combining the DC and DDDP methods was as follows:
Step 1: Start the whole program.
Step 2: Initialize the parameters and set n = 1, where n is the iteration number of the whole system. In this case, the parameters include the initial storage of the reservoir, the initial value of water quantity for each sub-area, and the water recession coefficient of this sub-area from previous sub-area(s).
Step 3: Begin calculation. Calculate the ecological release of the reservoir (M1t) and the total water supply of each sub-area (Mkt). Reservoir ecological release can be calculated using the Tennant method, and total water supply can be calculated based on the water balance equation. In this step, the initial allocation scheme is generated.
Step 4: Calculate the coordinative variable based on Equation (20). The calculated value is set as the initial coordinative variable.
Step 5: Begin the main method. In this step, the large system is divided into subsystems, and each subsystem is optimized by DDDP; set m = 1, where m is the iteration number of the kth subsystem. The optimization process is within the given width of the corridor by normal DP using the inverse sequence method to obtain the new allocation scheme and narrow the corridor. If the error-adjacent iteration of the allocation is less than ε, then go to the next step; otherwise, repeat this step, and set m = m + 1.
Step 6: Calculate the new coordinative variable and compare it with the initial one. If the convergence condition is satisfied or the maximum iteration is attained, then go to the next step; otherwise, update the coordinative variable and return to step 4.
Step 7: Prepare to optimize the next subsystem using the same method. If k = kmax, go to the next step; otherwise, go back to step 5 to optimize the next subsystem.
Step 8: In this step, the whole optimization is finished and it is time to prepare the next iteration of the whole system. If n = nmax or the convergence condition is satisfied, go to the next step; otherwise, go back to step 3 for the next iteration.
Step 9: The total optimal allocation scheme is generated, including the ecological release of the reservoir and socio-economic water allocation for each sub-area.
Step 10: End the program.
5. Conclusions
This study developed a large complex system of water sources, and the optimal solution of allocation scheme was solved using the system analysis technique. The optimal water resources allocation model takes into account both water supply and environmental needs, and the combination of the decomposition-coordination and discrete differential dynamic programming methods was used to optimize the model efficiently. These two main methods can reduce the dimensions of the complex large system to increase the solution efficiency by distributing the two objectives into different subsystems, and each objective can thus be taken into account by optimizing each subsystem. It can then be integrated into the process of water resources planning and management based on sustainable development. The following conclusions can be drawn based on this study:
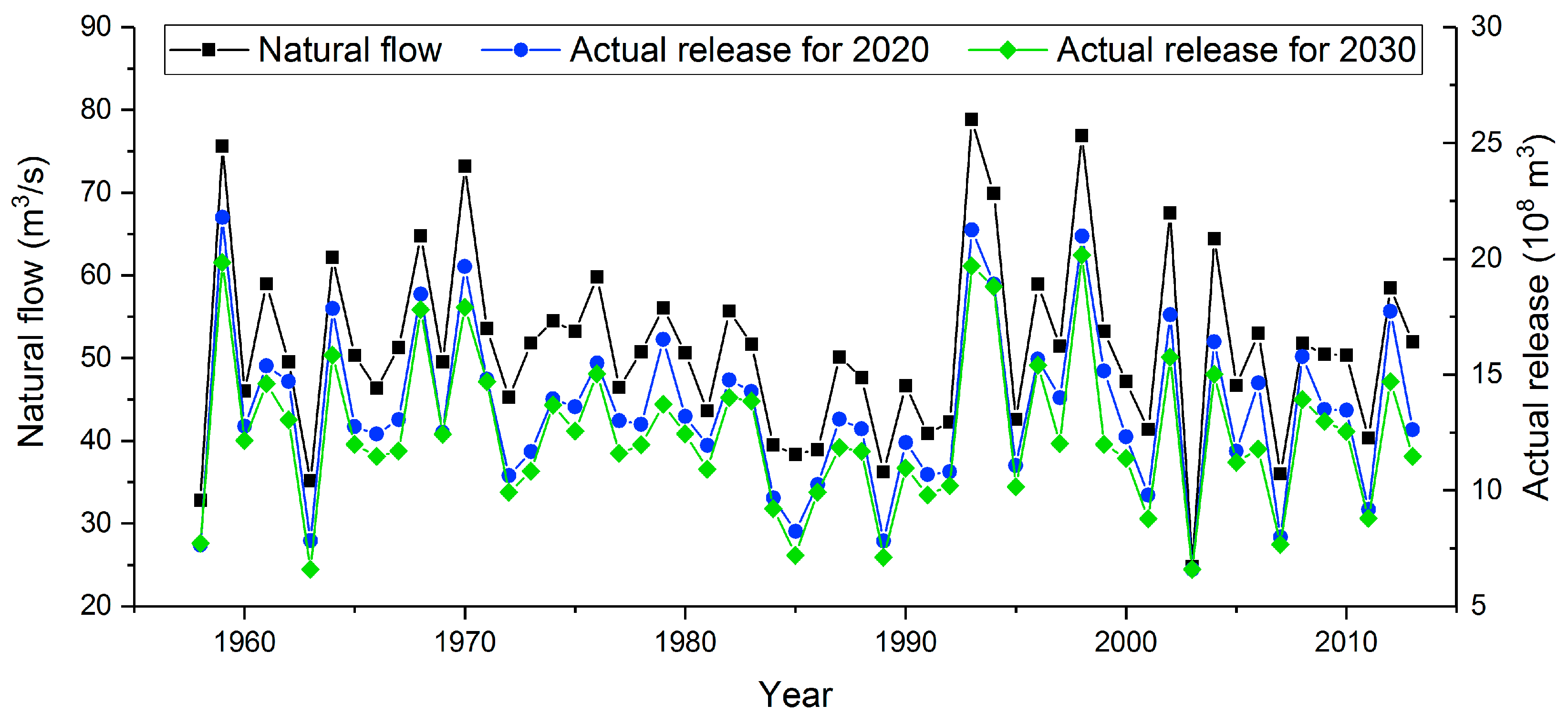
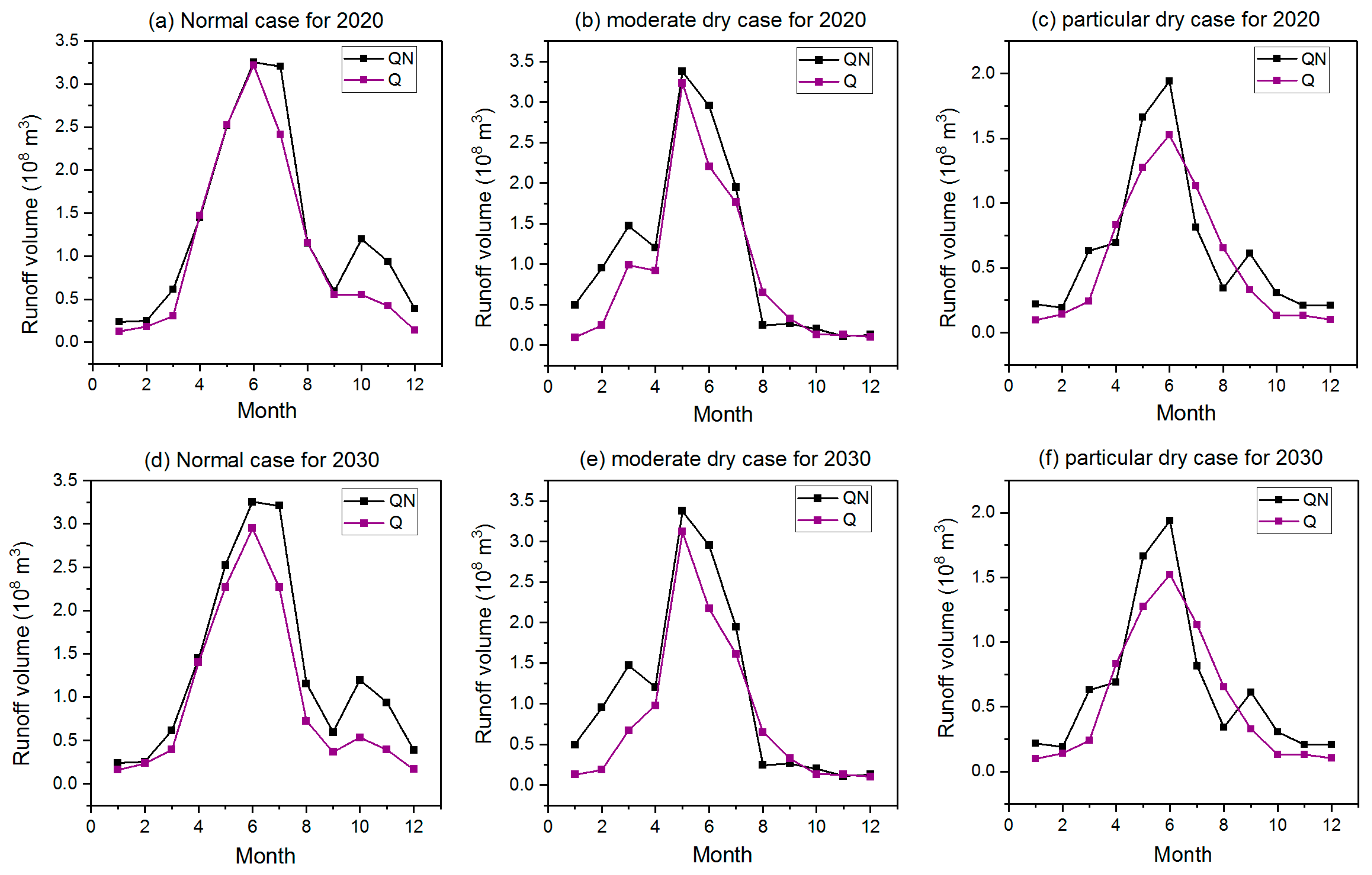
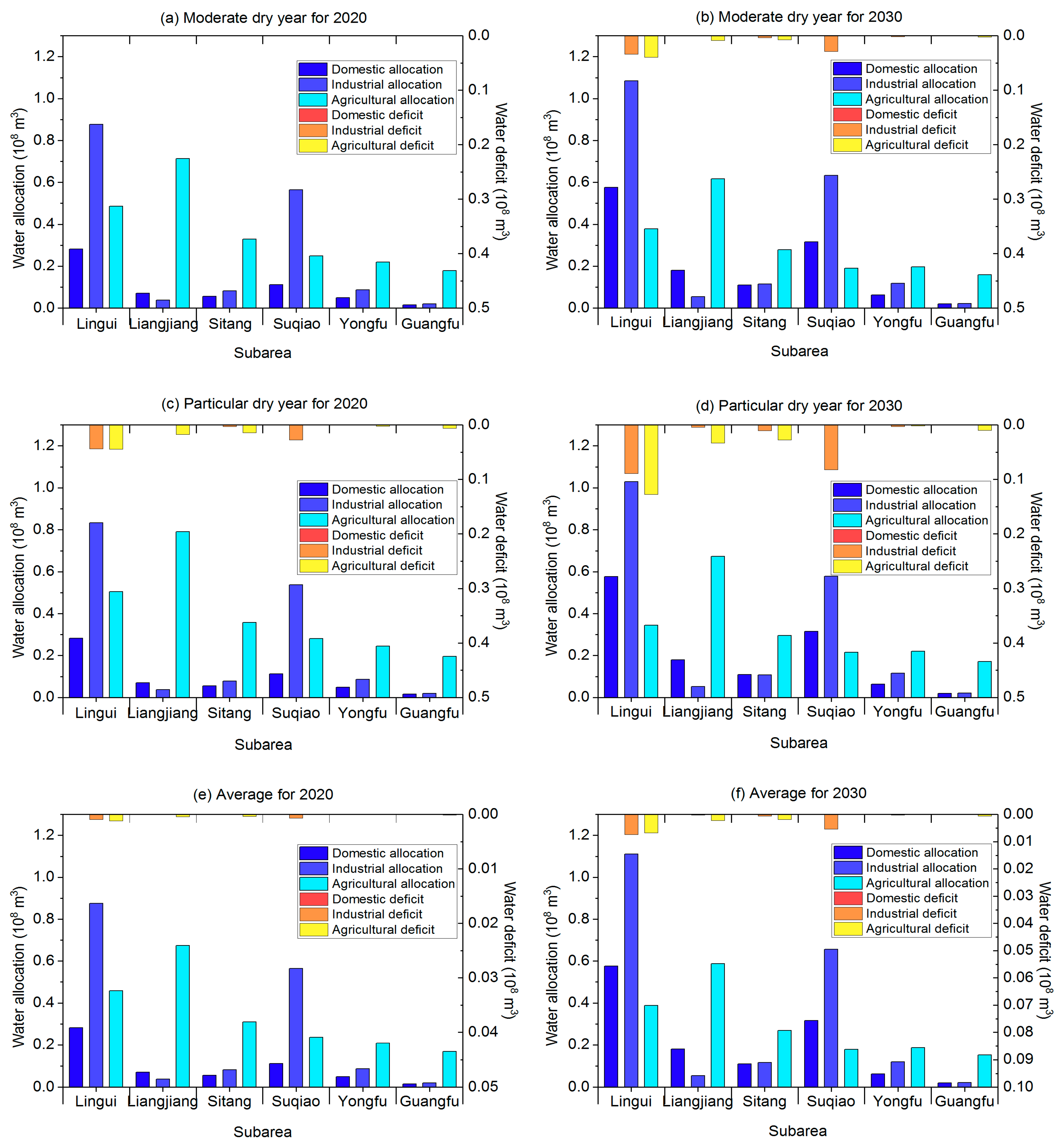
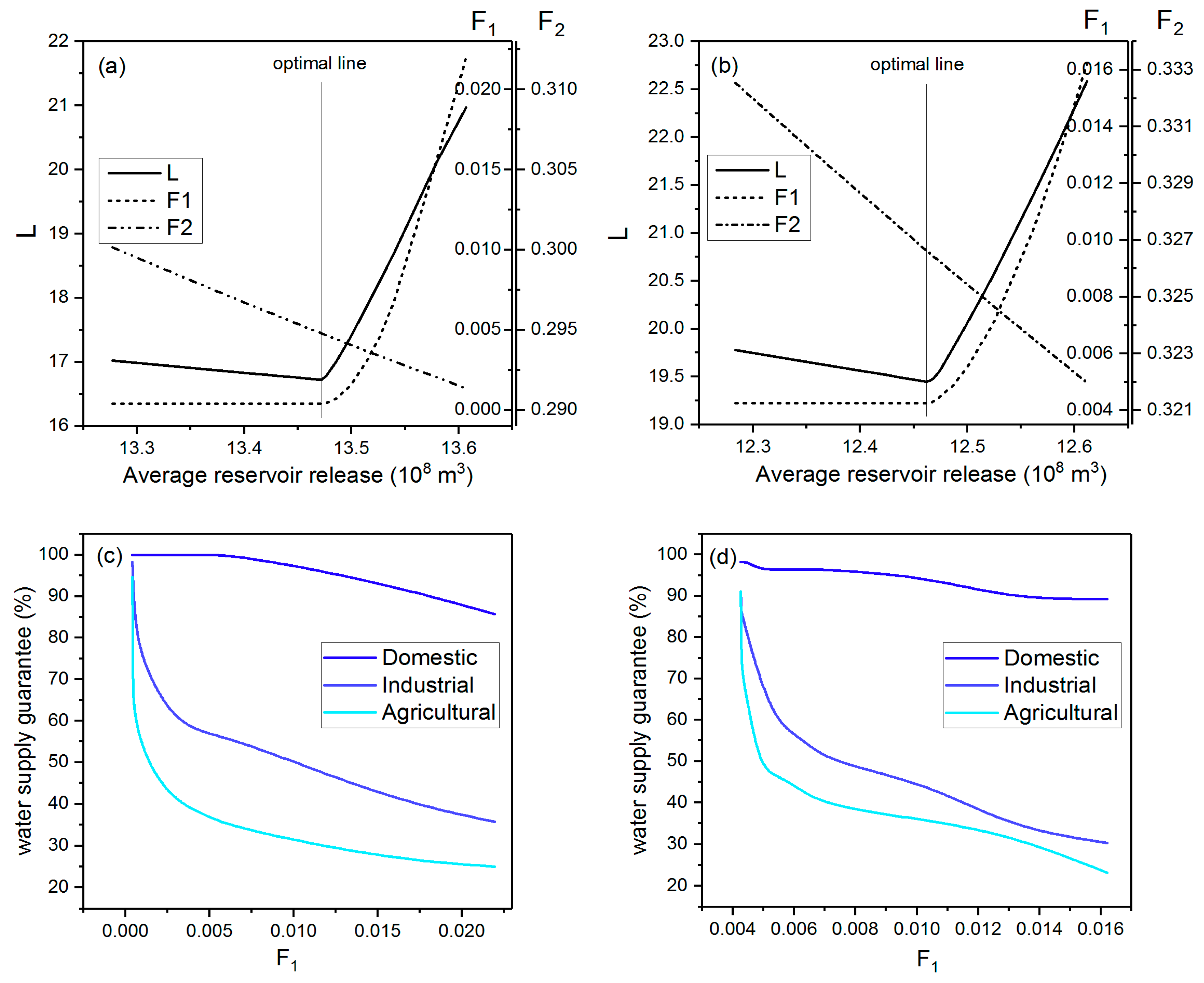
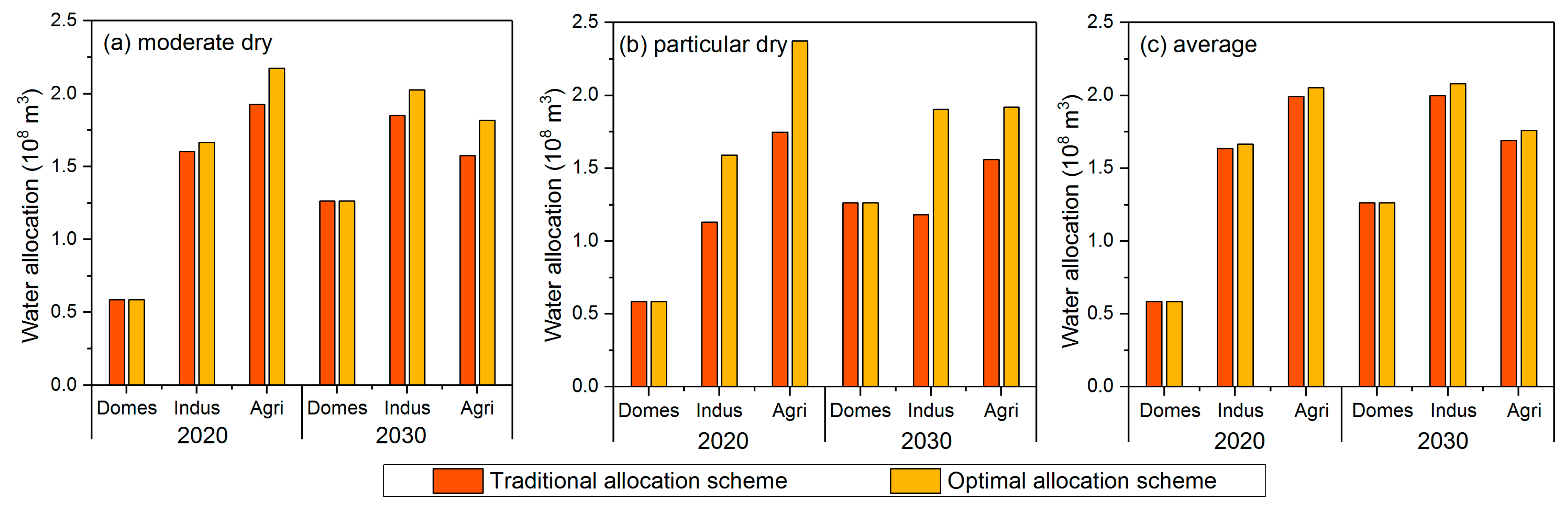
(1) There exists a balance between ecological and socio-economic targets, although they can be mutually contradictory. The total optimal allocation result will be obtained if the ecological release of the reservoir is as close as possible to the natural flow while achieving minimal water deficit. In the case study, the trend of ecological release of the reservoir was consistent with the natural flow on both year and multi-year scales, and the water supply to different water users could almost be satisfied in order to support economic development in different level years, which is, to some extent, beneficial to sustainable development.
(2) The water supply element is more sensitive to the water resources system model than the ecological element; thus, the actual release of the reservoir can be decreased slightly to increase the satisfaction of the demand for water in different sectors based on the minimum alteration of natural flow and the maintenance of basic ecological flow. This further indicates that the optimal allocation scheme can be flexibly adjusted as the external condition changes.
(3) The case study demonstrated that the proposed model is able to find the optimal water resources allocation scheme in consideration of sustainable water resources utilization in terms of both water supply and riverine ecological benefit, as compared to traditional model, and it can be applied in other, similar, fields where it is necessary to satisfy two conflicting aspects.
There is much space for the development in this study. For example, uncertainly is usually reflected in the random precipitation in both time and space, as well as the irregularity of water demands in different periods, which can be an important factor in water resources management. In addition, the riverine ecology itself is also a large complex system that includes a large number of elements. The amount and the distribution of actual release of the reservoir are just one of the most crucial elements in this system, but other subtle elements, such as sedimentation, water quality and aquatic condition, are also important in maintaining ecological health. Therefore, uncertainty analysis, comprehensive ecology, and also study on multi-function reservoirs [
47] are future research directions in our study.