Soil Water Dynamics in a Rainfed Mediterranean Agricultural System
Abstract
:1. Introduction
2. Materials and Methods
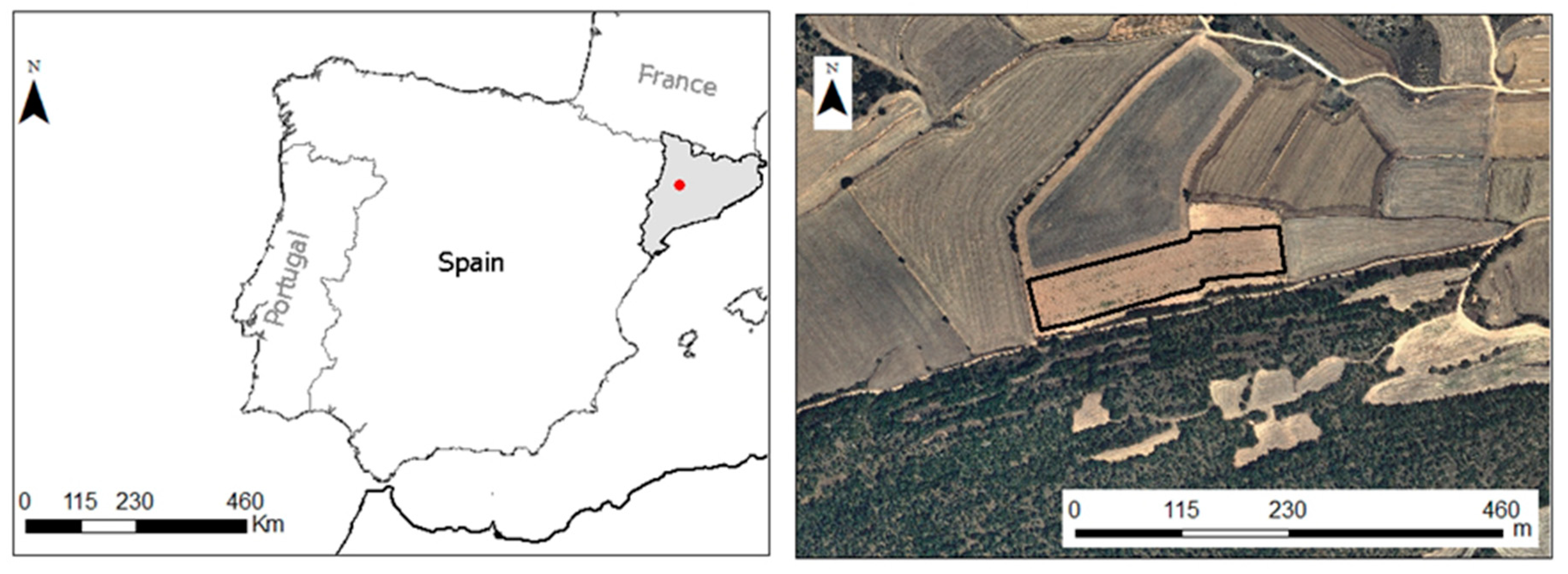
2.1. Study Area
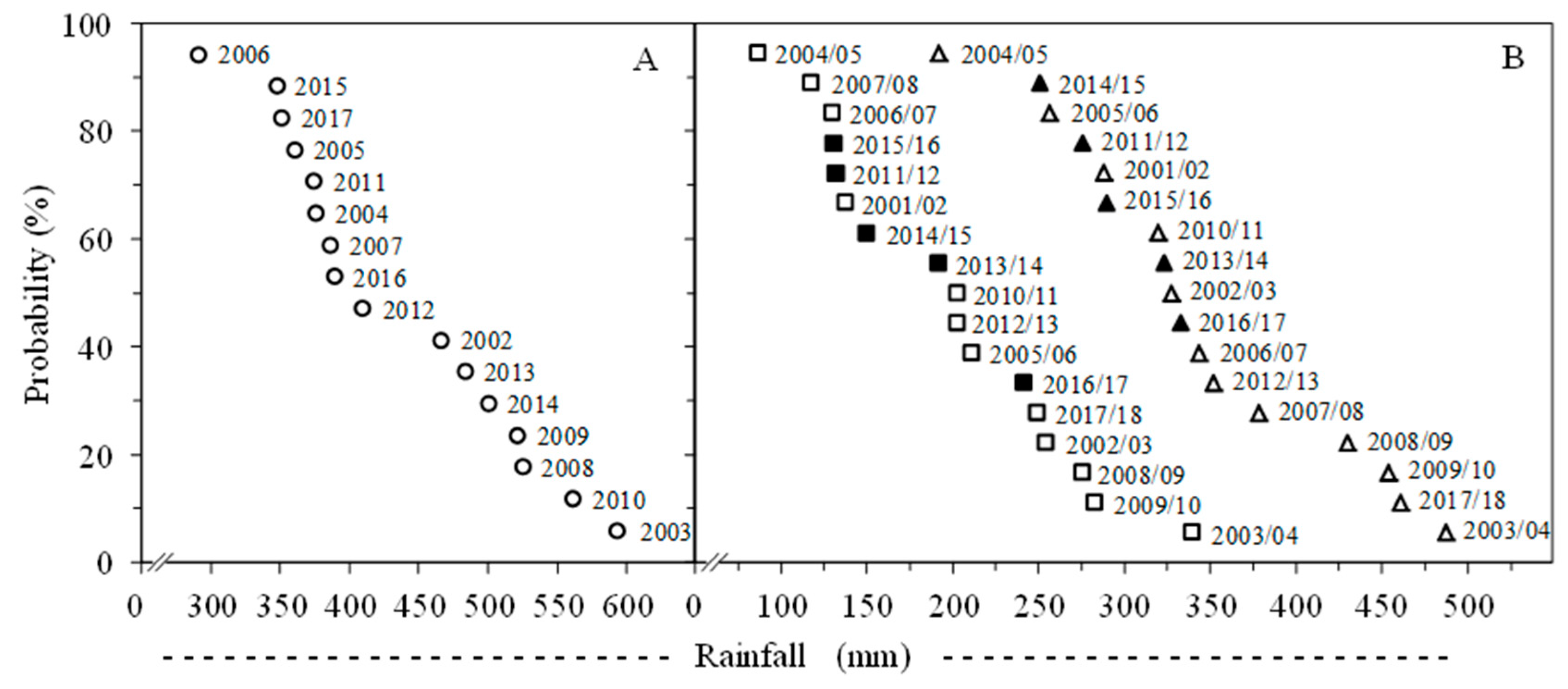
2.2. Climate Conditions
2.3. Soil Properties
2.4. Data Acquisition
2.5. LEACHM Model
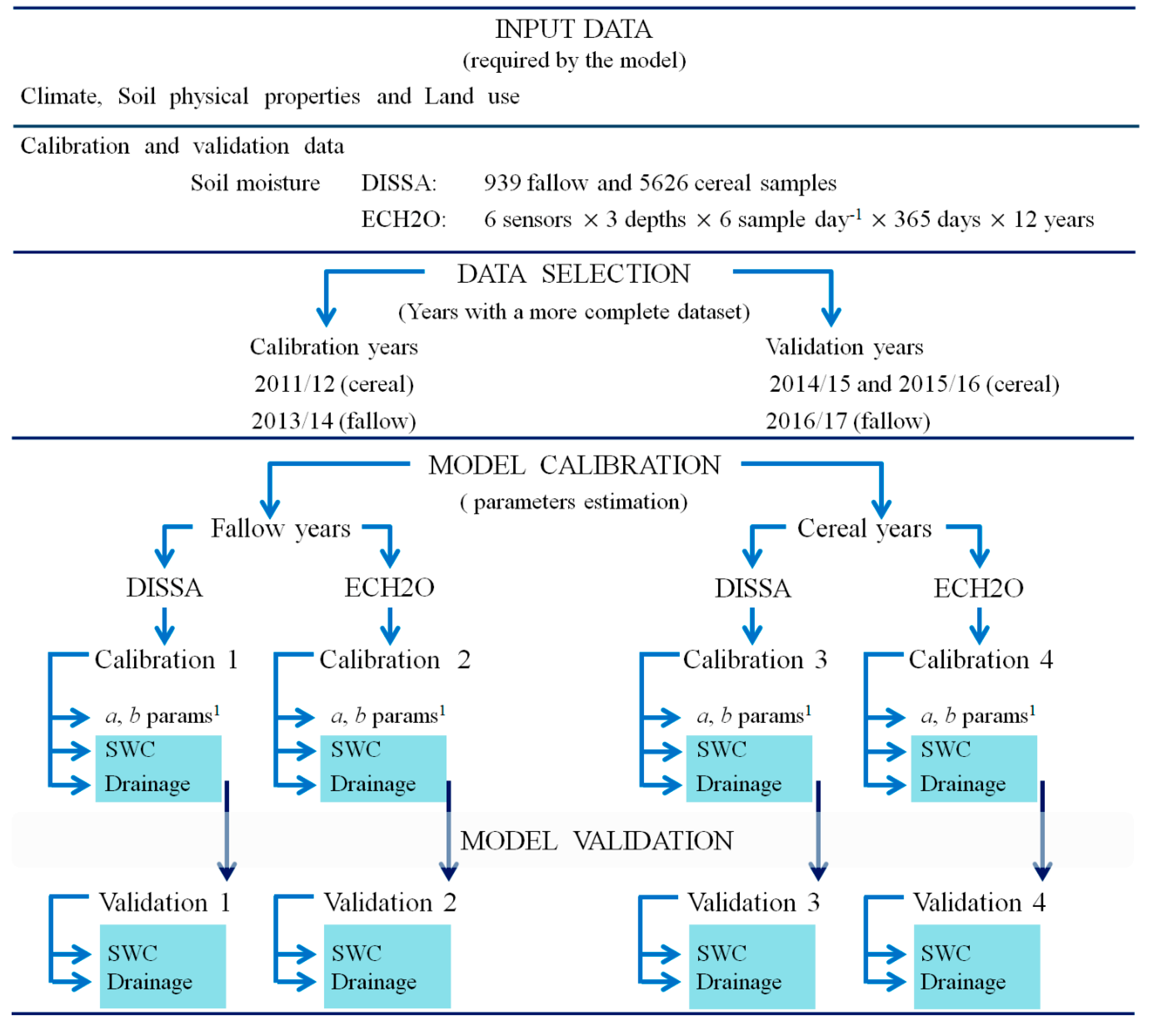
2.6. Model Calibration and Validation
3. Results
3.1. Parameters Calibration
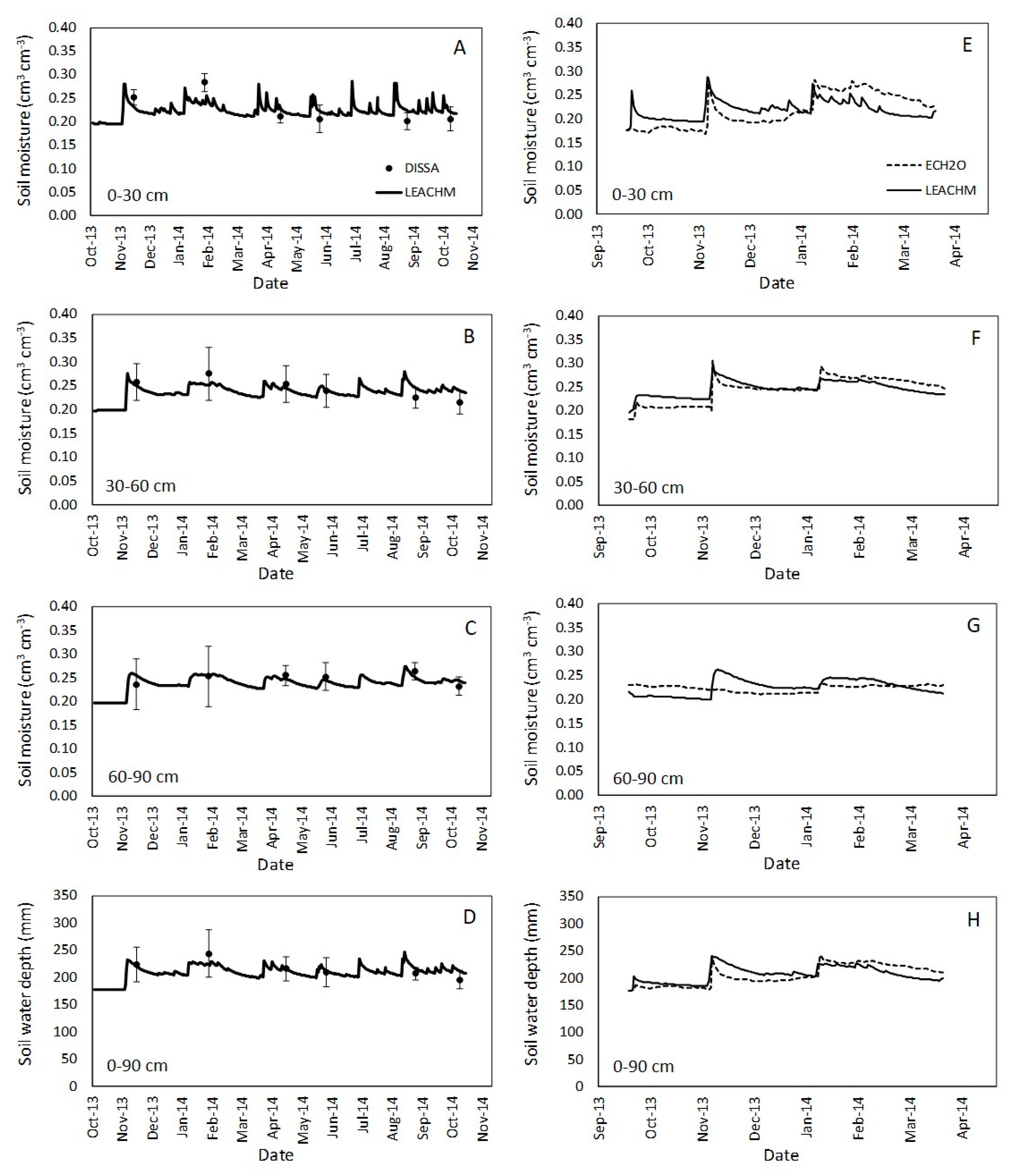
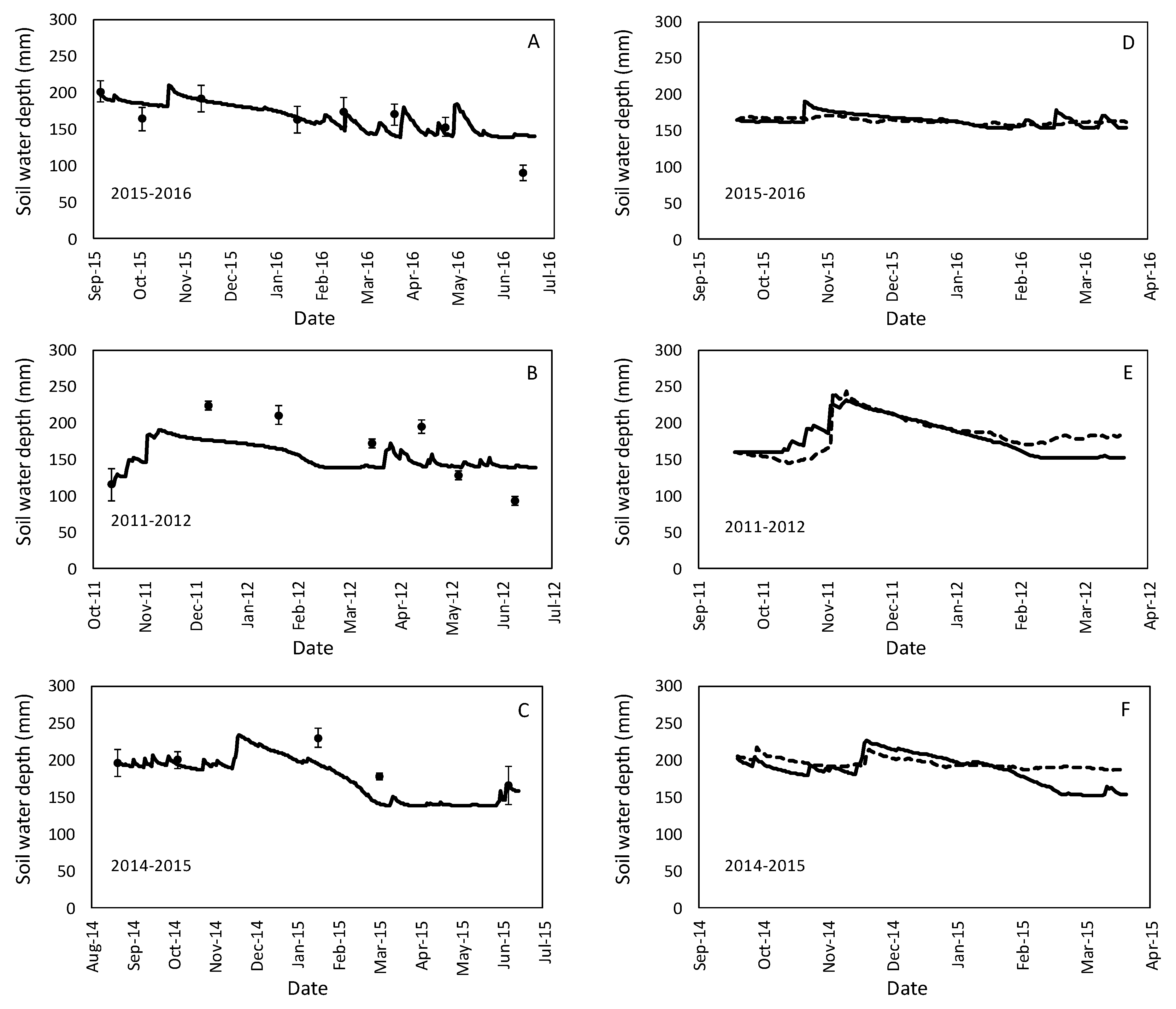
3.2. Soil Water Content Modelling in a Fallowing Period
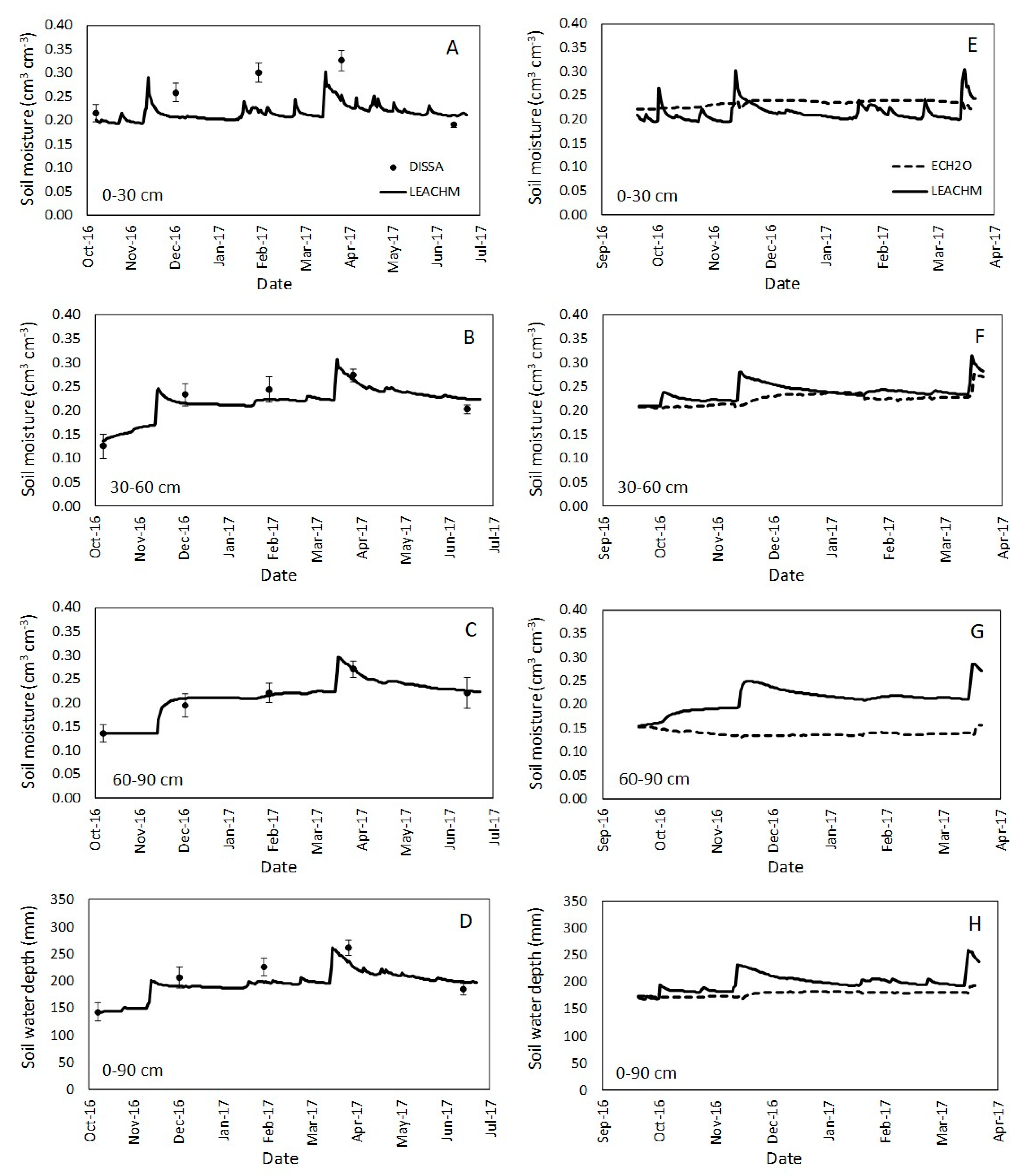
3.3. SWC Modelling in a Barley Crop Soil
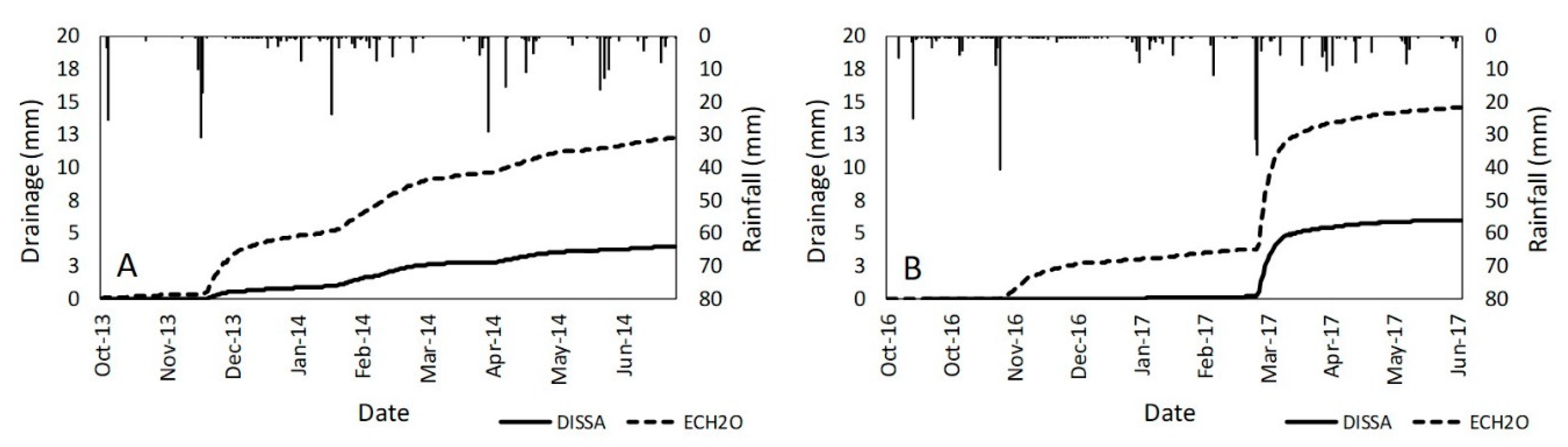
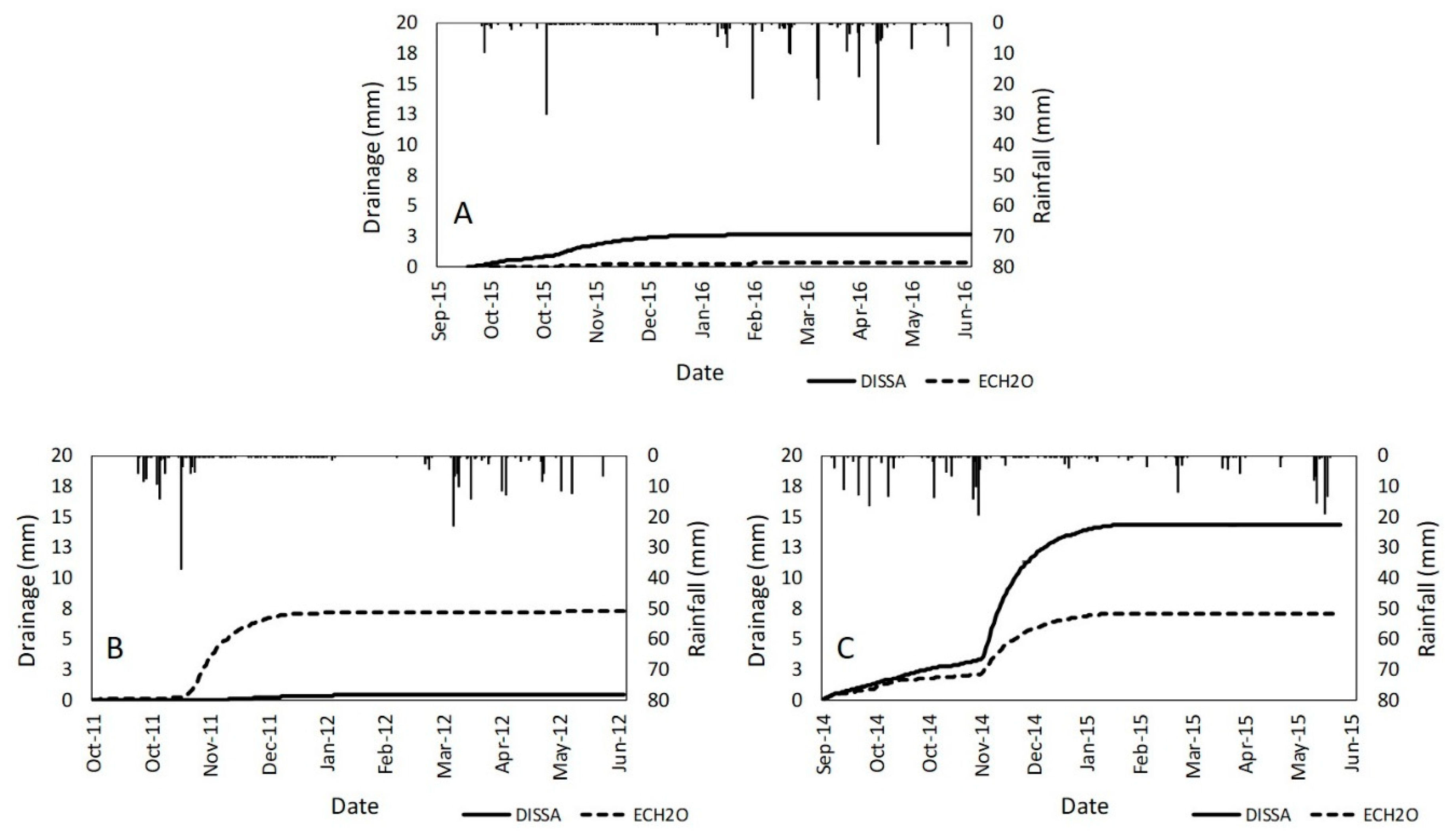
3.4. Water Balance
4. Discussion
4.1. Soil Water Dynamics
4.2. Drainage Modelling
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Union. Council Directive 91/676/EEC, of 12 December 1991, concerning the protection of waters against pollution caused by nitrates from agricultural sources. Off. J. Eur. Communities 1991, L375/1–L375/8. [Google Scholar]
- Mateo-Sagasta, J.; Marjani, S.; Turral, H. (Eds.) More People, More Food, Worse Water? A Global Review of Water Pollution from Agriculture; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy; International Water Management Institute (IWMI): Colombo, Sri Lanka, 2018; ISBN 978-92-5-130729-8. [Google Scholar]
- Sordo-Ward, A.; Granados, I.; Iglesias, A.; Garrote, L. Blue Water in Europe: Estimates of current and future availability and analysis of uncertainty. Water 2019, 11, 420. [Google Scholar] [CrossRef]
- Rockström, J.; Karlberg, L.; Wani, S.P.; Barron, J.; Hatibu, N.; Oweis, T.; Bruggeman, A.; Farahani, J.; Qiang, Z. Managing water in rainfed agriculture—The need for a paradigm shift. Agric. Water Manag. 2010, 97, 543–550. [Google Scholar] [CrossRef]
- Ministerio de Medio Ambiente y Medio Rural y Marino (MARM). National summary of area, yield and production, 2015. In Statistical Yearbook; NIPO 013-17-118-2; MARM: Madrid, Spain, 2017; p. 791. (In Spanish) [Google Scholar]
- Moret, D.; Arrúe, J.L.; López, M.V.; Gracia, R. Winter barley performance under different cropping and tillage systems in semiarid Aragon (NE Spain). Eur. J. Agron. 2007, 26, 54–63. [Google Scholar] [CrossRef]
- Meco, R.; Moreno, M.; Lacasta, C. Productividad de sistemas de secano semiárido en manejo ecológico. In La Reposición de la Fertilidad en los Sistemas Agrarios Tradicionales; Garrabou, R., González de Molina, M., Eds.; Icaria Editorial S.A.: Barcelona, Spain, 2010; pp. 85–108. ISBN 978-84-9888-215-5. [Google Scholar]
- Robinson, D.A.; Campbell, C.S.; Hopmans, J.W.; Hornbuckle, B.K.; Jones, S.B.; Knight, R.; Ogden, F.; Selker, J.; Wendroth, O. Soil moisture measurement for ecological and hydrological watershed-scale observatories: A review. Vadose Zone J. 2008, 7, 358–389. [Google Scholar] [CrossRef]
- Shukla, M.K. Soil Physics: An Introduction, 1st ed.; CRC Press: Boca Raton, FL, USA, 2013; pp. 119–156. ISBN 978-1-4398-8842-1. [Google Scholar]
- Gardner, C.M.K.; Robinson, D.; Blyth, K.; Cooper, J.D. Soil Water Content. In Soil and Environmental Analysis, 2nd ed.; Smith, K.A., Mullins, C.E., Eds.; Marcel Dekker Inc.: New York, NY, USA, 2000; pp. 1–84. ISBN 0-203-90860-0. [Google Scholar]
- Czarnomski, N.M.; Moore, G.W.; Pypker, T.G.; Licata, J.; Bond, B.J. Precision and accuracy of three alternative instruments for measuring soil water content in two forest soils of the Pacific Northwest. Can. J. For. Res. 2005, 35, 1867–1876. [Google Scholar] [CrossRef]
- Lidón, A.; Ramos, C.; Rodrigo, A. Comparison of drainage estimation methods in irrigated citrus orchards. Irrig. Sci. 1999, 19, 25–36. [Google Scholar] [CrossRef]
- Jakubínský, J.; Pechanec, V.; Procházka, J.; Cudlín, P. Modelling of Soil Erosion and Accumulation in an Agricultural Landscape—A Comparison of Selected Approaches Applied at the Small Stream Basin Level in the Czech Republic. Water 2019, 11, 404. [Google Scholar] [CrossRef]
- Hutson, J.L. LEACHM, Leaching Estimation and Chemistry Model. Model Description and User’s Guide. School of Chemistry, Physics and Earth Sciences, The Flinders University of South Australia: Adelaide, Australia, 2003. [Google Scholar]
- Marinov, I.; Marinov, A.M.A. Coupled mathematical model to predict the influence of nitrogen fertilization on crop, soil and groundwater quality. Water Resour. Manag. 2014, 28, 5231–5246. [Google Scholar] [CrossRef]
- Porter, J.R. AFRCWHEAT2: A model of the growth and development of wheat incorporating responses to water and nitrogen. Eur. J. Agron. 1993, 2, 69–82. [Google Scholar] [CrossRef]
- Addiscott, T.M.; Wagenet, R.J. Concepts of solute leaching in soils: A review of modelling approaches. Eur. J. Soil Sci. 1985, 36, 411–424. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Allen, R.G.; Droogers, P.; D’Urso, G.; Steduto, P. Twenty-five years modeling irrigated and drained soils: State of the art. Agric. Water. Manag. 2007, 92, 111–125. [Google Scholar] [CrossRef]
- Greenwood, D.J.; Zhang, K.; Hilton, H.W.; Thompson, A.J. Opportunities for improving irrigation efficiency with quantitative models, soil water sensors and wireless technology. J. Agric. Sci. 2010, 148, 1–16. [Google Scholar] [CrossRef]
- Hutson, J.L.; Wagenet, R.J. Simulating nitrogen dynamics in soils using a deterministic model. Soil Use Manag. 1991, 7, 74–78. [Google Scholar] [CrossRef]
- Sánchez de Óleo, C.M. Estimación de Parámetros en Modelos de Transporte de agua y Nitrógeno en el Suelo. Ph.D. Thesis, Technical University of Valencia, Valencia, Spain, 2015. [Google Scholar]
- Ramos, C.; Carbonell, E.A. Nitrate leaching and soil-moisture prediction with the LEACHM model. Fertil. Res. 1991, 27, 171–180. [Google Scholar] [CrossRef]
- Jabro, J.D.; Hutson, J.L.; Jabro, A.D. Parameterizing LEACHM model for simulating water drainage fluxes and nitrate leaching losses. In Advances in Agricultural Systems Modeling 2. Methods of Introducing System Models into Agricultural Research; Ahuja, L.R., Ma, L., Eds.; ASA-CSSA-SSSA: Madison, WI, USA, 2011; pp. 95–115. ISBN 978-0-89118-180-196-5. [Google Scholar]
- Lidón, A.; Ramos, C.; Ginestar, D.; Contreras, W. Assessment of LEACHN and a simple compartmental model to simulate nitrogen dynamics in citrus orchards. Agric. Water Manag. 2013, 121, 45–53. [Google Scholar] [CrossRef]
- Smith, W.N.; Reynolds, W.D.; De Jong, R.; Clemente, R.S.; Topp, B. Water flow through intact soil columns: Measurement and simulation using LEACHMN. J. Environ. Qual. 1995, 24, 874–891. [Google Scholar] [CrossRef]
- Akinremi, O.O.; Jame, Y.W.; Campbell, C.A.; Zentner, R.P.; Chang, C.; De Jong, R. Evaluation of LEACHMN under dryland conditions. I. Simulation of water and solute transport. Can. J. Soil Sci. 2005, 85, 223–232. [Google Scholar] [CrossRef]
- Soil Survey Staff. Keys to Soil Taxonomy, 12th ed.; USDA-Natural Resources Conservation Service: Washington, DC, USA, 2014.
- Santamaría, J. Máximas lluvias diarias en la España Peninsular; Serie Monografías. Dirección General de Carreteras y Centro de Estudios y Experimentación de Obras Públicas Ministerio de Fomento: Madrid, Spain, 1999; ISBN 9788449804199. (In Spanish)
- Casas, M.C. Análisis Espacial y Temporal de las Lluvias Extremas en Catalunya. Modelización y Clasificación Objetiva. Ph.D. Thesis, Universitat de Barcelona, Barcelona, Spain, 2005. [Google Scholar]
- Plaza-Bonilla, D.; Álvaro-Fuentes, J.; Hansen, N.C.; Lampurlanés, J.; Cantero-Martínez, C. Winter cereal root growth and aboveground–belowground biomass ratios as affected by site and tillage system in dryland Mediterranean conditions. Plant Soil 2014, 374, 925–939. [Google Scholar] [CrossRef]
- MAPA, Ministerio de Agricultura, Pesca y Alimentación. Métodos Oficiales de Análisis. Tomo III. 2(b) Textura (Método de la Pipeta), Pipet Method; Secretaria General de Alimentación, Dirección General de Política Alimentaria: Madrid, Spain, 1994; pp. 297–306. ISBN 8449100003. (In Spanish)
- Walkley, A.; Black, I.A. An examination of the Degtjareff method for determining soil organic matter and a proposed modification of the chromic acid titration method. Soil Sci. 1934, 37, 29–38. [Google Scholar] [CrossRef]
- Topp, G.C.; Davis, J.L.; Annan, A.P. Electromagnetic determination of soil water content: Measurements in coaxial transmission lines. Water Resour. Res. 1980, 16, 574–582. [Google Scholar] [CrossRef]
- Crank, J.; Nicolson, P. A practical method for numerical evaluation of solutions of partial differential equations of the heat-conduction type. Math. Proc. Camb. Philos. Soc. 1947, 43, 50–67. [Google Scholar] [CrossRef]
- Campbell, G.S. A simple method for determining unsaturated conductivity from moisture retention data. Soil Sci. 1974, 117, 311–314. [Google Scholar] [CrossRef]
- Hutson, J.L.; Cass, A. A retentivity function for use in soil–water simulation models. Eur. J. Soil Sci. 1987, 38, 105–113. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration Guidelines for Computing Crop Water Requirements—FAO Irrigation and Drainage Paper 56; FAO, Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; pp. 65–87. ISBN 92-5-104219-5. [Google Scholar]
- Childs, S.; Hanks, R.J. Model of soil salinity effects on crop growth. Soil Sci. Soc. Am. J. 1975, 39, 617–622. [Google Scholar] [CrossRef]
- Nimah, M.N.; Hanks, R.J. Model for Estimating Soil Water, Plant, and Atmospheric Interrelations: I. Description and Sensitivity. Soil Sci. Soc. Am. J. 1973, 37, 522–527. [Google Scholar] [CrossRef]
- Lidón, A. Simulación del movimiento del agua y nitrógeno en el suelo. In VI Jornadas de Investigación y Fomento de la Multidisciplinariedad; Editorial UPV: Valencia, Spain, 2004; pp. 207–221. (In Spanish) [Google Scholar]
- Jung, Y.W.; Oh, D.S.; Kim, M.; Park, J.W. Calibration of LEACHN model using LH-OAT sensitivity analysis. Nutr. Cycl. Agroecosyst. 2010, 87, 261–275. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder-Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Wallach, D. Evaluating crop models. In Working with Dynamic Crop Models Evaluation, Analysis, Parameterization, and Applications, 1st ed.; Wallach, D., Makowski, D., Jones, J.W., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; pp. 11–54. ISBN 978-0-444-52135-4. [Google Scholar]
- Jabro, J.D.; Jemison, J.M., Jr.; Lengnick, L.L.; Fox, R.H.; Fritton, D.D. Field validation and comparison of LEACHM and NCSWAP models for predicting nitrate leaching. Trans. ASAE 1993, 36, 1651–1657. [Google Scholar] [CrossRef]
- Jemison, J.M., Jr.; Jabro, J.D.; Fox, R.H. Evaluation of LEACHM: I. Simulation of drainage, bromide leaching, and corn bromide uptake. Agron. J. 1994, 86, 843–851. [Google Scholar] [CrossRef]
- Johnson, A.; Griffin, G. Estimating nitrate leaching and soil water dynamics with LEACHM. In Proceedings of the 1993 Georgia Water Resources Conference, University of Georgia, Athens, Georgia, 20–21 April 1993; pp. 371–374. [Google Scholar]
- Gasch, C.K.; Brown, D.J.; Brooks, E.S.; Yourek, M.; Poggio, M.; Cobos, D.R.; Campbell, C.S. A pragmatic, automated approach for retroactive calibration of soil moisture sensors using a two-step, soil-specific correction. Comput. Electron. Agric. 2017, 137, 29–40. [Google Scholar] [CrossRef]
- Plaza-Bonilla, D.; Cantero-Martínez, C.; Bareche, J.; Arrúe, J.L.; Lampurlanés, J.; Álvaro-Fuentes, J. Do no-till and pig slurry application improve barley yield and water and nitrogen use efficiencies in rainfed Mediterranean conditions? Field Crop Res. 2017, 203, 74–85. [Google Scholar] [CrossRef]
- Parsinejad, M.; Feng, Y. Field evaluation and comparison of two models for simulation of soil-water dynamics. Irrig. Drain. 2003, 52, 163–175. [Google Scholar] [CrossRef]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Zampieri, M.; Navarra, A. Heavy precipitation events over the Euro-Mediterranean region in a warmer climate: Results from CMIP5 models. Reg. Environ. Chang. 2016, 16, 595–602. [Google Scholar] [CrossRef]

| Approach | Maximum 24-h Precipitation (mm) | ||
|---|---|---|---|
| 25 Years | 50 Years | 100 Years | |
| Santamaría [28] | 72 | 82 | 93 |
| Casas [29] | 60–80 | 80–100 | 100 |
| Properties | Units | Depth (cm) | ||
|---|---|---|---|---|
| 0–30 | 30–60 | 60–90 | ||
| Sand | % | 15.2 | 31.1 | 11.5 |
| Silt | % | 58.1 | 48.6 | 60.3 |
| Clay | % | 26.7 | 20.3 | 28.2 |
| Textural class | Silty loam | Silty loam | Silty clay loam | |
| pH (1:2.5 soil:water) | 8.3 | 8.5 | 8.5 | |
| Organic carbon | g C kg−1 | 9.9 | 4.6 | 4.6 |
| Bulk density | kg m−3 | 1650 | 1600 | 1550 |
| Infiltration velocity | mm h−1 | 1.54 | − | − |
| Saturated hydraulic conductivity (Ks) | mm d−1 | 233 | 524 | 457 |
| Soil water retention 1 at: | ||||
| −33 kPa | cm3 cm−3 | 0.269/0.223 | 0.266/0.232 | − |
| −100 kPa | cm3 cm−3 | 0.234/0.194 | 0.237/0.213 | − |
| −500 kPa | cm3 cm−3 | 0.173 | 0.168 | − |
| −1500 kPa | cm3 cm−3 | 0.163 | 0.170 | − |
| Soil water content at saturation (θs) 2 | cm3 cm−3 | 0.37 | − | − |
| Cycle | Data Origin | Iterations Number | Error | Parameter | Depth (cm) | ||
|---|---|---|---|---|---|---|---|
| 0–30 | 30–60 | 60–90 | |||||
| Initial | a (kPa) | −2.500 | −5.000 | −5.000 | |||
| b | 7.400 | 9.600 | 9.600 | ||||
| 2013–14 | DISSA 1 | 65 | 0.22 | a (kPa) | −4.946 | −4.982 | −4.982 |
| Fallow | b | 9.873 | 9.143 | 8.376 | |||
| ECH2O 2 | 112 | 0.28 | a (kPa) | −4.995 | −4.995 | −4.995 | |
| b | 7.813 | 7.210 | 6.084 | ||||
| 2015–16 | DISSA 3 | 134 | 0.51 | a (kPa) | −2.000 | −2.500 | −2.500 |
| Barley | b | 7.591 | 6.513 | 6.895 | |||
| ECH2O 4 | 68 | 0.20 | a (kPa) | −2.382 | −3.000 | −3.000 | |
| b | 8.819 | 8.677 | 6.635 | ||||
| Statistic | Depth | Calibration (13/14) | Validation (16/17) | ||
|---|---|---|---|---|---|
| (cm) | DISSA | ECH2O | DISSA | ECH2O | |
| MD | 0–30 | 0.19 | −0.22 | 13.92 | 5.86 |
| (mm) | 30–60 | −0.08 | −0.49 | 1.77 | −4.40 |
| 60–90 | 0.22 | 5.12 | −1.05 | −21.86 | |
| 0–90 | 0.33 | 4.41 | 14.65 | −20.41 | |
| RMSE | 0–30 | 7.52 | 8.85 | 18.53 | 8.38 |
| (mm) | 30–60 | 5.07 | 4.63 | 5.33 | 6.02 |
| 60–90 | 3.37 | 7.82 | 2.47 | 23.37 | |
| 0–90 | 11.21 | 13.47 | 23.00 | 24.82 | |
| NRMSE | 0–30 | 0.11 | 0.14 | 0.23 | 0.12 |
| 30–60 | 0.07 | 0.06 | 0.07 | 0.09 | |
| 60–90 | 0.05 | 0.11 | 0.04 | 0.56 | |
| 0–90 | 0.05 | 0.06 | 0.10 | 0.14 | |
| R2 | 0–30 | 0.91 | 0.28 | 0.49 | 0.00 |
| 30–60 | 0.72 | 0.70 | 0.56 | 0.42 | |
| 60–90 | 0.02 | 0.10 | 0.94 | 0.24 | |
| 0–90 | 0.89 | 0.49 | 0.64 | 0.37 | |
| d | 0–30 | 0.52 | 0.66 | 0.57 | 0.26 |
| 30–60 | 0.50 | 0.86 | 0.83 | 0.65 | |
| 60–90 | 0.40 | 0.20 | 0.97 | 0.06 | |
| 0–90 | 0.65 | 0.81 | 0.78 | 0.31 | |
| Statistic | Depth | Calibration (15/16) | Validation (11/12) | Validation (14/15) | |||
|---|---|---|---|---|---|---|---|
| (cm) | DISSA | ECH2O | DISSA | ECH2O | DISSA | ECH2O | |
| MD | 0–30 | −0.12 | −0.47 | 5.17 | −1.38 | 10.24 | −1.58 |
| (mm) | 30–60 | −0.80 | −0.67 | 7.56 | 3.91 | 5.27 | 3.97 |
| 60–90 | −0.97 | 0.35 | 7.55 | 1,57 | 3.44 | 6.22 | |
| 0–90 | −1.89 | −0.80 | 20.27 | 4.10 | 18.94 | 8.61 | |
| RMSE | 0–30 | 9.48 | 4.41 | 17.51 | 10.44 | 13.03 | 6.06 |
| (mm) | 30–60 | 8.71 | 3.80 | 14.35 | 7.75 | 7.89 | 6.87 |
| 60–90 | 9.09 | 2.56 | 12.00 | 9.46 | 11.95 | 8.97 | |
| 0–90 | 25.45 | 6.73 | 41.77 | 17.76 | 25.84 | 18.46 | |
| NRMSE | 0–30 | 0.18 | 0.08 | 0.32 | 0.18 | 0.19 | 0.10 |
| 30–60 | 0.17 | 0.07 | 0.26 | 0.12 | 0.13 | 0.10 | |
| 60–90 | 0.16 | 0.05 | 0.20 | 0.16 | 0.19 | 0.13 | |
| 0–90 | 0.16 | 0.04 | 0.25 | 0.12 | 0.13 | 0.09 | |
| R2 | 0–30 | 0.23 | 0.05 | 0.69 | 0.54 | 0.66 | 0.16 |
| 30–60 | 0.33 | 0.12 | 0.62 | 0.54 | 0.62 | 0.50 | |
| 60–90 | 0.21 | 0.36 | 0.36 | 0.09 | 0.42 | 0.28 | |
| 0–90 | 0.28 | 0.31 | 0.56 | 0.57 | 0.52 | 0.47 | |
| d | 0–30 | 0.50 | 0.50 | 0.48 | 0.80 | 0.74 | 0.55 |
| 30–60 | 0.73 | 0.15 | 0.63 | 0.80 | 0.81 | 0.46 | |
| 60–90 | 0.68 | 0.68 | 0.64 | 0.12 | 0.70 | 0.44 | |
| 0–90 | 0.68 | 0.63 | 0.61 | 0.86 | 0.72 | 0.54 | |
| Component (mm) | Fallow | Barley | |||
|---|---|---|---|---|---|
| 2013–2014 | 2016–2017 | 2011–2012 | 2014–2015 | 2015–2016 | |
| Initial water depth | 176.1 | 173.4 | 159.9 | 205.2 | 164.1 |
| Final water depth | 196.1 | 191.1 | 153.0 | 171.9 | 152.9 |
| Soil water storage | 20.0 | 17.7 | −6.9 | −33.3 | −11.2 |
| Rainfall | 323.2 | 332.8 | 275.7 | 250.8 | 289.7 |
| Evaporation-Evapotranspiration 1 | 290.0 | 299.8 | 274.8 | 277.5 | 299.6 |
| Accumulated drainage | 12.2 | 14.5 | 7.3 | 6.2 | 0.3 |
| Drainage for Oct.–Feb. period | 7.0 | 3.1 | 7.2 | 5.9 | 0.2 |
| Drainage for Feb.–Jun. period | 5.2 | 11.3 | 0.1 | 0.3 | 0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez-de-Santiago, D.E.; Lidón, A.; Bosch-Serra, À.D. Soil Water Dynamics in a Rainfed Mediterranean Agricultural System. Water 2019, 11, 799. https://doi.org/10.3390/w11040799
Jiménez-de-Santiago DE, Lidón A, Bosch-Serra ÀD. Soil Water Dynamics in a Rainfed Mediterranean Agricultural System. Water. 2019; 11(4):799. https://doi.org/10.3390/w11040799
Chicago/Turabian StyleJiménez-de-Santiago, Diana E., Antonio Lidón, and Àngela D. Bosch-Serra. 2019. "Soil Water Dynamics in a Rainfed Mediterranean Agricultural System" Water 11, no. 4: 799. https://doi.org/10.3390/w11040799
APA StyleJiménez-de-Santiago, D. E., Lidón, A., & Bosch-Serra, À. D. (2019). Soil Water Dynamics in a Rainfed Mediterranean Agricultural System. Water, 11(4), 799. https://doi.org/10.3390/w11040799





