Optimised Triangular Weir Design for Assessing the Full-Scale Performance of Green Infrastructure
Abstract
1. Introduction
2. Materials and Methods
2.1. GI Monitoring: State of the Art
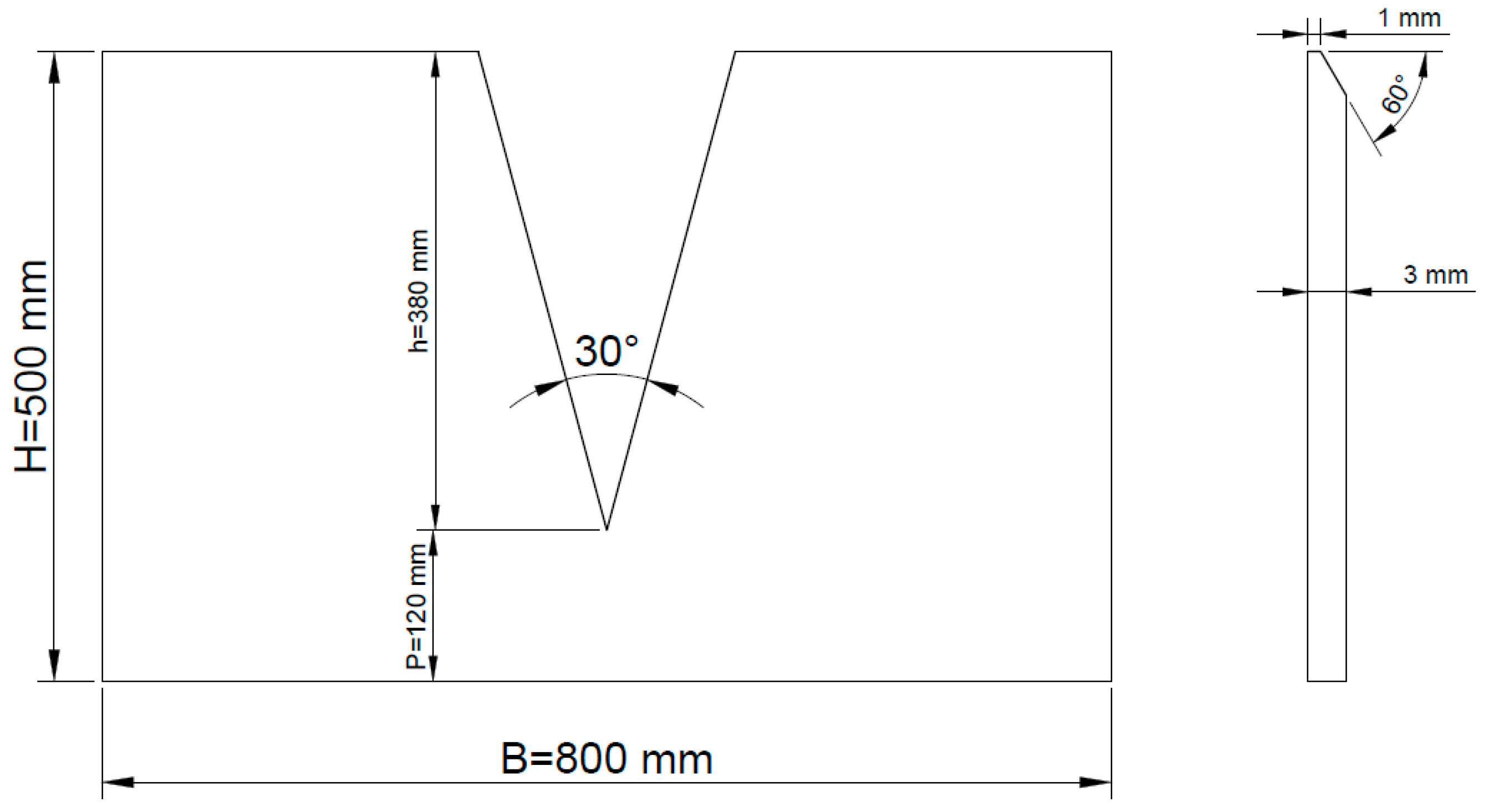
2.2. Weir Design for GI Full-Scale Performance Assessment
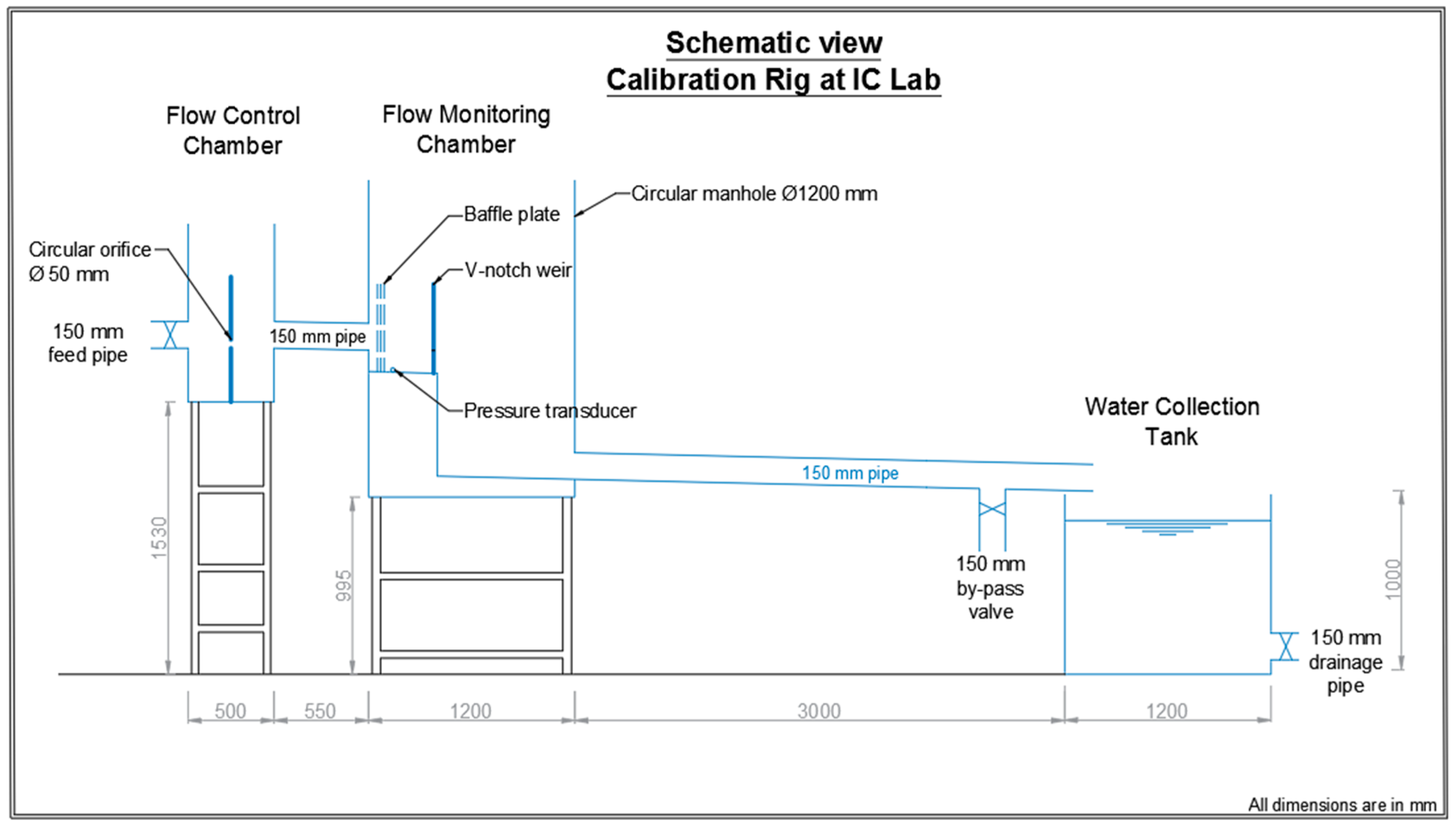
2.3. Experimental Facility
2.4. Experimental Procedure
3. Results and Discussions
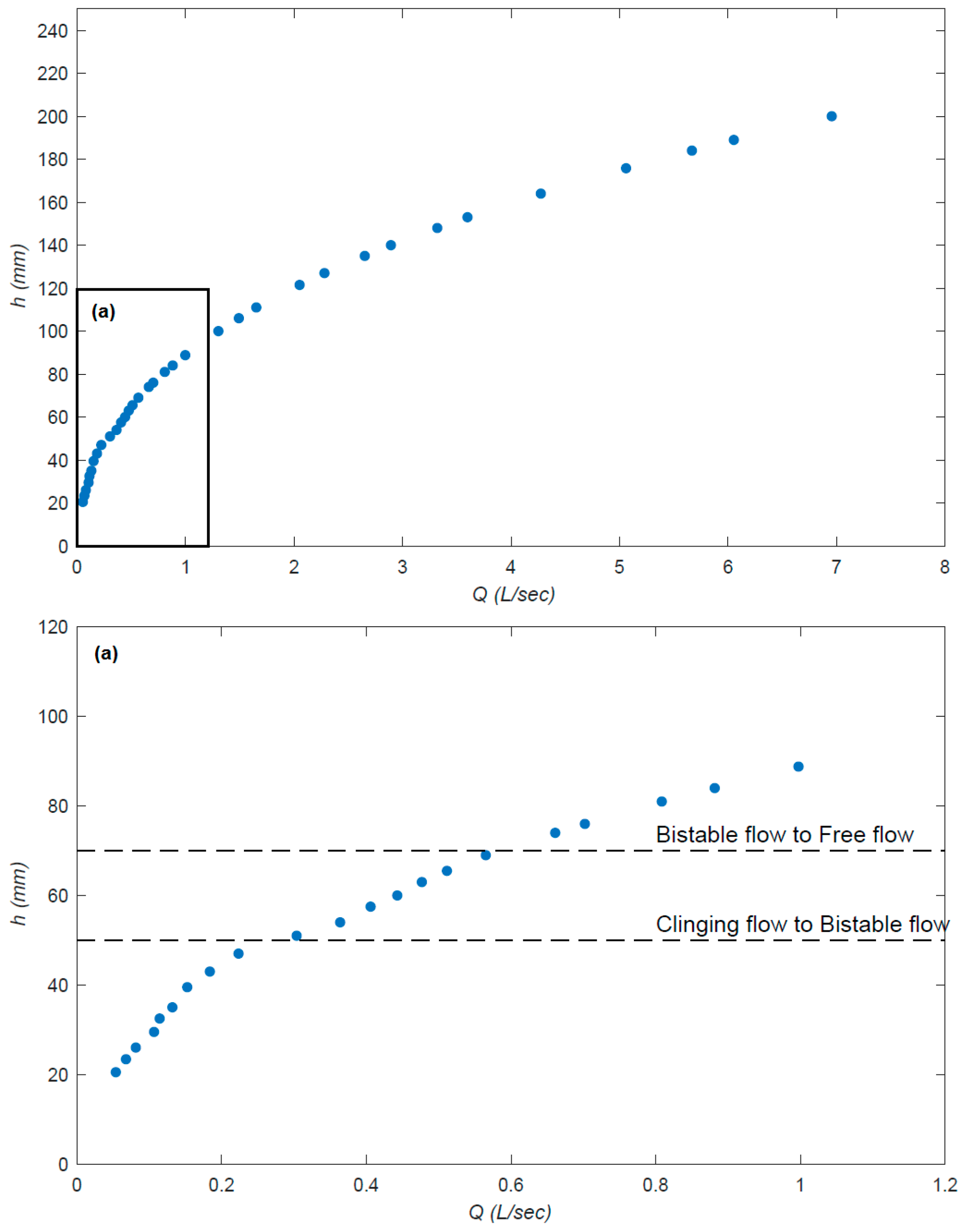
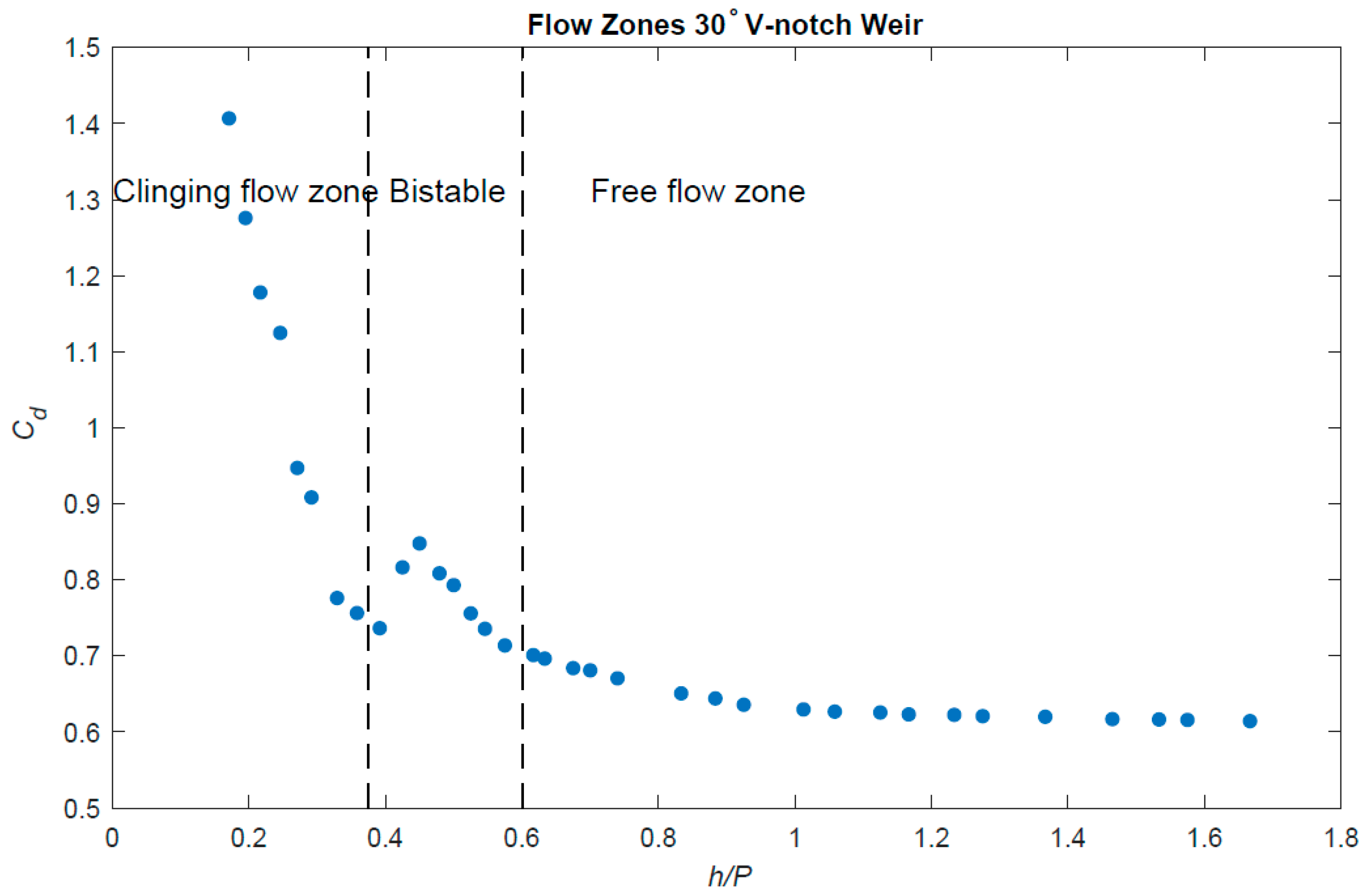
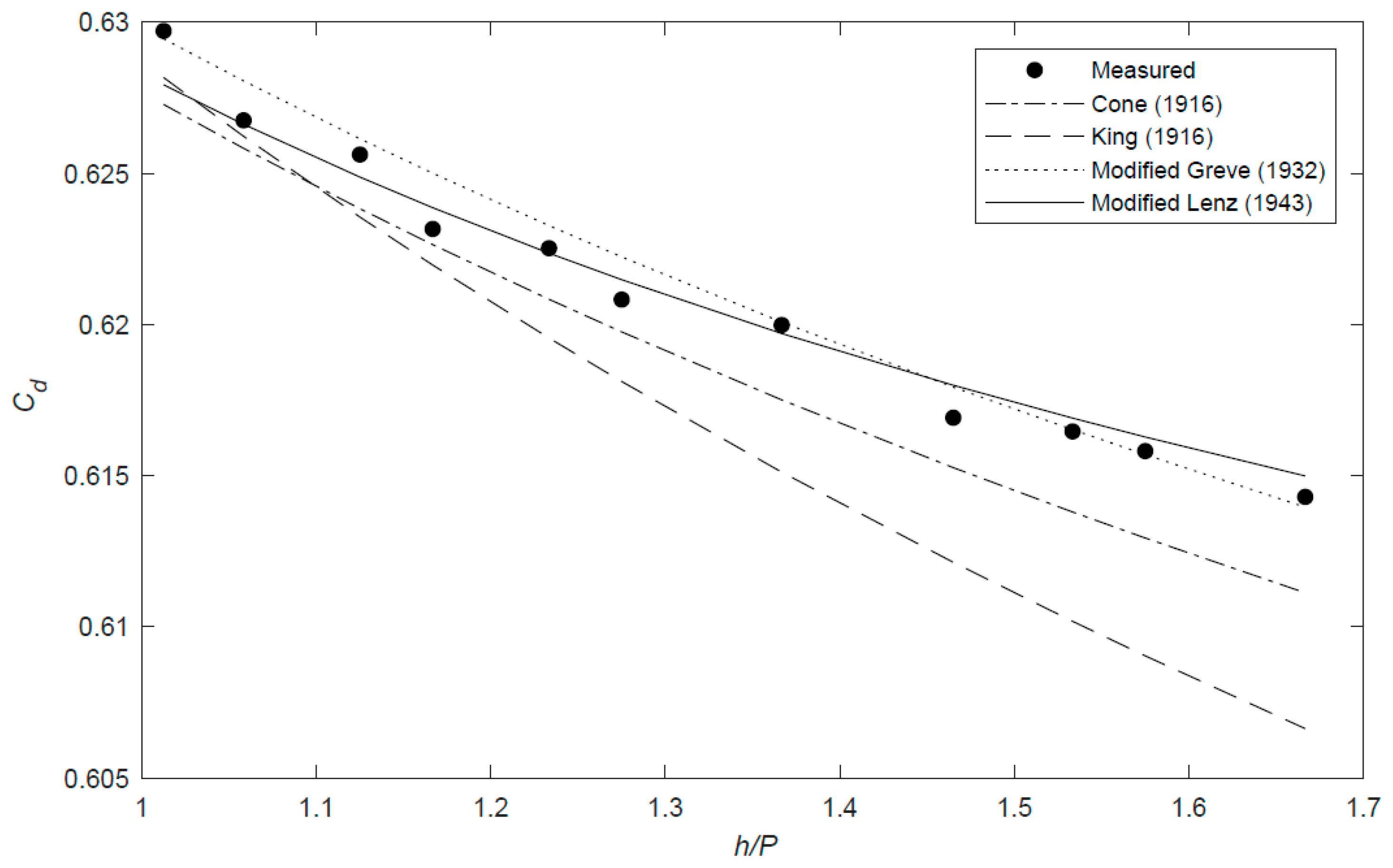
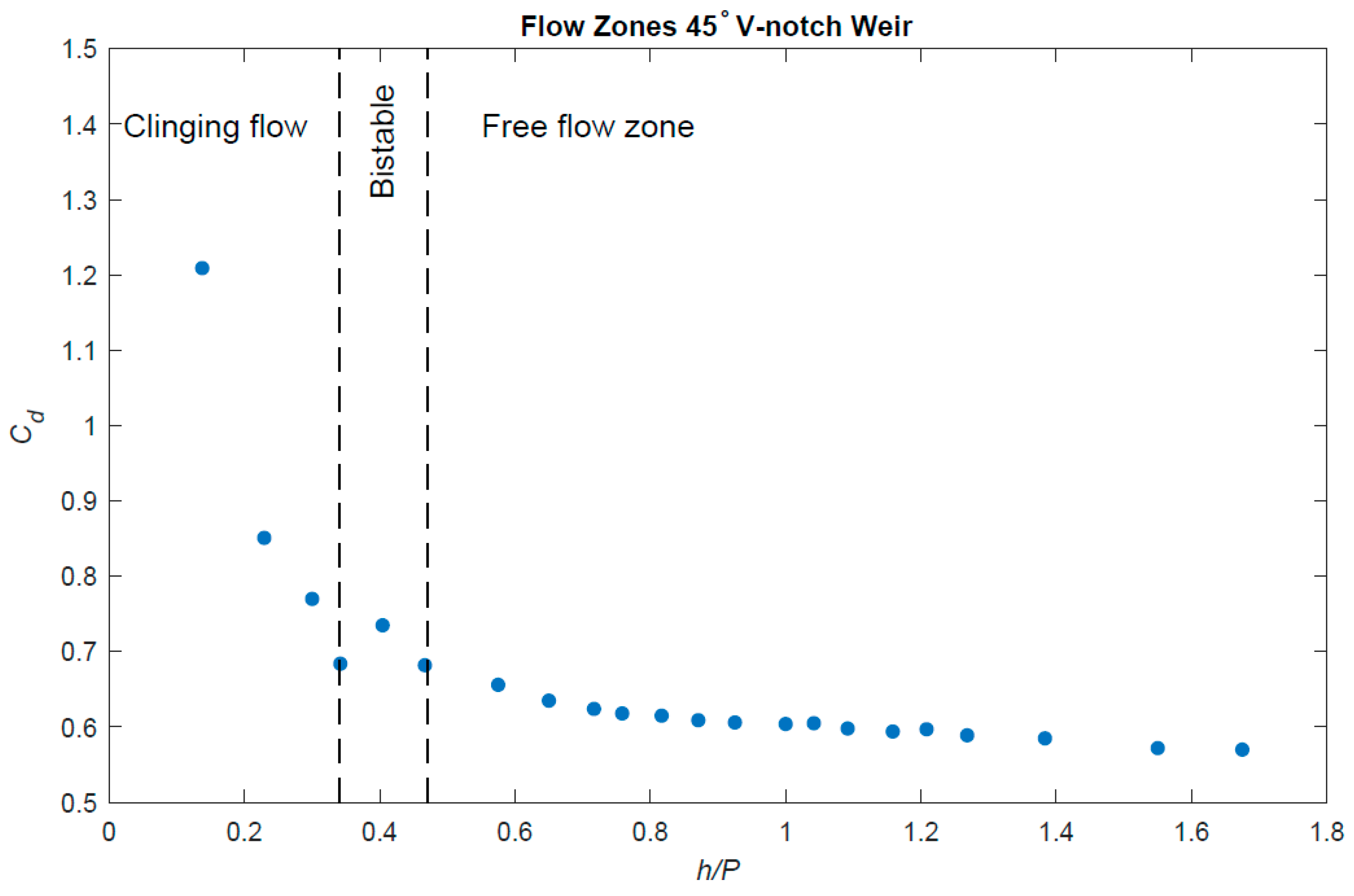
3.1. Head–Discharge relationship
3.2. Calibrated Rating Curve
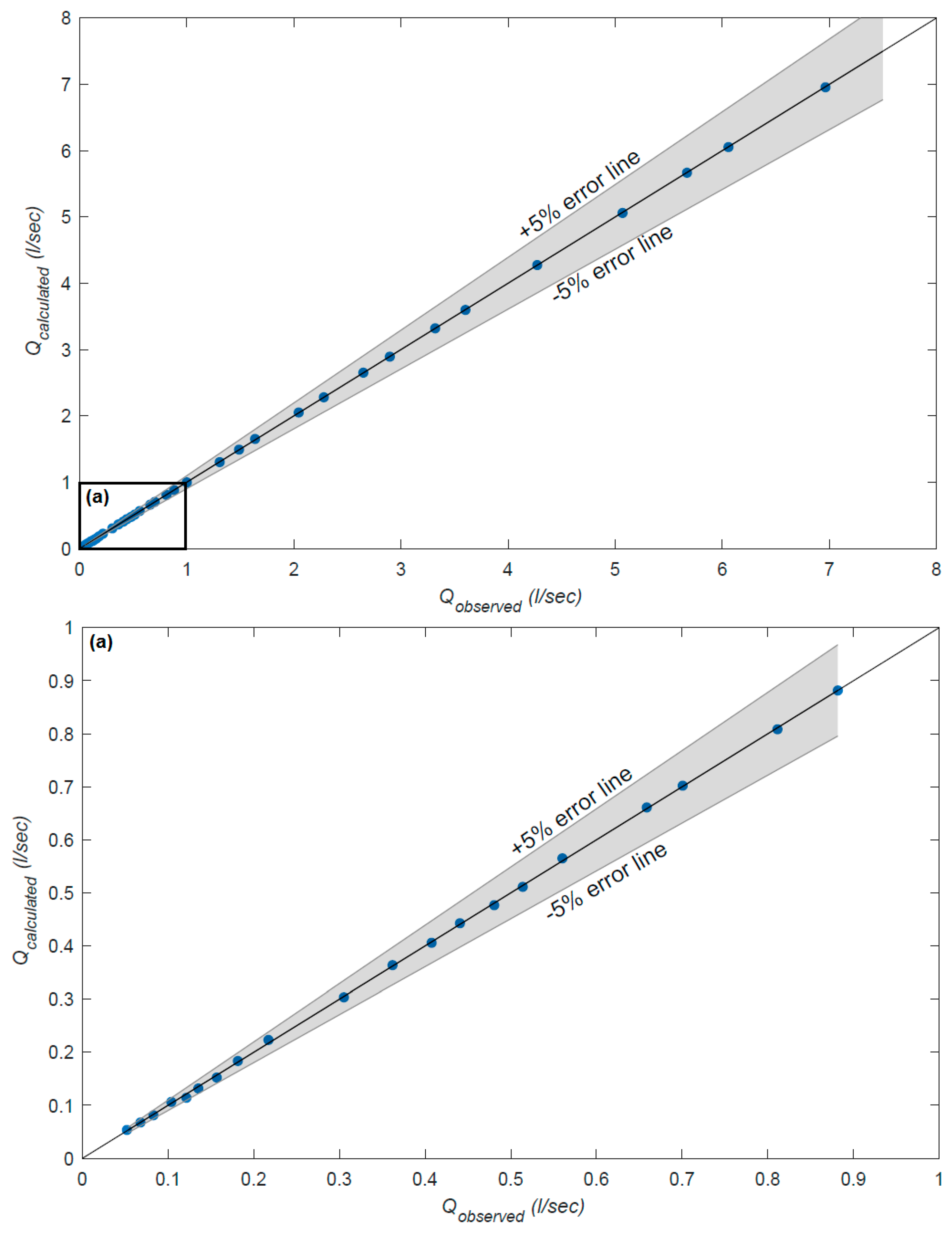
3.3. Uncertainty of the Proposed Discharge Equation
3.4. Transferability of the Observed Flow Behaviour
3.5. Significance of Obtained Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| B | width of the weir |
| Cd | discharge coefficient |
| g | gravitational acceleration |
| h | head of water over the weir |
| N | empirical constant in Lenz’s [55] equation |
| P | distance from channel bed to weir vertex |
| Q | discharge |
| θ | notch angle of the weir |
| R | Reynolds number |
| W | Weber number |
| ρ | mass density |
| σ | surface tension of liquid |
| μ | dynamic viscosity |
| λ | empirical constant in Lenz’s [55] equation |
References
- Halliday, S. The Great Stink of London: Sir Joseph Bazalgette and the Cleansing of the Victorian Metropolis; The History Press: Stroud, UK, 2001. [Google Scholar]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Zbigniew, W.; Lettenmaier, D.P.; Stouffer, R.J. Stationarity Is Dead: Whither Water Management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.R. Local Institutional Development and Organizational Change for Advancing Sustainable Urban Water Futures. Environ. Manag. 2008, 41, 221–233. [Google Scholar] [CrossRef]
- Ashley, R.M.; Digman, C.; Stovin, V.R.; Balmforth, D.; Glerum, J.; Shaffer, P. Retrofitting Surface Water Management Measures: Delivering Multiple Value. In Proceedings of the 12th International Conference on Urban Drainage, Porto Alegre, Brazil, 10−15 September 2011; pp. 10–15. [Google Scholar]
- Woods-Ballard, B.; Kellagher, R.; Martin, P.; Jefferies, C.; Bray, R.; Shaffer, P. The SUDS Manual; Construction Industry Research & Information Association (CIRIA): London, UK, 2015. [Google Scholar]
- Wright, T.J.; Liu, Y.; Carroll, N.J.; Ahiablame, L.M.; Engel, B.A. Retrofitting LID Practices into Existing Neighborhoods: Is It Worth It? Environ. Manag. 2016, 57, 856–867. [Google Scholar] [CrossRef] [PubMed]
- Ellis, J.B.; Lundy, L. Implementing Sustainable Drainage Systems for Urban Surface Water Management within the Regulatory Framework in England and Wales. J. Environ. Manag. 2016, 183, 630–636. [Google Scholar] [CrossRef]
- Jia, H.; Wang, X.; Ti, C.; Zhai, Y.; Field, R.; Tafuri, A.N.; Cai, H.; Yu, S.L. Field Monitoring of a LID-BMP Treatment Train System in China. Environ. Monit. Assess. 2015, 187, 373. [Google Scholar] [CrossRef] [PubMed]
- Eckart, K.; Mcphee, Z.; Bolisetti, T. Performance and Implementation of Low Impact Development—A Review. Sci. Total Environ. 2017, 607–608, 413–432. [Google Scholar] [CrossRef]
- Maheepala, U.K.; Takyi, A.K.; Perera, B.J.C. Hydrological Data Monitoring for Urban Stormwater Drainage Systems. J. Hydrol. 2001, 245, 32–47. [Google Scholar] [CrossRef]
- Hunt, W.F.; Jarrett, A.R.; Smith, J.T.; Sharkey, L.J. Evaluating Bioretention Hydrology and Nutrient Removal at Three Field Sites in North Carolina. J. Irrig. Drain. Eng. 2006, 132, 600–608. [Google Scholar] [CrossRef]
- Collins, K.A.; Hunt, W.F.; Hathaway, J.M. Hydrologic Comparison of Four Types of Permeable Pavement and Standard Asphalt in Eastern North Carolina. J. Hydrol. Eng. 2008, 13, 1146–1157. [Google Scholar] [CrossRef]
- Davis, A.P. Field Performance of Bioretention: Hydrology Impacts. J. Hydrol. Eng. 2008, 13, 90–95. [Google Scholar] [CrossRef]
- Dietz, M.E.; Clausen, J.C. Stormwater Runoff and Export Changes with Development in a Traditional and Low Impact Subdivision. J. Environ. Manag. 2008, 87, 560–566. [Google Scholar] [CrossRef]
- Hunt, W.F.; Smith, J.T.; Jadlocki, S.J.; Hathaway, J.M.; Eubanks, P.R. Pollutant Removal and Peak Flow Mitigation by a Bioretention Cell in Urban Charlotte, N.C. J. Environ. Eng. 2008, 134, 403–408. [Google Scholar] [CrossRef]
- Li, H.; Sharkey, L.J.; Hunt, W.F.; Davis, A.P. Mitigation of Impervious Surface Hydrology Using Bioretention in North Carolina and Maryland. J. Hydrol. Eng. 2009, 14, 407–415. [Google Scholar] [CrossRef]
- Aravena, J.; Dussaillant, A. Storm-Water Infiltration and Focused Recharge Modeling with Finite-Volume Two-Dimensional Richards Equation: Application to an Experimental Rain Garden. J. Hydraul. Eng. 2009, 135, 1073–1080. [Google Scholar] [CrossRef]
- Roseen, R.M.; Ballestero, T.P.; Houle, J.J.; Avellaneda, P.; Briggs, J.; Fowler, G.; Wildey, R. Seasonal Performance Variations for Storm-Water Management Systems in Cold Climate Conditions. J. Environ. Eng. 2009, 135, 128–137. [Google Scholar] [CrossRef]
- Debusk, K.M.; Wynn, T.M. Storm-Water Bioretention for Runoff Quality and Quantity Mitigation. J. Environ. Eng. 2011, 137, 800–808. [Google Scholar] [CrossRef]
- Lenhart, H.A.; Hunt, W.F., III. Evaluating Four Storm-Water Performance Metrics with a North Carolina Coastal Plain Storm-Water Wetland. J. Environ. Eng. 2011, 137, 155–162. [Google Scholar] [CrossRef]
- Brown, R.A.; Hunt, W.F.H., III. Impacts of Media Depth on Effluent Water Quality and Hydrologic Performance of Undersized Bioretention Cells. J. Irrig. Drain. Eng. 2011, 137, 132–143. [Google Scholar] [CrossRef]
- Central Kitsap Community Campus Low Impact Development Flow Monitoring Project; Final Project Report, Prepared for Kitsap County Public Works (Surface and Stormwater Management Program), Port Orchard, Washington; Herrera Environmental Consultants, Inc.: Seattle, WA, USA, 2013.
- Perales-Momparler, S.; Hernández-Crespo, C.; Vallés-Morán, F.; Martín, M.; Andrés-Doménech, I.; Andreu Álvarez, J.; Jefferies, C. SuDS Efficiency during the Start-up Period under Mediterranean Climatic Conditions. Clean Soil Air Water 2014, 42, 178–186. [Google Scholar] [CrossRef]
- Wilson, C.E.; Hunt, W.F.; Winston, R.J.; Smith, P. Comparison of Runoff Quality and Quantity from a Commercial Low-Impact and Conventional Development in Raleigh, North Carolina. J. Environ. Eng. 2015, 141, 1–10. [Google Scholar] [CrossRef]
- Winston, R.J.; Dorsey, J.D.; Hunt, W.F. Quantifying Volume Reduction and Peak Flow Mitigation for Three Bioretention Cells in Clay Soils in Northeast Ohio. Sci. Total Environ. 2016, 553, 83–95. [Google Scholar] [CrossRef]
- Cording, A.; Hurley, S.; Whitney, D. Monitoring Methods and Designs for Evaluating Bioretention Performance. J. Environ. Eng. 2017, 143, 1–10. [Google Scholar] [CrossRef]
- Braswell, A.S.; Anderson, A.R.; Hunt, W.F., III. Hydrologic and Water Quality Evaluation of a Permeable Pavement and Biofiltration Device in Series. Water 2018, 10, 33. [Google Scholar] [CrossRef]
- Winston, R.J.; Dorsey, J.D.; Smolek, A.P.; Hunt, W.F. Hydrologic Performance of Four Permeable Pavement Systems Constructed over Low-Permeability Soils in Northeast Ohio. J. Hydrol. Eng. 2018, 23, 1–13. [Google Scholar] [CrossRef]
- Brown, R.A.; Line, D.E.; Hunt, W.F. Case Study LID Treatment Train: Pervious Concrete with Subsurface Storage in Series with Bioretention and Care with Seasonal High Water Tables. J. Environ. Eng. 2012, 138, 689–697. [Google Scholar] [CrossRef]
- Jarden, K.M.; Jefferson, A.J.; Grieser, J.M. Assessing the Effects of Catchment-Scale Urban Green Infrastructure Retrofits on Hydrograph Characteristics. Hydrol. Process. 2016, 30, 1536–1550. [Google Scholar] [CrossRef]
- Rodriguez-Rojas, M.I.; Huertas-Fernandez, F.; Moreno, B.; Martínez, G.; Grindlay, A.L. A Study of the Application of Permeable Pavements as a Sustainable Technique for the Mitigation of Soil Sealing in Cities: A Case Study in the South of Spain. J. Environ. Manag. 2018, 205. [Google Scholar] [CrossRef] [PubMed]
- Drake, J.; Bradford, A.; Seters, T. Van. Stormwater Quality of Spring e Summer-Fall Effluent from Three Partial-in Filtration Permeable Pavement Systems and Conventional Asphalt Pavement. J. Environ. Manag. 2014, 139, 69–79. [Google Scholar] [CrossRef]
- LeFevre, N.-J.B.; Watkins, D.W.; Gierke, J.S.; Brophy-Price, J. Hydrologic Performance Monitoring of an Underdrained Low-Impact Development Storm-Water Management System. J. Irrig. Drain. Eng. 2010, 136, 333–339. [Google Scholar] [CrossRef]
- Jackisch, N.; Weiler, M. The Hydrologic Outcome of a Low Impact Development (LID) Site Including Superposition with Streamflow Peaks. Urban Water J. 2017, 14, 143–159. [Google Scholar] [CrossRef]
- Stewart, R.D.; Lee, J.G.; Shuster, W.D.; Darner, R.A. Modelling Hydrological Response to a Fully-Monitored Urban Bioretention Cell. Hydrol. Process. 2017, 31, 4626–4638. [Google Scholar] [CrossRef]
- Chanson, H. The Hydraulics of Open Channel Flow: An Introduction, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2004; ISBN 978-0750659789. [Google Scholar]
- Kindsvater, C.E.; Carter, R.W.C. Discharge characteristics of rectangular thin-plate weirs. J. Hydro. Div. 1957, 83, 1–36. [Google Scholar]
- Ackers, P.; White, W.R.; Perkins, J.A.; Harrison, A.J.M. Weirs and Flumes for Flow Measurement; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Bos, M.G. Discharge Measurement Structures, 3rd ed.; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1989; pp. 40–202. [Google Scholar]
- Montes, S. Hydraulics of Open Cannel Flow; American Society of Civil Engineers: Reston, VA, USA, 1998. [Google Scholar]
- Finnemore, J.E.; Franzini, J.B. Fluid Mechanics: With Engineering Applications, 10th ed.; McGraw-Hill Asia: Singapore, 2002; ISBN 9780-0712-7011-3. [Google Scholar]
- British Standards Institute. BS ISO 1438:2008: Hydrometry-Open Channel Flow Measurement Using Thin-Plate Weirs; BSI: London, UK, 2008. [Google Scholar]
- International Organization for Standardization. ISO 1438/1: Part 1: Water Flow Measurement in Open Channels Using Weirs and Venturi Flumes—Thin-Plate Weirs; ISO: Geneva, Switzerland, 1980. [Google Scholar]
- American Society for Testing and Materials. ASTM D5242: Standard Method for Open-Channel Flow Measurement of Water with Thin-Plate Weirs; ASTM: West Conshohocken, PA, USA, 1993. [Google Scholar]
- U.S. Bureau of Reclamation (USBR). Water Measurement Manual; U.S. Department of the Interior: Washington, WA, USA, 2001.
- Martínez, J.; Reca, J.; Morillas, M.T.; López, J.G. Design and Calibration of a Compound Sharp-Crested Weir. J. Hydraul. Eng. 2005, 131, 112–116. [Google Scholar] [CrossRef]
- Aydin, I.; Ger, A.M.; Hincal, O. Measurement of Small Discharges in Open Channels by Slit Weir. J. Hydraul. Eng. 2002, 3, 234–237. [Google Scholar] [CrossRef]
- Henderson, F.M. Open Channel Flow, 1st ed.; Prentice–Hall: Upper Saddle River, NJ, USA, 1966; ISBN 9780-0235-3510-9. [Google Scholar]
- Grant, D.M.; Dawson, B.D. Isco Open Channel Flow Measurement Handbook, 5th ed.; Isco: Lincoln, NE, USA, 2001; ISBN 9780-9622-7572-2. [Google Scholar]
- Zhang, X.; Yuan, L.; Peng, R.; Chen, Z. Hydraulic Relations for Clinging Flow of Sharp-Crested Weir. J. Hydraul. Eng. 2010, 136, 385–390. [Google Scholar] [CrossRef]
- Kumar, S.; Ahmad, Z.; Mansoor, T. A New Approach to Improve the Discharging Capacity of Sharp-Crested Triangular Plan Form Weirs. Flow Meas. Instrum. 2011, 22, 175–180. [Google Scholar] [CrossRef]
- Crookston, B.M.; Tullis, B.P. Hydraulic Design and Analysis of Labyrinth Weirs. II: Nappe Aeration, Instability, and Vibration. J. Irrig. Drain. Eng. 2013, 139, 371–377. [Google Scholar] [CrossRef]
- Swamee, P.K.; Pathak, S.K.; Ghodsian, M. Viscosity and Surface Tension effects on Rectangular Weirs. ISH J. Hydraul. Eng. 2001, 7, 45–50. [Google Scholar] [CrossRef]
- Bagheri, S.; Kabiri-samani, A.R.; Heidarpour, M. Discharge Coefficient of Rectangular Sharp-Crested Side Weirs, Part I: Traditional Weir Equation. Flow Meas. Instrum. 2014, 35, 109–115. [Google Scholar] [CrossRef]
- Lenz, A.T. Viscosity and surface tension effects on V-notch weir coefficients. Trans. Am. Soc. Civ. Eng. 1943, 108, 759–782. [Google Scholar]
- British Standards Institute. BS 3680:1965: Methods of Measurement of Liquid Flow in Open Channels, Part 4A: Thin-Plate Weirs and Venturi Flumes; BSI: London, UK, 1965. [Google Scholar]
- L’Association Francaise de Normalisation. Mesure de débit de l’eau dans les Chenaux au Moyen de Déversoire en Mince Paroi; X 10-311. ISO/TC 113/GT2; ISO: Montpellier, France, 1971; p. 152. [Google Scholar]
- Shen, J. Discharge Characteristics of Triangular-Notch Thin-Plate Weirs (No. 1617); United States Department of the Interior, Geological Survey: Reston, VA, USA, 1981.
- Rehbock, T. Discussion of precise weir measurement, by K. B. Turner. Trans. Am. Soc. Civ. Eng. 1929, 93, 1143–1162. [Google Scholar]
- Barr, J. Experiments upon the flow of water over Triangular Notches. Engineering 1910, 89, 435. [Google Scholar]
- Cone, V.M. Flow through weir notches with thin edges and full contractions. J. Agric. Res. 1916, 5, 1051. [Google Scholar]
- King, H.W. Flow of water over right-angled V-notch weir. Univ. Michigan Technic 1916, 29, 189. [Google Scholar]
- Greve, F.W. Flow of Water through Circular, Parabolic, and Triangular Vertical Notch-Weirs. Purdue Univ. Eng. Bull. 1932, 16, 84. [Google Scholar]
- Milburn, P.; Burney, J. V-notch weir boxes for measurement of subsurface drainage system discharges. Can. Agric. Eng. 1988, 30, 209–212. [Google Scholar]
- Hattab, M.E.; Vernon, D.; Mijic, A. Performance Evaluation of Retrofitted Low Impact Development Practices in Urban Environments: A Case Study from London, UK. In Proceedings of the International Conference on Sustainable infrastructure: Technology, New York, NY, USA, 26–28 October 2017; pp. 282–294. [Google Scholar] [CrossRef]



| Monitoring Type | Monitoring Instrument | GI Technology | Project Type (Retrofit/New Development) | Reference |
|---|---|---|---|---|
| Rating curve of hydraulic control structure | Pressure transducer + V-notch weir (30°) | Bioretention Cell | Retrofit | [11] |
| Pressure transducer + V-notch weir (30°) | Permeable Pavement, Porous Concrete | Retrofit | [12] | |
| Bubbler sampler + Flume | Bioretention Cell | Retrofit | [13] | |
| Bubbler sampler + Palmer-Bowlus flume | Swale, Rain Garden, Permeable Pavement, Bioretention Cell | Retrofit | [14] | |
| Bubbler sampler + V-notch weir (120°) | Bioretention Cell | Retrofit | [15] | |
| Pressure transducer + V-notch weir (30°, 45° and 60°) | Bioretention Cell | Retrofit | [16] | |
| Pressure transducer + V-notch weir | Rain Garden | Retrofit | [17] | |
| Bubbler sampler + Thel-Mar weir | Bioretention Cell, Sand Filter, Gravel Wetland, Street Tree, Porous Asphalt | Retrofit | [18] | |
| Bubbler sampler + Thel-Mar weir | Bioretention Cell | Retrofit | [19] | |
| Bubbler sampler + Compound V-notch/Rectangular Weir | Wetland | Retrofit | [20] | |
| Rating curve of hydraulic control structure | Bubbler sampler + V-notch weir (120°) | Pervious Concrete, Bioretention Cell | Retrofit | [21] |
| Pressure transducer + Thel-Mar weir + Palmer- Bowlus Flume | Bioretention Cell, Porous Pavement | Retrofit | [22] | |
| Pressure transducer + V-notch weir (90°) | Swale, Infiltration Pond | Site 1: RetrofitSite 2: New Development | [23] | |
| Bubbler sampler + V-notch weir (30°) | Bioretention Cell, Detention Pond, Swale, Infiltration Trench | New Development | [24] | |
| Pressure transducer + V-notch weir (45° and 60°) | Bioretention Cell | Retrofit | [25] | |
| Pressure transducer + V-notch weir (90°) | Bioretention Cell | Retrofit | [26] | |
| Bubbler sampler + V-notch weir (30°) | Permeable Pavement, Biofiltration | Retrofit | [27] | |
| Pressure transducer + V-notch weir (30°, and 60°) | Permeable Pavement | Retrofit | [28] | |
| Rating curve of hydraulic control structure | Bubbler sampler + V-notch weir (90°)and Flowmeter | Bioretention Cell | Retrofit | [29] |
| Flow meter | ||||
| Flow meter | Pressure transducer + Doppler ultrasonic velocity sensor | Bioretention Cell, Rain Garden | Retrofit | [30] |
| Flowmeter | Permeable Pavement | New Development | [31] | |
| Clamp-on ultrasonic flowmeter | Permeable Pavement | Retrofit | [32] | |
| Rating Curve determined by models | Pressure transducer + Manning’s equation | Rain Garden, Green Roof, Permeable Pavement, Bioswale, Detention Pond | New Development | [33] |
| Pressure transducer + HEC-RAS | Green Roof, Permeable Pavement, Swale | New Development | [34] | |
| Pressure transducer | Bioretention Cell | Retrofit | [35] |
| Expression for Cd | Reference | Application Range of the Head (mm) |
|---|---|---|
| Lenz [55] | 80–214 | |
| where | Cone [61] | 61–381 |
| a | King [62] | 50–450 |
| Greve [63] | 51–302 |
| Flow Phase | h/P |
|---|---|
| Clinging flow | Less than 0.358 |
| Bistable flow | 0.358 to 0.600 |
| Free-flow | Larger than 0.600 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El Hattab, M.H.; Mijic, A.; Vernon, D. Optimised Triangular Weir Design for Assessing the Full-Scale Performance of Green Infrastructure. Water 2019, 11, 773. https://doi.org/10.3390/w11040773
El Hattab MH, Mijic A, Vernon D. Optimised Triangular Weir Design for Assessing the Full-Scale Performance of Green Infrastructure. Water. 2019; 11(4):773. https://doi.org/10.3390/w11040773
Chicago/Turabian StyleEl Hattab, Mohamad H., Ana Mijic, and Dejan Vernon. 2019. "Optimised Triangular Weir Design for Assessing the Full-Scale Performance of Green Infrastructure" Water 11, no. 4: 773. https://doi.org/10.3390/w11040773
APA StyleEl Hattab, M. H., Mijic, A., & Vernon, D. (2019). Optimised Triangular Weir Design for Assessing the Full-Scale Performance of Green Infrastructure. Water, 11(4), 773. https://doi.org/10.3390/w11040773





