Integrating XAJ Model with GIUH Based on Nash Model for Rainfall-Runoff Modelling
Abstract
1. Introduction
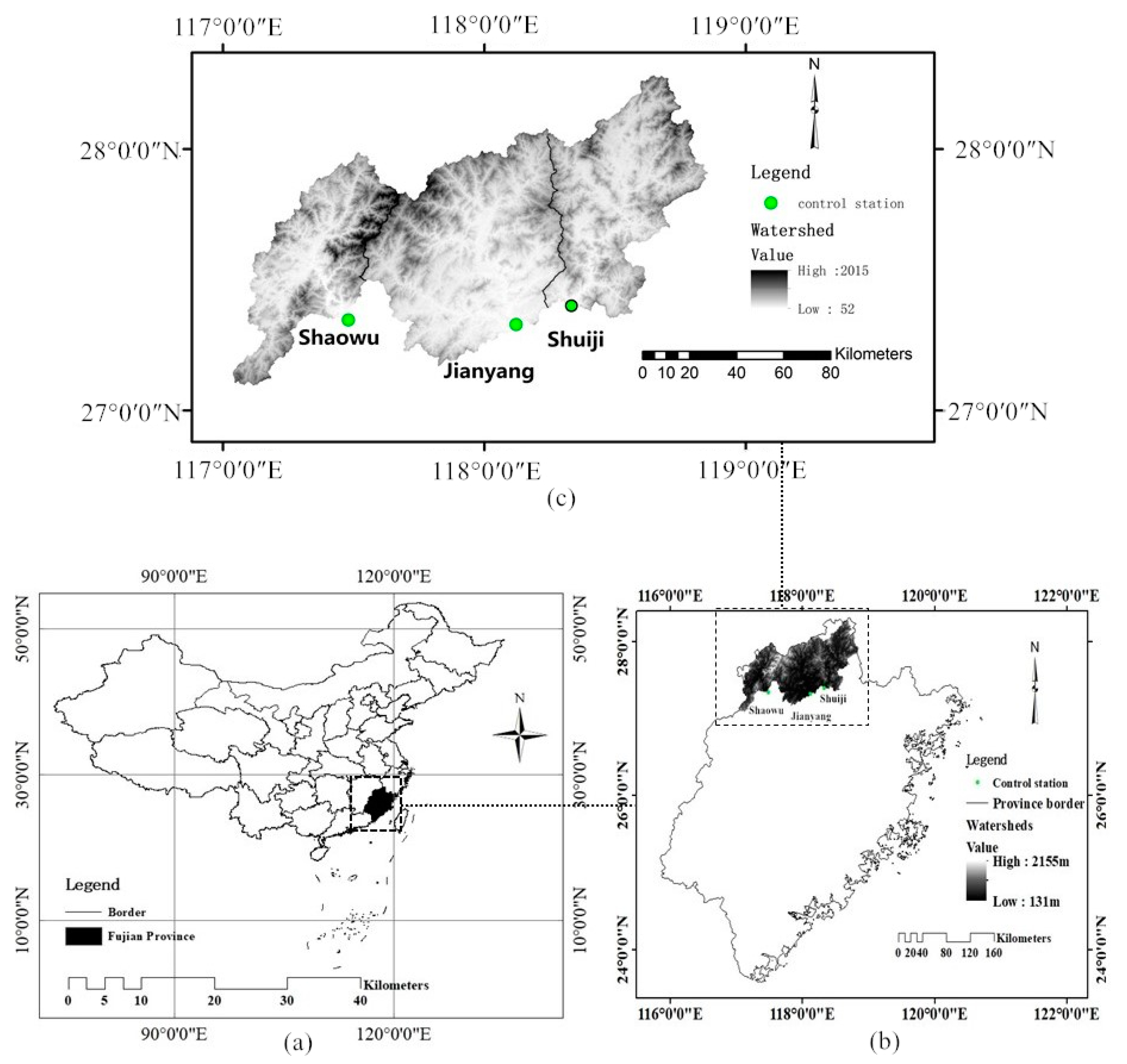
2. Study Area and Data Collection
2.1. Study Area
2.2. Hydrologic Data and Preprocessing
3. Methodology
3.1. XAJ Model
- (1)
- when ,
- (2)
- when and
- (3)
- when
- (4)
- when
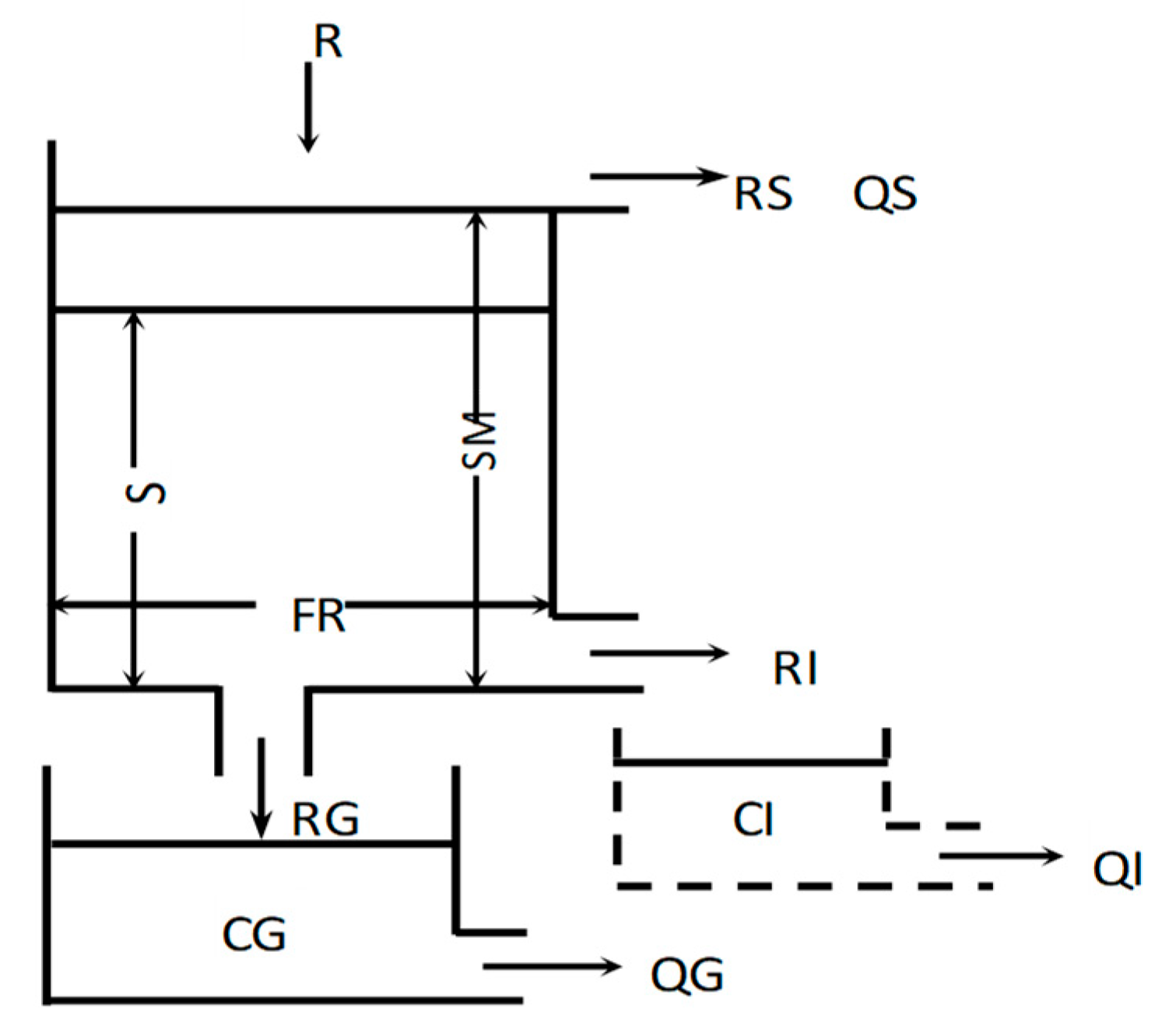
3.2. GIUH based on Nash Model
3.2.1. GIUH Derivation
3.2.2. Estimation of the Average Flow Velocity
- : the slope of the drainage area, m/m.
- : the sum of the mean length of each order channel, approximate to the length of flow concentration, m, .
3.3. Calibration and Validation on Model Parameters
3.4. Criteria on the Model Assessment
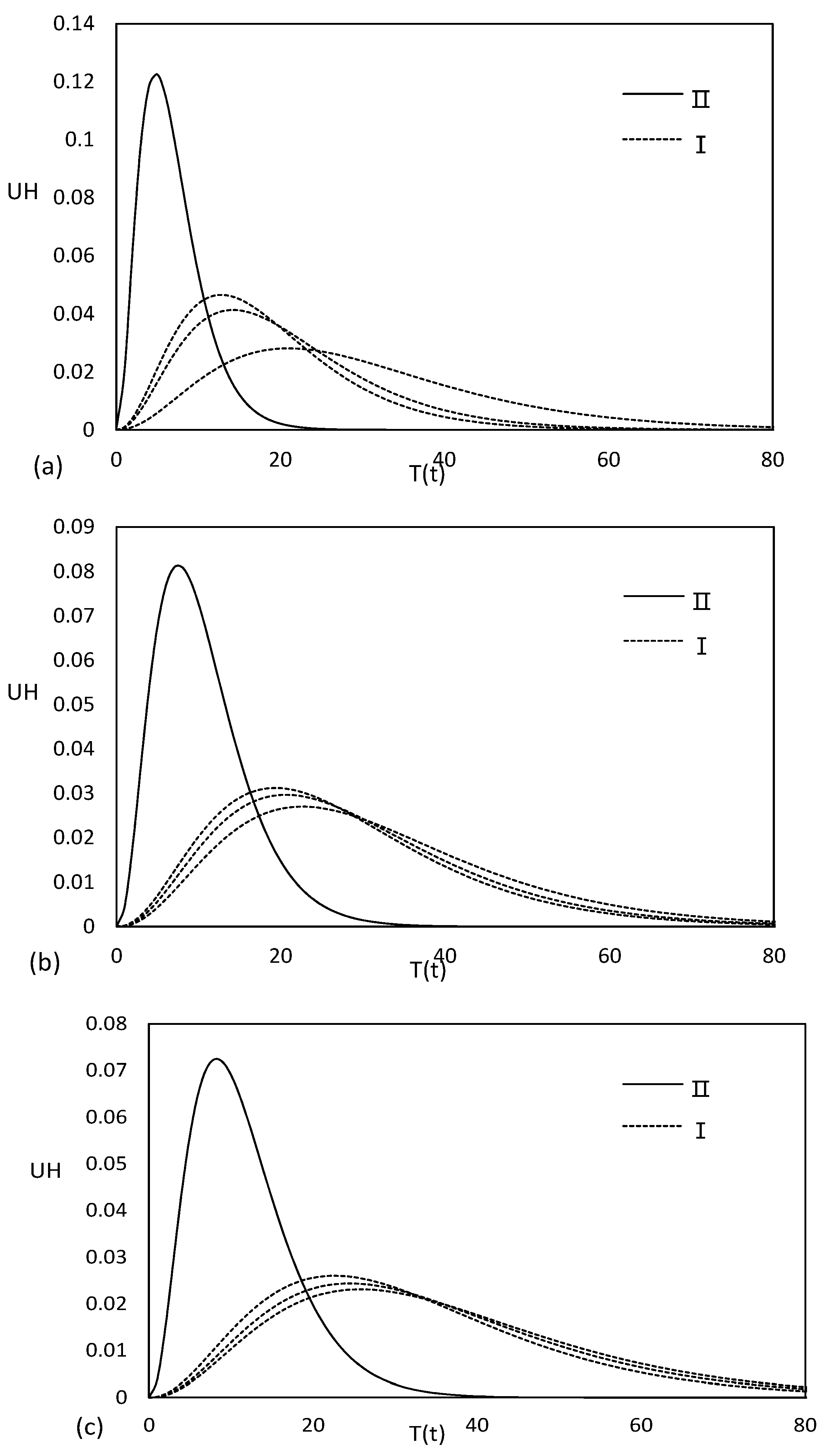
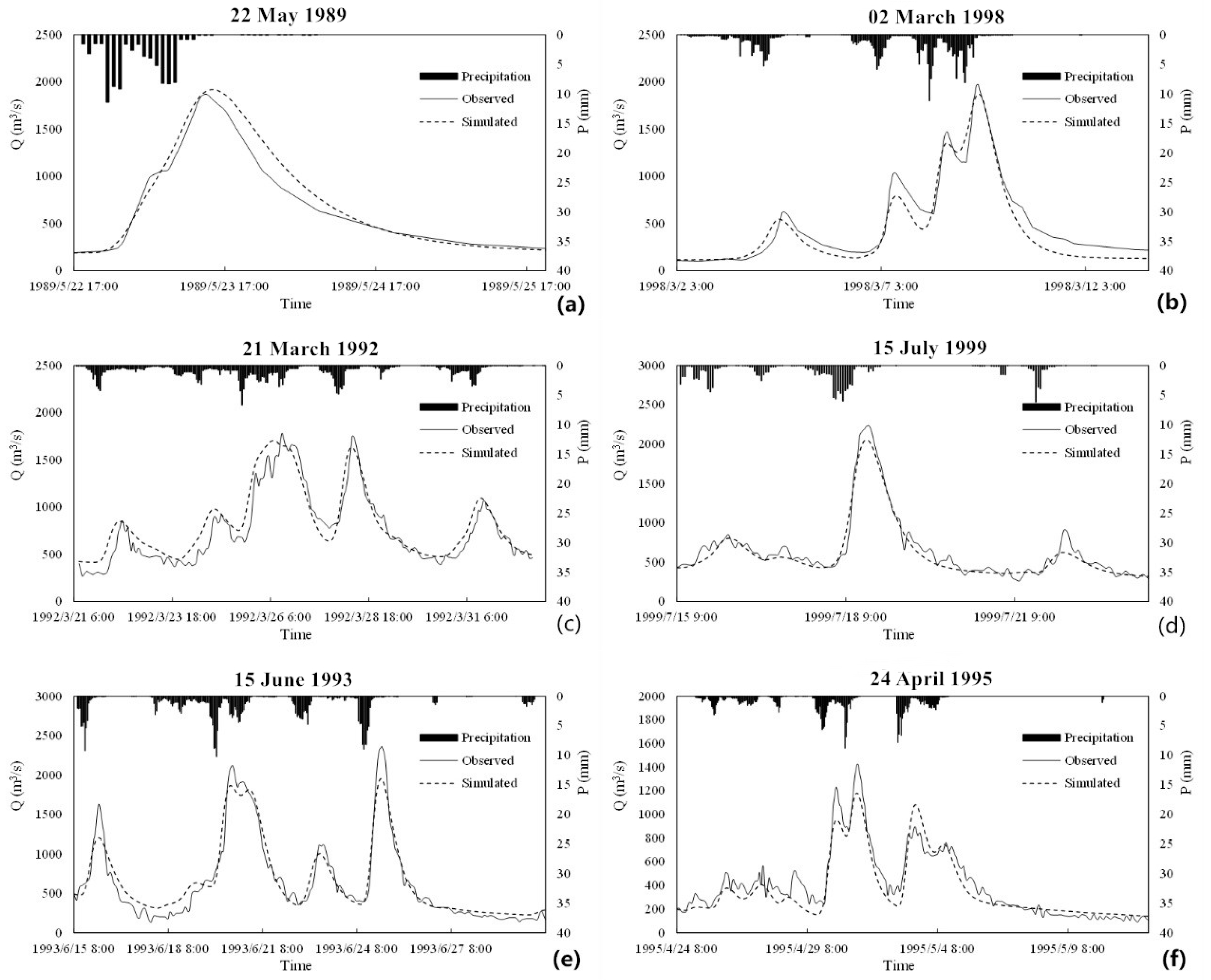
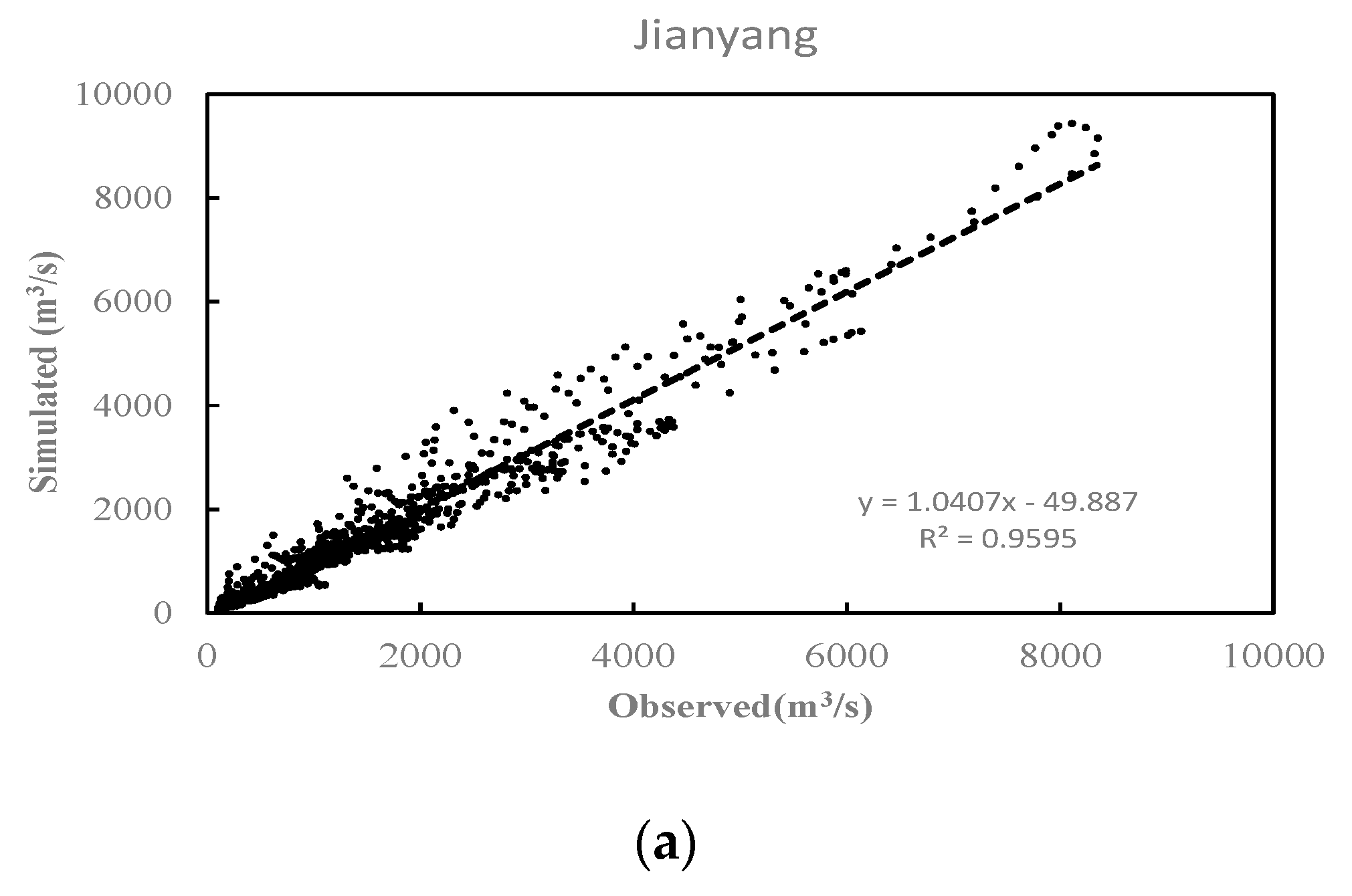
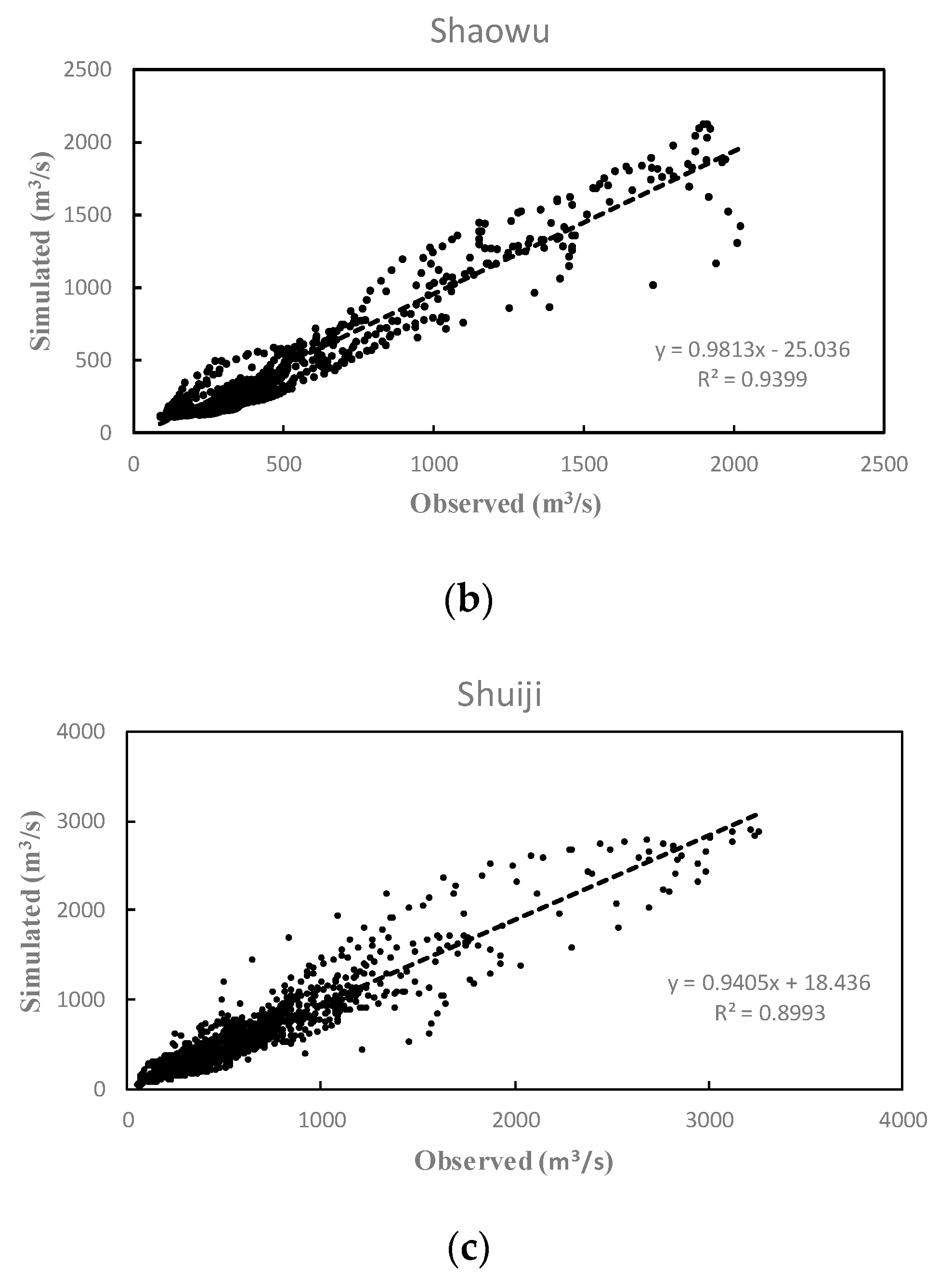
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Luo, P.; He, B.; Takara, K.; Xiong, Y.E.; Nover, D.; Duan, W.; Fukushi, K. Historical assessment of Chinese and Japanese flood management policies and implications for managing future floods. Environ. Sci. Policy 2015, 48, 265–277. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Valdes, J.B. The geomorphologic structure of hydrologic response. Water Resour. Res. 1979, 15, 1409–1420. [Google Scholar] [CrossRef]
- Valdes, J.B.; Fiallo, Y.; Rodriguez-Iturbe, I. A rainfall-runoff analysis of the geomorphologic IUH. Water Resour. Res. 1979, 15, 1421–1434. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E.C.; Wang, C.T. A representation of an instantaneous unit hydrograph from geomorphology. Water Resour. Res. 1980, 16, 855–862. [Google Scholar] [CrossRef]
- Horton, R.E. Erosional development of streams and their drainage basins; hydrophysical approach to quantitative morphology. Geol. Soc. Am. Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Strahler, A.N. Dynamic basis of geomorphology. Geol. Soc. Am. Bull. 1952, 63, 923–938. [Google Scholar] [CrossRef]
- Strahler, A.N. Hypsometric (Area-Altitude) analysis of erosional topography. Geol. Soc. Am. Bull. 1952, 63, 1117–1142. [Google Scholar]
- Gupta, V.K.; Waymire, E. On the formulation of an analytical approach to hydrologic response and similarity at the basin scale. J. Hydrol. 1983, 65, 95–123. [Google Scholar]
- Rosso, R. Nash Model Relation to Horton Order Ratios. Water Resour. Res. 1984, 20, 914–920. [Google Scholar] [CrossRef]
- Gupta, V.K.; Waymire, E.; Rodríguez-Iturbe. On Scales, Gravity and Network Structure in Basin Runoff. In Scale Problems in Hydrology; Springer: Dordrecht, the Netherlands, 1986; pp. 159–184. [Google Scholar]
- Mesa, O.J.; Mifflin, E.R. On the Relative Role of Hillslope and Network Geometry in Hydrologic Response. In Scale Problems in Hydrology; Springer: Dordrecht, the Netherlands, 1986; pp. 1–17. [Google Scholar]
- Gupta, V.K.; Mesa, O.J. Runoff generation and hydrologic response via channel network geomorphology—Recent progress and open problems. J. Hydrol. 1988, 102, 3–28. [Google Scholar] [CrossRef]
- Lu, G.H. The derivation of GIUH based on the deterministic method. J. Hohai Univ. 1990, 18, 79–84. [Google Scholar]
- Choi, Y.J.; Lee, G.; Kim, J.C. Estimation of the Nash Model Parameters Based on the Concept of Geomorphologic Dispersion. J. Hydrol. Eng. 2011, 16, 806–817. [Google Scholar] [CrossRef]
- Lee, K.T.; Yen, B.C. Geomorphology and kinematic-wave-based hydrograph derivation. J. Hydrol. Eng. 1997, 123, 73–80. [Google Scholar] [CrossRef]
- Rui, X.F.; Shi, P. Study on WGIUH by means of geomorphologic and hydrodynamic dispersion. Adv. Water Sci. 2002, 13, 439–444. [Google Scholar]
- Shi, P.; Rui, X. Construction of the basin geomorphological instantaneous unit hydrograph using SSNs. Adv. Water Sci. 2005, 16, 799. [Google Scholar]
- Sarkar, S.; Rai, R.K. Flood Inundation Modeling Using Nakagami-m Distribution Based GIUH for a Partially Gauged Catchment. Water Resour. Manag. 2011, 25, 3805–3835. [Google Scholar] [CrossRef]
- Moussa, R. Definition of new equivalent indices of Horton-Strahler ratios for the derivation of the Geomorphological Instantaneous Unit Hydrograph. Water Resour. Res. 2009, 45, 63–69. [Google Scholar] [CrossRef]
- Lee, K.T.; Chang, C.H. Incorporating subsurface-flow mechanism into geomorphology-based IUH modeling. J. Hydrol. 2005, 311, 91–105. [Google Scholar] [CrossRef]
- Sabzevari, T.; Fattahi, M.H.; Mohammadpour, R.; Noroozpour, S. Prediction of surface and subsurface flow in catchments using the GIUH. J. Flood Risk Manag. 2013, 6, 135–145. [Google Scholar] [CrossRef]
- Kumar, R.; Chatterjee, C.; Singh, R.D.; Lohani, A.K.; Kumar, S. GIUH based Clark and Nash models for runoff estimation for an ungauged basin and their uncertainty analysis. Int. J. River Basin Manag. 2004, 2, 281–290. [Google Scholar] [CrossRef]
- Kumar, R.; Chatterjee, C.; Singh, R.D.; Lohani, A.K.; Kumar, S. Runoff estimation for an ungauged catchment using geomorphological instantaneous unit hydrograph (GIUH) models. Hydrol. Process. 2007, 21, 1829–1840. [Google Scholar] [CrossRef]
- Sahoo, B.; Chatterjee, C.; Raghuwanshi, N.S.; Kumar, R. Flood Estimation by GIUH-Based Clark and Nash Models. J. Hydrol. Eng. 2006, 11, 515–525. [Google Scholar] [CrossRef]
- Iskender, I.; Sajikumar, N. Evaluation of surface runoff estimation in ungauged watersheds using SWAT and GIUH. Procedia Technol. 2016, 24, 109–115. [Google Scholar] [CrossRef]
- Kumar, A.; Kumar, D. Predicting direct runoff from hilly watershed using geomorphology and stream-order-law ratios: Case Study. J. Hydrol. Eng. 2008, 13, 570–576. [Google Scholar] [CrossRef]
- Rai, R.K.; Upadhyay, A.; Sarkar, S.; Singh, V.P. GIUH based transfer function for Gomti River Basin of India. J. Spatial Hydrol. 2009, 9, 24–50. [Google Scholar]
- Kumar, A. Geomorphologic Instantaneous Unit Hydrograph Based Hydrologic Response Models for Ungauged Hilly Watersheds in India. Water Resour. Manag. 2015, 29, 1–21. [Google Scholar] [CrossRef]
- Zhao, R.J. The Xinanjiang model applied in China. J. Hydrol. 1992, 135, 371–381. [Google Scholar]
- Zhao, R.J.; Liu, X.R.; Singh, V.P. The Xinanjiang model. Proc. Oxford Symp. Hydrol. Forecast. IAHS Publ. 1995, 135, 371–381. [Google Scholar]
- Nash, J.E. The Form of the Instantaneous Unit Hydrograph; International Association of Scientific Hydrology: Toronto, ON, Canada, 1957. [Google Scholar]
- Nash, J.E.; HRS. A Unit Hydrograph Study, with Particular Reference to British Catchments. In Proceedings of the Institution of Civil Engineers; 1960; pp. 249–282. Available online: https://hydrology.agu.org/wp-content/uploads/sites/19/2016/04/Nash_1960.pdf (accessed on 29 March 2019).
- Rui, X.F. Some reviews on Geomorphologic Instantaneous Unit Hydrograph. Adv. Water Sci. 1991, 2, 194–200. [Google Scholar]
- Bhaskar, N.R.; Parida, B.P.; Nayak, A.K. Flood Estimation for Ungauged Catchments Using the GIUH. J. Water Resour. Plan. Manag. 1997, 123, 228–238. [Google Scholar] [CrossRef]
- Kirpich, Z.P. Time of Concentration of Small Agricultural Watersheds. Civ. Eng. 1940, 10, 362. [Google Scholar]
- Ministry of Water Resources of the People’s Republic of China. Standard for Information and Hydrological Forecasting; GB/T22482—2008; China Standard Press: Beijing, China, 2008.
- Cheng, K.S.; Lien, Y.T.; Wu, Y.C.; Su, Y.F. On the criteria of model performance evaluation for real-time flood forecasting. Stoch. Environ. Res. Risk Assess. 2017, 31, 1123–1146. [Google Scholar] [CrossRef]
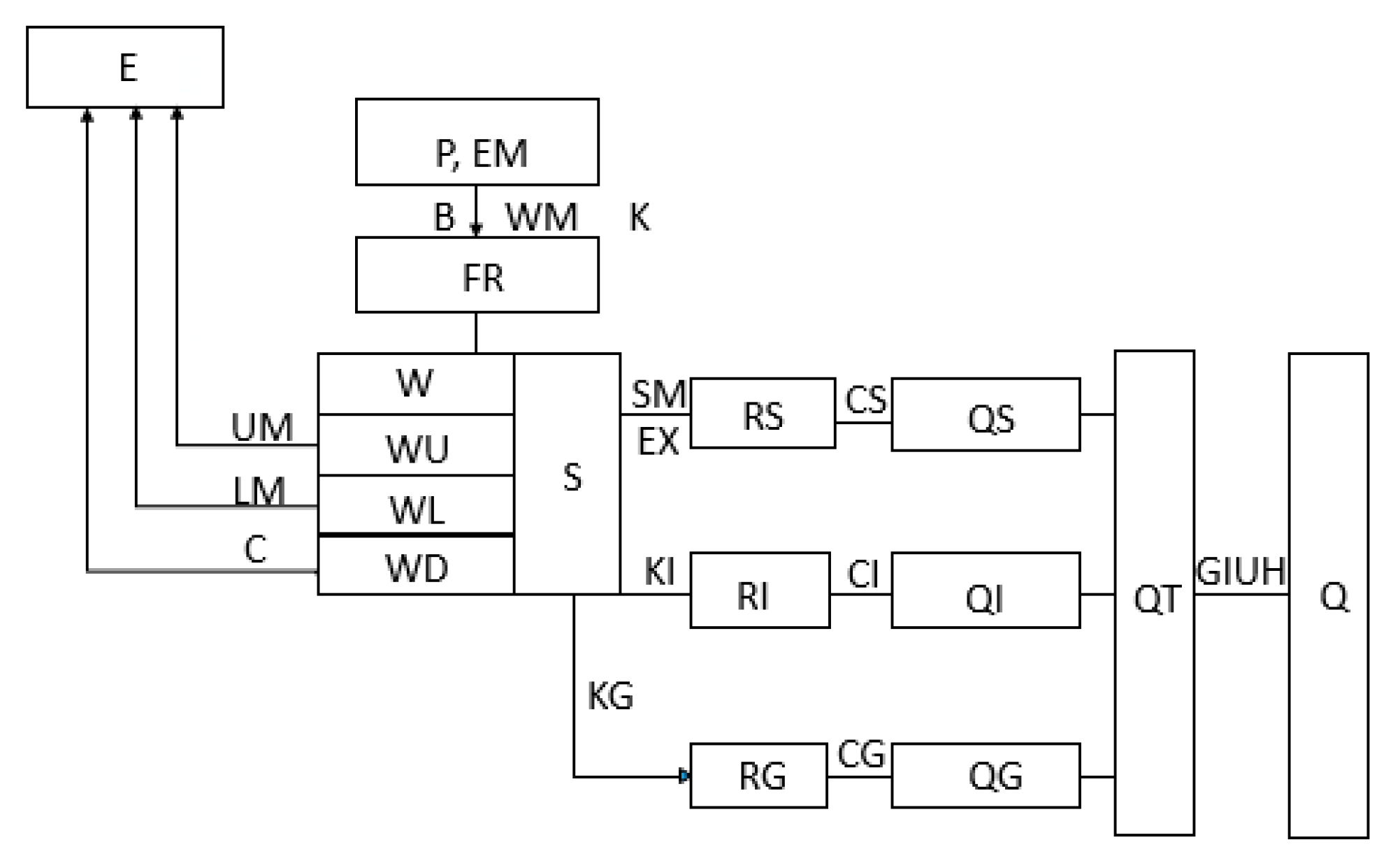
| E: Evapotranspiration | S: Free water storage |
| P: Precipitation | SM: Free water capacity |
| EM: Evapotranspiration capability | EX: Free water capacity distribution exponent |
| B: Exponent of tension water capacity distribution | KI: Outflow ratio of free water storage to interflow |
| K: Ratio of potential evapotranspiration to the pan evapotranspiration | KG: Outflow ratio of free water storage to groundwater |
| WM: Tension water capacity | RS: surface runoff |
| FR: Ratio of the runoff generation area to the basin area | RI: Interflow |
| UM: Upper layer tension water capacity | RG: Groundwater runoff |
| LM: Lower layer tension water capacity | QS: Surface runoff inflow to river network |
| C: Deep layer evapotranspiration coefficient | QI: Interflow to river network |
| W: Tension water storage | QG: Groundwater inflow to river network |
| WU: Upper soil moisture | QT: Total inflow to river network |
| WL: Lower soil moisture | Q: Total outflow |
| WD: Deep layer soil moisture |
| Watershed | S0 (km2) | (km) | Stream Area | Bifurcation | Stream Length |
|---|---|---|---|---|---|
| Shaowu | 2677 | 49.74 | 4.2 | 3.99 | 2.13 |
| Jianyang | 3253 | 72.77 | 4.292 | 4.345 | 2.211 |
| Shuiji | 3470.5 | 86.93 | 4.326 | 4.209 | 2.187 |
| Module | Parameter | Physical Significant (Unit) | Sensitive Degree | Range | Shaowu | Jianyang | Shuiji |
|---|---|---|---|---|---|---|---|
| Evaporation | KC | potential evaporation/pan evaporation | S | 0.8–1.2 | 0.8 | 0.9 | 1.35 |
| UM | Volume of upper layer soil moisture storage capacity (mm) | I | 5–20 | 20 | 20 | 20 | |
| LM | Volume of lower layer soil moisture storage capacity (mm) | I | 60–90 | 80 | 80 | 80 | |
| C | Conversion coefficient of deep layer evaporation | I | 0.1–0.2 | 0.15 | 0.16 | 0.16 | |
| Runoff generation | WM | Volume of average soil moisture storage capacity (mm) | I | 120–200 | 160 | 223 | 163 |
| B | The power in the curve of soil moisture storage capacity | I | 0.1–0.4 | 0.3 | 0.3 | 0.79 | |
| IM | A ratio impervious area/the area of saturated zone | I | 0.01–0.04 | 0.01 | 0.01 | 0.01 | |
| Runoff partition | SM | Free water capacity in the soil surface (mm) | S | 18 | 40 | 20 | |
| EX | The power in the curve of free water capacity in the soil surface | I | 1.0–1.5 | 0.9 | 0.9 | 1.5 | |
| KG | Outflow coefficient of free water storage to ground water | S | 0.4 | 0.6 | 0.45 | ||
| KI | Outflow coefficient of free water storage to subsurface runoff | S | 0.35 | 0.397 | 0.4 |
| Watershed | Method (I) | Method (II) | |||||
|---|---|---|---|---|---|---|---|
| Code of Flood Event | Average Effective Rainfall Intensity, (mm/h) | Mean Flow Velocity, (m/s) | The Mean Channel Slope of Whole Basin, | Length of Flow Concentration, (km) | Time of Concentration, (min) | Mean Flow Velocity, (m/s) | |
| Shaowu | 19890522 | 2.94 | 1.20 | 0.035 | 104.895 | 520.3 | 3.36 |
| 19960530 | 3.05 | 0.77 | |||||
| 19980302 | 2.17 | 1.13 | |||||
| Jianyang | 19880228 | 1.59 | 1.07 | 0.029 | 116.693 | 605.9 | 3.21 |
| 19950603 | 2.61 | 1.17 | |||||
| 19990715 | 2.65 | 1.17 | |||||
| Shuiji | 19880520 | 2.43 | 1.16 | 0.032 | 130.692 | 635.0 | 3.43 |
| 19950425 | 2.36 | 1.15 | |||||
| 19930615 | 1.83 | 1.10 | |||||
| Watershed | Stage | Flood Code | TPE | RPE (%) | RRDE (%) | NSE |
|---|---|---|---|---|---|---|
| Shaowu | Calibration | 19880228 | 1 | 1 | 20 | 0.854 |
| 19880512 | 0 | −19 | 6.7 | 0.892 | ||
| 19890515 | 8 | −11 | −16.3 | 0.905 | ||
| 19890522 | 1 | 3 | 8 | 0.941 | ||
| 19890621 | 0 | −16 | 3.5 | 0.924 | ||
| 19890629 | 2 | 19 | 13.3 | 0.812 | ||
| 19920321 | 0 | 17 | 12.2 | 0.851 | ||
| 19920514 | 0 | −14 | −16 | 0.877 | ||
| 19920831 | 1 | −29 | −22.4 | 0.834 | ||
| 19930615 | 0 | −22 | −1.6 | 0.846 | ||
| Validation | 19940501 | 0 | −5 | −9.9 | 0.832 | |
| 19960328 | −2 | −9 | 0 | 0.856 | ||
| 19960530 | 2 | 11 | −5.9 | 0.922 | ||
| 19980215 | 0 | 1 | −7.5 | 0.851 | ||
| 19980302 | 0 | −4 | −13.9 | 0.930 | ||
| 19980509 | 6 | −9 | −10.5 | 0.898 | ||
| Jianyang | Calibration | 19880228 | −1 | −5 | 6.9 | 0.943 |
| 19880620 | 1 | −15 | 14.6 | 0.883 | ||
| 19890629 | −2 | −5 | −3.3 | 0.880 | ||
| 19920321 | −5 | −4 | 12 | 0.871 | ||
| 19920616 | −1 | −14 | 5.1 | 0.897 | ||
| 19920704 | −1 | −8 | 2.0 | 0.905 | ||
| 19920831 | 0 | −8 | 11.9 | 0.817 | ||
| 19930615 | −2 | 8 | 19.5 | 0.887 | ||
| 19930630 | −3 | −17 | −17.9 | 0.842 | ||
| 19950603 | 1 | −9 | 0 | 0.948 | ||
| Validation | 19950622 | −2 | −5 | −5.8 | 0.844 | |
| 19950626 | 0 | 6 | 0.8 | 0.914 | ||
| 19970605 | 1 | 12 | 4.7 | 0.897 | ||
| 19980608 | −2 | 13 | 2.4 | 0.944 | ||
| 19990521 | 0 | −18 | −20 | 0.876 | ||
| 19990715 | 0 | −8 | −5.2 | 0.958 | ||
| Shuiji | Calibration | 19880228 | 2 | −5 | 25.0 | 0.875 |
| 19880520 | 11 | −18 | −1.7 | 0.894 | ||
| 19880620 | 3 | −36 | 4.2 | 0.827 | ||
| 19890520 | 1 | −17 | 5.9 | 0.882 | ||
| 19890621 | −1 | −12 | −5.9 | 0.817 | ||
| 19900629 | 1 | 7 | 11.1 | 0.864 | ||
| 19920321 | 1 | −4 | 14.6 | 0.861 | ||
| 19920514 | −1 | −11 | 10.2 | 0.912 | ||
| 19930615 | −1 | −20 | 2.1 | 0.933 | ||
| 19930502 | −2 | −7 | −2.4 | 0.890 | ||
| Validation | 19940521 | 4 | −28 | −4.7 | 0.883 | |
| 19940614 | −1 | −11 | 12 | 0.903 | ||
| 19950425 | 0 | −22 | −10.4 | 0.870 | ||
| 19950614 | −7 | −7 | −1.6 | 0.848 | ||
| 19980301 | 0 | −7 | −9.7 | 0.869 | ||
| 19990715 | 5 | −5 | −9.9 | 0.826 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Shi, P.; Qu, S.; Ji, X.; Zhao, L.; Gou, J.; Mou, S. Integrating XAJ Model with GIUH Based on Nash Model for Rainfall-Runoff Modelling. Water 2019, 11, 772. https://doi.org/10.3390/w11040772
Chen Y, Shi P, Qu S, Ji X, Zhao L, Gou J, Mou S. Integrating XAJ Model with GIUH Based on Nash Model for Rainfall-Runoff Modelling. Water. 2019; 11(4):772. https://doi.org/10.3390/w11040772
Chicago/Turabian StyleChen, Yingbing, Peng Shi, Simin Qu, Xiaomin Ji, Lanlan Zhao, Jianfeng Gou, and Shiyu Mou. 2019. "Integrating XAJ Model with GIUH Based on Nash Model for Rainfall-Runoff Modelling" Water 11, no. 4: 772. https://doi.org/10.3390/w11040772
APA StyleChen, Y., Shi, P., Qu, S., Ji, X., Zhao, L., Gou, J., & Mou, S. (2019). Integrating XAJ Model with GIUH Based on Nash Model for Rainfall-Runoff Modelling. Water, 11(4), 772. https://doi.org/10.3390/w11040772





