The Exact Groundwater Divide on Water Table between Two Rivers: A Fundamental Model Investigation

Abstract

The groundwater divide within a plane has long been delineated as a water table ridge composed of the local top points of a water table. This definition has not been examined well for river basins. We developed a fundamental model of a two-dimensional unsaturated–saturated flow in a profile between two rivers. The exact groundwater divide can be identified from the boundary between two local flow systems and compared with the top of a water table. It is closer to the river of a higher water level than the top of a water table. The catchment area would be overestimated (up to ~50%) for a high river and underestimated (up to ~15%) for a low river by using the top of the water table. Furthermore, a pass-through flow from one river to another would be developed below two local flow systems when the groundwater divide is significantly close to a high river.

1. Introduction

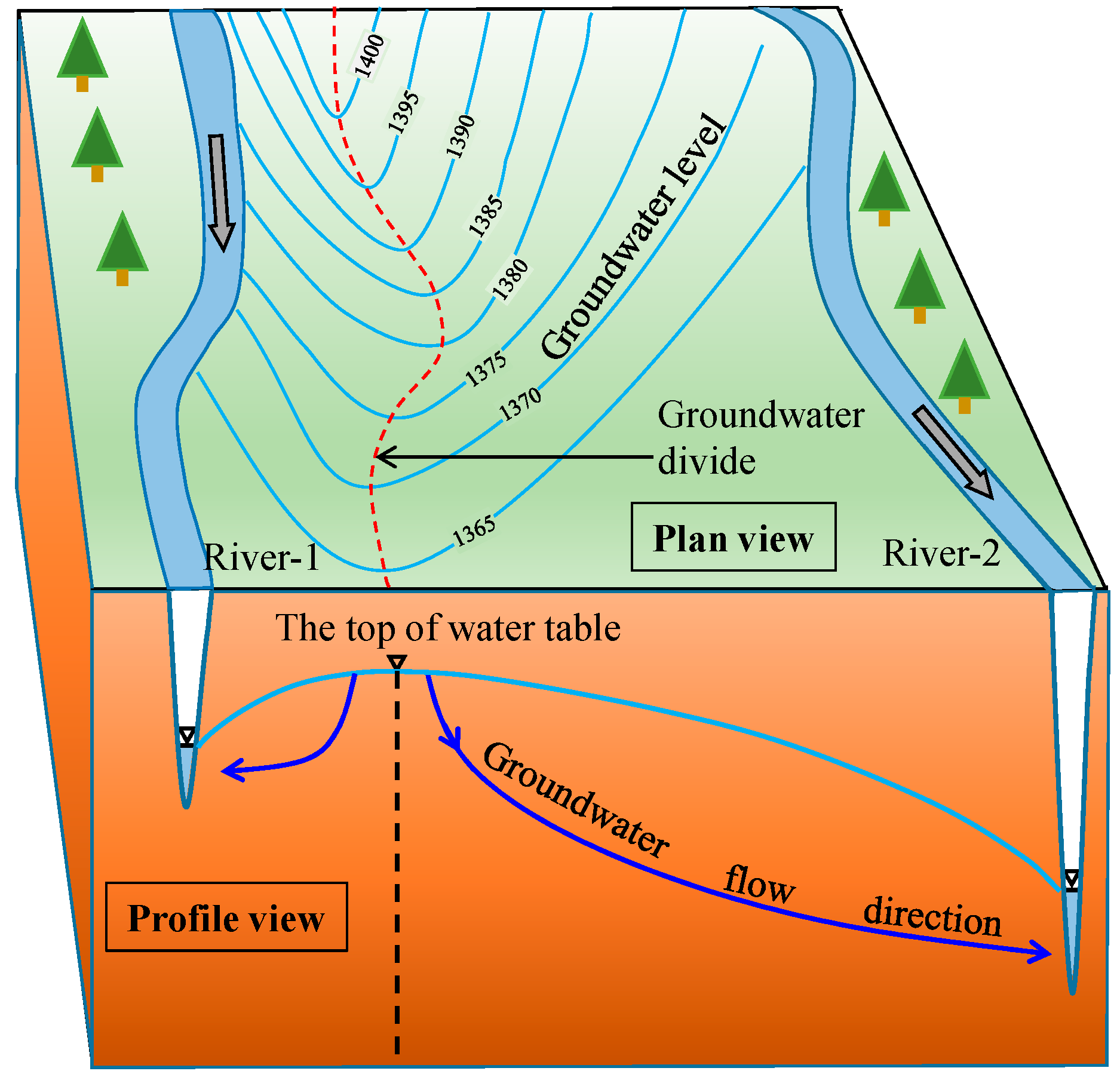
Hydrologists study the water cycle and transport of accompanying materials in regions based on watershed divisions. A watershed or drainage basin is an area enclosed by a divide line that can be described with topographic ridges, i.e., with local land surface top points. This definition is fine for surface water studies but is not always effective in groundwater studies. The groundwater divide between basins may be different from the topographic divide [1,2], and it causes inter-basin groundwater flow (IGF) that has been identified in hydrogeological surveys [2,3,4]. In the past few decades, researchers have highlighted the impacts of IGF on the geochemical characteristics [5,6,7], the regional climate–hydrological interactions [8], and the geomorphic evolution [9] of river basins. An exact description of groundwater divides is necessary to quantitatively interpret the features of IGF.

The definition of the groundwater divide is not as straightforward as it is for surface watersheds due to the complexities in aquifer media (geological and hydraulic diversity) and flow patterns (horizontal and vertical). At the regional scale, nested groundwater flow systems can develop [10,11], in which the flow system boundaries yield divide lines of groundwater on the profile and show how IGF occurs. In particular, water table highs linking with divide lines between local flow systems are comparable to surface watersheds [2]. In the horizontal plane, a groundwater divide has been conventionally defined as a curve representing the water table ridge (described with contours of the groundwater level) that separates the flow domain into subdomains [1]. For an unconfined aquifer with infiltration recharge between two rivers (Figure 1), in practice, people describe the groundwater divide as a line across the contours of the groundwater level at the turning points (in the plan view) that play a role as local top points of the water table (in the profile view). The point with the highest elevation on the water table between rivers is the theoretical place of groundwater divide, as in the Dupuit–Forchheimer model [12], where the vertical line below the point (dashed line in Figure 1) yields a no flow boundary. The Dupuit assumption ignores the vertical flow but this definition of groundwater divide is compatible with Tóth’s theory if only two local flow systems exist between the rivers. In most of the profile figures of nested flow systems [2,10,11,13,14], it is believed that water table highs separate the local flow systems. However, the relationship between the exact groundwater divide and the top of the water table in an inter-river unconfined aquifer, to our knowledge, has never been seriously examined in the literature.

The inaccuracy of using the water table ridge in defining the groundwater divide was recently noticed in an investigation of three-dimensional (3D) groundwater flow systems [15]. Groundwater circulation cells (GWCCs) have been defined as representing the unit space of groundwater flow from a recharge area to a discharge area. Local flow systems are characterized by open GWCCs with boundaries on the phreatic surface that are close to the local top of the water table. However, they do not coincide with and are not parallel to the water table ridges. The investigation was based on complex Tóthian basins where the flow patterns are controlled by an undulating water table which has a planar distribution of discharge zones. The water table plays a role as a subdued replica of the topography in these topography-controlled basins where the recharge is relatively high over the hydraulic conductivity of the aquifers [16]. In reality, for basins the flow systems are mostly controlled by areal recharge and linear discharge or local discharge at limited water table outcrops [17,18,19], especially for river basins. How is the groundwater divide different from the local top of the water table in a river basin? This question has not been well addressed. As an early investigation, we carried out a special examination of the groundwater divide between rivers in a fundamental two-dimensional (2D) profile model for an unconfined aquifer. Inconsistency between the exact groundwater divide and the top of the water table was found and quantitatively researched. We are aware that this is an essential effect for river basins with high ratios of groundwater discharge to streamflow.

2. Conceptual Model and Methods

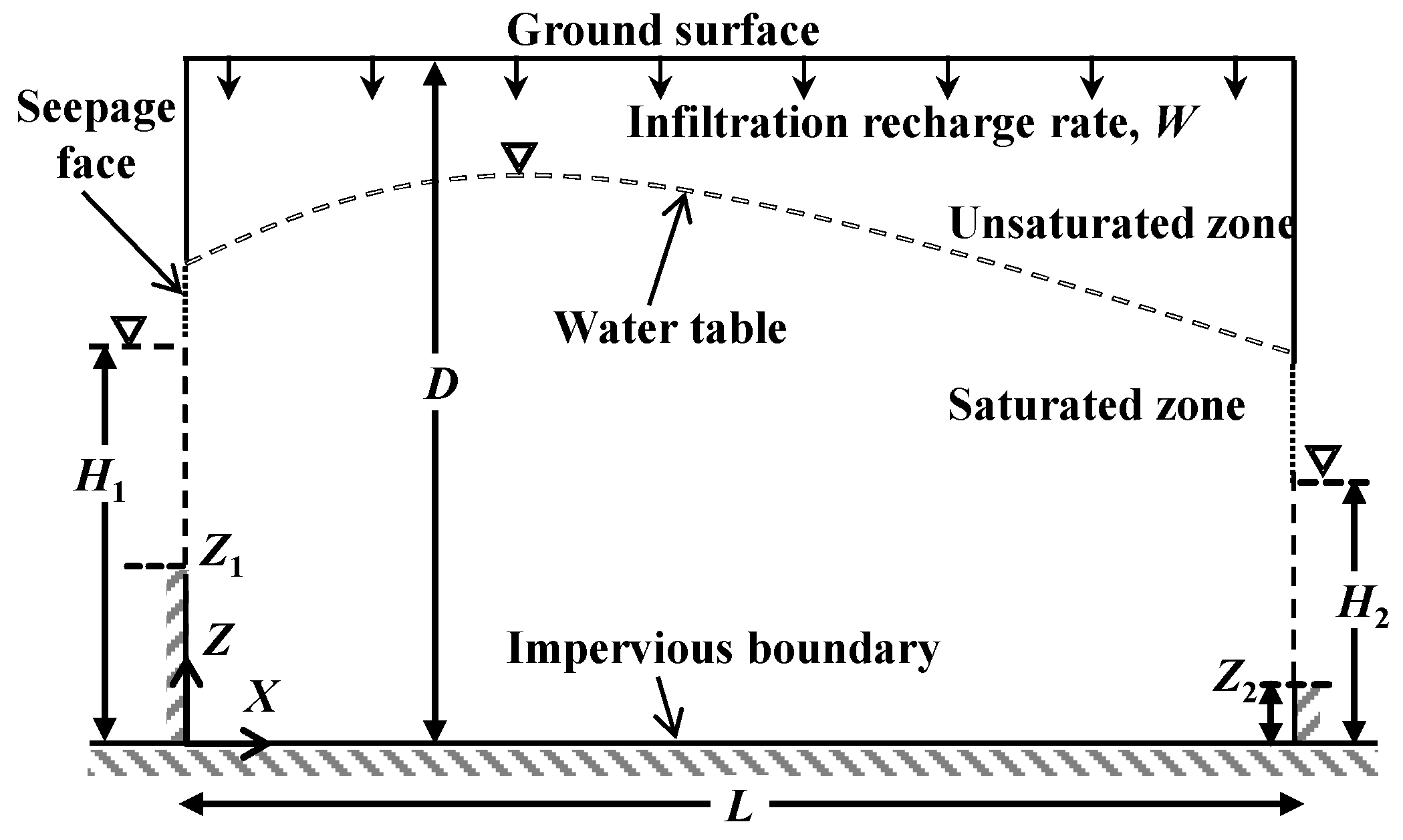
In this study, we analyzed the groundwater divide between rivers using a fundamental 2D model, as shown in Figure 2. The two rivers, numbered 1 and 2, partially cut into an unconfined aquifer with anisotropic homogeneous porous media. The water level in River 1 was higher than that in River 2. Precipitation infiltration proceeded at a constant uniform rate and drove a steady-state unsaturated–saturated flow from the ground surface to the rivers across the aquifer. A water table mound was formed, separating the saturated and unsaturated zones. Seepage faces were also formed along the interface between the aquifer and atmosphere when groundwater flowed to a surface body [1,12].

Assuming Darcy’s law was applicable, we adopted the Richards’ equation to describe the unsaturated–saturated flow in porous media [20]. The pressure head (L) of capillary water in the unsaturated zone, P_h, was used in the equation, which can be incorporated into the total hydraulic head (L), H, as [1]

$$H=Z+P_h$$

(1)

where Z is the height (L) of the position (positive upward). P_h < 0 for positions in the unsaturated zone whereas P_h ≥ 0 in the saturated zone. At the position of the water table, P_h = 0. For the 2D steady-state flow in the model shown in Figure 2, the control equation can be written as

$$K_{sx}\frac{\partial }{\partial X}\left[K_r(P_h)\frac{\partial H}{\partial X}\right]+K_{sz}\frac{\partial }{\partial Z}\left[K_r(P_h)\frac{\partial H}{\partial Z}\right]=0,0<X<L,0<Z<D$$

(2)

where K_sx and K_sz are the saturated hydraulic conductivities (LT⁻¹) in the horizontal and vertical flow, respectively. K_r is the ratio (-) of hydraulic conductivities between unsaturated and saturated flow, and is a function of P_h. X is the horizontal distance (L) from the side of River 1. Without loss of generality, we used the exponential formula for K_r when P_h < 0, K_r = exp(A_kP_h) [21], where A_k (L⁻¹) is a decay parameter; otherwise, K_r = 1. The empirical range of A_k for soils is 0.2–5.0 m⁻¹ [22].

The boundary conditions were specified as

$$K_{sz}{K}_r(P_h)\frac{\partial H}{\partial Z}=W, 0<X<L,Z=D$$

(3)

$$\frac{\partial H}{\partial Z}=0, 0<X<L,Z=0$$

(4)

$$H=H_1, X=0,Z_1\le Z\le H_1$$

(5)

$$H=H_2, X=L,Z_2\le Z\le H_2$$

(6)

$$\frac{\partial H}{\partial X}=0, X=0,Z<Z_1,\mathrm{or},X=L,Z<Z_2$$

(7)

$$\frac{\partial H}{\partial X}=C_b(H-Z), X=0,H_1<Z<D$$

(8)

$$\frac{\partial H}{\partial X}=-C_b(H-Z),X=L,H_2<Z<D$$

(9)

where W is the net infiltration rate (LT⁻¹), D is the total thickness of the aquifer (L), and L is the horizontal length of the aquifer between the two rivers (L). H₁ and H₂ are the water levels in River 1 and River 2 (L), respectively. Z₁ and Z₂ are the river bed heights of River 1 and River 2 (L), respectively. C_b is a parameter (LT⁻¹) dependent on the existence of a seepage face. Equation (8) is a simplified formula of the equation in Chui and Freyberg (2009) [23] used to switch the boundary condition between the Neumann type (C_b = 0 when H ≤ Z) for a place above the seepage face and the Dirichlet type (C_b→∞ when H > Z) for a portion at the seepage face. In practice, a large number is applied to estimate C_b→∞.

The mathematic model presented in Equations (2)–(8) can be solved in a general way with the dimensionless variables

$$x=\frac{2X}{L},z=\frac{Z}{D},h=\frac{H}{D},p_h=\frac{P_h}{D},$$

(10)

$$z_i=\frac{Z_i}{D},h_i=\frac{H_i}{D},k=\frac{4D^2}{L^2}\frac{K_{sx}}{K_{sz}},w=\frac{W}{K_{sz}},a=A_{k}D,c=C_{b}L/2$$

(11)

where i = 1 and 2 denotes River 1 and River 2, respectively. Equation (2) can then be rewritten as

$$k\frac{\partial }{\partial x}\left[K_r(p_h)\frac{\partial h}{\partial x}\right]+\frac{\partial }{\partial z}\left[K_r(p_h)\frac{\partial h}{\partial z}\right]=0,0<x<2,0<z<1$$

(12)

The boundary conditions can also be simplified with these dimensionless variables:

$$K_r(p_h)\frac{\partial h}{\partial z}=w,0<x<2,z=1$$

(13)

$$\frac{\partial h}{\partial z}=0,0<x<2,z=0$$

(14)

$$h=h_1,x=0,z_1\le z\le h_1$$

(15)

$$h=h_2,x=2,z_2\le z\le h_2$$

(16)

$$\frac{\partial h}{\partial x}=0,x=0,z<z_1,\mathrm{or},x=2,z<z_2$$

(17)

$$\frac{\partial h}{\partial x}=c(h-z),x=0,h_1<z<1$$

(18)

$$\frac{\partial h}{\partial x}=-c(h-z),x=2,h_2<z<1$$

(19)

There are difficulties in obtaining the general analytical solution of Equation (12) because it is a nonlinear second-order partial differential equation. Read and Broadbridge [24] developed series solutions only for the case of p_h < 0 so that the flow in the saturated zone was not incorporated. Tristscher et al. [25] extended the solutions to a condition with both unsaturated and saturated zones but an additional numerical approach has to be used. This analytical-numerical approach is not efficient for segmental boundaries such as that expressed in Equations (15)–(19). In this study, a numerical solution of the model was implemented using the COMSOL Multiphysics tool produced by COMSOL Inc., Sweden [26]. The maximum element size of the finite-element network was limited to 0.02. The water table was identified as the curve satisfying p_h = 0. In particular, this software yielded a streamline tracing technique used to identify local flow systems (different groups of streamlines) for groundwater discharge toward River 1 and River 2. The boundary between the local flow systems intersected the water table at a point that performs a role as the exact divide but may be different from the top of the water table.

3. Results

The modeling results in the dimensionless manner are dependent on the geometric parameters, z_i and h_i, that are limited between 0 and 1, and the physical parameters, a, k, and w, that are defined in Equation (11). In this study, we set the a value to the range between 2 and 300 for D varying from 10 m to 60 m and A_k varying from 0.2 m⁻¹ to 5.0 m⁻¹ [22]. The k value varies between 0.1 and 10 for normal conditions where D is significantly smaller than L but K_sx is significantly higher than K_sz. The w value is less than 1 because W is generally smaller than K_sz. The parameter c is not a control parameter because it is 0 or ∞. A large enough number is used to estimate c→∞.

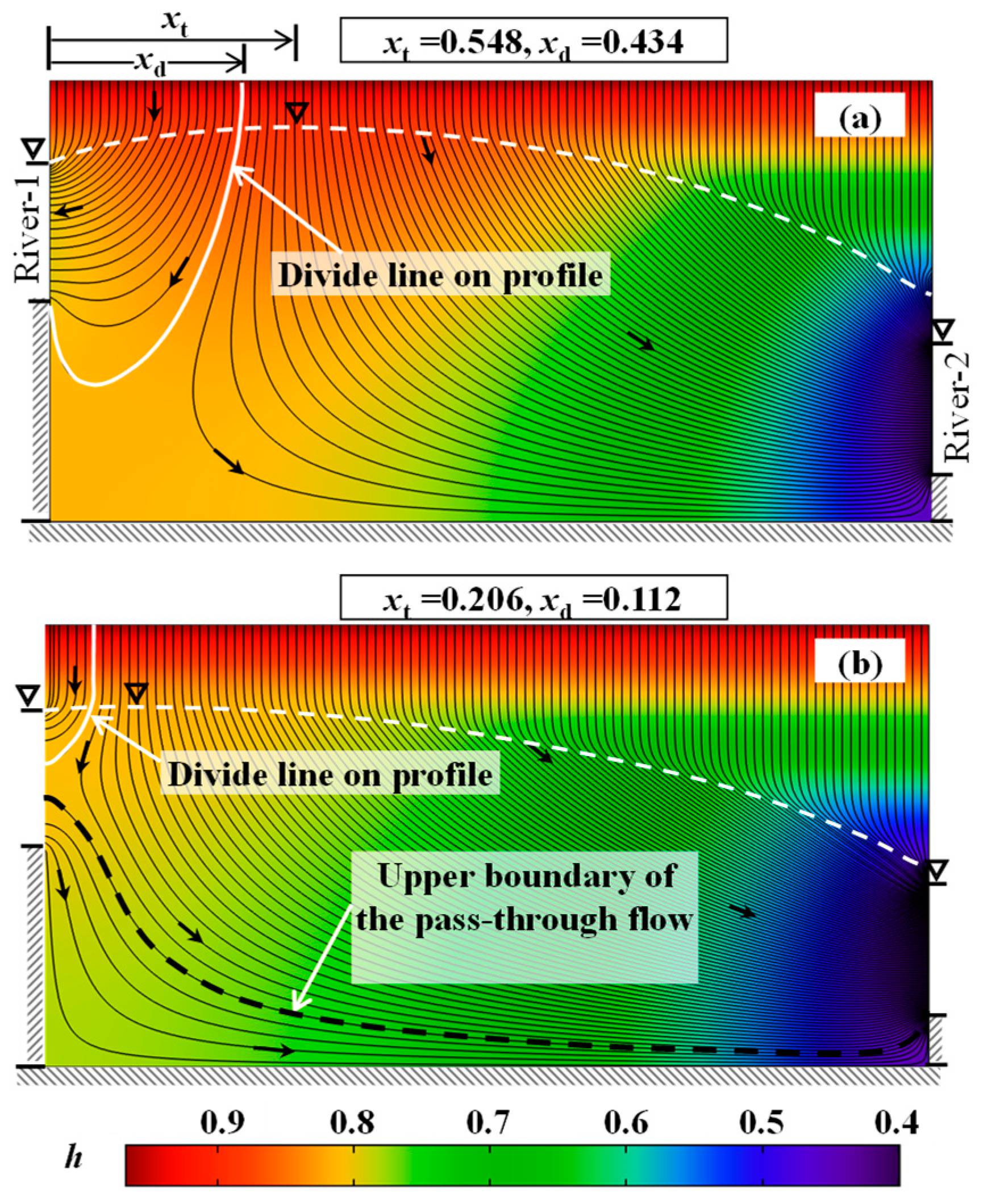
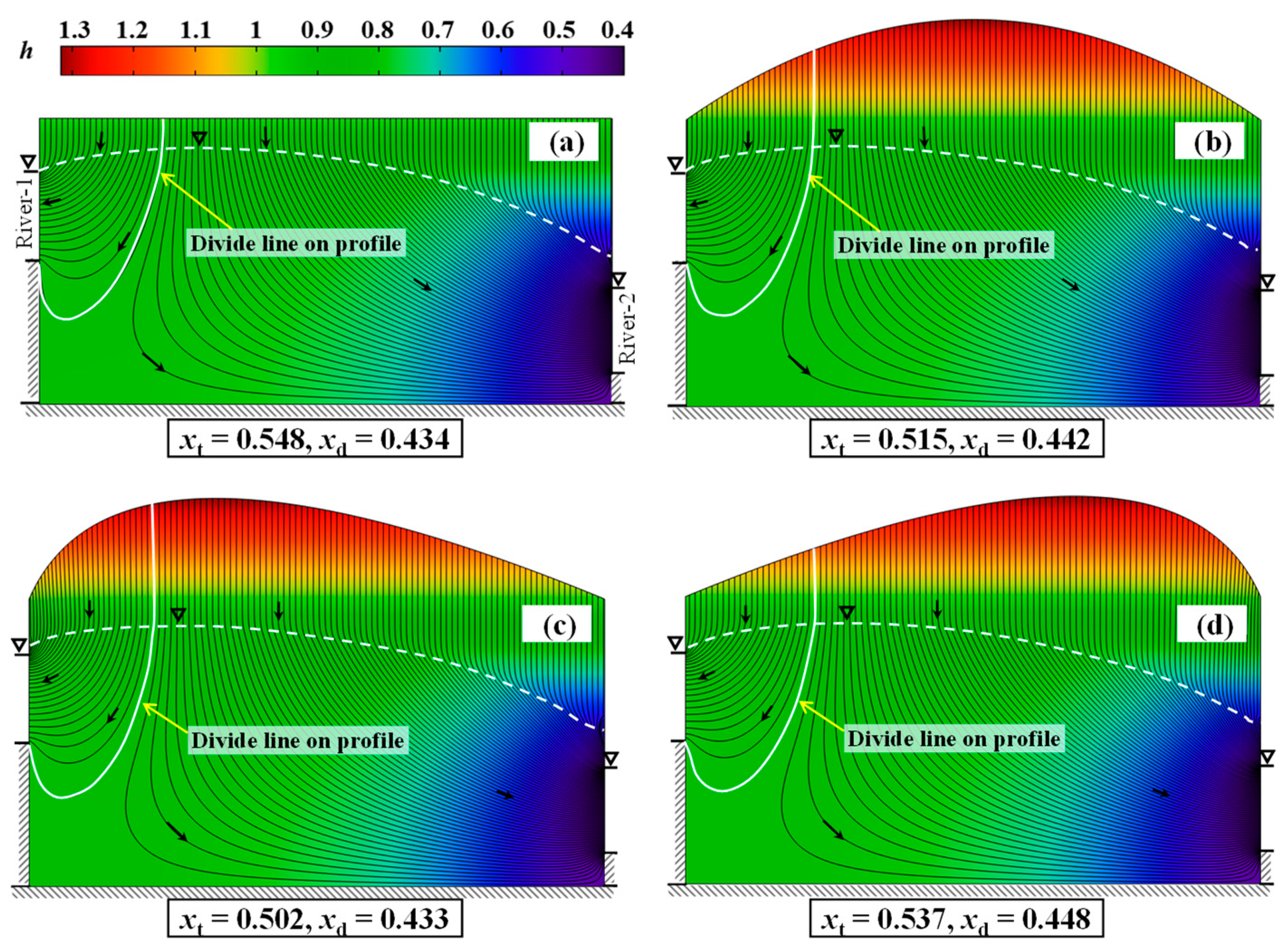
We show two typical cases in Figure 3 to indicate what will happen. In these cases, the water level in River 1 is double of that in River 2 so more infiltration recharge is contributed to River 2. Streamlines indicate the characteristics of the flow systems. A divide line exists between the local flow systems of the two rivers. The point of intersection between the divide line and the water table is not the top of the water table but closer to River 1. In the domain between the two points, a downward flow of shallow groundwater is accompanied by a weak horizontal flow toward River 1. However, in the deep zone, the flow changes direction in the horizontal direction toward River 2. This dynamic feature explains why the divide has to shift to a place that is closer to River 1. The relative errors can be calculated as

$$e_1=\frac{x_t-x_d}{x_t},e_2=\frac{x_d-x_t}{2-x_t}$$

(20)

where x_d and x_t are dimensionless horizontal coordinates of the groundwater divide and the top of the water table, respectively. The errors in the catchment area estimated for River 1 and River 2 by using the top of water table, are, respectively, e₁ and e₂. The value of e₁ in percentage denotes the overestimated proportion (e₁ ≥ 0) of the catchment area for the high river. The negative value of e₂ denotes underestimated proportion (e₂ ≤ 0) of the catchment area for the low river. For the situations in Figure 3, the e₁ values are +20.8% in Figure 3a and +45.6% in Figure 3b, respectively, showing a significant overestimation of the catchment area for River 1. The maximum e₁ value in other examples approximates to 50%. In comparison, the e₂ values are −7.9% for Figure 3a and −5.2% for Figure 3b, respectively. Thus, the catchment area was underestimated for River 2 but the absolute relative error was smaller than that for River 1.

A special feature was exhibited when the infiltration recharge was small, as shown in Figure 3b: a pass-through flow from River 1 to River 2 came into being below the local flow systems. This should not be the regional groundwater flow system or intermediate flow system that is defined in Tóth’s theory because the source head (River 1) of such a pass-through flow is a local discharge zone. When w is less than 0.06 without changes in other parameters, the divide of shallow groundwater disappears (x_d = 0) and only a local flow system of River 2 overlies the pass-through flow. Thus, Figure 3b shows a transition status of groundwater flow between that shown in Figure 3a and that of w < 0.06.

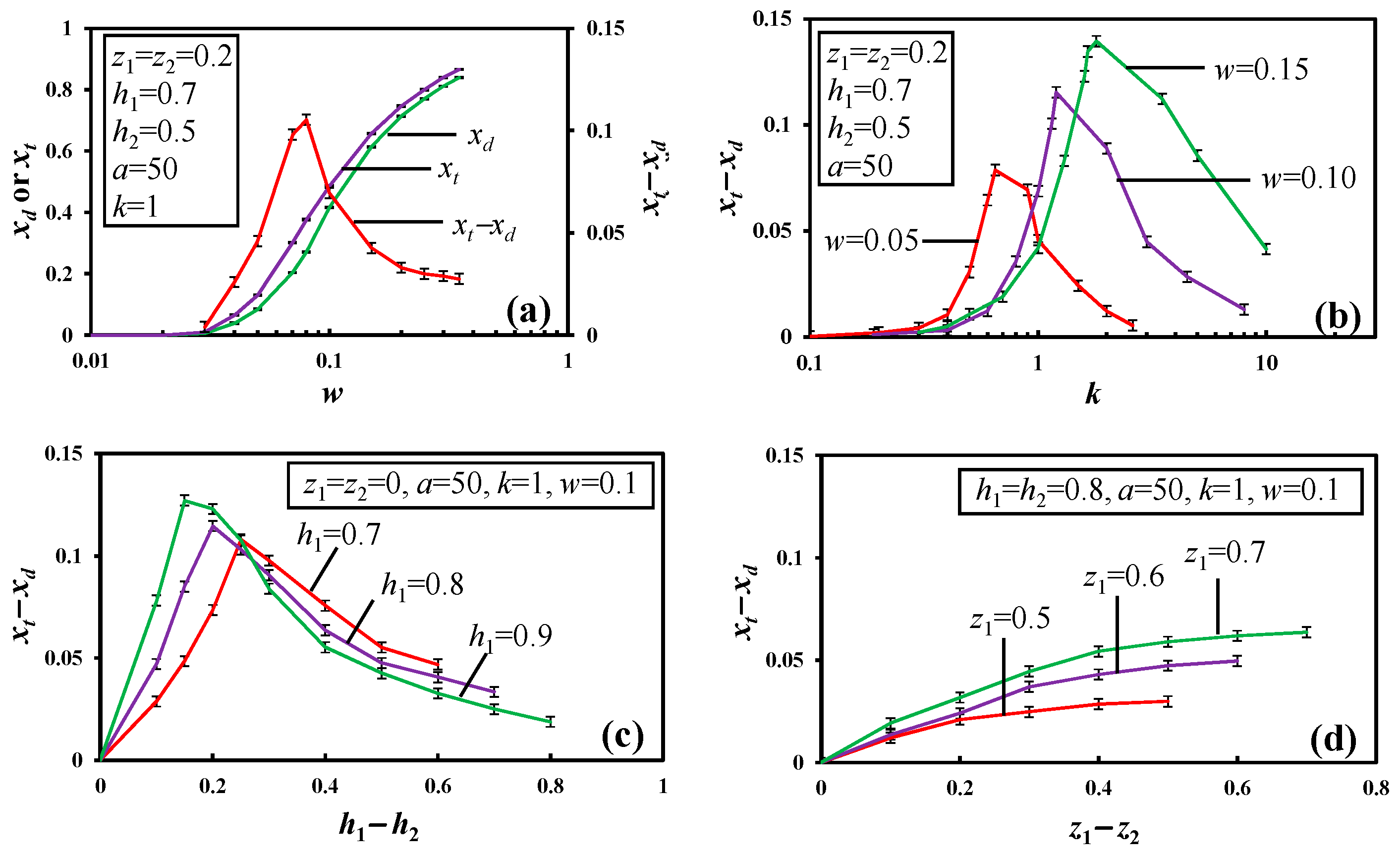
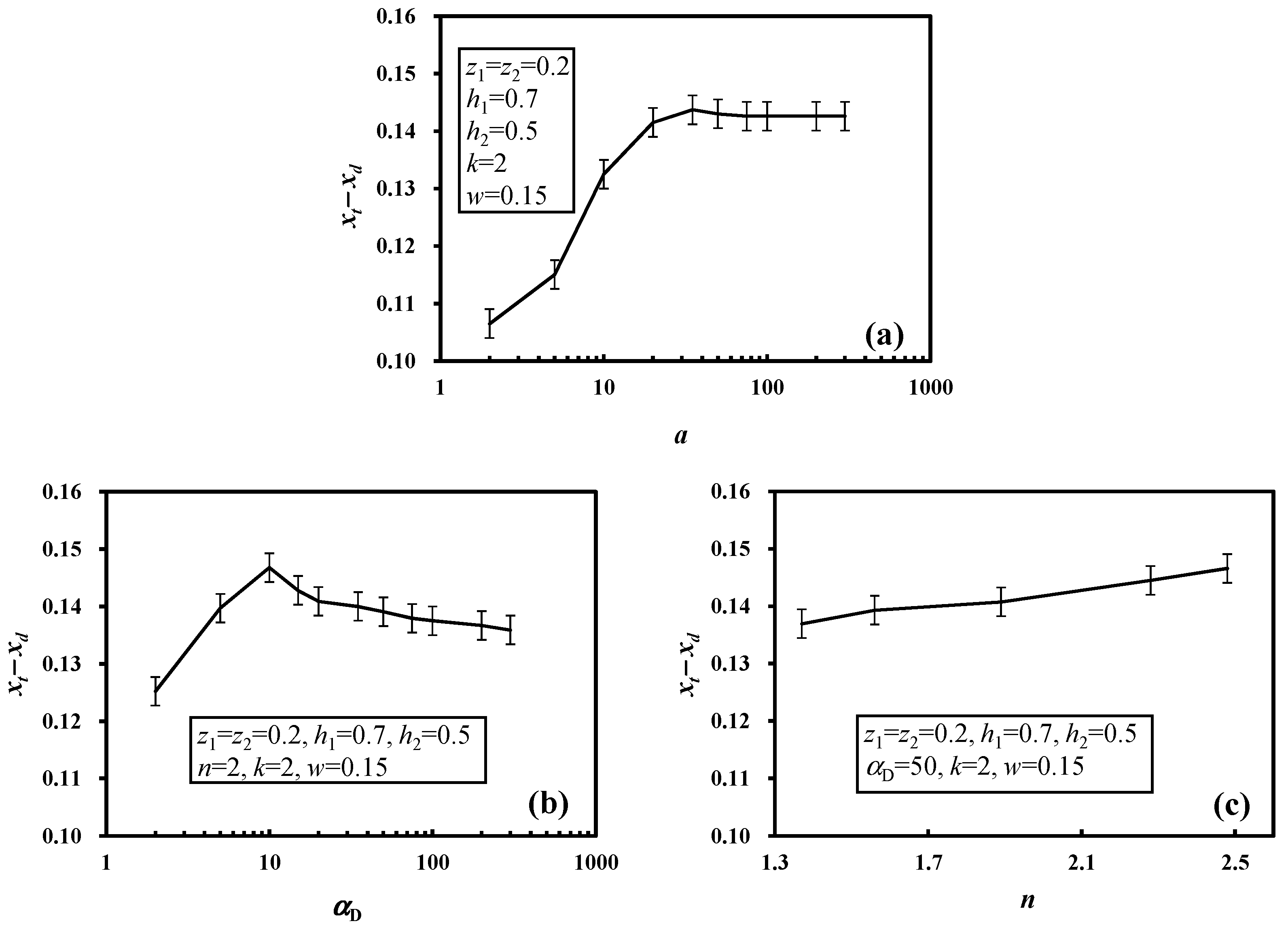
We checked the variation of the gap x_t−x_d with sensitivity analysis, as illustrated in Figure 4. Figure 4a shows the impact of the infiltration recharge w. In this case, there are four types of status of the flow. (1) The top of the water table lies on the side of River 1 (x_t = x_d = 0) when w < 0.03. (2) Two local flow systems overlie a pass-through flow when w ranges from 0.03 to 0.08. (3) The pass-through flow does not exist when w ranges from 0.08 to 0.35. (4) The top of the water table touches the ground surface when w > 0.35, leading to an overland flow. When w increases from 0.03 to 0.35, both x_t and x_d increase (the divide moves toward River 2) but x_t−x_d is raised to its maximum value when w = 0.08, after which point it decreases. Figure 4b shows similar rise–fall curves of x_t−x_d when k increases from 0.1 to 10.0. The peak value of x_t−x_d is raised with increasing w. A higher k value results in a divide closer to River 1 and increases the possibility of pass-through flow. Figure 4c explains the impact of the water level difference, h₁−h₂, for rivers that fully penetrate the aquifers (z₁ = z₂ =0). Increasing h₁−h₂ may push the divide toward River 1, whereas x_t−x_d varies along a rise–fall curve. The maximum x_t−x_d value is positively related to the water level in River 1. An equal water level does not mean the groundwater divide would lie on the top of the water table in the middle. As pointed out in Figure 4d, the difference in the penetrating depth of the rivers, z₁−z₂, is also a cause of the difference between x_t and x_d. Parameter a mainly controls the unsaturated flow and does not significantly influence the modeling results of the water table and streamlines.

The x_t−x_d values shown in Figure 4 are less than 0.15, showing that the e₂ value determined from Equation (12) is higher than −15% (because x_t is smaller than 1). Therefore, the underestimation of the catchment area for River 2 would be generally less than 15% by using the top of water table.

4. Discussion

The fundamental 2D model used in this study demonstrates how far a groundwater divide between two rivers would be removed from the top of the water table. The modeling results in a dimensionless manner which can be used directly to assess the actual difference between groundwater divides and water table highs if the conditions between rivers or drains are sufficiently similar to the model. However, this model includes assumptions and simplifications which should be carefully examined in practice.

4.1. The Effect of Using the Van Genuchten (1980) (VG) Formula for K_r

For the numerical modeling of flow in the unsaturated zone, the model used here may be enhanced by using more complex formulas of K_r that have been suggested by other researchers [27,28]. However, this would introduce a cost associated with using more empirical parameters. In this section, we examine the use of the VG formula for calculating K_r [27], the VG formula being

$$K_r(S_e)=S_e^l{\left[1-{\left(1-S_e^{1/m}\right)}^m\right]}^2$$

(21)

where

$$S_e={\left(1+|\alpha P_h{|}^n\right)}^{-m}={\left(1+|{\alpha }_D{p}_h{|}^n\right)}^{-m},m=1-\frac{1}{n}$$

(22)

and α is a parameter (L⁻¹) used for describing the soil retention curve, α_D (=αD) is a dimensionless parameter which was introduced in this research, and n and l are dimensionless parameters. The value of l has been suggested as being 0.5 [27]. Thus, α_D and n are the two dimensionless parameters considered in this study as being capable of rerunning the fundamental model on the basis of the VG formula. According to the database of soils proposed by Carsel and Parrish [29], the ranges of α and n are 0.2–14.5 m⁻¹ and 1.09–2.68, respectively. The value of α_D should range from 2 to 300 for normal conditions where D ranges from 10 m to 60 m.

Typical results obtained using the Gardner formula (with only one dimensionless parameter, a) and VG the formula are presented for comparison in Figure 5. The values of x_t−x_d show different sensitivities with variations in a, α_D, and n. As indicated in Figure 5a, the value of x_t−x_d generally increases with a when the value of a is less than 30, and then stays at an approximately constant value when the value of a is larger than 30. When the VG formula is used, as shown in Figure 5b, the relationship between x_t−x_d and α_D is not consistent, and a peak value of x_t−x_d exists when α_D is close to 10. It should be noted that both a and α_D control the decay of hydraulic conductivity with decreases in soil water saturation and thus the impact of α_D on x_t−x_d is comparable to the impact of a on x_t−x_d. Figure 5b shows a smaller variation range of x_t−x_d than that shown in Figure 5a. However, the maximum values of x_t−x_d obtained with the two K_r formulas are almost the same, being between 0.14 and 0.15. Compared to the results obtained using the Gardner formula, using the VG formula does not cause a significant underestimation of the maximum difference between the top of the water table and the groundwater divide. In addition, the x_t−x_d value is not significantly influenced by the n value, even though it increases with increasing n, as shown in Figure 5c. The e₁ and e₂ values estimated from the VG formulas were shown to be generally lower than 36% and higher than −10%, respectively. Therefore, it may be concluded that the use of the VG formula will not break the previously obtained boundary of relative difference between the top of the water table and the groundwater divide.

4.2. Examining the Effect of Topography

One of the assumptions of the fundamental model that should be examined is that regarding the flat horizontal ground surface. In mountain areas, two neighboring streams are generally separated by a hill, causing a surface water divide between them. We preliminarily checked the impact of such topography by reshaping the ground surface boundary in the model with a hill in the middle or on the left (closer to River 1) or right (closer to River 2). The boundary condition on the top may be rewritten from Equation (13) in this situation as

$$K_r(p_h)\frac{\partial h}{\partial z}=w,0<x<2,z=1+f(x)$$

(23)

where f(x) is a function used here to describe the shape of the hill. The other boundary conditions are not changed.

Figure 6 shows examples where the hydraulic conditions and parameters coincide with those of Figure 3a, except for the shape of the ground surface. The shape of the water table does not significantly change because the infiltration recharge is the same. A hill in the middle increases x_d but decreases x_t, as shown in Figure 6b, resulting in a smaller gap (x_t−x_d) in comparison to that of a flat ground surface. When the hill is closer to River 1, as shown in Figure 6c, both x_d and x_t decrease but x_t decreases more. When the hill is closer to River 2, as shown in Figure 6d, x_d increases and x_t decreases but x_d increases more. Therefore, the gap between the groundwater divide and the top of the water table seems to be smaller than that seen in the fundamental model when a hill exists between the rivers, regardless of whether the hill is in the middle or not. However, further research should examine this effect using more examples.

5. Conclusions

The groundwater divide has been traditionally delineated as the line of local top points on the water table, which is similar to the definition of the surface water divide where topographic ridges are used. In this work, we examined this approach for river basins by using a fundamental 2D model of unsaturated–saturated flow in an unconfined aquifer between two rivers. The boundary between two local flow systems of the two rivers was identified, and it was shown to intersect the water table at the exact groundwater divide. In comparison with the top of the water table, the groundwater divide is closer to the river of the higher water level. The gap between them depends nonlinearly on the shape, size, boundary conditions, and hydraulic properties of the aquifer. The catchment area of the high river may be overestimated from the top of the water table with an error of up to ~50%. The catchment area of the low river may be underestimated but the error is generally less than 15%. A pass-through flow from one river to another will also develop below two local flow systems when the groundwater divide is significantly close to the high river. This is a new type of IGF—in comparison to regional groundwater flow—from which the rivers directly exchange water even when a divide has developed between them.