Optimization of Tank Bottom Shape for Improving the Anti-Deposition Performance of a Prefabricated Pumping Station
Abstract
:1. Introduction
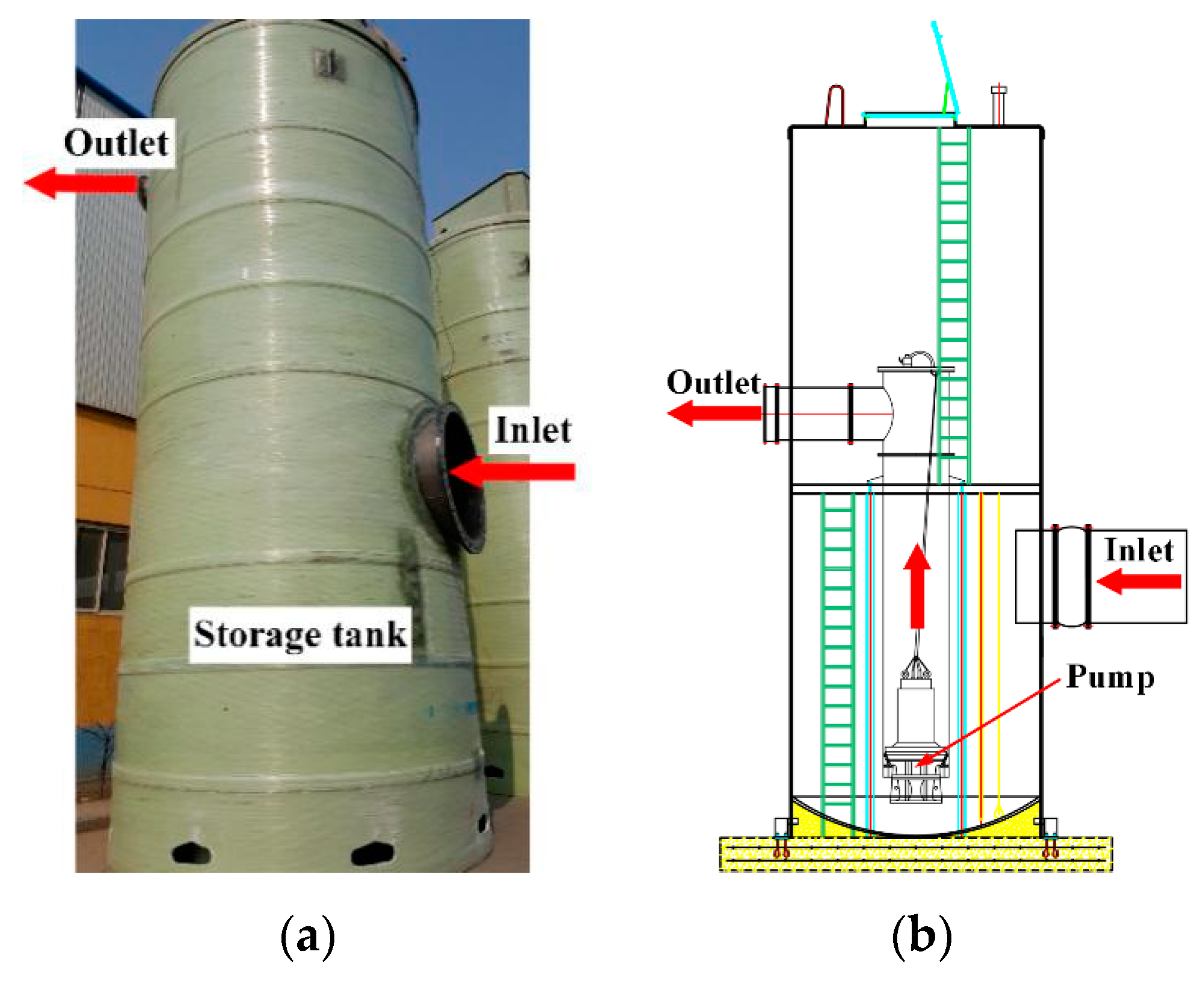
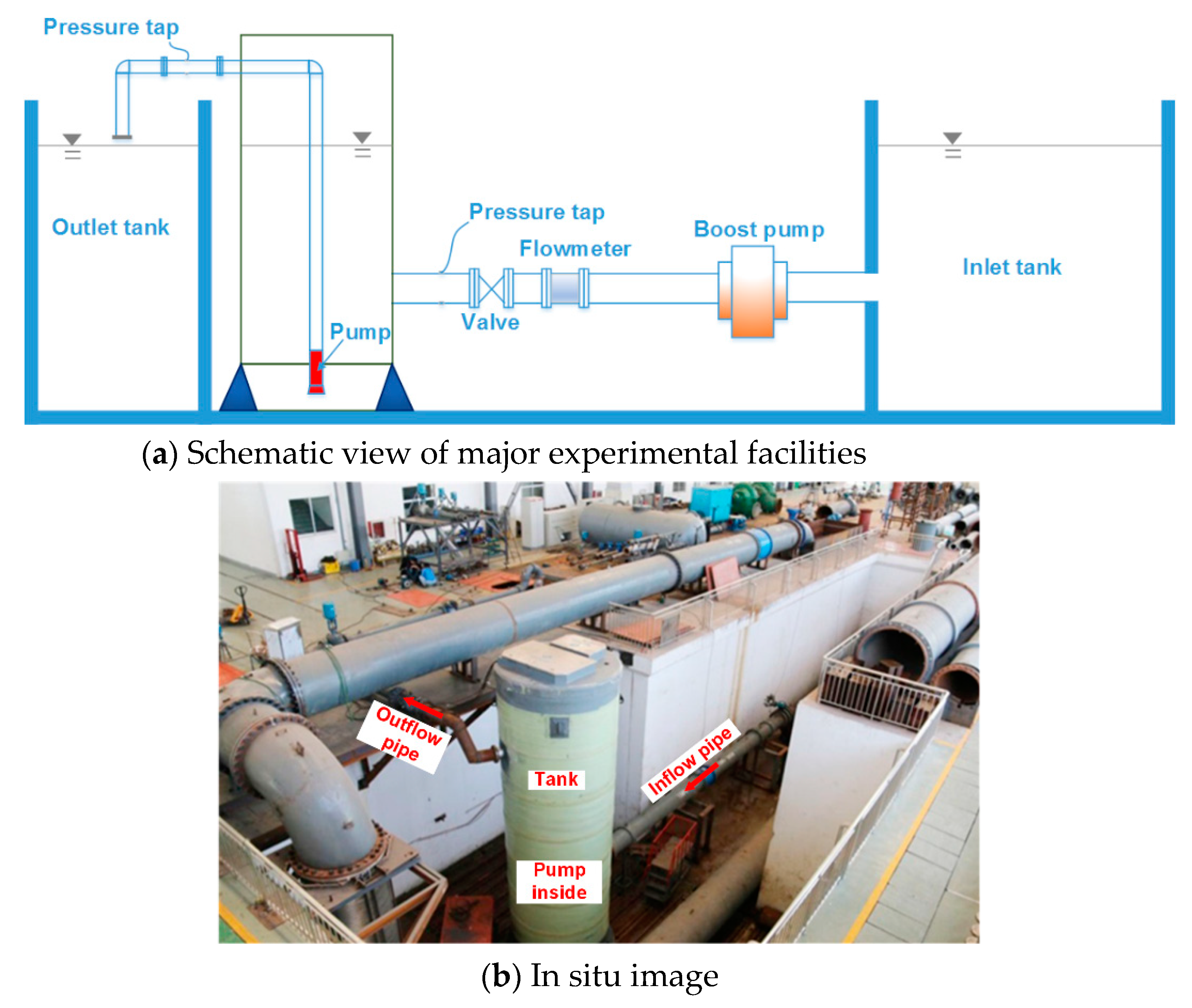
2. Prefabricated Pumping Station Model
3. Numerical Set-Up
3.1. Governing Equations
3.2. Turbulence Model
3.3. Boundary Conditions
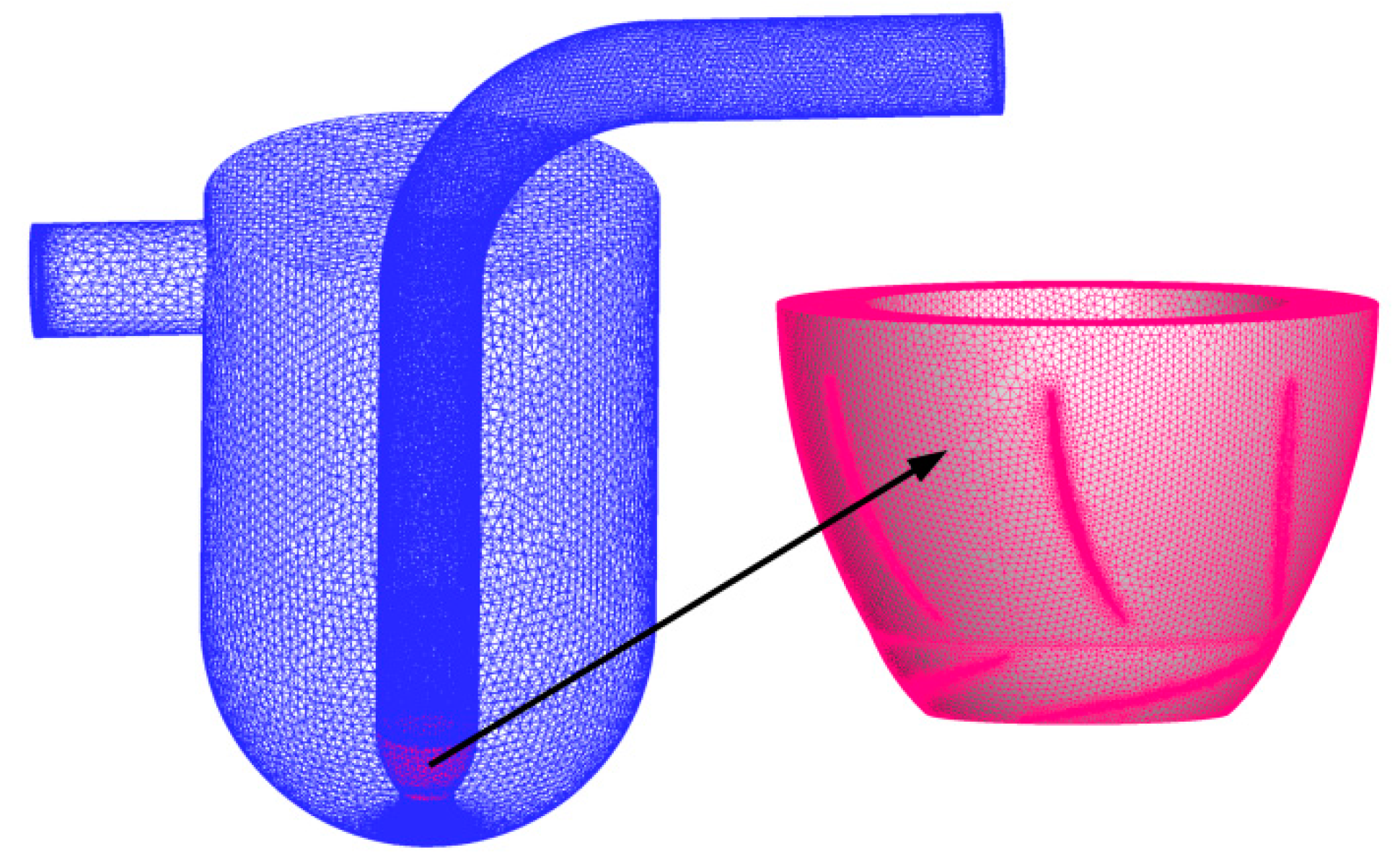
3.4. Grid Independence Examination
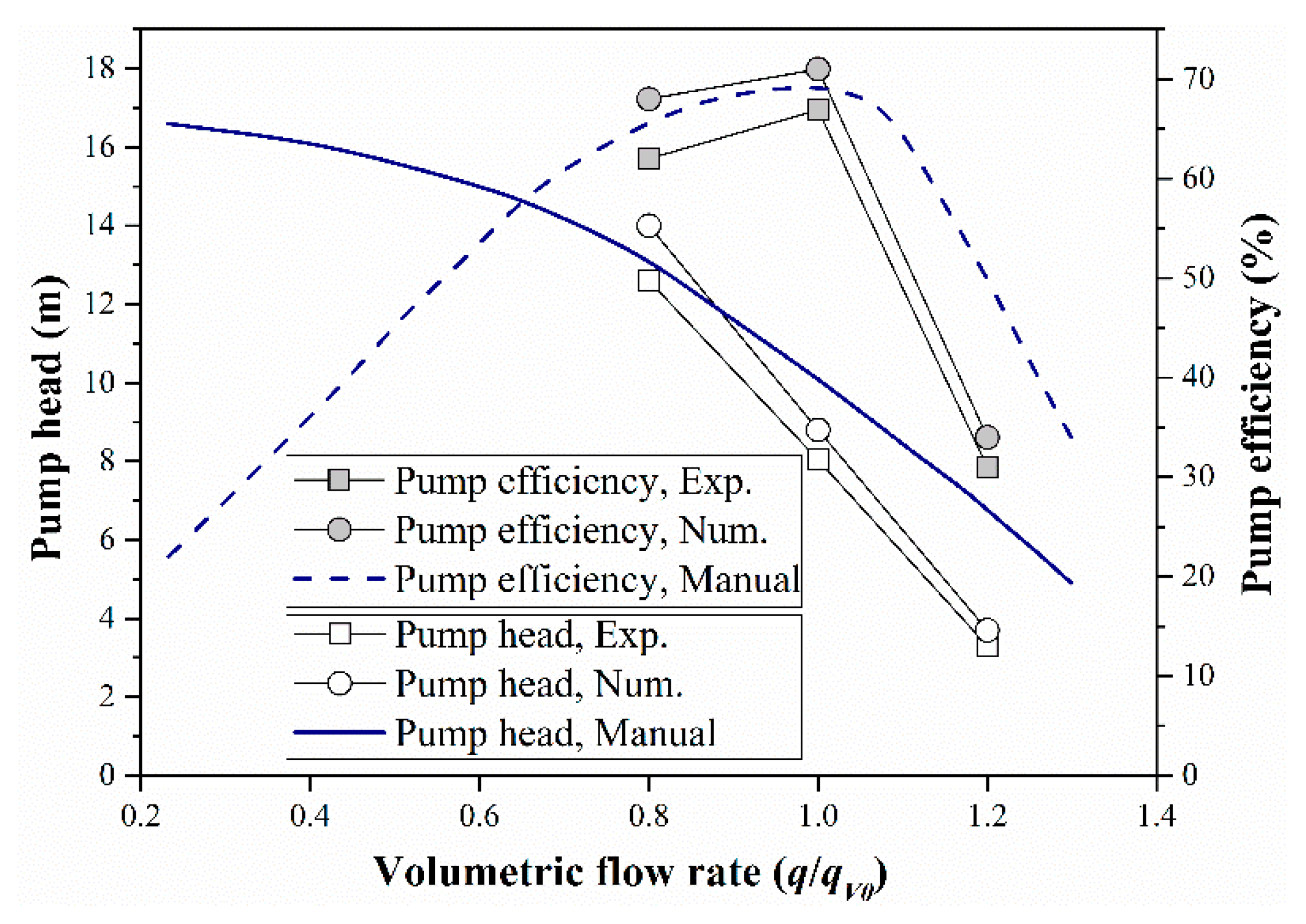
3.5. Validation of Numerical Results
4. Results and Discussion
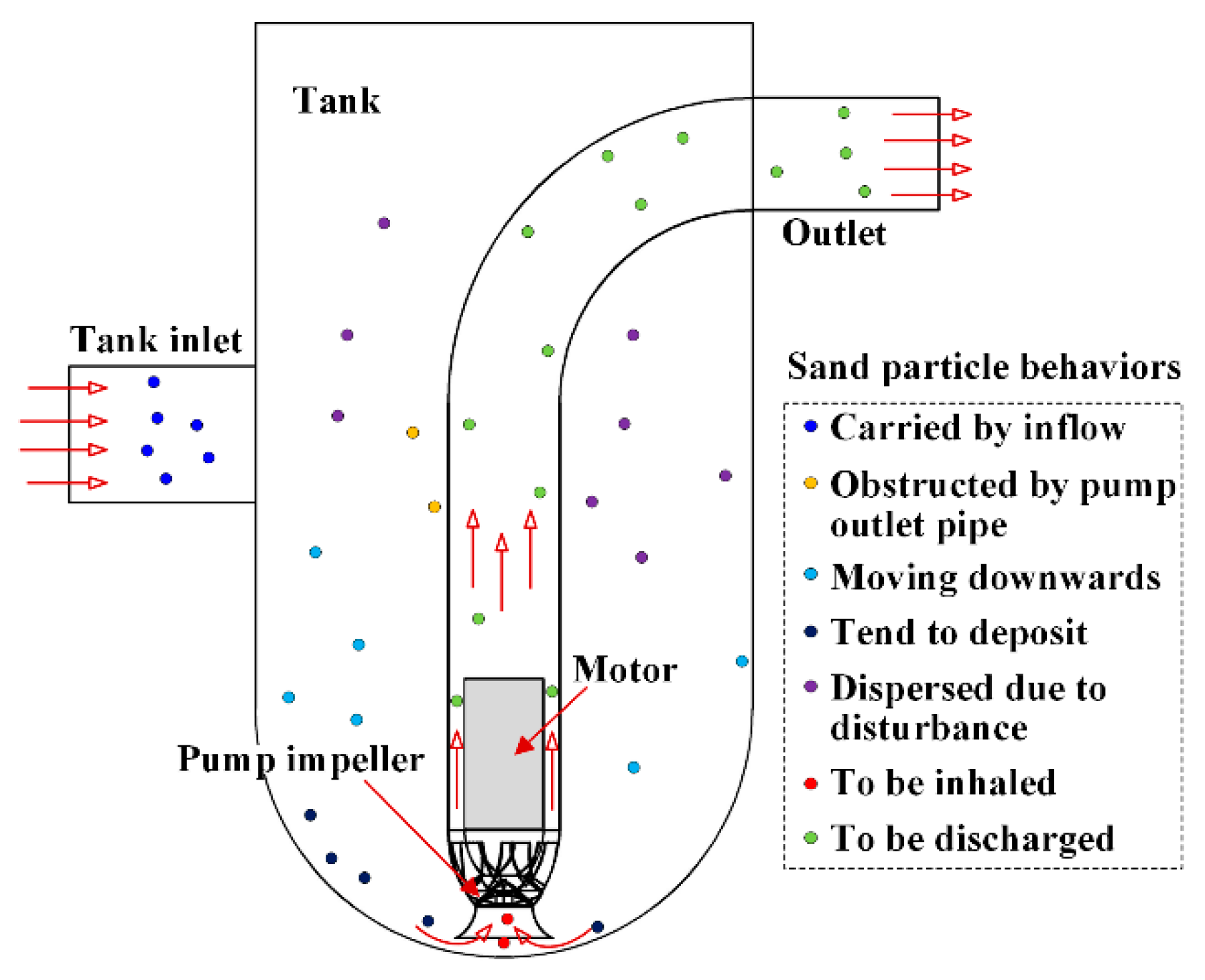
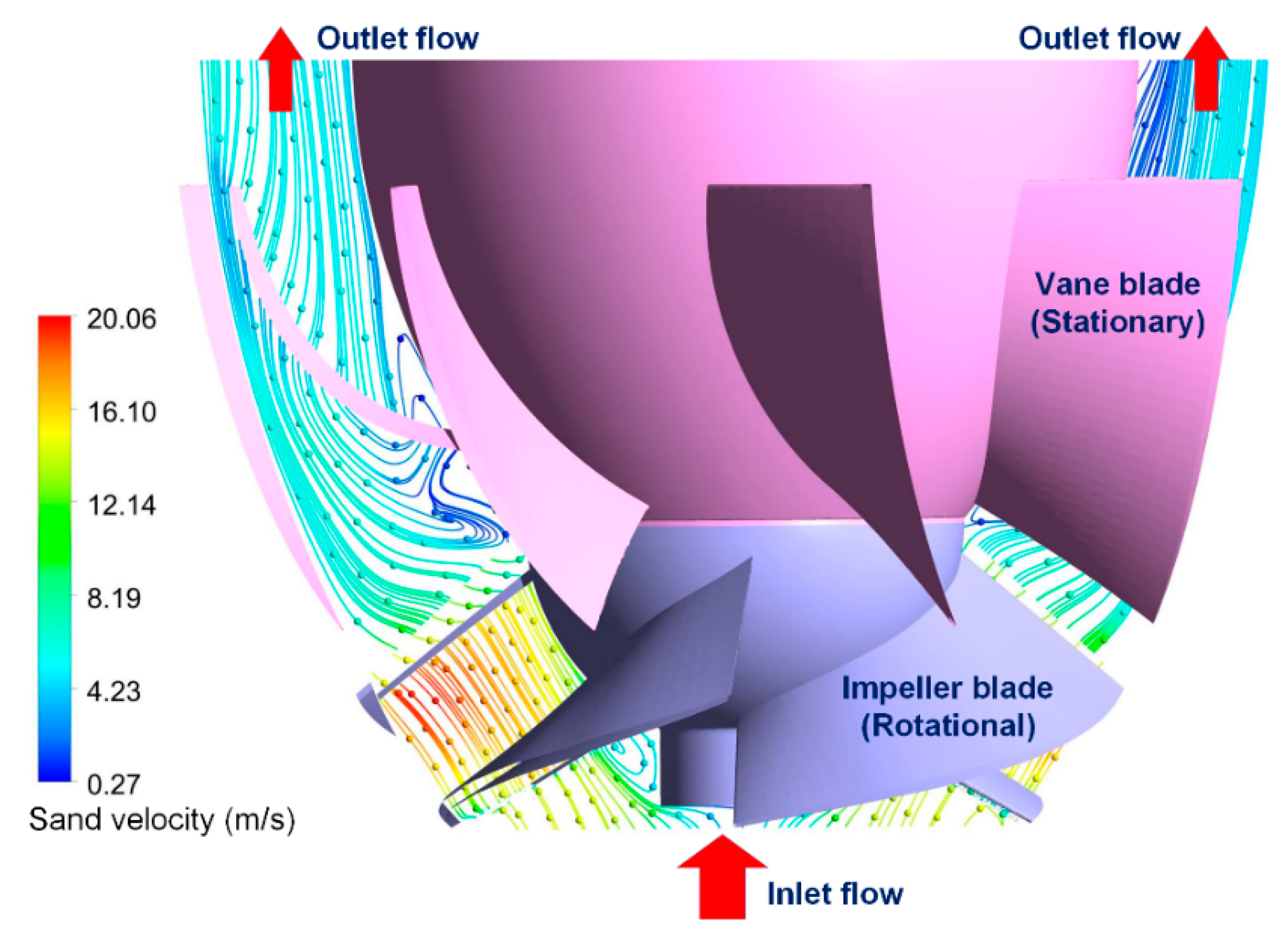
4.1. Motion of Sand Particles in the Pump
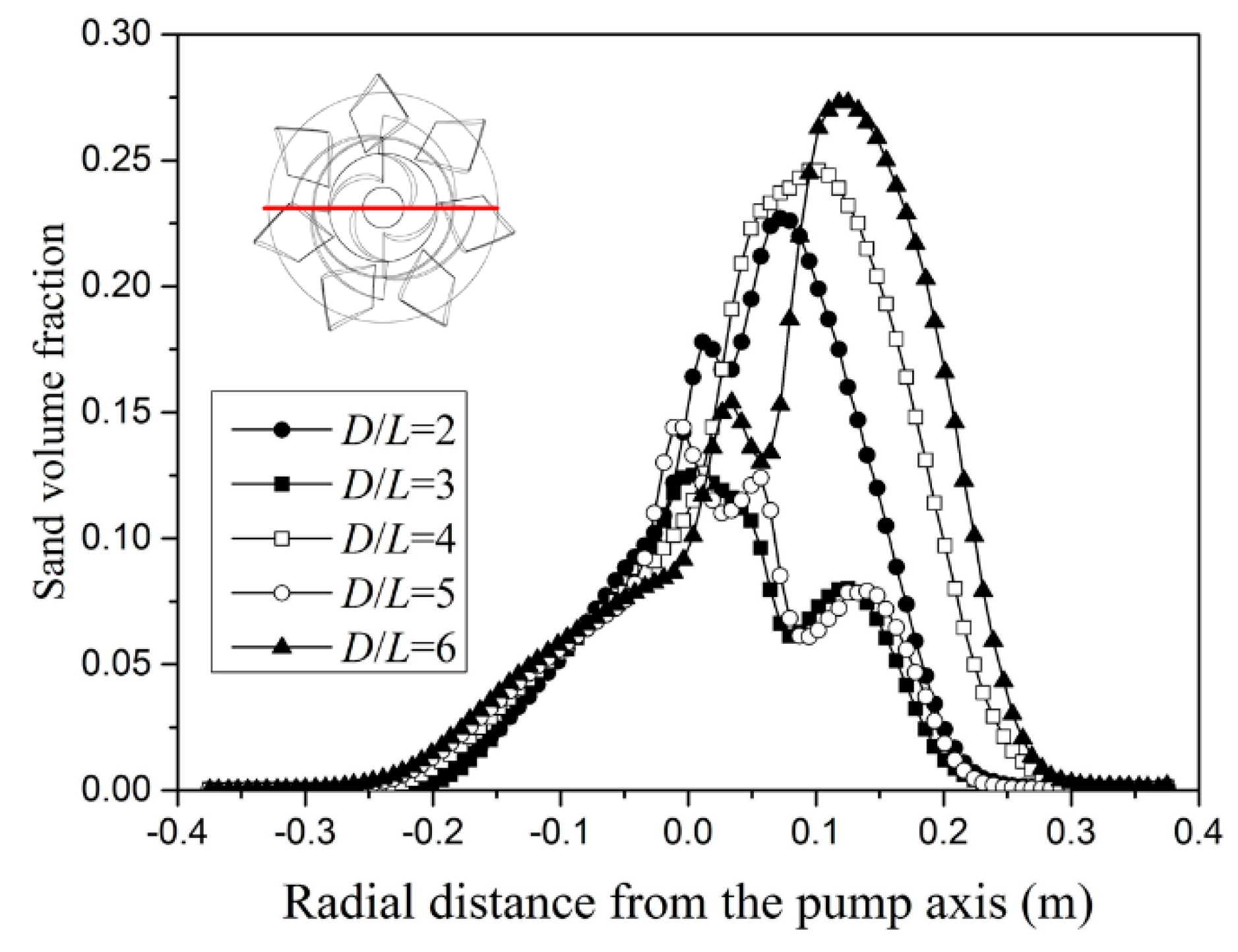
4.2. Distribution of Volume Fraction of Sand
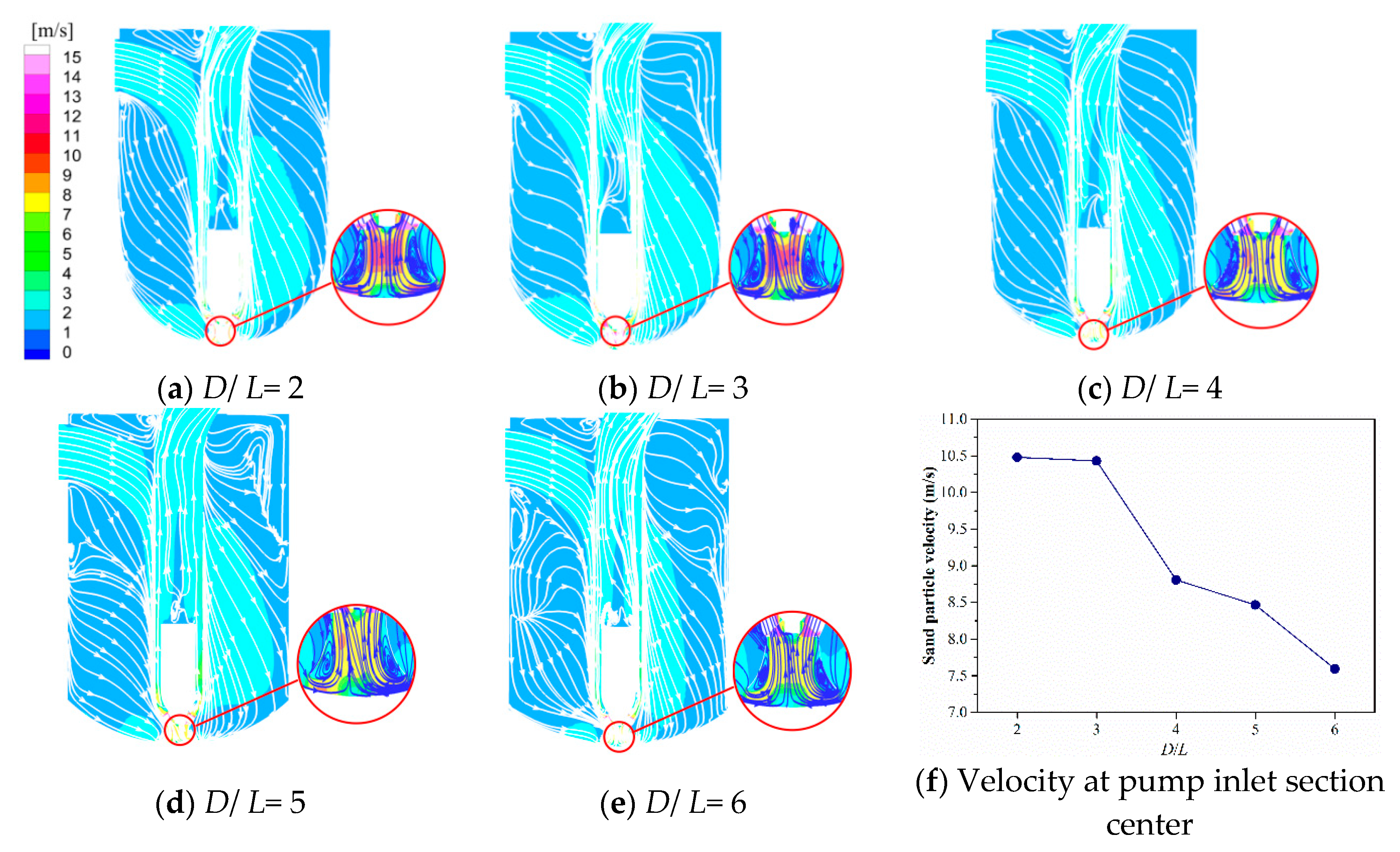
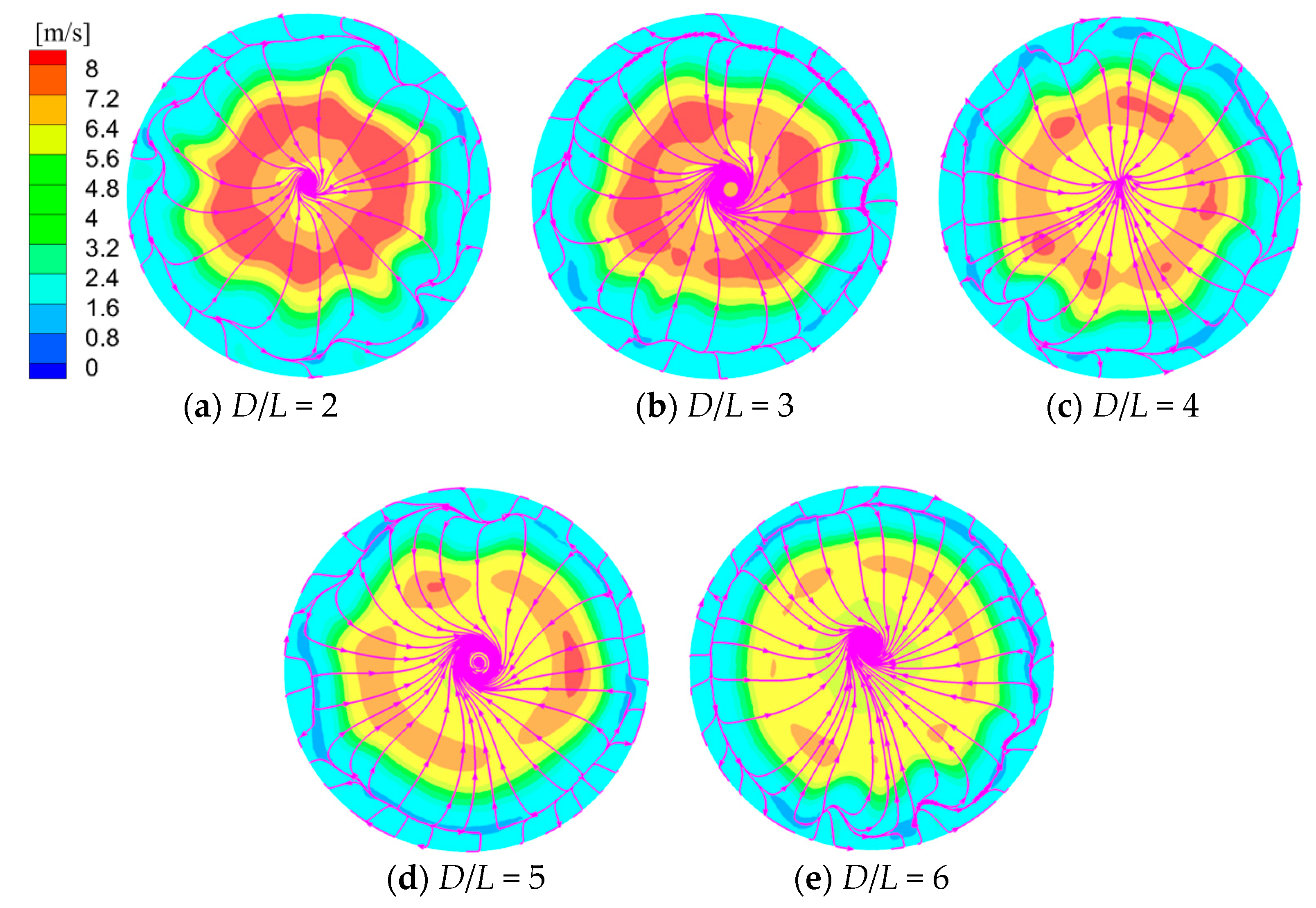
4.3. Velocity Distribution of Sand Particles
5. Conclusions
- Highly three-dimensional and non-uniform two-phase flow patterns in the prefabricated pumping station were revealed. The underlying mechanisms of sand particle sedimentation were explained from the flow aspect. The orientation of the tank inlet contributed to the high risk of sand deposition at the tank bottom side close to the tank inlet. Circumferential distribution of sand particles at the tank bottom was proved uneven.
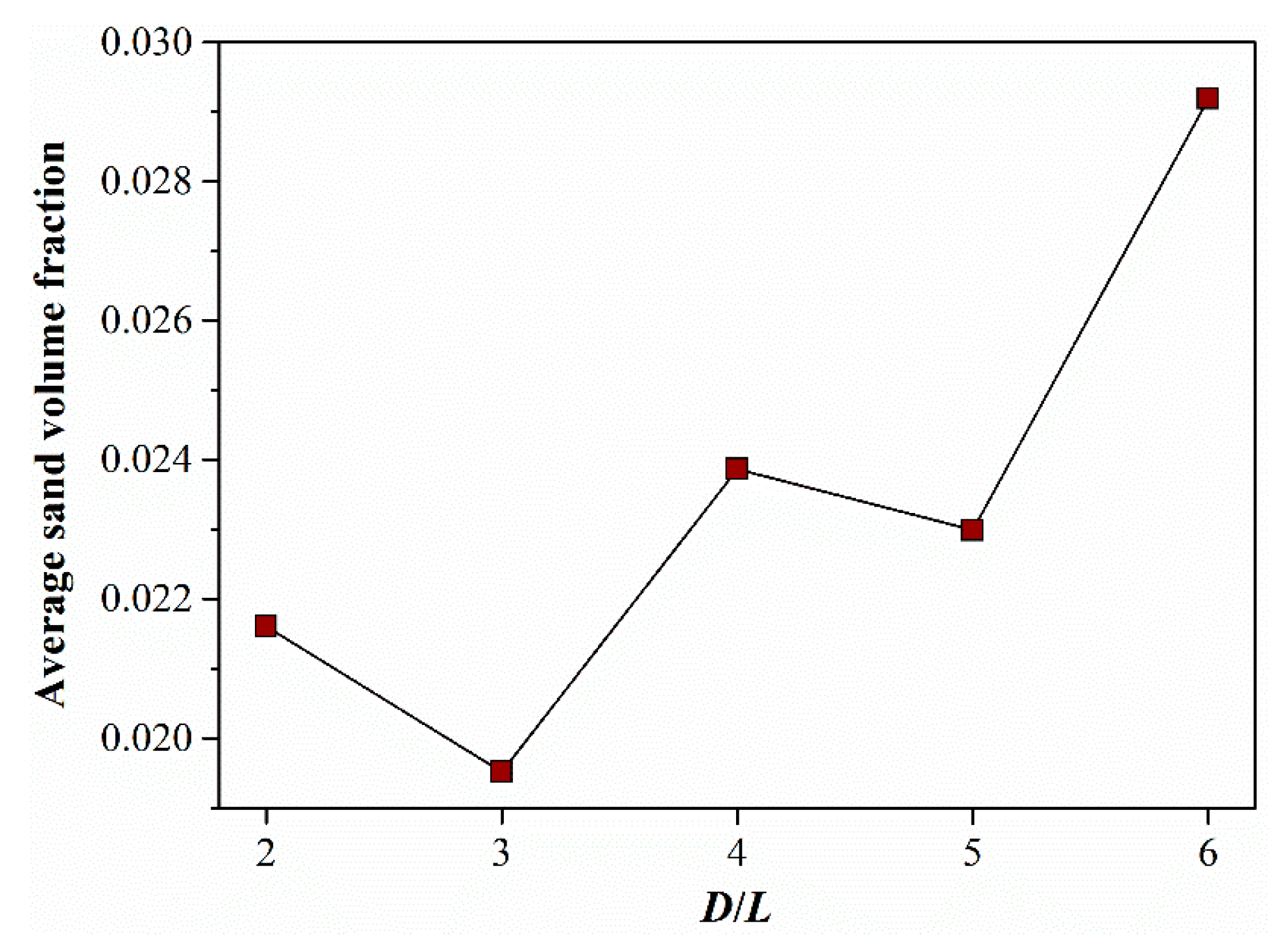
- The tank bottom geometry imposed a significant effect on the deposition of sand particles. Since the pump kept inhaling sand particles and imparting energy into them, a reasonable distribution of the sand volume fraction at the pump inlet was critical. Such a distribution varies considerably with D/L. The averaged sand volume fraction at the pump inlet reaches its minimum at D/L = 3, which signifies an efficient suction of sand particles.
- The motion of sand particles at the pump inlet should be sufficiently stimulated to restrict sand particle deposition. The sand particle velocity at the pump inlet decreased gradually with increasing D/L. The highest intensity of the large-scale vortex formed at the pump inlet arose at D/L = 3, which was also responsible for locally high sand particle velocity and active motion of sand particles. The best anti-sedimentation performance was attained at D/L = 3.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, H.; Jia, Y.; Niu, C. “Sponge city” concept helps solve China’s urban water problems. Environ. Earth Sci. 2017, 76, 473–477. [Google Scholar] [CrossRef]
- Zeferino, J.A.; Cunha, M.C.; Antunes, A.P. Adapted optimization model for planning regional wastewater systems: case study. Water Sci. Technol. 2017, 76, 1196–1205. [Google Scholar] [CrossRef]
- Li, Q.; Kang, C.; Li, M.Y. Flow features of a prefabricated pumping station operating under high flow rate conditions. Int. J. Fluid Mach. Syst. 2018, 11, 171–180. [Google Scholar] [CrossRef]
- Chen, H.X.; Guo, J.H. Numerical simulation of 3-D turbulent flow in the multi-intakes sump of the pump station. J. Hydrodyn. Ser. B 2007, 19, 42–47. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Z.; Zhu, Z.; Si, Q.; Li, Y. Entropy generation analysis for the cavitating head-drop characteristic of a centrifugal pump. P. I. Mech. Eng. C-J. Mec. 2018, 232, 4637–4646. [Google Scholar] [CrossRef]
- Teaima, I.R.; El-Gamal, T. Improving flow performance of irrigation pump station intake. J. Appl. Water Eng. Res. 2013, 1, 31–42. [Google Scholar] [CrossRef]
- Azimi, A.H.; Zhu, D.Z.; Rajaratnam, N. Computational investigation of vertical slurry jets in water. Int. J. Multiphas. Flow 2012, 47, 94–114. [Google Scholar] [CrossRef]
- Gandhi, B.K.; Singh, S.N.; Seshadri, V. Performance characteristics of centrifugal slurry pumps. J. Fluid. Eng.-T. ASME 2001, 123, 271–280. [Google Scholar] [CrossRef]
- Cheng, W.; Gu, B.; Shao, C.; Wang, Y. Hydraulic characteristics of molten salt pump transporting solid-liquid two-phase medium. Nucl. Eng. Des. 2017, 324, 220–230. [Google Scholar] [CrossRef]
- Lu, L.G. Basic flow patterns and optimum hydraulic design of a suction box of pumping station. J. Hydrodyn. Ser. B 2000, 12, 46–51. [Google Scholar]
- Cong, G.; Wang, F. Numerical investigation on the flow structure and vortex behavior at a large scale pump sump. In Proceedings of the ASME-JSME Joint Fluids Engineering Conference, San Diego, CA, USA, 30 July–2 August 2007. [Google Scholar]
- Tanweer, S.; Desmukh, V.K.G. Numerical study of flow behaviour in a multiple intake pump sump. Int. J. Adv. Eng. Technol. 2011, 2, 118–128. [Google Scholar]
- Li, W.; Zhong, W. CFD simulation of hydrodynamics of gas-liquid-solid three-phase bubble column. Powder Technol. 2015, 286, 766–788. [Google Scholar] [CrossRef]
- Virdung, T.; Rasmuson, A. Hydrodynamic properties of a turbulent confined solid-liquid jet evaluated using PIV and CFD. Chem. Eng. Sci. 2007, 62, 5963–5978. [Google Scholar] [CrossRef]
- Zhou, W.; Zhao, Z.; Lee, T.S.; Winoto, S.H. Investigation of flow through centrifugal pump impellers using computational fluid dynamics. Int. J. Rotating Mach. 2007, 9, 49–61. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Rocha, P.A.C.; Rocha, H.H.B.; Carneiro, F.O.M.; Vieira da Silva, M.E.; Bueno, A.V. k–ω SST (shear stress transport) turbulence model calibration: A case study on a small scale horizontal axis wind turbine. Energy 2014, 65, 412–418. [Google Scholar] [CrossRef]
- Isaev, S.A.; Baranov, P.A.; Zhukova, Y.V.; Usachov, A.E.; Kharchenko, V.B. Correction of the shear-stress-transfer model with account of the curvature of streamlines in calculating separated flows of an incompressible viscous fluid. J. Eng. Phys. Thermophys. 2014, 87, 1002–1015. [Google Scholar] [CrossRef]
- Kim, H.J.; Park, S.W.; Rhee, D.S. Numerical analysis of the effects of anti-vortex device height on hydraulic performance of pump sump. KSCE J. Civ. Eng. 2017, 21, 1484–1492. [Google Scholar] [CrossRef]
- Moshfeghi, M.; Song, Y.J.; Xie, Y.H. Effects of near-wall grid spacing on SST k-ω model using NREL Phase VI horizontal axis wind turbine. J. Wind Eng. Ind. Aerod. 2012, 107–108, 94–105. [Google Scholar] [CrossRef]
- Messa, G.V.; Ferrarese, G.; Malavasi, S. A mixed Euler–Euler/Euler–Lagrange approach to erosion prediction. Wear 2015, 342–343, 138–153. [Google Scholar] [CrossRef]
- Azimi, A.H.; Zhu, D.Z.; Rajaratnam, N. Effect of particle size on the characteristics of sand jets in water. J. Eng. Mech. 2011, 137, 822–834. [Google Scholar] [CrossRef]
- Duarte, C.R.; Murata, V.V.; Barrozo, M.A.S. A study of the fluid dynamics of the spouted bed using CFD. Braz. J. Chem. Eng. 2005, 22, 263–270. [Google Scholar] [CrossRef]
- Shi, D.-P.; Luo, Z.-H.; Zheng, Z.-W. Numerical simulation of liquid-solid two-phase flow in a tubular loop polymerization reactor. Powder Technol. 2010, 198, 135–143. [Google Scholar] [CrossRef]
- Gómez, L.C.; Milioli, F.E. A numerical simulation analysis of the effect of the interface drag function on cluster evolution in a CFB riser gas-solid flow. Braz. J. Chem. Eng. 2004, 21, 569–583. [Google Scholar] [CrossRef]
- Xu, L.; Xia, Z.; Guo, X.; Chen, C. Application of population balance model in the simulation of slurry bubble column. Ind. Eng. Chem. Res. 2014, 53, 4922–4930. [Google Scholar] [CrossRef]
- Panneerselvam, R.; Savithri, S.; Surender, G.D. CFD simulation of hydrodynamics of gas-liquid-solid fluidised bed reactor. Chem. Eng. Sci. 2009, 64, 1119–1135. [Google Scholar] [CrossRef]
- Choi, J.W.; Choi, Y.D.; Kim, C.G.; Lee, Y.H. Flow uniformity in a multi-intake pump sump model. J. Mech. Sci. Technol. 2010, 24, 1389–1400. [Google Scholar] [CrossRef]
- Park, I.; Kim, H.-J.; Seong, H.; Rhee, D.S. Experimental studies on surface vortex mitigation using the floating anti-vortex device in sump pumps. Water 2018, 10, 441. [Google Scholar] [CrossRef]
- Kang, W.T.; Shin, B.R.; Doh, D.H. An effective shape of floor splitter for reducing sub-surface vortices in pump sump. J. Mech. Sci. Technol. 2014, 28, 175–182. [Google Scholar] [CrossRef]
- Kabiri-Samani, A.R.; Borghei, S.M. Effects of anti-vortex plates on air entrainment by free vortex. Sci. Iran. 2013, 20, 251–258. [Google Scholar]
- Ahmad, Z.; Jain, B.; Kumar, S.; Mittal, M.K. Rational design of a pump-sump and its model testing. J. Pipeline Syst. Eng. 2011, 2, 53–63. [Google Scholar] [CrossRef]
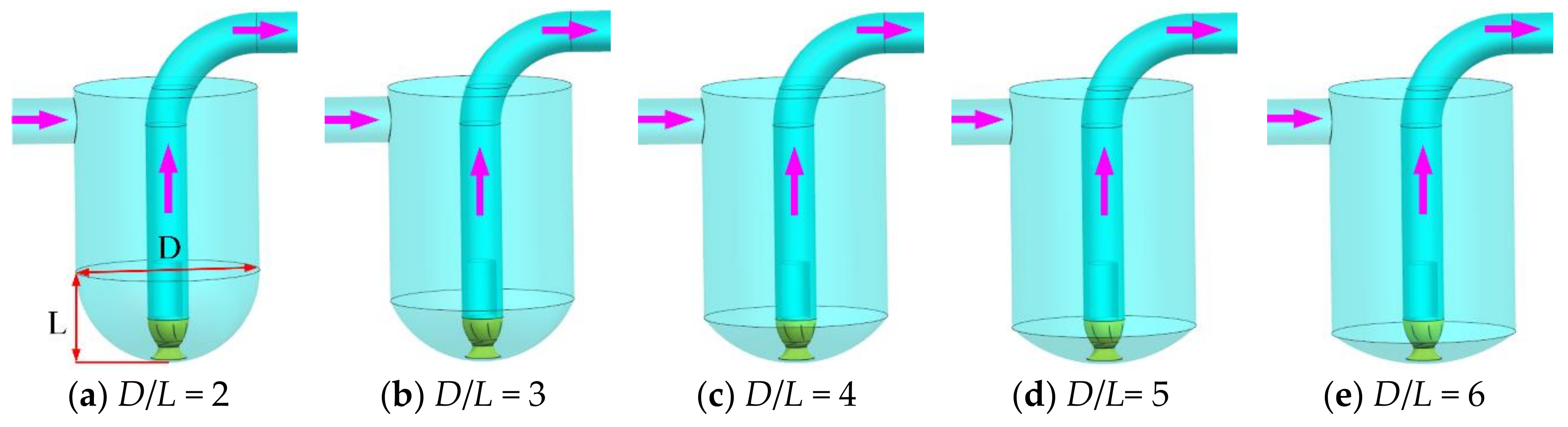


| Tank Scheme | D/L = 2 | D/L = 3 | D/L = 4 | D/L = 5 | D/L = 6 |
|---|---|---|---|---|---|
| Approximate grid number (×106) | 7.78 | 7.13 | 6.90 | 6.75 | 6.68 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Kang, C.; Teng, S.; Li, M. Optimization of Tank Bottom Shape for Improving the Anti-Deposition Performance of a Prefabricated Pumping Station. Water 2019, 11, 602. https://doi.org/10.3390/w11030602
Li Q, Kang C, Teng S, Li M. Optimization of Tank Bottom Shape for Improving the Anti-Deposition Performance of a Prefabricated Pumping Station. Water. 2019; 11(3):602. https://doi.org/10.3390/w11030602
Chicago/Turabian StyleLi, Qing, Can Kang, Shuang Teng, and Mingyi Li. 2019. "Optimization of Tank Bottom Shape for Improving the Anti-Deposition Performance of a Prefabricated Pumping Station" Water 11, no. 3: 602. https://doi.org/10.3390/w11030602
APA StyleLi, Q., Kang, C., Teng, S., & Li, M. (2019). Optimization of Tank Bottom Shape for Improving the Anti-Deposition Performance of a Prefabricated Pumping Station. Water, 11(3), 602. https://doi.org/10.3390/w11030602





