Analysis of Intra and Interseasonal Rainfall Variability and Its Effects on Pearl Millet Yield in a Semiarid Agroclimate: Significance of Scattered Fields and Tied Ridges
Abstract
1. Introduction
2. Materials and Methods
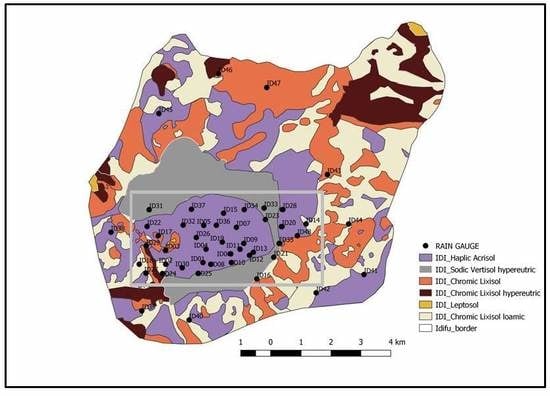
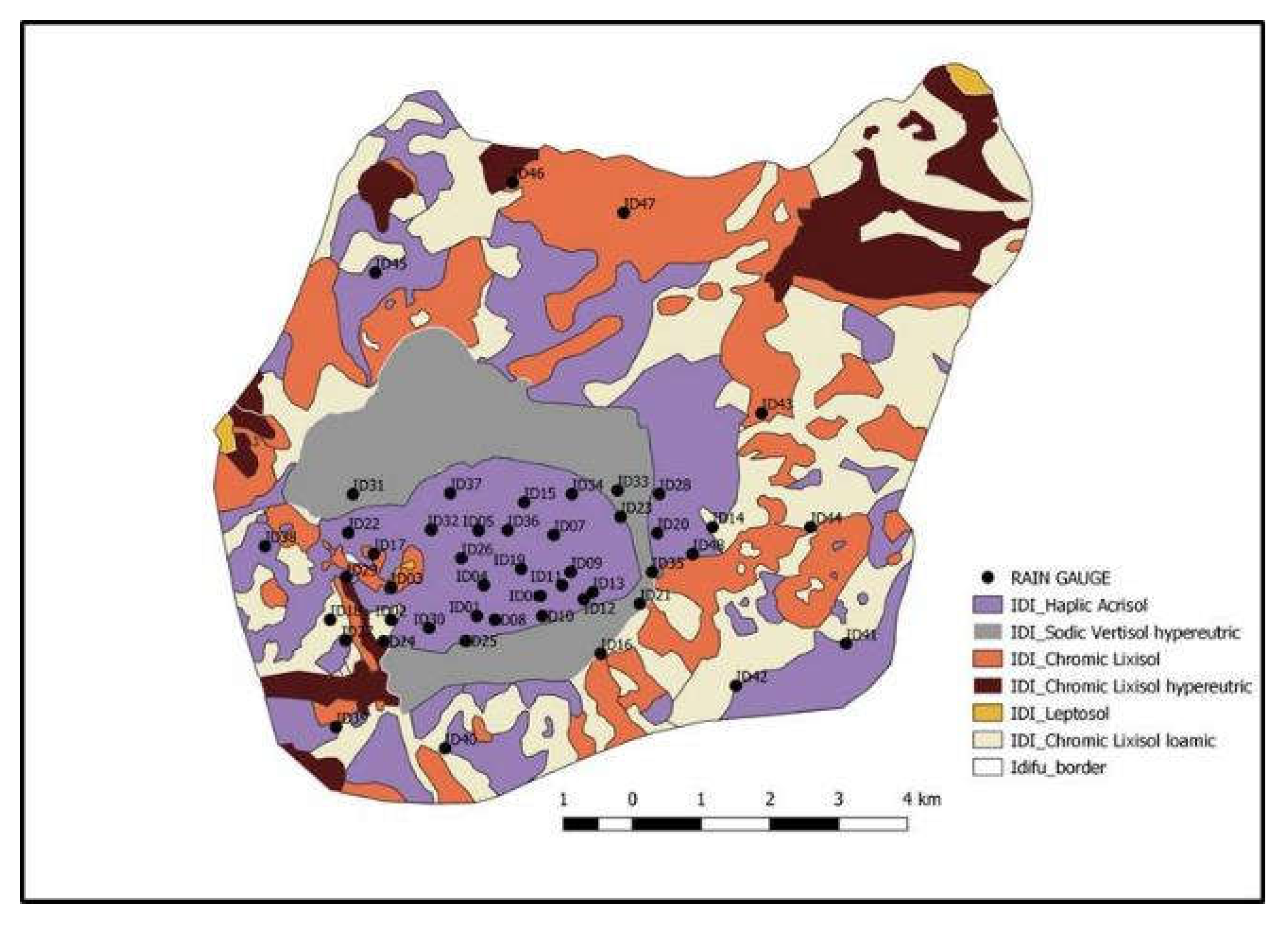
2.1. Study Area
2.2. Spatiotemporal Rainfall Data Collection
2.3. Pearl Millet Yield Data
2.4. Soil Physical and Chemical Properties
2.5. Data Analysis
3. Results
3.1. Spatiotemporal Rainfall Variability
3.1.1. Average Daily Rainfall and Variability
3.1.2. Seasonal Rainfall Variability
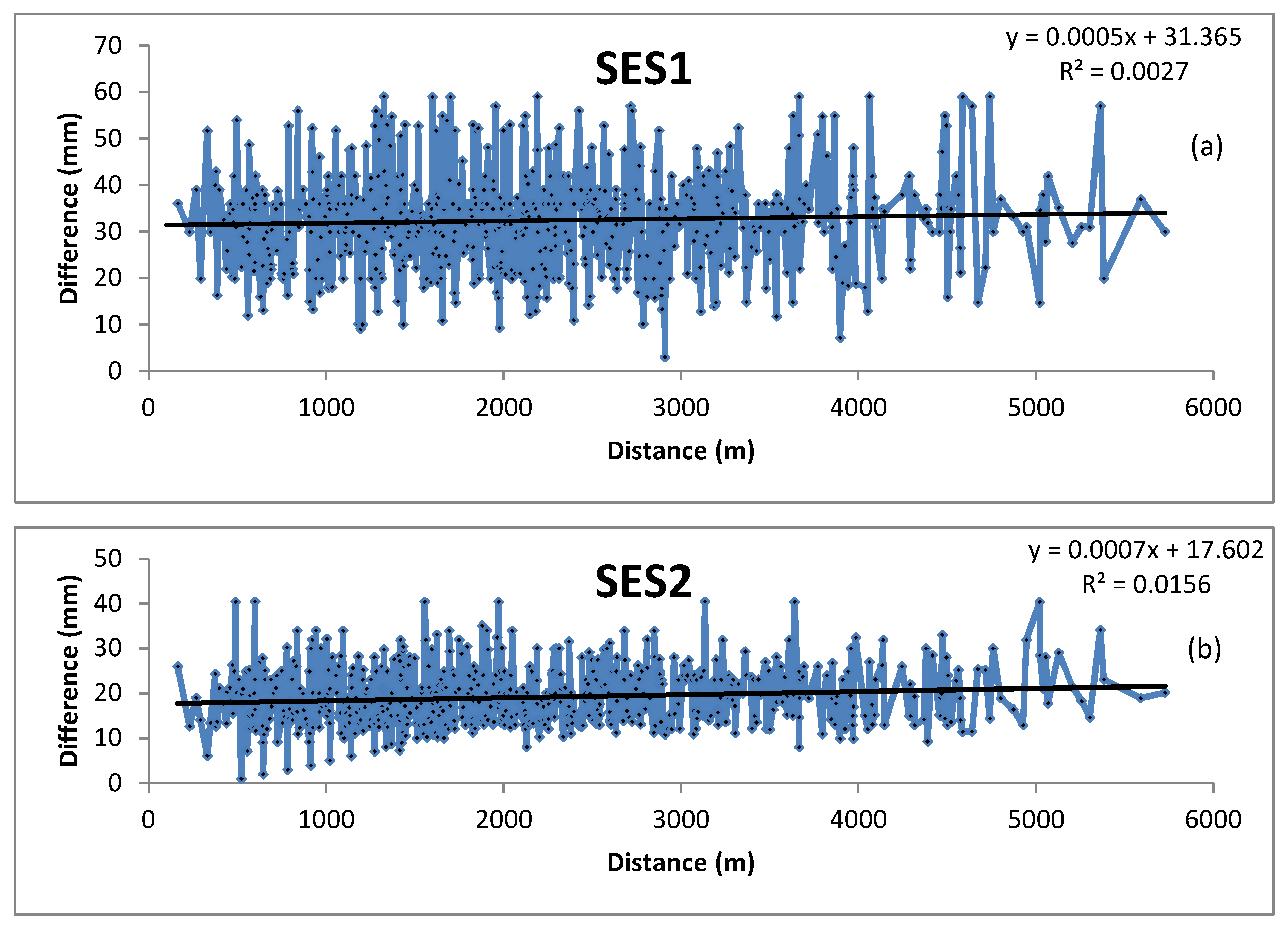
3.1.3. Rainfall Variability with Distance between Pairs of Gauges
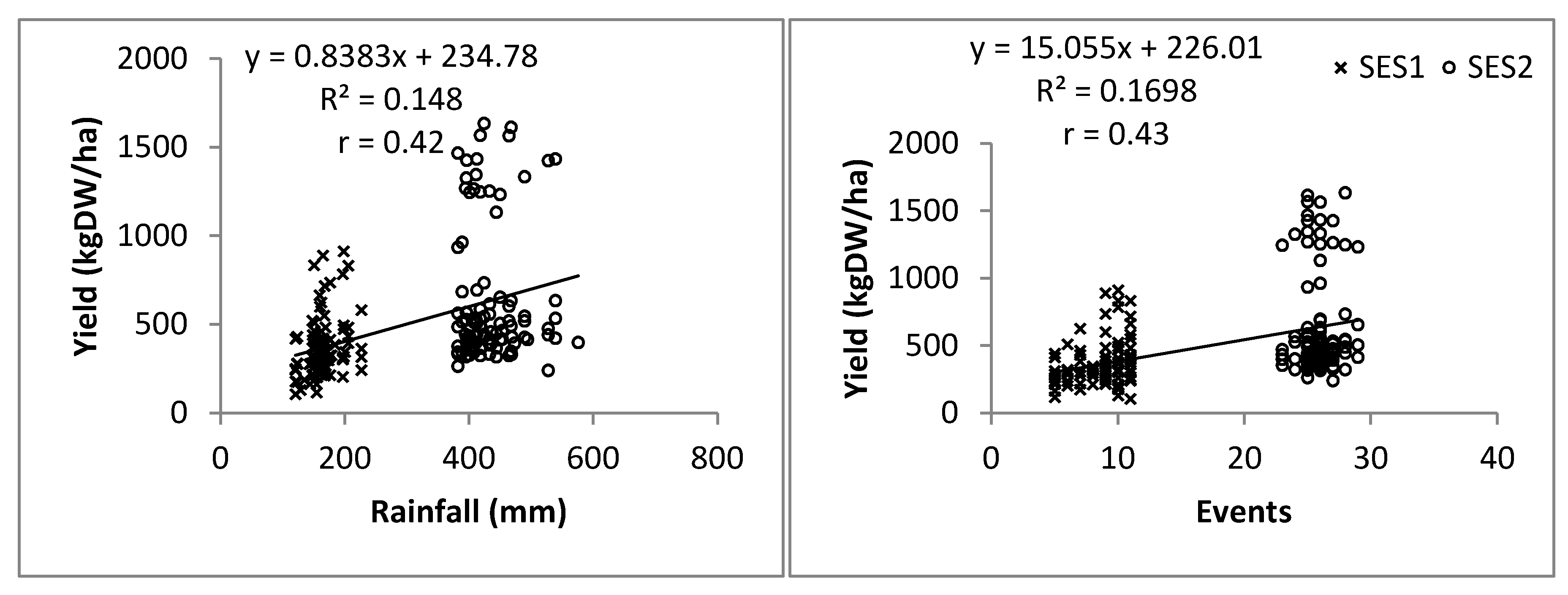
3.2. Effects of Spatiotemporal Rainfall Variability on Pearl Millet Grain Yield
3.3. Yield Variability by Soil and the Influence of the Tied Ridge Management Strategy
3.3.1. Yield Variations among Soil Types
3.3.2. Yield Variations between Flat and Tied Ridge Cultivations
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| SES1 | SES2 | |||||
|---|---|---|---|---|---|---|
| Distance (m) | Direction Angle (Degrees) | Difference | Variance | Covariance | Variance | Covariance |
| 164.45 | 52.34 | 0.2 | 0 | 4915.2 | 1346.9 | 68.6 |
| 231.71 | 212.44 | 29.3 | 858.5 | 2182.3 | 46.9 | 42.9 |
| 267.29 | 102.11 | 40.8 | 1664.6 | −43.3 | 262.4 | 165.9 |
| 292.97 | 175.98 | 11.8 | 139.2 | 161.4 | 324 | −43.6 |
| 329.77 | 198.87 | 15.6 | 243.4 | 549.7 | 22.6 | 307.9 |
| 347.02 | 63.96 | 26.2 | 686.4 | 278.2 | 46.9 | −11.4 |
| 374.59 | 122.58 | 35.9 | 1288.8 | 2408.7 | 1802 | −152.7 |
| 377.54 | 143.34 | 11.5 | 132.3 | 449.1 | 4.8 | 1662.1 |
| 386.54 | 353.24 | 73.1 | 5343.6 | −1093.8 | 228 | 15.8 |
| 397.86 | 203.91 | 16.1 | 259.2 | 2216.1 | 14.4 | 23.6 |
| 423.08 | 89.43 | 53 | 2809 | −81.8 | 691.7 | 305.2 |
| 437.56 | 132.71 | 6.4 | 41 | 4453.1 | 158.8 | −19.3 |
| 440.94 | 154.28 | 6.6 | 43.6 | 4465.8 | 2430.5 | −416.3 |
| 457.18 | 102.79 | 35.7 | 1274.5 | 2401.9 | 33.1 | −7.1 |
| 460.1 | 12.72 | 55.5 | 3080.3 | −627.1 | 5700.3 | −486.7 |
| 470.28 | 210.79 | 15.2 | 231 | 26.7 | 858.5 | 331.4 |
| 473.97 | 0.31 | 39.6 | 1568.2 | 955.5 | 22.6 | 162.3 |
| 477.42 | 211.69 | 93.5 | 8742.3 | −2163.9 | 2672.9 | −584.2 |
| 482.79 | 309.53 | 59.4 | 3528.4 | 1233.1 | 5.5 | 127.3 |
| 483.99 | 324.16 | 95.1 | 9044 | −705.4 | 27 | 23.3 |
| 488.99 | 216.32 | 164.9 | 27,192 | −5072.3 | 81 | 153.6 |
| 495.36 | 21.24 | 16.1 | 259.2 | 603.9 | 3058.1 | −760.3 |
Appendix B
References
- Granados, R.; Soria, J.; Cortina, M. Rainfall variability, rainfed agriculture and degree of human marginality in North Guanajuato, Mexico. Singap. J. Trop. Geogr. 2017, 38, 153–166. [Google Scholar] [CrossRef]
- Bayu, W.; Rethman, N.F.G.; Hammes, P.S. Effects of tied-ridge, nitrogen fertilizer and cultivar on the yield and nitrogen use efficiency of sorghum in semi-arid Ethiopia. Arch. Agron. Soil Sci. 2012, 58, 547–560. [Google Scholar] [CrossRef]
- van Ittersum, M.K.; Cassman, K.G.; Grassini, P.; Wolf, J.; Tittonell, P.; Hochman, Z. Yield gap analysis with local to global relevance—A review. Field Crops Res. 2013, 143, 4–17. [Google Scholar] [CrossRef]
- Hoffmann, M.P.; Haakana, M.; Asseng, S.; Höhn, J.G.; Palosuo, T.; Ruiz-Ramos, M.; Fronzek, S.; Ewert, F.; Gaiser, T.; Kassie, B.T.; et al. How does inter-annual variability of attainable yield affect the magnitude of yield gaps for wheat and maize? An analysis at ten sites. Agric. Syst. 2017. [Google Scholar] [CrossRef]
- Rockstrom, J. Making the best of climatic variability: Options for upgrading rainfed farming in water scarce regions. Water Sci. Technol. 2004, 49, 151–156. [Google Scholar] [CrossRef] [PubMed]
- Vanacker, V.; Linderman, M.; Lupo, F.; Flasse, S.; Lambin, E. Impact of short-term rainfall fluctuation on interannual land cover change in sub-Saharan Africa. Glob. Ecol. Biogeogr. 2005, 14, 123–135. [Google Scholar] [CrossRef]
- Cooper, P.J.M.; Dimes, J.; Rao, K.P.C.; Shapiro, B.; Shiferaw, B.; Twomlow, S. Coping better with current climatic variability in the rain-fed farming systems of sub-Saharan Africa: An essential first step in adapting to future climate change? Agric. Ecosyst. Environ. 2008, 126, 24–35. [Google Scholar] [CrossRef]
- Waongo, M.; Laux, P.; Kunstmann, H. Adaptation to climate change: The impacts of optimized planting dates on attainable maize yields under rainfed conditions in Burkina Faso. Agric. For. Meteorol. 2015, 205, 23–39. [Google Scholar] [CrossRef]
- Sithole, N.J.; Magwaza, L.S.; Mafongoya, P.L. Conservation agriculture and its impact on soil quality and maize yield: A South African perspective. Soil Tillage Res. 2016, 162, 55–67. [Google Scholar] [CrossRef]
- Bekele, D.; Alamirew, T.; Kebede, A.; Zeleke, G.; Melese, A.M. Analysis of rainfall trend and variability for agricultural water management in Awash River Basin, Ethiopia. J. Water Clim. Chang. 2017, 8, 127–141. [Google Scholar] [CrossRef]
- Wang, X.C.; Qadir, M.; Rasul, F.; Yang, G.T.; Hu, Y.G. Response of Soil Water and Wheat Yield to Rainfall and Temperature Change on the Loess Plateau, China. Agronomy 2018, 8, 101. [Google Scholar] [CrossRef]
- Graef, F.; Haigis, J. Spatial and temporal rainfall variability in the Sahel and its effects on farmers’ management strategies. J. Arid Environ. 2001, 48, 221–231. [Google Scholar] [CrossRef]
- Satyanarayana, P.; Srinivas, V.V. Regional frequency analysis of precipitation using large-scale atmospheric variables. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Batisani, N.; Yarnal, B. Rainfall variability and trends in semi-arid Botswana: Implications for climate change adaptation policy. Appl. Geogr. 2010, 30, 483–489. [Google Scholar] [CrossRef]
- Nasseri, M.; Zahraie, B. Application of simple clustering on space-time mapping of mean monthly rainfall pattern. Int. J. Climatol. 2011, 31, 732–741. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, L. Rainfall feature extraction using cluster analysis and its application on displacement prediction for a cleavage-parallel landslide in the Three-Gorges Reservoir area. Nat. Hazards Earth Syst. Sci. Discuss. 2016, 1–15. [Google Scholar] [CrossRef]
- Silungwe, F.R.; Graef, F.; Bellingrath-Kimura, S.D.; Tumbo, S.D.; Kahimba, F.C.; Lana, M.A. Crop Upgrading Strategies and Modelling for Rainfed Cereals in a Semi-Arid Climate—A Review. Water 2018, 10, 356. [Google Scholar] [CrossRef]
- Munishi, P.K.T. Analysis of Climate Change and its Impacts on Productive Sectors, Particularly Agriculture in Tanzania; Sokoine University of Agriculture: Morogoro, Tanzania, 2009; p. 72. [Google Scholar]
- Kassile, T. Trend Analysis of Monthly Rainfall Data in Central Zone. J. Math. Stat. 2013, 9, 1–11. [Google Scholar] [CrossRef]
- Mkonda, M.Y.; He, X.H. Are Rainfall and Temperature Really Changing? Farmer’s Perceptions, Meteorological Data, and Policy Implications in the Tanzanian Semi-Arid Zone. Sustainability 2017, 9, 1412. [Google Scholar] [CrossRef]
- Maestrini, B.; Basso, B. Drivers of within-field spatial and temporal variability of crop yield across the US Midwest. Sci. Rep. 2018, 8, 14833. [Google Scholar] [CrossRef]
- Falconnier, G.N.; Descheemaeker, K.; Van Mourik, T.A.; Giller, K.E. Unravelling the causes of variability in crop yields and treatment responses for better tailoring of options for sustainable intensification in southern Mali. Field Crops Res. 2016, 187, 113–126. [Google Scholar] [CrossRef]
- Kahimba, F.C.; Mbaga, S.; Mkoko, B.; Swai, E.; Kimaro, A.A.; Mpanda, M.; Liingilie, A.; Germer, J. Analysing the Current Situation Regarding Biophysical Conditions and Rainfed Crop, Livestock- and Agroforestry Systems: A Baseline Report; 031A249A; Trans-SEC Consortium: Müncheberg, Germany, 2015; p. 42. [Google Scholar]
- URT. National Sample Census of Agriculture 2007/2008 Small Holder Agriculture: Regional Report—Dodoma Region “[Volume Va],” United Republic of Tanzania; Regional Administration and Local Governments: Dodoma, Tanzania, 2012; p. 319.
- Li, Y.; Wu, H. A Clustering Method Based on K-Means Algorithm. Phys. Procedia 2012, 25, 1104–1109. [Google Scholar] [CrossRef]
- Reinhardt, N.; Herrmann, L. Fusion of indigenous knowledge and gamma spectrometry for soil mapping to support knowledge-based extension in Tanzania. Food Secur. 2017, 9, 1271–1284. [Google Scholar] [CrossRef]
- Chan, Y.; Walmsley, R.P. Learning and Understanding the Kruskal-Wallis One-Way Analysis of Variance-by-Ranks Test for Differences Among Three or More Independent Groups. Phys. Ther. 1997, 77, 1755–1762. [Google Scholar] [CrossRef] [PubMed]
- Sucozhañay, A.; Célleri, R. Impact of Rain Gauges Distribution on the Runoff Simulation of a Small Mountain Catchment in Southern Ecuador. Water 2018, 10, 1169. [Google Scholar]
- Buytaert, W.; Celleri, R.; Willems, P.; De Bievre, B.; Wyseure, G. Spatial and temporal rainfall variability in mountainous areas: A case study from the south Ecuadorian Andes. J. Hydrol. 2006, 329, 413–421. [Google Scholar] [CrossRef]
- Gao, R.Z.; Li, F.L.; Wang, X.X.; Liu, T.X.; Du, D.D.; Bai, Y. Spatiotemporal variations in precipitation across the Chinese Mongolian plateau over the past half century. Atmos. Res. 2017, 193, 204–215. [Google Scholar] [CrossRef]
- Akponikpe, P.B.; Minet, J.; Gérard, B.; Defourny, P.; Bielders, C.L. Spatial fields’ dispersion as a farmer strategy to reduce agro-climatic risk at the household level in pearl millet-based systems in the Sahel: A modeling perspective. Agric. For. Meteorol. 2011, 151, 215–227. [Google Scholar] [CrossRef]
- Bagayoko, M.; Maman, N.; Palé, S.; Sirifi, S.; Taonda, S.; Traore, S.; Mason, S. Microdose and N and P fertilizer application rates for pearl millet in West Africa. Afr. J. Agric. Res. 2011, 6, 1141–1150. [Google Scholar]
- Stein, A.; Brouwer, J.; Bouma, J. Methods for comparing spatial variability patterns of millet yield and soil data. Soil Sci. Soc. Am. J. 1997, 61, 861–870. [Google Scholar] [CrossRef]
- Usowicz, B.; Lipiec, J. Spatial variability of soil properties and cereal yield in a cultivated field on sandy soil. Soil Tillage Res. 2017, 174, 241–250. [Google Scholar] [CrossRef]
- Miller, M.P.; Singer, M.J.; Nielsen, D.R. Spatial variability of wheat yield and soil properties on complex hills. Soil Sci. Soc. Am. J. 1988, 52, 1133–1141. [Google Scholar] [CrossRef]
- Cox, M.; Gerard, P.; Wardlaw, M.; Abshire, M. Variability of selected soil properties and their relationships with soybean yield. Soil Sci. Soc. Am. J. 2003, 67, 1296–1302. [Google Scholar] [CrossRef]
- Belay, A.; Gebrekidan, H.; Uloro, Y. Effect of tied ridges on grain yield response of Maize (Zea mays L.) to application of crop residue and residual N and P on two soil types at Alemaya, Ethiopia. S. Afr. J. Plant Soil 1998, 15, 123–129. [Google Scholar] [CrossRef]
- Wright, J.P.; Posner, J.L.; Doll, J.D. The effect of tied ridge cultivation on the yield of maize and a maize cowpea relay in the gambia. Exp. Agric. 1991, 27, 269–279. [Google Scholar] [CrossRef]
- Mesfin, T.; Tesfahunegn, G.B.; Wortmann, C.S.; Nikus, O.; Mamo, M. Tied-ridging and fertilizer use for sorghum production in semi-arid Ethiopia. Nutr. Cycl. Agroecosyst. 2009, 85, 87–94. [Google Scholar] [CrossRef]
- Kiboi, M.N.; Ngetich, K.F.; Diels, J.; Mucheru-Muna, M.; Mugwe, J.; Mugendi, D.N. Minimum tillage, tied ridging and mulching for better maize yield and yield stability in the Central Highlands of Kenya. Soil Tillage Res. 2017, 170, 157–166. [Google Scholar] [CrossRef]
- Lana, M.A.; Vasconcelos, A.C.F.; Gornott, C.; Schaffert, A.; Bonatti, M.; Volk, J.; Graef, F.; Kersebaum, K.C.; Sieber, S. Is dry soil planting an adaptation strategy for maize cultivation in semi-arid Tanzania? Food Secur. 2018, 10, 897–910. [Google Scholar] [CrossRef]

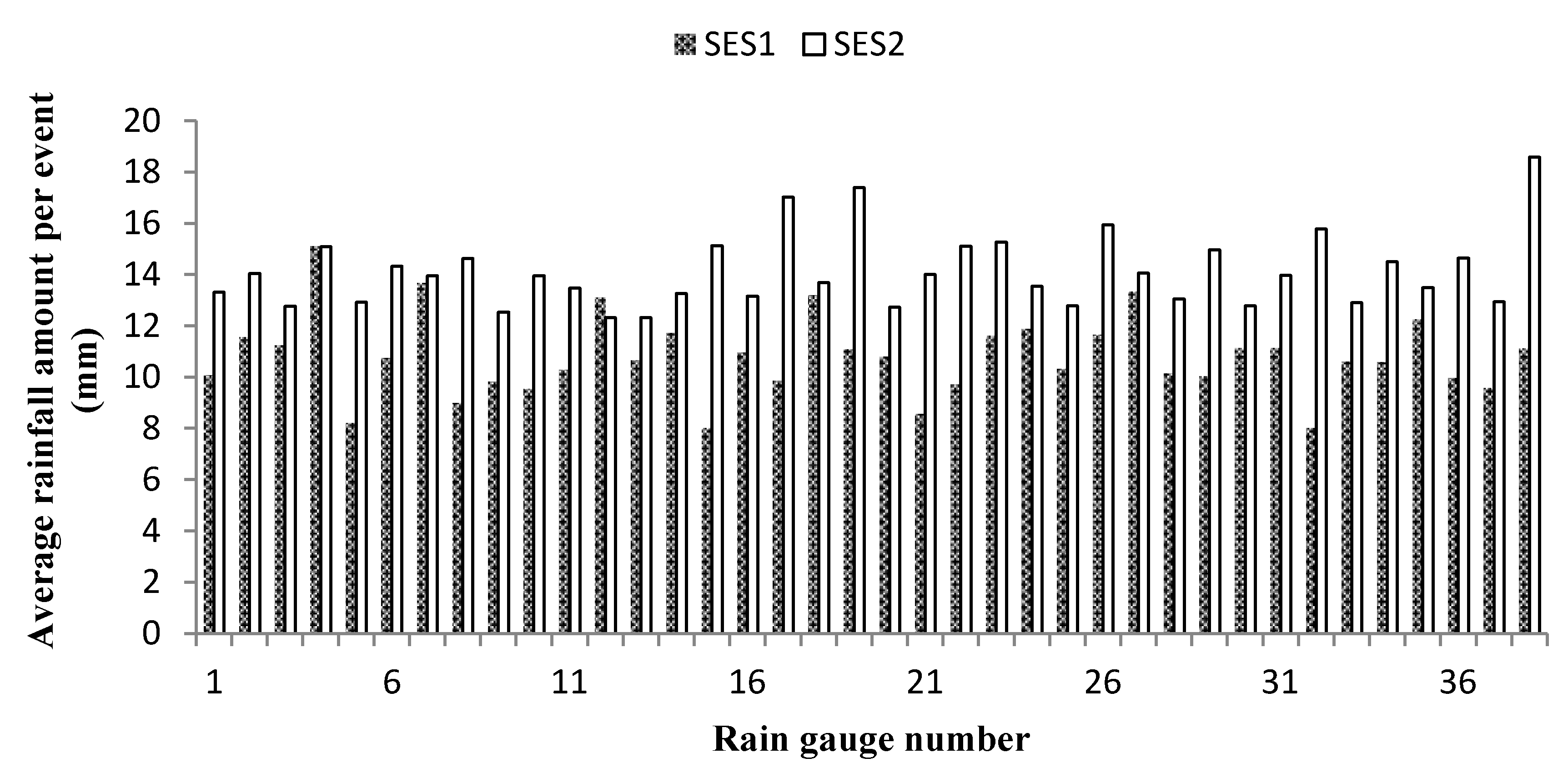
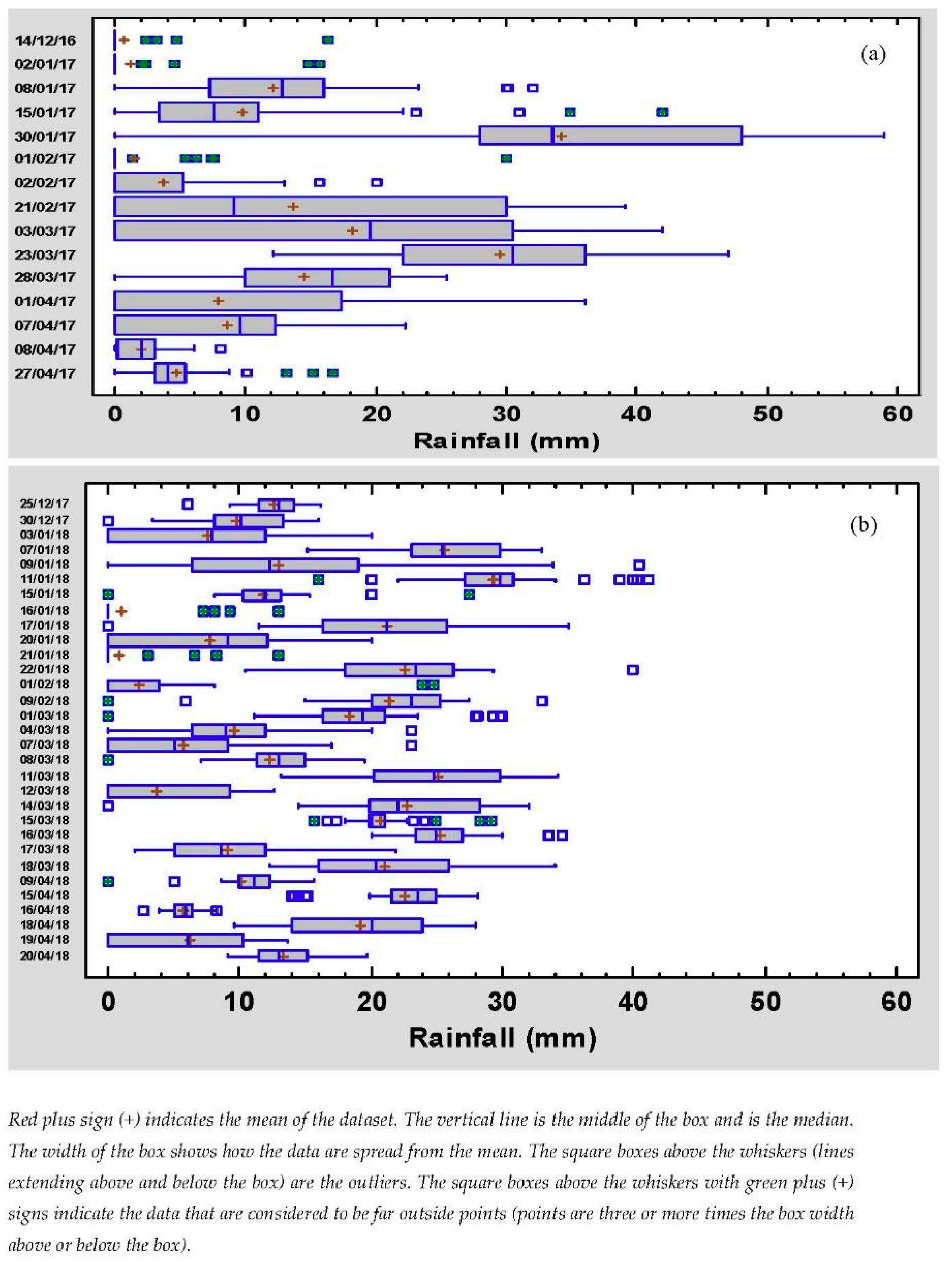
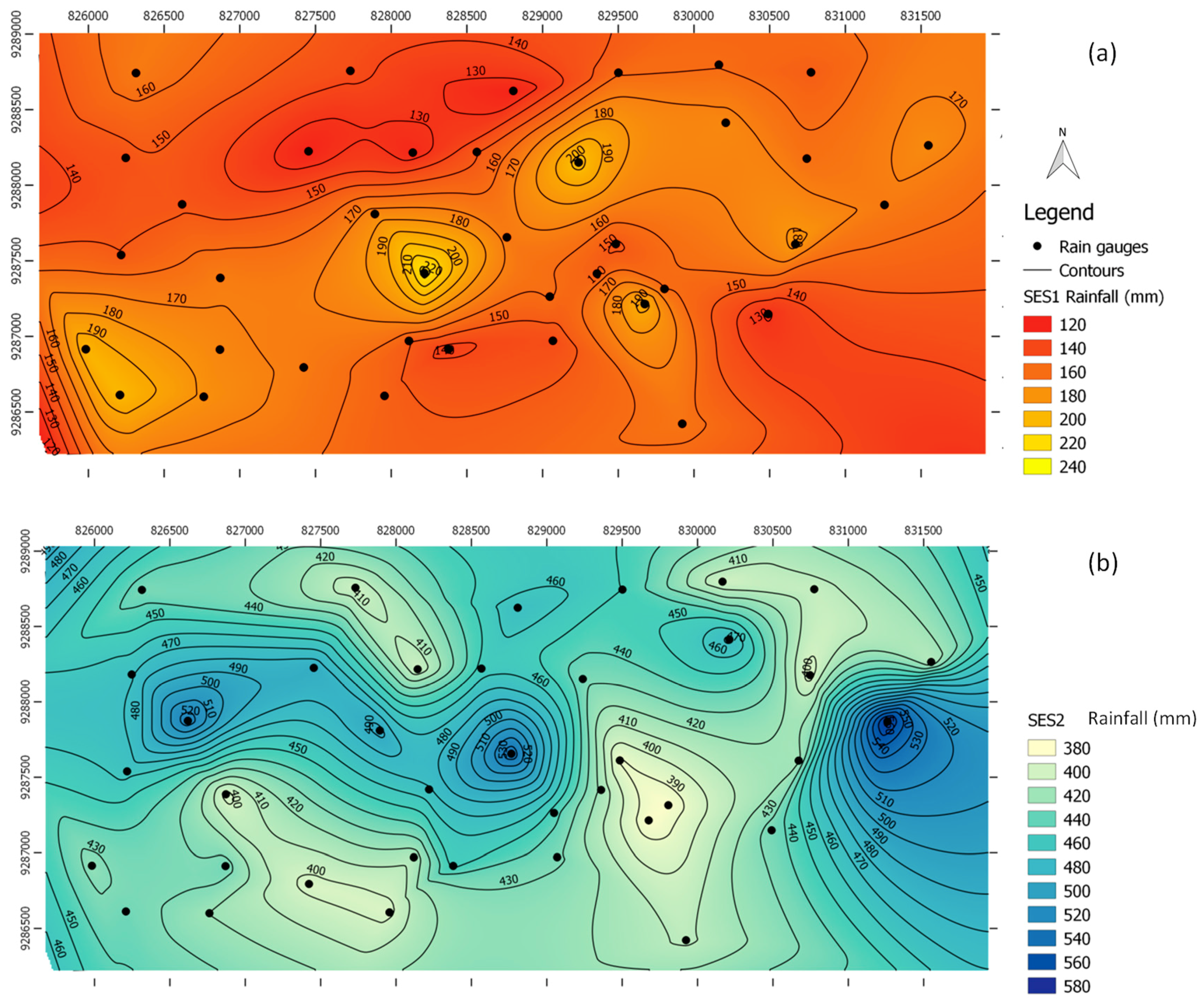
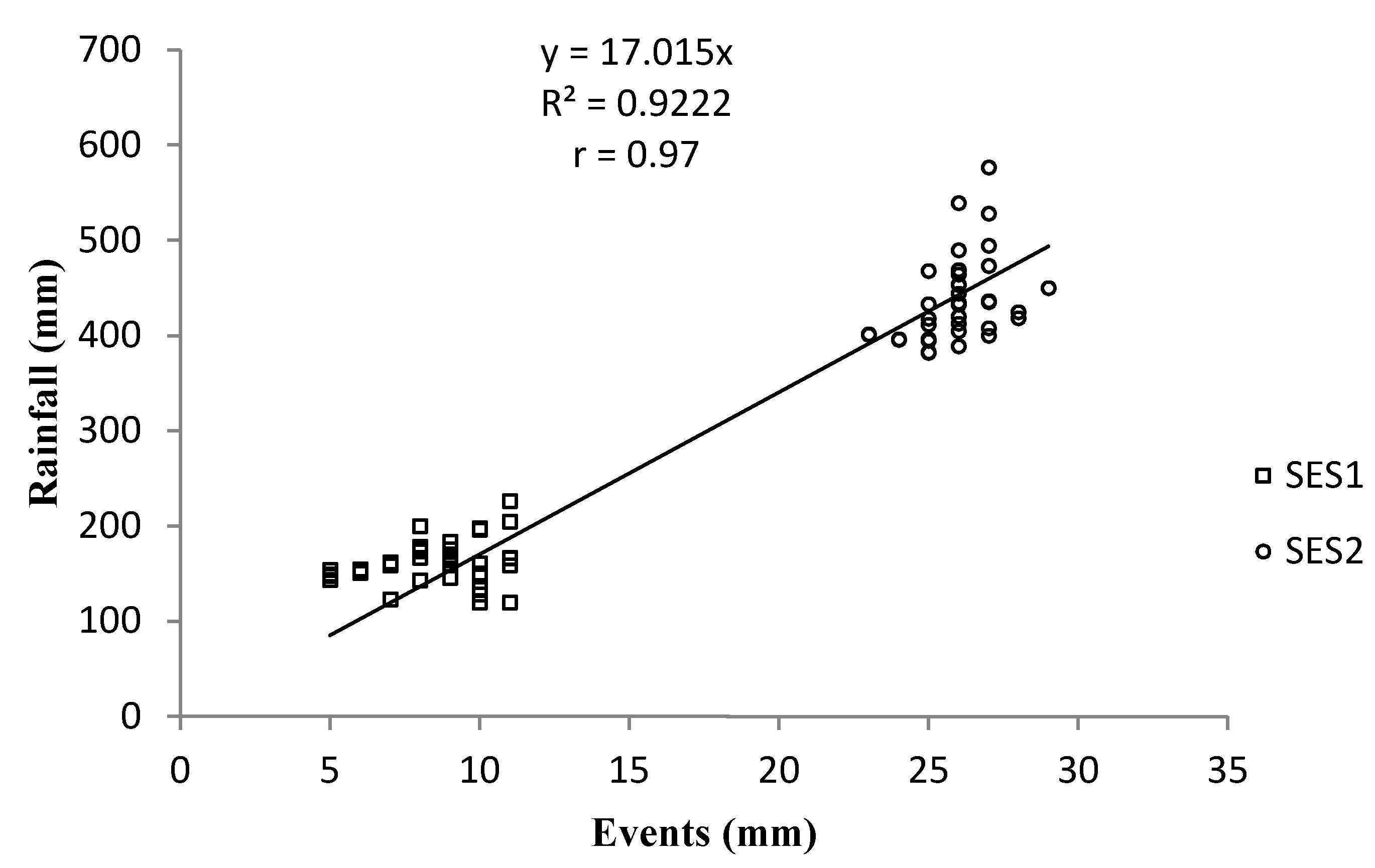
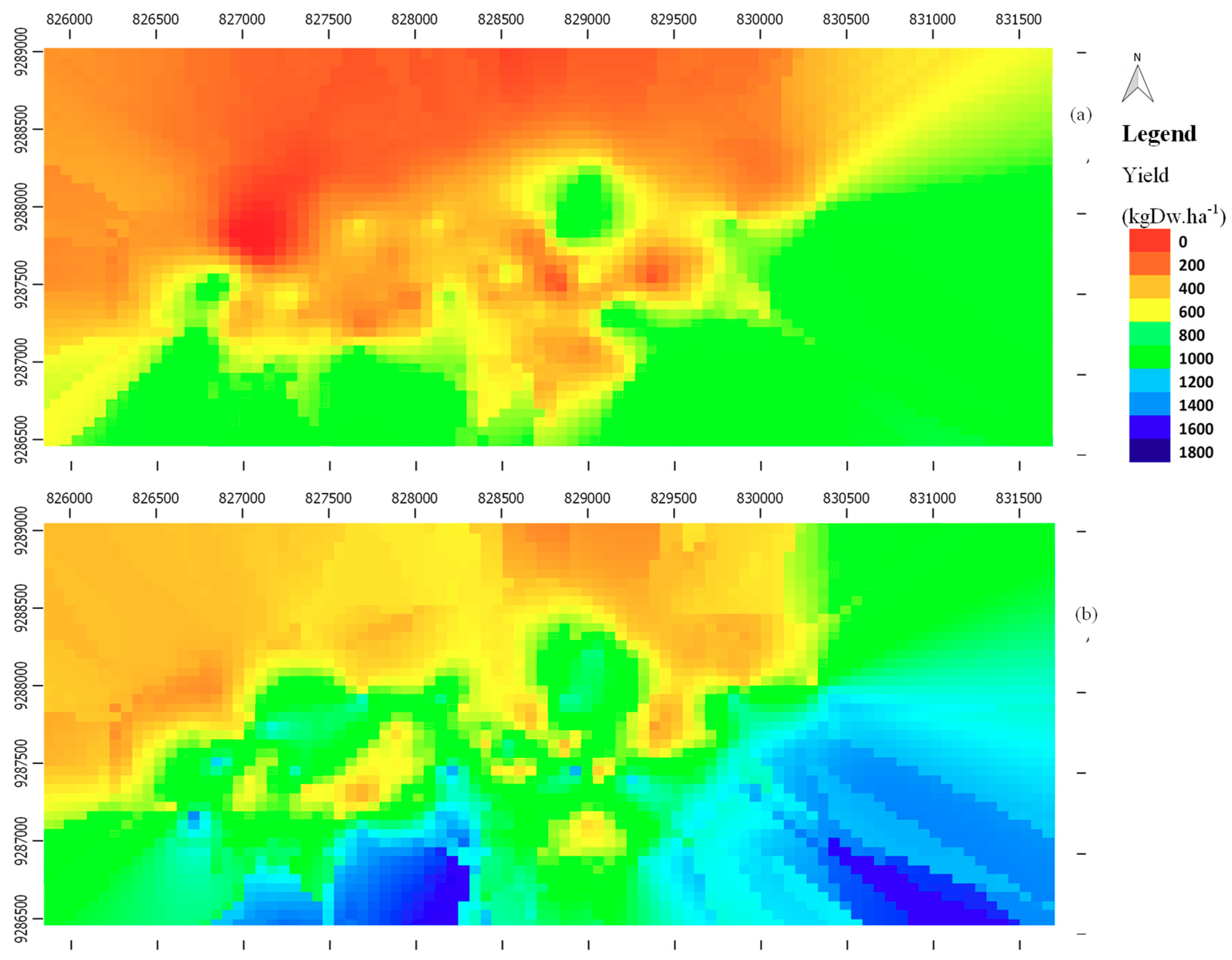
| Season | No. of Gauges | Average (mm) | SD (mm) | CV (%) | Minimum (mm) | Maximum (mm) | p-Value (within) | p-Value (between) |
|---|---|---|---|---|---|---|---|---|
| SES1 | 38 | 10.79 | 1.56 | 14.5 | 8.0 | 15.1 | 0.00 * | 0.00 * |
| SES2 | 38 | 14.11 | 1.44 | 10.2 | 12.3 | 18.6 | 0.00 * |
| Season | No. of Gauges | Average Number of Events | P100 | P50 |
|---|---|---|---|---|
| SES1 | 38 | 9 | 0.00 | 0.42 |
| SES2 | 38 | 25 | 0.56 | 0.87 |
| Season | No. of Plots | Average (kgDWha−1) | SD (kgDWha−1) | CV (%) | Minimum (kgDWha−1) | Maximum (kgDWha−1) | p-Value (within Season) | p-Value (between Seasons) |
|---|---|---|---|---|---|---|---|---|
| SES1 | 98 | 360.53 | 170.6 | 47.32 | 105 | 912 | 0.00 * | 0.00 * |
| SES2 | 101 | 637.66 | 381.26 | 59.79 | 239 | 1633 | 0.00 * |
| Soil Type | No. of Plots | Average (kgDWha−1) | SD (kgDWha−1) | CV (%) | Minimum Yield (kgDWha−1) | Maximum Yield (kgDWha−1) | Range (kgDWha−1) | p-Value (within Soil) | p-Value (among Soils) |
|---|---|---|---|---|---|---|---|---|---|
| CL | 16 | 497.9 | 360.85 | 72.47 | 216 | 1424 | 1208 | 0.00 * | 0.38 |
| CLL | 28 | 573.1 | 345.76 | 60.33 | 214 | 1633 | 1419 | 0.00 * | |
| HA | 141 | 477.9 | 320.88 | 64.75 | 105 | 1612 | 1507 | 0.00 * | |
| SVH | 14 | 415.6 | 266.21 | 64.05 | 130 | 1247 | 1117 | 0.00 * |
| Cultivation Practice | Number of Plots | Average (kgDWha−1) | SD (kgDWha−1) | CV (%) | Minimum (kgDWha−1) | Maximum (kgDWha−1) | Range (kgDWha−1) | p-Value (within Treatment) | p-Value (between Treatments) | Season |
|---|---|---|---|---|---|---|---|---|---|---|
| Flat | 58 | 288.5 | 88.26 | 30.5 | 105.0 | 474 | 369 | 0.37 | 0.00 * | SES1 |
| Tied Ridges | 40 | 470.72 | 189.29 | 40.2 | 163.0 | 912 | 749 | 0.04 * | ||
| Flat | 59 | 418.0 | 78.15 | 18.7 | 239.0 | 567 | 328 | 0.18 | 0.00 * | SES2 |
| Tied Ridges | 42 | 946.24 | 423 | 44.7 | 343.0 | 1633 | 1290 | 0.00 * |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silungwe, F.R.; Graef, F.; Bellingrath-Kimura, S.D.; Tumbo, S.D.; Kahimba, F.C.; Lana, M.A. Analysis of Intra and Interseasonal Rainfall Variability and Its Effects on Pearl Millet Yield in a Semiarid Agroclimate: Significance of Scattered Fields and Tied Ridges. Water 2019, 11, 578. https://doi.org/10.3390/w11030578
Silungwe FR, Graef F, Bellingrath-Kimura SD, Tumbo SD, Kahimba FC, Lana MA. Analysis of Intra and Interseasonal Rainfall Variability and Its Effects on Pearl Millet Yield in a Semiarid Agroclimate: Significance of Scattered Fields and Tied Ridges. Water. 2019; 11(3):578. https://doi.org/10.3390/w11030578
Chicago/Turabian StyleSilungwe, Festo Richard, Frieder Graef, Sonoko Dorothea Bellingrath-Kimura, Siza Donald Tumbo, Frederick Cassian Kahimba, and Marcos Alberto Lana. 2019. "Analysis of Intra and Interseasonal Rainfall Variability and Its Effects on Pearl Millet Yield in a Semiarid Agroclimate: Significance of Scattered Fields and Tied Ridges" Water 11, no. 3: 578. https://doi.org/10.3390/w11030578
APA StyleSilungwe, F. R., Graef, F., Bellingrath-Kimura, S. D., Tumbo, S. D., Kahimba, F. C., & Lana, M. A. (2019). Analysis of Intra and Interseasonal Rainfall Variability and Its Effects on Pearl Millet Yield in a Semiarid Agroclimate: Significance of Scattered Fields and Tied Ridges. Water, 11(3), 578. https://doi.org/10.3390/w11030578