1. Introduction
As an important productive resource, the economic characteristics of water are defined by its scarcity. With rapid population growth and economic development, water resources are becoming increasingly scarce; consequently, increasing attention is being paid to the economic characteristics of water resources. It is crucial to promote the efficient utilization and allocation of water resources and, thereby, facilitate both an incentive mechanism to save water and a restraint mechanism to avoid waste. In fact, water rights and water markets have proven to be effective economic approaches for realizing optimal water allocation. With the help of the water market, water rights are gradually transferred from users with low-efficiency use to those with high efficiency, thus, improving the overall level of water utilization and allocation.
The water rights trade market is usually categorized into the primary and secondary water markets. In the primary water market, public water use rights are distributed to organizations and individuals by authorized administrations through methods such as direct distribution, bidding, and so on. After the initial distribution, water rights can be transferred between users through commercial transactions in the secondary water market; this is considered as a readjustment of water rights distribution from the primary water market. As water rights transactions in the secondary water market are driven by individual benefit, allocation and utilization efficiency can be improved. Therefore, it is crucial to conduct research on the water rights transaction model in the secondary water market to ensure better water allocation.
Currently, major studies on the water market focus on its necessity, operation mechanisms, policies, economic efficiency, determination of transaction goals, transaction prices, and costs [
1,
2,
3]. Richard et al. [
4] evaluated the current policy of water shortage adaptation in the Colorado River Basin and proposed an interstate water market as an interesting reform that could be used for adapting to increased water scarcity and preserving core elements of the Colorado River Basin law. Zaman et al. [
5] discussed an economic trading model combined with a hydrologic water allocation model to estimate the impacts of temporary water trading and physical water transfers, considering the key trade drivers of commodity prices, seasonal water allocations, and irrigation deliveries. The Chinese government has conducted demonstration work regarding water markets in several regions in China. In the Inner Mongolia Autonomous Region, experimental work on water rights transactions has been undertaken in the upper reaches of the Yellow River. At present, it is generally believed that water rights transaction is an effective measure for solving the problem of water resources distribution in the context of water resources shortage.
Generally, an optimal water allocation model includes an administered system (AS) and a market-based system (MS) [
6]. In AS, information is completely transparent, and water resources are distributed and traded by authorities in accordance with their optimization goals. For instance, Roozbahani et al. [
7] determined the maximum water-use benefit for each user and introduced an allocation model to guarantee a maximization of the minimum ratio for each stakeholder’s profit to its highest possible benefit. Yu et al. [
8] used linear programming techniques to simulate the water market for maximizing the aggregate net return, subject to land, water, and crop restraints. Montilla et al. [
9] designed a basin-level water bank model that considered 15 representative farm types to simulate water trading. They also demonstrated that water banks are market mechanisms that facilitate the transfer of water toward uses of greater value, including environmental uses. Water banks reduce static transaction costs and help create more active water markets by increasing economic efficiency. Market operations are centralized, which allows the administration (or other agencies) to properly control potential negative externalities and prevent any kind of harmful speculation [
10].
Unlike AS, in which the role of the water trade market is limited, MS takes full account of the transaction process and the outcome for each water user under specific trading rules in the water market. In this context, transaction rules become major influential factors for water allocation. Giuliani et al. [
11] believed that each agent represents a decision maker and that its decisions are defined by an explicit optimization problem that only considers the agent’s local interests. A practical water transaction process includes both the supply and the demand sides, especially in the secondary water market. Tradable water rights and transaction prices are determined by the balance between supply and demand. It is, therefore,. necessary to continue the development of water market mechanisms to ensure that this reallocation/transaction process takes place as efficiently as possible. Under MS, water exchanges generally utilize two mechanisms: bulletin boards and sealed double-auctions [
12,
13]. Without the intervention of the relevant authorities, the bulletin-board approach is a relatively reasonable transaction method, as all traders, whether buyers or sellers, have to make decisions based on insufficient information. This approach requires buyers and sellers to post offers and requests for water, typically through an electronic platform. Trade transactions are executed by matching individual offers with corresponding quantity and price.
Many established water banks in the western United States are actually bulletin-board markets. The most active bulletin-board market is the Northern Colorado Water Conservancy District (NCWCD), where about 30% of the water allocated to the Colorado-Big Thompson (C-BT) project is utilized for rental transactions [
14]. However, some bulletin-board markets have been less successful; for example, the Texas Water Bank has conducted only one transaction since its establishment in 1993 [
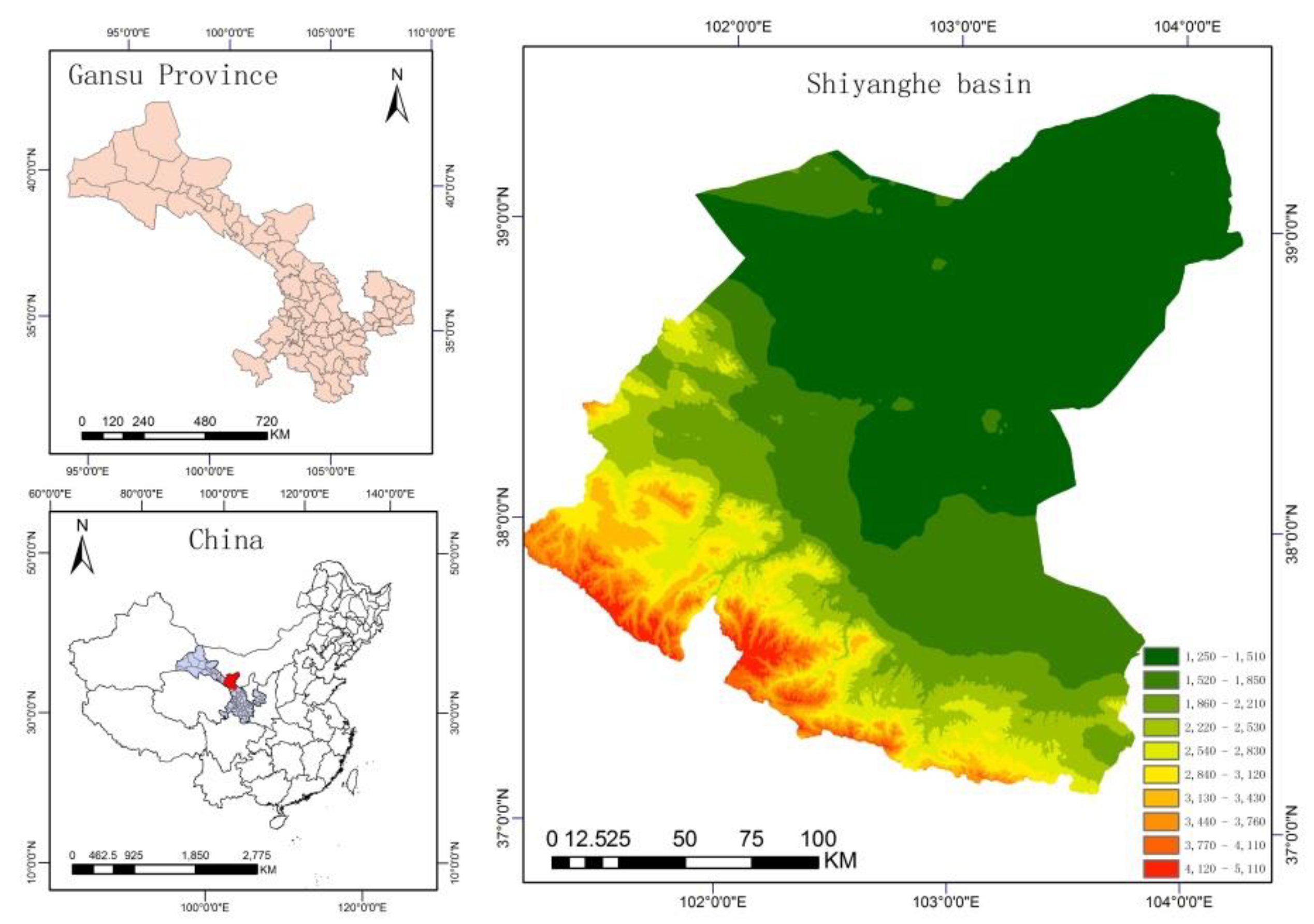
15]. In this study, we established the transaction rules for water markets by using the bulletin-board approach; this seems to be a more suitable approach for describing the operation system of the planned water markets in the Shiyang River Basin. Potential buyers and sellers make their offers simultaneously; each participant has no evidence of the marginal cost and the actual evaluation of others, but the participant’s decision can be influenced by other offers.
The comparison of the two systems has also garnered attention in recent decades. Many scholars have widely discussed the advantages and disadvantages of AS and MS [
16,
17], and others have also compared these systems directly. Matthew et al. [
18] pointed out that water markets did not always function efficiently because the features of some water rights were not designed for market transactions, and in particular, the impact of hydrological uncertainty was not adequately considered. Calatrava et al. [
1] showed that, compared to decentralized markets, centralized water markets lead to more efficient water resource allocation and utilization. However, such research requires more quantitative evidence.
In the context of water shortage, water saving is another important issue that has attracted people’s attention, especially in terms of water-saving techniques, costs, benefits, and quantities [
19]. Berbel et al. [
20] used cost-effectiveness analysis to rank and select policy measures for improving the ecological status of water bodies, based on the ratio between the equivalent annual cost and the reduction of impacts. Maeda et al. [
21] presented a multi-objective optimization model for allocating irrigation water in a rice paddy cultivation area after considering appropriate water-saving practices and providing an optimal solution for the water allocation problem at the regional level. Thus, it is crucial to fully consider the impact of water-saving behaviors on water resource policies and optimal allocation.
Following previous studies [
22], this study introduced a multi-agent and multi-objective optimization model based on a complex adaptive system to realize the administered allocation of water resources in the Shiyang River Basin and established a market-based water transaction model using the bulletin-board approach. The results of the market-based model were further compared with the output of the AS model. Furthermore, the influence of water-saving cost on optimal water allocation was also considered.
4. Results
Using the base year 2010, the water supply of and the water demand for the Shiyang River Basin in 2020 were forecasted and analyzed to facilitate optimal allocation planning. The optimization results obtained by using the two water rights trade models were also compared to facilitate further discussions.
4.1. Water Supply Forecast
The available water supply includes surface water, groundwater, and water supply from other sources. The available surface water supply is derived from water storage, diversion, lifting, and inter-basin transfer projects. The groundwater supply is mainly derived from water lifting projects, such as electro-mechanical wells. Other sources of water supply include wastewater re-usage and rainfall utilization.
According to the Water Resources Development Planning of the Shiyang River Basin, there will be no additional surface water supply projects, such as water storage and water lifting, in the next decade. Therefore, in accordance with the historical water supply curve, the exponential smoothing method has been adopted to predict that the surface water supply will be 1.77 billion m
3 in 2020. As the utilization rate of canal water in the irrigation area increases, the recharge amount of water infiltration will correspondingly decrease, and the total supply of groundwater will become relatively small. The groundwater supply volume is predicted to reach 570 million m
3 in 2020. According to the policy requirements of Jinchang City, the sewage treatment rate should reach 60% on average, and the amount of reused sewage treatment is likely to increase to 65 million m
3 in 2020. The amount of available rainwater is roughly estimated to reach 12 million m
3 in 2020 (
Table 5).
4.2. Water Demand Forecast
The norm method and analytic hierarchy process were adopted to predict the water demand (
Table 6) and initial water rights allocation (
Table 7) for each industry in 2020 [
22].
Domestic water demand was divided into urban water demand and rural water demand. The population was predicted by using the exponential smoothing method and then multiplied by the water quota. The estimated agricultural water needs included farmland irrigation and water needs for forestry, animal husbandry, fishing, and livestock. Three different types of irrigation were considered, namely canal irrigation, well irrigation, and combined well and canal irrigation. The water demands of forestry, animal husbandry, fishing, and livestock included two items: irrigation of forest fruit fields and water for livestock. The predictions for agricultural water demand were required to consider these four factors: (1) variations in the irrigation area, (2) irrigation regulations, (3) crop composition and irrigation norms, and (4) canal water utilization efficiency.
where
is the gross irrigation quota in planning year
t, and
,
, and
represent the net irrigation quota, irrigation area, and the utilization coefficient of canal water, respectively.
The industrial water demand forecast was based on historical industrial water consumption, the Key Management Plan Report of the Shiyang River Basin, and the research results of Industry Water Quota in Gansu Province.
The water demand of the construction industry was predicted by using the exponential smoothing method in accordance with Industry Water Quota in Gansu Province and the growth curve of the actual water quota for construction industries in the Shiyang River Basin.
Water demand in the tertiary industries was predicted according to trends in economic development and water consumption per unit of output value.
The ecological water demand forecast was calculated based on the forest-grass irrigation area, irrigation quota, and utilization coefficient of irrigation water.
4.3. Water Allocation Results for 2020
4.3.1. Under the Administered System
In 2020, the amount of water saved for agriculture in Wuwei is expected to reach 823 million m
3, while the figure for Jinchang is 356 million m
3, with corresponding investment amounts of up to 1632.8 and 317.8 million yuan (a total of USD 46.91 million; USD 1 is roughly equal to 6.77 yuan), respectively [
24]. The impact of variations in water prices and water-saving behaviors on water rights trade is undoubtedly non-negligible; this impact should be measured by introducing the water-saving amount and cost coefficient into the model. Because it was the dominant water-saving measure in Wuwei and Jinchang, only agricultural water saving was considered for calculations in the model (
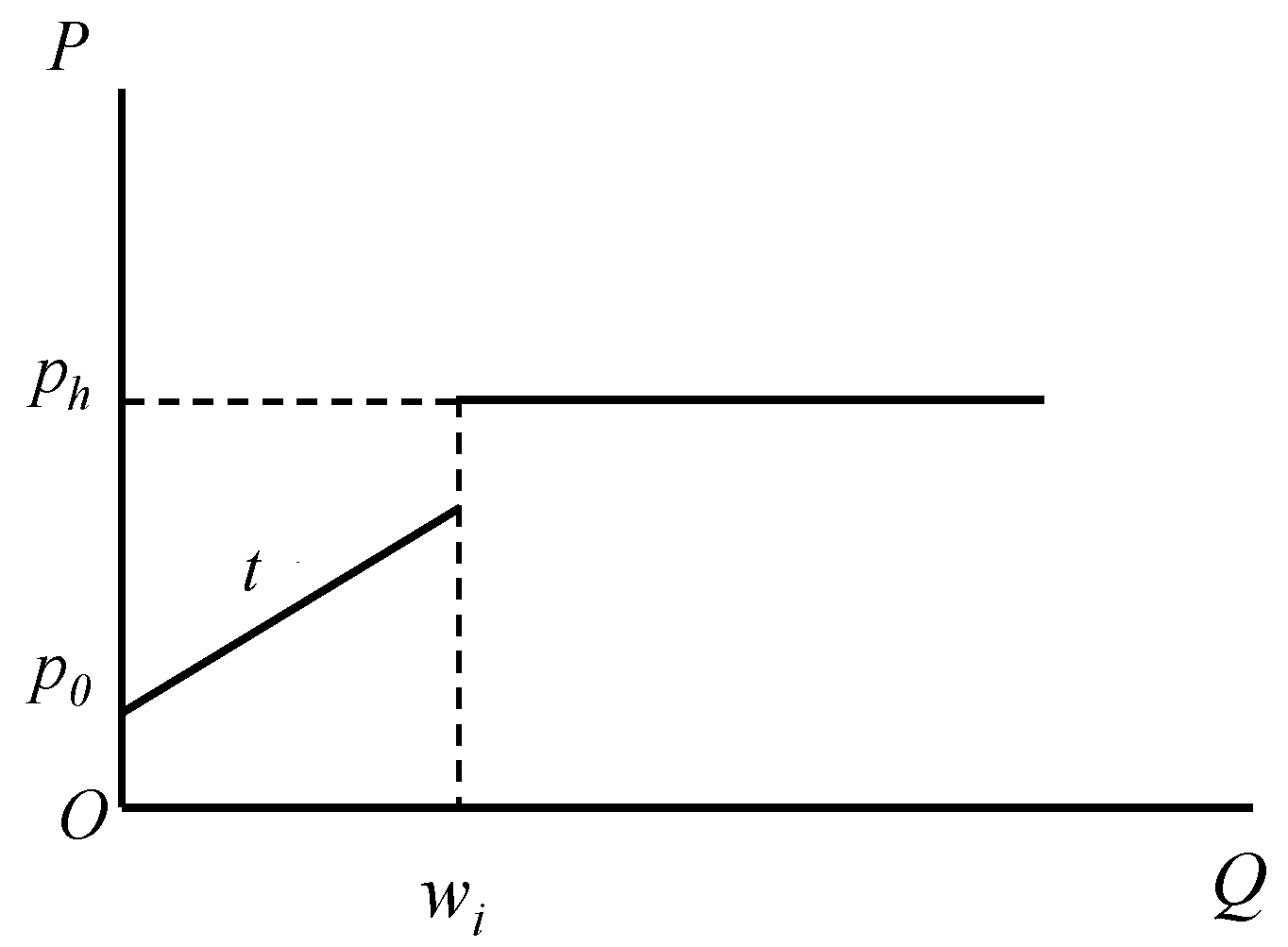
Table 8). To determine the water-saving cost coefficient
k for the two cities, the relationship of water-saving cost
and water-saving amount
was simplified linearly with a slope of
as follows:
Table 9,
Table 10 and
Table 11 show the optimized water price and corresponding industrial benefits in 2020; these factors reveal that the key influential factor is transaction price and not the industrial water price. A relatively low transaction price (0.793 yuan/m
3 in 2020) is necessary to achieve the optimal social benefit of the entire basin and increase the profits of the corresponding agents (
Table 9 and
Table 10). For this transaction, the sellers are two agents from Jinchang, while the buyers are two agents from Wuwei, who both succeeded in obtaining water rights in the market (compare data in the second and fourth rows of
Table 11). Simultaneously, Wuwei and Jinchang will not need to save as much water as possible, as both cities show strong capacities to cut down on cost and save water; this enables them to satisfy the water demand of the whole basin without reaching their full water-saving capacities (
Table 11).
In addition, cost accounting was utilized to analyze whether each agent took real action to save water in the trading process. Under the condition that the water demand of the
ith consumption agent
is less than its initial water rights
, the water use cost before saving water is
, where
is the slope of ladder water prices for the
ith agent. With effective water-saving behaviors, a volume equaling
(
is the water-saving coefficient) is saved, which decreases the cost to
. The system reaches its critical state when the values of the two costs are equal. As the linear function is used to depict the water-saving cost (Equation (14)), if the slope of ladder water prices
is omitted, the equation under critical state can be simplified as
where
is the transaction price,
is the basic industrial water price for the ith agent, and
is the water-saving coefficient of the
ith agent.
When the transaction price
,
represents the optimized water price of the
ith agent in the administrated model, while
is fixed in the water market. The agent is likely to demonstrate water-saving behavior until the full capacity of water saving is reached. Otherwise, the agent will reach the opposite conclusion, as more profits can be obtained through water rights trade than through water saving. When Equation (14) holds, the amount of water that should be saved is determined by the comprehensive optimization objective (
Table 12).
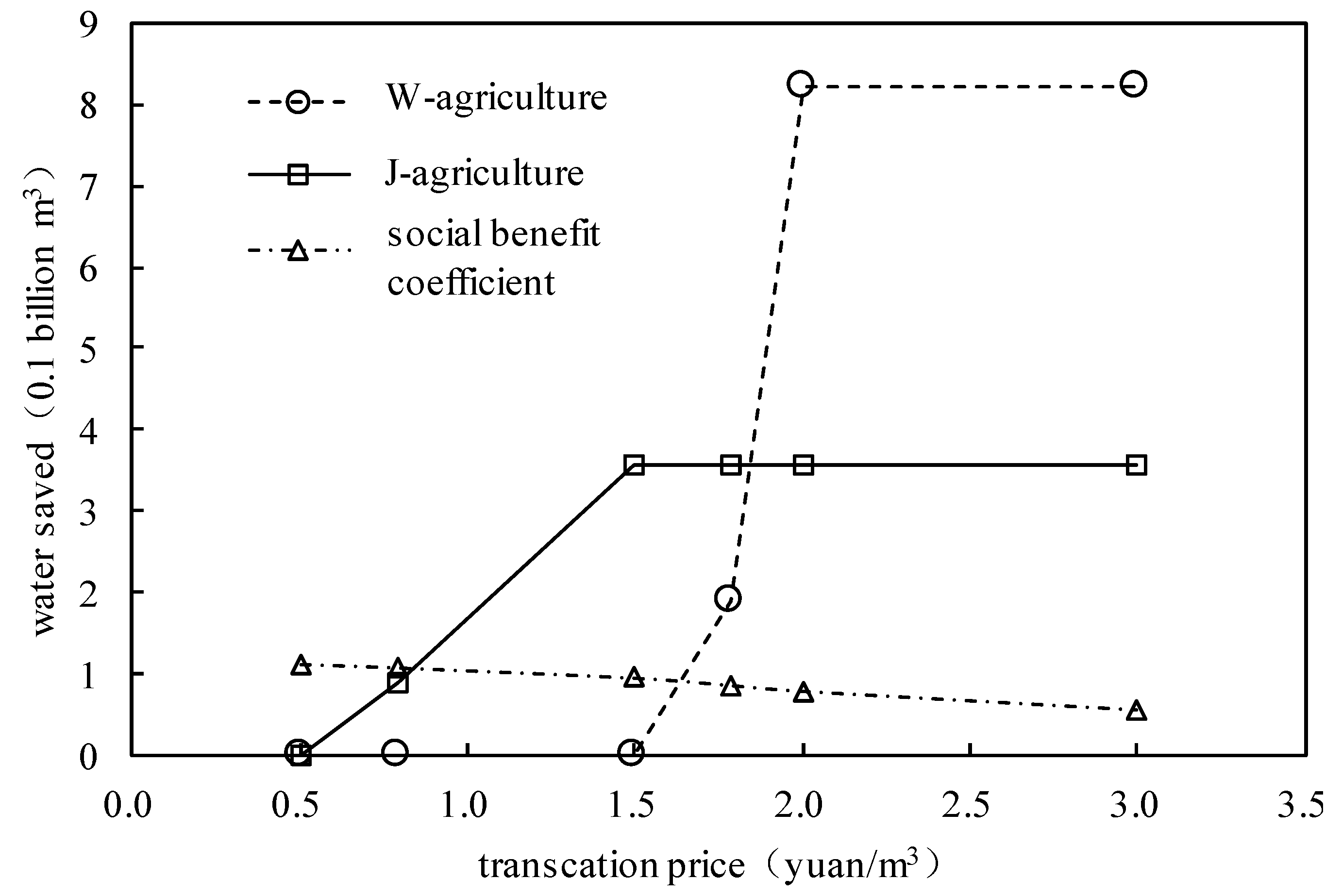
Figure 3 illustrates how transaction price
influences the water-saving behavior of each agent under the condition of fixed industrial water price. When
,
In this situation, Wuwei’s agricultural industry does not need to save water. However, for Jinchang, transaction price
exceeds its critical value, which will make the water quantity saved by agents reach its maximum amount of 355.6 million m
3 (6th row in
Table 11).
Moreover, it is noteworthy that when the transaction price increases, the social benefit coefficient
r decreases; this is attributed to the unreasonable utilization of water resources (
Figure 3). The transaction price parameter should, thus, be reduced to resolve the problem of supply exceeding demand.
4.3.2. Under the Market-Based System
The trading procedures of the MS model are as follows:
- (1)
The total water supply, water demand, and water price for each industry, initial water rights, and economic agent equations are the same as those under AS.
- (2)
Based on the economic agent equation of each industry, the optimal water consumption of each agent is calculated while considering the current water price. An agent whose optimal water consumption is less than its initial water rights is considered a seller. Thus, the surplus water resources for selling constitute the total water supply in the market, which will be purchased by the buyers whose optimal water consumption has not yet been satisfied.
- (3)
In a certain period, there are M sellers and N buyers in the market. Calculate the upper limit of the critical bid quotation and the corresponding water demand of each buyer.
- (4)
Rank the buyers’ quotations from high to low and the sellers’ quotations from low to high, thus, determining their prioritization. Check whether there are any role changes for the agents (for example, from buyer to seller).
- (5)
On the basis of each buyer’s quotation, compare the buyer’s water-saving cost with the cost of buying water, while simultaneously comparing each seller’s water-saving cost with the potential benefit of selling water. If more profit can be gained through saving water, the agent will participate in water-saving behavior. Otherwise, the agent will choose to directly trade with other agents in the market.
- (6)
Taking all current quotations into account, trade transactions should be conducted until the entire water supply is sold out or the water demands of all the buyers are satisfied. Next, calculate the purchasing price, purchasing amount, actual water consumption, and corresponding economic benefit for each agent.
Substitute all relevant parameters for the Shiyang River Basin into MS and define the termination as “all buyers’ water demands have been met” or “all sellers’ tradable water rights have been sold.” Accounting for the use of agricultural water-saving techniques, calculate the ultimate water consumption amount and corresponding benefit for each industry in the planning year by using the bulletin-board trading mechanism.
Table 13 shows the maximum purchasing amount for each buyer and its maximum affordable purchasing quotation. From high to low, the quotation ranks are as follows: Wuwei-Industry, Wuwei-Agriculture, and Jinchang-Agriculture. However, Jinchang-Industry rarely needs to purchase water rights from the market. The allocation results for MS under different sets of purchasing quotations can be calculated and compared with the corresponding results for AS to further analyze the differences between the two systems in terms of water allocation.
Table 14 displays the optimal allocation results for different sets of purchasing quotations. Define the benefit ratio of AS as 100% and calculate the ratio of the gross economic benefit under MS to that of AS. For instance, a quotation set for the four agents is [1.5, 2, seller, seller]; this means that Wuwei-Agriculture and Wuwei-Industry are planning to purchase water rights at the price of 1.5 yuan/m
3 and 2 yuan/m
3, respectively, but Jinchang-Agriculture and Jinchang-Industry are selling their surplus water rights. According to trading procedure nos. (2) and (4)–(6), with the highest transaction price of 2 yuan/m
3, Wuwei-Agriculture is prone to agricultural water-saving behavior, as the transaction price is higher than the critical water-saving price. In this situation, Wuwei-Agriculture, whose maximum water-saving reaches 823 million m
3, is converted from the buyer to the seller and becomes the first agent to trade with Wuwei-Industry in accordance with trading procedure no. (5). This result reveals that the water demand of Wuwei Industry, whose maximum purchasing amount is 284 million m
3, can be fully satisfied by Wuwei-Agriculture; thus, the two agents can finalize the trade transaction with an amount of 281.8 million m
3. Jinchang-Agriculture and Jinchang-Industry will no longer participate in the trade, and their water consumption will be determined by the economic agent equations in accordance with the limits of the initial water rights. Now, the potential tradable water rights exceed the water demand in the market; thus, the water resources in the basin are not fully utilized and hold a benefit ratio of 99.7%. The corresponding optimal gross economic benefit will be 48,303 million yuan (less than the figure obtained under AS), which is 48,439.5 million yuan.
When the quotation set is [0.7, 0.793, seller, seller], according to Equation (14), only Jinchang-Agriculture shows the tendency to save water, with the maximum amount reaching 356 million m3. The tradable water rights of Jinchang-Agriculture and Jinchang-Industry are 89.4 and 53.4 million m3, respectively; both are purchased by Wuwei-Industry, with none left for Wuwei-Agriculture. The benefit ratio under this condition is 99%, with a total economic benefit of 47,971.4 million yuan, which is still less than that obtained under AS.
The results above demonstrate that, as the basis of the decision to save water and participate in trade, the highest bid in the quotation set has a dominant influence over how the trade is conducted. This case includes an occasion where the benefit ratio improves with the increase in transaction price; this results from the use of cost-benefit accounting in agricultural water-saving. Only when the quotation is higher than the critical value does the agent become stimulated to adopt water-saving behavior to save as much water as possible and to introduce surplus water rights into the market.
Note that the economic benefits of MS are lower than that of AS because the water prices of industries in AS are obtained through optimization calculation to reap economic, social, and environmental benefits (
Table 10). In MS, the water prices of industries cannot be obtained through optimization calculation. Moreover, it cannot use the 2010 initial water prices; it can only use the predicted industry water price for 2020. Wuwei’s predicted agricultural water price is 0.28 yuan/m
3, which is higher than that of AS in the model optimization numerical (0.207 yuan/m
3). Thus, the water fee increases, while economic benefits decrease. The total benefit value is also smaller than the result in the AS model. For example, when the predicted water price is reduced in 2020, the agricultural water price in Wuwei is reduced to 0.22 yuan/m
3. Recalculation shows that the benefit value of MS exceeds that of AS. This result is due to the introduction of water-saving technology, which is similar to the emergence of additional water resource supplies. If water-saving measures are not introduced, and trading is conducted on the basis of existing total water resources, the benefit value of MS will not exceed that of AS.
5. Discussion and Conclusions
Based on previous studies, this study further explored the optimal allocation of regional water resources. Because they are centered on ideal economic agent equations, this study assumed that the behaviors of water use agents will only comply with the objective of achieving maximum economic benefit; therefore, the influence of market variation, environmental controls, development strategy, and so on were excluded. Additionally, the study demonstrates the important role of water-saving techniques and cost in water allocation; thus, a high transaction price in the market is considered as the incentive for agents to adopt water-saving behaviors.
The allocation results for both AS and MS were calculated and discussed. The AS model conceptually focuses on a top-down comprehensive transparent control facilitated by the government and builds an entirely ideal environment for conducting water rights transactions without the impacts of competition and game. However, for the MS model, which is better suited to real-world trade scenarios, the study introduced a bulletin-board approach to facilitate the calculation of allocation plans under different sets of quotations. In MS, as a basis for judging a given agent’s tendency to save water and participate in the trade transactions, the highest bid in the quotation set wields dominant influence over how the trade is conducted. The higher the transaction price is, the better the benefit ratio of MS will be. Therefore, a relatively low transaction price will result in inactivity in terms of water rights trade, and this will have a significant impact on the economic benefit of the basin.
With many influential factors and complex structures, the regional water resource management system is still underdeveloped and needs to be improved so that appropriate trading rules can be formulated in the water rights transaction market. Therefore, the discussion of the following questions in future research is of great scientific value:
- (1)
The oversimplification of water agents is a problem in this area. For example, all agricultural industries were assumed to have the same marginal value for water; however, different industries tend to have different values, and some even have negative marginal benefits. To determine the accuracy of the results, it is necessary to focus on the problem of how to choose and decide typical industry needs. In this study, we considered only one agricultural agent for convenience reasons.
- (2)
It is important for future research to analyze the influence of different policies and trading systems on trading results to elevate the results of the selected model to the level of macroscopic operability and suggestion.
- (3)
This study considered only agricultural water-saving techniques, but wider attention should be paid to the influence of industrial and domestic water-saving behaviors on the transaction price and amount in the market.
- (4)
The benefit ratio in this study was defined by using economic benefits; thus, it may not reflect the allocation efficiency of water trading systems precisely. Methods to comprehensively evaluate the working effect of water allocation still require more exploration. An evaluation mechanism for assessing the comprehensive utilization efficiency of water resources based on a basin scale should be established in the future.