1. Introduction
One of the main problems related to urban drainage systems are the frequent flooding events in urban areas. Various factors can cause these events, such as pipe size, structural failures in the system, objects causing obstructions or an increase in rainfall intensity due to climate change inducing increased runoff flow. Climate change undoubtedly affects the intensity and frequency of meteorological phenomena of present days, including a gradual increase in rainfall intensities in many cities throughout the world, making systems initially well designed begin to fail.
In order to have a better control over the systems and prevent the occurrence of urban flooding events, many mechanisms have been implemented to reduce runoff and increase the capacity of the system. Certainly, one of the most used methods in the last years has been the implementation of storm water detention tanks (STs). These methods refer to the installation of devices in the urban area that can hold back the flow that cannot be evacuated by the system. Later, when the system has regained its transport capacity, the devices return the water to the sewerage system for correct evacuation.
Howard [
1] published one of the first works related to STs where it is established that the effectiveness of the STs combined with Wastewater Treatment Plants (WTP) to control runoff depends on STs and WTP’s capacity as well as the duration and volume of the precipitation events they must control. Howard’s paper also lays out the possibility of using computational tools for the analysis of these devices. His work focused on the usage of probabilistic methods based on precipitation data.
These water storage structures are built to retain a portion of the just-fallen rainwater, a portion that varies according to every storm. Di Toro and Small [
2] posited a statistical method based on a probabilistic characterization of both rainwater and runoff that predicts the behavior of the storm water control devices. The long-term behavior of a ST is determined based on its size, operation method and both runoff and precipitation statistical characteristics. Based on these, Di Toro and Small studied the filling, storage and emptying of the retaining structures; flow variations caused by storm water; and first flush’s implications regarding water quality.
Early ST sizing methods were based on roughly simplified methods since simulation techniques require a high computational effort in terms of time and memory. Loganathan et al. [
3] presented a simplified method that could estimate ST’s capacity accounting for previous storms. This method is based on exponential probability density functions for the main hydrological variables involved (runoff volumes, runoff duration, time between events). These functions are used to generate a new statistical distribution that can estimate WTP’s capacity and retention volume for a given risk level. One of the main advantages of this method is that it permits us to determine the preliminary volume for an ST. With the same focus, Meredith et al. [
4] developed a procedure based on all available historical data for the dimension of a runoff storage structure. The dimensioning process uses the water quality concept because all runoff must pass through the cleaning water process in the WTP. The method was tested in several industrial areas, but it is limited to small areas where rational methods can be applied.
Most of these studies were focused on the treatment of rainwater runoff before the water enters the network. Due to urban area space restrictions, alternative systems for the treatment of runoff water are needed. For this, Takamatsu et al. [
5] presented the design of a rainwater storage system as part of the complementary structure of road drainage. They developed a mathematical model based on the hydraulic principals to estimate the efficiency of the pollutant elimination. The main idea was to evaluate the efficiency of a rectangular runoff ST removing suspended solids. In order to validate the mathematical model, a scaled (1/5) network model was built, on which several tests were run to study the influence of different inflows, functioning frequency and pollutant concentrations. The temporal concentration of suspended solids at the exit and the efficiency of the conceptual model were compared. They concluded that there is a correlation between the detention time and the removal efficiency.
Similar studies to Takamatsu et al. have been done to study the behavior of several draining areas under different rainfall scenarios. De Martino et al. [
6] proposed the usage of STs as structures that enable controlling the impact of the first-rain contamination, which has the highest pollutant load. As the design of this system depends on a large number of parameters, they consider that the design is not completely defined. In order to study the influence that the rainwater might have, De Martino et al. made several simulations with different rainfall-time series in Campania (Italy). This study made an analysis of the hydrographs and pollutographs generated for several network and tank configurations. The results showed that the rainfall does not have a direct influence in the reduction of pollutant concentration. Based on this, a new methodology for the preliminary design of STs was presented.
In line with analyzing different rainfall amounts, Li et al. [
7] analyzed 16 different rain events in three drainage areas. The objective of this study was to analyze the effect of a detention tank’s location on the polluted load reduction, mainly particles and metals. Thus, Fu et al. [
8] presented a model for optimum distribution of the STs in order to minimize the effect of new residential zones on the discharge water quality. The developed model considered three working scenarios; optimum flow control, minimization of deposit’s distribution and a combination of both. A step beyond was made by Vanrolleghem et al. [
9], who proposed a real time control system to manage the quality of water poured in the collectors in order to comply with the European Water Framework.
Most of the previous works about the usage of STs are focused on the issue of maximizing the quality of poured water, not to control the potential overflows that may occur due to excessive rainwater, but some studies have been carried out in order to show that STs can also reduce floods. One of the first studies that relate the usage of STs with the rainwater variation due to climate change was done by Andrés-Domenech et al. [
10]. The study focused on the effects originating from changes in the rainfall regimes on the efficiency of the actual drainage systems. The proposed analytical statistical model permits us to evaluate the overflow reduction efficiency and the retention tank’s volumetric efficiency as a function of the expected climate behavior and urban basins. The tank’s efficiency sensitivity is evaluated under the analysis of certain changes in the precipitation. The results show the ability of STs to partially mitigate the resulting effects of climate change. Andrés-Domenech et al. based their work in the same approach as Butler and Schütze [
11]: integrate simulation models to obtain an optimum control of the sanitary draining systems. For this purpose, Butler and Schütze developed a model (SYNOPSIS) consisting of a series of sub-models of the sewage network, the treatment plant and the behavior of the natural stream over which the system’s evacuation will be made. These sub-models, together with a developed control module, allow the development of water control strategies in order to minimize the impact on the water evacuation. The use of simulation techniques is simple for urban wastewaters. Moreover, the simulation techniques enable water control solutions that were not possible by the classic simplified methods. This work was extended by Fu et al. [
8] taking into account the optimization of urban wastewaters as a multi-objective problem. For this, they used a powerful multi-objective genetic model called NSGA II [
12] that allows obtaining the Pareto’s front for several optimum solutions. For the same topic, Wang et al. [
13] proposed a two-stage optimization framework to find an optimal scheme for STs using the storm water management model (SWMM) [
14]. As a result, the authors conclude that the use of STs not only reduces flooding, but also the total suspended solids.
Drainage network rehabilitation is a necessary operation to adapt an insufficient network to the new climatologic and environmental conditions. There are several ways to rehabilitate a drainage network with difficulties in the compliance of its design specifications. Traditional ones consist of pipes replaced with larger pipes. A newly developed option is the introduction of STs in the network to store water during the storm, draining it after the extreme events have passed. In this regard, Gaudio et al. [
15] proposed a methodology for the hydraulic rehabilitation of urban drainage networks combining a hydraulic analysis model, a data base of rainfall events and a series of synthetic hyetographs. The results statistically analyze the possible places where the flood occurs and the influence that the roughness of the pipes can have on it.
Considering the rehabilitation using pipe replacement and other actions, Sebti et al. [
16] proposed an algorithm to analyze the benefits of combining pipe substitution with other solutions installed to reduce the runoff. However, Sebti et al. did not consider hydraulic models to analyze the consequences of rehabilitation works in the network. Instead, they used the simplex algorithm for the optimization. Then, Ugarelli and Di Federico [
17] calculated the economic balance between replacing damaged infrastructures or maintaining them for a certain period of time.
The rehabilitation of drainage networks based on the mere substitution of pipes is an approach that has been traditionally carried out. However, this solution is not very applicable in consolidated cities in which the replacement of large parts of the network interferes with other services already installed and generates social problems for the population such as noise, inconvenience or traffic jams. That is why this work proposes a combined use of the installation of STs and the replacement of pipes. This is intended not only to reduce investment costs, but also to minimize the impact that changes may have on citizens.
In short, the objective of this paper is to propose a methodology for the rehabilitation of drainage networks that combines the installation of STs with the replacement of pipes. To do this, the mathematical model of the network is the starting point, using SWWM to conduct the hydraulic analysis and a pseudo-genetic optimization algorithm (PGA) [
18] to find the best solutions. The connection between the hydraulic calculation model and the optimization algorithm will be carried out through an adaptation of the SWMM calculation toolkit done by Martínez-Solano et al. [
19] in order to reduce the calculation time.
The solution of the optimization problem requires an elevated number of decision variables (DVs) generating a large space of feasible and unfeasible solutions. This search space entails not only a big computational effort, but also may cause the method to fall at local minima, limiting the ability to find the best solution. A reduction in the size of the problem and, subsequently, in the size of the search space might help the convergence of the method. In this paper, a methodology for the reduction of number of DVs based on pre-selection of potential locations of STs and the selection of conduits potentially substitutable is proposed. This is a worthwhile contribution because reducing the size of the search space and improving searching mechanisms are listed as current research challenges in the application of optimization algorithms to real world problems [
20,
21].
The methodology has been validated in several networks. Although this paper presents the results of application to the E-Chicó sector of the drainage network of Bogotá (Colombia), some model files and additional case studies can be found in the
supplementary material.
2. Problem Formulation
In order to formulate the problem of optimizing the rehabilitation of drainage networks based on the combined use of STs and the replacement of pipes, some hypothesis had to be established:
The computational models for the drainage networks are going to be tested with several rain scenarios, scenarios based on different climate change predictions [
22].
Potentially dangerous scenarios are the ones to be considered during the optimization process. The first selected rainfall is a synthetic design rainfall obtained from the IDF curves of 10-year return periods using the alternate block method. The second rainfall is obtained after processing the first through a climate change adaptive scenario. The rehabilitation will be carried out considering only the worst-case scenario.
The rainfall-runoff transformation model used is the one included in the SWMM model. Specifically, the Curve Number model is used. For this, according to the characteristics of the terrain, the curve number has been specified for each of the sub catchments defined in the model.
The drainage system models must go through a calibration process, since the analysis must be as accurate as possible. That is, the starting point of the process is a calibrated hydraulic model of the drainage network. The hydraulic model used would be SWMM. Traditionally, this type of simulation is performed considering uniform flow. However, in this case, each configuration is analyzed using the dynamic wave model, because it provides a better representation of floods than the kinetic wave model or uniform model.
A simplification process is necessary for every model, yet the accuracy of the result must not be compromised. This simplification will highly reduce computational times for every hydraulic simulation.
The optimization problem will be addressed in monetary units. Thus, the first step would be to find the cost functions that characterize the value of hydraulic variables in monetary units. So, the functions that together form the optimization total cost problem are: pipe replacement cost, ST installation cost and total flood damage cost as introduced by Cunha et al. [
23].
From all described mathematical approaches, it seems heuristics approaches can give the best advantages for the process. Therefore, based on previous experience [
24], a PGA method was used.
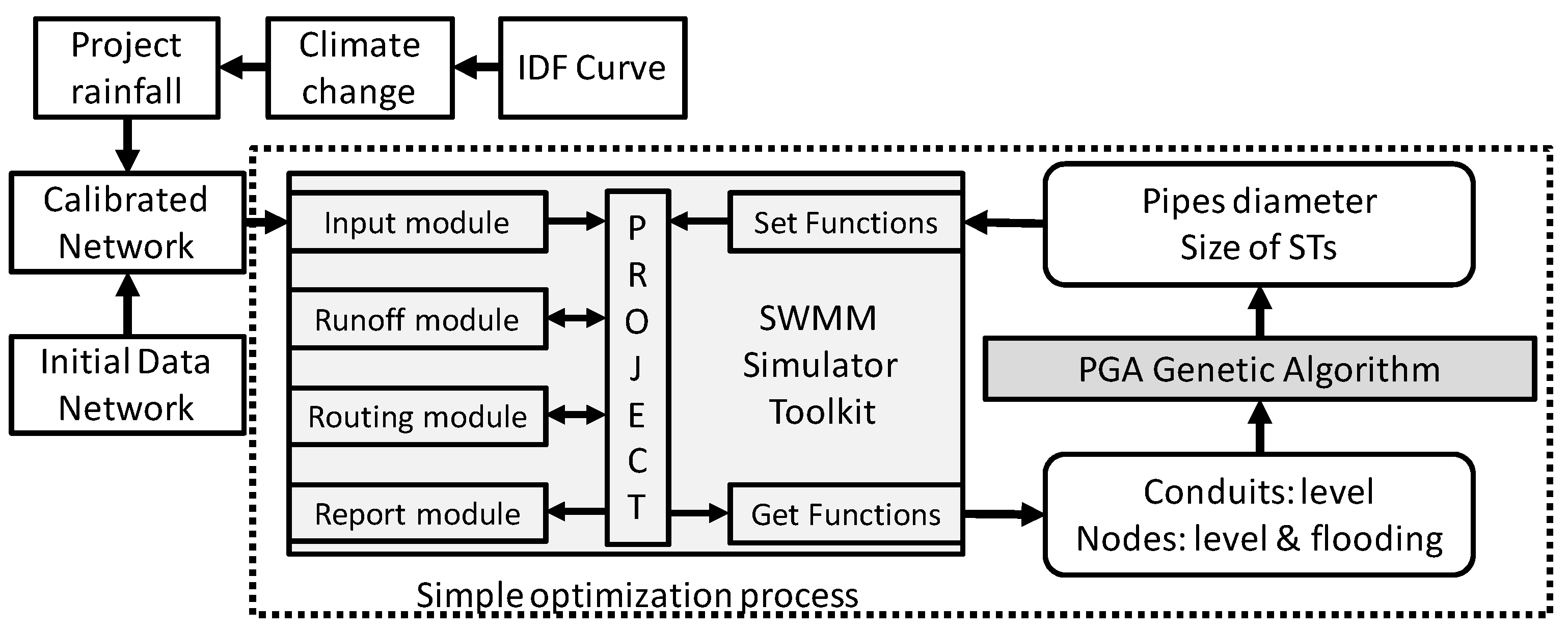
The main objective of drainage network rehabilitation is to allow the adaptation of the network to new climatologic and environmental condition while fulfilling assigned missions. Due to that importance, it is necessary to define an adequate optimization scenario in order to optimize the process. The formulation of the problem of rehabilitation of a drainage network, combining the installation of ST and the replacement of pipes, is summarized in the flow chart of
Figure 1. The first part consists of obtaining the calibrated model of the network, which is the starting point of the process. This network should represent, as faithfully as possible, the behavior of the network. Afterwards, a simple optimization process is used, with a hydraulic model based on the use of the SWMM Toolkit and a PGA that uses the levels in nodes and pipes and the flooding in nodes to determine the possible diameters of the rehabilitated conduits or the size of the installed STs. In order to define all the details of the optimization algorithm, the following sections describe the DVs, the objective function and the cost functions used.
2.1. Decision Variables
The process of rehabilitation of a drainage network (
Figure 1) involves modifying two types of DVs. On the one hand, there are variables related to pipe diameters, which seek to locate the best combination of sizes to obtain the minimum flooding. The optimization model analyzes the replacement of the pipes based on their transport capacity. The diameter may increase if the original pipe is insufficient to transport the flowing water or decrease if a hydraulic control device [
25] should be installed to introduce the same head loss as the calculated pipe’s diameter. Consequently, the DV is the size of the pipes, and can vary from 0 (not replace) to a maximum value set before beginning the optimization process. Obviously, if the result associated with a pipe is 0, it is because it is not necessary to replace it for the correct operation of the network. Then, for a better understanding of the optimization methodology, it is convenient to define some parameters related to the pipes. So,
NC is the number of network conduits;
m is the number of feasible conduits selected to be replaced, varying between 1 and
NC; and
ND is the number of candidate diameters, between
ND0 and
NDmax.
On the other hand, there are variables related to node storage capacity that seek the minimum volume of STs that reduce floods. The proposed methodology considers the possibility of installing an ST in each node of the network. This involves replacing an existing manhole with an underground ST. The land in which the rehabilitation of the drainage network is developed is mostly urban. Therefore, it is admitted that the depth of excavation is limited. Thus, the maximum depth of ST is what the manhole initially had, so the only parameter needed as DV is the ST cross section. Related to this, every node has a defined storage capacity related to its cross section and the model takes into account some nodes that could be modified into an ST. For this process, every node would have a DV representing the equivalent additional section corresponding to that of the STs in the case it would have been installed in the node location. The DV would vary between zero and a maximum value, predetermined before the optimization process and taking into account the restrictions of the urban geographical space of each node. If the nodes were not to be transformed into a tank, then the variable would have a value of 0, meaning that, it is not adequate to install a ST on the specific node’s location, maintaining thus the initial storage capacity of the node. In case the initial hydraulic model has any type of water deposit, the cross section of the deposit might be part of the optimization process.
For every node, whether it is regular or a storage node, its cross section
S would be expressed according to the following equation:
where
AS, BS and
CS are characteristic coefficients that adjust the tank’s section to different expressions, and z is the water level of the node. In the case of considering tanks of constant section,
A represents the cross section while the coefficients
B and
C are null. However, considering tanks with variable section does not imply a major difficulty in the problem implementation beyond choosing the right DVs.
Again, the definition of some parameters related to the nodes is important for the understanding of the methodology. NN is the number of network nodes and n is the number of nodes selected to potentially install a ST, varying between 1 and NN. Each node in which an ST can be installed has the cross section (S) as DV. Since a heuristic optimization model is used, it is necessary to perform a discretization of S. For this reason, a maximum value of the tank cross section (Smax) is defined for each node. In this way, N is the number of divisions in which Smax is divided. Therefore, N determines the resolution of the section S, varying between N0 and Nmax. A simulation performed with the ST cross section divided into N0 parts is faster than a simulation performed Nmax divisions. So, to obtain better calculation times, the number of divisions of the ST cross section could be reduced.
Additionally, to introduce tanks with a variable straight section does not imply major difficulty in the problem implementation beyond choosing the right DVs.
As stated before, the size of the problem is a key aspect when trying to optimize real problems. In this work, the optimization algorithm takes into consideration both pipes and nodes. The maximum size of each rehabilitation scenario can be expressed by the following equation:
2.2. Objective Function
The objective function of the optimization problem is addressed in monetary units and is represented as the sum of three cost functions:
The investment cost related to the substitution of each selected pipe of the network.
The investment cost linked to required volumes of STs to be installed in each solution.
The damage cost caused by the flooding level in various nodes of the network.
The mathematical expression of the objective function is given by Iglesias-Rey et al. [
26]:
In Equation (3), the first term represents the rehabilitation or replacement cost of the
m considered pipes in the network. The second term represents the construction or expansion cost of volume
VDR(
j) of the n STs installed in the drainage network. This cost concerns the existing STs whose volume will be expanded, and the network nodes where new STs will be installed. The third term represents the total flood damages costs [
27] caused by the
NF nodes in which a certain flooding volume
VI(
i) appears. All the terms of the objective function have a weight coefficient
λi, in order to prioritize one term versus another. If
λi is minimum (eventually null) the term is not considered, but if
λi is greater, the term is considered in the objective function.
2.2.1. Pipe Replacement Cost Functions
This function represents the cost of rehabilitation of those pipes that are replaced in the optimization process, either because they have poor internal conditions or because they have insufficient transport capacity. In this work, the proposed function is adjusted based on real data from manufacturers, relating the u
nit cost of the pipes with their diameter. Finally, the pipe substitution cost is in the form of a second-grade polynomial:
where
α and
β are coefficients that must be adjusted in each case considering the costs of the project.
2.2.2. Storm Tank Installation Cost Functions
This cost function links the associated investment to the installation of STs in the network. The tanks are installed on-line, simply said in series with the pipes existing in the network. The determination of this cost function is fundamental at the moment to establish the size of the adequate tanks to install. The function defines the tank installation cost based on its storage volume. Here, the idea is to build small and median tanks implying the increase of the storage capacity of the network and the water flow travelling time through the network. The mathematical expression of the cost function is:
In this expression, C(VDR) is the cost associated with the installation of an ST of volume VDR and A, B and C are coefficients that must be adjusted in each case according to the specifics of the project.
2.2.3. Flood Damage Cost functions
Representation of the flood cost function can be based on either total flooding volume or floods based on either total flooding volume or flood level. The first option allows us to eliminate totally the flood, but this option will need more investments. This total water volume can be obtained by summing the flooding volume of each flooding node. The second option allows reducing the flood and the cost of the flood depending on the flooding area. Lee and Kim [
27] showed that flooding damage is different from flooding volume and that it was necessary to create a resilience index based on flooding damage because some subareas are immediately damaged by a certain amount of flooding while other subareas are not. They represented flood damage costs as a function of the level reached by water.
Using the Lee and Kim approach, flood damage costs have been determined for a drainage network in Bogota (Colombia) analyzing the replacement costs of the damaged goods. A curve representing the flood cost by m
2 of area as a function of the flood level was obtained for 6 different social stratums, a commercial area and an industrial area [
23]. There is also a curve representing the average value of the study area. They can be observed in
Figure 2.
The formulation of the proposed problem considers that the resulting flood cost is defined according to land use. Thus, the damage function is mathematically characterized by the expression:
In this equation,
Cmax represents the maximum cost, when flood level
ymax is reached.
y is the existing flood level in the specific node;
λ = 4.89 and
b = 2 are adjustment coefficients of the curve; and the parameter
ymax = 1.4 is the level from which the maximal economic damage is produced. In all the cases, Equation (6) depends totally on the value of
Cmax, which is presented in
Table 1, for different land uses and represents the maximum per area unit.
The cost evaluation C(y) described in Equation (6) required the determination of the flood level in each node. Therefore, the SWMM’s ponded area model is used. This model assumes the definition of a ponded area (Af) in each node. In this way, the flood level is obtained as the relation between the flood volume Vf and the area Af.
3. Methodology
The optimal design or rehabilitation in drainage networks involves the search for solutions in very large spaces. Accordingly, the probability of finding minimum solutions is very small due to the immensity of SS and the existence of multiple local minima. Developments in the field of genetic algorithms (GAs) have proven to be useful in the optimization of drainage networks.
The GAs test the evolution of a random population via a parallelism that is similar to Darwin´s law of natural selection. Some calibration parameters, including crossover probability, mutation probability and the population size control the optimization process. In this sense, the performance of population-based algorithms is directly related to the balance of exploration and exploitation of the SS. Traditionally, small population sizes have been related to premature convergence, since the population of the algorithm loses diversity too early, converging too early with poor solutions. Conversely, larger population sizes help ensure diversity of individuals, avoiding premature convergence, but the algorithm might waste considerable time exploring regions of the SS without any kind of interest. Consequently, parameter choice should be a trade-off between solution quality and search time. It should be noted that this work uses a modified version of classical GA, PGA, whose complete description can be found in [
18].
In the same manner, the stopping criterion is important for population-based algorithms as GAs. Three genetic algorithm stopping conditions are usually found in the literature: the objective function value reaches a certain pre-defined value, a defined absolute number of generations are performed or there is no improvement in the population for X iterations. In this work, the third option was used, i.e., a maximal number of generations
G without a change in the objective function value. Considering the characteristics of the problem and based on previous experiences [
25], a stopping criterion of 1000 generations without change was selected. As in the calibration of the population size, the choice of stopping criteria must prevent premature convergence, guaranteeing a good exploration and exploitation of the SS.
Additionally, it should be noted that the DVs had to be discretized. On one hand, for STs a maximum area is used, which is a function of the available surface with minimal urban impact and divided into partitions. Therefore, STs can be discretized in N divisions (N = N0,…,Nmax). On the other hand, the number of candidate pipe diameters was ND (ND = ND0,…,NDmax).
As a previous step, some algorithm tests were performed considering the full SS, i.e., all the nodes and lines of the network. According to protocol, several tests were carried out, in which it was appreciated that the space of solutions is so large that the algorithm barely finds good solutions. The enormous amount of local minimums causes the algorithm to be lost. A smaller solution space allows the optimization algorithm to find minimum values more easily.
So, this work presents a methodology for the rehabilitation of large drainage networks, reducing the SS of the problem. Additionally, this SS reduction will improve the solutions found by the PGA when the entire SS was used. The different options to reduce the SS are the following:
Reduce the number of nodes (n) in which STs could potentially be installed.
Reduce the number of lines (m) in which there could potentially be a change in diameter.
Reduce the discretization N that is made of the section of each of the STs.
Reduce the number of candidate diameters ND in the pipes.
The four ways to reduce the SS have been organized in a specific methodology. The complete process is summarized in
Figure 3, and basically consists of three stages: the pre-location of STs, the pre-selection of conduits and the final optimization. In the following subsections, each of these stages is described in detail.
3.1. Pre-locating Storm Tanks
There are some previous studies oriented to the pre-locating of STs [
25]. However, in this case methodology described in
Figure 1 is used as a basic tool to determine the possible locations of the STs. The first step of the methodology is summarized on the left hand side of
Figure 3. Some runs (
Nit) are performed with all the nodes of the network (n =
NN), but without including the diameters in the optimization process (
m = 0). Thus,
Nit optimizations are made, considering only the cross section (S) of the tanks as DVs and without modifying the diameters of the network. Since the objective is the reduction of the SS, the discretization of the cross sections of the tanks (S) is carried out with the smallest number of divisions (
N =
N0). This coarse discretization of each section is carried out since the objective is not to calculate its exact value, but to determine in which nodes the installation of an ST is adequate. That is, the objective of this step is selecting the nodes where STs could be installed in the rehabilitation of the network, i.e., a pre-location of STs.
In this step, the obtained solutions of initial trial runs are ranked according the value of the objective function. Each of these solutions contains a distribution of STs in the network and a dimensioning, even if approximate, of the ST size required in each node. However, the analysis is not focused on the size of the STs but on their location. Therefore, a percentage pn of the best simulations is selected. The analysis of these simulations allows identifying the nodes where an ST could be installed and a list of ns possible locations is created. These nodes are selected because they are repeated as the location of an ST in all the pn selected solutions.
3.2. Locating Lines of Possible Pipe Substitutions
The objective of this second step is to reduce the number of pipes in which the diameter can be modified. Another set of Nit optimizations is run. The DVs of each optimization are the cross section of the ns selected nodes in the previous process and the Nc conduits of the network. For both types of variables the reduction of the SS is applied. Therefore, the discretization of the cross section of the tanks is the coarsest (N = N0) and the range of pipes available is the smallest (ND = ND0). In this step, the aim is to find a pre-location of pipes to be substituted.
Analogous to what happened in the previous step, an analysis of the solutions with the best value of the objective function is carried out. This analysis is not focused on the section of the tanks or on the diameter of the ducts. The analysis is centered on locating the conduits whose dimensions have been modified with respect to the initial situation.
Finally, a percentage pm of the best solutions are selected. The conduits selected are those that appear repeated in the solutions defined by the percentage pm. Analyzing these solutions, the list of ms pipes whose replacement is repeated in the pm best solutions is selected.
3.3. Final Optimization, Location and Optimization of Storm Tanks and Pipe Diameters
The last step considers the results of the two previous steps: the pre-location of the STs and the location of the pipes that could potentially be rehabilitated. A simulation is defined with the ns selected nodes and the ms selected lines. Although the number of DVs is smaller, the exploration of each of these variables must now be greater. Therefore, the STs are discretized to the maximum (N = Nmax) and the list of candidate diameters for the conduits is also the largest (ND = NDmax). This final optimization determines the location and size of the STs to be installed and the diameters of the pipes to be rehabilitated.
In short, the reduction of SS in a problem with continuous and discrete variables has been based on two aspects: the reduction of the number of DVs and the level of detail of each of the variables. During the first two stages, the number of DVs is reduced by two with a lower level of exploration of each variable. In the final simulation, a smaller number of variables is used, but with a higher level of exploration. This reduction of the SS allows obtaining solutions to problems with large SS and multiple local minimums.
4. Case Study
The drainage network is called E-Chicó. It is divided into 35 hydrological sub-catchments over an area of 51 hectares. All the conduits are circular with diameters between 300 and 1400 mm, with a total length around 5000 m. The network works completely by gravity with a maximum difference of 39.28 m.
The diagnosis of the network and the evaluation of the possible solutions have been carried out using projected rain obtained by means of the alternative blocks method and the IDF curve. This process has been done with the original IDF curve (actual rain), the one with which the network was designed, and the one obtained after applying several climate change models [
22]. As can be seen (
Figure 4), the consideration of the climate change effects on the study area implies an increase in the intensity of rainfall above 45%.
The results of the first simulation considering the current IDF curve barely cause flooding in any node of the network. On the other hand, if the network is analyzed with the IDF curve obtained from climate change analysis, flooding occurs in 11 nodes of the network with a volume of 3833 m
3, representing 18% of the total runoff of the network (21,233 m
3).
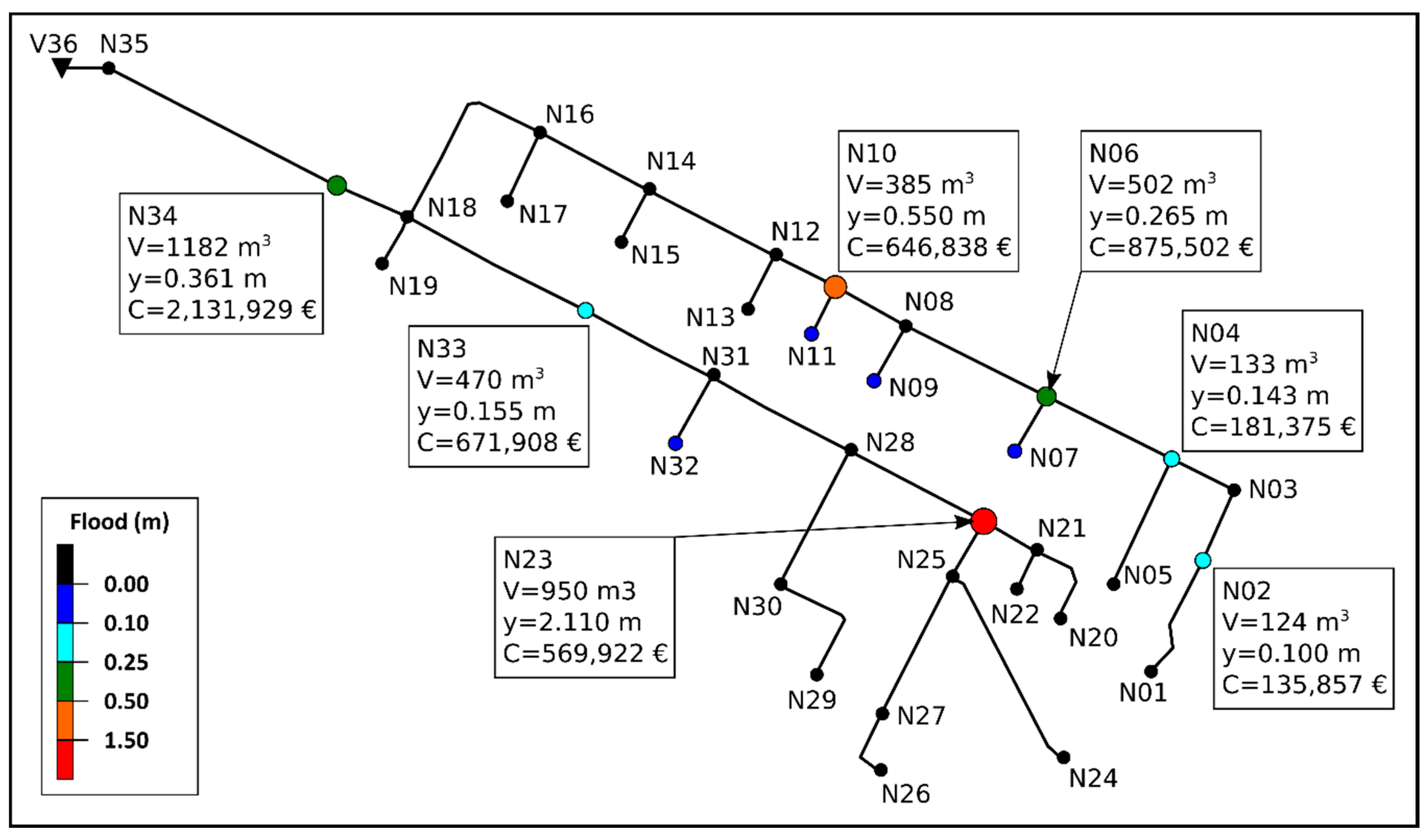
Figure 5 shows the nodes in which the main floods occur (flood level over 10 cm), indicating the flood volume V; the maximum level
y reached by the water in the node and the cost associated with flood damage.
Table 2 shows the detail of the flooded nodes: the flood volume, area and level, and the damage cost obtained from Equation (6). The nodes shown in
Figure 5 are highlighted in bold in
Table 2.
The total cost of flood damage in the study area amounts to 5.24 million euros, which suggests the importance of rehabilitating this sector of the network and applying the proposed methodology.
4.1. Application of the Drainage Network Rehabilitation Methodology to E Chico
In the first place, the validity of the methodology described in
Figure 1 will be tested. Taking as a starting point the simulation whose results are obtained in
Figure 3, three different simulation scenarios are considered:
Scenario 1: Rehabilitation of the network based only on the modification of conduits of the network and substituted them by another with different diameter. This scenario has 35 DVs, as all the conduits are potentially changed.
Scenario 2: Rehabilitation of the network by installing only STs. This scenario also has 35 DVs, corresponding to the 35 potential nodes in which STs can be installed. The maximum section to be installed in the tank potentially installable is defined in each node. Subsequently, the optimization method selects the cross section according to the discretization (N) of this variable. It should be noted that the section minimum value corresponds to a diameter of 1.2 meters, corresponding to the cross-sectional value of a manhole.
Scenario 3: Rehabilitation of the network combining the installation of conduits and STs. The number of DVs is 70.
In order to be able to simulate the previous scenarios, all the data described in the formulation of the problem should be defined. That is, it is necessary to specify the values of the installation cost functions of the new conduits and the investment cost for the construction of the new STs to be installed at the nodes. This involves determining the values of the parameters
α and
β of Equation (4) and parameters A, B and C of Equation (5). In this case, price databases have been used for the area where the network is located (Colombia). In this way, the values of the characteristic parameters of Equations (4) and (5) are shown in
Table 3.
At the same time, simulation of scenarios 1 and 3 requires defining a full range of pipe diameters. The full range of diameters used in this case is shown in
Table 4. This table assumes a value of the parameter
ND =
NDmax = 25, since it must be combined with an additional state corresponding to the event of leaving the drainage line as it is in the model; that is, without rehabilitation.
Table 4 also shows the installation cost of each diameter. These costs are obtained from the application of Equation (4) with the coefficients defined in
Table 3.
The results of the optimization of the first three scenarios will allow comparing the effect of carrying out the rehabilitation of the drainage network by different methods. The results will show the benefits of rehabilitation through the combined use of STs and the replacement of pipes. One of the main conclusions obtained from this first analysis is the time necessary to complete the simulations due to the high number of DVs and the wide of solutions space. In addition, after performing numerous simulations, a large dispersion in the results was also observed. Additionally, it could be concluded that the combination of diameter changes and ST installation gave better results than the optimization of any of them separately.
For the Scenario 3 corresponding to the rehabilitation of the whole network, some previous simulations have been performed with the following characteristics: n = 35, m = 35, N = 40 and ND = 25. The best objective function value obtained was 268,292 €, corresponding to the substitution of 21 pipes and the installation of 16 STs. Afterwards, a sensitivity analysis with different population sizes and different maximum number of generations was done, but no improvement was obtained.
So, the presented methodology has undergone an improvement process in order to obtain optimal results without the need to significantly modify the parameters of the genetic algorithm used to perform the simulations. Since these parameters are estimated based on the number of DVs and the complexity of the problem, the objective was now focused on reducing the number of nodes and lines that can be modified.
4.2. Application of the Solution Space Reduction Methodology to E-Chicó
The application of the proposed methodology (
Figure 3) to the E-Chicó network begins with the process of
pre-locating STs. The parameters used in this process are:
The number of simulations defined is one hundred (Nit = 100).
The discretization of the ST area is reduced to its minimum value (N = N0 = 10).
Only the sections of the tanks potentially to be installed in the nodes of the network are considered as DVs (n = NN = 35).
No conduit can be modified during the process (m = 0).
The basic parameters of the PGA algorithm, population size (Npop) and the end criterion based on a number of generations (Ngen) without change, are fixed at 100.
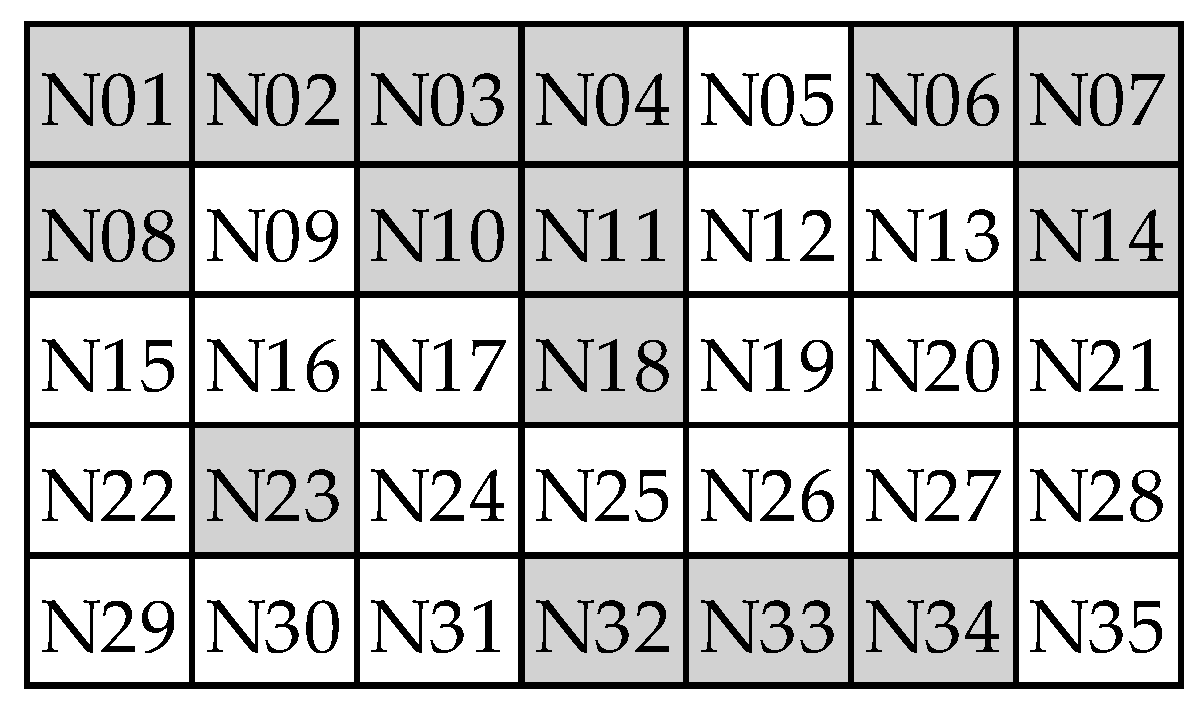
Once all the simulations have been carried out, the percentage
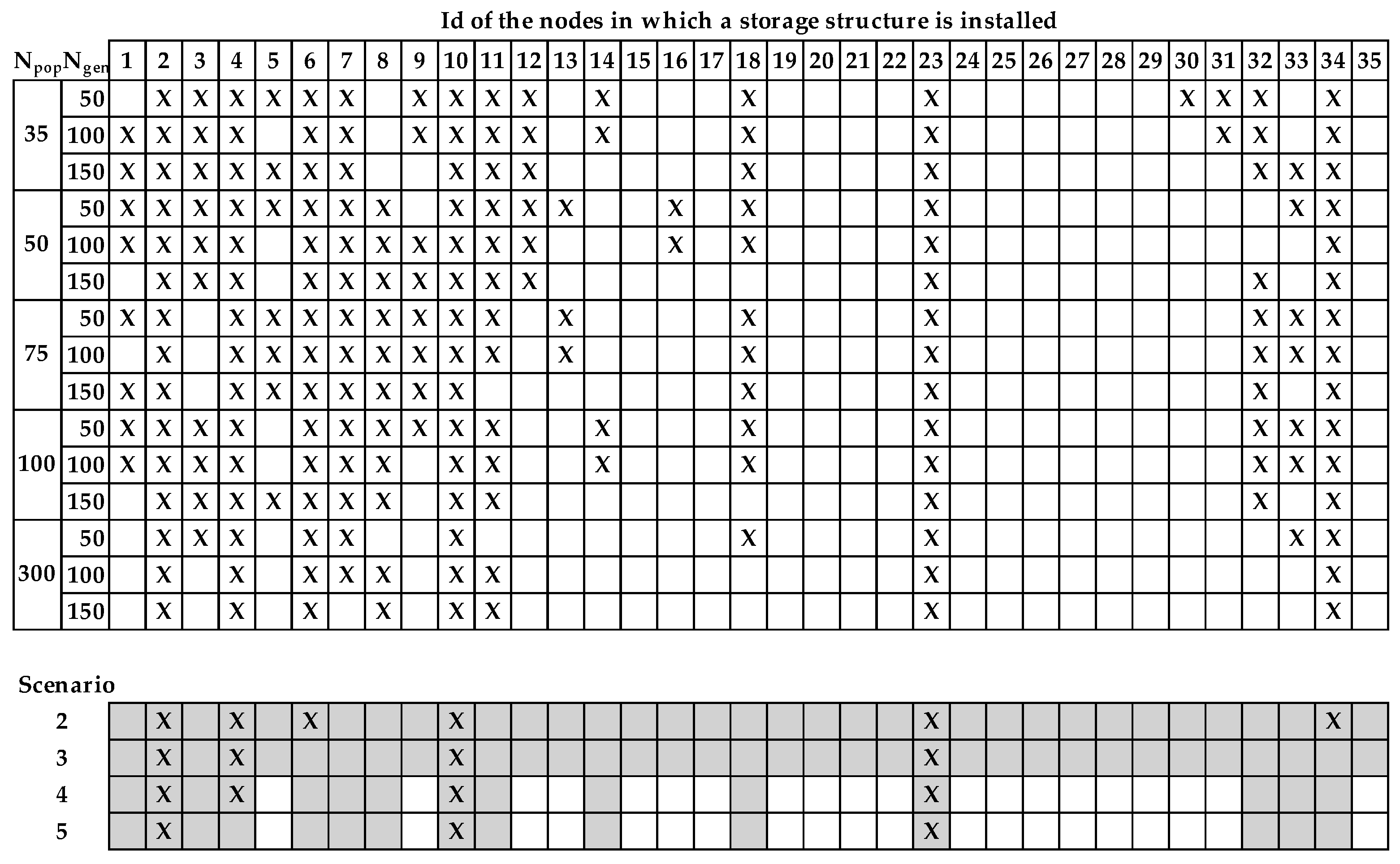
pn of solutions with the best value in the objective function is selected. In short, the 10 best solutions are selected. In each one, it is analyzed in which nodes an ST is installed. This generates a list of pre-locations of STs in the network. In this case, this list contains a total of 15 possible locations of the STs. In
Figure 6, the shaded cells represent the selected nodes.
In order to validate the methodology of pre-localization of STs, the previous process has been repeated, but by expanding the discretization of the tank area to the maximum value (
N =
Nmax = 40). The results obtained lead to the same list of selected nodes as indicated in
Figure 6.
The second stage of the SS reduction process is the pre-selection of conduits. For this, the pre-location of STs from the previous stage is used and a reduction in the number of potentially substitutable pipes is sought. The parameters used in this process are:
The number of simulations is the same as in the previous stage (Nit = 100).
The DVs are the areas of the ns nodes selected in the first stage and the diameters of all the conduits (n = NC = 35) of the network.
The discretization of the area of the STs is kept at the minimum value, as it happened with the previous stage of the process.
The basic parameters of the PGA algorithm are the same as in the previous phase (Npop = 100, Ngen = 100).
Instead of using the full range of diameters (
Table 4), a range of reduced diameters is used, the details of which can be seen in
Table 5. This table shows the diameters
D of the reduced range and the unit costs (
C) obtained from the application of the cost function (4) with the parameters of the
Table 3. Note that although
Table 5 only has 9 values, the number of options for the DV is
ND = 10. This additional value corresponds to the option of not taking any action on the pipe.
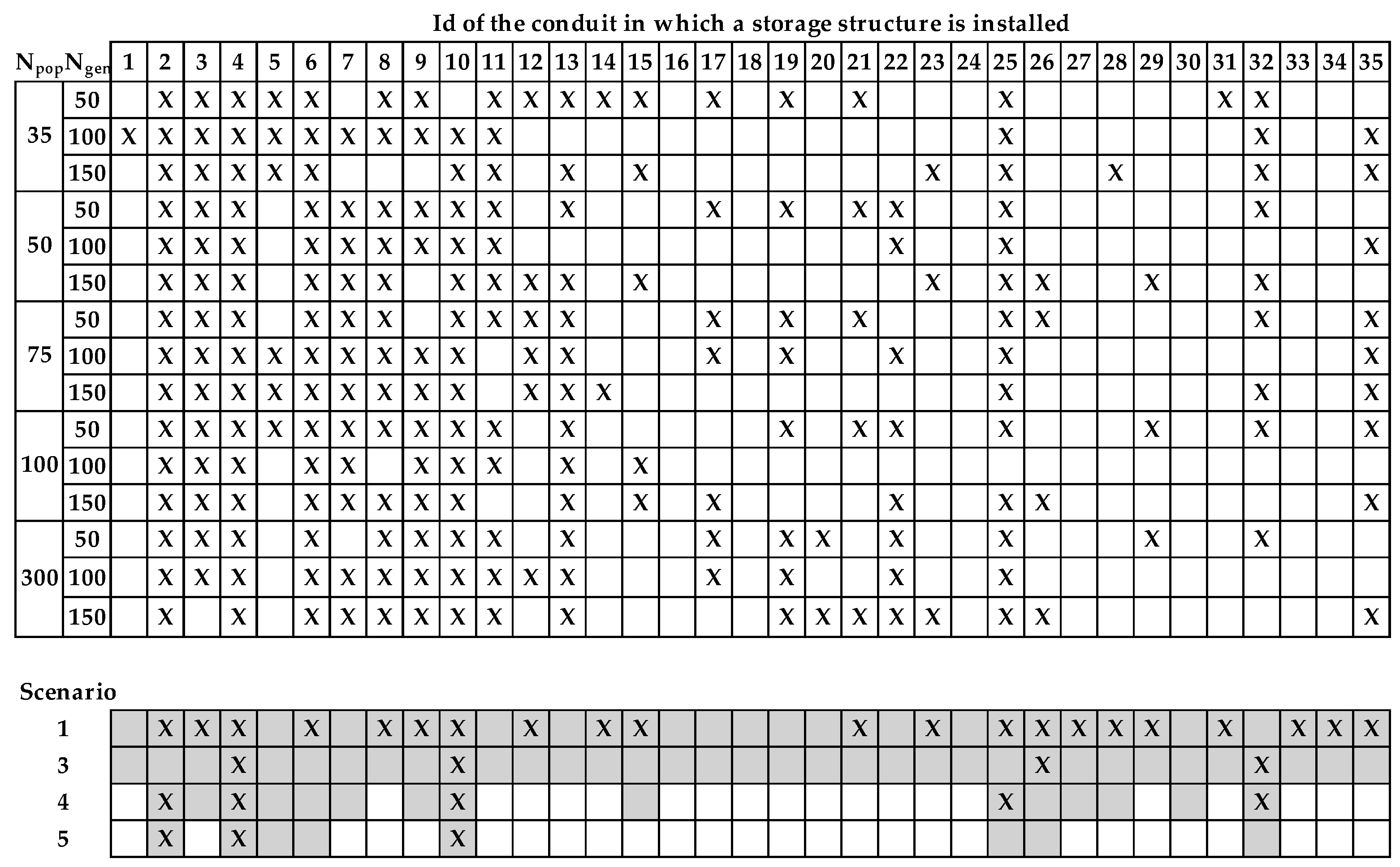
Once the simulations have been carried out, it has been decided to define two different conduit pre-selections. One is considering a probability of 10% of the best solutions (
pm1 = 10%) and another one considering only 5% of solutions with a lower value of the objective function (
pm2 = 5%). The preselected lines in each case are shown in
Figure 7. In the left part of the figure, the values corresponding to 10% are collected, highlighting the preselected lines by gray color. On the right hand side, the pipes selected for 5% of the best solutions obtained in this process are represented in an analogous way.
The pre-selection of ducts has been tested to validate performing the same simulations but using the full range of diameters (ND = NDmax = 25). The results obtained, in terms of the lines that would be pre-selected, are the same as those obtained in the case of using only the reduced range (ND = ND0 = 10).
In short, the process of conduits pre-selection leads to select 15 pipes in case of selecting 10% of the best solutions or only 8 lines when the 5% of best simulations is considered. At this moment, the final stage of the process is the final optimization. In this phase, the reduction of the SS is used: 15 possible locations of STs and 8 or 15 possible lines to be rehabilitated. Therefore, the analysis of the network requires the definition of two new scenarios:
Scenario 4: Rehabilitation of the network combining the possible installation of STs in the 15 selected nodes and the 15 conduits that can be substituted.
Scenario 5: It is the same scenario as the previous one (scenario 4), with the difference that the number of potentially replaceable conduits is only 8.
4.3. Results Analysis
The results obtained from the optimization in the five scenarios considered are shown in
Table 6. In each scenario, the following values appear: the number of DVs (nodes in which STs can potentially be installed and lines where their diameter could potentially be modified), the value of the objective function (divided into flood costs, investment costs in STs and investment costs in pipes), the number of elements to install of each type (STs and conduits) and the size of the SS of the problem. The scenario that offers the worst results (scenario 1) would be classic rehabilitation based solely on the replacement of pipes. The solution based on the use of STs has better results than the rehabilitation based on pipe substitution (scenario 2). However, the combined use of pipe substitution and installation of STs is shown as the best option of all (scenario 3).
Comparing the solutions that use joint rehabilitation pipes-STs, it is observed that the reduction of the SS significantly improves the solutions. That is, pre-location of STs and pre-selection of conductions reduce the SS in an amount that allows a better exploration. Therefore, according to
Table 6, the best solution is the one proposed by scenario 5, which considers the installation of 3 STs and the replacement of 3 conduits. As it is observed, the reduction of the SS between scenario 3 and scenarios 4 and 5 is many orders of magnitude, which helps to explain the improvement in the solutions.
The methodology used assesses the flood economically. Therefore, the solutions of scenarios 4 and 5 present flood costs (8353 and 12,701 respectively). These flood costs correspond to nodes whose flood level does not exceed 1.5 cm. However, from the point of view of the function defined in Equation (6), any level of flooding has an associated cost. Additionally,
Table 7 and
Table 8 present the results of the flood nodes for scenarios 4 and 5. As can be seen, the cost of flooding is not zero. However, both flood volumes (52.77 and 75.78 m
3) and flood levels are very low. Therefore, from a practical point of view it can be considered that the solutions are acceptable.
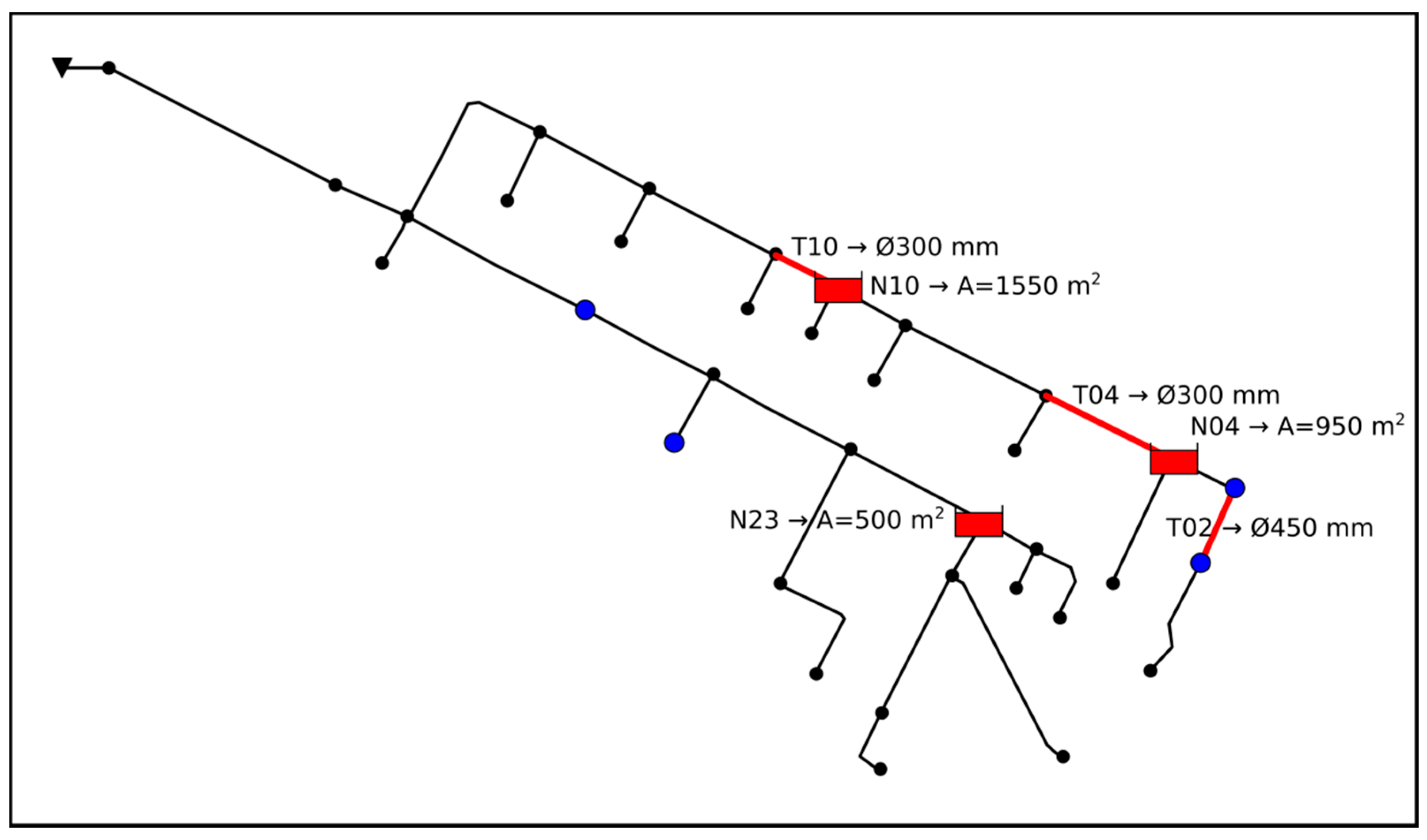
Figure 8 represents the location of the STs obtained in scenario 5, as well as their size. Also, the flooded nodes are represented (blue nodes). Additionally, the figure represents the lines that have been necessary to modify and the size of the new conduits. It should be noted that in the case of conduits T04 and T10, the solution obtained involves the installation of a diameter smaller than the original one. This clearly indicates the need to install in these sections a resistant element (a gate or an orifice) that introduces a head loss equivalent to the one that involves the installation of the new smaller diameter.
The installation of control devices in drainage networks allows the accumulation of water in certain points of the network, decreasing the time of concentration downstream, and thereby reducing flooding. This is why this “hydraulic control” is one of the techniques that is often used to improve the efficiency of STs. In this case, the appearance of solutions, such as those of conduits T04 and T10, supposes the need to install a gate or an orifice at the outlet of the STs that introduces a certain head loss. This head loss must be such that the equivalent capacity of the original pipeline together with the control device used is equal to the transport capacity of the calculated pipeline.
In short, two of the three STs installed should have hydraulic control. Therefore, these tanks must have a control element at the exit that contains the avenue of water in the tanks and reduces the water travel time towards the downstream sections. If
Figure 8 is compared with
Figure 5, the installation of the STs together with the hydraulic control elements allows not only a reduction of flooding upstream, but also control of flooding that occurred in nodes downstream from these STs (i.e., nodes N31 and N34).
Simulations with a larger number of DVs are usually associated with a longer calculation time. However, the real difficulty of a problem is expressed by its size (
PSmax) according to Equation (2). Therefore, in
Table 9 the size of the problem of each scenario is presented. The table also includes a measurement of the calculation time, expressed as the number of times it is necessary to evaluate the objective function.
As can be seen, the larger the size of the problem, the greater the number of evaluations of the objective function required to find the solution. It is for this reason that the use of an SS reduction technique and reduction of the size of the problem has been effective.
The reduction in the number of DVs allows a better exploration of the SS, which means the smaller the number of decision variables, the better the solution found. However, reducing the number of DVs entails another effect. Simulations performed with large numbers of DVs cause a large dispersion of solutions, while solutions obtained with fewer DVs offer a much narrower range of solutions. Thus,
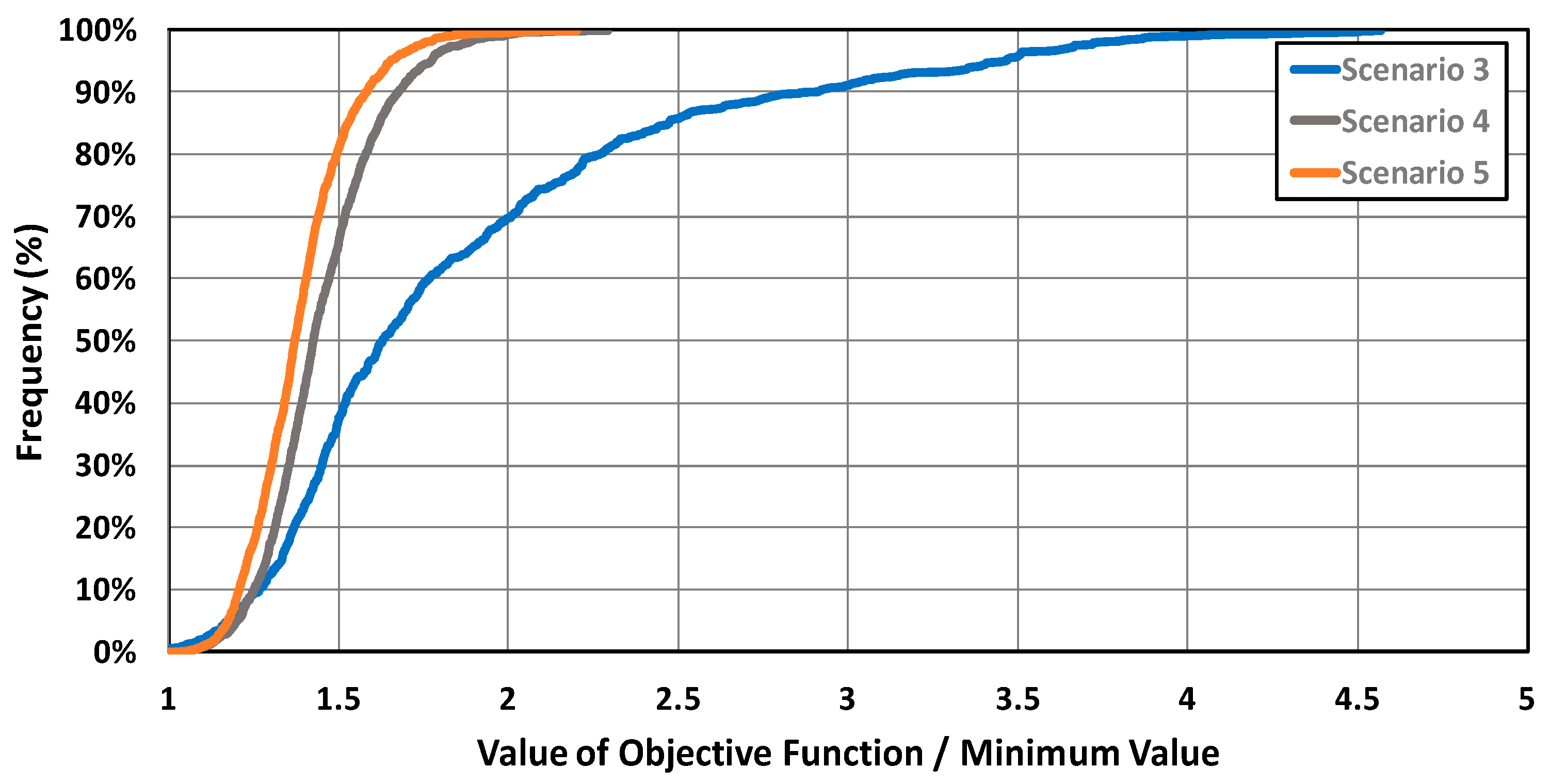
Figure 9 represents a comparison of the solution variability range offered in scenarios 3, 4 and 5. It shows on the X-axis the relation between the value of the objective function in a simulation and the minimum global value for this scenario. On the Y-axis is represented the frequency of the different solutions obtained with respect to the minimum value obtained. That is, the more vertical the curve, the greater concentration of solutions. On the contrary, if the slope of the curve is smaller, it indicates that there is a greater dispersion of the solutions. Suppose that a value of 1.5 is set as a reference (the solution obtained has a maximum extra cost of 50% over the optimal solution). In that case, only 37% of the solutions obtained with scenario 3 are below that level. In the case of scenario 4, 66% of solutions present a cost smaller than 1.5 times the minimum value of the objective function. For scenario 5, this percentage is even greater (81%). In short, the reduction of the SS not only allows obtaining better solutions but at the same time it makes the range of good solutions (solutions close to the minimum) greater.
4.4. Sensitivity Analysis of the SS Reduction
The main uncertainty is whether the SS reduction methodology could affect the final solution. It must be borne in mind that STs pre-localization and conduits pre-selection were performed using the PGA algorithm with a population size
Npob = 100 and a termination criterion
Ngen = 100. In order to validate the selection, a sensitivity analysis of the selection process of STs and conduits has been carried out. The process of reducing the SS was repeated with different values of
Npop and
Ngen. The different values of the population size were 35, 50, 75, 100 and 300 elements, while the values used as finalization criteria were 50, 100 and 150 generations without a change in the value of the objective function. The results obtained are shown in the following figures. In
Figure 10, the nodes that could potentially be a ST location are collected for each combination of values of
Npop and
Ngen. On the other hand,
Figure 11 shows the lines potentially replaceable. In both cases, the node or line selected has been indicated with an X in the corresponding cell.
The sensitivity analysis of
Figure 10 and
Figure 11 validates the SS reduction methodology based on the pre-location of STs and the pre-selection of conduits. In the lower part of
Figure 10, the DVs used in each scenario are indicated by a shaded cell, and X indicates the nodes that finally provide a solution for the installation of a ST. The nodes that finally appear as solutions in the scenarios are those that had been selected mostly in the process of pre-selection of STs. In short, regardless the value of
Npop and
Ngen the preselected nodes would have been almost the same, and in any case those that appear in the final solutions of scenarios 3, 4 and 5 would have always been selected.
Something similar happens in the case of pre-selection of conduits.
Figure 11 shows the results of the sensitivity analysis and the results of scenarios 1, 3, 4 and 5. As in
Figure 10, the DVs used are indicated as shaded cells, and the lines that are finally replaced are indicated with an X. The results show that the lines selected for different values of
Npop and
Ngen are almost the same. That is, selected lines are those that are finally found in the final solutions of scenarios 3, 4 and 5. Moreover,
Npop and
Ngen parameters have no influence on the pre-location of STs or on the pre-selection of pipes. Therefore, the SS reduction methodology can be considered reliable.
5. Conclusions
The proposed methodology for the rehabilitation of drainage networks, based on the combined use of STs and the replacement of conduits, has been shown to be effective in solving the problems of insufficient drainage networks. Despite the effectiveness of the presented methodology, a certain disparity is detected in the obtained solutions due to the enormous size of the SS. Therefore, a complementary strategy that allows the reduction of SS is presented. Once the methodologies area applied to the case study, it is possible to extract the following conclusions:
The increase in rainfall intensities caused by climate change causes originally well-designed networks to present flooding problems. The use of STs has been shown as an effective technique to solve this problem. However, the effectiveness of this method is even greater when it is combined with the rehabilitation of some pipes of the drainage network. The results shown by scenarios 1, 2 and 3 presented above show how the combined action of STs and pipe renewal (scenario 3) is much more effective than the isolated action of any of the other two actions (scenarios 1 and 2).
The number of DVs required for the rehabilitation of a drainage network can be very high. This may cause (
Figure 9) the optimization model to give solutions that are quite dispersed and sometimes far from the optimal values required. It is well known that the importance of meta-heuristic algorithms does not lie in the optimality of their solutions, but in the ability to obtain large sets of good solutions. That is why the disparity of solutions observed with large numbers of DVs can become a problem.
An alternative methodology has been proposed for the reduction of the SS that permit us to locate solutions that are better and less dispersed than those obtained with the initial model. This methodology is based on the pre-location of STs and the pre-selection of possible conduits. The methodology uses the PGA developed, reducing the SS by using a smaller discretization of the size of the STs, a smaller range of diameters of pipes, and a smaller number of elements (tanks and pipes). The final result has proven to be effective for the cases analyzed, not only because it reduces SS and computing times, but also because it obtains better solutions (scenario 4 and 5). Likewise, the solutions obtained with the scenarios that use a reduced SS (scenarios 4 and 5) are much more concentrated and less dispersed (
Figure 9) than those obtained initially.
The SS reduction methodology in the case study has been shown to be reliable and stable since variations in the Npop and Ngen parameters of the PGA model hardly modify the preselected lines and nodes.
The best solutions suggest the suitability of installing control devices as a strategy to improve the operation of drainage networks. These control elements are static: either orifices or gates in a fixed position. In the solutions of scenarios 4 and 5, the installation of STs is complemented with the presence of this devices at the exit of the ST. This additional hydraulic resistance has been represented by a conduit with a diameter lower than the original one. As indicated previously, this type of operation helps to increase the concentration times in the critical nodes of the network.
The methodology based on the use of STs is adequate for the rehabilitation of drainage networks. The optimization model and the SS reduction methodology allow obtaining good solutions to a really complex problem. The resolution methodology used in the E-Chicó network can be extended to any type of drainage network, since the approach of the method has been so general to be easily extrapolated to other cases.
The extrapolation of the method to other networks generates some interesting uncertainties, such as the possible behavior of drainage networks with pumping stations. In this case, where the network has already installed pumping systems, the start and stop levels of the pumps and the size of the suction tank can be defined as DV. In the case of installing new pumping systems, the DVs would be the flows to be evacuated by each pump. In this case, it would be necessary to include in the objective function the investment cost associated with the construction of the new pumping equipment. In any case, it seems that the exposed methodology would be applicable to this situation.
It should be noted that the best solutions do not always eliminate the presence of floods in the network. In the case that solutions without flood are desirable, there are two possibilities. The first one is to allocate higher costs to the presence of floods that shift the optimum to solutions where the installation of STs or new conduits is profitable. The second option would be to run the problem statement from a multi-criteria point of view. With this type of approach, one could determine the level of investment required for each level of expected flood damage.