Storm Energy Flux Characterization along the Mediterranean Coast of Andalusia (Spain)
Abstract
1. Introduction
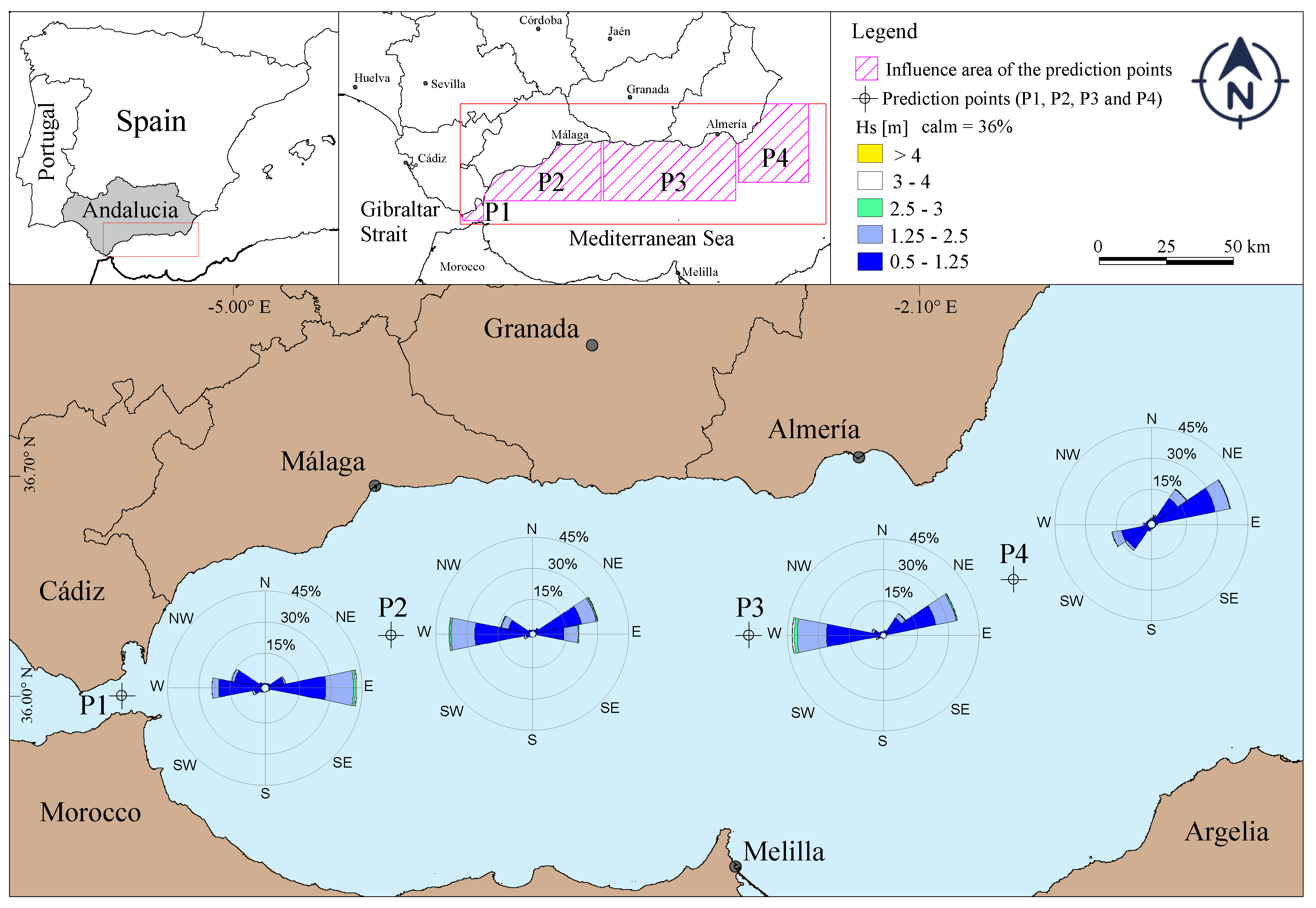
2. The Study Area
3. Methods
3.1. Wave Climate Preliminary Analysis
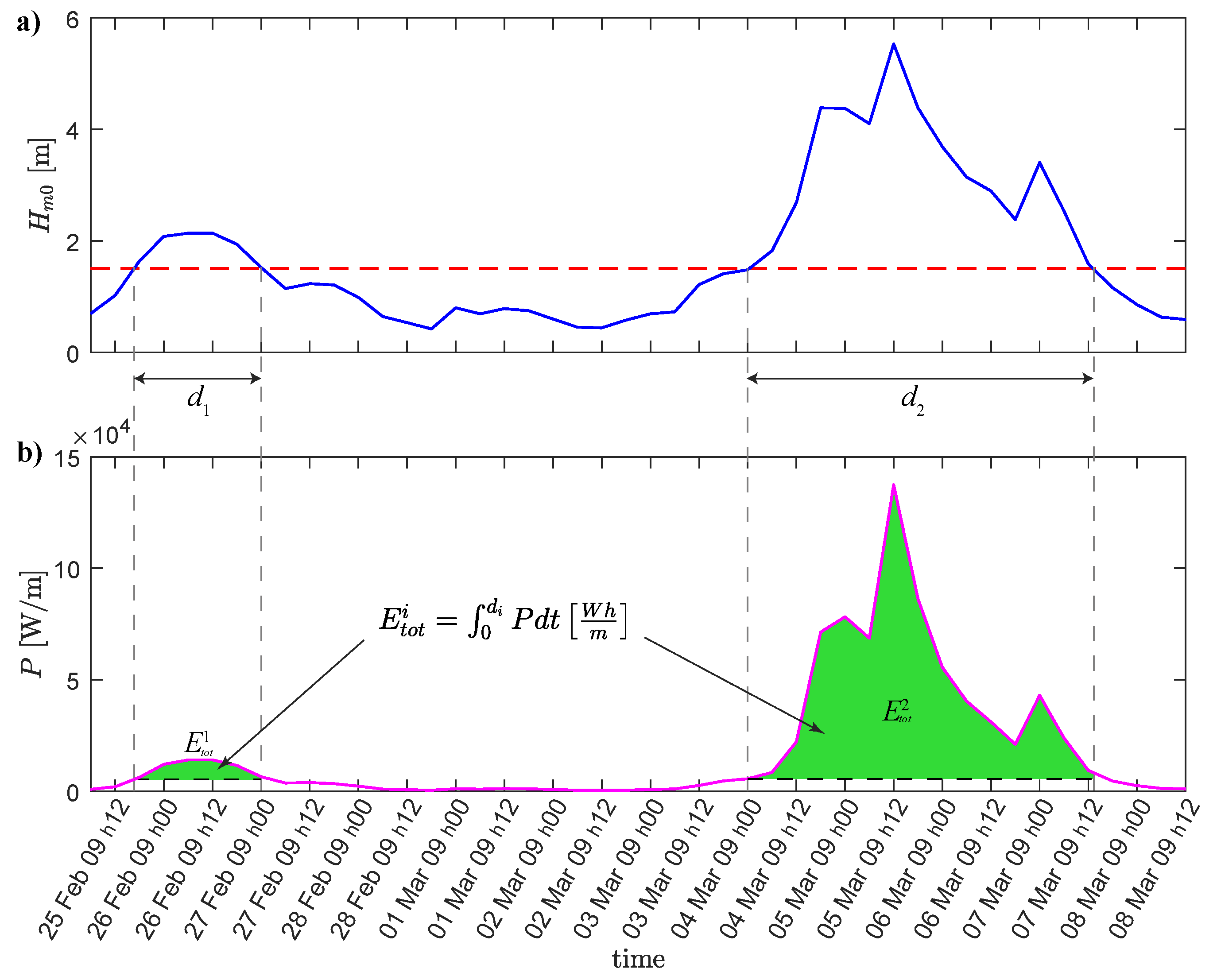
3.2. Storm Classification Using the Energy Flux
The Return Period of the Energy Flux of Storms
3.3. Stormy Year
4. Results and Discussion
4.1. Wave Height Characterization
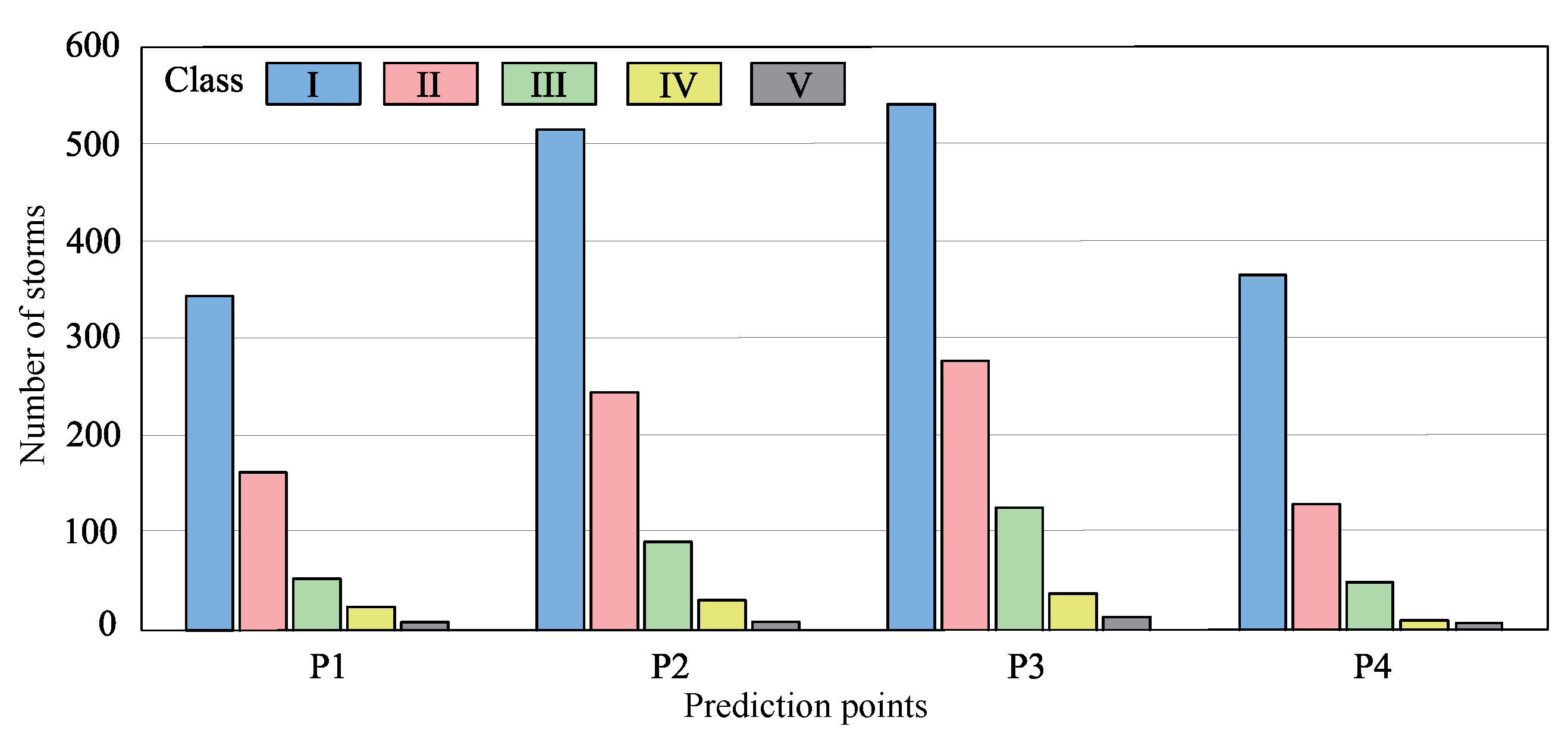
4.2. Storm Characterization
4.3. Characterization of Stormy Years
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CDF | Cumulative Distribution Function |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| ERA-Interim | ECMWF Reanalysis (from January 1979 onward) |
| POT | Peak Over Threshold |
| WAM | Wave Model |
Symbols
| Duration of i-th storm | |
| Total energy i-th storm | |
| Weibull Cumulative Distribution Function of energy flux | |
| Frequency of occurrence related to the empirical recurrence interval | |
| g | Gravity acceleration |
| Spectral significant wave height | |
| Monthly mean of maximum spectral wave height within the studied date-range (35 years) | |
| Wave height threshold for storm definition | |
| Mean number of events per year | |
| m | Number of events (upper threshold) within the studied date-range (35 years) |
| Mean of total energy within the studied date-range (35 years) | |
| N | Number of storm events |
| P | Energy flux or wave power per unit of wave-front length |
| The stormy year empirical recurrence interval | |
| Water volumetric mass density | |
| Standard deviation of total energy within the studied date-range (35 years) | |
| Energy period | |
| Return period related to the probability of exceedance | |
| u | Weibull function second parameter |
| w | Weibull function first parameter |
| X | Abscissa of auxiliary variable for linear fitting |
| Y | Ordinate of auxiliary variable for linear fitting |
References
- Ministerio de Medio Ambiente y Medio Rural y Marino. Evolución de las Zonas Costeras en Europa; Editorial Ministerio de Medio Ambiente: Madrid, Spain, 2008; Volume 1, p. 108.
- Garcia, G.M.; Pollard, J.; Rodriguez, R.D. Origins, management, and measurement of stress on the coast of southern Spain. Coast. Manag. 2000, 28, 215–234. [Google Scholar]
- Manno, G.; Lo Re, C.; Ciraolo, G. Uncertainties in shoreline position analysis: The role of run-up and tide in a gentle slope beach. Ocean Sci. 2017, 13, 661–671. [Google Scholar] [CrossRef]
- Bacon, S.; Carter, D.T. Wave climate changes in the North Atlantic and North Sea. Int. J. Climatol. 1991, 11, 545–558. [Google Scholar] [CrossRef]
- Komar, P.D.; Allan, J.C. Increasing hurricane-generated wave heights along the US east coast and their climate controls. J. Coast. Res. 2008, 24, 479–488. [Google Scholar] [CrossRef]
- Rodrıguez-Ramırez, A.; Ruiz, F.; Cáceres, L.; Vidal, J.R.; Pino, R.; Muñoz, J. Analysis of the recent storm record in the southwestern Spanish coast: Implications for littoral management. Sci. Total Environ. 2003, 303, 189–201. [Google Scholar] [CrossRef]
- Mendoza, E.T.; Jiménez, J.A. Clasificación de tormentas costeras para el litoral catalán (Mediterráneo NO). Tecnología y Ciencias del Agua 2008, 23, 21–32. [Google Scholar]
- Mendoza, E.; Jimenez, J.; Mateo, J.; Salat, J. A coastal storms intensity scale for the Catalan sea (NW Mediterranean). Nat. Hazards Earth Syst. Sci. 2011, 11, 2453–2462. [Google Scholar] [CrossRef]
- Guisado, E.; Malvárez, G.C. Multiple scale morphodynamic mapping: methodological considerations and applications for the coastal atlas of Andalusia. J. Coast. Res. 2009, 56, 1513–1517. [Google Scholar]
- Pintado, E.G.; García, G.C.M. El estado morfodinámico de las playas a través de modelización numérica de propagación y asomeramiento del oleaje: El frente litoral de Doñana. GeoFocus. Revista Internacional de Ciencia y Tecnología de la Información Geográfica 2015, 1, 163–180. [Google Scholar]
- Anfuso, G.; Rangel-Buitrago, N.; Cortés-Useche, C.; Castillo, B.I.; Gracia, F. Characterization of storm events along the Gulf of Cadiz (eastern central Atlantic Ocean). Int. J. Climatol. 2016, 36, 3690–3707. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Anfuso, G. Coastal storm characterization and morphological impacts on sandy coasts. Earth Surf. Processes Landf. 2011, 36, 1997–2010. [Google Scholar] [CrossRef]
- Rangel-Buitrago, N.; Anfuso, G. Winter wave climate, storms and regional cycles: The SW Spanish Atlantic coast. Int. J. Climatol. 2013, 33, 2142–2156. [Google Scholar] [CrossRef]
- Halsey, S. Proposed classification scale for major northeast storms: East coast, USA based on extent of damage. In Geological Society of America, Abstracts with Programs (Northeastern Section); Geological Society of America: Boulder, CO, USA, 1986; Volume 18, p. 21. [Google Scholar]
- Dolan, R.; Davis, R.E. An intensity scale for Atlantic coast northeast storms. J. Coast. Res. 1992, 8, 840–853. [Google Scholar]
- Orford, J.; Hinton, A.; Carter, R.; Jennings, S. A tidal link between sea level rise and coastal response of a gravel-dominated barrier in Nova Scotia. Geophys. Monogr. 1992, 11, 71–79. [Google Scholar]
- Orford, J.; Carter, R. Examination of mesoscale forcing of a swash-aligned, gravel barrier from Nova Scotia. Mar. Geol. 1995, 126, 201–211. [Google Scholar] [CrossRef]
- Kriebel, D.; Dalrymple, R.; Pratt, A.; Sakovich, V. Shoreline risk index for northeasters. In Proceedings of the 1996 Conference on Natural Disaster Reduction, Washington, DC, USA, 3–5 December 1996. [Google Scholar]
- Zhang, K.; Douglas, B.; Leatherman, S. Beach erosion potential for severe nor’easters. J. Coast. Res. 2001, 17, 309–321. [Google Scholar]
- Manno, G.; Anfuso, G.; Messina, E.; Williams, A.; Suffo, M.; Liguori, V. Decadal evolution of coastline armouring along the Mediterranean Andalusia littoral (South of Spain). Ocean Coast. Manag. 2016, 124, 84–99. [Google Scholar] [CrossRef]
- Fernandez-Nunez, M.; Díaz-Cuevas, P.; Ojeda, J.; Prieto, A.; Sánchez-Carnero, N. Multipurpose line for mapping coastal information using a data model: The Andalusian coast (Spain). J. Coast. Conserv. 2015, 19, 461–474. [Google Scholar] [CrossRef]
- Guisado, E.; Malvárez, G.C.; Navas, F. Morphodynamic environments of the Costa del Sol, Spain. J. Coast. Res. 2013, 65, 500–505. [Google Scholar] [CrossRef]
- Boccotti, P. Wave Mechanics for Ocean Engineering; Elsevier: Amsterdam, The Netherlands, 2000; Volume 64. [Google Scholar]
- Dee, D.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Puerto del Estado. Recomendaciones para Obras Marítimas R.O.M. 0.3-91. Oleaje. Anejo I. Clima Marítimo en el Litoral Español; Technical Report; Ministerio de Obras Públicas y Transportes: Madrid, Spain, 1992.
- Monteforte, M.; Lo Re, C.; Ferreri, G.B. Wave energy assessment in Sicily (Italy). Renew. Energy 2015, 78, 276–287. [Google Scholar] [CrossRef]
- Lo Re, C.; Manno, G.; Ciraolo, G.; Besio, G. Wave Energy Assessment around the Aegadian Islands (Sicily). Energies 2019, 12, 333. [Google Scholar]
- Iglesias, G.; Carballo, R. Wave energy potential along the Death Coast (Spain). Energy 2009, 34, 1963–1975. [Google Scholar] [CrossRef]
- Vicinanza, D.; Cappietti, L.; Ferrante, V.; Contestabile, P. Estimation of the wave energy in the Italian offshore. J. Coast. Res. 2011, 64, 613–617. [Google Scholar]
- Jenks, G.; Caspall, F. Error on Choroplethic Maps: Definition, Measurement, Reduction. Ann. Assoc. Am. Geogr. 1971, 61, 217–244. [Google Scholar] [CrossRef]
- Lo Re, C.; Cannarozzo, M.; Ferreri, G.B. Present-day use of an empirical wave prediction method. Proc. Inst. Civ. Eng. Marit. Eng. 2016, 169, 3–14. [Google Scholar] [CrossRef]
- Almeida, L.; Vousdoukas, M.; Ferreira, Ó.; Rodrigues, B.; Matias, A. Thresholds for storm impacts on an exposed sandy coastal area in southern Portugal. Geomorphology 2012, 143–144, 3–12. [Google Scholar] [CrossRef]
- Dorman, C.; Beardsley, R.; Limeburner, R. Winds in the strait of gibraltar. Q. J. R. Meteorol. Soc. 1995, 121, 1903–1921. [Google Scholar] [CrossRef]
- Moritz, H.; Moritz, H. Evaluating extreme storm power and potential implications to coastal infrastructure damage, Oregon Coast USA. In Proceedings of the 9th International Workshop on Wave Hindcasting and Forecasting, Victoria, BC, Canada, 24–29 September 2006. [Google Scholar]
- Ferreira, Ó. Storm groups versus extreme single storms: Predicted erosion and management consequences. J. Coast. Res. 2005, 42, 221–227. [Google Scholar]
- Menéndez, M.; Mendez, F.J.; Losada, I.J.; Medina, R.; Abascal, A.J. Variaciones del régimen extremal del clima marítimo en el litoral español en el periodo 1958–2001. In El Clima entre el Mar y la Montaña. Asociación Española de Climatología y Universidad de Cantabria, Santander, Serie A; García Codron, J.C., Diego Liaño, C.F., De Arróyabe Hernáez, P., Garmendia Pedraja, C., Rasilla Álvarez, D., Eds.; Asociación Española de Climatología (AEC): Santander, Spain, 2004; Volume 4, pp. 73–84. [Google Scholar]

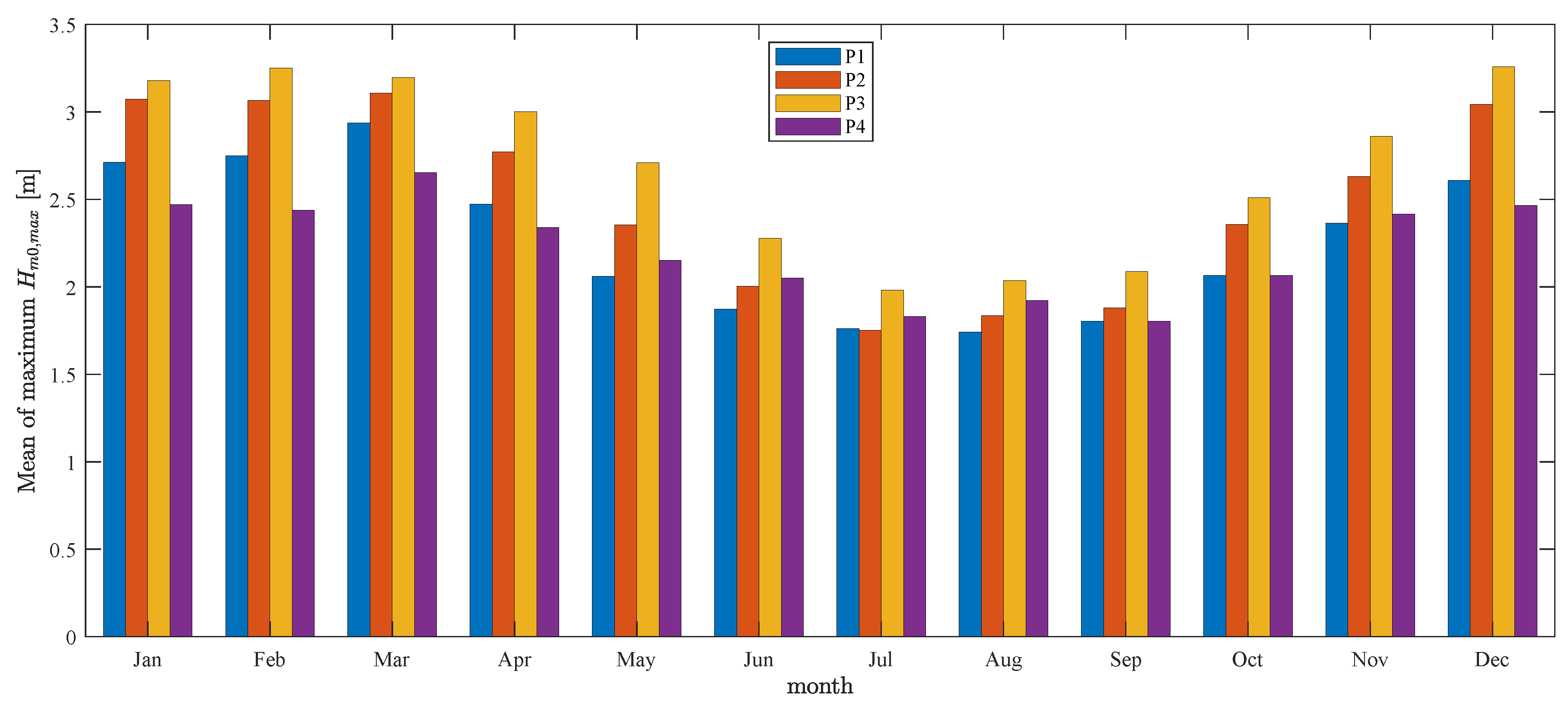
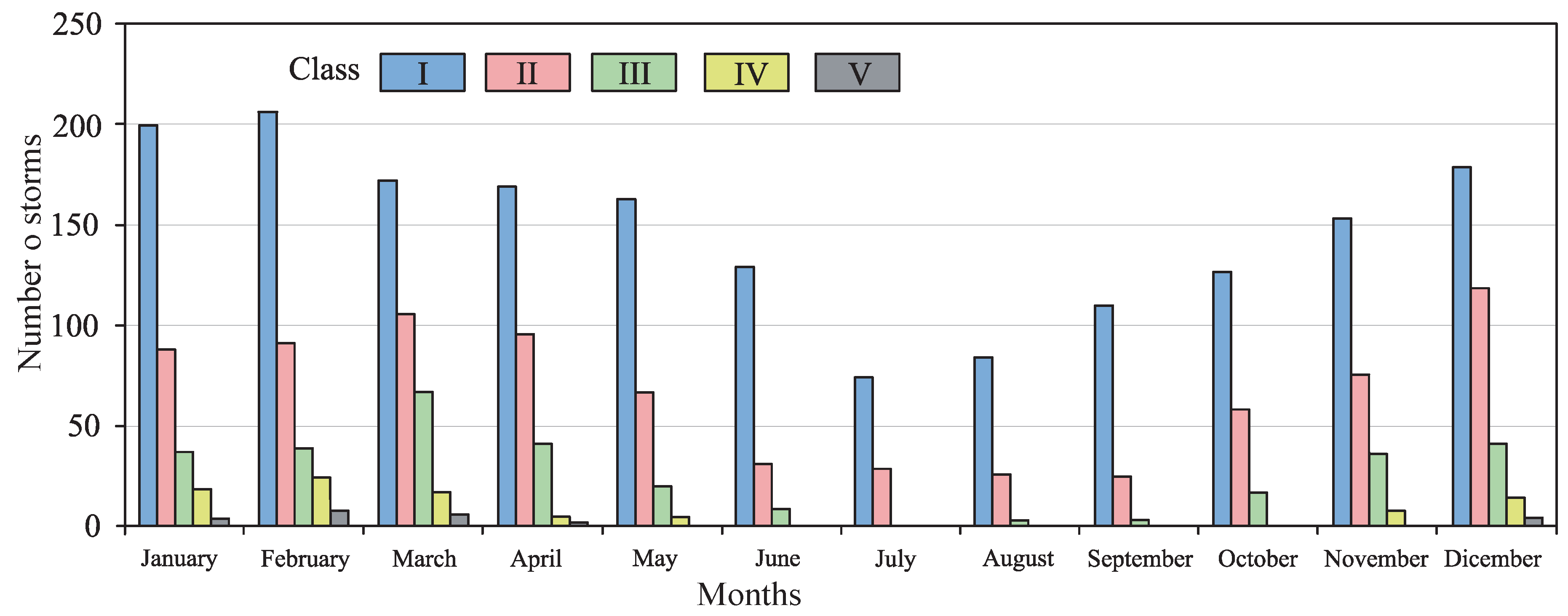
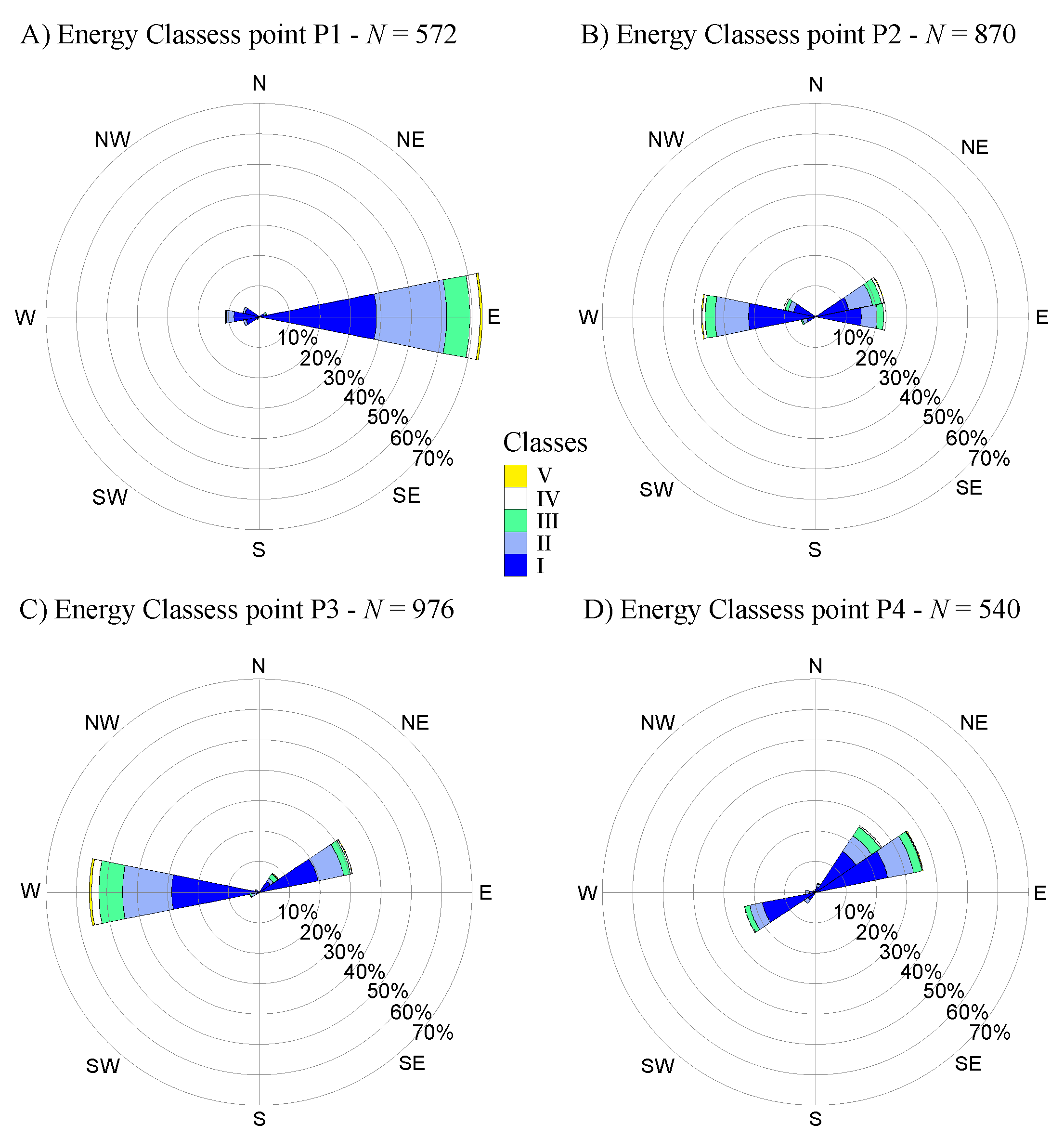
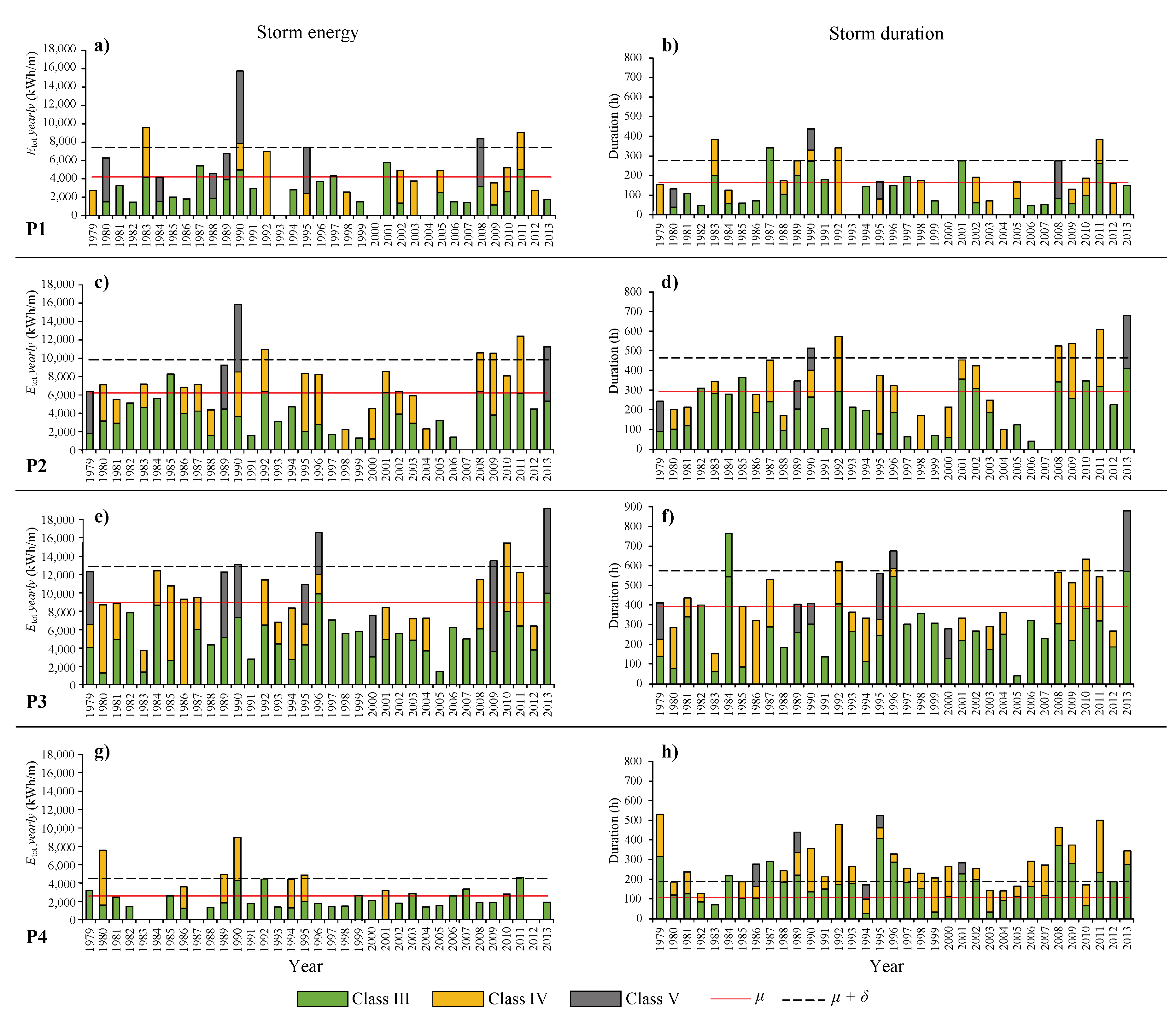
| Point | Class | [kWh/m] | Frequency [%] | [m] | [s] | D [days] | |||
|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | Mean | Standard Deviation | Mean | Mean | |||
| I | 108 | 503 | 265 | 59.6 | 2.01 | 0.26 | 6.5 | 0.9 | |
| II | 503 | 1100 | 730 | 27.8 | 2.61 | 0.37 | 7.4 | 1.9 | |
| 1 | III | 1100 | 2102 | 1509 | 8.3 | 3.27 | 0.48 | 8.1 | 2.9 |
| IV | 2102 | 4179 | 2624 | 3.5 | 3.64 | 0.65 | 8.5 | 4.2 | |
| V | 4179 | 9165 | 5635 | 0.7 | 4.68 | 0.98 | 9.7 | 4.8 | |
| I | 108 | 503 | 272 | 58.9 | 2.05 | 0.29 | 6.5 | 0.9 | |
| II | 503 | 1100 | 749 | 27.6 | 2.65 | 0.38 | 7.4 | 2.0 | |
| 2 | III | 1100 | 2102 | 1484 | 9.9 | 3.13 | 0.50 | 7.9 | 3.3 |
| IV | 2102 | 4179 | 2752 | 2.3 | 3.76 | 0.62 | 8.6 | 4.8 | |
| V | 4179 | 9165 | 5551 | 0.4 | 4.73 | 0.76 | 9.2 | 6.9 | |
| I | 108 | 503 | 270 | 55.0 | 2.05 | 0.28 | 6.5 | 0.9 | |
| II | 503 | 1100 | 739 | 28.0 | 2.69 | 0.39 | 7.4 | 1.9 | |
| 3 | III | 1100 | 2102 | 1460 | 12.4 | 3.22 | 0.47 | 8.0 | 3.1 |
| IV | 2102 | 4179 | 2775 | 3.4 | 3.99 | 0.52 | 8.9 | 4.4 | |
| V | 4179 | 9165 | 5632 | 0.9 | 4.87 | 0.74 | 9.5 | 7.0 | |
| I | 108 | 503 | 280 | 67.1 | 2.03 | 0.27 | 6.8 | 0.9 | |
| II | 503 | 1100 | 712 | 23.2 | 2.52 | 0.35 | 7.6 | 2.0 | |
| 4 | III | 1100 | 2102 | 1408 | 8.3 | 3.12 | 0.46 | 8.3 | 3.0 |
| IV | 2102 | 4179 | 2802 | 0.9 | 4.34 | 0.60 | 9.6 | 3.3 | |
| V | 4179 | 9165 | 5248 | 0.3 | 5.18 | 0.49 | 10.6 | 3.7 | |
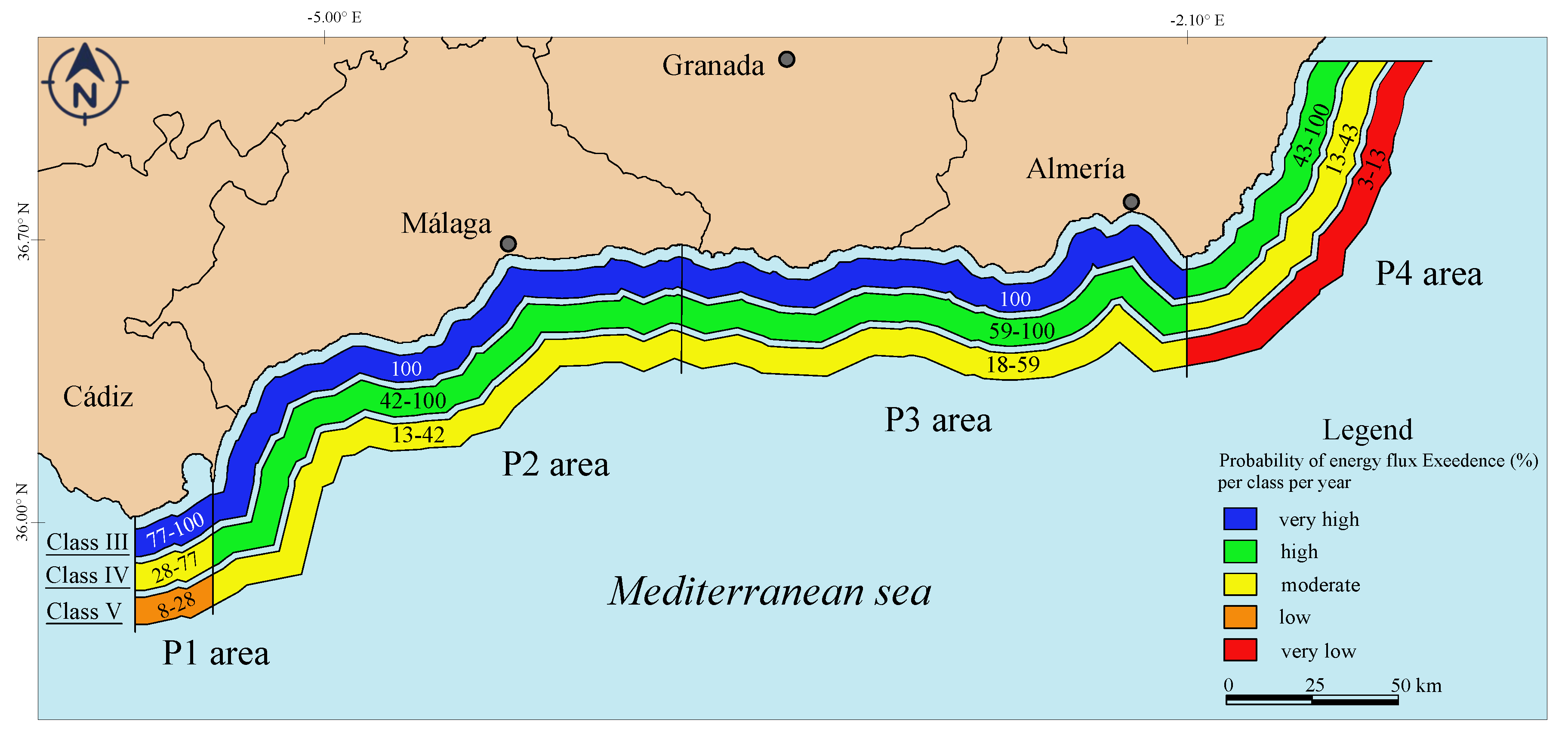
| Point | Class III | Class IV | Class V | ||||
|---|---|---|---|---|---|---|---|
| min | max | min | max | min | max | ||
| P1 | [year] | <1 | 1.3 | 1.3 | 3.6 | 3.6 | 11.9 |
| [%] | 76.9 | 100 | 27.8 | 76.9 | 8.4 | 27.8 | |
| P2 | - | <1 | <1 | 2.4 | 2.4 | 7.9 | |
| - | 100 | 41.7 | 100 | 12.7 | 41.7 | ||
| P3 | - | <1 | <1 | 1.7 | 1.7 | 5.4 | |
| - | 100 | 58.8 | 100 | 18.5 | 58.8 | ||
| P4 | <1 | 2.3 | 2.3 | 7.9 | 7.9 | 30.1 | |
| 43.5 | 100 | 12.7 | 43.5 | 3.3 | 12.7 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina, R.; Manno, G.; Lo Re, C.; Anfuso, G.; Ciraolo, G. Storm Energy Flux Characterization along the Mediterranean Coast of Andalusia (Spain). Water 2019, 11, 509. https://doi.org/10.3390/w11030509
Molina R, Manno G, Lo Re C, Anfuso G, Ciraolo G. Storm Energy Flux Characterization along the Mediterranean Coast of Andalusia (Spain). Water. 2019; 11(3):509. https://doi.org/10.3390/w11030509
Chicago/Turabian StyleMolina, Rosa, Giorgio Manno, Carlo Lo Re, Giorgio Anfuso, and Giuseppe Ciraolo. 2019. "Storm Energy Flux Characterization along the Mediterranean Coast of Andalusia (Spain)" Water 11, no. 3: 509. https://doi.org/10.3390/w11030509
APA StyleMolina, R., Manno, G., Lo Re, C., Anfuso, G., & Ciraolo, G. (2019). Storm Energy Flux Characterization along the Mediterranean Coast of Andalusia (Spain). Water, 11(3), 509. https://doi.org/10.3390/w11030509









