Abstract
Irrigated agriculture has considerable impacts on the environment. To minimize negative effects and maximize positive effects, it is necessary to provide comprehensive analyses beyond the strictly technical domain. In this study, we apply a methodology for determining priorities in implementing irrigation plans using multi-criteria analysis methods on a specific case study area in the sub-catchment area of the Orljava River in Požega–Slavonia County, Croatia. Five potential irrigation areas (Orljava–Londža, Pleternica, Ovčare, Treštanovci, and Venje–Hrnjevac) were analyzed according to five selected criteria: environmental protection, water-related (four sub-criteria), social, economic, and time criteria with different criteria importance (weight). The aim of this study was to confirm the adequacy of using six multi-criteria analysis (MCA) methods (mostly used: PROMETHEE, AHP, ELECTRE TRI, and the less used: DEXi, PRIME, and PCA) in determining priorities for fulfilling irrigation plans, present models for preparation of the input data, apply certain methods, and compare the results on the selected case study area. The methods’ adequacy was confirmed during the research. Five of the six MCA methods identified the Ovčare area as the most appropriate for irrigation development (i.e., it has priority in implementing the irrigation plan). According to one (AHP) of the six methods, Orljava–Londža has more advantages over other areas. All MCA methods, except PCA, chose Venje–Hrnjevac as the least advisable (last to be implemented) alternative. Conclusions from this research confirm findings from recently published research regarding the application of MCA on water management problems.
1. Introduction
Irrigated agricultural land comprises more than 250 million hectares all over the world, and is essential for ensuring food security and stimulating rural socio-economic development [1]. However, this land’s impact on water resources, soil, and the environment in general is unquestionable. Implementation of irrigation systems is a considerable investment involving operation and maintenance costs. Therefore, improving the performance of irrigation systems by increasing the efficiency and transparency of those systems is essential.
Making decisions regarding the implementation of water management plans as irrigation system plans is a complex task due to the multiple objectives that must be satisfied, different and numerous criteria (economic, social, and environmental) and different measures (quantitative and qualitative) are used for objective fulfillment assessment with the involvement of multiple stakeholders [2,3]. Ranking alternatives to be implemented by priority, and in some cases selecting the first alternative to be implemented as a pilot project, represents this kind of decision-making problem [4,5].
The use of the traditional cost-benefit method, where only the quantified direct cost and benefits are incorporated in the analyses, is not sufficient when the decision involves consideration of variables that cannot be easily quantified into monetary units or if sufficient information for monetarization of all variables and criteria is not available [6]. In these situations, there are numerous procedures, classified as multi-criteria decision analysis methods (MCDM), which provide support to the complex decision-making process [7,8,9].
Multi-criteria analysis (MCA) provides a systematic methodology to integrate heterogeneous and uncertain information with cost-benefit information and stakeholders views in an understandable framework to rank project alternatives [10]. MCA is highly useful as a tool for project evaluation during the developing phase when decision makers do not have sufficient knowledge regarding details, but the importance of making the right decision is considerable.
MCA has been used for analyses of various types of water management problems [11], for ranking and selection of: water management strategies [12,13], alternatives of water supply systems [14,15], desalination procedures for drinking water production [16], reservoir use alternatives [17], wastewater disposal locations [18], urban stormwater drainage management alternatives [19], locations for hydropower plants and dams [20], and alternatives for irrigation [4,5,21,22,23,24].
ELimination and (Et) Choice Translating Reality (ELECTRE TRI) method was applied for minimizing flood damages and minimizing damages in agricultural areas caused by deficits in water supply in Iran [25]. For effective management of irrigation networks in farms, based on the example of ranking and selecting check and intake structures for irrigation canals, in Iran, the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method was applied [26]. Often, multi-criteria methods are applied with GIS (Geographic Information System), as in site selection for certain types of fruit cultivation where multi-criteria analyses overlay method and Analytic Hierarchy Process (AHP) method with GIS were analyzed in Antalya, Turkey [27]. Evaluation of potential irrigation expansion using spatial fuzzy multi-criteria decision framework, which includes AHP in ARCGIS environment, was analyzed in the limestone coast region of South Australia [28]. MCA methods, such as Preference Ranking Organization METHod for Enrichment Evaluations (PROMETHEE), ELECTRE TRI, AHP, and Decision EXpert (DEXi), have been used to provide support decision making for defining priorities in the implementation of agricultural irrigation plans in different parts of Croatia [4,5,23]. A review of irrigation system performance evaluation using fuzzy set theory, direct measurement for indicators, AHP, and remote sensing was performed by Elshaikh et al. [29].
An overview of multi-criteria decision analysis in environmental sciences [10] shows that in water management, during the period 2000–2009 the most used methods were: Multi-Attribute Utility Theory (MAUT)/Multi-Attribute Value Theory (MAVT), AHP/Analytic Network Process (ANP), ELECTRE, and PROMETHEE. This is confirmed by more recent research [15,30,31,32]. If multiple methods are applied on the same decision making problem, then the methods that are used beside already mentioned are mostly: TOPSIS, Compromise Programming (CP), Simple product weighting, and Weighted average [10,31].
This led to the selection of six MCA methods: the three most used are PROMETHEE, AHP, and ELECTRE TRI; and three not so often used on this kind of problems are DEXi, Preference Ratios In Multi-attribute Evaluation (PRIME), and Principal Component Analysis (PCA), to be applied and compared on the specific case study in Croatia for defining priorities in implementation of the Irrigation plan of Požega–Slavonia County.
The aims of this study are: confirm the adequacy of using all the selected methods, especially DEXi, PRIME, and PCA, when determining priorities in fulfilling irrigation plans on the Požega–Slavonia County irrigation plan, present the model for preparation of the input data for selected MCA methods application, use the selected MCA methods on the specific case study and compare the results.
2. Materials and Methods
2.1. Description of Study Area
Priorities in implementation of irrigation plans are defined on the case study area located in Požega–Slavonia County (north-eastern part of Croatia, Figure 1), in the sub-catchment area of the Orljava River that belongs to the Sava River Basin [23,33].
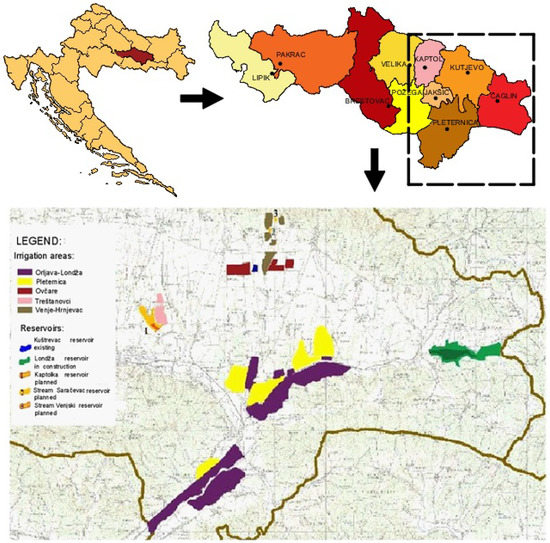
Figure 1.
Study area: Požega–Slavonia County [23,33].
According to the spatial plan of the Požega–Slavonia County [34], agricultural land occupies the largest share in the county. In this area, wheat, maize, sugar beet, tobacco, grape, fruits, and vegetables are grown, and agricultural land can be divided into three categories: especially valuable soil, valuable soil, and other cultivable soil.
Considering the cultivability of agricultural areas, it was found that of the total area of 894.9 km2, the cultivated area covers 782.9 km2 or 87.48% [33,34,35].
According to data from 2003 [36], only 1085.6 ha were irrigated in the Požega–Slavonia County, representing only 2.55% of its total area suitable for irrigation. This percentage is higher than the average in Croatia, which amounted to only 0.86%, but it was still insufficient to realize its own potential.
To intensify the agricultural production, enable development in the area, raise the standard and quality of life, a significant contribution can be expected if irrigation is applied to agricultural areas. Analyses carried out in the Požega area show that the total surface where irrigation is required is 40,772 hectares of gross (29,327 ha net).
These analyses have shown that the need for irrigation exists as a supplementary measure for the improvement of agricultural production. The amount of water from 1500 to 2500 m3/ha per year can meet the water needs of all crops. Areas that could potentially be irrigated are located in the central part of the Orljava River basin and amount to 29,237 ha.
The entire study area is characterized by small quantities of groundwater and high potential for building multipurpose reservoirs and micro-reservoirs; therefore, water for irrigation, ~77 mil.m3, can be provided by reservoirs of various sizes [34].
The planning of irrigation is based on selecting water resources that will provide the required quantities and can be divided into three phases. The first phase involves using existing reservoirs, construction of micro-reservoirs, and preparation of pilot irrigation areas. The second phase is the development of small and medium-sized systems based on the first stage knowledge and preparation for the performance of larger systems, where coordination is needed in terms of aligning plans with other relevant factors. The third phase is the performance of medium and large systems [33].
2.2. Alternatives and Criteria
Planned irrigation areas in the 1st phase represent only a small part of the area of Požega–Slavonia County that can be irrigated. Planned irrigation areas (alternatives) in the 1st phase are Orljava–Londža (1), Pleternica (2), Ovčare (3), Treštanovci (4), and Venje–Hrnjevac (5) (Figure 1).
Based on analyses done in the study “Basics for irrigation in Požega–Slavonia County” [34], the most important characteristics of all areas (alternatives) were extracted by authors for this article research and are presented in Figure 2 and Table 1 [23].
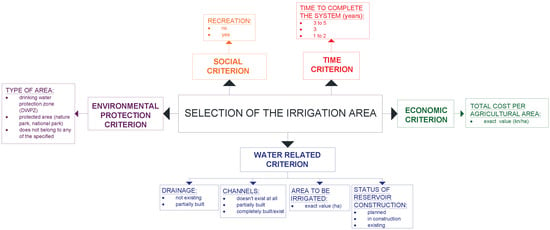
Figure 2.
Selected criteria for MCA (Multi-Criteria Analysis).

Table 1.
Characteristics of all areas (alternatives) [23].
Criteria development was a very sensitive process. To achieve sustainable irrigation systems, beside the criteria that include natural and technical potentials, environmental, social, and economic criteria were selected. Finally, authors defined five groups of criteria: “environmental protection”, “water-related”, “social”, “economic”, and “time” criteria (Table 2) [23].

Table 2.
Characteristics of all alternatives sorted by selected criteria [23].
The “environmental protection” criterion (e.g., “environment”) evaluates whether the agricultural area is in the drinking water protection zone—DWPZ (worst case)—other protected areas, e.g., nature park or national park, or does not belong to any of the specified (best case). The weight factor/importance for the “environmental protection” criterion is 20%. This information is qualitative but was easy to obtain via a comparison of available maps.
The “water-related” criterion comprises four sub-criteria. The first is “drainage”. This sub-criterion evaluates whether the drainage from agricultural areas is partially built (best case), or non-existent (worst case). The weight factor for sub-criterion “drainage” (subsurface drainage) is 5%.
The second sub-criterion is “channel” (surface drainage) and is evaluated depending on whether the channel networks are completely built/exist (best case), partially built, or do not to exist at all (worst case). The weight factor for “channel” network sub-criterion is 5%. Both of these sub-criteria assessments are qualitative and expert-opinion-based.
The third sub-criterion is related to the size of the “area to be irrigated”. The larger the area is, the better the alternative. The weight factor for sub-criteria of the irrigated area is 10%. Assessment of irrigation areas has been done in detail in the plan [33], so this information enables the use of exact quantitative values. If a qualitative assessment is used, then the following principle is applied: three classes of areas are defined 0–149 (worst alternatives), 150–449, and over 450 ha (best alternatives).
The fourth sub-criterion is related to “status of reservoir construction” ranking for an already existing reservoir that could be used for irrigation (best case), a reservoir for which construction has already started and a reservoir for which construction is only planned (worst case). This sub-criterion is qualitative. The total weight factor for this last sub-criterion is 10%.
The total weight factor for the “water-related” criterion is 30%.
The “social” criterion is related to the possibility of using reservoirs for recreation, i.e., whether reservoirs can be used for recreation (best case) or not (worst case). This sub-criterion is qualitative and expert-opinion-based. The weight factor for the “social” criteria is 5%.
The “economic” criterion covers the total cost of the irrigation systems (the cost of designing the project and all needed documentation as well as the cost of building the complete system, in Croatian currency Kuna i.e., kn) divided by the size of the irrigated area. Assessment of irrigation areas has been done in detail in the plan; therefore, this information enables the use of exact quantitative values. If a qualitative assessment is done, the alternatives are sorted in three classes: less than 2,500,000 (best case); 2,500,000 to 5,500,000, and over 5,500,000 kn/ha (worst case). The weight for the “economic” criterion is 30%.
The “time” criterion describes the time needed to build a system, which can be 1–2 years (best case), 2–3 years, and 3–5 years (worst case). This is a qualitative sub-criterion and expert-opinion-based. The weight factor for the “time” criterion is 15%.
Although there are different techniques that can be used for elicitation of weight factors [37] in this paper weight factors were determined directly by authors as experts, considering awareness of the local population for environmental protection and its value, economic development and value of money, National Irrigation Strategy and County Irrigation Plan. The above explained weight factors represent Scenario 1 (Table 3). For sensitivity analysis three additional weight factors scenarios (2, 3, and 4) were applied (Table 3).

Table 3.
Scenarios for criteria weighting factors.
In comparison to Scenario 1: for Scenario 2 the “water related” criteria “area” and “reservoir status” were given greater importance (10% more), while the “environmental” and “economic” criteria were given less importance (10% less); for Scenario 3 the “water related” criterion “drainage” and “economic” criteria were given greater importance (5 and 10% more), while the “environmental” and “reservoir status” criteria were given less importance (10 and 5% less); and for Scenario 4 the “social” and “time” criteria were given greater importance (5% more), while the “economic” criterion was given less importance (10% less).
2.3. Multi-Criteria Analyses Methods
In this study, six MCA methods were applied: PROMETHEE, AHP, ELECTRE TRI, DEXi, PRIME, and PCA, all of which are briefly described. Selected methods represent different MCA models. PROMETHEE and ELECTRE are outranking models, while AHP is a value measurement model based on pairwise comparison [31], DEXi combines “traditional” multi-attribute decision making with some elements of expert systems and machine learning [38], and PRIME incorporates the value tree analysis [39]. From ELECTRE family methods, the ELECTRE TRI as a sorting model was selected. PCA in many ways forms the basis for multivariate data analysis [40]. In this research, the main goal of PCA is to extract the most important characteristics of irrigation plans and compress the data set’s size by keeping only this important information.
PROMETHEE are multi-criteria outranking methods used for partial (PROMEHEE I) or total pre-order of alternatives (PROMETHEE II) [41,42]. In PROMETHEE methods, the notion of criterion is extended by introducing the preference function, giving the preference of the decision maker for an alternative a as opposed to b, for each criterion. The preference value is between 0 and 1. The smaller the value, the higher the indifference of the decision maker, whereas the closer it is to 1, the higher his preference. In case of strict preference, the value of the preference function is 1. Six different types of criterion functions, for which the decision maker has to define a maximum of two parameters (indifference and preference thresholds), cover most of the cases that can happen in practice: usual criterion, quasi criterion, criterion with linear preference, level criterion, criterion with linear preference and indifference area, and Gaussian criterion. A valued outranking graph is considered by using a preference index. In this study, the PROMETHEE II method and usual criterion function were used.
AHP is a priority method applicable to problems that can be represented by a hierarchical structure [43,44]. The top of the hierarchy is the goal, one level lower are criteria, and even lower sub-criteria. The lowest level is represented by alternatives. AHP method is conceived based on estimating relative priorities (weights) of criteria and alternatives on which pair-wise comparison criteria matrix and pair-wise comparison alternatives matrices (one matrix for each criterion) are generated. The matrices are normalized in order to calculate the priority weightings for criteria (the priority vector for criteria) and for alternatives on the basis of each criterion (the priority vector of alternatives for each criterion). Combining the criterion priorities and the priorities of each alternative relative to each criterion enables the development of an overall priority ranking of the alternative, which is termed the priority matrix.
ELECTRE are multi-criteria optimization methods that enable the choice, ranking, and sorting of alternative problem solutions (depending of the ELECTRE version) considering decision-makers’ criteria and preferences [45,46]. The ELECTRE method was developed for a partial order in the set of solutions based on the decision maker’s preferences. A graph with nodes that represent possible solutions and a kernel that defines preferred solutions can be constructed. The ELECTRE method is useful in the case when criterion functions are weakly defined. The first developed method was ELECTRE I and on the basis of it, ELECTRE II, III, IV, and TRI followed. The ELECTRE TRI is a multi-criteria sorting method that assigns alternatives to predefined categories. The assignment of an alternative results from the comparison between the profiles that define the limits of the categories. The built outranking relation validates or invalidates the assertion of the alternative as to a predefined category. The ELECTRE TRI method gives the decision-maker a possibility to use pseudo-criteria with indifference and preference thresholds.
The DEXi decision model is a qualitative decision model that divides the decision-making problem into less complex decision-making problems (sub-problems) [23,38]. Criteria are hierarchically organized and linked to the utility function that evaluates each criterion in relation to its goal in the hierarchy. Instead of numerical variables, DEXi uses qualitative variables, the values of which are usually presented in words. To display and evaluate the utility function, DEXi uses “if-then” decision-making rules. The utility function is defined throughout the hierarchy for each set of criteria, and the decision rule is described. The value of the aggregate criterion for each combination of input criteria is described and the relative importance of each criterion is expressed. Within each criterion, the ranking is performed depending on whether its value is good, neutral, or poor.
PRIME is an analytic decision-making tool, where preferred data are given in intervals because the exact value is often not known, and it is easier to define a rough estimate [39,47]. In PRIME, the decision makers’ preferences are assumed to have an additive structure in which the total value of an alternative equals the sum of its attribute-specific scores. Determination of preferences can be score assessments, holistic comparisons, and weight assessments. PRIME uses the Swing Weighting Method, where the most important attribute is assigned with 100 points, and weights of other attributes are compared to the most important attribute in the interval from 0 to 100. PRIME has two styles to make weight assessments: bottom-up and top-down. In this study, the bottom-up weight assessment is used, where the decision maker compares sub-attribute weights of the main goal with each other.
PCA is a multivariate technique that analyzes a data table in which observations are described by several inter-correlated quantitative dependent variables. The goals of PCA are to (a) extract the most important information from the data table, (b) compress the size of the data set by keeping only this important information, (c) simplify the description of the data set, and (d) analyze the structure of the observations and the variables [40]. PCA in many ways forms the basis for multivariate data analysis and it was first formulated in statistics by Pearson in 1901 [48]. There are many possibilities of using PCA; representation of spatial cause-effect data, in investigation of causal connections between spatial rainfall-runoff and rainfall-drought [49], as well as description of regional characteristics and differences among low-flow regimes at multiple hydrological stations, have been demonstrated [50].
3. Results and Discussion
3.1. PROMETHEE
To apply the PROMETHEE method, data from Table 2 were transformed into quantitative values for all criteria, on a scale of 1–3, where 1 is the lowest value of the assessment and 3 the highest, except for “social” criterion that had two values (1 and 2), “water-related”, “area” and “economic” criteria are already quantitative (Table 4).

Table 4.
Quantitative assessment of alternatives by criteria.
The PROMETHEE II was applied using the usual preference function for all criteria. The results for criteria weights defined by Scenario 1 (Table 3) are presented in Figure 3a, where the area Ovčare had the highest rank/priority, followed by Orljava–Londža, Treštanovci, and Pleternica. Figure 3b shows the Geometrical Analysis for Interactive Decision Aid (GAIA) plane, and it can be observed that, based on the direction and length of the decision stick (red color), Ovčare and then Orljava–Londža should have priority in implementation of irrigation.
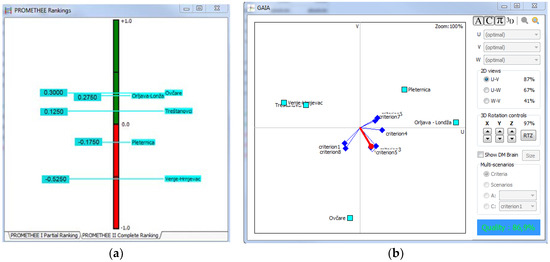
Figure 3.
Results of PROMETHEE II application for Scenario 1: (a) complete ranking scheme of proposed alternatives, and (b) GAIA (Geometrical Analysis for Interactive Decision Aid) plane.
Results for Scenario 2 ranked alternatives Orljava–Londža and Ovčare in the first place, followed by Pleternica and then Treštanovci; for Scenario 3 Orljava–Londža was ranked in the first place, followed by Ovčare, Treštanovci, Pleternica; for Scenario 4 Ovčare was ranked as first to be implemented followed by Orljava–Londža, Treštanovci, Pleternica. Venje–Hrnjevac was the worst alternative that should to be implemented last in all scenarios.
3.2. AHP
The application of AHP was performed in two ways, the first using the direct assessment of each alternative by each criterion and each criterion in regard to the goal, and second by using pairwise comparison of criteria and alternatives.
The direct assessment of each alternative by each criterion, and each criterion with regard to the goal, was based on data from Table 3 and Table 4. Results for criteria weights defined by Scenario 1 (Table 3) ranked the alternatives as per priority: the first alternative to be implemented was Orljava–Londža, the second alternative was Ovčare but with a very small difference, followed by Treštanovci, Pleternica, and Venje–Hrnjevac (Figure 4).
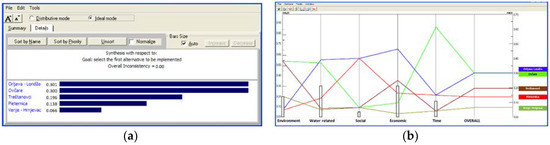
Figure 4.
AHP (Analytic Hierarchy Process) results for direct assessment of each alternative by each criterion, and each criterion with regard to the goal for Scenario 1: (a) the final ranking, and (b) graphical presentation of all alternatives’ assessment by each group of criteria.
Applying criteria weights defined by Scenarios 2 and 3 resulted in the same priority ranking as for Scenario 1. The results in case of applying Scenario 4 criteria weights differed and the priority was given to Ovčare alternative, followed by Orljava–Londža.
Pairwise comparisons of criteria with regard to the goal, sub-criteria to criteria and alternatives to each criterion according to the scale in Table 5 were based on data from Table 2 and Table 3, and are presented partially in Table 6 for pair-wise comparison of all groups of criteria to the goal, all water-related criteria to the group criterion, and pairwise comparison of alternatives to the criterion “environment”, as an example using criteria weights defined by Scenario 1.

Table 5.
AHP (Analytic Hierarchy Process) pair-wise comparison scale [48].

Table 6.
Pair-wise assessment of: all groups of criteria in regard to the goal, all water-related criteria to the group criterion “water-related criteria”, and all alternatives to the criterion “environment” based on Scenario 1.
The results of using AHP with pairwise comparison of criteria and alternatives (for Scenario 1) ranked the Orljava–Londža alternative as the first to be implemented, Ovčare as the second, followed by Treštanovci, Pleternica, and Venje–Hrnjevac (Figure 5).
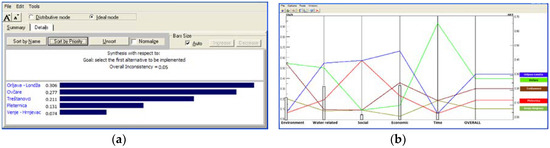
Figure 5.
AHP results based on pairwise assessment of criteria and alternatives for Scenario 1: (a) the final ranking, and (b) graphical presentation of all alternatives assessment by each group of criteria.
3.3. ELECTRE TRI
ELECTRE TRI as a sorting method was applied on the same input data as those for the PROMETHEE method, i.e., data from Table 3 and Table 4, to sort alternatives in three predefined categories: first to be implemented, middle, and last to be implemented alternatives. The thresholds between categories are presented in Table 7, and in case of Ovčare, in Figure 6.

Table 7.
Thresholds between categories.
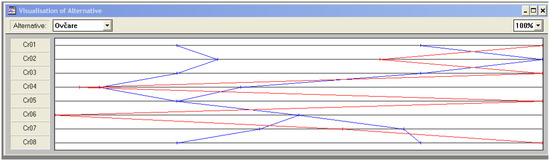
Figure 6.
Visualization of alternative Ovčare (red) with categories thresholds (blue) for Scenario 1.
The results for criteria weights defined by Scenario 1 (Table 3) are presented in Table 8. ELECTRE TRI had two ways to rank the alternatives, using pessimistic or optimistic sorting. According to pessimistic sorting, there was no alternative in the first category (alternatives to be implemented first), whereas in the second, there was one, Ovčare, while all others were in the last category. For optimistic sorting, Orljava–Londža and Ovčare were sorted in the first category (alternatives to be implemented first), while Pleternica, Treštanovci, and Venje–Hrnjevac were to be implemented second. Sorting alternatives based on criteria weights defined in Table 3 for Scenarios 2, 3, and 4 produced the same result.

Table 8.
Results of ELECTRE TRI for Scenario 1.
It can be concluded that the first alternative to be implemented suggested by ELECTRE TRI was Ovčare, followed by Orljava–Londža, and the last ones to be implemented were Pleternica, Treštanovci, and Venje–Hrnjevac.
3.4. DEXi
DEXi method was applied on data from Table 2 and Table 3, and the results for criteria weights defined by Scenario 1 are presented in Figure 7 [23]. DEXi software allows the display of results in multiple graphical modes. The first way was to display the final evaluation in which all the results of the analysis were combined (Figure 7a), and the recommended alternatives, partially recommended, or not recommended were displayed. The results can also be presented according to a certain criterion, which also specify the areas that are recommended, partially recommended, or not recommended according to that criterion. The results can also be presented for two criteria. In this case, the results were no longer presented in line but were projected at the point at the intersection for both criteria (Figure 7b). The presentation of results for three or more criteria is done on a polygon. An ideal alternative would represent an unbroken line that moves at the top of the polygon. If the results vary between good and medium, the line is in the space between the center and the top of the polygon, while for the worse results, there is no line, i.e., there is no shift from the point that indicates the center of the polygon.
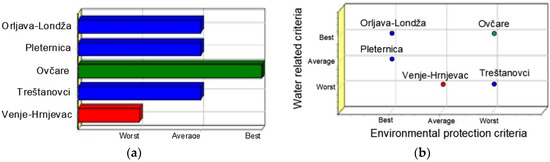
Figure 7.
Presentation of results of DEXi application for Scenario 1: (a) result based on evaluation of all criteria, and (b) result for two criteria [23].
An example of results only for the area Ovčare has been presented in Figure 8 [23].

Figure 8.
Result of alternative Ovčare analyses for Scenario 1 [23].
An example of results for only the area Ovčare has been presented in Figure 8 [23].
Based on the conducted analyses, using the DEXi software for Scenario 1, the area of Ovčare was recommended as the first in which the irrigation should be implemented (Figure 7a). The other three areas Orljava–Londža, Pleternica, and Treštanovci were partially recommended, while the area of Venje–Hrnjevac was not recommended (i.e., it is the last that should be implemented) [23]. Using Scenarios 2, 3, and 4 (from Table 3) the difference in the result was that both Orljava–Londža and Ovčare were recommended as the first in which the irrigation should be implemented.
3.5. PRIME
The PRIME method was applied on data from Table 2 and Table 3, and the results for criteria weights defined by Scenario 1 are presented in Figure 9, Figure 10 and Figure 11. There are four ways to sort the results after importing the input data. The results are available in the following forms: value intervals, weights, dominance, and decision rules. A value interval represents the range of possible values, and every alternative has a value interval for each attribute, and each goal has its range of possible values.
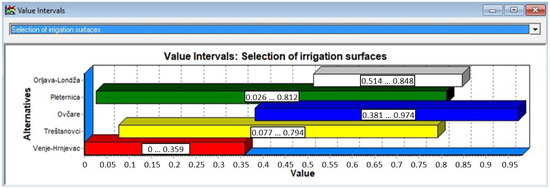
Figure 9.
Range of possible values of alternatives for Scenario 1.
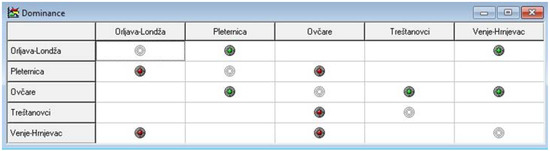
Figure 10.
Dominance matrix of mutual relationships among alternatives for Scenario 1.
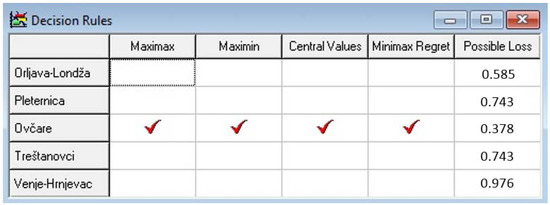
Figure 11.
Advised alternative for decision maker for Scenario 1.
Form Figure 9, the alternative Venje–Hrnjevac was dominated by the alternatives Orljava–Londža and Ovčare because the least possible value of the latter was higher than the highest possible value of the former ones. The value interval did not tell which one of alternatives was the best, but it showed which had good chances.
Dominance showed which alternative was preferred to another, for all the permissible combinations of preference information. Dominance is needed when the value intervals of two alternatives overlap, and a unique single alternative that would be preferred to the other may not exist. Absolute dominance means that the value intervals of the alternatives do not overlap and one alternative is preferred to the other without any doubt.
Dominance window contains a dominance matrix, as shown in Figure 10. A red dot in the matrix indicates that the alternative on that row is dominated by the alternative of that column, and the green dot means the opposite. Grey dots denote the diagonal of the matrix.
Decision rules help the decision maker select the best alternative. There are four decision rules that can apply to different situations: maximax, maximin, central values, and minimax regret. Maximax supposes that the most likely value lies at or near the great bound of the value intervals, and selects the alternative with the greatest upper bound. Maximin supposes that the worst case for the alternative will happen and selects the alternative with the greatest lower bound of the value interval. Central values select the alternative with the greatest midpoint, while minimax regret takes a different approach and calculates the possible loss of value, which means that it selects the alternative with the least possible loss of value. These decision rules only give advice, and the decision makers should pick the alternative that they find best (Figure 11).
Using Scenarios 1, 2, and 4 (from Table 3) all the results suggest that the first alternative to be implemented should be Ovčare, followed by Orljava–Londža, Pleternica, Treštanovci, and as the last one Venje–Hrnjevac. Results based on Scenario 3 suggest that the first alternative to be implemented should be Orljava–Londža, followed by Ovčare, Pleternica, Treštanovci, and Venje–Hrnjevac.
3.6. PCA
Input data for PCA are adopted from Table 1 by introducing mark “2” instead of “best” and mark “1” instead of “worst” and based on Scenario 1 from Table 3. Application of PCA defined three key factors, and each of them is a combination of several criteria (Table 9). The contribution of key factor F1 is 44% and it consists of two criteria: environmental protection and recreation. Contribution of key factor F2 is 37%. It is a combination of four criteria: drainage, irrigation area, reservoirs, and time for completion. The third key factor F3 has a contribution of 19% with the contribution of two criteria: cost/unit area and channel network.

Table 9.
Factor loadings according to PCA (Principal Component Analysis) for Scenario 1.
The irrigation area of priority depends on the value of cos2. Squared cosines of the observations are presented in Table 10. The value of a contribution is between 0 and 1 and, for a given component, the sum of the contributions of all observations is equal to 1. The larger the value of the contribution, the more the observation contributes to the component. It is clear that Ovčara has high priority mostly because of the contribution of F2 key factor.

Table 10.
Squared cosines of the observations for Scenario 1.
Locations Venje–Hrnjevac and Treštanovci are ranked on the second position dominantly under the influence of environmental protection criterion and criteria of F2 key factor. Pleternica is under the influence of the F2 key factor, dominantly a channel network. All four locations have similar and rather close rankings, but Pleternica has been evaluated as the least advisable location even though the differences are almost negligible.
The major advantage of Ovčara location is the time required to complete and the existing reservoir, which is obvious from the biplot of key factors F1 and F2 and observed locations (Figure 12). Locations Venje–Hrnjevac and Treštanovci are ranked on the second position dominantly under the influence of environmental protection criterion and criteria of F2 key factor. Pleternica is under the influence of the F2 key factor, dominantly the channel network. All four locations have similar and rather close rankings, but Pleternica has been evaluated as the least advisable location.
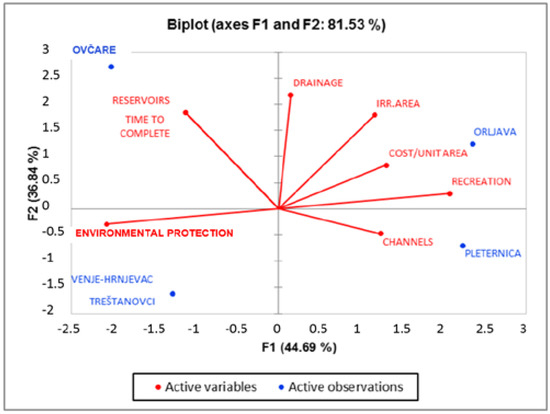
Figure 12.
Biplot of key factors and observed locations.
Results presented in Figure 12 are based upon Scenario 1, and show a clear conclusion about the Ovčare location as the most acceptable alternative. PCA was also applied on scenarios 2 to 4 and the conclusion was the same, there was no change in alternatives ranking.
3.7. Comparison of Results
Previously described applications of six multi-criteria analysis (PROMETHEE, AHP, ELECTRE TRI, DEXi, PRIME, and PCA) in the Croatian case study showed similar results. According to criteria importance defined as Scenario 1 (Table 3) the Ovčare area has been estimated as the first to be implemented (most recommended) by all methods, except AHP (Table 11). The reservoir for irrigation already exists, the time to complete the irrigation system is up to 2 years, the agricultural area is not in any restricted (protected) zone, the status of the drainage system is mostly built, and the cost is not the highest, although the reservoir is not used for recreation. Except for the PCA method, the least favorable location is Venje–Hrnjevac, mostly owing to its position close to the nature park.

Table 11.
Comparison of results from different MCA (multi-criteria analysis) methods for different criteria weight scenarios.
To test the robustness of MCA methods application, the sensitivity analyses was performed according to three additional criteria weight scenarios defined in Table 3 and the results are presented in Table 11.
The sensitivity analyses mostly confirmed Ovčare as the first alternative to be implemented. Exception were the results for the AHP method in case of Scenarios 1, 2, and 3, and in case of PROMETHEE, and PRIME methods for Scenario 3 where Orljava–Londža is suggested to be the first to be implemented. For Scenario 2 in case of the PROMETHEE method application and for Scenarios 2, 3, and 4 for DEXi both Orljava–Londža and Ovčare were ranked as first to be implemented. ELECTRE TRI and PCA ranked Ovčare as the first alternative to be implemented independently of the criteria weight scenario applied, while all methods except PCA pointed out Venje–Hrnjevac as the last alternative to be implemented. Most similar results were obtained by PROMETHEE, DEXi, and PRIME although their algorithms were different. In case of AHP application the differences in the final score between alternatives Ovčare and Orljava–Londža for all scenarios are small. ELECTRE TRI and PCA were the least sensitive to criteria weight changes.
All selected MCA methods have demonstrated to be adequate for defining priorities in the irrigation plans implementation, and the following conclusions about their application on the case study were made.
The PROMETHEE method demands all alternatives’ assessments to be quantitative and gives the criteria importance too, so the qualitative ones had to be transformed into quantitative ones. The method was simple to use and not time-consuming. The GAIA method gave additional information for decision making.
For AHP application input data can be both quantitative and qualitative. In case of direct assessment with quantitative values, the use of the method was simple and not time-consuming. If pairwise comparison was applied, there was no need for quantitative data, but more time was needed for pairwise assessment of all alternatives by each criterion, and of criteria to the goal.
Since ELECTRE TRI is a method that sorts alternatives in predefined categories, categories’ thresholds had to be defined. The method demands all alternatives assessments to be quantitative and gives the criteria importance too, so the qualitative values had to be transformed into quantitative ones. The method use was simple and not time-consuming.
For DEXi decision model the quantitative assessment of alternatives had to be transformed into qualitative ones (i.e., words). Input data had to be hierarchically sorted for each criterion. It was simple to use, and allowed various display options for output data: graphical display for all alternatives or one alternative or a comparison of two criteria, with very good visualization.
For PRIME method application quantitative assessment of alternatives was given in intervals. Input data must be compared with the most important attribute that may require slightly more time. Output data were a combination of graphical and tabular views, that are only advisory in nature, and the decision maker should pick the alternative he/she finds the best. PCA offers the possibility to combine several criteria and define key factors essential for specific process. A group of criteria were ranked according to their importance. In this way, some parameters could be neglected. PCA has good visualization and graphical presentation.
Regarding the specific case study in Croatia, defining priorities in implementation of the irrigation plan of Požega–Slavonia County, more appropriate methods were the ones that have the possibility to use qualitative assessment of alternatives because in the planning phase the input data for the assessment of alternatives were not precise.
Comparing results from this study with published research [51,52] confirmed that different multi-criteria decision making methods identify mostly the similar ranking among water management alternatives in case objective weights are assigned to the criteria. Selecting the MCA technique has proven in this research (including methods DEXi, PRIME, and PCA) to have lesser importance than the initial structuring of the decision problem (selection of criteria, generating alternatives, weighting the criteria and assessing the alternatives) as stated by Hajkowicz and Higgins in [51]. The difference occurs because the weights and the resulting distributions of the scores within the criteria do not have the same impact on all the methods [31]. The slight sensitivity to the weight assignment to the criteria [52] was observed in this case study too. It can be confirmed that the application of several methods, but also the sensitivity analysis, is necessary to check the consistency and increase the reliability of the results [31] for the analyzed case study.
4. Conclusions
Currently, the irrigation of agricultural areas is essential to ensure food security and stimulate rural socio-economic development. In the 21st century, water resources will certainly be one of the major issues. Water consumption in irrigation is very large and very often non-sustainable. Improving the performance of irrigation systems by increasing the efficiency and transparency of those systems is essential. The proposed analysis should be done prior to the more detailed project development in order to avoid potential negative irrigation effects on environment and conflicts among water consumers.
In the case study area of Požega–Slavonia county (Croatia), five potential irrigation areas were analyzed according to the defined criteria using six multi-criteria analysis methods PROMETHEE, AHP, ELECTRE TRI, DEXi, PRIME, and PCA. Five of the six methods identified Ovčare as the most appropriate area for an irrigation development case study for criteria weights defined by Scenario 1. The sensitivity analysis based on three additional criteria weight scenarios confirmed these conclusions with small variations, ranking Ovčare and Orljava–Londža both as alternatives that could be implemented first (PROMETHEE and DEXi), and in some cases pointed Orljava–Londža as the alternative that should be implemented first (PROMETHEE, AHP and PRIME). Five of the six methods have the same result for the least advisable alternative, Venje–Hrnjevac.
The results show that selected methods can be applied for defining priorities in irrigation project development. The novelty in this research is the application of DEXi, PRIME, and PCA methods that were not used so often on this kind of problems. For the case study in Croatia, more appropriate MCA methods are the ones that can perform qualitative assessment of alternatives, since the input data for the assessment of alternatives were not precise.
Initial structuring of the decision problem, especially the criteria’s definition, is the most sensitive part in the multi-criteria evaluation. The criteria should present realistic and objective characteristics of the study field in order to achieve results with an objective and valuable decision. As the weighting factors in this research were defined by authors (considering awareness of the local population for environmental protection and its value, economic development and value of money), although the sensitivity analysis was done, further research should involve stakeholders in the definition of weight factors.
The selected methods confirmed to be a useful tool for informing decision-makers about the sustainability of catchment scale water use in a relatively simple way and help them to develop strategies for further improvement of water resources management in irrigation districts.
Author Contributions
Conceptualization, B.K.; methodology, B.K., A.H., and L.T.; formal analysis, B.K., A.H., and L.T.; investigation, B.K., A.H., and L.T.; resources, B.K.; data curation, B.K., A.H., and L.T.; writing—original draft, B.K., A.H., and L.T.; writing—review/editing, B.K.; visualization, B.K., A.H., and L.T.; supervision, B.K.; project administration, B.K.; funding acquisition, B.K.
Funding
The research for this article and the publication of this article were funded by the University of Rijeka within projects: “Development of New Methodologies in Water and Soil Management in Karstic, Sensitive and Protected Areas” (13.05.1.3.08) and “Implementation of Innovative Methodologies, Approaches and Tools for Sustainable River Basin management” (UNIRI-TEHNIC-18-129).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Masia, S.; Sušnik, J.; Marras, S.; Mereu, S.; Spano, D.; Trabucco, A. Assessment of Irrigated Agriculture Vulnerability under Climate Change in Southern Italy. Water 2018, 10, 209. [Google Scholar] [CrossRef]
- Đorđević, B. Vodoprivredni sistema; Naučna knjiga: Beograd, Serbia, 1990. [Google Scholar]
- Margeta, J. Osnove Gospodarenja Vodama/Basis of Water Management; Građevinski fakultet: Split, Croatia, 1992. [Google Scholar]
- Karleuša, B.; Ožanić, N. Određivanje prioriteta u realizaciji vodnogospodarskih planova/Determination of priorities during realization of water management plans. Građevinar 2011, 63, 2. Available online: http://www.casopis-gradjevinar.hr/archive/article/371 (accessed on 1 November 2018).
- Karleuša, B.; Ožanić, N.; Deluka-Tibljaš, A. Improving decision making in defining priorities for implementation of irrigation plans using AHP methodology. Tech. Gazette 2014, 21, 673–680. Available online: https://hrcak.srce.hr/index.php?show=clanak&id_clanak_jezik=182226 (accessed on 11 January 2018).
- Tiwari, D.N.; Loof, R.; Paudyal, G.N. Environmental-economic decision-making in lowland irrigated agriculture using multi-criteria analysis techniques. Agric. Syst. 1999, 60, 99–112. [Google Scholar] [CrossRef]
- Opricović, S. Višekriterijumska optimizacija/Multi-criteria optimization; Naučna knjiga: Beograd, Yugoslavia, 1986. [Google Scholar]
- Triantaphyllou, E. Multi-Criteria Decision Making Methods: A Comparative Study; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Figueira, J.; Greco, S.; Ehrogott, M. Multiple Criteria Decision Analysis: State of the Art Surveys. In International Series in Operations Research & Management Science; Springer: New York, NY, USA, 2005; Volume 78. [Google Scholar]
- Huang, I.B.; Keisler, J.; Linkov, I. Multi-criteria decision analysis in environmental sciences: Ten years of applications and trends. Sci. Total Environ. 2011, 409, 3578–3794. [Google Scholar] [CrossRef] [PubMed]
- Hajkowicz, S.; Collins, K. A Review of Multiple Criteria Analysis for Water Resource Planning and Management. Water Resour. Manag. 2007, 21, 1553–1566. [Google Scholar] [CrossRef]
- Raju, K.S.; Pillai, C.R.S. Multi-criterion decision making in river basin planning and development. Eur. J. Oper. Res. 1999, 112, 249–257. [Google Scholar] [CrossRef]
- Duckstein, L.; Treichel, W.; El Magnouni, S. Ranking Ground-water Management Alternatives by Multi-criterion Analysis. J. Water Resour. Plan. Manag. 1994, 120, 546–565. [Google Scholar] [CrossRef]
- Paneque Salgado, P.; Corral Quintana, S.; Guimaraes Pereira, A.; del Moral Ituarte, L.; Pedregal Mateos, B. Participative multi-criteria analysis for the evaluation of water governance alternatives. A case study in the Costa del Sol (Malaga). Ecol. Econ. 2009, 68, 990–1005. [Google Scholar] [CrossRef]
- Sapkota, M.; Arora, M.; Malano, H.; Sharma, A.; Moglia, M. Integrated Evaluation of Hybrid Water Supply Systems Using a PROMETHEE–GAIA Approach. Water 2018, 10, 610. [Google Scholar] [CrossRef]
- Srđević, B.; Jandrić, Z.; Potkonjak, S. Vrednovanje alternativa korištenja akumulacije pomoću analitičkog hijerarhijskog procesa. Jugoslavenski časopis: Vodoprivreda 2000, 32, 237–242. [Google Scholar]
- Afify, A. Prioritizing desalination strategies using multi-criteria decision analysis. Desalination 2010, 250, 928–935. [Google Scholar] [CrossRef]
- Margeta, J. Izbor optimalnog rješenja dispozicije otpadnih voda Poljičke rivijere/Selection of the optimal solution for waste water disposal of Poljička riviera. Vodoprivreda 1986, 18, 79–87. [Google Scholar]
- Martin, C.; Ruperd, Y.; Legret, M. Urban stormwater drainage management: The development of a multicriteria decision aid approach for best management practices. Eur. J. Oper. Res. 2007, 181, 338–349. [Google Scholar] [CrossRef]
- Margeta, J.; Mladineo, N.; Petričec, M. Višekriterijsko rangiranje lokacija za male hidroelektrane/Multicriteria ranking of locations for small hydropower plants. Građevinar 1987, 39, 239–244. [Google Scholar]
- Raju, K.S.; Pillai, C.R.S. Multicriterion decision making in performance evaluation of an irrigation system. Eur. J. Oper. Res. 1999, 112, 479–488. [Google Scholar] [CrossRef]
- Goncalves, J.M.; Pereira, L.S.; Fang, S.X.; Dong, B. Modelling and multicriteria analysis of water saving scenarios for an irrigation district in the upper Yellow River Basin. Agric. Water Manag. 2007, 94, 93–108. [Google Scholar] [CrossRef]
- Karleuša, B.; Hajdinger, A.; Tadić, L. Use of Multicriteria Analysis Method DEXi to Define Priorities in Implementation of Irrigation Plans. Proceedings 2018, 2, 663. [Google Scholar] [CrossRef]
- Assefa, T.; Jha, M.; Reyes, M.; Srinivasan, R.; Worqlul, A.W. Assessment of Suitable Areas for Home Gardens for Irrigation Potential, Water Availability, and Water-Lifting Technologies. Water 2018, 10, 495. [Google Scholar] [CrossRef]
- Malekmohammadi, B.; Zahraie, B.; Kerachian, R. Ranking solutions of multi-objective reservoir operation optimization models using multi-criteria decision analysis. Expert Syst. Appl. 2011, 38, 7851–7863. [Google Scholar] [CrossRef]
- Hosseinzade, Z.; Pagsuyoin, S.; Ponnambalam, K.; Monem, M.J. Decision-making in irrigation networks: Selecting appropriate canal structures using multi-attribute decision analysis. Sci. Total Environ. 2017, 601–602, 177–185. [Google Scholar] [CrossRef] [PubMed]
- Selim, S.; Koc-San, D.; Selim, C.; San, B.T. Site selection for avocado cultivation using GIS and multi-criteria decision analyses: Case study of Antalya, Turkey. Comput. Electron. Agric. 2018, 154, 450–459. [Google Scholar] [CrossRef]
- Chen, Y.; Paydar, Z. Evaluation of potential irrigation expansion using a spatial fuzzy multi-criteria decision framework. Environ. Model. Softw. 2012, 38, 147–157. [Google Scholar] [CrossRef]
- Elshaikh, A.E.; Xiyun, J.; Shi-hong, Y. Performance evaluation of irrigation projects: Theories, methods, and techniques. Agric. Water Manag. 2018, 203, 87–96. [Google Scholar] [CrossRef]
- Montazar, A.; Gheidari, O.N.; Snyder, R. A fuzzy analytical hierarchy methodology for the performance assessment of irrigation projects. Agric. Water Manag. 2013, 121, 113–123. [Google Scholar] [CrossRef]
- Tscheikner-Gratl, F.; Egger, P.; Rauch, W.; Kleidorfer, M. Comparison of Multi-Criteria Decision Support Methods for Integrated Rehabilitation Prioritization. Water 2017, 9, 68. [Google Scholar] [CrossRef]
- Sun, H.; Wang, S.; Hao, X. An Improved Analytic Hierarchy Process Method for the evaluation of agricultural water management in irrigation districts of north China. Agric. Water Manag. 2017, 179, 324–337. [Google Scholar] [CrossRef]
- Hidroprojek-ing, D.O.O.; Hidroing, D.O.O. Osnove navodnjavanja na području Požeško-slavonske županije/Basics for irrigation in Požega-Slavonia County; Osijek: Zagreb, Croatia, 2005. [Google Scholar]
- Prostorni plan Požeško-slavonske županije. Spatial plan of Požega-Slavonia County; Požeško-slavonski službeni glasnik 5/02, 5A/02, 05/2015; Požega-Slavonia County: Požega, Croatia, 2015. [Google Scholar]
- Razvojna strategija Požeško-slavonske županije za razdoblje 2011–2013/Development strategy of Požega-Slavonia County; Požega-Slavonia County: Požega, Croatia, 2011.
- Kantoci, D. Navodnjavanje/Irrigation. Glasnik zaštite bilja 2012, 35, 66–72. Available online: https://hrcak.srce.hr/index.php?show=clanak&id_clanak_jezik=240422 (accessed on 10 May 2018).
- Riabacke, M.; Danielson, M.; Ekenberg, L. State-of-the-Art Prescriptive Criteria Weight Elicitation. Adv. Decis. Sci. 2012, 276584. [Google Scholar] [CrossRef]
- Rozman, Č.; Pažek, K. Introduction to DEXi multi criteria decision models: What they are and how to use them in agriculture? Agricultura 2012, 9, 23–30. Available online: http://www.agricultura-online.com/portal/issues/50-issue-16/153-introduction-to-dexi-multi-criteria-decision-models-what-they-are-and-how-to-use-them-in-agriculture (accessed on 23 November 2017).
- Gustafsson, J.; Salo, A.; Gustafsson, T. PRIME Decisions: An Interactive Tool for Value Analysis; University of Technology, System Analysis Laboratory: Helsinki, Finland, 2011. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal Component Analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Roy, B.; Vincke, P.; Mareschal, B. How to select and how to rank project: The PROMETHEE method. Eur. J. Oper. Res. 1981, 24, 228–238. [Google Scholar] [CrossRef]
- Brans, J.P.; Vincke, P. Preference Ranking Organization Method: The Promethee Method for MCDM. Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process, 2nd ed.; RWS Publications: Pittsburg, PA, USA, 1996. [Google Scholar]
- Saaty, T.L. Fundamentals of Decision Making and Priority Theory; RWS Publications: Pittsburg, CA, USA, 1994. [Google Scholar]
- Mousseau, V.; Slowinski, R. Inferring an ELECTRE TRI Model from Assignment Examples. J. Glob. Optim. 1998, 12, 157–174. [Google Scholar] [CrossRef]
- Mousseau, V.; Slowinski, R.; Zielniewicz, P. ELECTRE TRI 2.0 a Methodological Guide and User’s Manual; Universite Paris-Dauphine-Paris-Francuska and Poznan University of Technology: Piotrowo, Polland, 1998. [Google Scholar]
- Gustafsson, T. A Comparison of PRIME Decisions with Other Tools for Decision Analysis; University of Technology, System Analysis Laboratory: Helsinki, Finland, 2000. [Google Scholar]
- Wold, S.; Kim Esbensen, K.; Paul Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1998, 2, 37–52. [Google Scholar] [CrossRef]
- Rao, A.R.; Burke, T.T. Principal Component Analysis of Hydrologic Data. In Integrated Approach to Environmental Data Management Systems; Harmancioglu, N.B., Alpaslan, M.N., Ozkul, S.D., Singh, V.P., Eds.; NATO ASI Series (Series: 2: Environment); Springer: Dordrecht, The Netherlands, 1997; Volume 31. [Google Scholar]
- Daigle, A.; St-Hilaire, A.; Beveridge, D.; Caissie, D.; Benyahya, L. Multivariate analysis of the low-flow regimes in eastern Canadian rivers. Hydrol. Sci. J. 2011, 56, 51–67. [Google Scholar] [CrossRef]
- Hajkowicz, S.; Higgins, A. A comparison of multiple criteria analysis techniques for water resource management. Eur. J. Oper. Res. 2008, 184, 255–265. [Google Scholar] [CrossRef]
- Yilmaz, B.; Harmancioglu, N.B. Multi-criteria decision making for water resource management: A case study of the Gediz River Basin, Turkey. Water 2010, 36, 5. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).