Generating Scenarios of Cross-Correlated Demands for Modelling Water Distribution Networks
Abstract
1. Introduction
2. Description of Methodology
2.1. Scaling Laws
2.2. Generation of Scenarios
- Step 1.
- Create a random (S, N) dimensional matrix Z*, containing S Latin Hypercube Samples of size N from a standardized normal distribution, where S is the number of scenarios and N the number of the demand nodes in the WDN. For this purpose, the Matlab function lhsnorm was used. Owing to the finite size of the samples their correlation matrix I* (Here, the asterisk is used to distinguish data and corresponding correlation matrices to be corrected) does not coincide with the identity matrix I, that is they are not independent. Then, the lower triangular Cholesky decomposition is applied to induce the desired correlation [27]. Specifically:and the (S, N) dimensional matrix Z of perfectly independent S samples of size N from a standardized normal distribution is obtained. In order to obtain the Cholesky root, the Matlab function chol was used.
- Step 2.
- Create a random (S, N) dimensional matrix G containing S standardized normal samples with the correlation matrix Corr from the scaling laws for nodal demand. To this aim the desired correlation is induced in Z also applying the lower triangular Cholesky decomposition [27], that is:
- Step 3.
- Transform the matrix G in the (S, N) dimensional matrix D* which complies with the desired marginal distributions at each demand ith node. Transformation is based on the inverse cumulative distribution function, CDF, of the desired marginals, Fi. Specifically, for each element D*i of matrix D*, i.e., a non-normal random sample with the desired CDF, the following equation holds:where is the CDF of the ith samples of G and it is uniformly distributed. This procedure is known as the inverse transformation method [28]. Function can also be interpreted as a realization from the Gaussian copula. Applying the inverse CDF to the uniform random variable ensures that is distributed according to . Unfortunately, the transformation in Equation (1) is non-linear, and therefore the correlation matrix Corr* of D* is not equal to the desired correlation matrix Corr.
- Step 4.
- Apply the Iman-Conover algorithm proposed by Ekström [29] in order to get a better approximation of the desired correlation matrix Corr for the (S, N) matrix of nodal demand scenarios D*. The algorithm is described in the following steps:
- 4.1
- Calculate lower triangular Cholesky decomposition V of Corr, i.e., Corr = V∙VT.
- 4.2
- Calculate lower triangular Cholesky decomposition Q of Corr*, i.e., Corr* = Q∙QT.
- 4.3
- Obtain T such that Corr = T∙Corr∙TT, can be calculated as T = V∙Q−1.
- 4.4
- Obtain the matrix ScoreD* by rank-transforming D and convert to van der Waerden scores, defined as where ϕ is the CDF of the standard normal distribution, i is the assigned rank and N is the total number of samples.
- 4.5
- Calculate the target scores matrix ScoreD = ScoreD*·TT.
- 4.6
- Match up the rank pairing in D* according to ScoreD, obtaining the new (S,N) dimensional matrix D containing the S scenarios of the N nodal demand in the WDS. The N samples are distributed according to the desired marginals and their correlation matrix is close to the correlation matrix derived from the scaling laws.
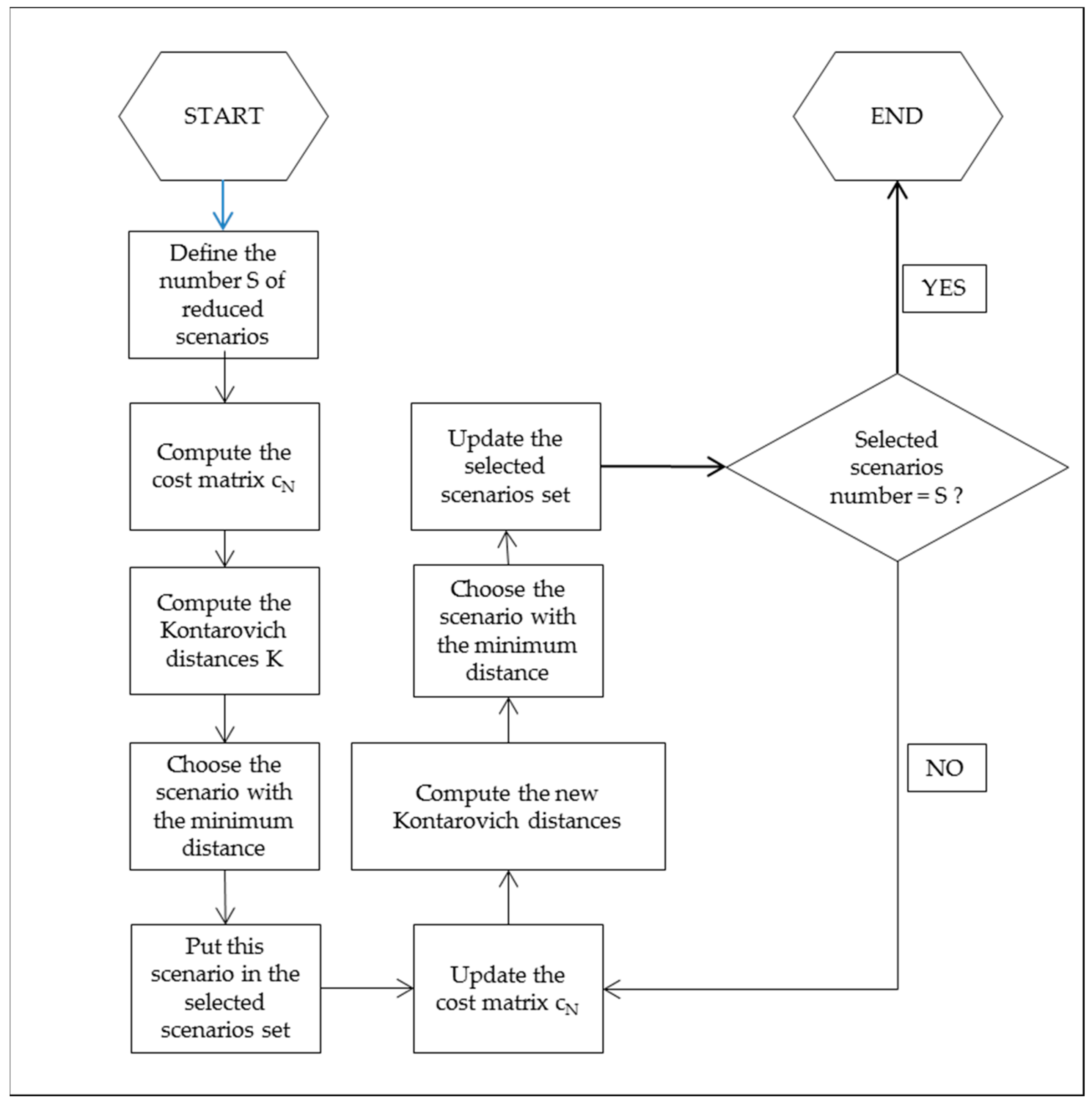
2.3. Scenario Reduction
3. Application Example
3.1. Theoretical WDN: The Apulian Network
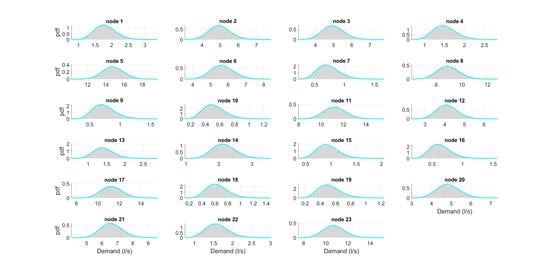
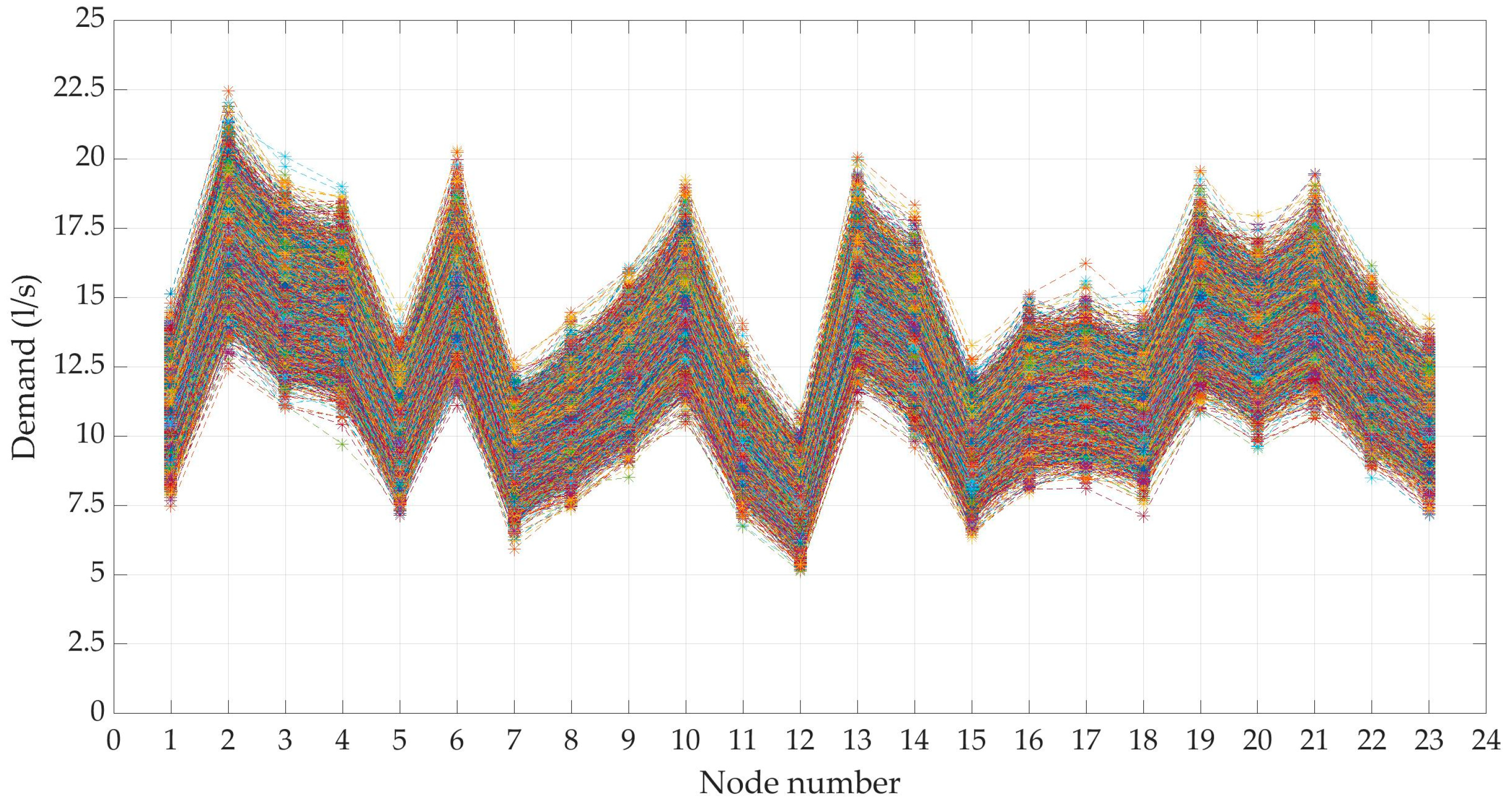
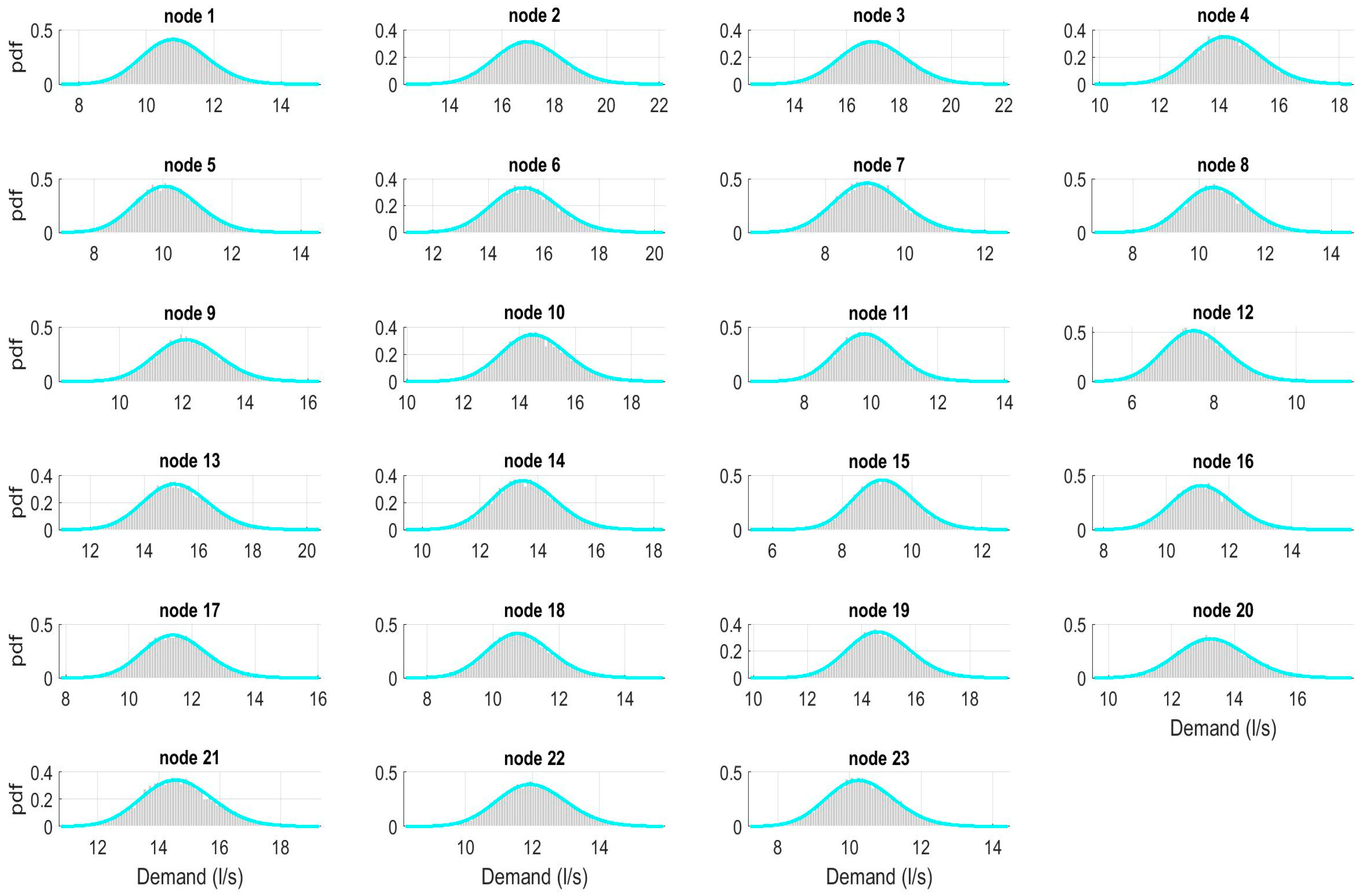
3.2. Generation of Demand Scenarios
3.2.1. DemandA
3.2.2. DemandB
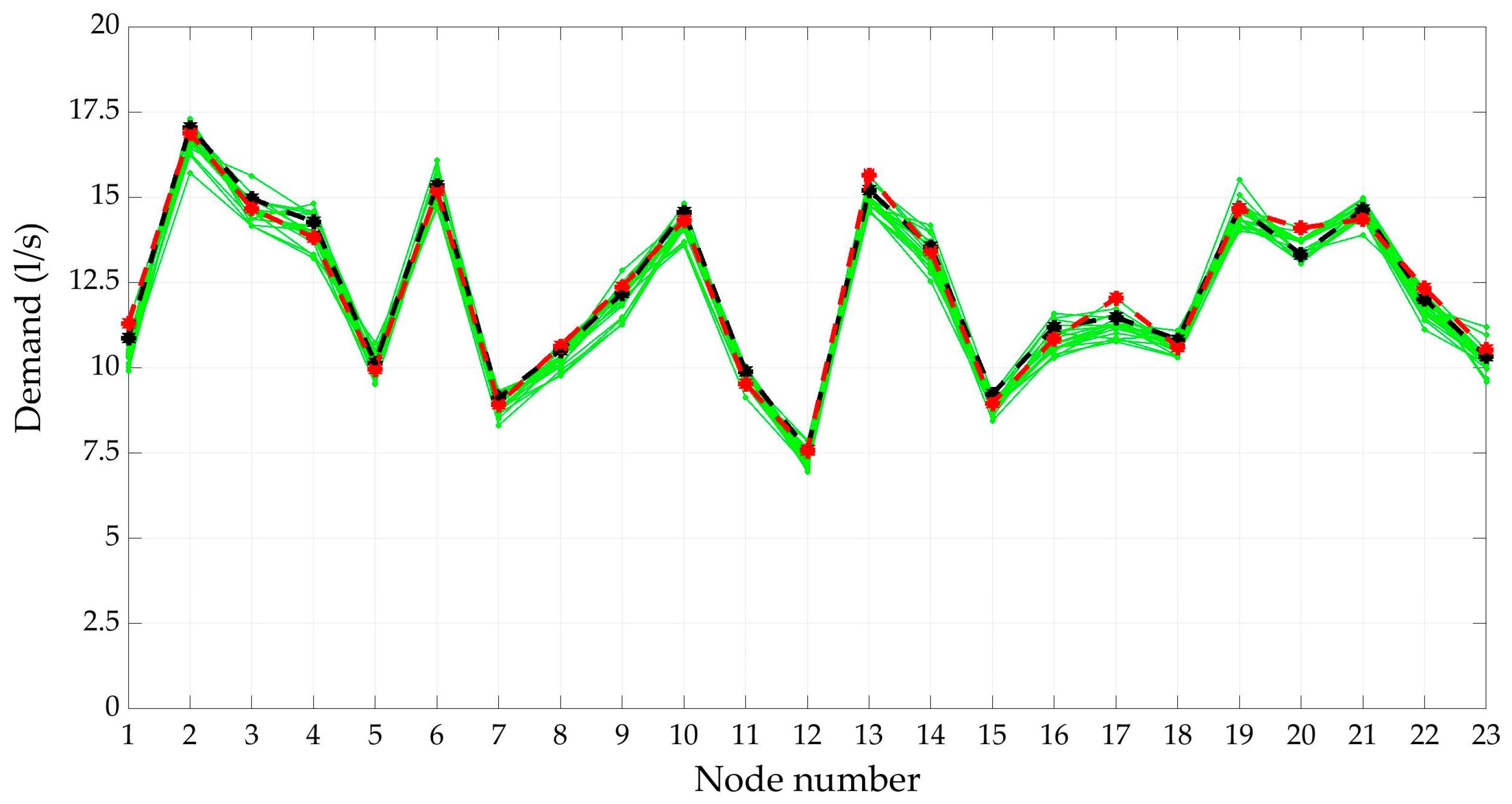
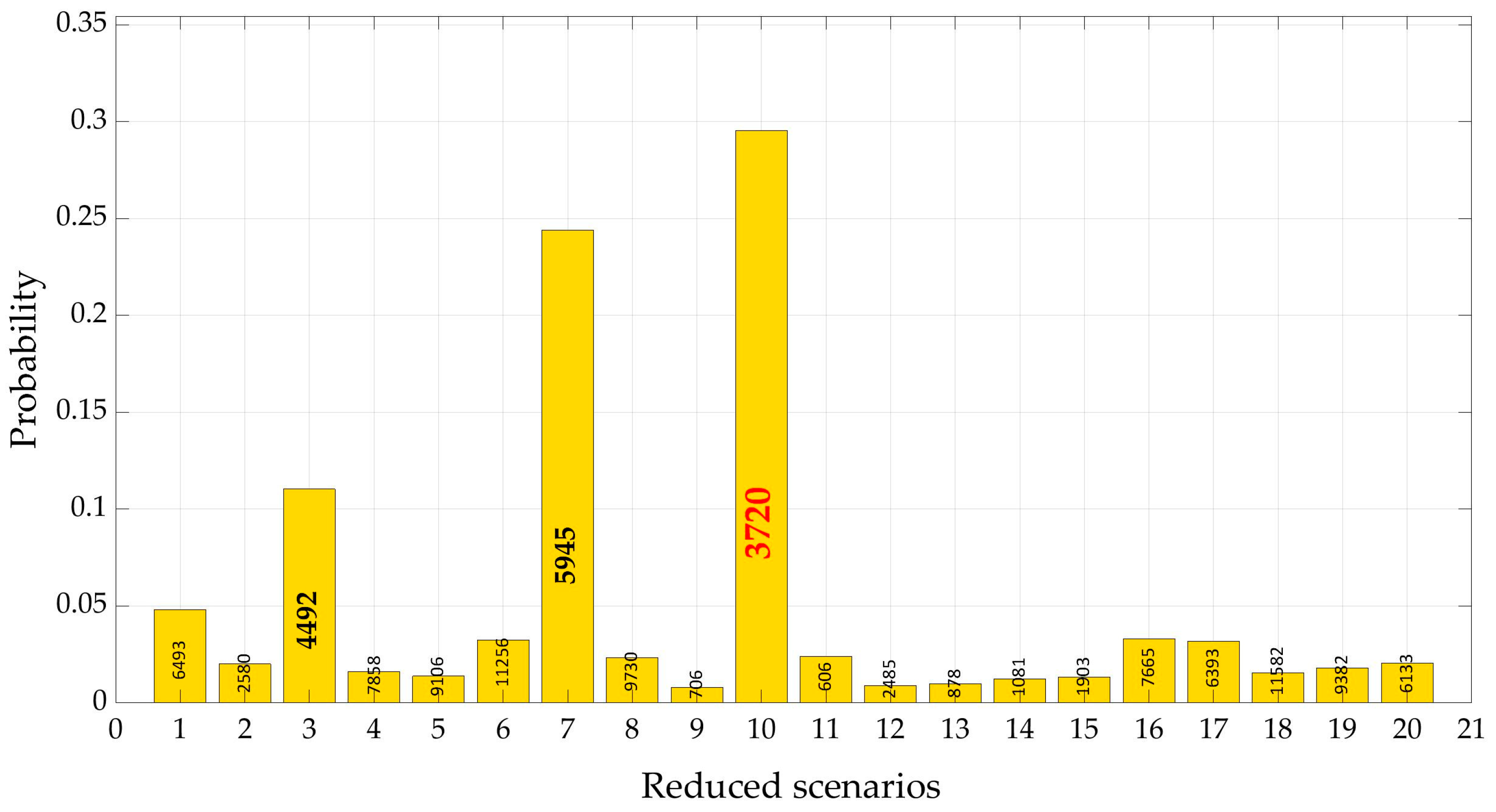
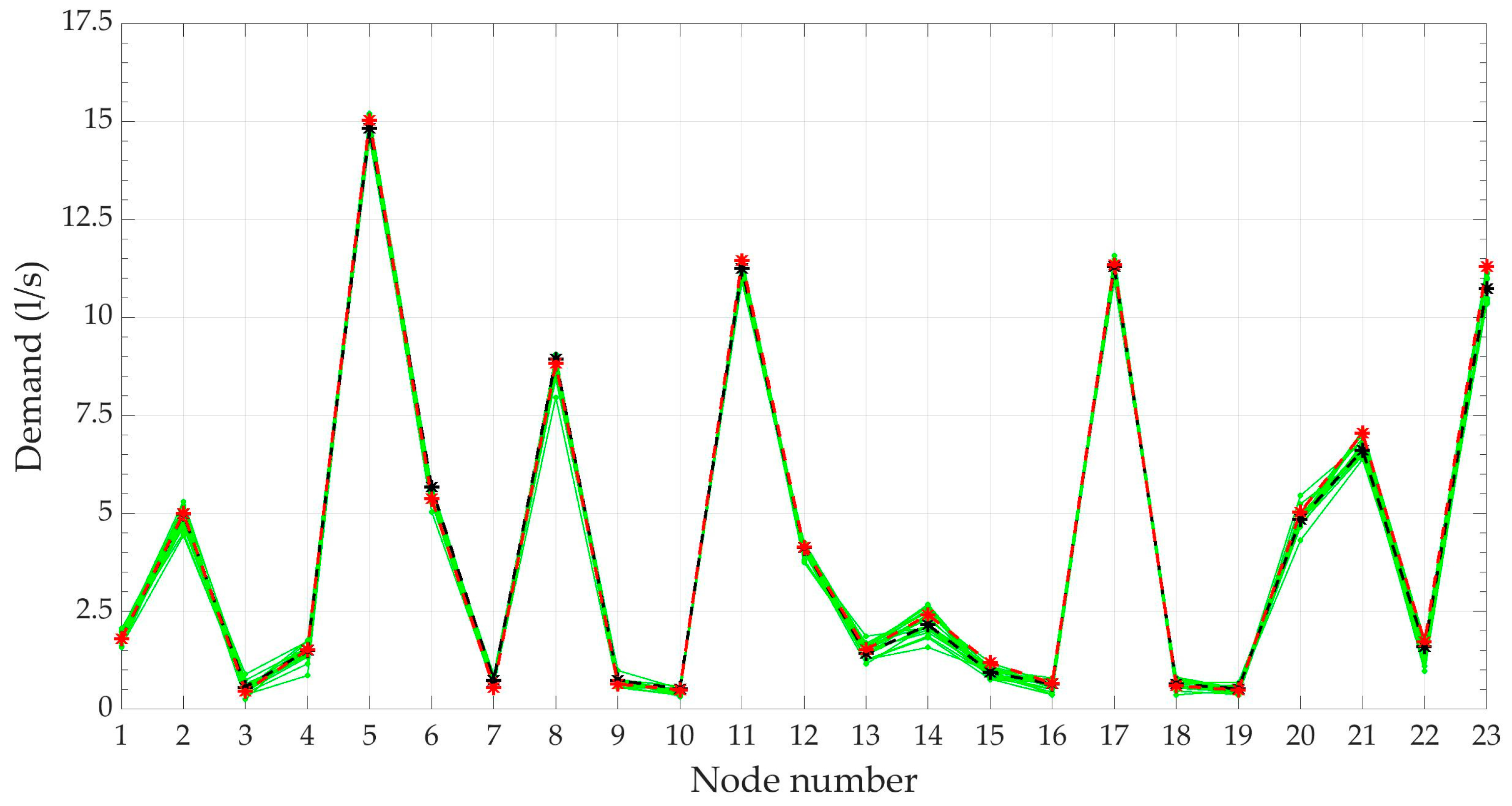
3.3. Reduction of Demand Scenarios
3.3.1. DemandA
3.3.2. DemandB
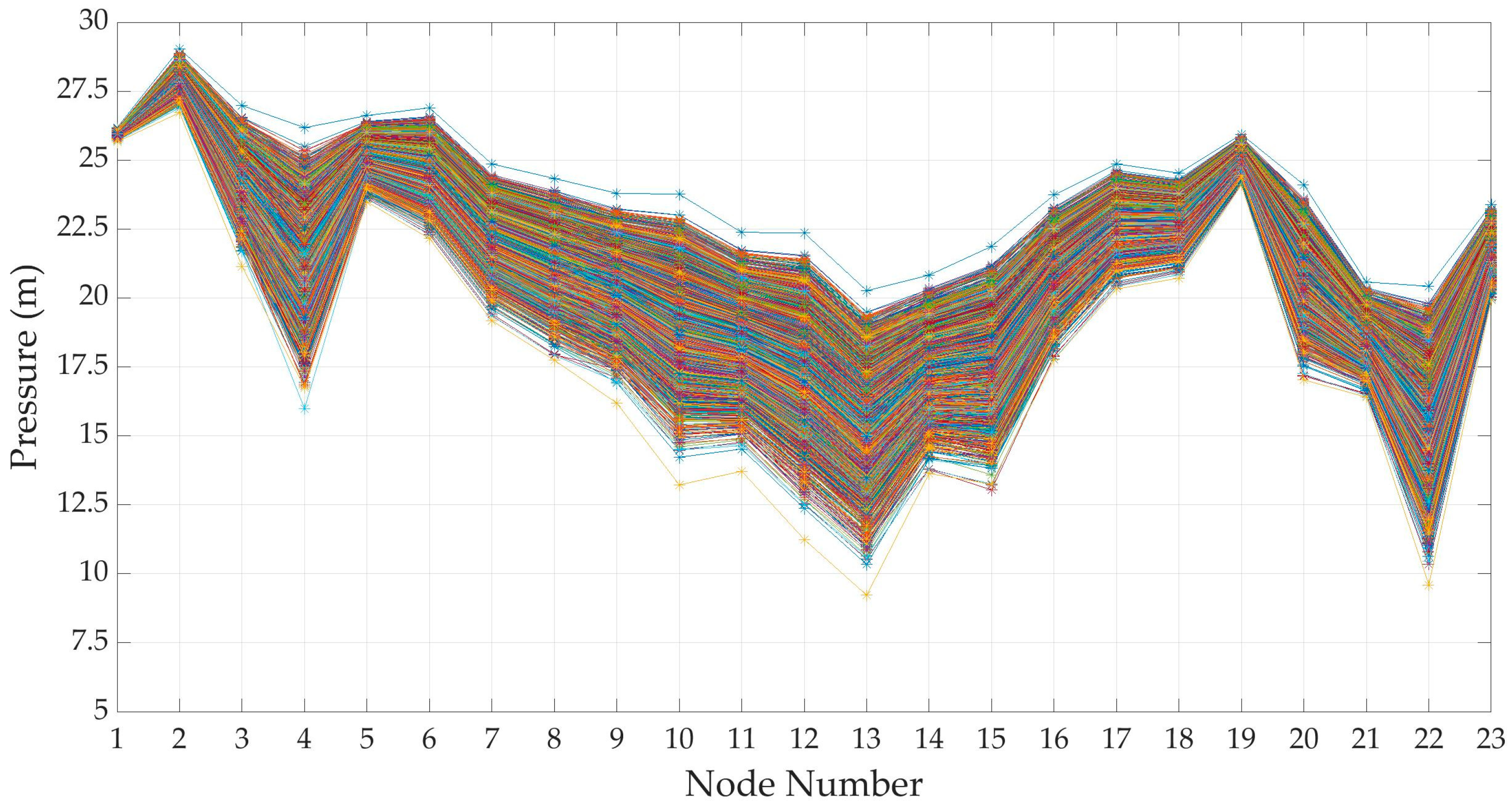
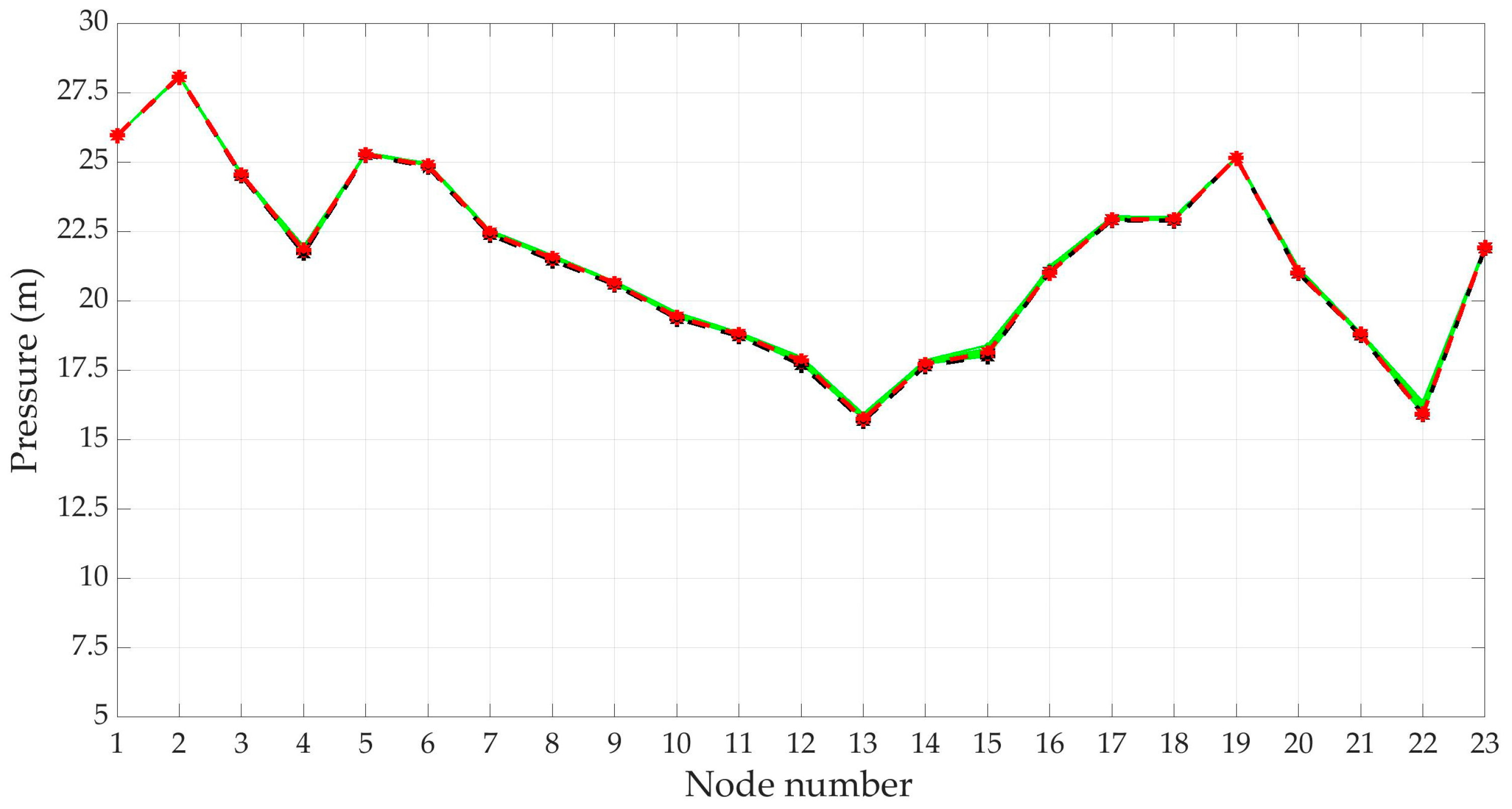
3.4. Hydraulic Simulation with Scenarios from DemandA
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Magini, R.; Pallavicini, I.; Guercio, R. Spatial and Temporal Scaling Properties of Water Demand. J. Water Resour. Plan. Manag. 2008, 134, 276–284. [Google Scholar] [CrossRef]
- Bargiela, A.; Sterling, M. Adaptive forecasting of daily water demand. In Comparative Model for Electrical Load Forecasting; Bunn, D.W., Farmer, E.D., Eds.; John Wiley and Sons: New York, NY, USA, 1985. [Google Scholar]
- Perelman, L.; Housh, M.; Ostfeld, A. Robust optimization for water distribution systems least cost design. Water Resour. Res. 2013, 49, 6795–6809. [Google Scholar] [CrossRef]
- Xu, C.C.; Goulter, I.C. Reliability-based optimal design of water distribution networks. J. Water Resour. Plan. Manag. 1999, 125, 352–362. [Google Scholar] [CrossRef]
- Steffelbauer, D.; Neumayer, M.; Günther, M.; Fuchs-Hanusch, D. Sensor Placement and Leakage Localization considering Demand Uncertainties. Procedia Eng. 2014, 89, 1160–1167. [Google Scholar] [CrossRef]
- Pallavicini, I.; Magini, R.; Guercio, R. Assessing the spatial distribution of pressure head in municipal water networks. In Proceedings of the Eighth International Conference on Computing and Control for the Water Industry, Exeter, UK, 5–7 September 2005. [Google Scholar]
- Kapelan, Z.S.; Savic, D.A.; Walters, G.A. Multiobjective design of water distribution systems under uncertainty. Water Resour. Res. 2005, 41, W11407. [Google Scholar] [CrossRef]
- Iman, R.L.; Conover, W.J. A distribution-free approach to inducing rank correlation among input variables. Communun. Stat. 1982, 11, 311–334. [Google Scholar] [CrossRef]
- Tolson, B.A.; Maier, H.R.; Simpson, A.R.; Lence, B.J. Genetic algorithms for reliability-based optimisation of water distribution systems. J. Water Resour. Plan. Manag. 2004, 130, 63–72. [Google Scholar] [CrossRef]
- Vertommen, I.; Magini, R.; Cunha, M.D.C. Generating Water Demand Scenarios Using Scaling Laws. Procedia Eng. 2014, 70, 1697–1706. [Google Scholar] [CrossRef]
- Eck, B.; Fusco, F.; Taheri, N. Scenario Generation for Network Optimization with Uncertain Demands. In Proceedings of the 17th Water Distribution Systems Analysis Symposium, World Environmental and Water Resources Congress, Austin, TX, USA, 17–21 May 2015; pp. 844–852. [Google Scholar]
- Ridolfi, E.; Vertommen, I.; Magini, R. Joint probabilities of demands on a water distribution network: A non-parametric approach. AIP Conf. Proc. 2013, 1558, 1681–1684. [Google Scholar]
- Vertommen, I.; Magini, R.; Cunha, M.C.; Guercio, R. Water demand uncertainty: The scaling law approach. In Water Supply Systems Analysis: Selected Topics; Ostfeld, D.A., Ed.; InTech: London, UK, 2012; pp. 1–25. ISBN 978-953-51-0889-4. [Google Scholar]
- Vertommen, I.; Magini, R.; Cunha, M. Scaling Water Consumption Statistics. J. Water Resour. Plan. Manag. 2015, 141, 04014072. [Google Scholar] [CrossRef]
- Giustolisi, O.; Kapelan, Z.; Savic, D. Algorithm for Automatic Detection of Topological Changes in Water Distribution Networks. J. Hydraul. Eng. 2008, 134, 435–446. [Google Scholar] [CrossRef]
- Vershik, A. Kantorovich metric: Initial history and little-known applications. J. Math. Sci. 2006, 133, 1410–1417. [Google Scholar] [CrossRef]
- Blokker, E.J.M.; Vreeburg, J.H.G.; Dijk, J.C.V. Simulating Residential Water Demand with a Stochastic End-Use Model. J. Water Resour. Plan. Manag. 2010, 136, 19–26. [Google Scholar] [CrossRef]
- Creaco, E.; Alvisi, S.; Farmani, R.; Vamvakeridou-Lyroudia, L.; Franchini, M.; Kapelan, Z.; Savic, D. Preserving Duration-intensity Correlation on Synthetically Generated Water Demand Pulses. Procedia Eng. 2015, 119, 1463–1472. [Google Scholar] [CrossRef]
- Filion, Y.R.; Karney, B.W.; Moughton, L.; Buchberger, S.G.; Adams, B.J. Cross Correlation Analysis of Residential Demand in the City of Milford, Ohio. In Proceedings of the Water Distribution Systems Analysis Symposium, Cincinnati, OH, USA, 27–30 August 2006; ASCE: Reston, VA, USA, 2008. [Google Scholar]
- Filion, Y.; Adams, B.; Karney, B. Cross Correlation of Demands in Water Distribution Network Design. J. Water Resour. Plan. Manag. 2007, 133, 137–144. [Google Scholar] [CrossRef]
- Savic, D. Coping with risk and uncertainty in urban water infrastructure rehabilitation planning. In Proceedings of the Acqua e Città-1° Convegno Nazionale di Idraulica Urbana, Sorrento, Italy, 28–30 September 2005. [Google Scholar]
- Hutton, C.J.; Kapelan, Z.; Vamvakeridou-Lyroudia, L.; Savic, D. Dealing with Uncertainty in Water Distribution System Models: A Framework for Real-Time Modeling and Data Assimilation. J. Water Resour. Plan. Manag. 2014, 140, 169–183. [Google Scholar] [CrossRef]
- Kossieris, P.; Makropoulos, C. Exploring the Statistical and Distributional Properties of Residential Water Demand at Fine Time Scales. Water 2018, 10, 1481. [Google Scholar] [CrossRef]
- Ponomareva, K.; Roman, D.; Date, P. An algorithm for moment-matching scenario generation with application to financial portfolio optimization. Eur. J. Oper. Res. 2015, 240, 678–687. [Google Scholar] [CrossRef]
- Magini, R.; Capannolo, F.; Ridolfi, E.; Guercio, R. Demand uncertainty in modelling WDS: Scaling laws and scenario generation. WIT Trans. Ecol. Environ. 2016, 210, 735–746. [Google Scholar] [CrossRef]
- Mitra, S. Scenario Generation for Stochastic Programming; White Paper Series, Optirisk Systems, Domain: Finance Reference Number: OPT 004; SINTEF Technology and Society: Uxbridge, UK, 2006. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 3rd ed.; Johns Hopkins: Baltimore, MD, USA, 1996; ISBN 978-0-8018-5414-9. [Google Scholar]
- Ross, S.M. Introduction to Probability and Statistics for Engineers and Scientists, 5th ed.; Academic Press: Cambridge, MA, USA, 2014; ISBN 978-0-1239-48113. [Google Scholar]
- Ekstrom, P.A. A Simulation Toolbox for Sensitivity Analysis. Master‘s Thesis, Faculty of Science and Technology, Uppsala Universitet, Uppsala, Sweden, 2005. [Google Scholar]
- Dupacová, J.; Gröwe-kuska, N.; Römisch, W. Scenario reduction in stochastic programming. An approach using probability metrics. Math. Program 2003, 95, 493–511. [Google Scholar] [CrossRef]
- Morales, J.M.; Pineda, S.; Conejo, A.J.; Carrión, M. Scenario Reduction for Future Market Trading in Electricity Markets. IEEE Tras. Power Syst. 2009, 24, 878–888. [Google Scholar] [CrossRef]
- Heitsch, H.; Romisch, W. Scenario reduction in stochastic programming. Comput. Optim. Appl. 2003, 24, 187–206. [Google Scholar] [CrossRef]
- Giustolisi, O.; Laucelli, D.; Colombo, A.F. Deterministic versus stochastic design of water distribution networks. J. Water Resour. Plan. Manag. 2009, 135, 117–127. [Google Scholar] [CrossRef]
- Todini, E.; Pilati, S. A gradient algorithm for the analysis of pipe networks. In Computer Applications in Water Supply; Research Studies Press: Letchworth, UK, 1988. [Google Scholar]
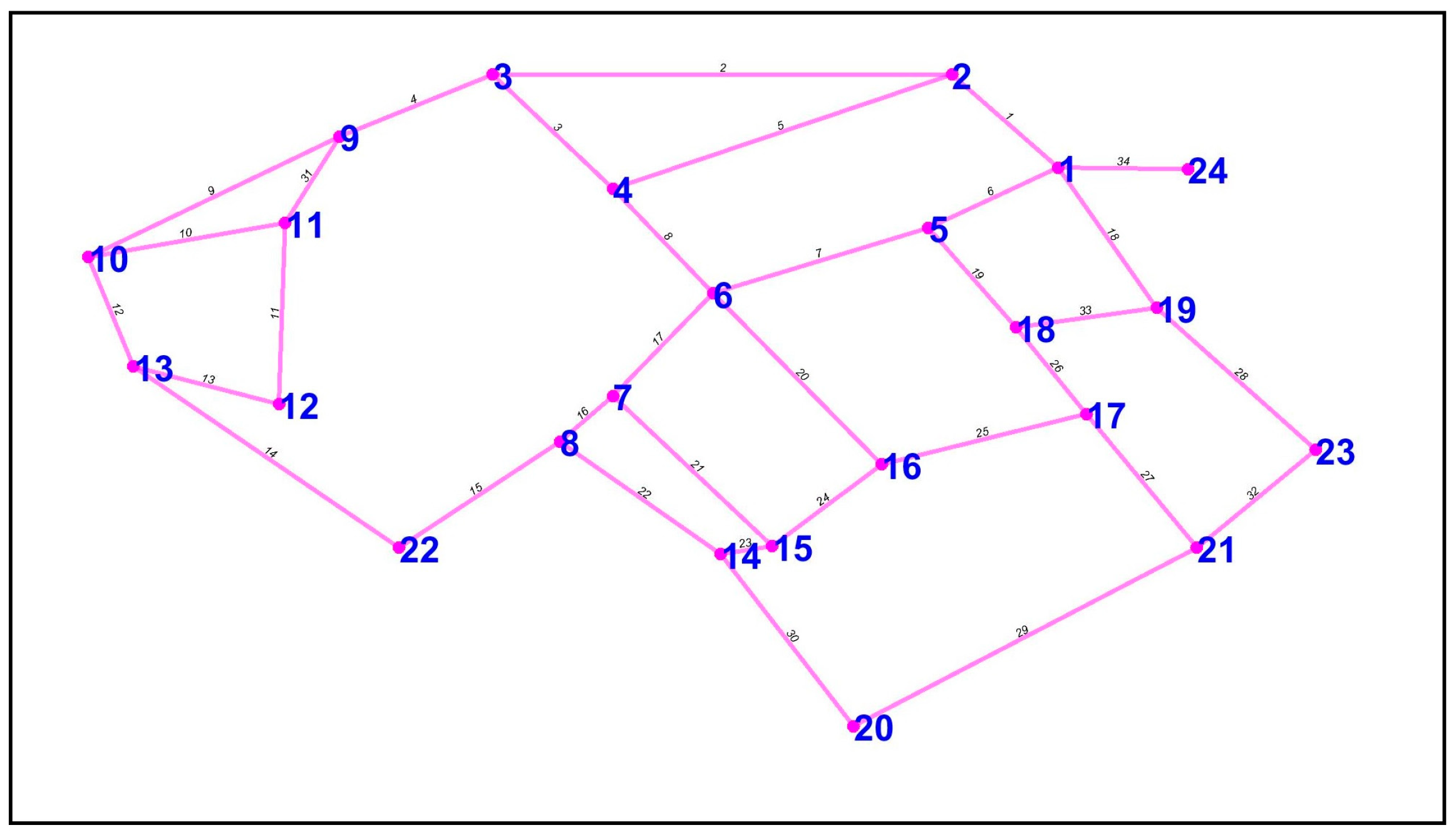




| PIPES | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Pipe Number | Start Node | End Node | Length (m) | C Hazen Williams | D (m) | Pipe Number | Start Node | End Node | Length (m) | C Hazen Williams | D (m) |
| 1 | 1 | 2 | 348.5 | 100 | 0.327 | 18 | 1 | 19 | 583.9 | 100 | 0.164 |
| 2 | 2 | 3 | 955.7 | 100 | 0.29 | 19 | 5 | 18 | 452 | 100 | 0.229 |
| 3 | 3 | 4 | 483 | 100 | 0.1 | 20 | 6 | 16 | 794.7 | 100 | 0.1 |
| 4 | 3 | 9 | 400.7 | 100 | 0.29 | 21 | 7 | 15 | 717.7 | 100 | 0.1 |
| 5 | 2 | 4 | 791.9 | 100 | 0.1 | 22 | 8 | 14 | 655.6 | 100 | 0.258 |
| 6 | 1 | 5 | 404.4 | 100 | 0.368 | 23 | 15 | 14 | 165.5 | 100 | 0.1 |
| 7 | 5 | 6 | 390.6 | 100 | 0.327 | 24 | 16 | 15 | 252.1 | 100 | 0.1 |
| 8 | 6 | 4 | 482.3 | 100 | 0.1 | 25 | 17 | 16 | 331.5 | 100 | 0.1 |
| 9 | 9 | 10 | 934.4 | 100 | 0.1 | 26 | 18 | 17 | 500 | 100 | 0.204 |
| 10 | 11 | 10 | 431.3 | 100 | 0.184 | 27 | 17 | 21 | 579.9 | 100 | 0.164 |
| 11 | 11 | 12 | 513.1 | 100 | 0.1 | 28 | 19 | 23 | 842.8 | 100 | 0.1 |
| 12 | 10 | 13 | 428.4 | 100 | 0.184 | 29 | 21 | 20 | 792.6 | 100 | 0.1 |
| 13 | 12 | 13 | 419 | 100 | 0.1 | 30 | 20 | 14 | 846.3 | 100 | 0.184 |
| 14 | 22 | 13 | 1023.1 | 100 | 0.1 | 31 | 9 | 11 | 164 | 100 | 0.258 |
| 15 | 8 | 22 | 455.1 | 100 | 0.164 | 32 | 23 | 21 | 427.9 | 100 | 0.1 |
| 16 | 7 | 8 | 182.6 | 100 | 0.29 | 33 | 19 | 18 | 379.2 | 100 | 0.1 |
| 17 | 6 | 7 | 221.3 | 100 | 0.29 | 34 | 24 | 1 | 158.2 | 100 | 0.368 |
| NODES | |||||||||||
| node ID | elevation (m) | users A | DemandA (l/s) | users B | DemandB (l/s) | ||||||
| 1 | 6.4 | 932 | 10.86 | 155 | 1.8 | ||||||
| 2 | 7 | 1461 | 17.03 | 427 | 4.98 | ||||||
| 3 | 6 | 1282 | 14.95 | 48 | 0.56 | ||||||
| 4 | 8.4 | 1224 | 14.28 | 129 | 1.5 | ||||||
| 5 | 7.4 | 869 | 10.13 | 1270 | 14.81 | ||||||
| 6 | 9 | 1316 | 15.35 | 486 | 5.67 | ||||||
| 7 | 9.1 | 782 | 9.11 | 63 | 0.73 | ||||||
| 8 | 9.5 | 901 | 10.51 | 766 | 8.93 | ||||||
| 9 | 8.4 | 1045 | 12.18 | 63 | 0.73 | ||||||
| 10 | 10.5 | 1249 | 14.57 | 45 | 0.52 | ||||||
| 11 | 9.6 | 848 | 9.88 | 964 | 11.24 | ||||||
| 12 | 11.7 | 650 | 7.58 | 354 | 4.12 | ||||||
| 13 | 12.3 | 1303 | 15.2 | 122 | 1.42 | ||||||
| 14 | 10.6 | 1162 | 13.55 | 185 | 2.15 | ||||||
| 15 | 10.1 | 791 | 9.23 | 81 | 0.94 | ||||||
| 16 | 9.5 | 960 | 11.2 | 55 | 0.64 | ||||||
| 17 | 10.2 | 984 | 11.47 | 968 | 11.29 | ||||||
| 18 | 9.6 | 928 | 10.82 | 55 | 0.64 | ||||||
| 19 | 9.1 | 1258 | 14.68 | 45 | 0.52 | ||||||
| 20 | 13.9 | 1142 | 13.32 | 416 | 4.85 | ||||||
| 21 | 11.1 | 1255 | 14.63 | 567 | 6.61 | ||||||
| 22 | 11.4 | 1030 | 12.01 | 137 | 1.59 | ||||||
| 23 | 10 | 886 | 10.33 | 920 | 10.73 | ||||||
| 24 (Reservoir) | 36.4 | 24258 | 282.86 | 8321 | 96.97 | ||||||
| Statistical Parameter | Value |
|---|---|
| 0.365 | |
| 0.700 | |
| 0.870 | |
| scaling law exponent α | 1.230 |
| INPUT | OUTPUT | INPUT | OUTPUT | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Node ID | a | b | a | b | Node ID | a | b | a | b |
| 1 | 125.20 | 0.0868 | 125.21 | 0.0868 | 13 | 162.06 | 0.0938 | 162.07 | 0.0938 |
| 2 | 176.99 | 0.0963 | 177.01 | 0.0963 | 14 | 148.38 | 0.0914 | 148.39 | 0.0914 |
| 3 | 160.04 | 0.0935 | 160.06 | 0.0934 | 15 | 110.35 | 0.0836 | 110.36 | 0.0836 |
| 4 | 154.44 | 0.0925 | 154.45 | 0.0925 | 16 | 128.09 | 0.0874 | 128.10 | 0.0874 |
| 5 | 118.63 | 0.0855 | 118.65 | 0.0855 | 17 | 130.55 | 0.0879 | 130.56 | 0.0879 |
| 6 | 163.30 | 0.0940 | 163.32 | 0.0940 | 18 | 124.79 | 0.0868 | 124.80 | 0.0868 |
| 7 | 109.38 | 0.0834 | 109.39 | 0.0834 | 19 | 157.73 | 0.0930 | 157.75 | 0.0930 |
| 8 | 121.98 | 0.0862 | 122.00 | 0.0862 | 20 | 146.41 | 0.0910 | 146.42 | 0.0910 |
| 9 | 136.73 | 0.0892 | 136.75 | 0.0892 | 21 | 157.44 | 0.0930 | 157.46 | 0.0930 |
| 10 | 156.86 | 0.0929 | 156.88 | 0.0929 | 22 | 135.22 | 0.0889 | 135.24 | 0.0889 |
| 11 | 116.42 | 0.0850 | 116.43 | 0.0850 | 23 | 120.42 | 0.0858 | 120.43 | 0.0858 |
| 12 | 94.86 | 0.0799 | 94.87 | 0.0799 | - | - | - | - | - |
| E[ρ1] = 0.0043 | ||
|---|---|---|
| ρ Input Correlation Matrix (Scaling Laws) | ρ Output Correlation Matrix (Scenarios) | |
| min | 0.7542 | 0.7542 |
| average | 0.8147 | 0.8147 |
| max | 0.8568 | 0.8567 |
| INPUT | OUTPUT | INPUT | OUTPUT | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Node ID | a | b | a | b | Node ID | a | b | a | b |
| 1 | 31.46 | 0.0575 | 31.46 | 0.0575 | 13 | 26.16 | 0.0544 | 26.16 | 0.0544 |
| 2 | 68.64 | 0.0726 | 68.65 | 0.0726 | 14 | 36.05 | 0.0599 | 36.05 | 0.0599 |
| 3 | 12.76 | 0.0439 | 12.76 | 0.0439 | 15 | 19.08 | 0.0495 | 19.09 | 0.0495 |
| 4 | 27.31 | 0.0551 | 27.31 | 0.0551 | 16 | 14.17 | 0.0453 | 14.17 | 0.0453 |
| 5 | 158.89 | 0.0933 | 158.90 | 0.0932 | 17 | 128.91 | 0.0876 | 128.92 | 0.0876 |
| 6 | 75.83 | 0.0748 | 75.84 | 0.0748 | 18 | 14.17 | 0.0453 | 14.17 | 0.0453 |
| 7 | 15.73 | 0.0467 | 15.73 | 0.0467 | 19 | 12.14 | 0.0433 | 12.14 | 0.0432 |
| 8 | 107.65 | 0.0830 | 107.66 | 0.0830 | 20 | 67.28 | 0.0721 | 67.28 | 0.0721 |
| 9 | 15.73 | 0.0467 | 15.73 | 0.0467 | 21 | 85.39 | 0.0775 | 85.40 | 0.0775 |
| 10 | 12.14 | 0.0433 | 12.14 | 0.0432 | 22 | 28.60 | 0.0559 | 28.61 | 0.0559 |
| 11 | 128.50 | 0.0875 | 128.51 | 0.0875 | 23 | 123.96 | 0.0866 | 123.97 | 0.0866 |
| 12 | 59.41 | 0.0695 | 59.42 | 0.0695 | - | - | - | - | - |
| E[ρ1] = 0.0043 | ||
|---|---|---|
| ρ Input Correlation Matrix (Scaling Laws) | ρ Output Correlation Matrix (Scenarios) | |
| min | 0.1627 | 0.1627 |
| average | 0.4329 | 0.4330 |
| max | 0.8261 | 0.8261 |
| Node ID | Scenario 3720 | Scenario 5945 | Scenario 4492 | Mean Scenario | Node ID | Scenario 3720 | Scenario 5945 | Scenario 4492 | Mean Scenario |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 10.87 | 11.31 | 10.29 | 10.73 | 13 | 15.20 | 15.66 | 14.98 | 14.94 |
| 2 | 17.04 | 16.88 | 15.71 | 17.27 | 14 | 13.56 | 13.43 | 13.09 | 13.53 |
| 3 | 14.96 | 14.67 | 14.15 | 14.66 | 15 | 9.23 | 8.96 | 8.44 | 8.90 |
| 4 | 14.28 | 13.82 | 13.32 | 14.35 | 16 | 11.20 | 10.85 | 10.40 | 11.01 |
| 5 | 10.14 | 9.97 | 10.73 | 10.40 | 17 | 11.48 | 12.04 | 10.77 | 11.59 |
| 6 | 15.35 | 15.19 | 14.71 | 16.08 | 18 | 10.83 | 10.61 | 10.31 | 10.64 |
| 7 | 9.12 | 8.94 | 8.31 | 8.71 | 19 | 14.68 | 14.65 | 14.11 | 14.71 |
| 8 | 10.51 | 10.64 | 9.92 | 10.24 | 20 | 13.32 | 14.10 | 13.45 | 13.40 |
| 9 | 12.19 | 12.38 | 11.26 | 12.85 | 21 | 14.64 | 14.35 | 14.39 | 13.89 |
| 10 | 14.57 | 14.33 | 14.19 | 14.41 | 22 | 12.02 | 12.34 | 11.12 | 12.19 |
| 11 | 9.89 | 9.53 | 9.53 | 9.96 | 23 | 10.34 | 10.53 | 10.12 | 10.37 |
| 12 | 7.58 | 7.58 | 7.33 | 7.25 | - | - | - | - | - |
| Node ID | Scenario 6232 | Scenario 9392 | Scenario 9550 | Mean Scenario | Node ID | Scenario 6232 | Scenario 9392 | Scenario 9550 | Mean Scenario |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.81 | 1.81 | 1.75 | 1.80 | 13 | 1.42 | 1.52 | 1.27 | 1.39 |
| 2 | 4.98 | 5.01 | 4.80 | 4.71 | 14 | 2.16 | 2.41 | 1.58 | 2.13 |
| 3 | 0.56 | 0.46 | 0.64 | 0.48 | 15 | 0.94 | 1.19 | 0.99 | 1.06 |
| 4 | 1.50 | 1.52 | 1.39 | 1.55 | 16 | 0.64 | 0.66 | 0.65 | 0.58 |
| 5 | 14.82 | 15.03 | 14.55 | 14.92 | 17 | 11.29 | 11.34 | 11.24 | 11.16 |
| 6 | 5.67 | 5.38 | 5.38 | 5.62 | 18 | 0.64 | 0.60 | 0.83 | 0.64 |
| 7 | 0.73 | 0.56 | 0.59 | 0.68 | 19 | 0.52 | 0.49 | 0.45 | 0.55 |
| 8 | 8.94 | 8.82 | 8.45 | 8.82 | 20 | 4.85 | 5.04 | 4.86 | 4.91 |
| 9 | 0.73 | 0.65 | 0.76 | 0.69 | 21 | 6.61 | 7.05 | 6.65 | 6.59 |
| 10 | 0.52 | 0.50 | 0.34 | 0.46 | 22 | 1.60 | 1.72 | 1.53 | 1.10 |
| 11 | 11.25 | 11.45 | 11.04 | 11.24 | 23 | 10.73 | 11.30 | 11.12 | 10.64 |
| 12 | 4.13 | 4.14 | 4.04 | 4.05 | - | - | - | - | - |
| Node ID | Scenario 7577 | Scenario 6780 | Scenario Mean Pressure | Scenario 3720 | Scenario Mean Demand | Node ID | Scenario 7577 | Scenario 6780 | Scenario Mean Pressure | Scenario 3720 | Scenario Mean Demand |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 25.965 | 25.962 | 25.963 | 25.966 | 25.965 | 13 | 15.754 | 15.904 | 15.684 | 15.839 | 15.723 |
| 2 | 28.077 | 28.052 | 28.061 | 28.085 | 28.070 | 14 | 17.727 | 17.850 | 17.661 | 17.697 | 17.692 |
| 3 | 24.548 | 24.543 | 24.512 | 24.592 | 24.534 | 15 | 18.135 | 18.278 | 18.001 | 18.107 | 18.041 |
| 4 | 21.829 | 21.852 | 21.714 | 21.963 | 21.755 | 16 | 21.023 | 21.222 | 21.042 | 21.138 | 21.068 |
| 5 | 25.280 | 25.314 | 25.254 | 25.289 | 25.267 | 17 | 22.946 | 23.040 | 22.908 | 22.930 | 22.927 |
| 6 | 24.875 | 24.929 | 24.829 | 24.888 | 24.849 | 18 | 22.933 | 22.966 | 22.895 | 22.906 | 22.911 |
| 7 | 22.453 | 22.522 | 22.383 | 22.449 | 22.407 | 19 | 25.149 | 25.185 | 25.147 | 25.139 | 25.155 |
| 8 | 21.545 | 21.618 | 21.454 | 21.522 | 21.483 | 20 | 21.019 | 21.193 | 20.997 | 21.021 | 21.026 |
| 9 | 20.647 | 20.691 | 20.592 | 20.694 | 20.620 | 21 | 18.794 | 18.859 | 18.768 | 18.731 | 18.785 |
| 10 | 19.421 | 19.553 | 19.366 | 19.501 | 19.404 | 22 | 15.926 | 16.363 | 15.908 | 16.111 | 15.959 |
| 11 | 18.808 | 18.864 | 18.731 | 18.855 | 18.764 | 23 | 21.919 | 21.976 | 21.894 | 21.862 | 21.909 |
| 12 | 17.846 | 17.902 | 17.700 | 17.901 | 17.747 | - | - | - | - | - | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magini, R.; Boniforti, M.A.; Guercio, R. Generating Scenarios of Cross-Correlated Demands for Modelling Water Distribution Networks. Water 2019, 11, 493. https://doi.org/10.3390/w11030493
Magini R, Boniforti MA, Guercio R. Generating Scenarios of Cross-Correlated Demands for Modelling Water Distribution Networks. Water. 2019; 11(3):493. https://doi.org/10.3390/w11030493
Chicago/Turabian StyleMagini, Roberto, Maria Antonietta Boniforti, and Roberto Guercio. 2019. "Generating Scenarios of Cross-Correlated Demands for Modelling Water Distribution Networks" Water 11, no. 3: 493. https://doi.org/10.3390/w11030493
APA StyleMagini, R., Boniforti, M. A., & Guercio, R. (2019). Generating Scenarios of Cross-Correlated Demands for Modelling Water Distribution Networks. Water, 11(3), 493. https://doi.org/10.3390/w11030493