Abstract
The high-resolution topography is very crucial to investigate the hydrological and hydrodynamic process. To resolve the deficiency problem of high resolution terrain data in rivers, the Quartic Hermite Spline with Parameter (QHSP) method constructing the river channel terrain based on the limited cross-section data is presented. The proposed method is able to not only improve the reliability of the constructed river terrain, but also avoid the numerical oscillations caused by the existing constructing approach, e.g., the Cubic Hermite Spline (CHS) method. The performance of the proposed QHSP method is validated against two benchmark tests. Comparing the constructed river terrains, the QHSP method can improve the accuracy by at least 15%. For the simulated flood process, the QHSP method could reproduce more acceptable modeling results as well, e.g., in Wangmaogou catchment, the numerical model applying the Digital Elevation Model (DEM) produced by the QHSP method could increase the reliability by 18.5% higher than that of CHS method. It is indicated that the QHSP method is more reliable for river terrain model construction than the CHS and is a more reasonable tool investigating the hydrodynamic processes in river channels lacking of high resolution topography data.
1. Introduction
When investigating the hydrological and hydrodynamic process in rivers, high-resolution topography for river channels is indispensable. For instance, river channel terrain plays a very importance role in reliably simulating the flood propagation and inundation processes by using 2D shallow water models [1,2,3,4,5]. River channel terrain, a key spatial layer estimating channel networks in a catchment, slope gradients, flow direction and other controlling factors of the water movement, is one of the most important spatial input data sets in hydrological modeling [6]. Without high-resolution topography, there will be deviations in computed hydraulic factors, such as water depth and flow velocity, and in turn the rain-runoff process, thus affecting flood assessment and management.
The LiDAR (Light Detection And Ranging) technique is an ideal way to obtain topographical data [7,8], but it is difficult to survey the river bed under water, due to the limit existing in the Airborne LiDAR bathymetry device [9,10,11,12]. An alternative way to measure the river bed topography is the SONAR (Sound Navigation And Ranging) technique [13,14]. The river channel terrain acquired through SONAR has fine resolution, but the equipment is not feasible everywhere, e.g., it cannot work in very shallow water. The traditional method expressing a river channel is to employ the measured cross sections of the river bed at the distance from tens to hundreds of meters, but it is difficult to provide continuous 3D terrain.
To overcome the shortcomings of existing techniques, some numerical methods were developed to create whole river bed terrain according to the available cross-section data. Merwade et al. [15]; Mateo Lazaro et al. [16] interpolated river bed bathymetry on the basis of the ArcGIS environment, introducing different spatial interpolating methods in Cartesian and flow-oriented coordinate systems to evaluate anisotropic effects [17]. Flanagin et al. [18] and Schappi et al. [19] used Kochanek–Bartels splines and a bilinear techniques to reproduce the river bed terrain from cross sections, respectively. The troublesome thing for these methods is that breaklines need to input to define river banks. In order to efficiently generate river channel, Caviedes-Voulli et al. [20] implemented the Cubic Hermite Spline (CHS) method to create a continuous and smooth river channel topography from the cross-section data, but the river channel interpolated by CHS method cannot adjust river trend to fit the surrounding terrain. In the actual situation, the river trend is complicated and it may be meandering. That means an independent variable, x, is not monotonically increasing, and there may be a regression of x value (a fixed x may correspond to two y values) as shown in Figure 1a. In this case, it is prone to cause constructing errors by using CHS approach as plotted in Figure 1b in section A.
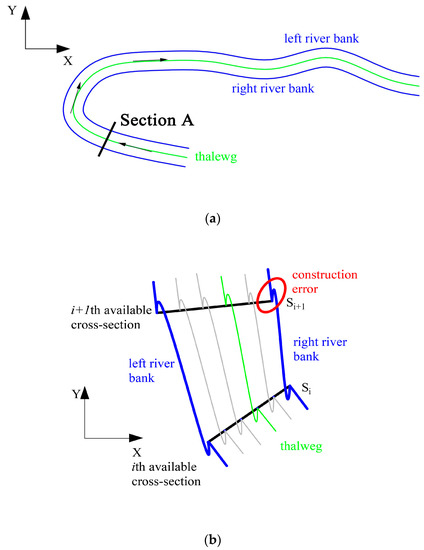
Figure 1.
(a) Meandering river channel and (b) erroneous river trend constructed by using the Cubic Hermite Spline (CHS) method.
Base on the research of Jun-Cheng et al. [21], this work developed an approach termed as Quartic Hermite Spline with Parameter (QHSP) method to construct more accurate river terrain from the available cross sections. The paper is structured as follows: Section 2 presents the QHSP method constructing river bed terrain; Section 3 illustrates the improved accuracy of the QHSP method against a benchmark test of a synthetic sinusoidal river; Section 4 applies the QHSP method to generate a realistic river bed terrain and demonstrates the higher accuracy of the terrain itself and the modeled results on it; and finally, brief conclusions are drawn in Section 5.
2. Constructing Method for River Bed Terrain from Available Cross Sections
2.1. Procedure for River Terrain Model Construction
When generating 3D river bed terrain, the approach applying the available cross-section data to interpolate the required points for the river channel are commonly used, e.g., Caviedes-Voulli et al. [20]. In this type of approach, two coordinate systems termed as planar and cross-section coordinates are applied as plotted in Figure 2. The planar coordinates have the variables of x and y describing the planar information. The cross-section coordinate system expresses the spatial information at a cross section consisting of surveyed points with the variables of n and Z, where n denotes the point number from the left bank to the right one, Z represents the elevation of a point (Figure 3). On the defined coordinate systems, the procedure generating the point clouds of river channel follows the four steps:
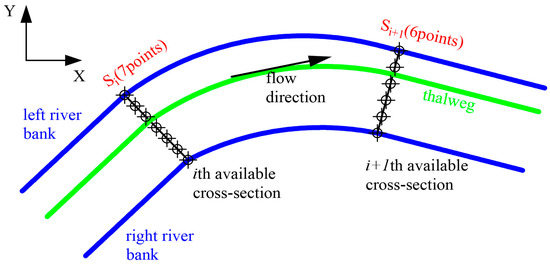
Figure 2.
The planar view of a river channel with measured cross sections.
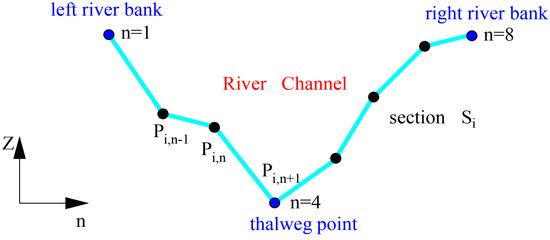
Figure 3.
An available cross section with surveyed points.
Step 1: preliminary treatment. In the planar coordinate system, the thalweg is produced by connecting the lowest point of the river-sections. The left and right bank lines are defined by respectively connecting the highest points at the left and right hand sides of the cross sections, as shown in Figure 2;
Step 2: reconstructing cross sections and generating the basic point clouds. For each cross section, the shape is reconstructed linearly from the measured points in cross-section coordinate, i.e., the section is divided into a fixed amount of points from the thalweg to the top of the left and right banks. For example, the sections Si and Si+1 have 3 and 7 points with the same planar distance respectively at the left and right banks (Figure 4). The basic point clouds are generated according to the reconstructed points;
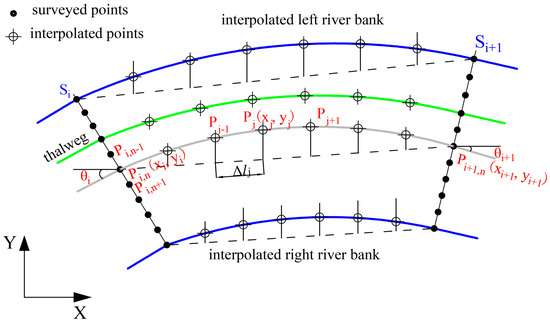
Figure 4.
River channel construction using the QHSP (Quartic Hermite Spline with Parameter) method.
Step 3: determining the planar positions of the interpolated river channel points. The new points should be interpolated between the two corresponding basic points at the existing neighbor sections. In this step, the planar locations of the interpolated points are determined by using the CHS method or the proposed one termed as QHSP in this work (Figure 4);
Step 4: computing the elevation of the interpolated river channel points. The elevation of each interpolated point in Step is computed through linearly interpolating the elevation of the corresponding basic points in existing cross section. The point cloud data (x, y, z) of the whole river is obtained and could be converted into raster data for model use.
As the Step 3 is a key step to produce more reliable results, the method generating the planar trend of the river and the locations of the interpolated points is improved in this work to obtain higher accuracy.
2.2. River Terrain Model Construction in the Planar Coordinate System
Caviedes-Voulli et al. [20] have developed the Cubic Hermite Spline (CHS) method to obtain a smooth and consecutive interpolated river channel. A sole river channel can be interpolated by using the CHS method if the two adjacent cross sections are given. However, the CHS method may cause unrealistic river trend as shown in Figure 1, especially when the river section data is rare. To solve this problem, the Quartic Hermite Spline with Parameter μ (QHSP) is proposed in this work. The key task is to determine the location of a newly inserted point Pj between the nth points of the sections Si and Si+1. The xj coordinate of the Pj is defined by equally dividing the straight line connecting the points of Pi,n and Pi+1,n, e.g., the line is divided into 7 segments in Figure 4. The interpolating formula for the considered point Pj using the QHSP method can be expressed as:
where tanθi and tanθi+1 are the tangent of the main flow direction at the cross section Si and Si+1. The coefficients of , , and can be evaluated from:
where, the parameter modifying the position of the interpolated channel points along the x-axis in the planar coordinate system can be depicted as:
In this method, the novelty is the introduction of the parameter μ which is used to flexibly adjust the trend of the river channel. As sketched in Figure 5, different value of μ can reconstruct different thalweg, e.g., if μ = 0, the reconstructed thalweg by the QHSP method is the same as that of the CHS method, if μ = 1 or μ = −1, the trend of thalweg is deflected to the left and right river bank, respectively.
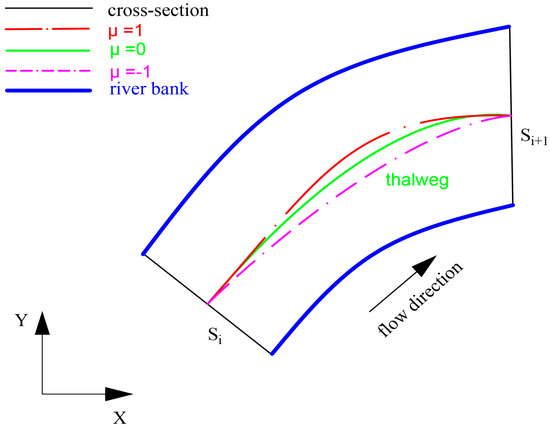
Figure 5.
The constructed thalweg affected by different values of the parameter μ.
When choosing a proper value of μ, a high-resolution aerial-view image or high accurate map of the river can be used to verify the performance of different μ, through comparing the constructed river tendency and that shown in the image or map between Si and Si+1. This procedure is repeated for all cross sections to produce the continuous and reliable river channel point cloud.
2.3. Constructing Error Treatment
As plotted in Figure 4, the x value of the river sections used for interpolation is increasing. But for meandering river, it is impossible to ensure the river trend always towards an irreversible direction. In this case, the method could encounter drastic oscillations, e.g., Figure 6a displays such an error occurring in interpolation process. To resolve this problem, the y-coordinate is applied instead when the river trend in x direction is reversed. Under such condition, the modified interpolating formula for the considered point Pj using the QHSP method is
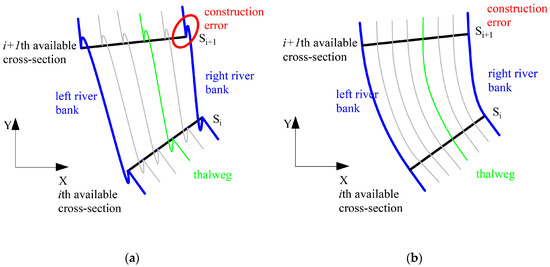
Figure 6.
Constructing error and the treatment. (a) Constructing errors occurring by using the existing method; (b) the corrected river trend construction using the proposed QHSP method.
In Equation (4), the parameter a and b are obtained as that in Equation (2) and accordingly, the parameter is modified as
2.4. Elevation Interpolation of River Channel
The Section 2.2 and Section 2.3 present the approach determining the planar locations of the interpolated points. The elevation of the point needs to be evaluated as well. In this work, the elevation zj of the considered point Pj is linearly interpolated from the corresponding given data in the sections Si and Si+1. In other words, the zj can be computed by interpolating the elevation at Pi,n and Pi+1,n as plotted in Figure 4 in a linear way as
where, m denotes the number of segments divided equally between the line connecting the Pi,n and Pi+1,n.
After this step, both the planar and the vertical positions of the new point Pj are known. In a sum, Equation (1) is used to determine the y valued of the considered point Pj whose x value of xj is a given one linear interpolated between sections Si and Si+1. I. The parameters applied in Equation (1) are computed by Equations (2) and (3), while when Equation (6) is utilized to compute the z value of the point Pj. Other inserted points can be interpolated in the same way and terrain point clouds between the given sections can be generated.
3. Channel Construction for a Synthetic Sinusoidal River
3.1. Benchmark Introduction
A synthetic sinusoidal river is applied to test the reliability of the proposed QHSP method. In this benchmark test, the planar location of the river channel can be presented as that by Morales-Hernandez et al. [22].
where A denotes the amplitudes; The period L = 2000 m is taken into account; The length of the river along the x axis is 4350 m. The river-section is defined by a function z(n) where n is an arbitrary point along the cross section
In Equation (8) has two independent variables x and n, where the thalweg position of the considered cross section is determined by x; n means the variable changing along the cross section. The river depth d = 5 m; the channel gradient G = 0.001; the width of the cross section W = 50 m and the elevation of the river bank E = 2800 m. The river channel is plotted in Figure 7. To consider general conditions, three types of the river channel with A = 400, 600 and 800 m are employed in this work to depict the performance of the QHSP method.

Figure 7.
Synthetic sinusoidal river with the amplitude of 400 m. Unit: m.
3.2. Channel Terrain Construction for the Synthetic Sinusoidal River
In this work, for each type of river channel, four test cases termed as A, B, C, and D are used by considering different given cross sections as shown in Figure 8a–d, respectively, where the given cross sections with the available measured points are marked in black. The distance between the given cross sections for case A, B, C, D are 500, 1000, 1000, and 750 m respectively. The difference between case B and C is that the locations of the cross sections are at the inflection points and those with the highest gradient, respectively. The QHSP and CHS methods are applied to construct the river terrains and the accuracy is compared by evaluating the constructed thalweg, cross sections (x = 1750, 2750, and 3250 m) and quantitative errors.
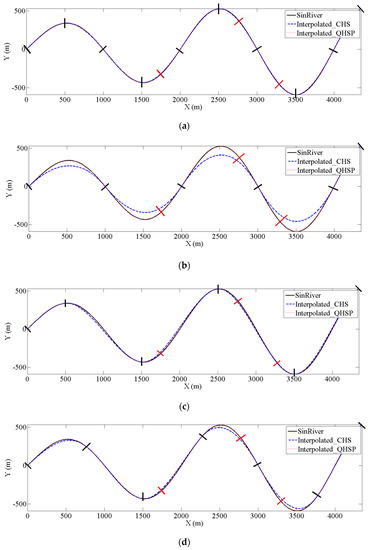
Figure 8.
Constructed river thalweg in Case (a) A, (b) B, (c) C, and (d) D with the amplitude of 600 m.
3.2.1. River Thalweg Construction
Constructing the thalweg could reflect the accuracy of a method. As plotted in Figure 8, the black curve represents the realistic sinusoidal river with the amplitude of 600 m, while the interpolated thalwegs by CHS and QHSP method are indicated by blue dashed lines and red dotted curves, respectively.
When using CHS method, the interpolated thalweg does not agree well with synthetic sinusoidal river in test cases B, C and D, especially for the test case B. The constructed thalweg in case A fit the river trend well, indicating that the CHS method requires more cross sections to produce reliable results. The QHSP method could considerably improve the accuracy for thalweg construction in cases B, C, and D through adjusting the parameter μ, showing that the QHSP method is able to correct the river trend deviation caused by the exiting method. The same results can also be found for the sinusoidal river with the amplitudes of 400 and 600 m which are not plotted herein but the accuracy is analyzed in Table 1.

Table 1.
Errors of constructed elevation for the sinusoidal rivers with 3 amplitudes.
3.2.2. Cross-Section Construction
A reliable interpolated planar river trend does not mean the accurate elevation, to test the performance of the interpolating methods, the constructed cross sections are compared with the realistic one. Figure 9 plots three constructed cross sections S1, S2, and S3 (x = 1750, 2750, and 3250 m) from the interpolated point clouds by using the QHSP and CHS methods for the river with the amplitude of 600 m. The constructed river channel is not exactly the same as the realistic one, but the QHSP method could generate more accurate results than the CHS method for all test cases, especially in the case B. The similar patterns can also be detected when constructing the river channels with the amplitudes of 400 and 800 m.
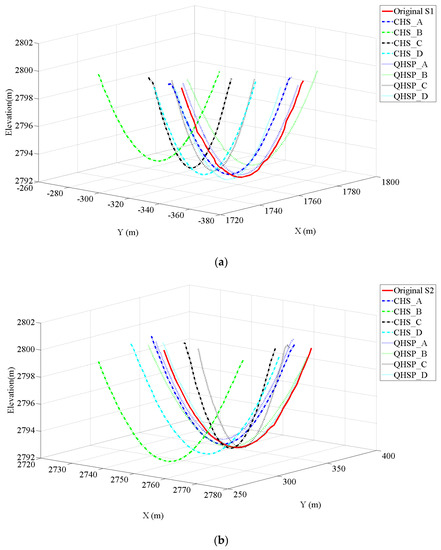
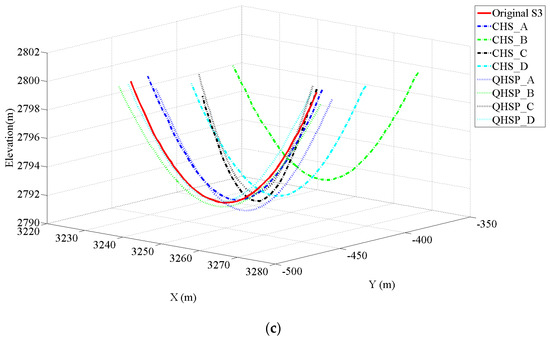
Figure 9.
Constructed cross section (a) S1, (b) S2, and (c) S3 for the river with the amplitude of 600 m.
3.2.3. Error Assessment for the Interpolating Method
To quantitatively show the performance of the QHSP method, the Mean Error (ME in Equation (9)) and Root Mean Square Error (RMSE in Equation (10)) of the constructed river terrain are employed as
To facilitate the comparison, the realistic and constructed river channels are converted into 2 m × 2 m raster data and the elevation values are compared at each cell. In Equations (9) and (10), N is the number of the raster cells, and are the constructed and exact or measured elevation data at the ith cell, respectively. The results of the ME and EMSE are listed in Table 1.
On the whole, the river channel constructed by the QHSP method is more accurate than that of the CHS method. For example, in test case B, comparing with the CHS method, the constructing ME of the QHSP method is at least 1 m lower. In test case C and D, the accuracy of the QHSP method can be improved by at least 15%, indicating the QHSP method has better performance than the CHS method when interpolating river channels.
A numerical hydrodynamic model with the framework of a finite-volume Godunov-type scheme [6] is used to simulate a flood process on the constructed river bed, in order to further investigate the performance of the QHSP method constructing river channels. Under the same inflow condition on the left hand boundary (Figure 10), the simulated hydrograph at different cross sections in the four test cases mentioned above on the constructed and the original river beds are compared in Figure 11, Figure 12 and Figure 13. Take the computed results on the original river bed as a reference, the accuracy of the computed hydrograph on the constructed river beds is shown in Table 2 in the form of ME and RMSE.
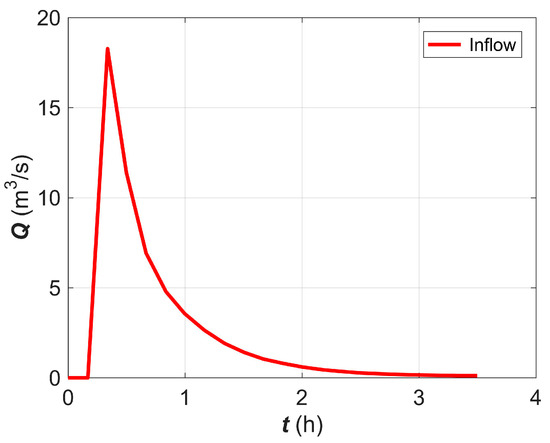
Figure 10.
Inflow hydrograph.
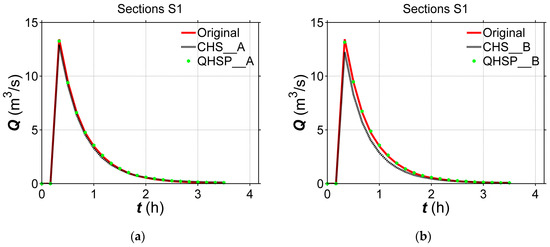
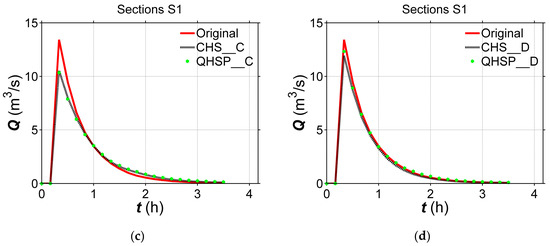
Figure 11.
Computed hydrograph for test case (a) A, (b) B, (c) C, and (d) D at Section S1 in the constructed river with the amplitude of 600 m.
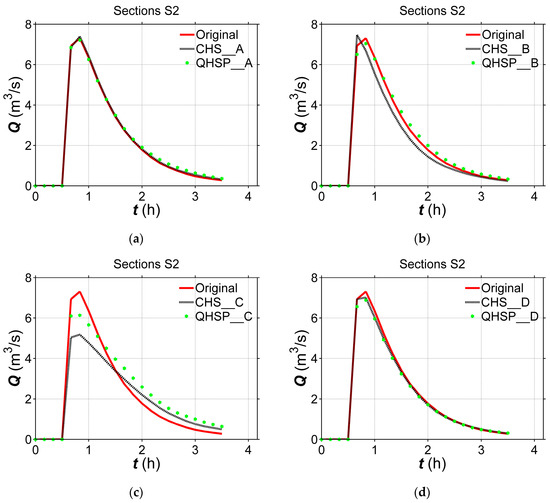
Figure 12.
Computed hydrograph for test case (a) A, (b) B, (c) C, and (d) D at Section S2 in the constructed river with the amplitude of 600 m.
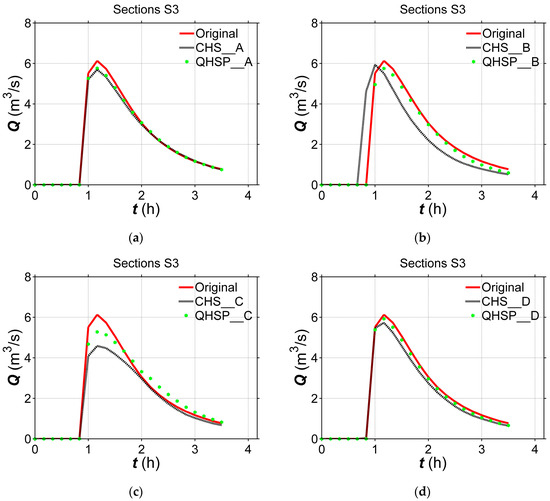
Figure 13.
Computed hydrograph for test case and (d) D at Section S3 in the constructed river with the amplitude of 600 m. (a) case A; (b) B, (c) C.

Table 2.
Mean Error (ME) and Root Mean Square Error (RMSE) of the computed hydrograph on the constructed river bed by CHS and QHSP method.
From Figure 11, Figure 12 and Figure 13 and Table 2, the computed hydrographs on the constructed river bed using the QHSP method display an overall higher accuracy, comparing to that using the CHS method. It is indicated again the CHS method is less applicable than the QHSP method, the latter could generate more reliable river channel terrain, through introducing a parameter μ to modify the river channel closer to the realistic one when having the same available river-section data.
4. Channel Construction for a Realistic River
4.1. River Channel Construction
In order to test the performance of the proposed QHSP method constructing river channel for a realistic river, a surveyed river channel in Wangmaogou catchment is employed. For this test case, a Digital Elevation Model (DEM) with 2 m resolution and 51 cross sections highlighted in green lines are available through survey (Figure 14).
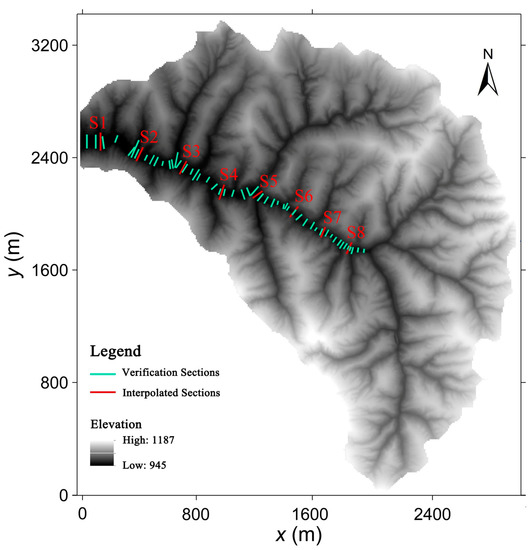
Figure 14.
DEM (Digital Elevation Model) and available cross sections for Wangmaogou catchment. Unit: m.
The available cross sections are utilized to construct the river bed terrain by using the CHS and the QHSP methods, the accuracy is compared in terms of ME and RMSE in Table 3. The result illustrates the QHSP method could increase the reliability by 15% to 16%, comparing to the CHS method.

Table 3.
Errors of constructed river channel at Wangmaogou catchment by using CHS and QHSP methods.
4.2. Flood Process Simulation on the Constructed River Bed
To further validate the higher accuracy of the proposed QHSP method used for river channel terrain construction, a flood process in the river channel caused by a storm in Wangmaogou catchment is simulated on the constructed river terrain. Since the terrain for the whole catchment is required, the constructed river channel is embedded into the available DEM of the catchment by using the ArcGIS tools provided by ESRI (Environmental Systems Research Institute, Inc, Redlands, CA, USA) (Figure 15).
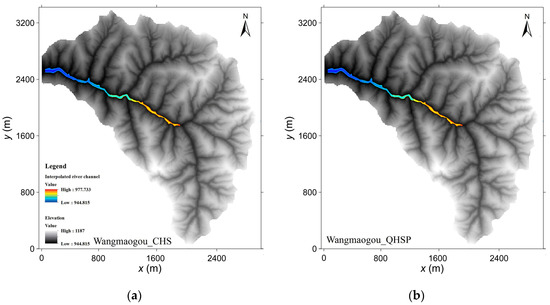
Figure 15.
Constructed river channel at Wangmaogou catchment by using (a) CHS and (b) QHSP methods. Unit: m.
The net rainfall process evaluated by considering the hydrological factors such as the hyetograph representing a heavy storm with the return period of about 300 years and the infiltration processes is used as shown in Table 4. The flood event is modeled and the propagation process at t = 2 h in the constructed river channel are plotted in Figure 16. To quantitatively reflect the net improvement of the QHSP method, the computed hydrographs at 8 cross sections (Figure 14) on the original and constructed river channel using QHSP and CHS methods are compared in Figure 17 and the simulating errors are listed in Table 5.

Table 4.
The net rainfall process.
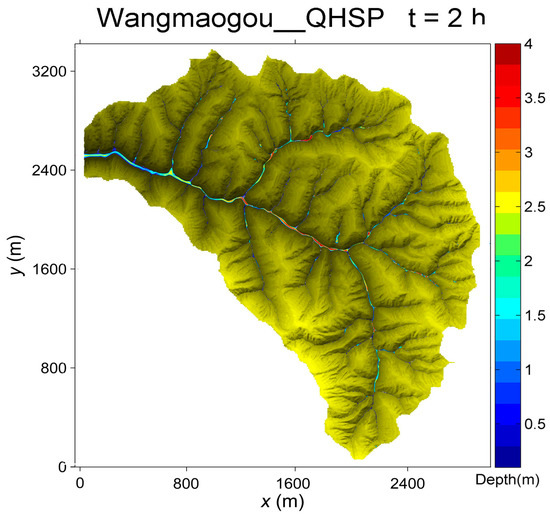
Figure 16.
Flood simulation on the DEM constructed by using QHSP method at t = 2.
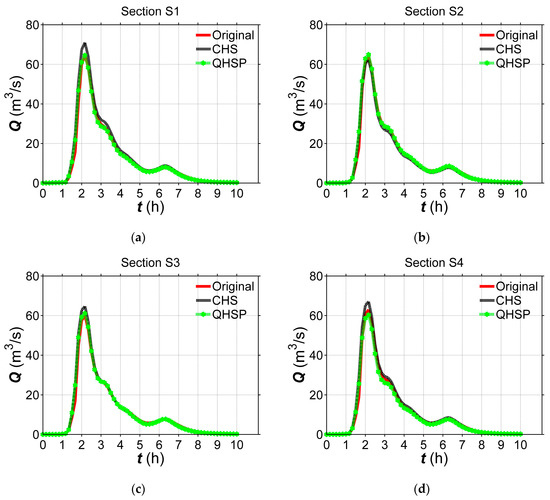
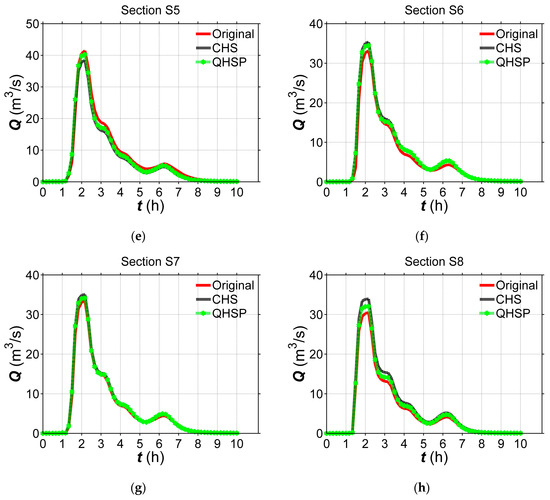
Figure 17.
Comparison between the computed hydrographs at considered cross sections in Wangmaogou catchment. (a) Section S1; (b) Section S2; (c) Section S3; (d) Section S4; (e) Section S5; (f) Section S6; (g) Section S7; (h) Section S8.

Table 5.
Simulating errors of hydrographs at considered cross sections on the DEM constructed by using CHS and QHSP methods.
Figure 17 plots that the simulated flood peak of the QHSP method is closer to that on the surveyed 3D bed than the CHS method. Besides, the computed hydrographs of the QHSP method are always in better agreement with those on the surveyed 3D bed. The phenomenon is also expressed in Table 5, demonstrating the computed errors by using the QHSP method are much lower than the CHS method at the considering sections. The accuracy of the QHSP method in terms of ME is increased by 18.5% and higher than 30% than the CHS method at Section S6 and other sections, respectively. The similar result can also be indicated by the RMSE factor. The proposed QHSP method is therefore more suitable than the CHS method for the river bed construction.
5. Conclusions
This work proposed a new approach termed as QHSP method to construct river channel terrain based on the limited available cross-section data. The QHSP method is able to not only improve the reliability of the constructed river terrain, but also avoid the numerical failures in terms of unrealistic oscillations caused by the existing constructing approach, e.g., CHS method. After validated against two benchmark tests including a synthetic sinusoidal river and a realistic river channel, it is concluded that
- The QHSP method can effectively resolve the unrealistic oscillations in the plane interpolation process by modifying the reversing tendency of x and y coordinates.
- Comparing to the CHS method, the proposed QHSP method can produce a more accurate river channel by using the same amount of the cross sections. The accuracy of the constructed river bed terrain can be improved by higher than 15% in terms of ME for the two test cases.
- On the constructed river channel by using the QHSP method, the computed hydrograph of flood process is more reliable than that employing the CHS methods, e.g., the former can improve the simulating accuracy by at least 18.5% in all cross sections in the Wangmaogou catchment.
The QHSP method is therefore an ideal approach for reliable river channel construction from limited available cross-section data. It is also more applicable to generate terrain date for hydrodynamic modeling, providing a more proper tool to investigate hydrologic and hydrodynamic process in the regions without sufficient topography data.
Author Contributions
P.H. and J.H. proposed the novel method and prepared the manuscript. Z.Z. run the numerical model. B.L. and K.G. prepared figures and tables. P.H. and J.H. contributed equally.
Funding
This research was funded by the National Key Research and Development Program of China (Grant No. 2016YFC0402704), National Natural Science Foundation of China (Grant No. 19672016), State Key Program of National Natural Science Foundation of China (Grant No. 41330858), International cooperation and exchange program for science and technology (Grant No. 2017KW-014) and the Water Conservancy Science and Technology Project of Shanxi Province (Grant No. 2017slkj-14).
Conflicts of Interest
The authors declare no conflict of interest.
References
- BurguetePilar, J.; Garcia-Navarro, P. Efficient construction of high-resolution TVD conservative schemes for equations with source terms: Application to shallow water flows. Int. J. Numer. Methods Fluids 2001, 37, 209–248. [Google Scholar] [CrossRef]
- Bernetti, R.; Titarev, V.A.; Toro, E.F. Exact solution of the Riemann problem for the shallow water equations with discontinuous bottom geometry. J. Comput. Phys. 2008, 227, 3212–3243. [Google Scholar] [CrossRef]
- Liang, Q.; Marche, F. Numerical resolution of well-balanced shallow water equations with complex source terms. Adv. Water Resour. 2009, 32, 873–884. [Google Scholar] [CrossRef]
- Schippa, L.; Pavan, S. Bed evolution numerical model for rapidly varying flow in natural streams. Comput. Geosci. 2009, 35, 390–402. [Google Scholar] [CrossRef]
- Hou, J.; Liang, Q.; Simons, F.; Hinkelmann, R. A 2D well-balanced shallow flow model for unstructured grids with novel slope source term treatment. Adv. Water Resour. 2013, 52, 107–131. [Google Scholar] [CrossRef]
- Bourdin, D.R.; Fleming, S.W.; Stull, R.B. Stream flow modelling: A primer on applications, approaches and challenges. Atmos.-Ocean 2012, 50, 507–536. [Google Scholar] [CrossRef]
- Negishi, J.N.; Sagawa, S.; Sanada, S.; Kume, M.; Ohmori, T.; Miyashita, T.; Kayaba, Y. Using airborne scanning laser altimetry (LiDAR) to estimate surface connectivity of floodplain water bodies. River Res. Appl. 2012, 28, 258–267. [Google Scholar] [CrossRef]
- Straatsma, M.W.; Middelkoop, H. Airborne laser scanning as a tool for lowland floodplain vegetation monitoring. Hydrobiologia 2006, 565, 87–103. [Google Scholar] [CrossRef]
- Casas, A.; Benito, G.; Thorndycraft, V.R.; Rico, M. The topographic data source of digital terrain models as a key element in the accuracy of hydraulic flood modelling. Earth Surf. Process. Landf. 2010, 31, 444–456. [Google Scholar] [CrossRef]
- Wang, C.; Philpot, W.D. Using airborne bathymetric lidar to detect bottom type variation in shallow waters. Remote Sens. Environ. 2007, 106, 123–135. [Google Scholar] [CrossRef]
- Hilldale, R.C.; Raff, D. Assessing the ability of airborne LiDAR to map river bathymetry. Earth Surf. Process. Landf. 2010, 33, 773–783. [Google Scholar] [CrossRef]
- Liu, X. Airborne LiDAR for DEM generation: some critical issues. Prog. Phys. Geogr. 2008, 32, 31–49. [Google Scholar] [CrossRef]
- Cin, C.D.; Moens, L.; Dierickx, P.; Bastin, G.; Zech, Y. An integrated approach for realtime floodmap forecasting on the Belgian Meuse River. Nat. Hazards 2005, 36, 237–256. [Google Scholar] [CrossRef]
- Eilertsen, R.S.; Hansen, L. Morphology of river bed scours on a delta plain revealed by interferometric sonar. Geomorphology 2008, 94, 58–68. [Google Scholar] [CrossRef]
- Merwade, V.M.; Maidment, D.R.; Goff, J.A. Anisotropic considerations while interpolating river channel bathymetry. J. Hydrol. 2006, 331, 731–741. [Google Scholar] [CrossRef]
- Lazaro, M.J.; Sanchez Navarro, J.A.; Garcia Gil, A.; Edo Romero, V. Developing and programming a watershed traversal algorithm (WTA) in GRID-DEM and adapting it to hydrological processes. Comput. Geosci. 2013, 51, 418–429. [Google Scholar] [CrossRef]
- Schauble, H.; Marinoni, O.; Hinderer, M. A GIS-based method to calculate flow accumulation by considering dams and their specific operation time. Comput. Geosci. 2008, 34, 635–646. [Google Scholar] [CrossRef]
- Flanagin, M.; Ratcliff, J.; Shaw, K.B.; Sample, J.; Abdelguerfi, M. Hydraulic splines: A hybrid approach to modeling river channel geometries. Comput. Sci. Eng. 2007, 9, 4–15. [Google Scholar] [CrossRef]
- Schappi, B.; Perona, P.; Schneider, P.; Burlando, P. Integrating river cross section measurements with digital terrain models for improved flow modelling applications. Comput. Geosci. 2010, 36, 707–716. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; Morales-Hernández, M.; López-Marijuan, I.; García-Navarro, P. Reconstruction of 2D river beds by appropriate interpolation of 1D cross-sectional information for flood simulation. Environ. Model. Softw. 2014, 61, 206–228. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.; Yang, L. Quartic Hermite interpolating splines with parameters. J. Comput. Appl. 2012, 32, 1868–1870. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Murillo, J.; García-Navarro, P. The formulation of internal boundary conditions in unsteady 2-D shallow water flows: Application to flood regulation. Water Resour. Res. 2013, 49, 471–487. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).