Dominant Influencing Factors of Groundwater Recharge Spatial Patterns in Ergene River Catchment, Turkey
Abstract
1. Introduction
2. Materials and Methods
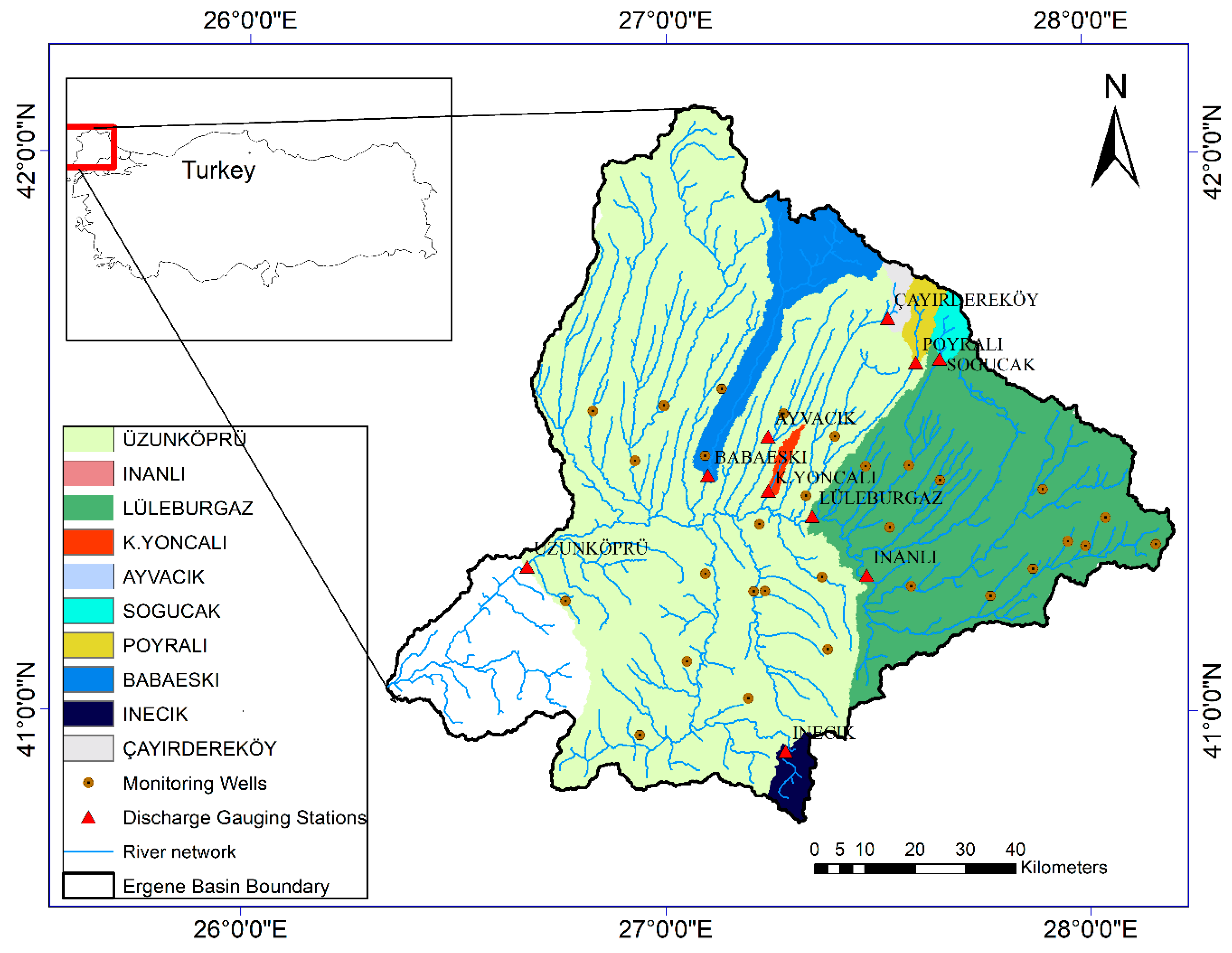
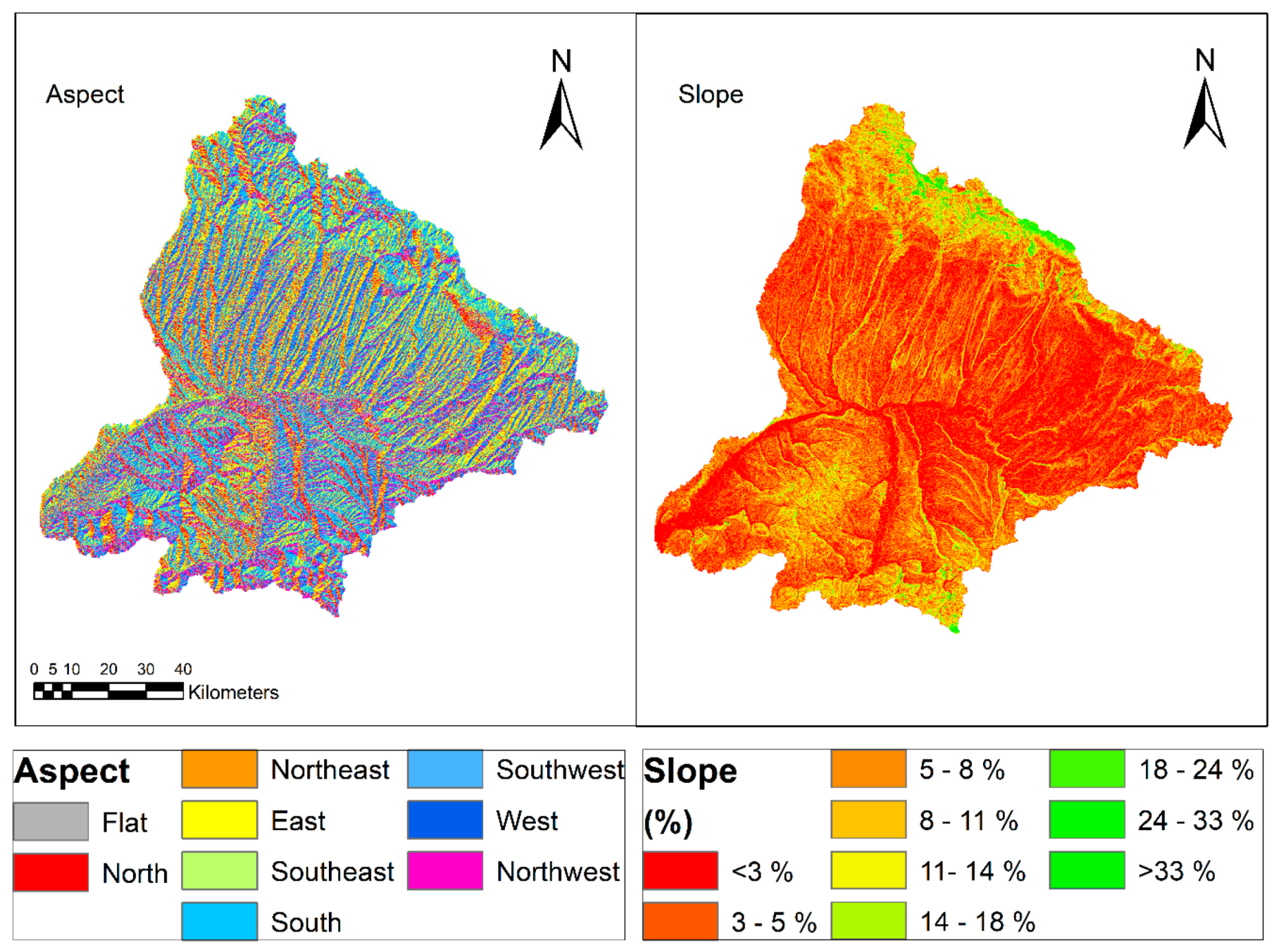
2.1. Study Area
2.2. Water Balance Modelling Based on the mGROWA Model
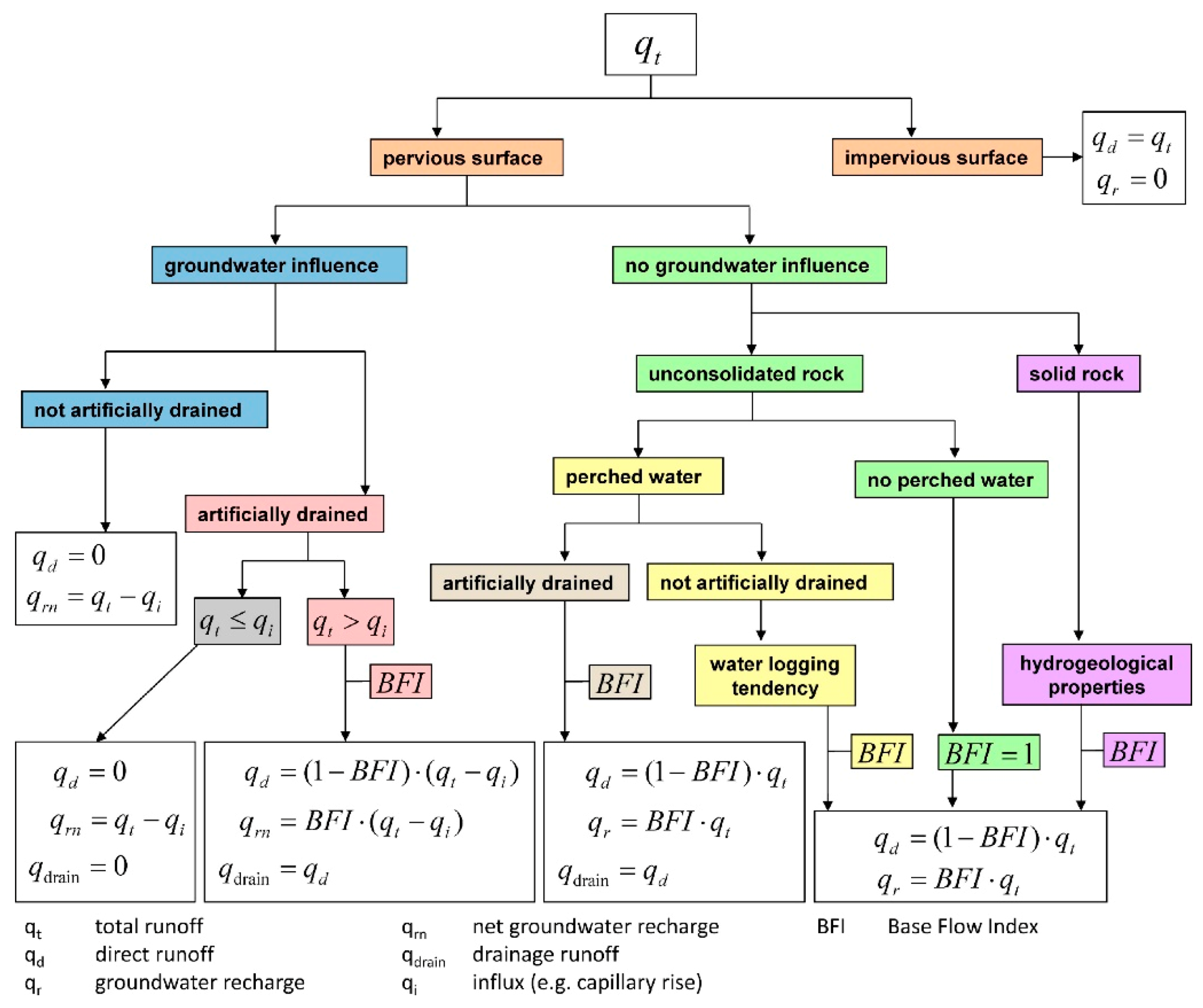
2.3. Baseflow Determination
2.4. Statistical Analysis
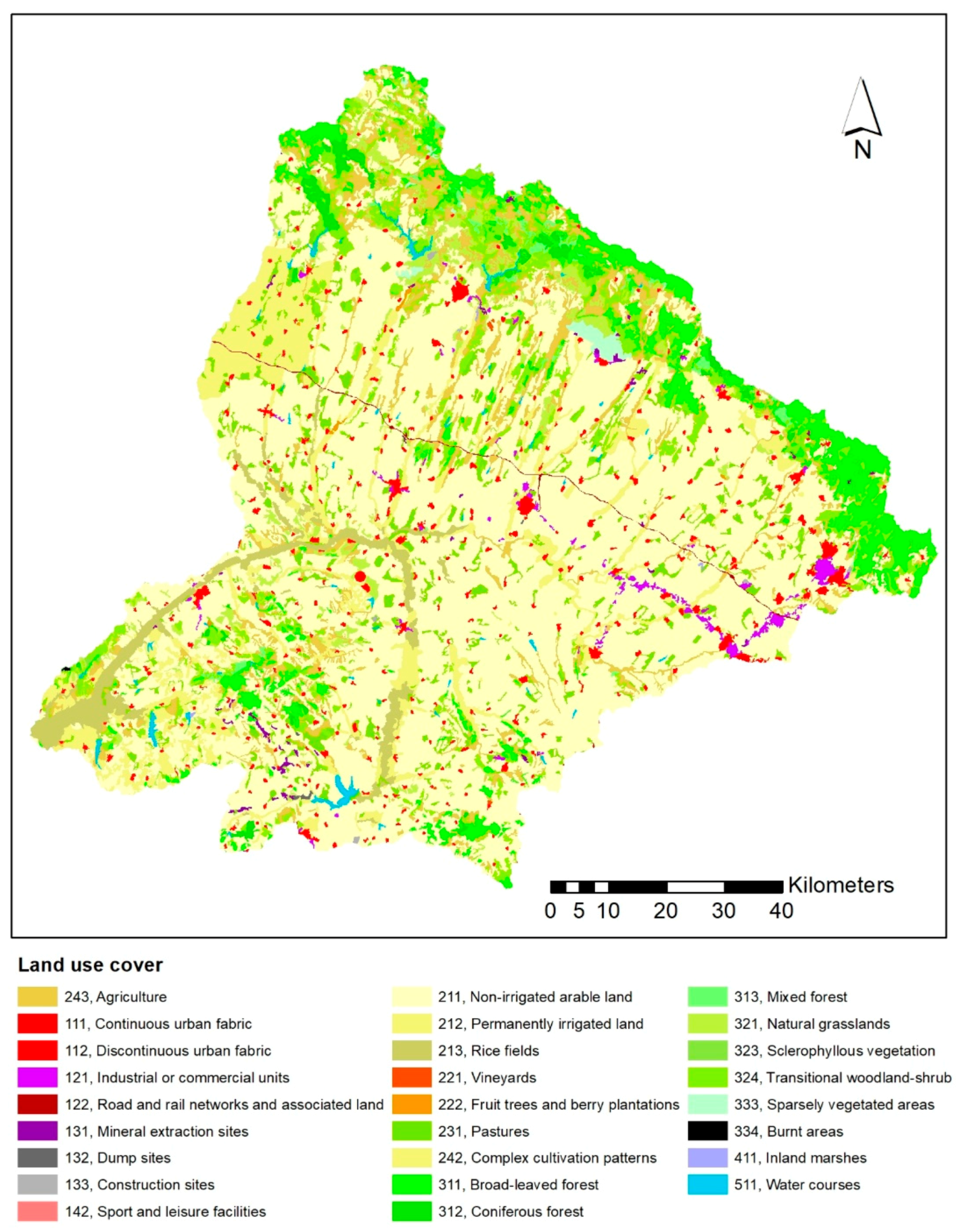
2.5. Input Data
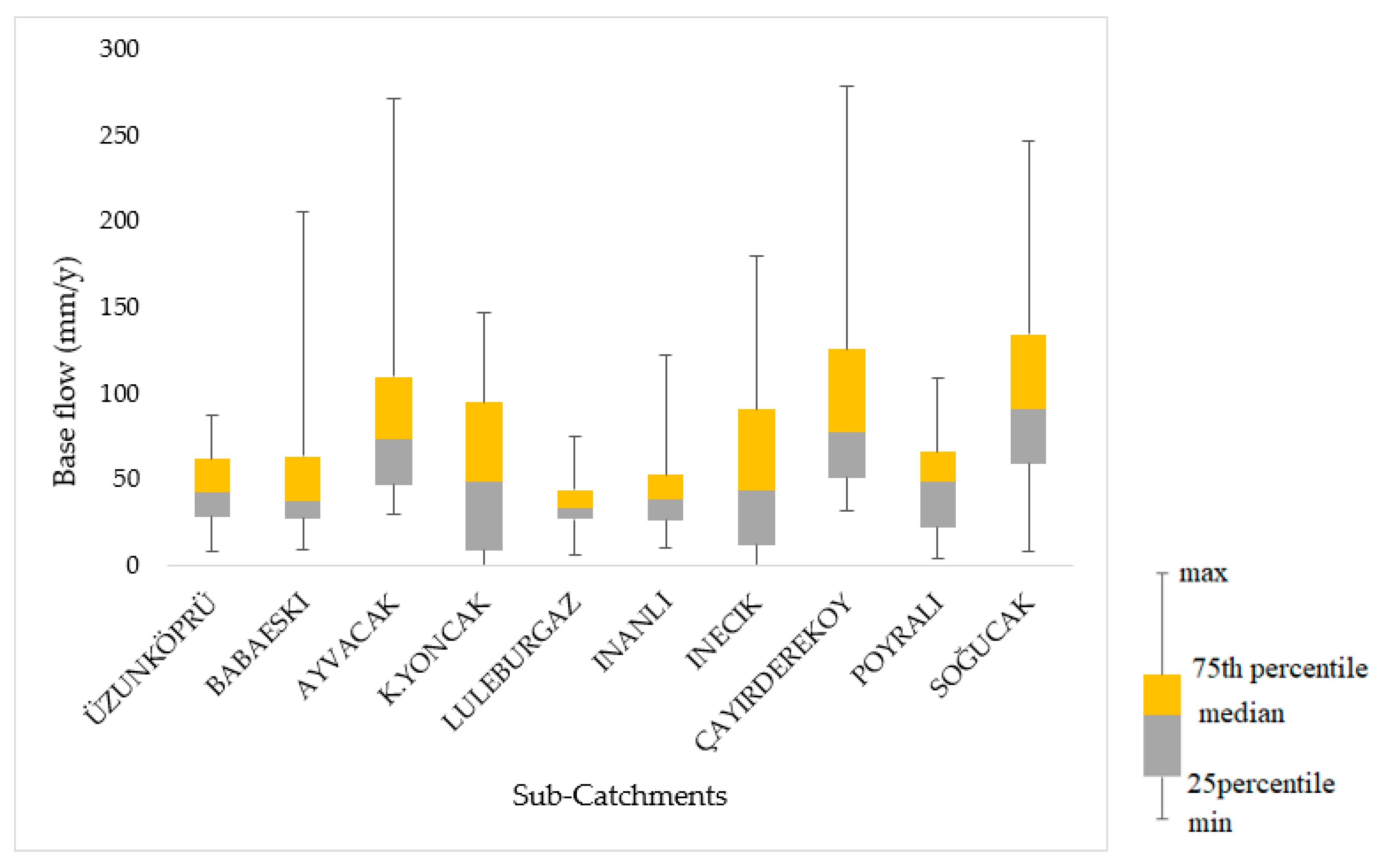
3. Results
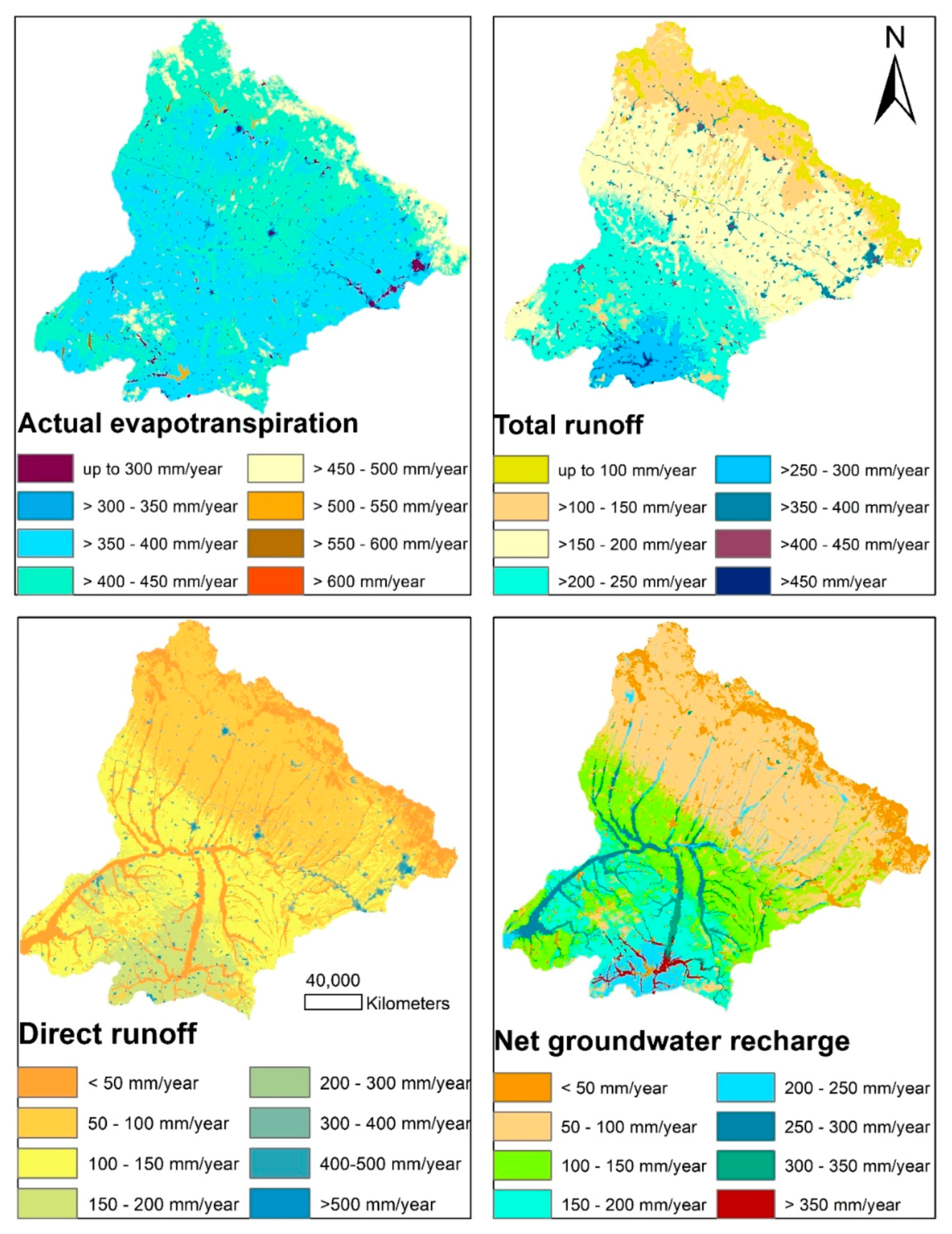
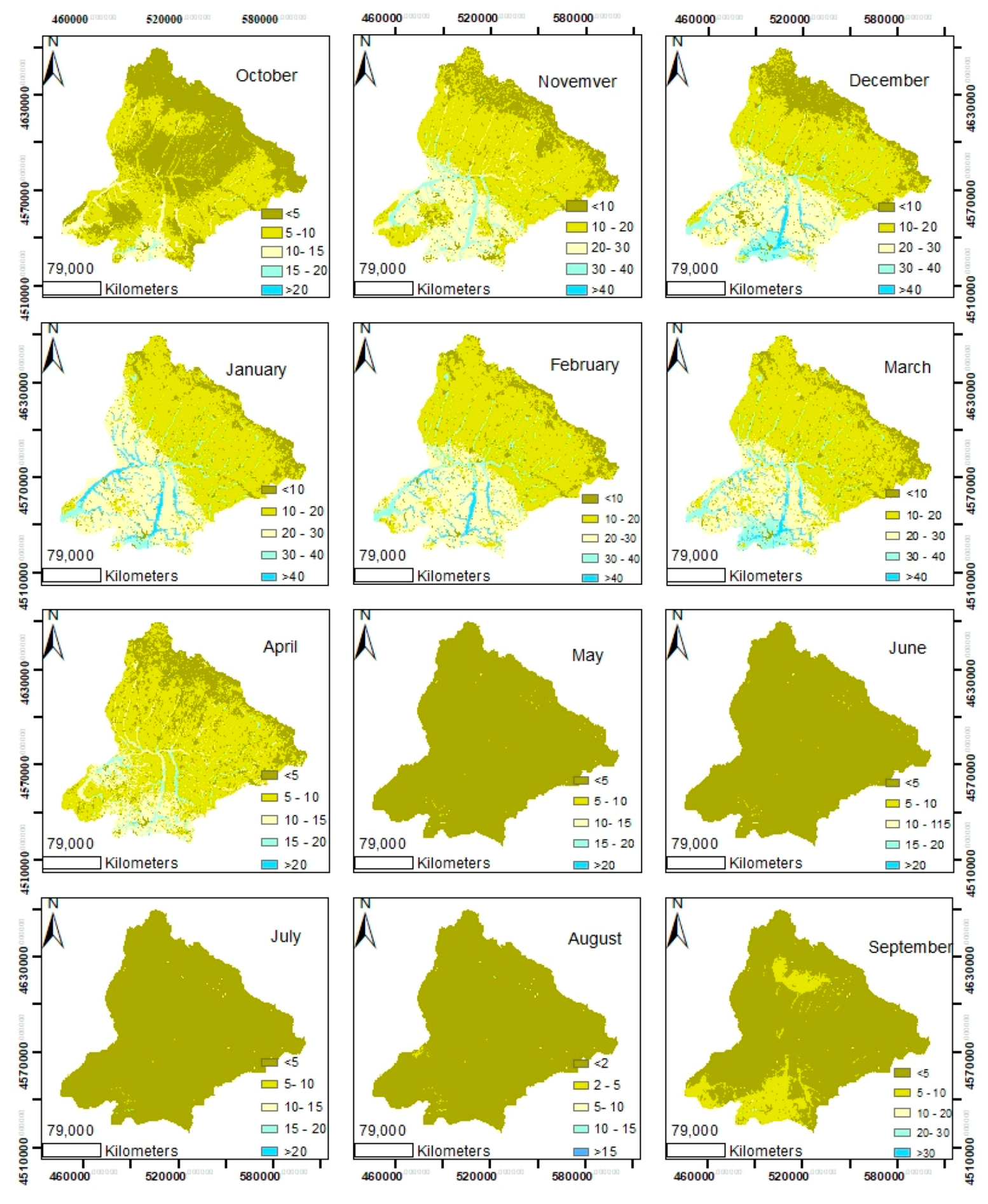
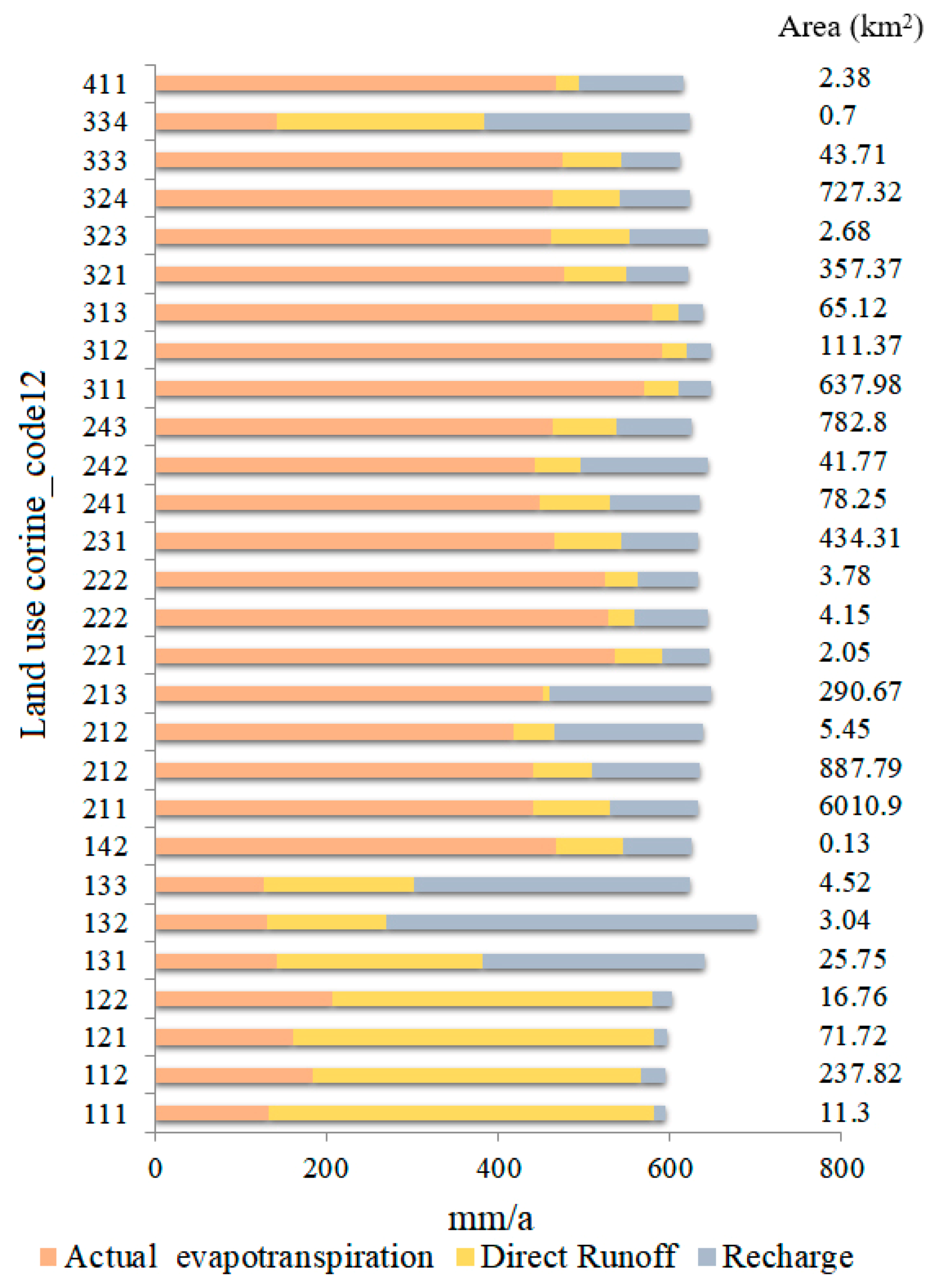
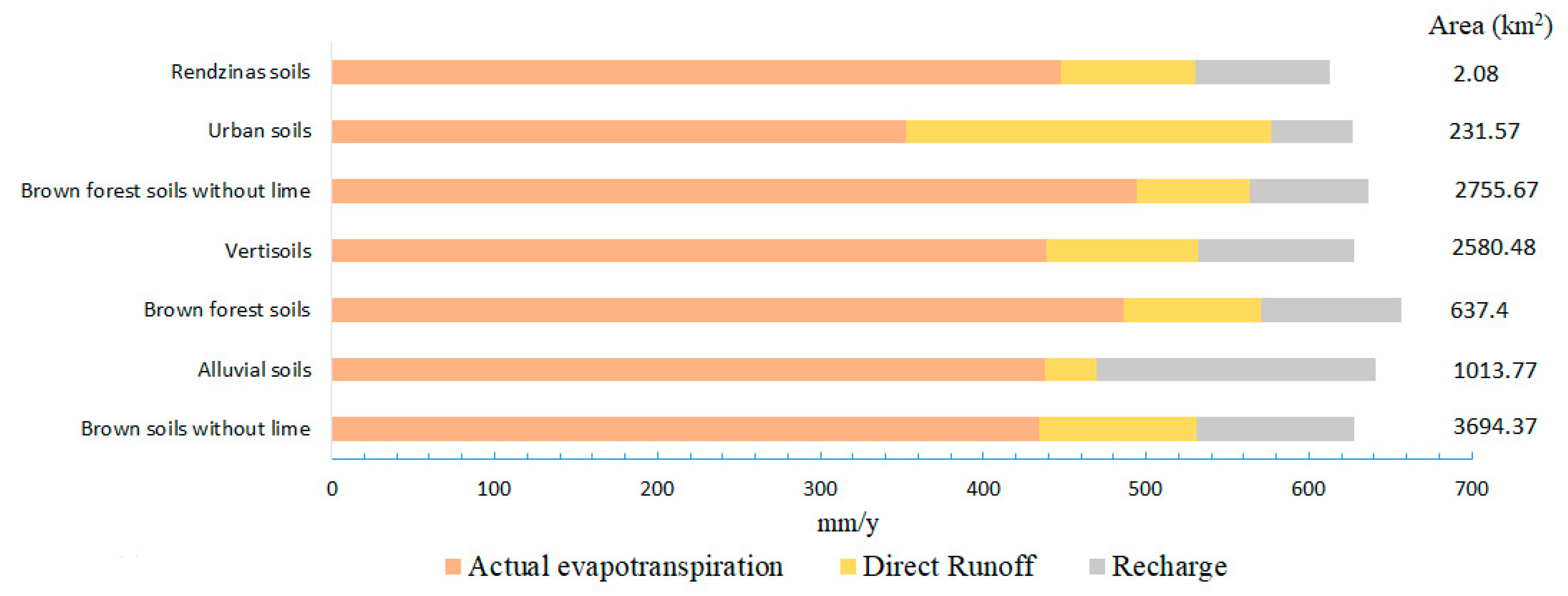
3.1. Simulation of Water Balance Quantities
3.2. Model Evaluation
3.3. Determination of Dominant Factors
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shah, T.; Burke, J.; Villholth, K.G.; Angelica, M.; Custodio, E.; Daibes, F.; Hoogesteger, J.; Giordano, M.; Girman, J.; Van Der Gun, J.; et al. Groundwater: A Global Assessment of Scale and Significance; International Water Management Institute (IWMI): Supriyo Das, India, 2007. [Google Scholar]
- Yenehun, A.; Walraevens, K.; Batelaan, O. Spatial and temporal variability of groundwater recharge in Geba bain. Northern Ethiopia. J. Afr. Earth Sci. 2017, 134, 198–212. [Google Scholar] [CrossRef]
- Seiler, K.P.; Gat, J.R. Groundwater Recharge from Run-Off, Infiltration and Percolation; Water Science and Technology Library: New York, NY, USA, 2007; Volume 55. [Google Scholar]
- Simmers, I. Estimation of Natural Groundwater Recharge; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1988; Volume 70, p. 510. [Google Scholar]
- Arkoc, O. Heavy metal concentrations of groundwater in the east of Ergene Basin, Turkey. Bull. Environ. Contam. Toxicol. 2014, 93, 429–433. [Google Scholar] [CrossRef]
- Füsun, E.; Zehra, B. Linear Alkylbenzene Sulfonates in the Groundwater and Surface Waters: Ergene Basin Case Study. J. Agric. Sci. Technol. A 2017, 7, 369–376. [Google Scholar] [CrossRef]
- Arkoç, O. Assessment of scaling properties of groundwater with elevated sulfate concentration: A case study from Ergene Basin, Turkey. Arab. J. Geosci. 2012, 6, 4377–4385. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Healy, R.W.; Cook, P.G. Choosing appropriate techniques for quantifying groundwater recharge. Hydrogeol. J. 2002, 10, 18–39. [Google Scholar] [CrossRef]
- Sharma, M.L. Measurement and prediction of natural groundwater recharge—An overview. J. Hydrol. 1989, 25, 49–56. [Google Scholar]
- Assefa, K.A.; Woodbury, A.D. Transient, spatially varied groundwater recharge modeling. Water Resour. Res. 2013, 49, 4593–4606. [Google Scholar] [CrossRef]
- Herrmann, F.; Keller, L.; Kunkel, R.; Vereecken, H.; Wendland, F. Determination of spatially differentiated water balance components including groundwater recharge on the Federal State level—A case study using the mGROWA model in North Rhine-Westphalia (Germany). J. Hydrol. Reg. Stud. 2015, 4, 294–312. [Google Scholar] [CrossRef]
- Zomlot, Z.; Verbeiren, B.; Huysmans, M.; Batelaan, O. Spatial distribution of groundwater recharge and base flow: Assessment of controlling factors. J. Hydrol. Reg. Stud. 2015, 4, 349–368. [Google Scholar] [CrossRef]
- Risser, D.W.; Gburek, W.J.; Folmar, G.J. Comparison of recharge estimates at a small watershed in east-central Pennsylvania, USA. Hydrogeol. J. 2008, 17, 287–298. [Google Scholar] [CrossRef]
- Meyer, S.C. Analysis of base flow trends in urban streams, northeastern illinois, USA. Hydrogeol. J. 2004, 13, 871–885. [Google Scholar] [CrossRef]
- Delin, G.N.; Healy, R.W.; Lorenz, D.L.; Nimmo, J.R. Comparison of local- to regional-scale estimates of ground-water recharge in Minnesota, USA. J. Hydrol. 2007, 334, 231–249. [Google Scholar] [CrossRef]
- Kunkel, R.; Wendland, F. The GROWA98 model for water balance analysis in large river basins-the river Elbe case study. J. Hydrol. 2002, 259, 152–162. [Google Scholar] [CrossRef]
- Rumsey, C.A.; Miller, M.P.; Susong, D.D.; Tillman, F.D.; Anning, D.W. Regional scale estimates of baseflow and factors influencing baseflow in the Upper Colorado River Basin. J. Hydrol. Reg. Stud. 2015, 4, 91–107. [Google Scholar] [CrossRef]
- Grinevskii, S.O.; Pozdnyakov, S.P. Principles of regional estimation of infiltration groundwater recharge based on geohydrological models. Water Resour. 2010, 37, 638–652. [Google Scholar] [CrossRef]
- Healy, R.W.; Cook, P.G. Using groundwater levels to estimate recharge. Hydrogeol. J. 2002, 10, 91–109. [Google Scholar] [CrossRef]
- Bogena, H.; Kunkel, R.; Schöbel, T.; Schrey, H.P.; Wendland, F. Distributed modeling of groundwater recharge at the macroscale. Ecol. Model. 2005, 187, 15–26. [Google Scholar] [CrossRef]
- Cooper, D.J.; Wolf, E.C.; Ronayne, M.J.; Roche, J.W. Effects of groundwater pumping on the sustainability of a mountain wetland complex, Yosemite National Park, California. J. Hydrol. Reg. Stud. 2015, 3, 87–105. [Google Scholar] [CrossRef]
- Rukundo, E.; Dogan, A. Assessment of Climate and Land Use Change Projections and their Impacts on Flooding. Pol. J. Environ. Stud. 2016, 25, 2541–2551. [Google Scholar] [CrossRef]
- Ehlers, L.; Herrmann, F.; Blaschek, M.; Duttmann, R.; Wendland, F. Sensitivity of mGROWA-simulated groundwater recharge to changes in soil and land use parameters in a Mediterranean environment and conclusions in view of ensemble-based climate impact simulations. Sci. Total Environ. 2016, 543, 937–951. [Google Scholar] [CrossRef]
- Bücker, A.; Crespo, P.; Frede, H.-G.; Vaché, K.; Cisneros, F.; Breuer, L. Identifying Controls on Water Chemistry of Tropical Cloud Forest Catchments: Combining Descriptive Approaches and Multivariate Analysis. Aquat. Geochem. 2009, 16, 127–149. [Google Scholar] [CrossRef]
- Karataş, A. Identifying Surface Runoff Distribution and Amount in Stream Basins: Ergene River Basin. Turk. J. Water Sci. Manag. 2018, 2, 40–81. [Google Scholar] [CrossRef]
- Bostan, P.A. Analysis and Modeling of Spatially and Temporally Varying Meteorological Parameter: Precipitation Over Turkey. Ph.D. Thesis, Middle East Technical University, Ankara, Turkey, 2013. [Google Scholar]
- Bostan, P.A.; Heuvelink, G.B.M.; Akyurek, S.Z. Comparison of regression and kriging techniques for mapping the average annual precipitation of Turkey. Int. J. Appl. Earth Obs. Geoinf. 2012, 19, 115–126. [Google Scholar] [CrossRef]
- Cobaner, M.; Citakoğlu, H.; Haktanir, T.; Kisi, O. Modifying Hargreaves–Samani equation with meteorological variables for estimation of reference evapotranspiration in Turkey. Hydrol. Res. 2017, 48, 480–497. [Google Scholar] [CrossRef]
- Golf, W. Ermittlung der Wasserressourcen im Mittelgebirge. Wasserwirtsch. Wassertech. 1981, 30, 90–95. [Google Scholar]
- Kunkel, R.; Wendland, F. Der Landschaftswasserhaushalt im Flubeinzugsgebiet der Elbe—Verfahren. Datengrundlagen und Bilanzgröben; Schriften des Forschungszentrum Jülich. Reine Umwelt.: Jülich, Germany, 1998; Volume 12. [Google Scholar]
- Dörhöfer, G.; Josopait, V. Eine Methode zur flächendifferenzierten Ermittlung der Grundwasserneubildungsrate. Geol. Clays 1980, 27, 45–65. [Google Scholar] [CrossRef]
- Hennings, V. Methodendokumentation Bodenkunde—Auswertemethoden zur Beurteilung der Empfindlichkeit und Belastbarkeit von Böden; Geologisches Jahrbuch, Reihe F: Hannover, Germany, 2000. [Google Scholar]
- Wessolek, G.; Facklam, M. Standorteigenschaften und Wasserhaushalt von versiegelten Flächen. Pflanzenernähr. Bodenk. 1997, 160, 41–46. [Google Scholar] [CrossRef]
- Bogena, H.; Kunkel, R.; Schöbel, T.; Schrey, H.P.; Wendland, F. Die Grundwasserneubildung in Nordrhein-Westfalen; FZ Jülich GmbH: Jülich, Germany, 2003; Volume 37, p. 148. [Google Scholar]
- Wendland, F.; Blum, A.; Coetsiers, M.; Gorova, R.; Griffioen, J.; Grima, J.; Hinsby, K.; Kunkel, R.; Marandi, A.; Melo, T.; et al. European aquifer typology: A practical framework for an overview of major groundwater composition at European scale. Environ. Geol. 2007, 55, 77–85. [Google Scholar] [CrossRef]
- Karpuzcu, M.A.; Alpaslan, N.; Engin, G.; Görmann, H.; Gunduz, M.; Kocal, M.; Oncel, S.; Pekdeger, A.; Voigt, H.; Kuhr, P.; et al. Integrated Modelling of Nutrients in Selected Rşver Basins of Turkey; Forschungszentrum Jülich GmbH: Jülich, Germany, 2008; Volume 17. [Google Scholar]
- Tetzlaff, B.; Andjelov, M.; Kuhr, P.; Uhan, J.; Wendland, F. Model-based assessment of groundwater recharge in Slovenia. Environ. Earth Sci. 2015, 74, 6177–6192. [Google Scholar] [CrossRef]
- Panagopoulos, A.; Arampatzis, G.; Kuhr, P.; Kunkel, R.; Tziritis, E.; Wendland, F. Area-differentiated modeling of water balance in Pinios river basin, central Greece. Glob. Nest 2015, 17, 221–235. [Google Scholar]
- Cheo, A.E.; Voigt, H.J.; Wendland, F. Modeling groundwater recharge through rainfall in the Far-North region of Cameroon. Groundw. Sustain. Dev. 2017, 5, 118–130. [Google Scholar] [CrossRef]
- Wundt, W. Die Kleinstwasserf¨ uhrung der Fl¨ usse als Maß f¨ ur die verf¨ ugbaren Grundwassermengen; Forsch Deutsch Landeskunde: Jülich, Germany, 1958; Volume 104. [Google Scholar]
- Kille, K. Das Verfahren MoMNQ, ein Beitrag zur Berechnung der mittleren langjährigen Grundwasserneubildung mit Hilfe der monatlichen Niedrigwasserabflüsse. Zeitschrift der Deutschen Geologischen Gesellschaft 1970, 122, 89–95. [Google Scholar]
- Demuth, S. Untersuchung zum Niedrigwasser in West-Europa. Freiburger Schriften xur Hydrologie; Universitat Freiburg: Freiburg, Germany, 1993. [Google Scholar]
- Andjelov, M.; Mikulic, Z.; Tetzlaff, B.; Uhan, J.; Wendland, F. Groundwater recharge in Slovenia: Results of a Bilateral German-Slovenia Research Project; Forschungszentrums Jülich GmbH: Jülich, Germany, 2016; Volume 339. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptiual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- McCuen, R.H.; Knight, Z.; Cutter, A.G. Evaluation of the Nash–Sutcliffe Efficiency Index. J. Hydrol. Eng. 2006, 11, 597–602. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Knudson, E.J.; Duewer, D.L.; Christian, G.D.; Larson, T.V. Application of Factor Analysis to the Study of Rain Chemistry in the Puget Sound Region; ACS Symposium Series; Amercan Chemestry Society: Washington, DC, USA, 1977; pp. 80–116. [Google Scholar]
- Wang, Y.; Shao, M.A.; Liu, Z.; Horton, R. Regional-scale variation and distribution patterns of soil saturated hydraulic conductivities in surface and subsurface layers in the loessial soils of China. J. Hydrol. 2013, 487, 13–23. [Google Scholar] [CrossRef]
- Abou Zakhem, B.; Al-Charideh, A.; Kattaa, B. Using principal component analysis in the investigation of groundwater hydrochemistry of Upper Jezireh Basin, Syria. Hydrol. Sci. J. 2017, 62, 2266–2279. [Google Scholar] [CrossRef]
- George, H.H.; Zohrab, A.S. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agric. Water Manag. 2014, 140, 20–25. [Google Scholar] [CrossRef]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Dudgeon, C.R. Effects of non-Darcy flow and partial penetration on water levels near open-pit excavations. In Proceedings of the 18th Congress of the International Association of Hydrogeologists, Cambridge, UK, 8–13 September 1985; pp. 122–132. [Google Scholar]
- Younger, P.L.; Banwart, S.A.; Hedin, R.S. Mine Water. Hdrology, Pollution, Remediation; Springer Science & Business Media: London, UK, 2002. [Google Scholar]
- Buttle, J.M.; Hazlett, P.W.; Murray, C.D.; Creed, I.F.; Jeffries, D.S.; Semkin, R. Prediction of groundwater characteristics in forested and harvested basins during spring snowmelt using a topographic index. Hydrol. Process. 2001, 15, 3389–3407. [Google Scholar] [CrossRef]
- Price, K. Effects of watershed topography, soils, land use, and climate on baseflow hydrology in humid regions: A review. Prog. Phys. Geogr. Earth Environ. 2011, 35, 465–492. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar]
- Richard, K. Development of Groundwater Recharge Model for the Sumanpa Catchment at Ashanti-Mampong-Ashanti Area in Ghana. Sci. Res. 2015, 3, 289. [Google Scholar] [CrossRef]
- Krishnaswamy, J.; Bonell, M.; Venkatesh, B.; Purandara, B.K.; Rakesh, K.N.; Lele, S.; Kiran, M.C.; Reddy, V.; Badiger, S. The groundwater recharge response and hydrologic services of tropical humid forest ecosystems to use and reforestation: Support for the “infiltration-evapotranspiration trade-off hypothesis”. J. Hydrol. 2013, 498, 191–209. [Google Scholar] [CrossRef]
- Wolock, D.M.; Winter, T.C.; McMahon, G. Delineation and Evaluation of Hydrologic-Landscape Regions in the United States Using Geographic Information System Tools and Multivariate Statistical Analyses. Environ. Manag. 2004, 34, S71–S88. [Google Scholar] [CrossRef]
- Kim, J.H.; Jackson, R.B. A Global Analysis of Groundwater Recharge for Vegetation, Climate, and Soils. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Jan, C.-D.; Chen, T.-H.; Lo, W.-C. Effect of rainfall intensity and distribution on groundwater level fluctuations. J. Hydrol. 2007, 332, 348–360. [Google Scholar] [CrossRef]


| Degree of Sealing | Groundwater Depth | Waterlogging Tendency | Slope | Baseflow Indices |
|---|---|---|---|---|
| <2 m | No water logging | <1% | 1 | |
| 1.3–2 m | 1 (very low) | 1–3.5% | 0.9 | |
| I (10–45%) | 0.82 | |||
| 3.5–7% | 0.67 | |||
| 7–10% | 0.59 | |||
| 0.8–1.3 m | 2 (low) | 10–13% | 0.5 | |
| 0.4–0.8 m | 3–4 (medium – high) | 13–15% | 0.44 | |
| <0.4 m | 5 (very high) | >15% | 0.4 | |
| II (45–75%) | 0.33 | |||
| III (75–90%) | 0.28 | |||
| IV (>90%) | 0.2 |
| Hydrogeological Class | Permeability | Hydraulic Conductivity | Baseflow Indices |
|---|---|---|---|
| I | Very high | >10−2 m/sec | 0.9 |
| II | High | >10−3–10−2 m/sec | 0.6 |
| III | Medium | >10−4–10−3 m/sec | 0.57 |
| IV | Moderate | >10−5–10−4 m/sec | 0.3 |
| V | Low | >10−7–10−5 m/sec | 0.29 |
| VI | Very low | >10−9–10−7 m/sec | 0.18 |
| VII | Extremely low | <10−9 m/sec | 0.12 |
| Data | Data Base | Scale/Spatial Resolutions | Data Source |
|---|---|---|---|
| Climate data | Precipitation (1991 to 2010) Temperature (1991 to 2010) | 100 × 100 m | General Directorate of State Hydraulic Works (DSI) |
| Soil data | Main soil groups | 1/25,000 | National soil database by General Directorate of State Hydraulic Works (DSI) |
| The depth of the groundwater table, Perching water influence Root depth, effective field capacity | Derived based on pedo-transfer functions | National soil database by General Directorate of State Hydraulic Works (DSI) and fields studies | |
| Capillary rise from the groundwater table | |||
| Land cover | Land use types Percentage imperviousness | 1/25,000 | National soil database by General Directorate of State Hydraulic Works (DSI) |
| Hydrogeology | Geological map | 1/500,000 | General Directorate of State Hydraulic Works (DSI) and fields studies |
| Relief | Digital elevation model SRTM Ground surface slope Ground surface exposition | 30 × 30 m | SRTM/X-SAR by National imaging and mapping agency |
| Runoff | Station data Monthly and daily resolution | General Directorate of State Hydraulic Works (DSI) and fields studies |
| Catchment Attributes | Abbreviation | Units | Correlation with the Groundwater Recharge |
|---|---|---|---|
| Soil types | |||
| Alluvial soil | AS | % | 0.671 |
| Brown forest soils | BFS | % | −0.293 |
| Brown forest soils without lime | BFSWL | % | −0.752 |
| Rendzinas | R | % | −0.277 |
| Brown soils without lime | BSWL | % | −0.020 |
| Vertisol | V | % | 0.302 |
| Urban soils | US | % | −0.062 |
| Land cover characteristics | |||
| Artificial surface Land | ASL | % | 0.130 |
| Agriculture area | AA | % | 0.676 |
| Forest | F | % | −0.659 |
| Semi natural area | ANA | % | −0.300 |
| Wetland and water bodies | WWB | % | −0.072 |
| Area and topography | |||
| Basin drainage area | BDA | Km2 | 0.541 |
| Basin slope | BS | % | −0.058 |
| Elevation | E | M | −0.469 |
| Depth to water table | DWT | M | 0.185 |
| Climate | |||
| Precipitation | P | mm/year | 0.817 |
| Actual evapotranspiration | AE | mm/year | −0.686 |
| Variables | GR | BSWL | AS | BFS | V | BFSWL | US | R | AS | AA | F | ANA | WWB | BDA | BS | P | AE | DWT | E |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GR | 1.00 | ||||||||||||||||||
| BSWL | −0.02 | 1.00 | |||||||||||||||||
| AS | 0.67 | 0.21 | 1.00 | ||||||||||||||||
| BFS | −0.29 | −0.61 | 0.11 | 1.00 | |||||||||||||||
| V | 0.30 | −0.04 | −0.16 | −0.43 | 1.00 | ||||||||||||||
| BFSWL | −0.75 | −0.23 | −0.30 | −0.12 | −0.53 | 1.00 | |||||||||||||
| US | −0.06 | 0.20 | 0.47 | −0.21 | −0.25 | 0.23 | 1.00 | ||||||||||||
| R | −0.28 | −0.30 | −0.42 | 0.41 | −0.20 | 0.07 | −0.16 | 1.00 | |||||||||||
| AS | 0.13 | 0.43 | 0.55 | −0.47 | 0.15 | −0.13 | 0.62 | −0.23 | 1.00 | ||||||||||
| AA | 0.68 | 0.41 | 0.33 | −0.34 | 0.73 | −0.85 | −0.08 | −0.46 | 0.34 | 1.00 | |||||||||
| F | −0.66 | −0.44 | −0.37 | 0.38 | −0.72 | 0.83 | 0.02 | 0.47 | −0.42 | −1.00 | 1.00 | ||||||||
| ANA | −0.30 | 0.20 | 0.18 | −0.33 | −0.16 | 0.36 | −0.03 | −0.16 | 0.18 | −0.24 | 0.20 | 1.00 | |||||||
| WWB | −0.07 | 0.29 | −0.15 | −0.57 | 0.45 | −0.08 | −0.27 | −0.32 | −0.16 | 0.30 | −0.29 | 0.57 | 1.00 | ||||||
| BDA | 0.54 | 0.24 | 0.53 | −0.28 | 0.14 | −0.15 | 0.28 | −0.15 | 0.37 | 0.34 | −0.36 | −0.03 | 0.06 | 1.00 | |||||
| BS | −0.06 | −0.39 | 0.07 | 0.49 | −0.56 | 0.43 | −0.25 | −0.17 | −0.59 | −0.54 | 0.58 | 0.35 | 0.08 | −0.24 | 1.00 | ||||
| P | 0.82 | −0.22 | 0.51 | 0.59 | −0.01 | −0.53 | −0.35 | −0.25 | −0.33 | 0.34 | −0.29 | −0.17 | −0.07 | 0.19 | 0.44 | 1.00 | |||
| AE | −0.69 | −0.42 | −0.60 | 0.25 | −0.43 | 0.69 | −0.30 | 0.30 | −0.72 | −0.80 | 0.83 | 0.25 | 0.11 | −0.57 | 0.64 | −0.19 | 1.00 | ||
| DWT | 0.19 | 0.31 | 0.12 | −0.52 | 0.70 | −0.50 | 0.06 | −0.13 | 0.68 | 0.64 | −0.69 | 0.15 | 0.28 | 0.12 | −0.69 | −0.26 | −0.68 | 1.00 | |
| E | −0.47 | −0.58 | −0.39 | 0.45 | −0.57 | 0.72 | 0.02 | 0.40 | −0.45 | −0.85 | 0.87 | −0.24 | −0.55 | −0.23 | 0.43 | −0.17 | 0.68 | −0.75 | 1.00 |
| Statistical Procedure | Indicators | PC1 | PC2 |
|---|---|---|---|
| PC Analysis | Eigenvalue | 3.946 | 1.090 |
| Variability (%) | 65.774 | 18.174 | |
| Cumulative (%) | 65.774 | 83.948 | |
| Variables | |||
| AS | 0.582 | 0.621 | |
| BFSWL | −0.894 | 0.087 | |
| AA | 0.939 | −0.277 | |
| F | −0.941 | 0.289 | |
| P | 0.516 | 0.719 | |
| AE | −0.880 | 0.139 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rukundo, E.; Doğan, A. Dominant Influencing Factors of Groundwater Recharge Spatial Patterns in Ergene River Catchment, Turkey. Water 2019, 11, 653. https://doi.org/10.3390/w11040653
Rukundo E, Doğan A. Dominant Influencing Factors of Groundwater Recharge Spatial Patterns in Ergene River Catchment, Turkey. Water. 2019; 11(4):653. https://doi.org/10.3390/w11040653
Chicago/Turabian StyleRukundo, Emmanuel, and Ahmet Doğan. 2019. "Dominant Influencing Factors of Groundwater Recharge Spatial Patterns in Ergene River Catchment, Turkey" Water 11, no. 4: 653. https://doi.org/10.3390/w11040653
APA StyleRukundo, E., & Doğan, A. (2019). Dominant Influencing Factors of Groundwater Recharge Spatial Patterns in Ergene River Catchment, Turkey. Water, 11(4), 653. https://doi.org/10.3390/w11040653




