Statistical and Numerical Assessments of Groundwater Resource Subject to Excessive Pumping: Case Study in Southwest Taiwan
Abstract
:1. Introduction
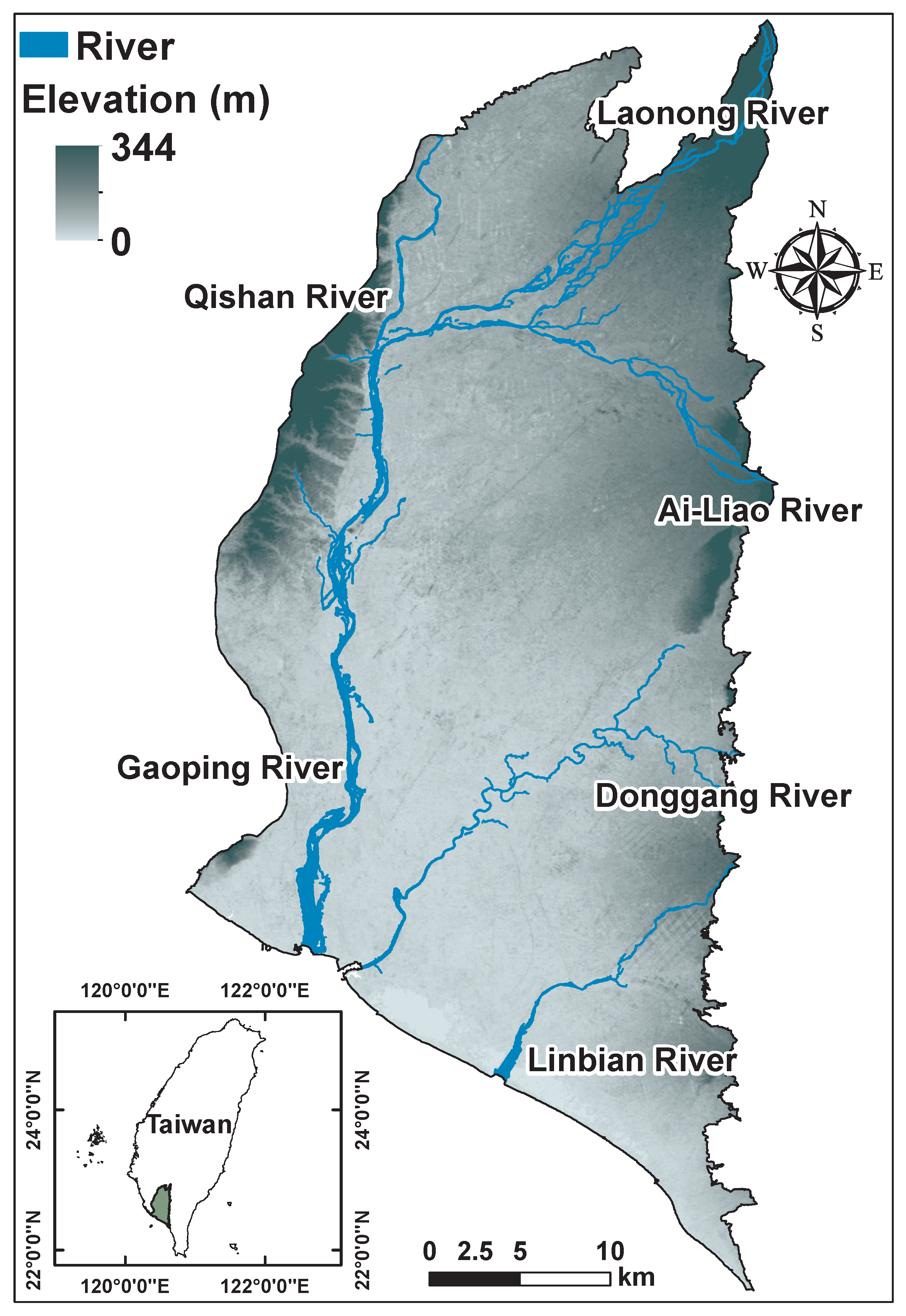
2. Study Area and Data
3. Methodology
3.1. Statistical Assessment
3.1.1. Trend Analysis
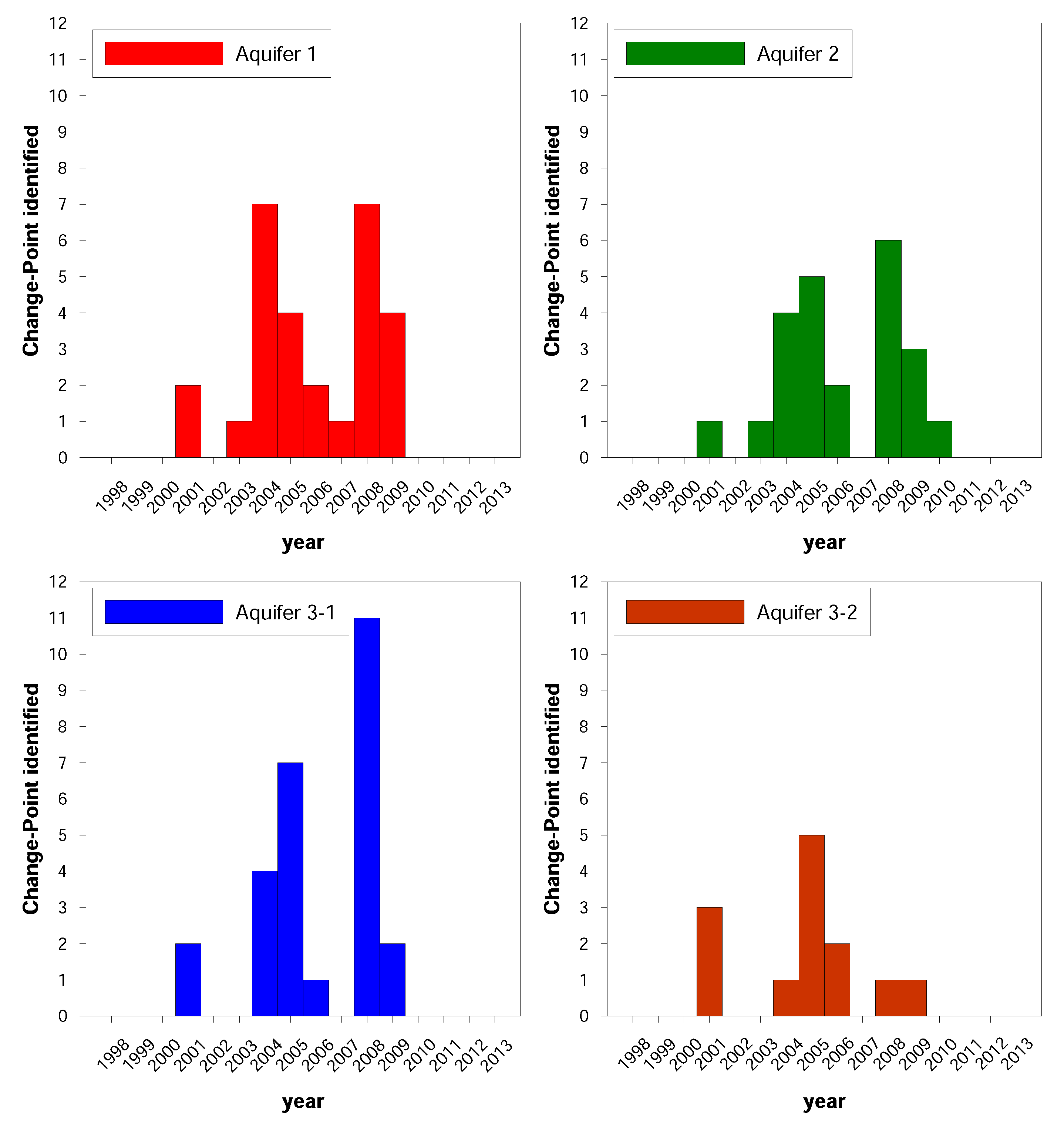
3.1.2. Change-Point Analysis
3.2. Numerical Assessment
3.2.1. Groundwater Model: WASH123D
3.2.2. Hydrogeological Analysis
3.2.3. Mesh Generation
3.2.4. Boundary Conditions
4. Results and Discussion
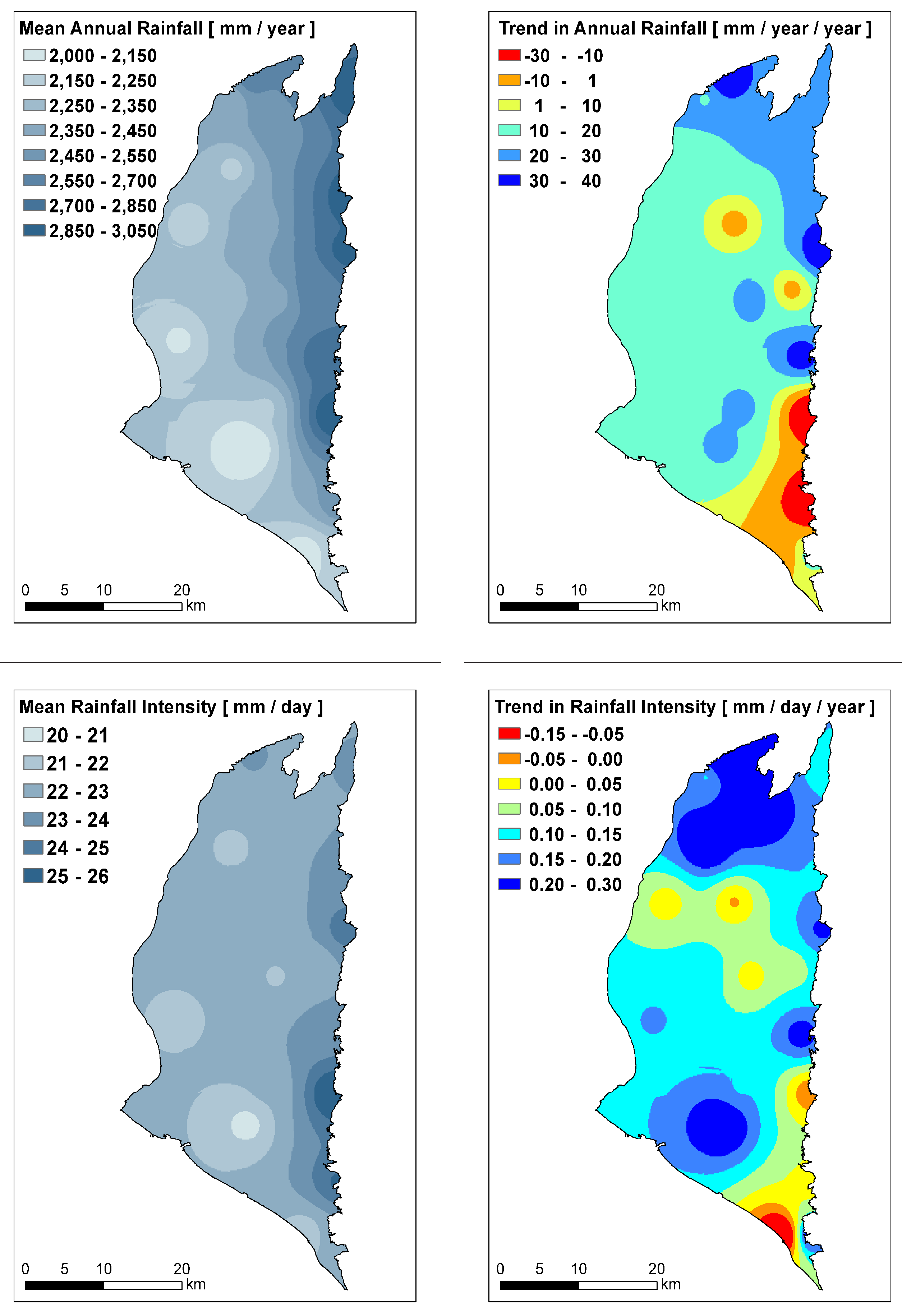
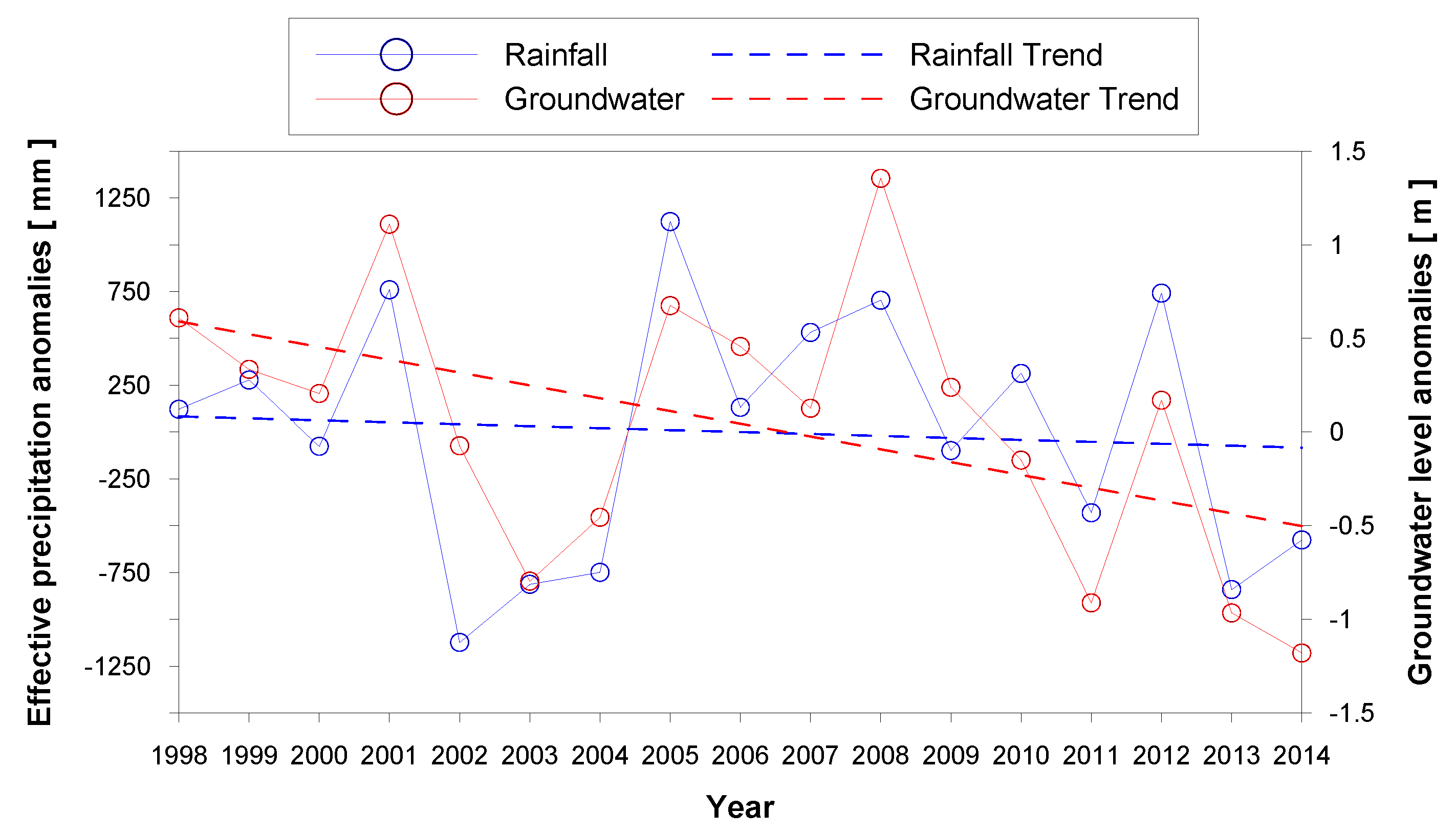
4.1. Interannual Variations in Hydro-Meteorological Conditions
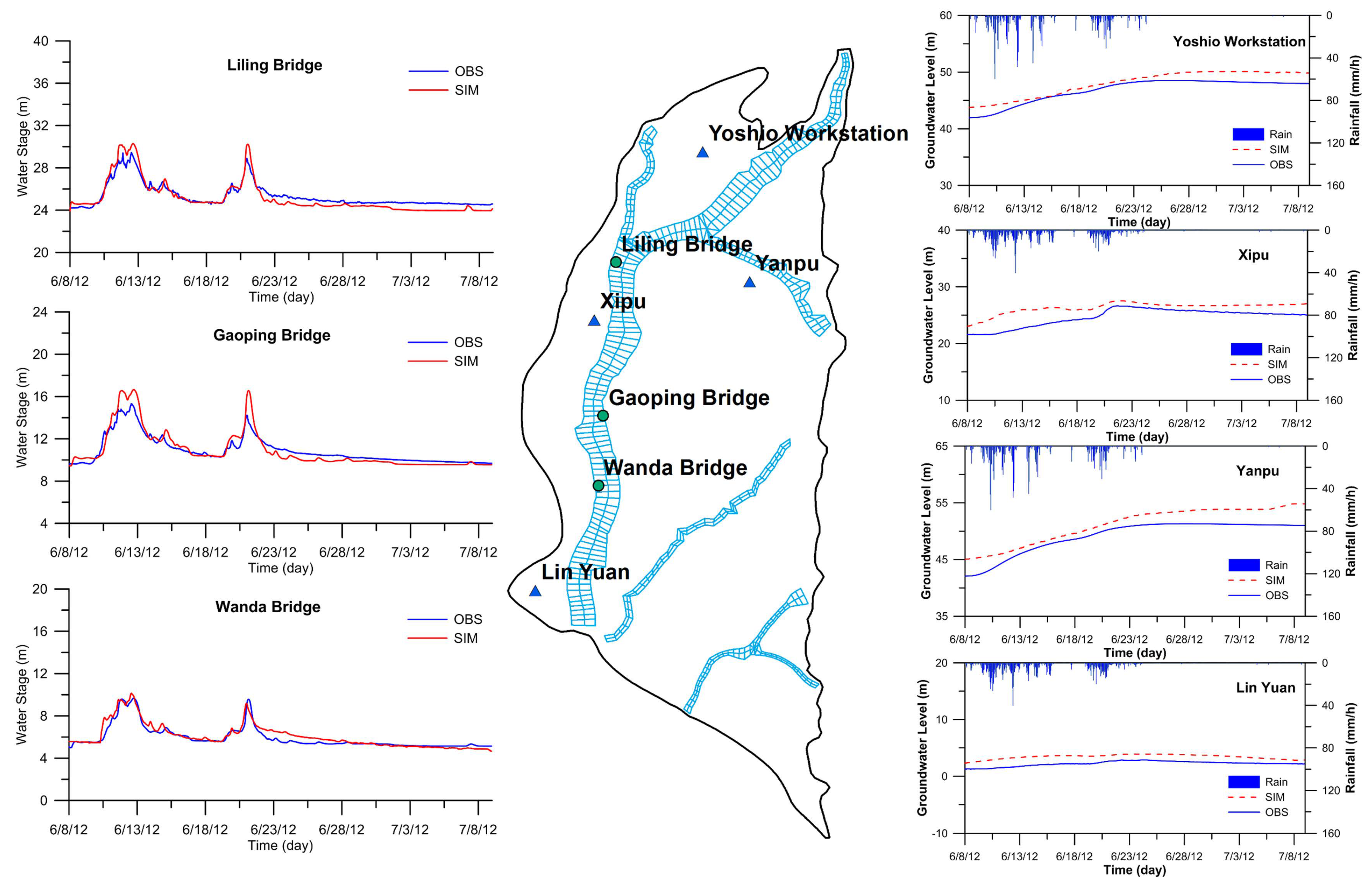
4.2. Calibration/Validation of WASH123D
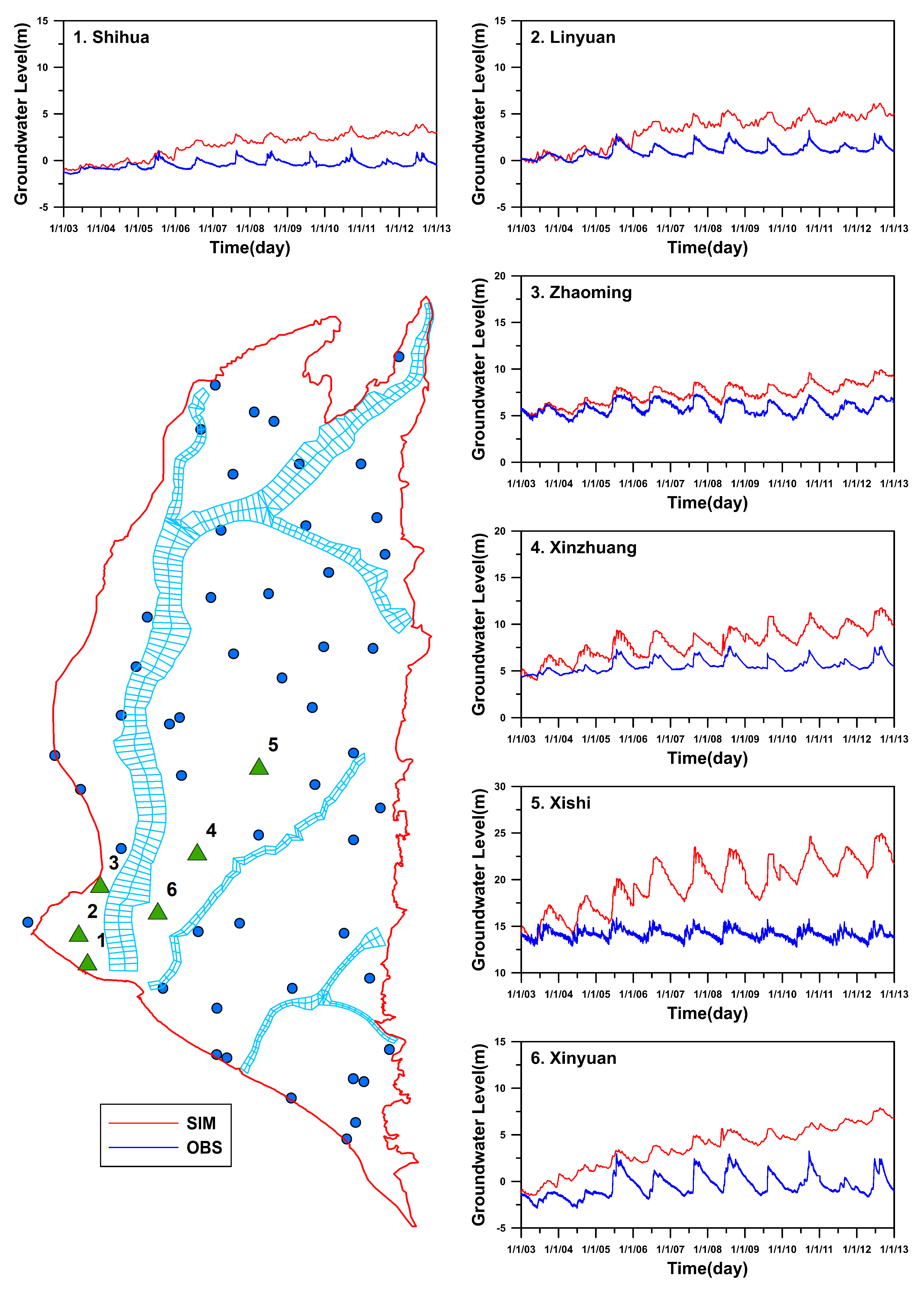
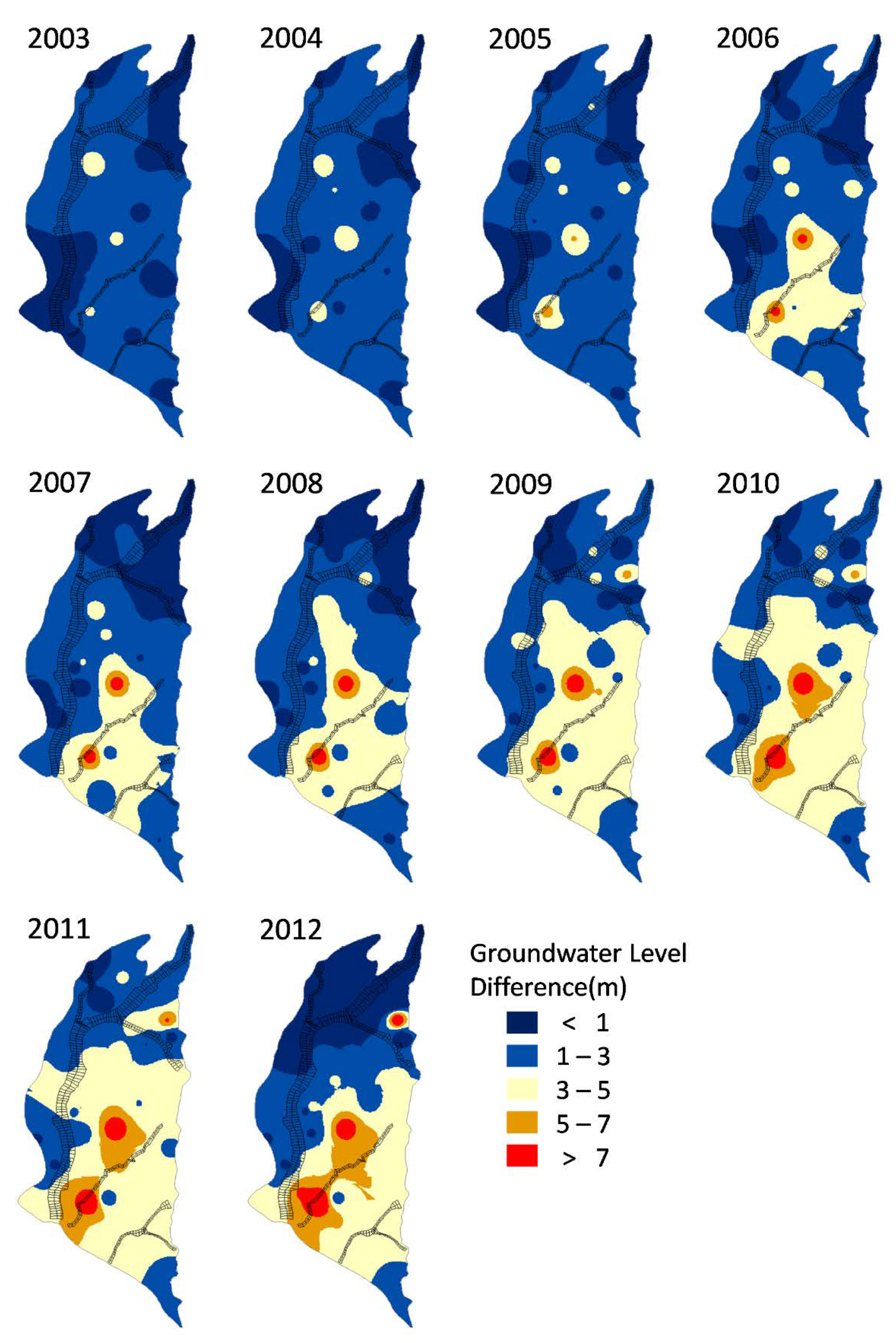
4.3. Assessment of Unregulated/Illegal Pumping Using WASH123D
5. Conclusions and Recommendations
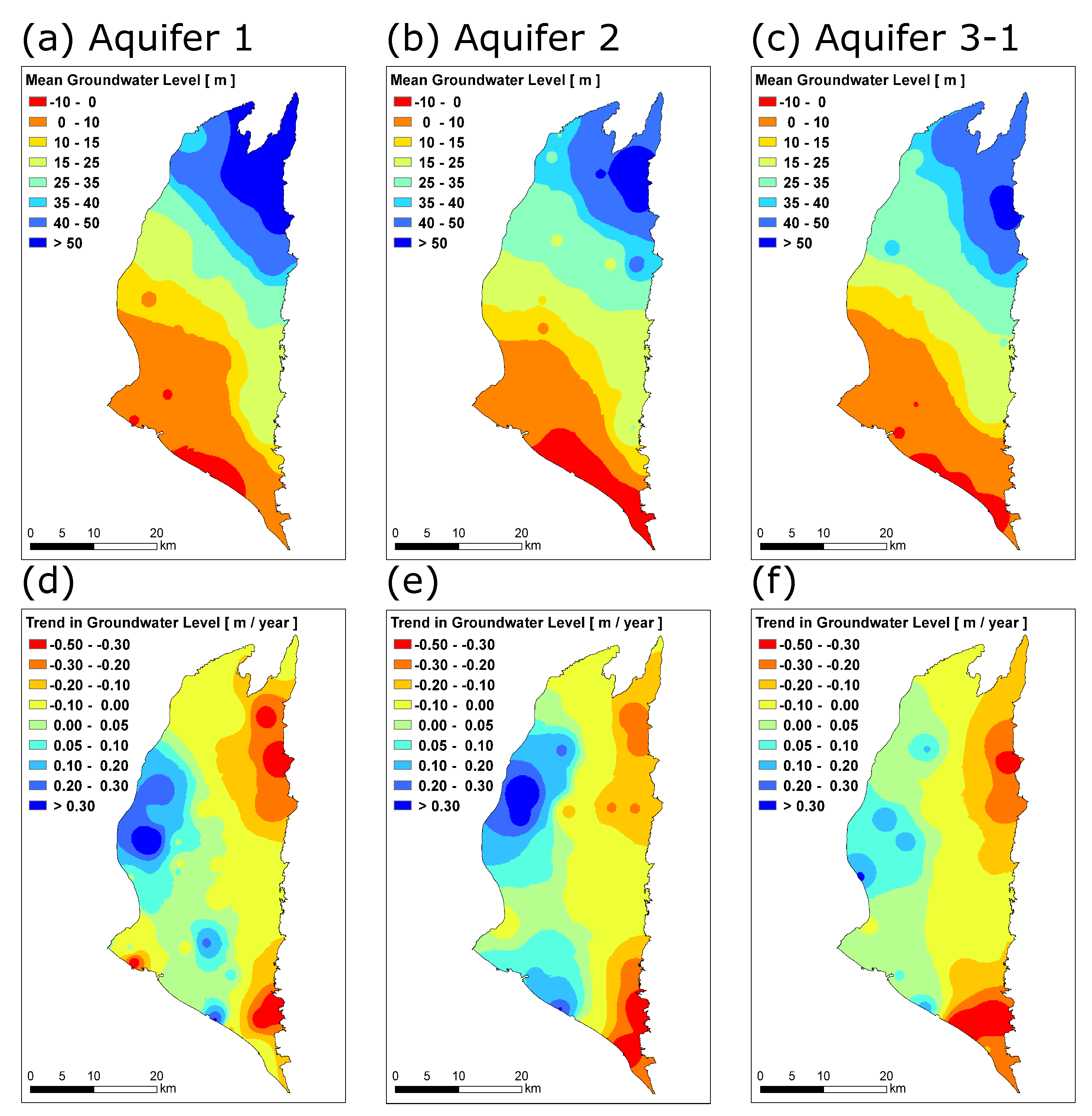
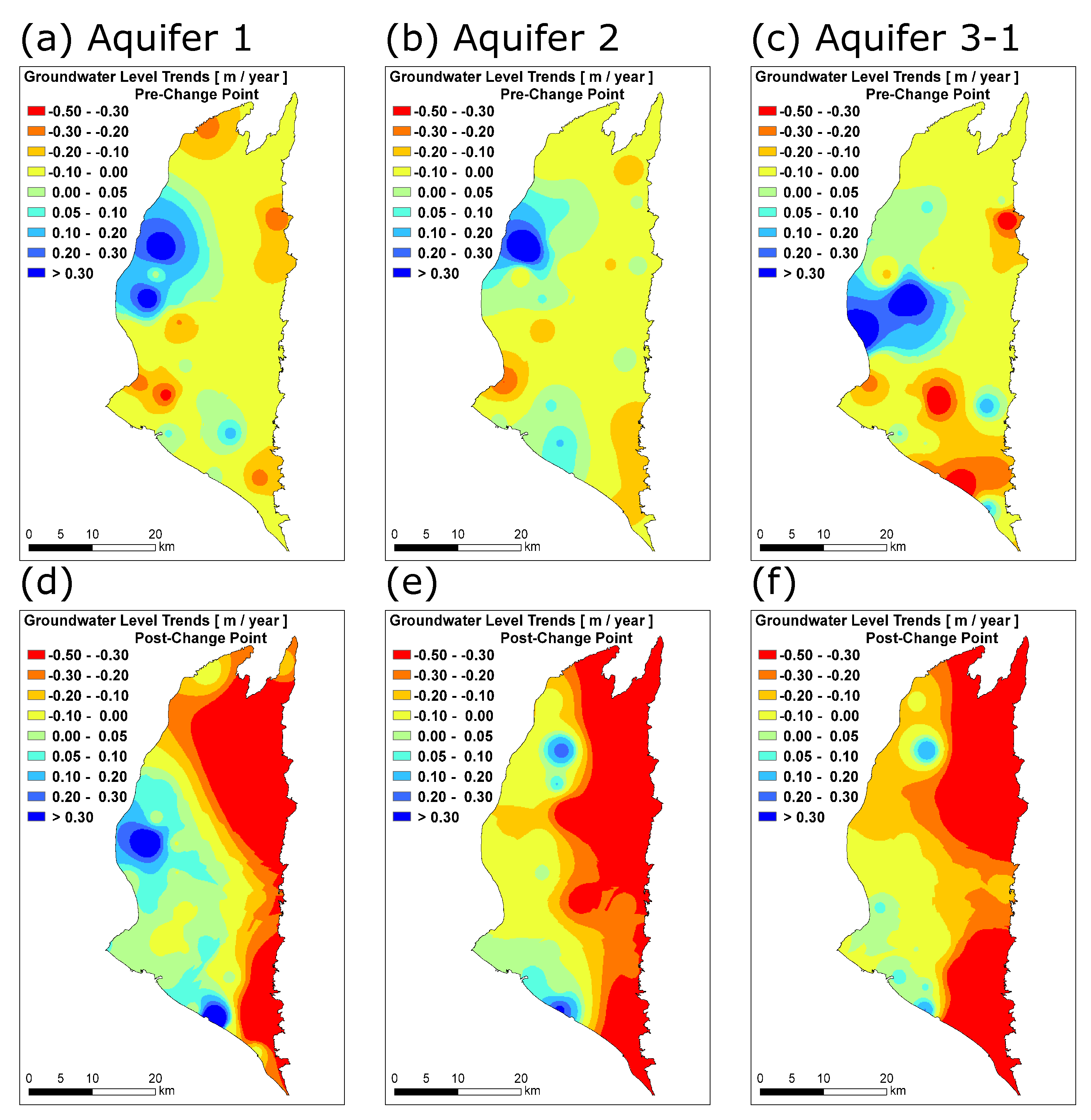
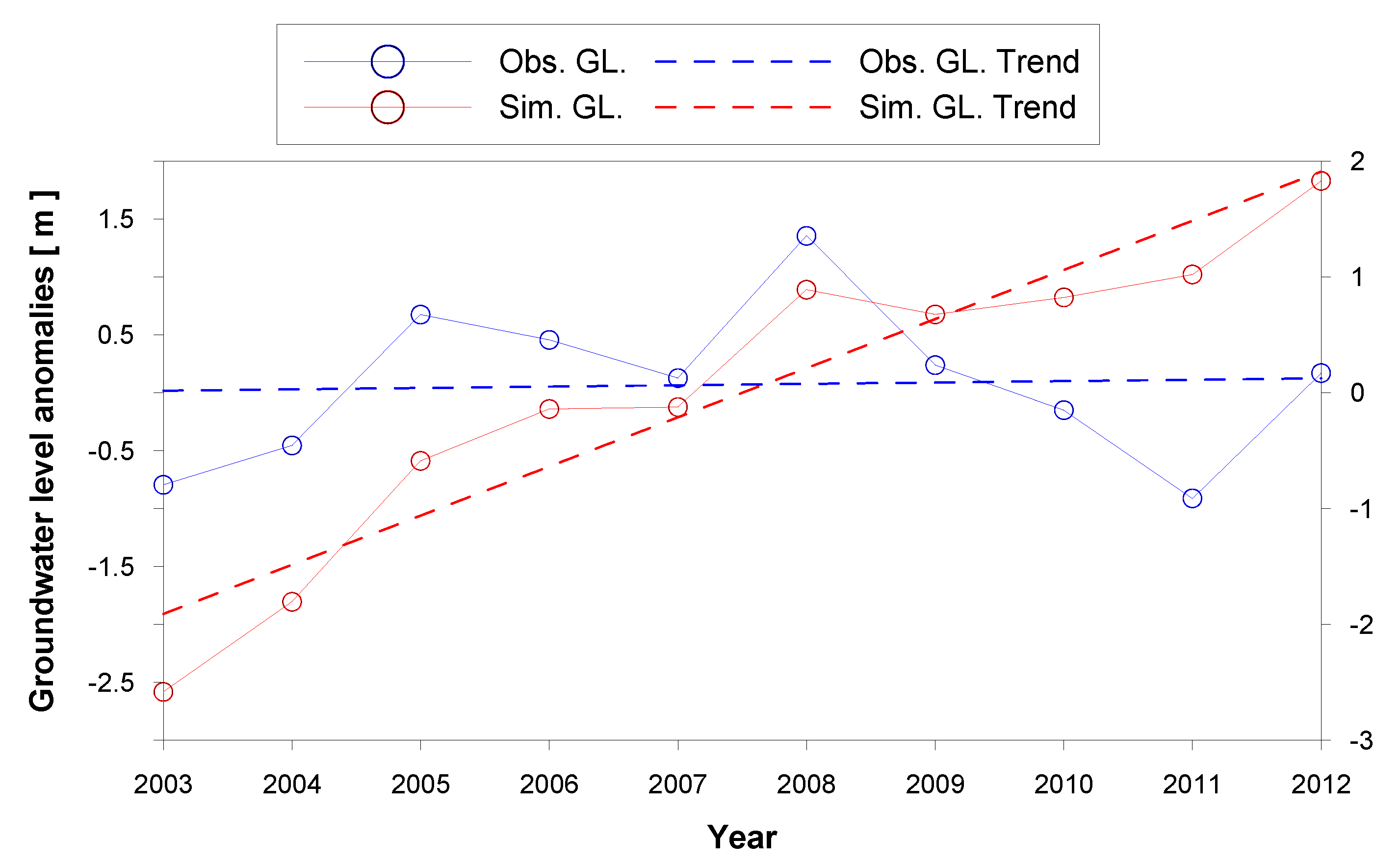
- At the annual scale, quasi-stationary rainfall is not able to provide enough recharge to the PAP aquifers with the observed decline of GLs, especially over the eastern-southeastern part. The decline, aggravated after the identified change points around 2005–2008, suggests a clear association with land subsidence.
- The pumping-free numerical experiment reveals significant discrepancies between simulated and observed GLs, and these discrepancies develop in both space and time. Our findings not only corroborate the evidence of unregulated/illegal pumping, but also propose a remote connection between pumping and land subsidence.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Castle, S.L.; Thomas, B.F.; Reager, J.T.; Rodell, M.; Swenson, S.C.; Famiglietti, J.S. Groundwater depletion during drought threatens future water security of the Colorado River Basin. Geophys. Res. Lett. 2014, 41, 5904–5911. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Calow, R.C.; Robins, N.S.; Macdonald, A.M.; Macdonald, D.M.J.; Gibbs, B.R.; Orpen, W.R.G.; Mtembezeka, P.; Andrews, A.J.; Appiah, S.O. Groundwater management in drought-prone areas of Africa. Int. J. Water Resour. Dev. 1997, 13, 241–261. [Google Scholar] [CrossRef]
- Chai, J.C.; Shen, S.L.; Zhu, H.H.; Zhang, X.L. Land subsidence due to groundwater drawdown in Shanghai. Géotechnique 2004, 54, 143–148. [Google Scholar] [CrossRef]
- Phien-wej, N.; Giao, P.H.; Nutalaya, P. Land subsidence in Bangkok, Thailand. Eng. Geol. 2006, 82, 187–201. [Google Scholar] [CrossRef]
- Nishikawa, T.; Siade, A.J.; Reichard, E.G.; Ponti, D.J.; Canales, A.G.; Johnson, T.A. Stratigraphic controls on seawater intrusion and implications for groundwater management, Dominguez Gap area of Los Angeles, California, USA. Hydrogeol. J. 2009, 17, 1699–1725. [Google Scholar] [CrossRef]
- Petrone, K.C.; Hughes, J.D.; Biel, T.G.V.; Silberstein, R.P. Streamflow decline in southwestern Australia, 1950–2008. Geophys. Res. Lett. 2010, 37, L11401. [Google Scholar] [CrossRef]
- Hughes, J.D.; Petrone, K.C.; Silberstein, R.P. Drought, groundwater storage and streamflow decline in southwestern Australia. Geophys. Res. Lett. 2012, 39, L03408. [Google Scholar] [CrossRef]
- Khan, H.F.; Yang, Y.E.; Ringler, C.; Wi, S.; Cheema, M.J.M.; Basharat, M. Guiding groundwater policy in the Indus Basin of Pakistan using a physically based groundwater model. J. Water Resour. Plan. Manag. 2017, 143, 05016014. [Google Scholar] [CrossRef]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology; Wiley: New York, NY, USA, 1998; p. 506. [Google Scholar]
- Das, B.M. Principles of Geotechnical Engineering; Thomson-Engineering: New York, NY, USA, 2001. [Google Scholar]
- Kiely, G.; Albertson, J.D.; Parlange, M.B. Recent trends in diurnal variation of precipitation at Valentia on the west coast of Ireland. J. Hydrol. 1998, 207, 270–279. [Google Scholar] [CrossRef] [Green Version]
- Yu, P.S.; Yang, T.C.; Kuo, C.C. Evaluating long-term trends in annual and seasonal precipitation in Taiwan. Water Resour. Manag. 2006, 20, 1007–1023. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of precipitation and drought data in Serbia over the period 1980–2010. J. Hydrol. 2013, 494, 32–42. [Google Scholar] [CrossRef]
- Mahinthakumar, G.; Sayeed, M. Hybrid genetic algorithm–local search methods for solving groundwater source identification inverse problems. J. Water Resour. Plan. Manag. 2005, 131, 45–57. [Google Scholar] [CrossRef]
- Ayvaz, M.T.; Karahan, H. A simulation/optimization model for the identification of unknown groundwater well locations and pumping rates. J. Hydrol. 2008, 357, 76–92. [Google Scholar] [CrossRef]
- Sun, P.L.; Yang, C.C.; Lin, T.W. How to amend land subsidence treatment policies to solve coastal subsidence problems in Taiwan. Reg. Environ. Chang. 2011, 11, 679–691. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Hafner Pub. Co.: New York, NY, USA, 1962; p. 199. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-parametric Approach to the Change-point Problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Kruskal, W.H.; Wallis, W.A. Use of ranks in one-criterion variance analysis. J. Am. Stat. Assoc. 1952, 47, 583–621. [Google Scholar] [CrossRef]
- Yeh, G.T.; Cheng, H.P.; Cheng, J.R.; Lin, H.C.; Martin, W.D. A Numerical Model Simulating Water Flow and Contaminant and Sediment Transport in WAterSHed Systems of 1-D Stream-River Network, 2-D Overland Regime, and 3-D Subsurface Media (WASH123D: Version 1.0); U.S. Army Corps of Engineers: Vicksburg, MS, USA, 1998.
- Yeh, G.T.; Huang, G.B.; Cheng, H.P.; Zhang, F.; Lin, H.C.; Edris, E.; Richards, D. A First-Principle, Physics-Based Watershed Model: WASH123D; CRC Press: Boca Raton, FL, USA, 2005; Chapter 9; pp. 211–244. [Google Scholar]
- Yates, D.; Purkey, D.; Sieber, J.; Huber-Lee, A.; Galbraith, H.; West, J.; Herrod-Julius, S.; Young, C.; Joyce, B.; Rayej, M. Climate driven water resources model of the Sacramento Basin, California. J. Water Resour. Plan. Manag. 2009, 135, 303–313. [Google Scholar] [CrossRef]
- Yeh, G.T.; Shih, D.S.; Cheng, J.R.C. An integrated media, integrated processes watershed model. Comput. Fluids 2011, 45, 2–13. [Google Scholar] [CrossRef]
- Shih, D.S.; Yeh, G.T. Identified model parameterization, calibration, and validation of the physically distributed hydrological model WASH123D in Taiwan. J. Hydrol. Eng. 2010, 16, 126–136. [Google Scholar] [CrossRef]
- Shih, D.S.; Liau, J.M.; Yeh, G.T. Model assessments of precipitation with a unified regional circulation rainfall and hydrological watershed model. J. Hydrol. Eng. 2011, 17, 43–54. [Google Scholar] [CrossRef]
- Hsu, T.W.; Shih, D.S.; Li, C.Y.; Lan, Y.J.; Lin, Y.C. A study on coastal flooding and risk assessment under climate change in the mid-western coast of Taiwan. Water 2017, 9, 390. [Google Scholar] [CrossRef]
- Wu, R.S.; Shih, D.S. Modeling hydrological impacts of groundwater level in the context of climate and land cover change. Terr. Atmos. Ocean. Sci. 2018, 29, 341–353. [Google Scholar] [CrossRef]
- Ting, C.S.; Zhou, Y.; de Vries, J.J.; Simmers, I. Development of a preliminary ground water flow model for water resources management in the Pingtung Plain. Groundwater 1998, 36, 20–36. [Google Scholar] [CrossRef]
- Yang, C.C. The Observation and Investigation of Cross Sections in the Valley of Donggang River and Gaoping River; Water Resources Agency: Taipei, Taiwan, 2015. (In Chinese)
- Li, M.H.; Jang, C.S.; Chen, C.J.; Shih, D.S. Applying Integrated Numerical Modeling of Surface Water and Subsurface Water to Study Groundwater Resources Management (3/3); Water Resources Agency: Taipei, Taiwan, 2016. (In Chinese)
- Lin, K.P.; Chou, P.C.; Shih, D.S. To study hydrological variabilities by using surface and groundwater coupled model–A case study of Pingtung plain, Taiwan. Procedia Eng. 2016, 154, 1034–1042. [Google Scholar] [CrossRef]
- Hamon, R.W. Computation of direct runoff amounts from storm rainfall. Int. Assoc. Hydrol. Sci. 1963, 63, 52–62. [Google Scholar]
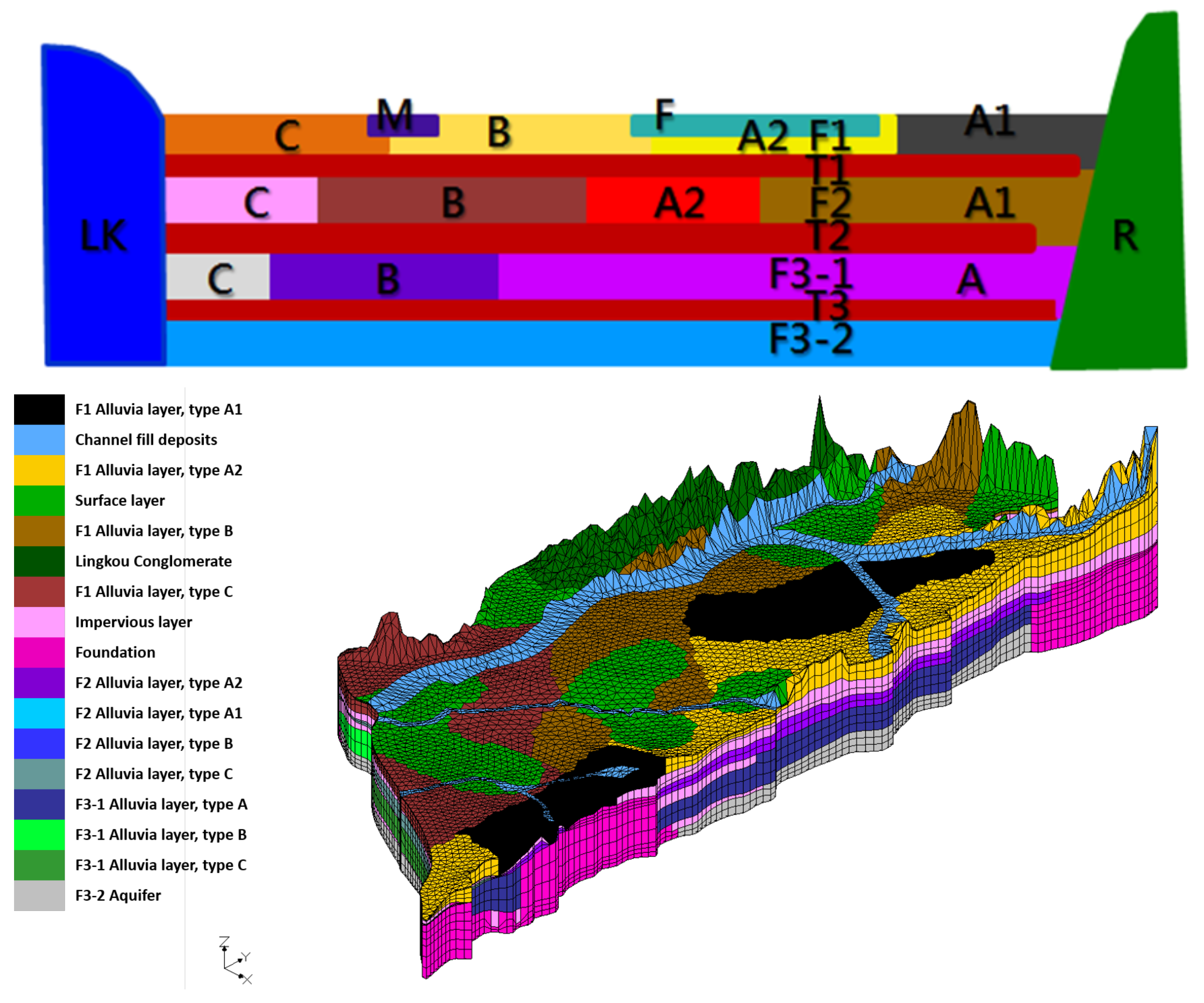

| Hydrogeological Unit | ID | Pumping Test Results | Lateral K | |||
|---|---|---|---|---|---|---|
| Name | Abbr. | No. Tests | Ave.K | Std. Log(K) | ||
| Mud Layer | M | 13 | - | - | - | m/s |
| Fluvial Deposit | F | 14 | - | - | - | m/s |
| Aquifer 1/A1 | F1/A1 | 1 | 7 | m/s | 0.32 | m/s |
| Aquifer 1/A2 | F1/A2 | 2 | 8 | m/s | 0.33 | m/s |
| Aquifer 1/B | F1/B | 3 | 13 | m/s | 0.5 | m/s |
| Aquifer 1/C | F1/C | 4 | 13 | m/s | 0.75 | m/s |
| Aquifer 2/A1 | F2/A1 | 5 | 4 | m/s | 0.06 | m/s |
| Aquifer 2/A2 | F2/A2 | 6 | 18 | m/s | 0.44 | m/s |
| Aquifer 2/B | F2/B | 7 | 15 | m/s | 0.38 | m/s |
| Aquifer 2/C | F2/C | 8 | 4 | m/s | 0.23 | m/s |
| Aquifer 3-1/A | F3-1/A | 9 | 30 | m/s | 0.5 | m/s |
| Aquifer 3-1/B | F3-1/B | 10 | 12 | m/s | 0.59 | m/s |
| Aquifer 3-1/C | F3-1/C | 17 | 5 | m/s | 0.48 | m/s |
| Aquifer 3-2 | F3-2 | 11 | 16 | m/s | 0.55 | m/s |
| Aquitards | T1–T3 | 15 | - | - | - | m/s |
| Lingkou Cg † | LK | 12 | - | - | - | m/s |
| Bedrock | R | 16 | - | - | - | m/s |
| Channels (1D) | Land Surfaces (2D) |
|---|---|
| 0.028–0.040 | Agricultural (0.20) |
| Forestry (0.30) | |
| Traffic (0.10) | |
| Water (0.05) | |
| Building (0.10) | |
| Other (0.15) |
| Year | Hengchun | Kaohsiung | Year | Hengchun | Kaohsiung |
|---|---|---|---|---|---|
| 1981 | 25.21 | 25.00 | 1998 | 26.06 | 25.83 |
| 1982 | 24.82 | 24.83 | 1999 | 25.12 | 25.19 |
| 1983 | 24.90 | 24.76 | 2000 | 25.32 | 25.13 |
| 1984 | 24.54 | 24.33 | 2001 | 25.20 | 25.16 |
| 1985 | 24.72 | 24.22 | 2002 | 25.44 | 25.66 |
| 1986 | 24.21 | 24.43 | 2003 | 25.27 | 25.43 |
| 1987 | 25.30 | 25.16 | 2004 | 25.12 | 25.22 |
| 1988 | 25.16 | 24.87 | 2005 | 25.05 | 25.05 |
| 1989 | 24.77 | 24.95 | 2006 | 25.90 | 25.68 |
| 1990 | 25.12 | 25.13 | 2007 | 25.77 | 25.46 |
| 1991 | 25.14 | 25.34 | 2008 | 25.37 | 25.14 |
| 1992 | 24.95 | 24.88 | 2009 | 25.40 | 25.35 |
| 1993 | 25.20 | 25.11 | 2010 | 25.37 | 25.44 |
| 1994 | 25.37 | 25.21 | 2011 | 24.72 | 24.95 |
| 1995 | 24.95 | 24.65 | 2012 | 25.48 | 25.43 |
| 1996 | 24.97 | 24.83 | 2013 | 25.56 | 25.55 |
| 1997 | 24.97 | 24.98 | 2014 | 25.59 | 25.59 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shih, D.-S.; Chen, C.-J.; Li, M.-H.; Jang, C.-S.; Chang, C.-M.; Liao, Y.-Y. Statistical and Numerical Assessments of Groundwater Resource Subject to Excessive Pumping: Case Study in Southwest Taiwan. Water 2019, 11, 360. https://doi.org/10.3390/w11020360
Shih D-S, Chen C-J, Li M-H, Jang C-S, Chang C-M, Liao Y-Y. Statistical and Numerical Assessments of Groundwater Resource Subject to Excessive Pumping: Case Study in Southwest Taiwan. Water. 2019; 11(2):360. https://doi.org/10.3390/w11020360
Chicago/Turabian StyleShih, Dong-Sin, Chia-Jeng Chen, Ming-Hsu Li, Cheng-Shin Jang, Che-Min Chang, and Yuan-Ya Liao. 2019. "Statistical and Numerical Assessments of Groundwater Resource Subject to Excessive Pumping: Case Study in Southwest Taiwan" Water 11, no. 2: 360. https://doi.org/10.3390/w11020360
APA StyleShih, D.-S., Chen, C.-J., Li, M.-H., Jang, C.-S., Chang, C.-M., & Liao, Y.-Y. (2019). Statistical and Numerical Assessments of Groundwater Resource Subject to Excessive Pumping: Case Study in Southwest Taiwan. Water, 11(2), 360. https://doi.org/10.3390/w11020360








