Abstract
Pan evaporation (Epan) is an important indicator of regional evaporation intensity and degree of drought. However, although more evaporation is expected under rising temperatures, the reverse trend has been observed in many parts of the world, known as the “pan evaporation paradox”. In this paper, the Haihe River Basin (HRB) is divided into six sub-regions using the Canopy and k-means (The process for partitioning an N-dimensional population into k sets on the basis of a sample is called “k-means”) to cluster 44 meteorological stations in the area. The interannual and seasonal trends and the significance of eight meteorological indicators, including average temperature, maximum temperature, minimum temperature, precipitation, relative humidity, sunshine duration, wind speed, and Epan, were analyzed for 1961 to 2010 using the trend-free pre-whitening Mann-Kendall (TFPW-MK) test. Then, the correlation between meteorological elements and Epan was analyzed using the Spearman correlation coefficient. Results show that the average temperature, maximum temperature, and minimum temperature of the HRB increased, while precipitation, relative humidity, sunshine duration, wind speed and Epan exhibited a downward trend. The minimum temperature rose 2 and 1.5 times faster than the maximum temperature and average temperature, respectively. A significant reduction in sunshine duration was found to be the primary factor in the Epan decrease, while declining wind speed was the secondary factor.
1. Introduction
Global warming has become an indisputable fact [1]. Temperature records indicate that the earth has warmed by approximately 0.6 °C during the 20th century [2]. This increase in global temperature has significantly impacted the natural environment, ecosystem, and social economy [3], and has led to a series of changes in hydrological factors, such as precipitation, evaporation, water infiltration, soil moisture, river runoff, and groundwater flow, all of which affect the global hydrological cycle. This, in turn, causes temporal and spatial redistribution of water resources, and thereby threatens water security, food security, social security, and national security [4,5]. As a key component in the hydrological cycle, evapotranspiration is associated with water balance and water exchange, as well as surface energy balance; hence, of all components of the water cycle, evapotranspiration is the factor most directly affected by climate change [6]. Therefore, analyzing the climate sensitivity of evapotranspiration has important theoretical and practical implications for understanding the impact of climate change on the hydrological cycle [7].
Evapotranspiration is the process of water transport from the earth’s surface to the atmosphere [8]. As a core process of the climate system, evapotranspiration closely links the hydrological cycle, energy budget, and carbon cycle [9]. Pan evaporation (Epan) [10] is the most universal and simplest way to measure evapotranspiration, which is often used to indicate the humidity level of a given regional climate [11]. Although Epan cannot directly represent the evaporation of the water surface, it has a close correlation with water surface evaporation. Therefore, it has remained an important reference indicator in the assessment of water resources, water resources planning, and the design of irrigation systems, to name a few examples [12]. As the global temperature rises, Epan should theoretically gradually increase. However, in reality, only certain regions in the world have an Epan value that is consistent with theoretical expectations, and the majority of the world’s regions have been found to have declining Epan values. This phenomenon is called the “pan evaporation paradox” [3]. Specifically, countries such as Spain [13], Iran [14], Israel [15], and Brazil [16] have been found to have increasing Epan values, and countries such as the former Soviet Union, the United States [17,18], New Zealand [19], China [20,21,22,23], Thailand [24], India [12], Nigeria [25], and Australia [26,27] have been found to have declining Epan values. Correctly interpreting the overall declining trend of Epan in the context of rising global temperatures and uncovering the main meteorological factors that affect the reduction of Epan is of great importance to accurately predict future hydrological cycles.
Many scholars have studied the temporal and spatial changes of Epan at global and regional scales, as well as the causes of such changes. According to their findings, the causes of Epan reduction can be categorized as follows. (1) An increase in humidity in the surrounding environment of the evaporation pan: Brutsaert and Parlange ascertained that the decrease in Epan value was due to an increase in the volume of evaporation from the land surface, considering the difference between evaporation from the land surface and the evaporation volume observed through the evaporation pan [28]. Zuo et al. employed observational data from 62 conventional meteorological stations with solar-radiation observation equipment in China to analyze in detail the relationship between Epan and corresponding environmental factors, as well as the environmental factors’ responses to global climate change. The researchers discovered that Epan was most correlated to atmospheric relative humidity [20]. (2) Changes in precipitation: Tebakari et al. [24] analyzed the temporal and spatial variation of Epan in Thailand from 1982 to 2000 and concluded that both Epan and precipitation showed a declining trend. This conclusion was inconsistent with findings from the United States, where Epan was found to be decreasing while precipitation was increasing [29]. Jaswal et al. utilized evaporation and rainfall data from 1971 to 2000 from 58 stations that were evenly distributed in India to analyze the overall correlation between evaporation and rainfall in a year, as well as their correlation in winter, summer, monsoon season, and post-monsoon season. The results showed that, in southern India, the evaporation trend had a complementary relationship with rainfall during the same period [30]. (3) A decrease in the diurnal temperature range: Peterson et al. compared data from both the United States and the former Soviet Union from 1950 to 1990 and found a steady decline in Epan values in all investigated regions (except Central Asia), as well as a decline in diurnal temperature range. Epan and diurnal temperature range were thus clearly correlated. Therefore, the researchers concluded that the reduction in the diurnal temperature range, caused by an increase in cloud cover, consequently caused the reduction in Epan [17]. (4) A reduction in solar radiation: Roderick and Farquhar found that Epan values observed in many parts of the world over the past 50 years showed a clear downward trend and asserted that such a decline was caused by the reduction in overall solar radiation resulting from an increase in cloud cover and aerosol concentrations [3]. (5) A reduction in wind speed: Burn and Hesch conducted a trend analysis on the evaporation data of 48 sites in the Canadian Prairies over three analysis periods and concluded that wind speed has a substantial influence on the decreasing trend of evaporation, while vapor-pressure deficit has a significant influence on the increasing trend of evaporation [31]. Hoffman et al. studied the changes in Epan, rainfall, wind speed, temperature, and vapor-pressure deficit from 1974 to 2005 taken from 20 climate stations in the Cape Floristic Region (CFR), South Africa, and suggested that the reduction in Epan was likely due to a reduction in wind speed [32]. Yang and Yang analyzed the daily Epan, temperature, wind speed, solar radiation, and relative humidity of 54 meteorological stations in China for 1961 to 2001 and concluded that the reduction in Epan in the majority of regions in China is due to a decrease in wind speed [33]. (6) The comprehensive impact of meteorological elements: Roderick and Farquhar analyzed data from Australia for 1970 to 2002 and found that Epan values showed a downward trend. The results showed that such a change might be related to a decrease in solar radiation, wind speed, and diurnal temperature range [26]. Sheng examined Epan data and other meteorological factors from 468 meteorological stations in China, measured simultaneously from 1957 to 2001, and found that the main influential factors of Epan were solar radiation, diurnal temperature range, and wind speed, while the influence of humidity was the weakest factor [21]. Liu et al. investigated data for 1955 to 2001 taken from 671 sites in China. The results revealed an overall decline in Epan. In addition, diurnal temperature range and wind speed were found to have the greatest correlation with such a decline [22]. Based on the aforementioned studies, the causes of the reduction of Epan appear to be very complicated. Owing to the location, climate, atmospheric differences, and even the differences in the length of the data series, the conclusions of these studies are inconsistent. Therefore, identifying the impact of various meteorological variables on Epan trends is critical to quantifying the impact of global warming.
The HRB is located in a region with a warm semi-arid climate and a continental monsoon climate. This area is sensitive to climate change and is a region with a fragile ecological environment. Owing to the area’s dense population and rapid economic development, as well as its status as one of China’s major wheat producers, the contradiction between water supply and water demand is prominent in the area. Water shortages have become a major factor restricting sustainable economic and social development in the HRB [34]. Epan in the HRB generally exhibits a decreasing trend [35,36,37], which is largely consistent with Epan trends in other regions of China [38,39,40,41,42,43,44,45,46,47,48]. However, scholars have differing views on the causes of the Epan trend in the HRB. Zheng et al. analyzed the effects of temperature, wind speed, solar radiation, and atmospheric pressure on Epan in the HRB for 1957 to 2001 and concluded that wind speed is the main factor leading to the decrease of Epan in the region [49]. Hao et al. selected eight meteorological elements from 34 climate stations for 1958 to 2011 in order to analyze the spatial and temporal variations in the HRB. The results showed that the potential evapotranspiration in the region was negatively correlated with relative humidity and was positively correlated with diurnal temperature range [50]. Guo and Ren examined data observed from the evaporation pans of 117 meteorological stations for 1956 and 2000 and analyzed the changes in evaporation in the Huang-Huai-Hai River Basin. The findings showed that the direct climatic cause of the decrease in evaporation may be a reduction in sunshine duration and solar radiation. In addition, a reduction in wind speed and diurnal temperature range may also play an important role [51]. In summary, though most of the papers consider that the decrease of wind speed is a main factor causing the Epan declining, but different literatures have different conclusions on the influence of other meteorological factors on the Epan decreasing. So, this study aimed to analyze the trend of changes in Epan in the HRB using data collected by 44 meteorological stations for 1961 to 2010, and to explore the temporal and spatial variation laws of Epan, as well as the main driving forces of declining Epan trend in the region.
2. Materials and Methods
The HRB is located between 112–120° E longitude and 35–43° N latitude, with the Bohai Sea to the east, the Yellow River to the south, the Yunzhong and Taiyue Mountains to the west, and the Inner Mongolia Plateau to the north. The total area of the HRB is 320,600 km2, accounting for 3.3% of the total area of the country. The HRB spans eight provinces: Beijing, Tianjin, Hebei, Shanxi, Shandong, Henan, Inner Mongolia, and Liaoning. It is a political and cultural center and an economically developed region of strategic significance in China. The HRB has two major rivers: the Hai River and the Luan River. The Hai River, which is the main water system for the area, consists of the Ji Canal River, Chaobai River, North Canal, Yongding River, Daqing River, Ziya River, and Zhangwei River, as well as plains rivers, such as the Tuhai River and Majia River, each of which enters the sea individually. The Luan River includes itself and the rivers along the eastern coast of Hebei Province. The annual average temperature range of the basin is between 1.5 °C and 14 °C, the annual average relative humidity is between 50% and 70%, and the average annual precipitation is 539 mm (semi-arid climate). The annual average land-surface evaporation is 470 mm, and the water surface evaporation is 1100 mm. The geographical location and topographic distribution of the study area are shown in Figure 1.
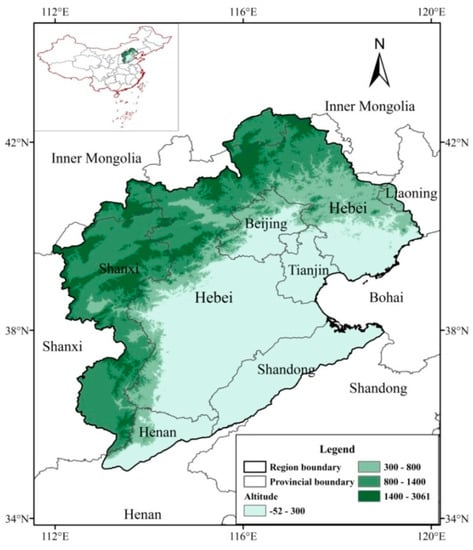
Figure 1.
Location and topography of the HRB.
Meteorological data from the HRB and 55 meteorological stations in the surrounding area, provided by the National Meteorological Center of the China Meteorological Administration, were used in this study, including the daily average temperature, highest, and lowest temperatures, average relative humidity, sunshine duration, wind speed, precipitation, and daily evaporation from an evaporation pan 20 cm in diameter. In terms of missing data, the following rules were respected: when the daily data for five or more days were missing for a specific meteorological element in a month, the data of the entire month were considered missing; when the data for one or more months were missing, the data of the entire year were considered invalid. The time series of the data was from 1961 to 2010, and the length of the time series was 50 years. After excluding the station data that did not satisfy the time series requirements, data for 44 stations were retained.
In order to better analyze the seasonal changes of the elements, the data were divided into spring (March to May), summer (June to August), fall (September to November), and winter (December to February). The annual temperature (average, maximum, and minimum), annual average relative humidity, annual average sunshine duration, and annual average wind speed of each station were calculated based on the mean of the daily data. The annual Epan and precipitation were calculated by summing the daily data. The same methods were applied to obtain the seasonal data for each element.
2.1. Canopy and k-means Clustering
In order to explore patterns in the spatial and temporal variations of the HRB climate, as well as geomorphological differences in the region and the climatic characteristics, this study selected eight representative indicators as references to categorize the HRB into several sub-regions. The indicators included geodetic coordinates (X and Y values), elevation, average temperature, precipitation, relative humidity, sunshine duration, and wind speed. The Canopy and k-means clustering technique was adopted. This method performs clustering in two stages. In Stage 1, the Canopy clustering algorithm is used to calculate the similarity of the objects and to categorize similar objects in the same subset (canopy). In Stage 2, the k-means clustering algorithm [52] is used to cluster the points in each canopy. Once Stage 1 is complete, the algorithm only needs to accurately cluster the points in each canopy, which greatly reduces the time spent on the accurate calculation of all data points that was performed in a traditional clustering algorithm. In addition, the number of canopies obtained in Stage 1 can be used as the K value in K-means clustering, which may minimize the irrational selection of the K value to a certain degree. The Canopy and k-means clustering technique not only greatly reduces the calculation of distance between points, the result is also more accurate when compared to general clustering methods [53,54].
MATLAB software (MATLAB 9.0, R2016a, MathWorks, Natick, MA, USA) was used to train the algorithm. The clustering results of the stations and their spatial distribution are presented in Figure 2. According to the clustering results, the HRB could be divided into six sub-regions (Figure 3). Detailed information for each sub-region is shown in Table 1.
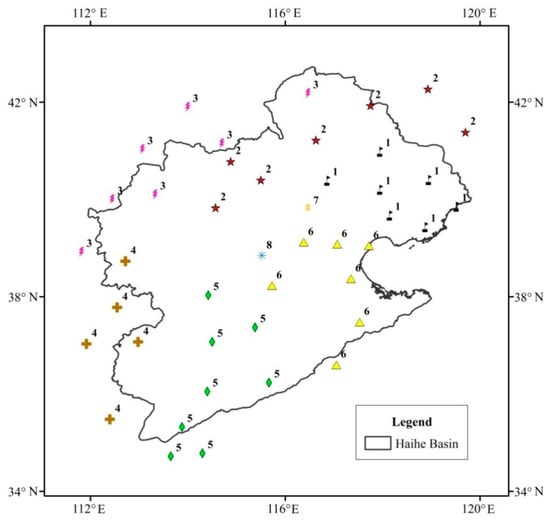
Figure 2.
The Canopy and k-means clustering results and spatial distribution of the stations in the HRB.
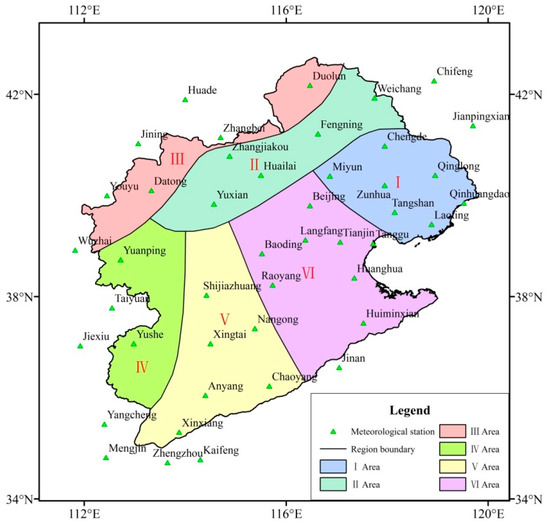
Figure 3.
The sub-region categorization of the HRB.

Table 1.
Basic information for the sub-regions of the HRB.
2.2. Trend-Free Pre-Whitening Mann-Kendall Test (TFPW-MK)
The Mann-Kendall (M-K) test [55,56] is a non-parametric statistical method. Compared to parametric statistical methods, the M-K test does not require samples to follow a certain distribution, the results are not subject to interference from a few outliers, and the method is simple and efficient in calculations. Therefore, it is commonly used to detect trends in a series of values. For that reason, the M-K test is suitable for examining the trend of the hydrological variables in this study [57,58,59]. Assuming is a time series, n is the length of the time series; then, the M-K method defines the statistical variable S as follows:
where xj and xk are the measured values of years j and k, respectively; and and .
When the number of samples is greater than 10, Z is calculated as follows:
where, Z is a normally distributed statistic, and Var(S) is the variance. If the Z value is positive, the data shows an increasing trend; if the Z value is negative, the data shows a decreasing trend [60]. Given the level of significance α, if , the null hypothesis is rejected, and the trend of the time series data (increasing or decreasing) is statistically significant at α.
The existence of serial correlation increases the probability that the M-K test will detect a significant trend [61,62]. The meteorological and hydrological data are mostly skewed and do not follow the same distribution, and there may be autocorrelation. Thus, in this paper, the TFPW method proposed by Yue et al. [62] is used to limit the influence of serial correlation; then, the significance of the time series is assessed by the M-K test.
The TFPW-MK steps are as follows:
Step 1. Use the Theil–Sen estimator(TSA) [63,64,65,66] to estimate the slope of a trend in sample data.
The slope of a trend is estimated using the TSA [63,64,65,66], and it is estimated as follows:
where is the estimate of the slope of the trend, and is the th observation. The slope determined by the TSA is a robust estimate of the magnitude of a trend. Since the publication of Hirsch et al. [67], the TSA has been popularly employed to identify the slope of trends in hydrological time series [68,69,70].
Step 2. If , there is no need to continue trend analysis; if , it is assumed to be linear, and the sample data are detrended as:
Step 3. The lag-1 serial correlation coefficient of is calculated using Equation (7), and then the autocorrelation is removed by Equation (9).
Step 4. The identified trend and the residual are blended by
Step 5. Verify the significance of trend of the blended series using the MK test.
2.3. Spearman Correlation Coefficient
The Spearman correlation coefficient [71] is a nonparametric test method independent of distribution and can be used as an indicator to measure the relationship between two variables. If there are no repeated values in the data, the Spearman correlation coefficient is +1 or 1 when two variables are monotonously correlated. For a sample of size , the raw scores , are converted to ranks , , and the Spearman correlation coefficient can be calculated as [72,73].

Table 2.
Grading table of Spearman correlation coefficient ().
3. Results
3.1. Trend and Significance Analysis
This study adopted the M-K test to analyze Epan, temperature (average, maximum, and minimum), precipitation, relative humidity, sunshine duration, and wind speed of the HRB. The TFPW method was used to eliminate the trends and autocorrelation of meteorological sequence data before the M-K Test was applied. If the value of Z was positive, the data exhibited an upward trend, while if the value of Z was negative, the data exhibited a downward trend. The threshold of the significance level was defined as . If the change trend of a given meteorological variable was found to be significant at this level, then [75]. The results of significance test of the interannual variations are shown in Figure 4, and that of the seasonal variations are shown in Table 3.
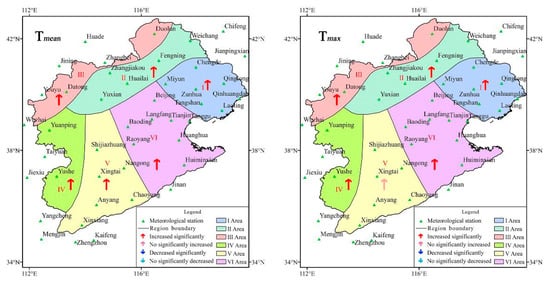
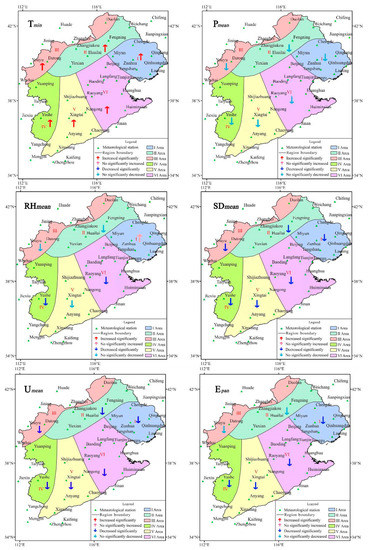
Figure 4.
Results of significance test on the interannual variations of the meteorological elements.

Table 3.
Z-Value of the Mann-Kendall test on the meteorological variables ().
For TFPW-MK test detrending, the TSA method is used to calculate the magnitude of the trend of the meteorological variables. The rates of the meteorological elements of each sub-region for 1961 to 2010 are shown in Table 4.

Table 4.
Climate tendency rates of the meteorological elements per sub-region from 1961 to 2010.
As shown in Figure 4, the interannual average temperatures (Tmean) in sub-regions I to VI presented a significant upward trend. With the exception of sub-region V, the average maximum temperatures (Tmax) of all sub-regions also increased significantly. The significance level of the trend of the average minimum temperatures (Tmin) was consistent with that of the Tmean. The Tmean in spring and winter in sub-regions I to VI increased significantly; in summer, it increased significantly only in sub-regions II and III. In fall, it increased significantly in the majority of sub-regions (except for sub-region I). Only the significance levels for Tmax in winter of sub-regions I to VI were consistent with those of Tmax. The Tmin of sub-regions I to VI in all four seasons significantly increased. However, it can be seen from Table 2 that the Tmin rose more rapidly, followed by the Tmean, with the Tmax rising the most slowly.
The interannual variations of average precipitation (Pmean) showed a downward trend of the six sub-regions: the decline rates were 22.50, 5.02, 4.07, 23.49, 5.35 and 19.71 mm/10a, respectively. However, the trend is not significant. The Pmean in spring showed an upward trend; only the trends of sub-regions II and VI were significant. In summer, it was found to be declining, except for sub-region V; the declining trends of sub-regions I, II, and VI were significant. The Pmean in fall showed an upward trend, except for sub-regions IV and V; The Pmean in winter showed an upward trend except for sub-region VI. The trends were not statistically significant in fall and in winter. As the decline of precipitation in summer offsets the increase of precipitation in spring, the interannual Pmean of the region showed a general downward trend.
The interannual variations of average relative humidity (RHmean) of all sub-regions showed a downward trend, except for sub-region I; however only the trends of sub-regions IV and VI were statistically significant. The change rates of sub-regions I to VI were 0.20%/10a, −0.35%/10a, −0.30%/10a, −0.71%/10a, −0.56%/10a, and −0.78%/10a, respectively. As the increase in the RHmean in fall and winter was larger than the sum of the reduction of the RHmean in spring and summer, the RHmean in sub-region I was found to be increasing. The RHmean in spring, summer, and fall of sub-regions I to VI was found to be declining, except for sub-region I in fall and sub-region V in summer; however, the trends of the majority of sub-regions were not significant. The changes in the RHmean of winter were not consistent across sub-regions I to VI, and none of the analyzed trends were significant.
The interannual variations of the average sunshine duration (SDmean) in sub-regions I to VI showed a significant downward trend; the decline rates were 0.27, 0.13, 0.17, 0.29, 0.31, and 0.32 h/10a, respectively. In addition, the significance values for the changes in the SDmean per season in sub-regions I to VI were consistent with those of the interannual variation.
The interannual average wind speed (Umean) of sub-regions I to VI had significantly decreased; the rates were 0.16, 0.15, 0.28, 0.05, 0.17, and 0.16 m/(s·10a), respectively. The seasonal variation of the Umean was showed a downward trend in all sub-regions, except for sub-region VI in summer. The Umean in summer and fall in sub-region IV was not significant, while the declining trends of the Umean per season of the other sub-regions were found to be significant.
The interannual Epan of sub-regions I to VI was found to be decreasing over the research period at speeds of 55.2, 11.7, 24.4, 30.7, 82.6, and 65.7 mm/10a, respectively. However, the trends of Epan for all sub-regions were significant except for sub-regions II and III. The Epan of sub-region II presented an upward trend in summer, fall, and winter, while the Epan of other sub-regions showed a downward trend in all seasons. Apart from sub-region IV, the Epan of other regions was significantly decreased in spring. The significance test results in summer aligned with those of the interannual variations. The changes of Epan in fall and winter in the majority of sub-regions were not statistically significant.
3.2. Sensitivity Analysis
Changes in meteorological variables led to temporal and spatial fluctuations in Epan, and their roles appeared to be different in different sub-regions. The influence of each meteorological element on changes in Epan depended on two factors: the sensitivity of the meteorological elements toward Epan and the change trend and corresponding significance level of the meteorological element. Therefore, it was necessary to analyze the meteorological elements that drive changes in Epan for each sub-region, to qualitatively evaluate the contribution of each meteorological element on the changes of Epan. The Spearman correlation coefficient was applied to qualitatively analyze the effects of Tmax, Tmean, Tmin, Pmean, RHmean, SDmean, and Umean on Epan. The results are shown in Table 5.

Table 5.
The Spearman correlation coefficients between Meteorological Elements and Epan per Sub-Region.
The sensitivity factors that caused changes in Epan in the HRB were different. It can be seen from Table 5 that there were significant correlations between Epan and Tmin, Pmean, RHmean, SDmean, and Umean in sub-region I. Although the correlations between Epan and Pmean and RHmean were significant, the trends of Pmean and RHmean were not significant. Therefore, the meteorological elements that affected the interannual changes in Epan of sub-region I were Tmin, SDmean, and Umean. Epan was found to have a negative correlation with Tmin, which does not align with what is commonly expected. Epan and SDmean and Umean were positively correlated. The significant decline in SDmean and Umean directly led to the significant decline of Epan. Based on the above analysis, the significant decrease in Epan in sub-region I was mainly due to the significant reduction in the SDmean and Umean. The Spearman correlation coefficient between Epan and SDmean was 0.75, indicating that the correlation is strong (see Table 2). The Spearman correlation coefficient between Epan and Umean was 0.46, indicating a moderate correlation. Thus, the primary factor affecting Epan decline in sub-region I was SDmean, followed by Umean. According to the same analysis method, the factors responsible for Epan decline in each sub-region were also analyzed. The primary factor affecting the decline of Epan in sub-regions I, III, IV, V, and VI was SDmean, followed by Umean, while the reasons for the changes in Epan in sub-regions II was the significant reduction in the SDmean.
In addition, the contributing factors to Epan in sub-regions I to VI for each season were also analyzed. In spring, the decrease in Epan in sub-regions I to VI was primarily caused by a significant decrease in SDmean, followed by a decline in Umean. In summer, significant decreases in SDmean and Umean were the primary and secondary driving factors of Epan in sub-regions I, V, and VI, respectively; the decrease in Epan for sub-regions III and IV was mainly due to the significant decrease in SDmean. Moreover, the change trend of Epan in sub-region II was found to be the opposite to that for other sub-regions, which could be due to a significant increase in temperature, as well as a significant drop in Pmean and RHmean. In fall, the decline in Epan in sub-regions I, III, V, and VI was attributed to a significant reduction in SDmean and Umean, while the decline in Epan in sub-region IV was caused by a significant reduction in SDmean. In addition, the change trend of Epan in sub-region II was the opposite of that for other sub-regions, which was mainly caused by a significant increase in Tmax and Tmean. In winter, apart from sub-region II, where a significant increase in temperature resulted in an upward trend in Epan, the reduction of Epan in all sub-regions was caused by a significant reduction in SDmean and Umean.
In summary, the primary factor responsible for the decline in Epan in the HRB was a reduction in sunshine duration, followed by a reduction in wind speed. The factors responsible for the reduction in Epan in each sub-region were consistent with the overall reduction in Epan of the HRB. However, the correlation between Umean and Epan was not significant in sub-region II, where the only influential factor was the decrease of sunshine duration.
4. Discussion
As noted above, when global temperature increases, the overall temperature of the HRB increases. However, there are differences in the spatial and temporal distribution. From 1961 to 2010, the lowest temperature increased approximately two times faster than the highest temperature, and approximately 1.5 times faster than the average temperature. This result is consistent with the results from an analysis of variations in annual temperatures by Zheng et al. [49] in the HRB for 1957 to 2001, but it is different from the results obtained by Salinger and Griffiths [76], which indicated that the lowest temperature rose approximately three times faster than the highest temperature globally from 1951 to 1998. Meanwhile, the average temperature, highest temperature, and lowest temperature in spring and winter increased much more quickly than the corresponding values in summer and autumn, for both the HRB and every sub-region. The temperatures in winter increased most significantly, three times faster than those in summer, and two times faster than those in autumn. Additionally, temperatures decreased to some extent in some areas of the HRB. For example, unlike the highest temperature in other sub-regions, which increased, the highest temperature in area V decreased.
The “evaporation paradox” also exists in the HRB. With respect to both the whole area and the sub-regions in the HRB, except for the slight increase in Epan in sub-region II in autumn and winter, Epan decreased, and this decline mostly occurred in spring and summer. This result agrees with the conclusions of Zheng et al. [49] and Liu et al. [77]. However, it contradicts with the findings in Liu et. al. [78] that from 1992 to 2007, Epan significantly increased in North China, including the HRB. The correlation between the general decrease in Epan and the temperature variation was weak, suggesting that the increase in temperature was not directly related to the decrease in Epan. The main factors responsible for the decline in Epan in the HRB included decreases in sunshine duration, which was the main factor, and in wind speed. This result differed from the conclusions of Zheng et al. [49], which stated that the decrease in wind speed is the main factor responsible for the decrease in Epan. In addition, this result does not agree with the conclusions from Liu et al. [79] that in the semi-humid/semi-arid region of China (including the HRB), decreases in diurnal temperature range, sunshine duration and wind speed were found to be the main factors contributing to the pan evaporation declines. Liu et al. [78] concluded that wind speed and solar radiation are the main factors that led to the decline in pan evaporation in North China, which differs from our findings. However, it is generally accepted that wind speed is one of the main driving factors of the decrease in Epan in the HRB. This statement is consistent with the conclusion that wind speed is one of the main factors driving the decrease in Epan in areas such as the Canadian Prairies [31], the Cape Floristic Region in South Africa [32], and Australia [26].
The factors attributed to the decrease in sunshine duration and wind speed also vary among studies [36,80,81,82]. For sunshine duration, multiple studies have concluded that this decrease may be related to the increase in aerosols and other air pollutants [3,83]. In other studies, it is argued that the decrease may be related to the increase in cloud cover. In addition, several studies have reported a correlation between a decrease in sunshine duration and urbanization [84]. Recently, Wei Pan [85] reported that the number of haze days significantly increased in North China (including in the HRB). Therefore, a decrease in sunshine duration may be related to the increase in haze days in the HRB. Regarding the decrease in wind speed, conclusions of various areas also differ; however, the main consensus is that the decrease in wind speed may be related to variations in global circulation [86,87], as well as the increase in surface roughness caused by afforestation and urbanization near the observation sites [88]. Based on the present studies, it is difficult to determine the reasons for the decrease in wind speed, and further studies are required.
5. Conclusions
In this study, the Canopy and k-means clustering method was employed to categorize the HRB into six sub-regions. Then, 44 out of the 55 meteorological stations in the surrounding area that had relatively complete data were selected, and the trends and significance of the interannual and seasonal variations of the pan evaporation, temperature, precipitation, relative humidity, sunshine duration, and wind speed for 1961 to 2010 were analyzed using TFPW-MK. Based on this analysis, the sensitivities of the average, maximum, and minimum temperatures, and precipitation, relative humidity, sunshine duration, and average wind speed to Epan were qualitatively analyzed using the Spearman correlation coefficient. In the whole basin, the primary cause of declining Epan was a significant reduction in sunshine duration, followed by a significant reduction in wind speed. In sub-regions, Epan showed a downward trend; however, the influential factors on Epan reduction per sub-region were slightly different from those of the entire region. Except for sub-region II, which was only affected by sunshine duration, reductions in Epan in other sub-regions were due to the joint influence of decreasing sunshine duration and wind speed.
In this paper, only a qualitative analysis was performed on the reduction of sunshine duration and wind speed in the HRB, and an explanation for this reduction is still lacking, and thus further research is needed.
Author Contributions
This paper is a joint effort by several authors. S.W. conceived and designed the paper’s structure; B.L. performed the Canopy-Kmeans clustering; Z.Y. compiled the code for the Mann-Kendall Test; Z.Y. and D.M. analyzed the data; H.L. and S.L. drew the figures; and Z.Y. wrote the paper.
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. 71573274; grant No. 51879066), the National Water Pollution Control and Management Science and Technology Major Project of China (2014ZX07203-008), the Science and Technology Project of Hebei Province (Grant No. 15227005D), and the Science and Technology Research and Development Program of Handan (1723209055-4).
Acknowledgments
The authors are very grateful to the editor and the anonymous reviewers whose suggestions significantly contributed to improving this work. The authors are also thankful for support from the Hebei University of Engineering, and Editage [www.editage.cn] for English language editing.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- IPCC. Climate Change 2001: The Science Basis, Contribution of Working Group I to the Third Assessment Report of Inter-Government Panel on Climate Change; The Press Syndicate of University of Cambridge: Cambridge, UK, 2001. [Google Scholar]
- IPCC. Climate Change 2007: Synthesis Report. Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; The Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2007. [Google Scholar]
- Roderick, M.L.; Farquhar, G.D. The cause of decreased pan evaporation over the past 50 years. Science 2002, 298, 1410–1411. [Google Scholar] [PubMed]
- Kang, S.Z. Towards water and food security in China. Chin. J. Eco Agric. 2014, 22, 880–885. (In Chinese) [Google Scholar]
- Gleick, P.H. Climate change, hydrology, and water resource. Rev. Geophys. 1989, 27, 329–344. [Google Scholar] [CrossRef]
- Limjirakan, B.S.; Limsakul, A. Trends in Thailand pan evaporation from 1970 to 2007. Atmos. Res. 2012, 108, 122–127. [Google Scholar] [CrossRef]
- Liu, X.M.; Zheng, H.X.; Liu, C.M.; Cao, Y.J. Sensitivity of the potential evapotranspiration to key climatic variables in the Haihe River Basin. Res. Sci. 2009, 31, 1470–1476. (In Chinese) [Google Scholar]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jou, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Eagleman, J.R. Pan evaporation, potential and actual evapotranspiration. J. Appl. Meteorol. 1967, 6, 482–488. [Google Scholar] [CrossRef]
- Wang, S.Q.; Chen, N.X. Water Resources Evaluation and Management, 1st ed.; Water Resources and Electric Power Press: Beijing, China, 1996; ISBN 7-120-01998-8. (In Chinese) [Google Scholar]
- Jhajharia, D.; Shrivastava, S.K.; Sarkar, D.; Sarkar, S. Temporal characteristics of pan evaporation trends under the humid conditions of northeast India. Agric. For. Meteorol. 2009, 149, 763–770. [Google Scholar] [CrossRef]
- Azorin-Molina, C.; Vicente-Serrano, S.M.; Sanchez-Lorenzo, A.; McVicar, T.R.; Morán-Tejeda, E.; Revuelto, J.; Kenawy, A.E.; Martín-Hernández, N.; Tomas-Burguera, M. Atmospheric evaporative demand observations, estimates and driving factors in Spain (1961–2011). J. Hydrol. 2015, 523, 262–277. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S. Changes of pan evaporation in the west of Iran. Water Resour. Manag. 2011, 25, 97–111. [Google Scholar] [CrossRef]
- Cohen, S.; Ianetz, A.; Stanhill, G. Evaporative climate changes at Bet Dagan, Israel, 1964–1998. Agric. For. Meteorol. 2002, 111, 83–91. [Google Scholar] [CrossRef]
- Silva, V.D.P.R.D. On climate variability in Northeast of Brazil. J. Arid Environ. 2004, 58, 575–596. [Google Scholar] [CrossRef]
- Peterson, T.C.; Golubev, V.S.; Groisman, P.Y. Evaporation losing its strength. Nature 1995, 377, 687–688. [Google Scholar] [CrossRef]
- Golubev, V.S.; Lawrimore, J.H.; Groisman, P.Y.; Speranskaya, N.A.; Zhuravin, S.A.; Menne, M.J.; Peterson, T.C.; Malone, R.W. Evaporation changes over the contiguous United States and the former USSR: A reassessment. Geophys. Res. Lett. 2001, 28, 2665–2668. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. Changes in New Zealand pan evaporation since the 1970s. Int. J. Climatol. 2005, 25, 2031–2039. [Google Scholar] [CrossRef]
- Zuo, H.C.; Li, D.L.; Hu, Y.Q.; Bao, Y.; Lv, S.H. The relationship between climate change trends and its changes in evaporation observed by evaporating dishes in the past 40 years in China. Chin. Sci. Bull. 2005, 11, 1125–1130. (In Chinese) [Google Scholar]
- Sheng, Q. The Variation and Causes of Small Pan Evaporation over the Past 45 Years in China. Master’s Thesis, Nanjing University of Information Science & Technology, Nanjing, China, May 2006. (In Chinese). [Google Scholar]
- Liu, M.; Shen, Y.J.; Ceng, Y.; Liu, C.M. Changing trend of pan evaporation and its cause over the past 50 years in China. Acta Geogr. Sin. 2009, 64, 259–269. (In Chinese) [Google Scholar]
- Ren, G.Y.; Guo, J. Change in pan evaporation and the influential factors over China: 1956–2000. J. Nat. Res. 2006, 1, 31–44. (In Chinese) [Google Scholar]
- Tebakari, T.; Yoshitani, J.; Suvanpimol, C. Time-space trend analysis in pan evaporation over Kingdom of Thailand. J. Hydrol. Eng. 2005, 10, 205–215. [Google Scholar] [CrossRef]
- Oguntunde, P.G.; Abiodun, B.J.; Olukunle, O.J.; Olufayoa, A.A. Trends and variability in pan evaporation and other climatic variables at Ibadan, Nigeria, 1973–2008. Meteorol. Appl. 2012, 19, 464–472. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. Changes in Australian pan evaporation from 1970–2002. Int. J. Climatol. 2004, 24, 1077–1090. [Google Scholar] [CrossRef]
- Jovanovic, B.; Jones, D.A.; Collins, D. A high-quality monthly pan evaporation data set for Australia. Clim. Chang. 2008, 87, 517–535. [Google Scholar] [CrossRef]
- Brutsaert, W.; Parlange, M.B. Hydrologic cycle explains the evaporation paradox. Nature 1998, 396, 30. [Google Scholar] [CrossRef]
- Lawrimore, J.; Peterson, T.C. Pan evaporation in dry and humid regions of the United States. J. Hydrometeorol. 2000, 1, 543–546. [Google Scholar] [CrossRef]
- Jaswal, A.K.; Rao, G.S.P.; De, U.S. Spatial and temporal characteristics of evaporation trends over India during 1971–2000. Mausam 2008, 59, 149–158. [Google Scholar]
- Burn, D.H.; Hesch, N.M. Trends in evaporation for the Canadian prairies. J. Hydrol. 2007, 336, 61–73. [Google Scholar] [CrossRef]
- Hoffman, M.T.; Cramer, M.D.; Gillson, L.; Wallace, M. Pan evaporation and wind run decline in the Cape Floristic Region of South Africa (1974–2005): Implications for vegetation responses to climate change. Clim. Chang. 2011, 109, 437–452. [Google Scholar] [CrossRef]
- Yang, H.; Yang, D. Climatic factors influencing changing pan evaporation across china from 1961 to 2001. J. Hydrol. 2012, 414, 184–193. [Google Scholar] [CrossRef]
- Cao, Y.Q.; Zhang, T.T.; Xu, D.; Yang, C.X. Analysis of evapotranspiration of temporal-space evolution in the Haihe Basin. Res. Sci. 2014, 36, 1489–1500. (In Chinese) [Google Scholar]
- Bao, Z.X.; Yan, X.L.; Wang, G.Q.; Liu, C.S.; He, R.M. Mechanism of effect of meteorological factors in paradox theory of pan evaporation of Haihe River basin. J. Water Res. Water Eng. 2014, 25, 1–7. (In Chinese) [Google Scholar]
- Li, X.C. Spatio-Temporal Variation of Actual Evapotranspiration in the Pearl, Haihe and Tarim River Basins of China. Ph.D. Thesis, Nanjing University of Information Science & Technology, Nanjing, China, May 2013. (In Chinese). [Google Scholar]
- Liu, M.; Shen, Y.J. Change trend of hydrological elements in Haihe River Basin over the last 50 years. J. China Hydrol. 2010, 30, 74–77. (In Chinese) [Google Scholar]
- Rong, Y.S.; Zhang, X.N.; Jiang, H.Y.; Bai, L.Y. Pan evaporation change and its impact on water cycle over the upper reach of the Yangtze River. Chin. J. Geophys. 2012, 55, 2889–2897. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, F.N.; Zhao, M.; Wang, Y.; Zhang, P.F. Variation characteristics of reference evapotranspiration and pan evaporation during 1960–2009 in Shiyang River Basin. J. Arid Meteorol. 2014, 32, 560–568. (In Chinese) [Google Scholar]
- Li, L.P.; Li, Y.Y.; Liu, M.C. Change trend of pan evaporation and its causes in Shiyang River Basin during 1961–2005. J. Desert Res. 2012, 32, 832–841. (In Chinese) [Google Scholar]
- Zhang, T.T. Analysis on Pan Evaporation Trend And Its Impacted Factors in Xiangjiang River Basin. Master’s Thesis, Hunan Normal University, Changsha, China, May 2013. (In Chinese). [Google Scholar]
- Rong, Y.S.; Zhou, Y.; Wang, W. Analysis of pan evaporation changes in the Huaihe River basin. Adv. Water Sci. 2011, 22, 15–22. (In Chinese) [Google Scholar]
- Xie, P.; Chen, X.H.; Wang, Z.L.; Xie, Y.W. Comparison of actual evapotranspiration and pan evaporation. Acta Geogr. Sin. 2009, 64, 270–277. (In Chinese) [Google Scholar]
- Wang, Z.L.; Qin, J.X.; Chen, X.H. Variation characteristics and impact factors of pan evaporation in Pearl River Basin. Trans. CSAE 2010, 26, 73–77. (In Chinese) [Google Scholar]
- Qiu, X.F.; Liu, C.M.; Zeng, Y. Changes of evaporation in the recent 40 years over the Yellow River Basin. J. Nat. Res. 2003, 18, 437–441. (In Chinese) [Google Scholar]
- Huang, Y.; Wang, Y. Analysis on temporal spatial distribution and inter-annual change of the evaporation capacity in Yunnan Province. Hydrology 2003, 23, 36–40. (In Chinese) [Google Scholar]
- Xu, Z.X.; He, W.L. Analysis on the long-term trend of pan evaporation in the Yellow River Basin over the past 40 years. Hydrology 2005, 06, 6–11. (In Chinese) [Google Scholar]
- Song, M.B.; Chen, J.Q.; Zhang, X.J.; Zhang, W.J. Pan evaporation trend in Yangtze River Basin from 1951 to 2000. Water Res. Prot. 2011, 27, 24–27. (In Chinese) [Google Scholar]
- Zheng, H.; Liu, X.; Liu, C.; Dai, X.; Zhu, R. Assessing contributions to pan evaporation trends in Haihe River Basin, China. J. Geophys. Res. Atmos. 2009, 114, D24105. [Google Scholar] [CrossRef]
- Hao, Z.C.; Yan, L.Z.; Ju, Q.; Dunzhu, J.C. Spatiotemporal characteristics of climate variation in different kinds of landforms of Haihe River Basin. Res. Soil Water Conserv. 2014, 21, 56–60. (In Chinese) [Google Scholar]
- Guo, J.; Ren, G.Y. Recent change of pan evaporation and possible climate factors over the Huang-Huai-Hai watershed, China. Adv. Water Sci. 2005, 16, 666–672. (In Chinese) [Google Scholar]
- Mac Queen, J.B. Some methods for classification and analysis of multivariate observations. In Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966; Volume 1, pp. 281–297. [Google Scholar]
- Guha, S.; Rastogi, R.; Shim, K. Cure: An efficient clustering algorithm for large databases. Inf. Syst. 2001, 26, 35–58. [Google Scholar] [CrossRef]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: An efficient data clustering method for very large database. In Proceedings of the 1996 ACM SIGMOD International Conference on Management of data, Montreal, QC, Canada, 4–6 June 1996; Volume 25, pp. 103–114. [Google Scholar]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Measures; Charles Griffin: London, UK, 1975. [Google Scholar]
- Kottegoda, N.T. Stochastic Water Resources Technology; Wiley: New York, NY, USA, 1980; ISBN 978-1-349-03467-3. [Google Scholar]
- Burn, D.H.; Elnur, M.A.H. Detection of hydrologic trends and variability. J. Hydrol. 2002, 55, 107–122. [Google Scholar] [CrossRef]
- Abdul Aziz, O.I.; Burn, D.H. Trends and variability in the hydrological regime of the Mackenzie River Basin. J. Hydrol. 2006, 319, 282–294. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Changes in extreme precipitation in Texas. J. Geophys. Res. Atmos. 2010, 115, D14. [Google Scholar] [CrossRef]
- Von Storch, H. Misuses of statistical analysis in climate research. In Analysis of Climate Variability: Applications of Statistical Techniques; Von Storch, H., Navarra, A., Eds.; Springer: New York, NY, USA, 1995; pp. 11–26. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis, I. Nederlands Akad. Wetensch. Proc. 1950, 53, 386–392. [Google Scholar]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis, II. Nederlands Akad. Wetensch. Proc. 1950, 53, 52–525. [Google Scholar]
- Theil, H. A rank-invariant method of linear and polynomial regression analysis, III. Nederlands Akad. Wetensch. Proc. 1950, 53, 1397–1412. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Demaree, G.R.; Nicolis, C. Onset of Sahelian drought viewed as a fluctuation-induced transition. Q. J. R. Meteorol. Soc. 1990, 116, 221–238. [Google Scholar] [CrossRef]
- Burn, D.H. Hydrologic effects of climatic change in west-central Canada. J. Hydrol. 1994, 160, 53–70. [Google Scholar] [CrossRef]
- Gan, T.Y. Hydroclimatic trends and possible climatic warming in the Canadian Prairies. Water Resour. Res. 1998, 34, 3009–3015. [Google Scholar] [CrossRef]
- Spearman’s Rank Correlation Coefficient. Available online: https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient (accessed on 20 January 2019).
- Myers, J.L.; Well, A.D. Research Design and Statistical Analysis, 2nd ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2003; ISBN 0-8058-4037-0. [Google Scholar]
- Maritz, J.S. Distribution-Free Statistical Methods, 1st ed.; Chapman & Hall: New York, NY, USA, 1981; ISBN 978-0-412-15940-4. [Google Scholar]
- Spearman’s correlation. Available online: http://www.statstutor.ac.uk/resources/uploaded/spearmans.pdf (accessed on 20 January 2019).
- Wei, F.Y. Modern Climate Statistical Diagnosis and Prediction Technology, 2nd ed.; China Meteorological Press: Beijing, China, 2007; ISBN 9787502942991. (In Chinese) [Google Scholar]
- Salinger, M.J.; Griffiths, G.M. Trends in New Zealand daily temperature and rainfall extremes. Int. J. Climatol. 2001, 21, 1437–1452. [Google Scholar] [CrossRef]
- Liu, B.H.; Xu, M.; Henderson, M.; Gong, W.G. A spatial analysis of pan evaporation trends in China, 1955–2000. J. Geophys. Res. Atmos. 2004, 109, D15102. [Google Scholar] [CrossRef]
- Liu, X.M.; Luo, Y.Z.; Zhang, D.; Zhang, M.H.; Liu, C.M. Recent changes in pan-evaporation dynamics in China. Geophys. Res. Lett. 2011, 38, 142–154. [Google Scholar] [CrossRef]
- Liu, M.; Shen, Y.J.; Zeng, Y.; Liu, C.M. Trend in pan evaporation and its attribution over the past 50 years in China. J. Geogr. Sci. 2010, 20, 557–568. [Google Scholar] [CrossRef]
- Kaiser, D.P.; Qian, Y. Decreasing trends in sunshine duration over China for 1954–1998: Indication of increased haze pollution? Geophys. Res. Lett. 2002, 29, 38-1–38-4. [Google Scholar] [CrossRef]
- Yildirim, U.; Yilmaz, I.O.; Akinoglu, B.G. Trend analysis of 41 years of sunshine duration data for Turkey. Turk. J. Eng. Environ. Sci. 2013, 37, 286–305. [Google Scholar] [CrossRef]
- Niroula, N.; Kobayashi, K.; Xu, J. Sunshine duration is declining in Nepal across the period from 1987 to 2010. J. Agric. Meteorol. 2015, 71, 15–23. [Google Scholar] [CrossRef]
- Ren, J.; Lei, X.; Zhang, Y.; Wang, M.; Xiang, L. Sunshine duration variability in Haihe River Basin, China, during 1966–2015. Water 2017, 9, 770. [Google Scholar] [CrossRef]
- Wang, Y.; Wild, M.; Sánchez-Lorenzo, A.; Manara, V. Urbanization effect on trends in sunshine duration in china. Ann. Geophys. 2017, 35, 839–851. [Google Scholar] [CrossRef]
- Pan, W. Interdecadal Variation of Haze Days over China and the Atmospheric Causes in Recent 50 Years. Master’s Thesis, Chinese Academy of Meteorological Sciences, Beijing, China, April 2017. (In Chinese). [Google Scholar]
- Liu, X.M.; Zheng, H.X.; Zhang, M.H.; Liu, C.M. Identification of dominant climate factor for pan evaporation trend in the Tibetan Plateau. J. Geogr. Sci. 2011, 21, 594–608. [Google Scholar] [CrossRef]
- Wang, Z.Y.; Ding, Y.H.; He, J.H.; Yu, J. An updating analysis of the climate change in China in recent 50 years. Acta Meteorol. Sin. 2004, 62, 228–236. (In Chinese) [Google Scholar]
- Shen, Y.J.; Liu, C.M.; Liu, M.; Zeng, Y.; Tian, C.Y. Change in pan evaporation over the past 50 years in the arid region of China. Hydrol. Process. 2010, 24, 225–231. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).