Transmissibility Upscaling on Unstructured Grids for Highly Heterogeneous Reservoirs
Abstract
1. Introduction
- (1)
- (2)
2. Local Transmissibility Upscaling Method
- (1)
- Remeshing each reservoir cell with a high-resolution geological mesh finer than the geological mesh;
- (2)
- Decomposing each reservoir cell in local sub-domain containing geological cells;
- (3)
- Calculate an upper and lower admissible half-transmissibility values on each sub-domain of each reservoir cell, by defining for each shifted block, 1D local problems with linear pressure boundary conditions [11] and apply a finite-volume numerical scheme to discretize these local problems;
- (4)
- Calculate upscaled transmissibility values between each reservoir cells using half-transmissibility values of corresponding cells weighted by the surface exchange between these cells.
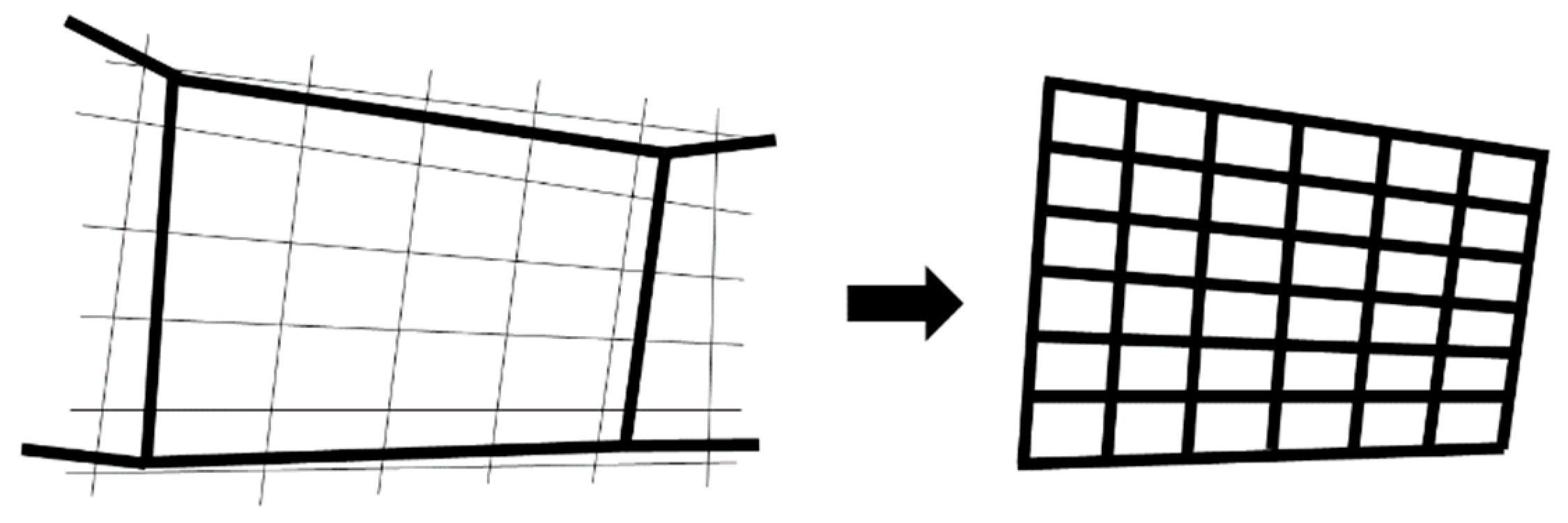
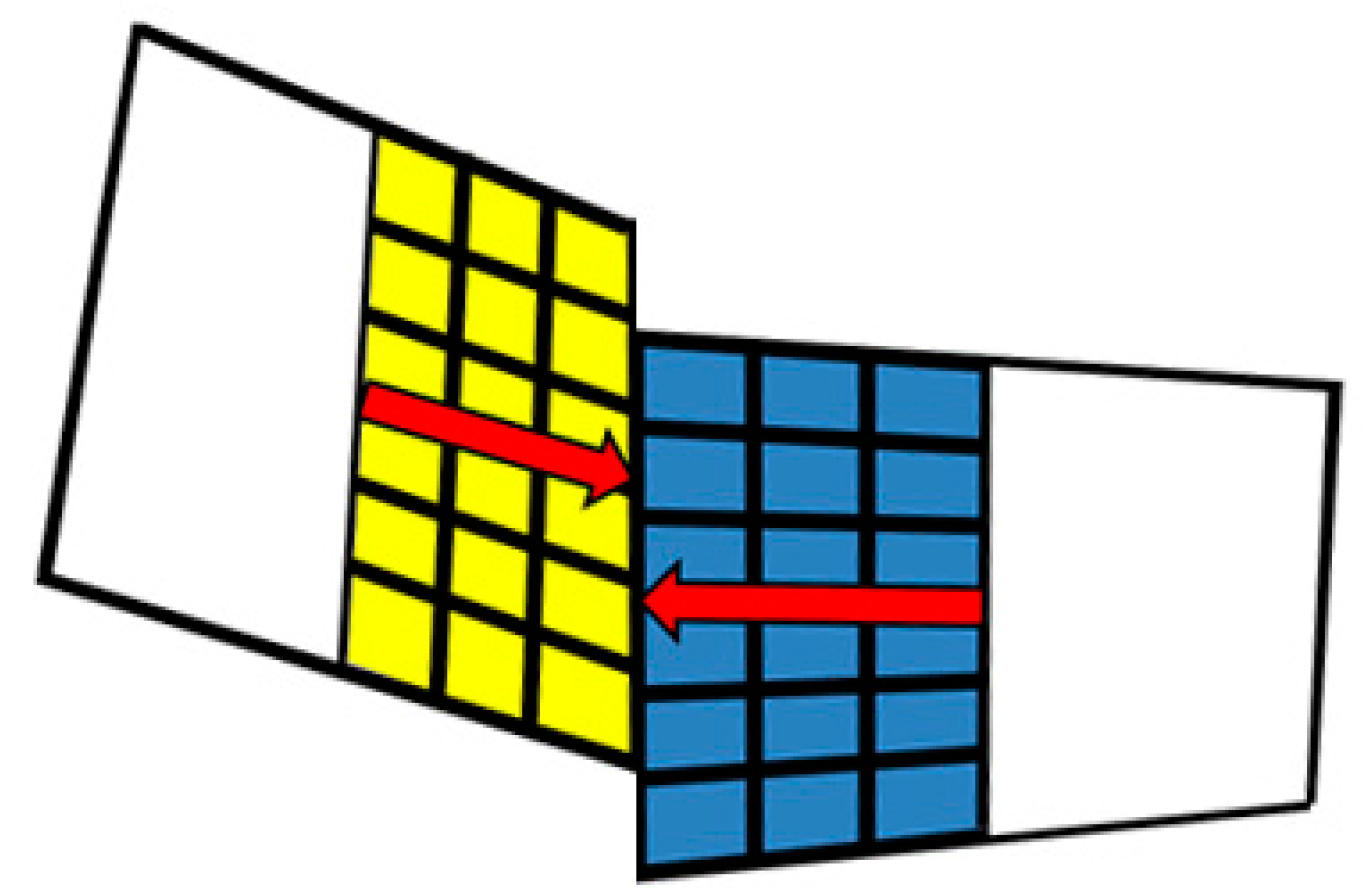
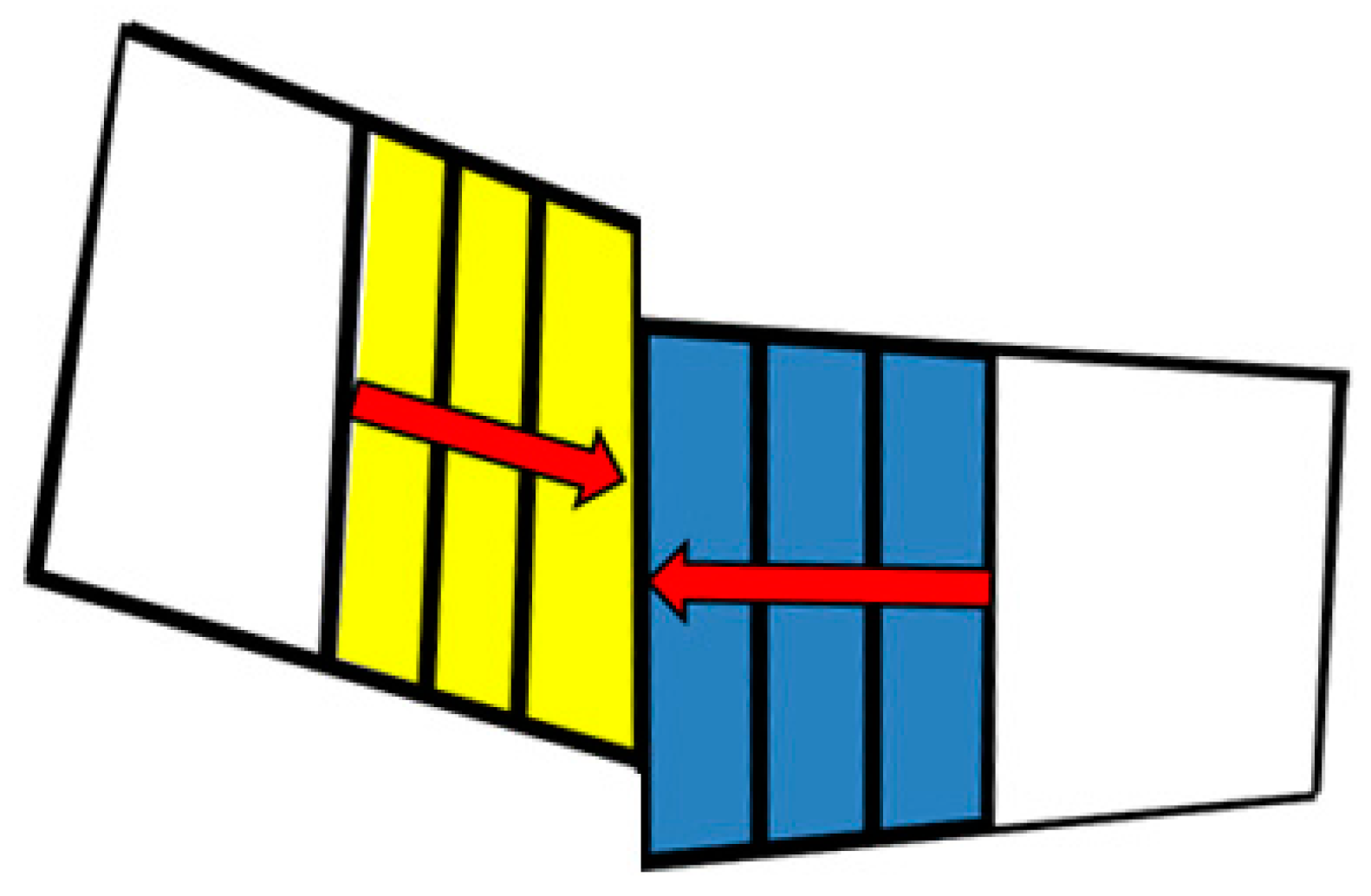
2.1. Remeshing
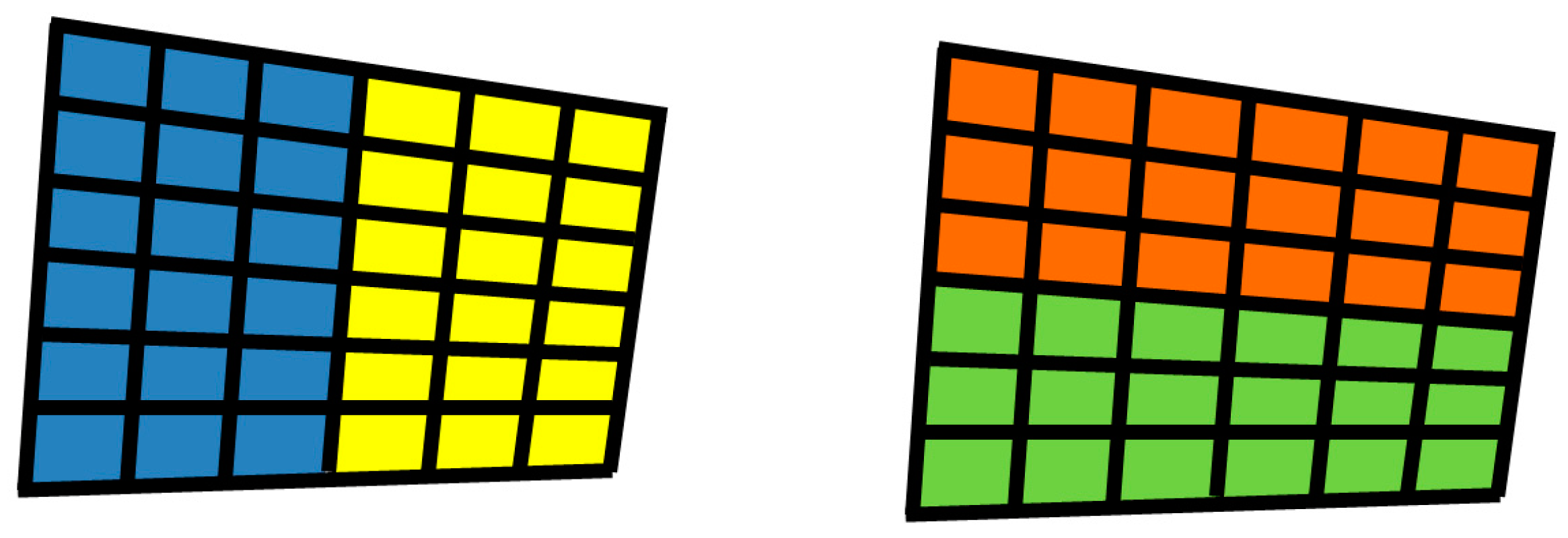
2.2. Sub-Domains Decomposition
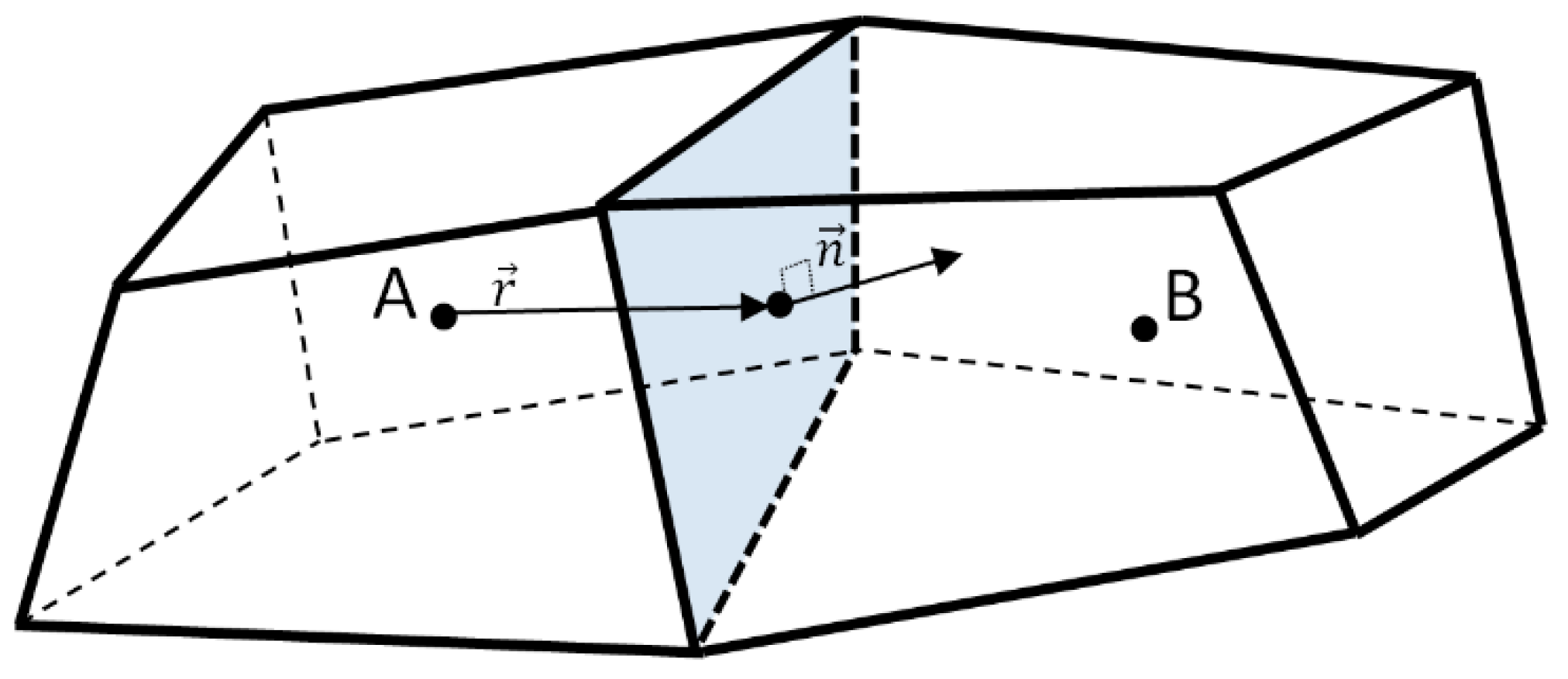
2.3. Lower and Upper Bounds Transmissibility
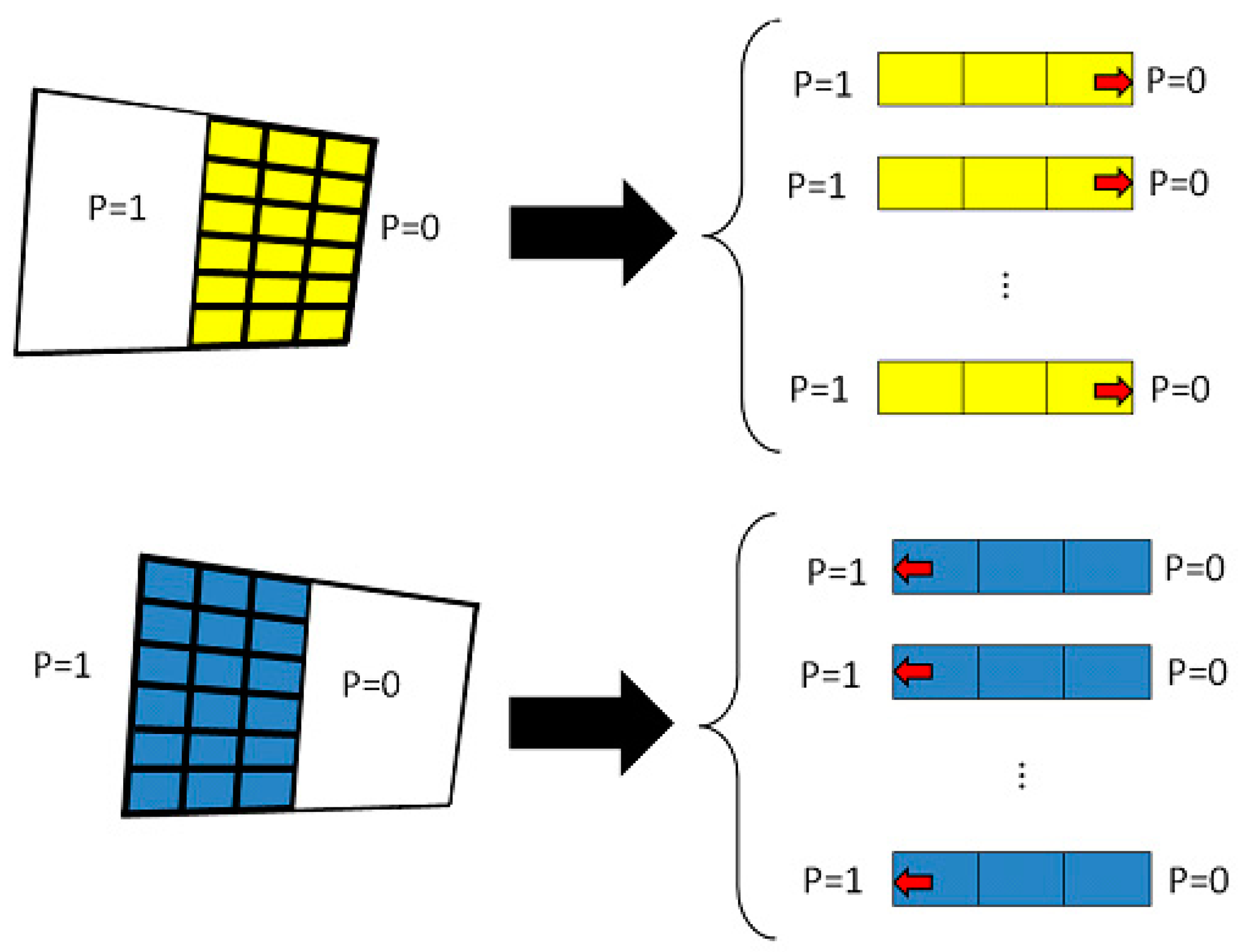
2.3.1. Implementation of the Lower Bound Transmissibility
2.3.2. Implementation of the Upper Bound Transmissibility
- is the arithmetic mean of the permeability for each slice perpendicular to the considered direction. The upper bound of the admissible permeability value and the exact value for a stratified medium considering a parallel flow is given by arithmetic mean of the permeability values;
- is a normalized vector through each cell;
- is the sum of the areas of the interfaces of the high-resolution geological cells;
- is the arithmetic mean of the vector connecting the centers of each high-resolution geological cell with the center of the interface.
2.4. Quality Control of the Upscaling and Gridding
- For cells with : .
- For cells with : reconsidering of gridding.
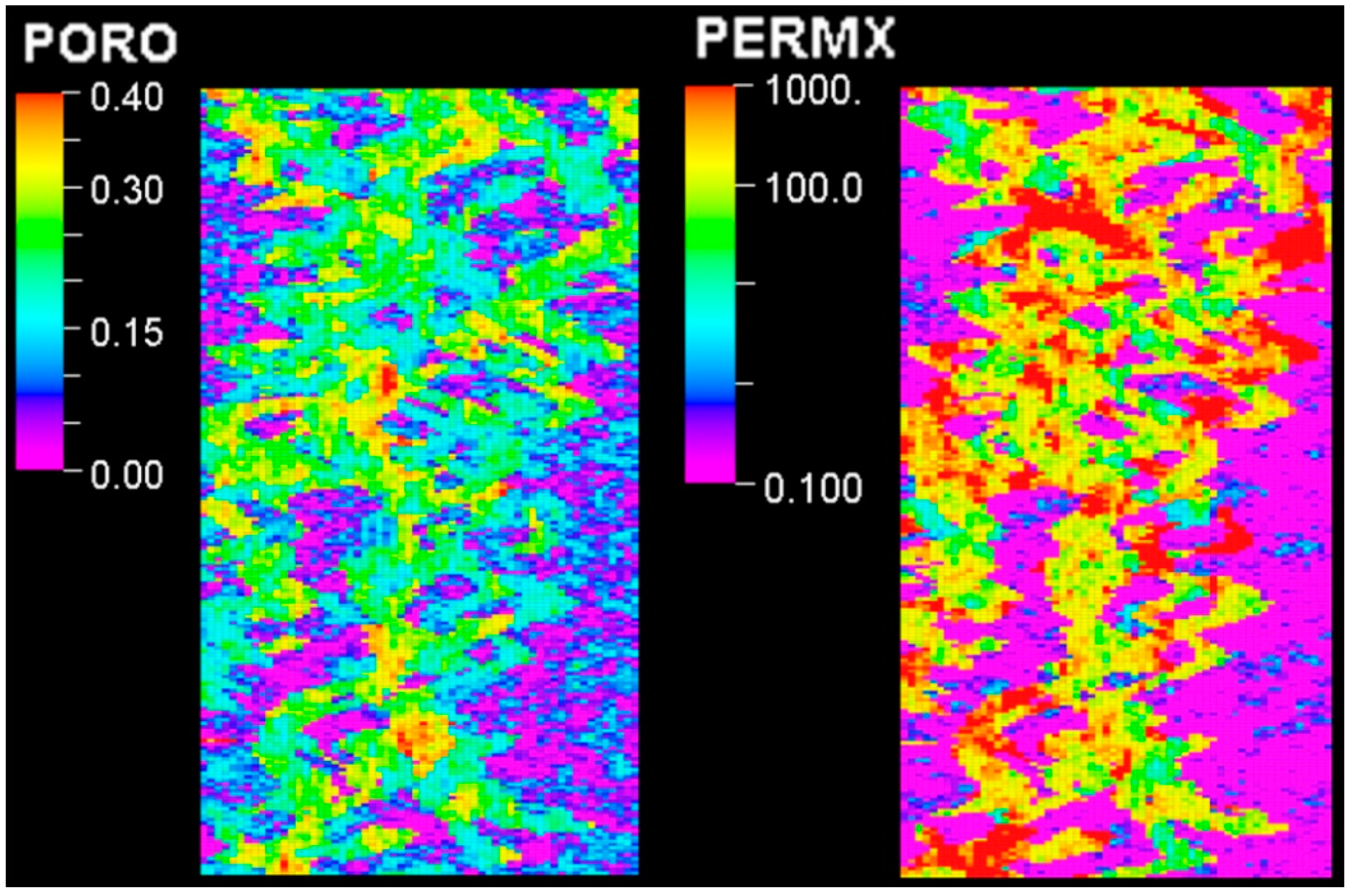
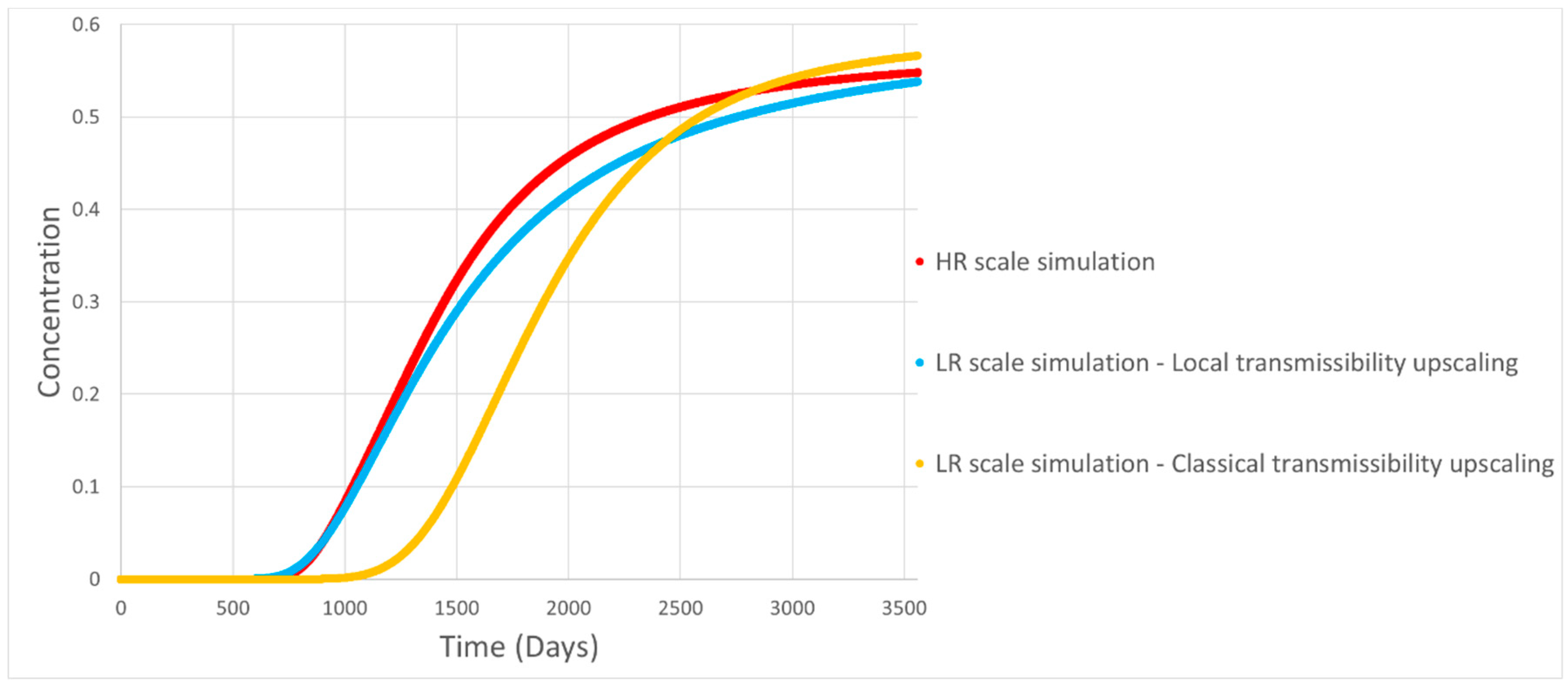
3. Application to the SPE-10 Model
4. Conclusions
- (1)
- This approach is more accurate than classical transmissibility upscaling method based on flow simulation;
- (2)
- This approach keeps the contrast of transmissibility values observed at the high-resolution geological scale and improves the accuracy of field-scale flow simulation for highly heterogeneous reservoirs;
- (3)
- The upper and lower bounds delivered by the algebraic method allow checking the quality of the upscaling and the gridding.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| the matrix containing the transmissibility values terms | |
| the vector containing the boundary condition terms | |
| the domain: Right, Left, North, South, Top or Bottom | |
| the opposite domain of the domain | |
| the cell permeability value in the direction α () | |
| the number of geological cells at the interface between the two reservoir cells | |
| the number of cells in each 1D system | |
| a normal vector going through the center of a face | |
| the pressure in the cell () | |
| the high-resolution scale flux () | |
| the Darcy’s flux at the interface of the cells and () | |
| a vector connecting the center of the cell with the center of the interface | |
| the cell interface area between the cells A and B () | |
| the surface area between the cell A and the connected cells on the domain () | |
| the upper estimated bound value for the transmissibility () | |
| the lower estimated bound value for the transmissibility () | |
| the lower bound half-transmissibility value () | |
| the upper bound half-transmissibility value () | |
| the vector containing the pressure unknown | |
| the large reservoir cell index | |
| the half-transmissibility value for the cell () |
References
- Corvi, P.; Heffer, K.; King, P.; Tyson, S.; Verly, G.; Ehlig-Economides, C.; Le Nir, I.; Ronen, S.; Shultz, P.; Corbett, P.; et al. Reservoir characterization using expert knowledge, data and statistics. Oilfield Rev. 1992, 4, 25–31. [Google Scholar]
- Sbaï, A.; Amraoui, N. Development and application of diagnostic tools for seawater intrusion analysis in highly heterogeneous coastal aquifers. In E3S Web of Conferences; EDP Sciences: Ullis, France, 2018; Volume 54. [Google Scholar]
- Mansoori, J. A Review of Basic Upscaling Procedures: Advantages and Disadvantages; The American Association of Petroleum Geologists: Tulsa, OK, USA, 1994; pp. 65–74. [Google Scholar]
- Kumar, A.; Noh, M.H.; Ozah, R.C.; Pope, G.A.; Bryant, S.L.; Sepehrnoori, K.; Lake, L.W. Reservoir simulation of CO2 storage in aquifers. SPE J. 2005, 10, 336–348. [Google Scholar] [CrossRef]
- Liang, Y.; Wen, B.; Hesse, M.A.; DiCarlo, D. Effect of dispersion on solutal convection in porous media. Geophys. Res. Lett. 2018, 45, 9690–9698. [Google Scholar] [CrossRef]
- Christie, M.A. Upscaling for Reservoir Simulation; Society of Petroleum Engineers: St. John’s, NL, Canada, 1996. [Google Scholar] [CrossRef]
- Renard, Ph.; De Marsily, G. Calculating equivalent permeability: A review. Adv. Water Resour. 1997, 20, 253–278. [Google Scholar] [CrossRef]
- Durlofsky, J. Upscaling of geocellular models for reservoir flow simulation: A review of recent progress. In Proceedings of the 7th International Forum on Reservoir Simulation Bühl, Baden-Baden, Germany, 12–27 June 2003. [Google Scholar]
- Nœtinger, B.; Vincent, A.; Ghassem, Z. The future of stochastic and upscaling methods in hydrogeology. Hydrogeol. J. 2005, 13, 184–201. [Google Scholar] [CrossRef]
- King, P.R. The use of renormalization for calculating effective permeability. Transp. Porous Media 1989, 4, 37–58. [Google Scholar] [CrossRef]
- Guérillot, D.; Rudkiewicz, J.L.; Ravenne, C.; Renard, G.; Galli, A. An integrated model for computer aided reservoir description: From outcrop study to fluid flow simulations. Revue de l’Institut français du pétrole 1990, 45, 71–77. [Google Scholar] [CrossRef]
- Gallouët, T.; Guérillot, D. An optimal method for averaging the absolute permeability. In Proceedings of the International Reservoir Characterization Technical Conference, Tulsa, OK, USA, 3–5 November 1991. [Google Scholar]
- Gallouët, T.; Guérillot, D. Averaged Heterogeneous Porous Media by Minimisation of the Error on the Flow Rate. In Proceedings of the ECMOR IV—4th European Conference on the Mathematics of Oil Recovery, Roros, Norway, 7–10 June 1994. [Google Scholar]
- Terpolilli, P.; Hontans, T. Boundary effects in the upscaling of absolute permeability–A new approach. In Proceedings of the ECMOR VII—7th European Conference on the Mathematics of Oil Recovery, Baveno, Italy, 5–8 September 2000. [Google Scholar]
- Samier, P. A Finite Element Method for Calculating Transmissibilities in N-point Difference Equations using a Non-Diagonal Permeability Tensor. In Proceedings of the ECMOR II—2nd European Conference on the Mathematics of Oil Recovery, Arles, France, 11–14 September 1990. [Google Scholar]
- Ding, Y.; Urgelli, D. Upscaling of transmissibility for field scale flow simulation in heterogeneous media. In Proceedings of the Proceedings of the SPE Symposium on Reservoir Simulation, Dallas, TX, USA, 8–11 June 1997. [Google Scholar]
- Urgelli, D. Upscaling of Transmissibility Applied to Corner Point Geometry; Society of Petroleum Engineers: St. John’s, NL, Canada, 1998. [Google Scholar] [CrossRef]
- Wang, W.; Gupta, A. Transmissibility Scale-up In Reservoir Simulation; Petroleum Society of Canada: St. John’s, NL, Canada, 1999. [Google Scholar] [CrossRef]
- Panfili, P.; Cominelli, A.; Calabrese, M.; Albertini, C.; Savitskiy, A.; Leoni, G. Advanced upscaling for Kashagan reservoir modeling. SPE Reserv. Eval. Eng. 2012, 15, 150–164. [Google Scholar] [CrossRef]
- Albertini, M.; Prisco, M.; Villa, F.; Kolyubaeva, O.; Stefanucci, M. High-Resolution Reservoir Simulator and Transmissibility Upscaling as a Key to Reservoir Modelling Optimization in an Extra-Heavy Oil Field. Proccedings of the Offshore Mediterranean Conference, Ravenna, Italy, 29–31 March 2017. [Google Scholar]
- Qi, D.; Hesketh, T. Quantitative Evaluation of Information Loss in Reservoir Upscaling; Society of Petroleum Engineers: St. John’s, NL, Canada, 2004. [Google Scholar] [CrossRef]
- Sablok, R.; Aziz, K. Upscaling and Discretization Errors in Reservoir Simulation; Society of Petroleum Engineers: St. John’s, NL, Canada, 2005. [Google Scholar] [CrossRef]
- Ganjeh-Ghazvini, M.; Masihi, M.; Baghalha, M. Study of heterogeneity loss in upscaling of geological maps by introducing a cluster-based heterogeneity number. Phys. A Stat. Mech. Appl. 2015, 436, 1–13. [Google Scholar] [CrossRef]
- Preux, C. About the use of quality indicators to reduce information loss when performing upscaling. Oil Gas Sci. Technol.–Revue d’IFP Energies nouvelles. 2016, 71, 7. [Google Scholar] [CrossRef]
- Preux, C.; Le Ravalec, M.; Enchéry, G. Selecting an appropriate upscaled reservoir model based on connectivity analysis. Oil Gas Sci. Technol.–Revue d’IFP Energies nouvelles 2016, 71, 60. [Google Scholar] [CrossRef][Green Version]
- Christie, M.A.; Blunt, M.J. Tenth SPE Comparative Solution Project: A Comparison of Upscaling Techniques; Society of Petroleum Engineers: St. John’s, NL, Canada, 2001. [Google Scholar]
- Kfoury, M.; Ababou, R.; Noetinger, B.; Quintard, M. Upscaling fractured heterogeneous media: Permeability and mass exchange coefficient. J. Appl. Mech. 2006, 73, 41–46. [Google Scholar] [CrossRef]
- Vitel, S.; Souche, L. Unstructured upgridding and transmissibility upscaling for preferential flow paths in 3D fractured reservoirs. In SPE Reservoir Simulation Symposium; Society of Petroleum Engineers: St. John’s, NL, Canada, 2007. [Google Scholar] [CrossRef]
- Lemonnier, P.; Bernard, B. Simulation of naturally fractured reservoirs. state of the art-part 1–physical mechanisms and simulator formulation. Oil Gas Sci. Technol.–Revue de l’Institut Français du Pétrole 2010, 65, 239–262. [Google Scholar] [CrossRef]
- Lemonnier, P.; Bourbiaux, B. Simulation of naturally fractured reservoirs. state of the art-Part 2–matrix-fracture transfers and typical features of numerical studies. Oil Gas Sci. Technol.–Revue de l’Institut Français du Pétrole 2010, 65, 263–286. [Google Scholar] [CrossRef]

| Wells | I-Coordinate | J-Coordinate |
|---|---|---|
| Injector | 3 | 3 |
| Producer | 58 | 218 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guérillot, D.; Bruyelle, J. Transmissibility Upscaling on Unstructured Grids for Highly Heterogeneous Reservoirs. Water 2019, 11, 2647. https://doi.org/10.3390/w11122647
Guérillot D, Bruyelle J. Transmissibility Upscaling on Unstructured Grids for Highly Heterogeneous Reservoirs. Water. 2019; 11(12):2647. https://doi.org/10.3390/w11122647
Chicago/Turabian StyleGuérillot, Dominique, and Jérémie Bruyelle. 2019. "Transmissibility Upscaling on Unstructured Grids for Highly Heterogeneous Reservoirs" Water 11, no. 12: 2647. https://doi.org/10.3390/w11122647
APA StyleGuérillot, D., & Bruyelle, J. (2019). Transmissibility Upscaling on Unstructured Grids for Highly Heterogeneous Reservoirs. Water, 11(12), 2647. https://doi.org/10.3390/w11122647






