Feasibility of Multi-Year Forecast for the Colorado River Water Supply: Time Series Modeling
Abstract
1. Introduction
2. Materials and Methods
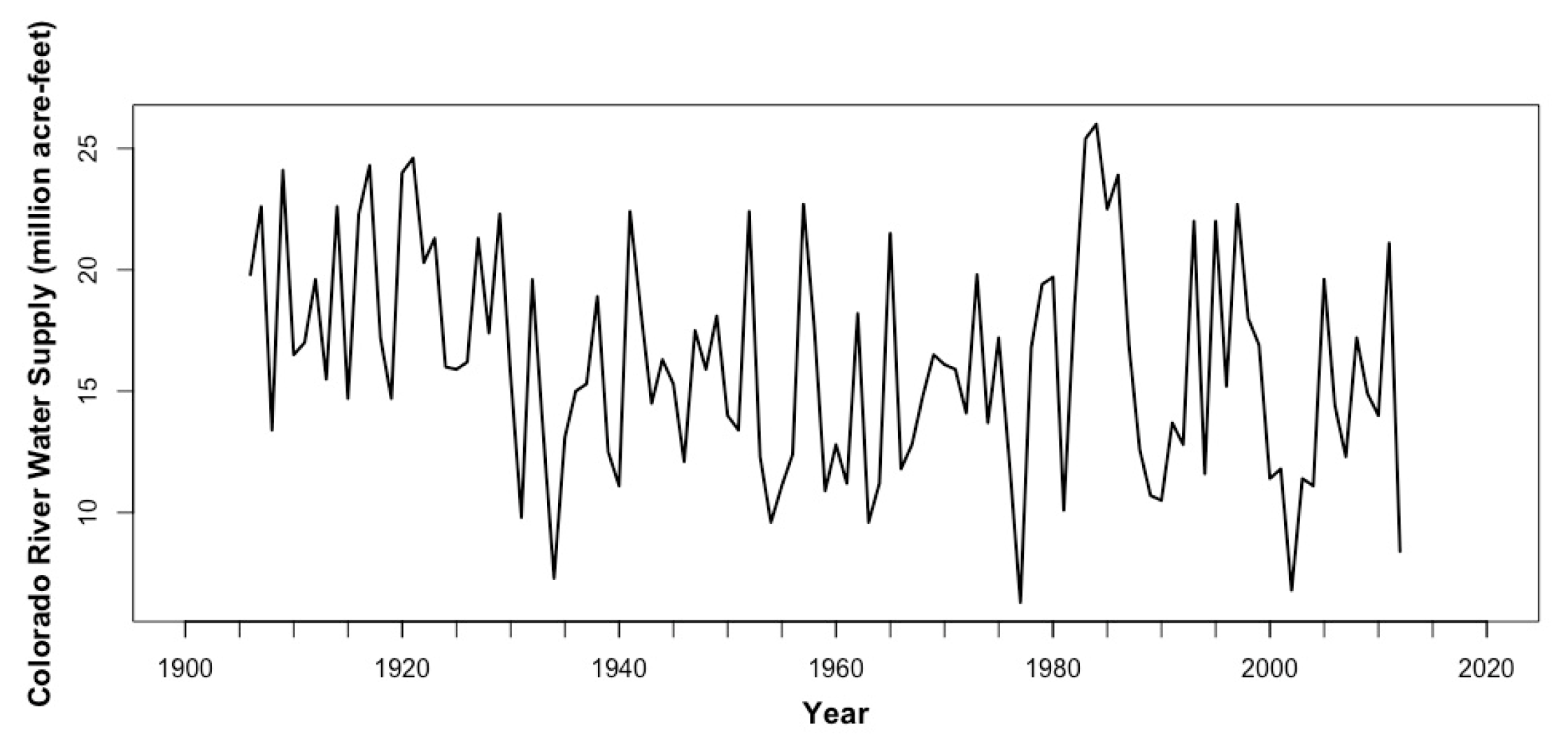
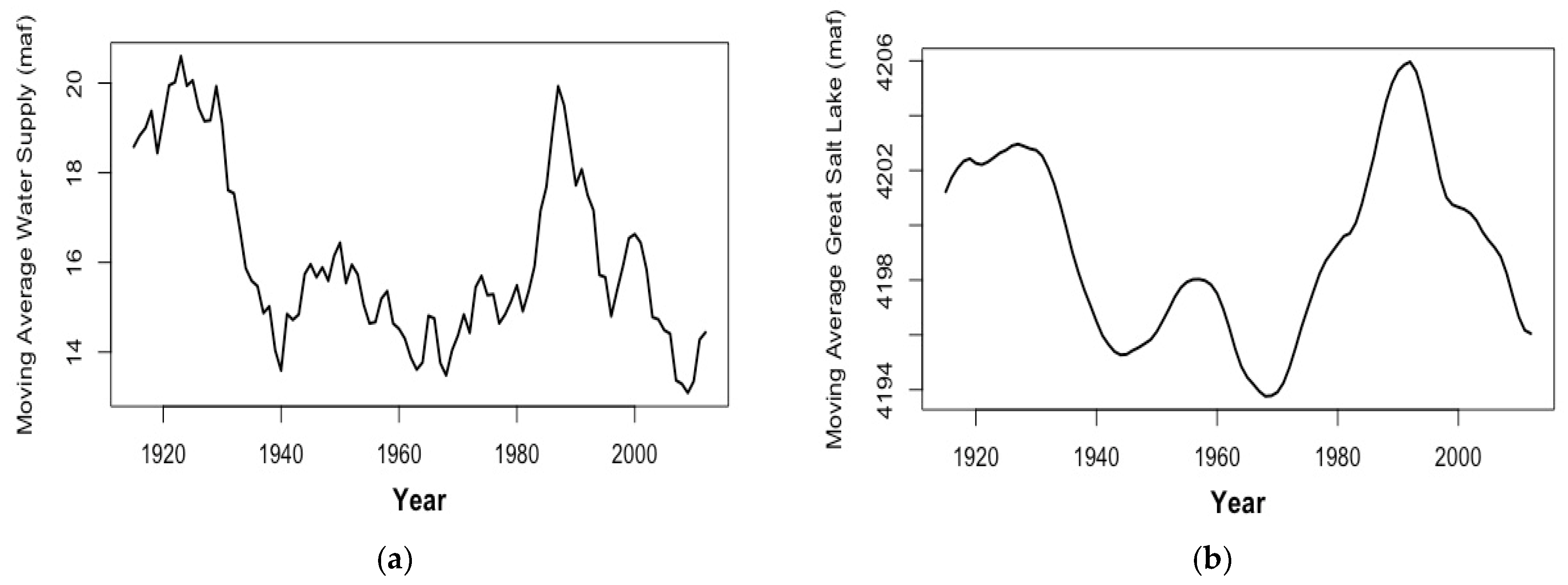
2.1. Data and Methodology
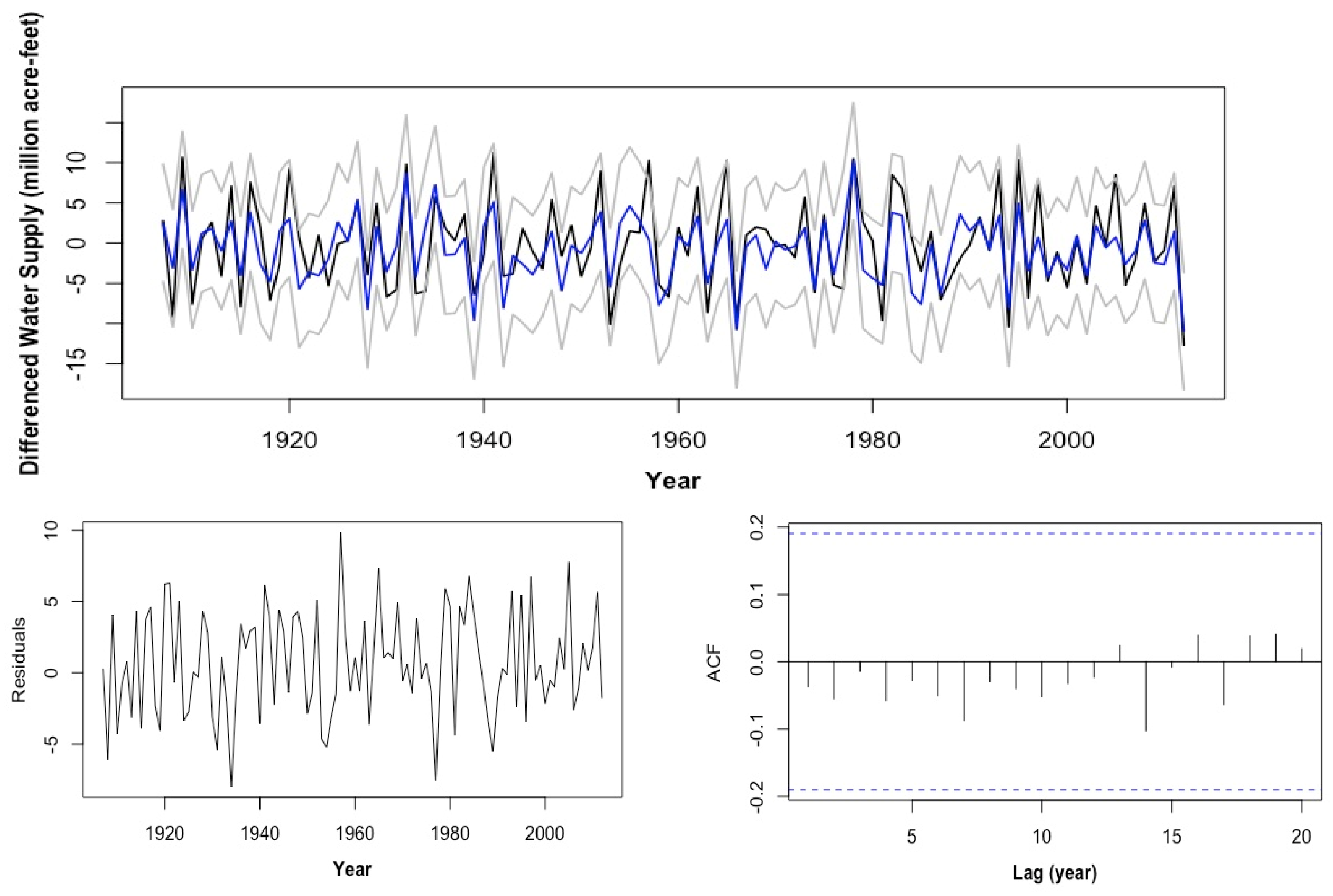
2.2. Univariate Time Series Models
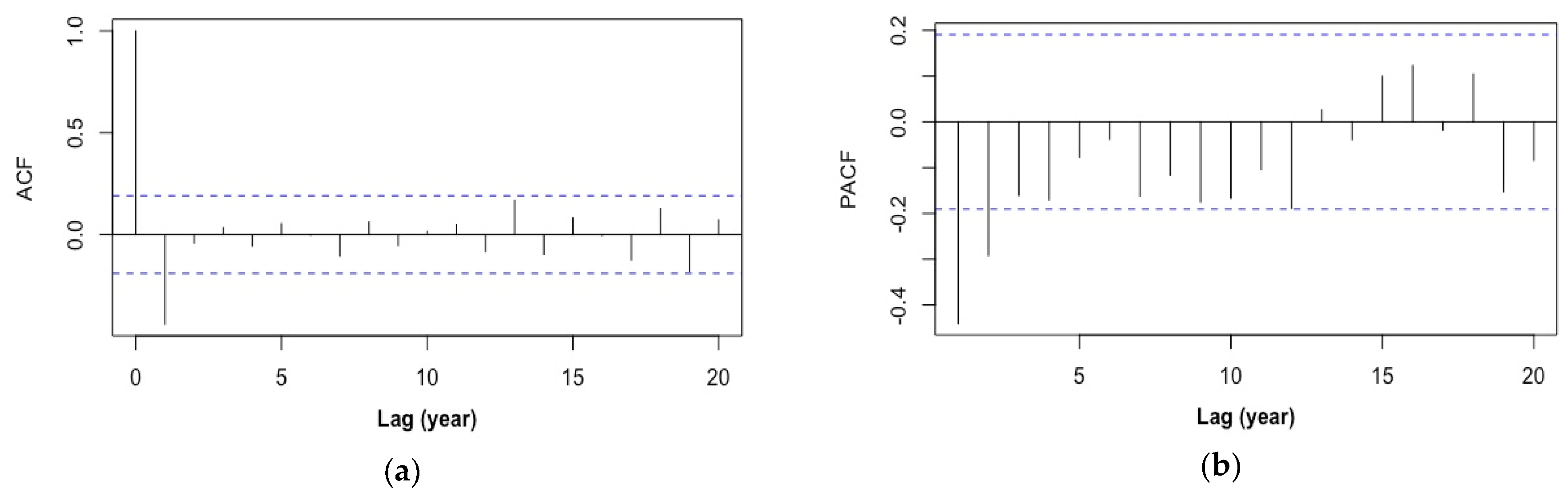
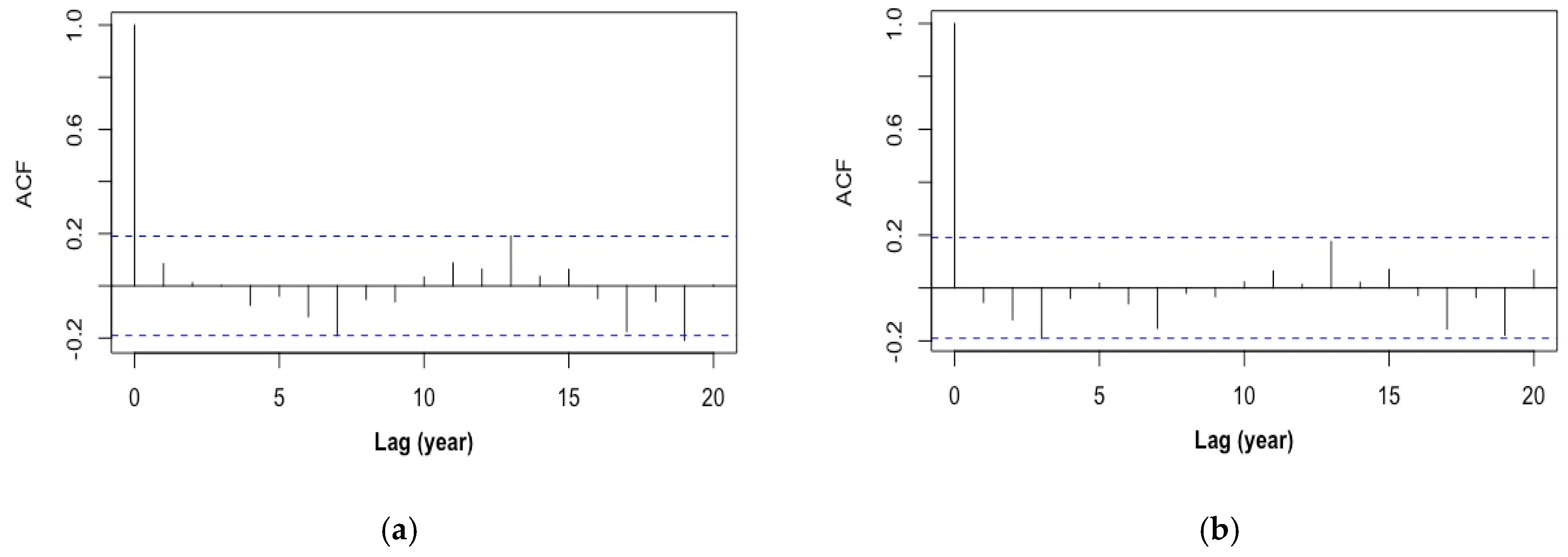
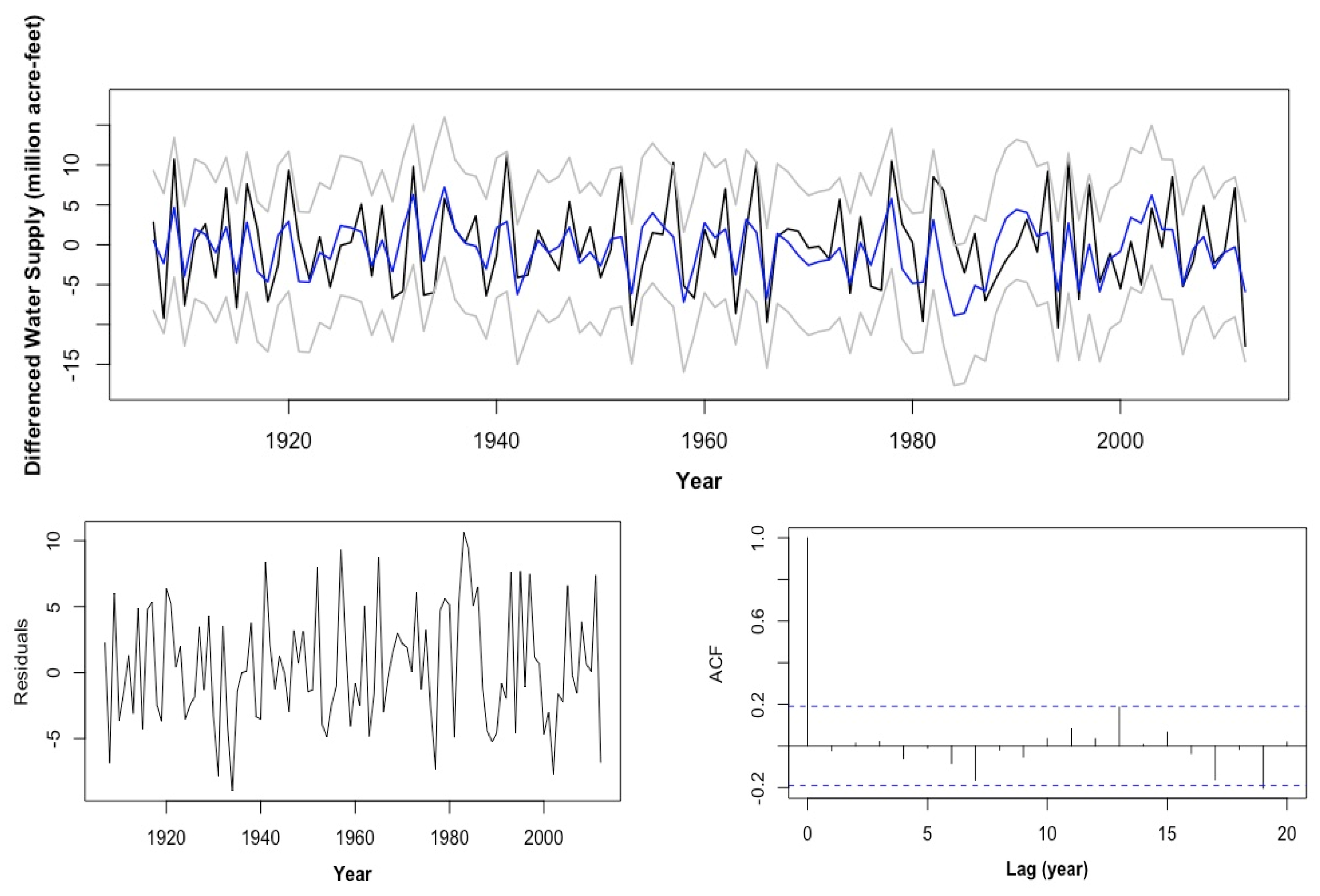
2.2.1. ARMA (1, 1)
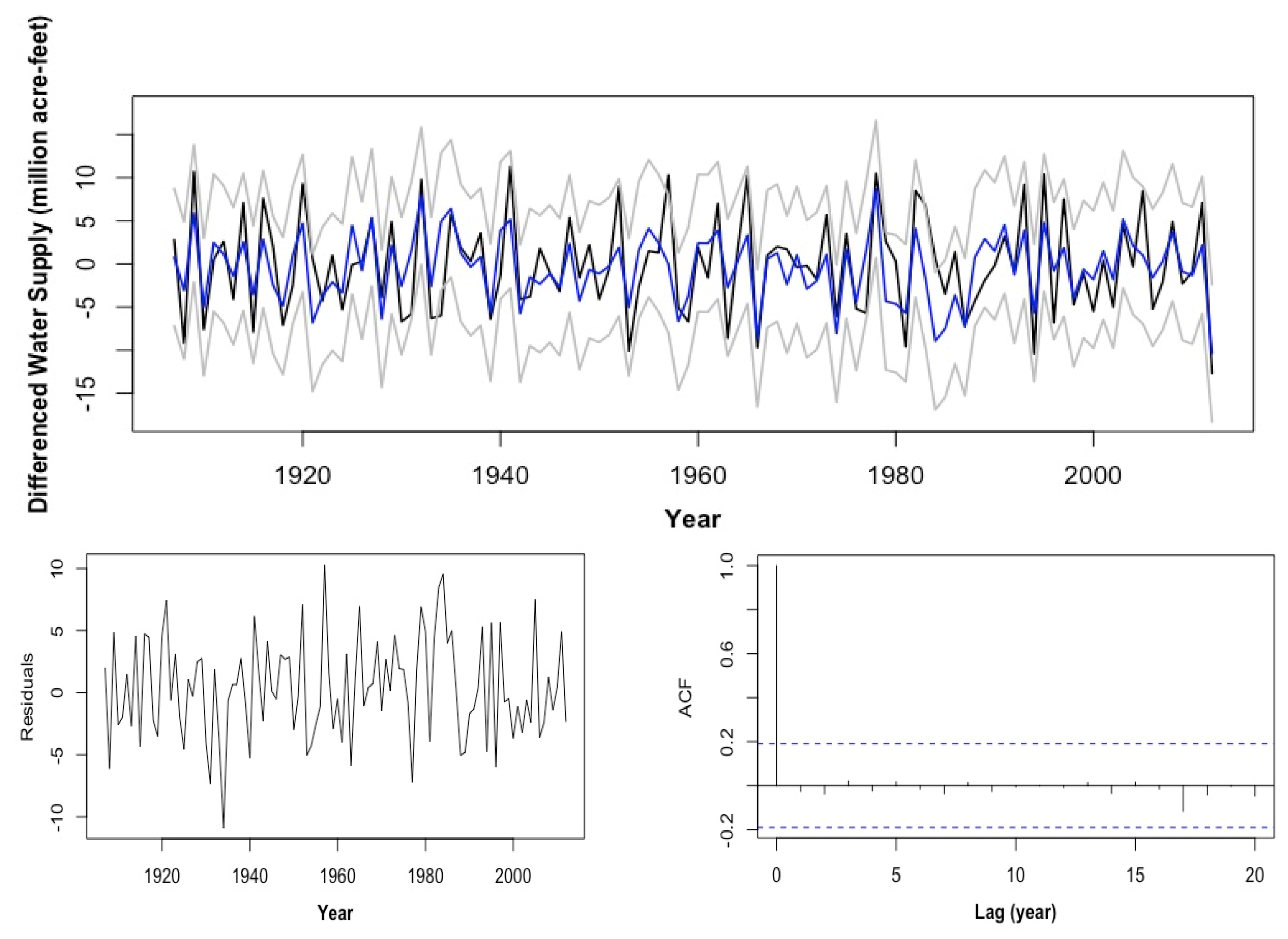
2.2.2. Sparse AR (19)
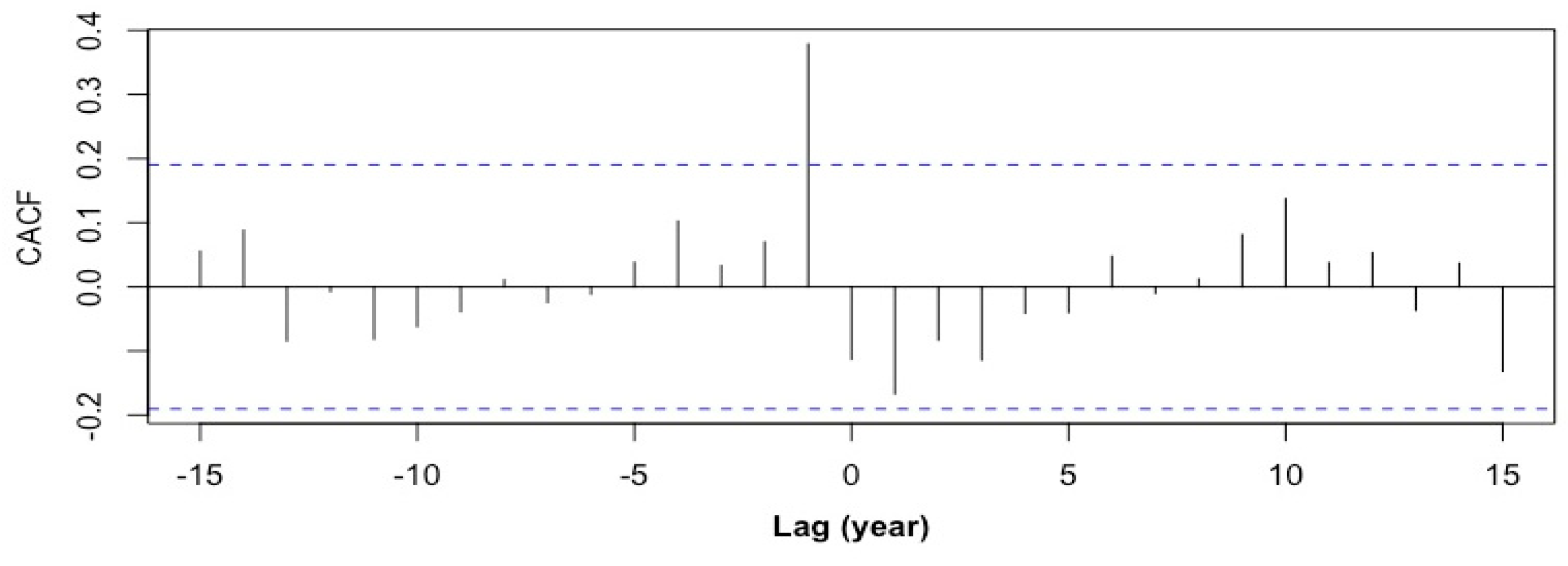
2.3. ARMA Models with Exogenous Variables
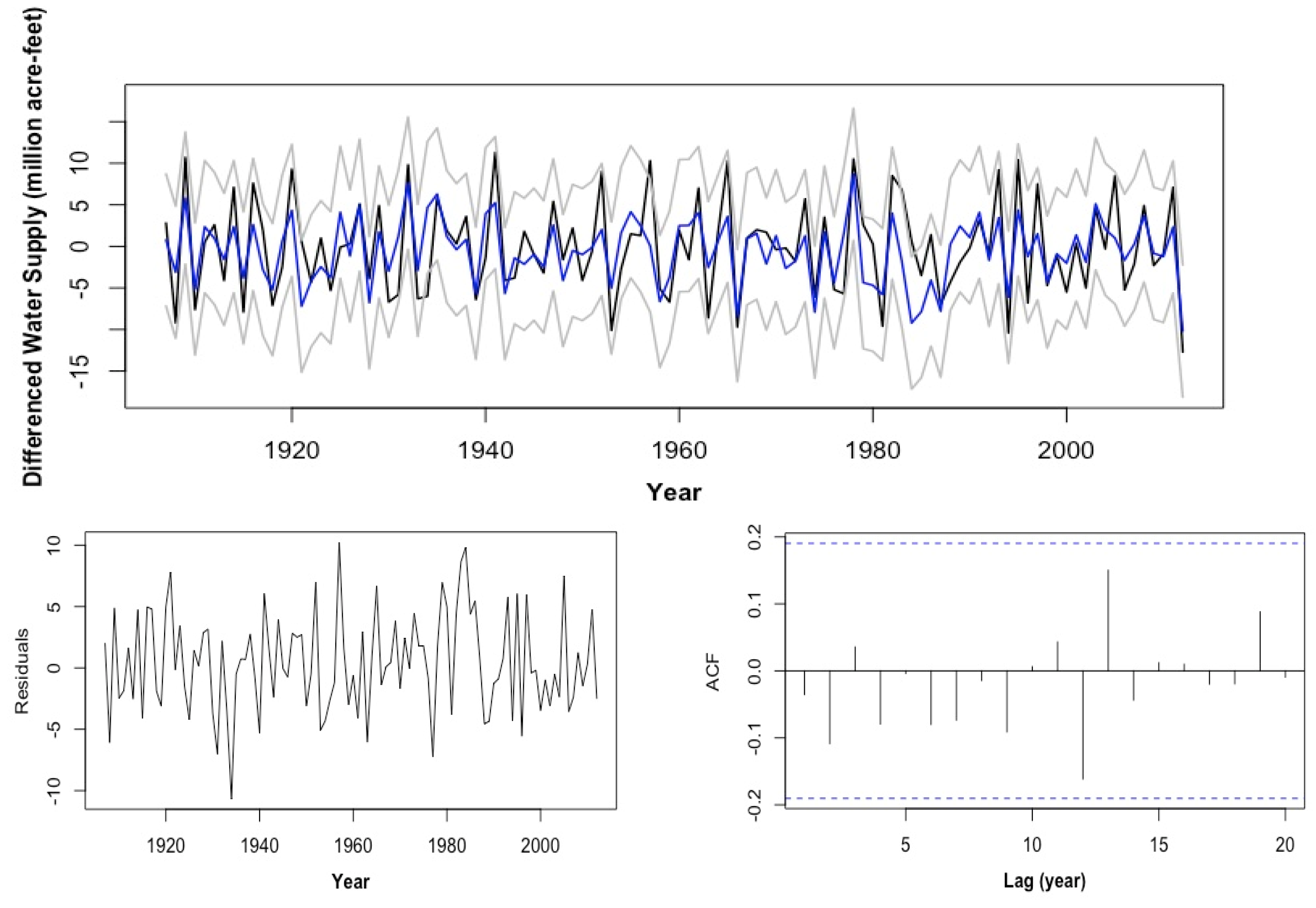
2.3.1. SARX (19, 1, 0)
2.3.2. ARMAX (19, 1, 2, 0)
2.4. Cross-Validation
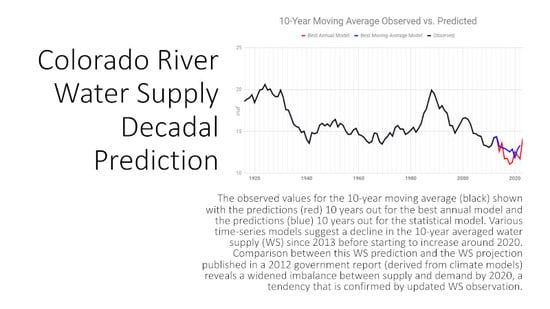
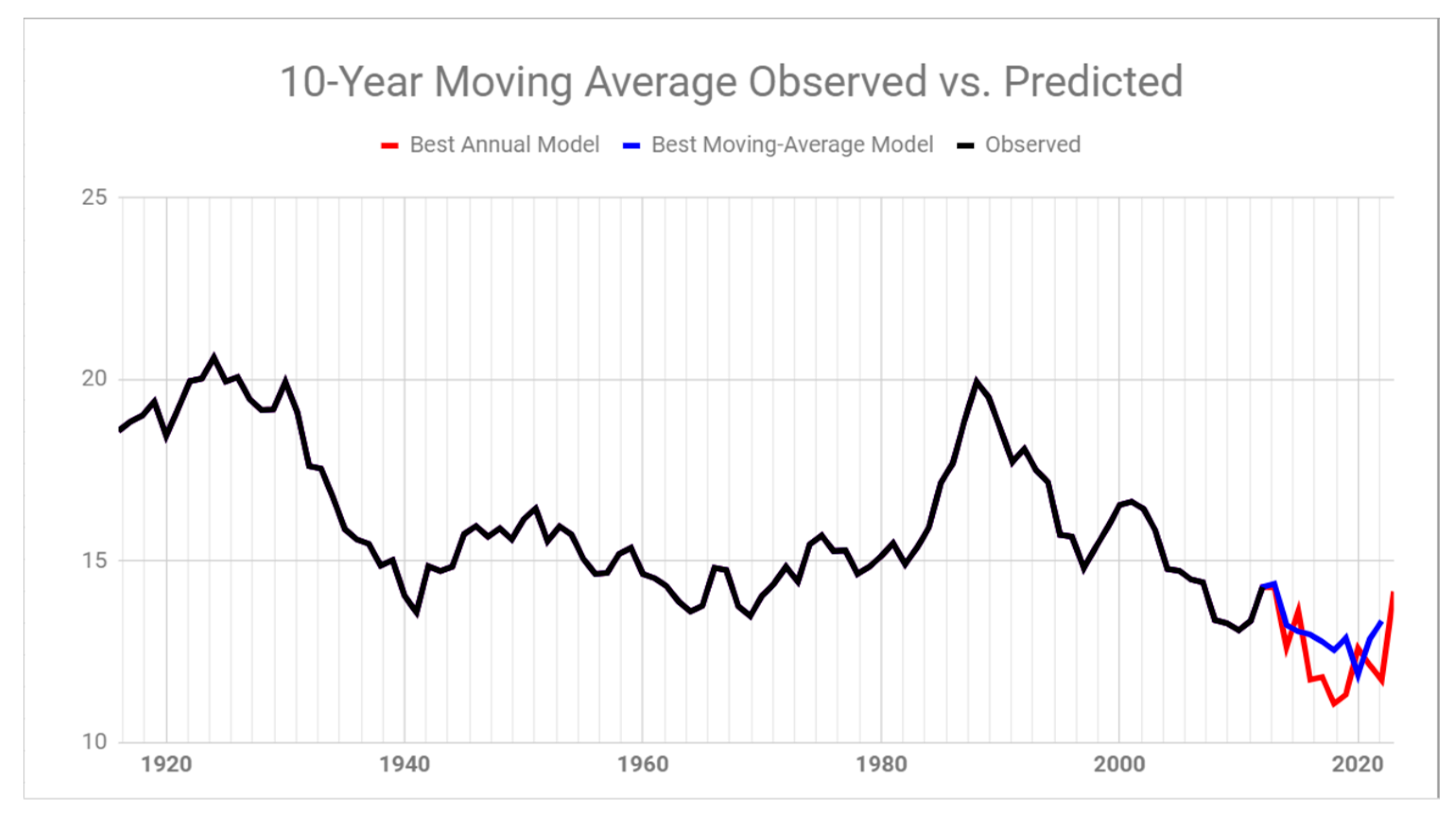
2.5. Benchmark Modeling Using the 10-Year Moving-Average Data
- Ten-Year Moving-Average Univariate Model AR (19)The best univariate model chosen for the 10-year moving-average WS is an AR (19) model; this is consistent with the raw-data model in Section 2.2. The fitted model iswhere is a white-noise process with an estimated variance of 0.1946.
- Ten-Year Moving-Average ARMAX (13, 10, 7, 0)One of the ARMAX models chosen had an ARMA (13, 10) base, and it includes 7 GSL elevation lags. The model equation iswhere is a white noise process with an estimated variance of 0.2051.
- Ten-Year Moving-Average ARMAX (19, 10, 7, 0)The other competitive ARMAX model for the ten-year moving-average WS also included 7 GSL lags and had an ARMA (19, 10) base. The equation is estimated aswhere is a white noise process with an estimated variance of 0.2018.
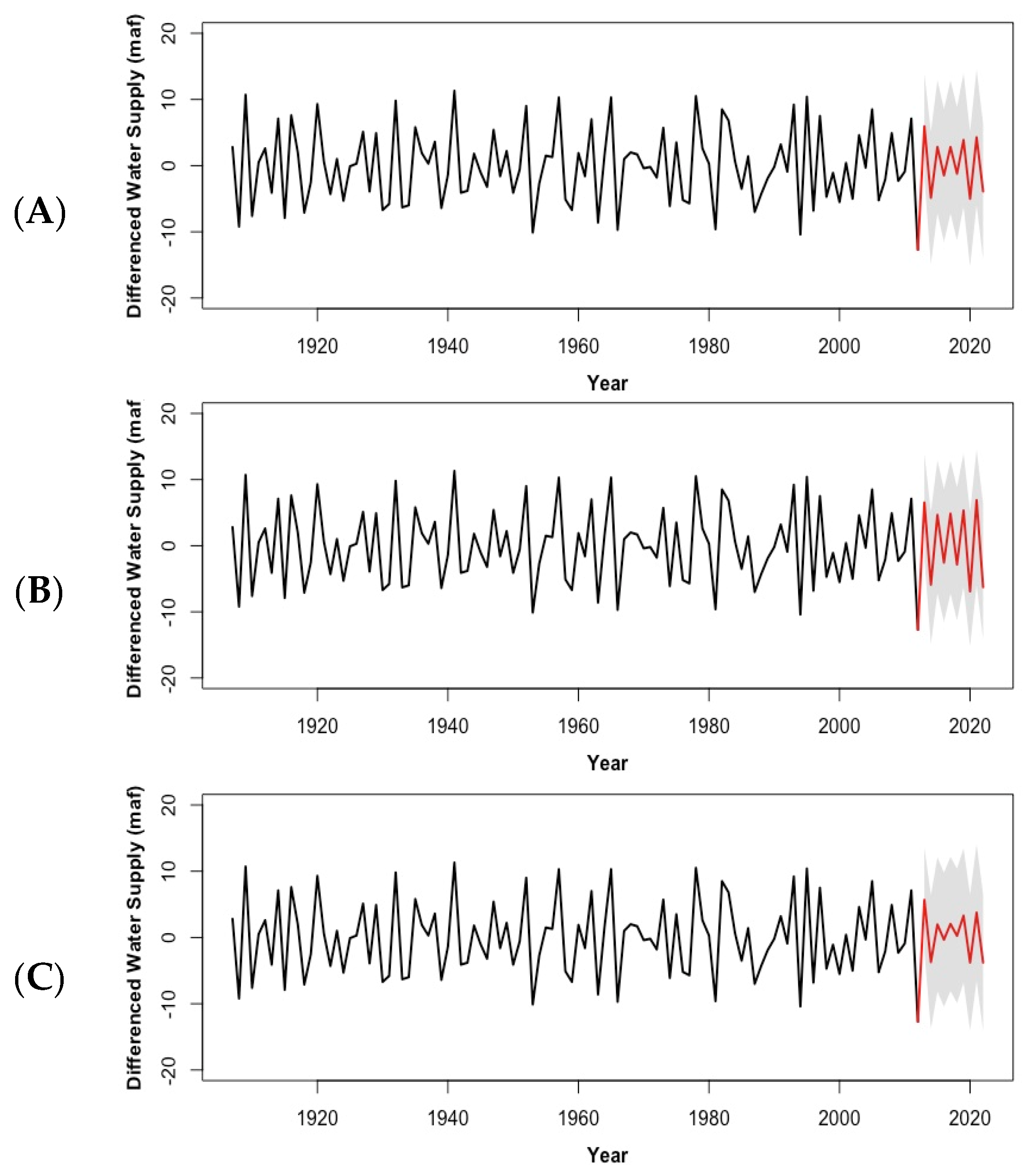
3. Prediction Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Colorado River Research Group. It’s Hard to Fill a Bathtub when the Drain is Wide Open: The Case of Lake PowellRep; CRRG: Boulder, CO, USA, 2018. [Google Scholar]
- Barnett, T.P.; Pierce, D.W. When will Lake Mead go dry? Water Resour. Res. 2008, 44, W03201. [Google Scholar] [CrossRef]
- McCabe, G.J.; Wolock, D.M. Warming may create substantial water supply shortages in the Colorado River basin. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Udall, B.; Overpeck, J. The twenty-first century Colorado River hot drought and implications for the future. Water Resour. Res. 2017, 53, 2404–2418. [Google Scholar] [CrossRef]
- BOR. Colorado River Basin Water Supply and Demand Study; BOR: Washington, DC, USA, 2012; p. 34. [Google Scholar]
- Gangopadhyay, S.; McCabe, G.J. Predicting regime shifts in flow of the Colorado River. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Gillies, R.R.; Chung, O.-Y.; Shen, C. Cross-Basin Decadal Climate Regime Connecting the Colorado River with the Great Salt Lake. J. Hydrometeorol. 2018, 19, 659–665. [Google Scholar] [CrossRef]
- Lall, U.; Mann, M.E. The Great Salt Lake: A barometer of low-frequency climatic variability. Water Resour. Res. 1995, 31, 2503–2515. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Gillies, R.R.; Jin, J.; Hipps, L.E. Coherence between the Great Salt Lake Level and the Pacific Quasi-Decadal Oscillation. J. Clim. 2010, 23, 2161–2177. [Google Scholar] [CrossRef]
- Gillies, R.R.; Chung, O.Y.; Wang, S.Y.S.; DeRose, R.J.; Sun, Y. Added value from 576 years of tree-ring records in the prediction of the Great Salt Lake level. J. Hydrol. 2015, 529, 962–968. [Google Scholar] [CrossRef]
- Gillies, R.R.; Chung, O.Y.; Wang, S.Y.S.; DeRose, R.J.; Sun, Y. Incorporation of Pacific SSTs in a time series model towards a longer-term forecast for the Great Salt Lake elevation. J. Hydrometeorol. 2011, 12, 474–480. [Google Scholar] [CrossRef]
- Neri, A.; Villarini, G.; Salvi, K.A.; Slater, L.J.; Napolitano, F. On the decadal predictability of the frequency of flood events across the US Midwest. Int. J. Climatol. 2019, 39, 1796–1804. [Google Scholar] [CrossRef]
- Wang, S.Y.; Hakala, K.; Gillies, R.R.; Capehart, W.J. The Pacific quasi-decadal oscillation (QDO): An important precursor toward anticipating major flood events in the Missouri River Basin? Geophys. Res. Lett. 2014, 41, 991–997. [Google Scholar] [CrossRef]
- Brockwell, P.; Davis, R.A. Introduction to Time Series and Forecasting, 2nd ed.; Springer: Berlin, Germany, 2002. [Google Scholar]
- Brockwell, P.; Davis, R.A. Time Series: Theory and Methods, 2nd ed.; Springer: Berlin, Germany, 1991. [Google Scholar]
- Cryer, J.D.; Chan, K.S. Time Series Analysis with Applications in R, 2nd ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Akaike, H. Fitting autoregressive models for prediction. Ann. Inst. Stat. Math. 1969, 21, 243–247. [Google Scholar] [CrossRef]
- Sang, H.; Sun, Y. Simultaneous sparse model selection and coefficient estimation for heavy-tailed autoregressive processes. Statistics 2015, 49, 187–208. [Google Scholar] [CrossRef]
- Murphy, A.H. Skill scores based on the mean squared error and their relationships to the correlation coefficient. Mon. Weather Rev. 1988, 116, 2417–2424. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Gillies, R.R.; Reichler, T. Multi-decadal drought cycles in the Great Basin recorded by the Great Salt Lake: Modulation from a transition-phase teleconnection. J. Clim. 2012, 25, 1711–1721. [Google Scholar] [CrossRef]
- O’Connor, R. Colorado River Basin Story Map Highlights Importance of Managing Water below the Ground. Available online: http://blogs.edf.org/growingreturns/2019/10/24/colorado-river-basin-story-map-highlights-importance-of-managing-water-below-the-ground/ (accessed on 24 October 2019).
- Fang, K.; Shen, C. Full-flow-regime storage-streamflow correlation patterns provide insights into hydrologic functioning over the continental US. Water Resour. Res. 2017, 53, 7499–8314. [Google Scholar] [CrossRef]
- Pagano, T.C.; Garen, D.C.; Perkins, T.R.; Pasteris, P.A. Daily Updating of Operational Statistical Seasonal Water Supply Forecasts for the Western US. JAWRA J. Am. Water Resour. Assoc. 2009, 45, 767–778. [Google Scholar] [CrossRef]
- Dai, A. The influence of the Inter-decadal Pacific Oscillation on US precipitation during 1923–2010. Clim. Dyn. 2012, 41, 633–646. [Google Scholar] [CrossRef]
- Smith, K.; Strong, C.; Wang, S.-Y. Connectivity between historical Great Basin precipitation and Pacific Ocean variability: A CMIP5 model evaluation. J. Clim. 2015, 28, 6096–6112. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Gillies, R.R.; Jin, J.; Hipps, L.E. Recent rainfall cycle in the Intermountain Region as a quadrature amplitude modulation from the Pacific decadal oscillation. Geophys. Res. Lett. 2009, 36, L02705. [Google Scholar] [CrossRef]
- Switanek, M.B.; Troch, P.A. Decadal prediction of Colorado River streamflow anomalies using ocean-atmosphere teleconnections. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Lehner, F.; Wood, A.W.; Llewellyn, D.; Blatchford, D.B.; Goodbody, A.G.; Pappenberger, F. Mitigating the impacts of climate nonstationarity on seasonal streamflow predictability in the US southwest. Geophys. Res. Lett. 2017, 44, 12–208. [Google Scholar] [CrossRef]
- Bedford, D. The Great Salt Lake America’s Aral Sea? Environ. Sci. Policy Sustain. Dev. 2009, 51, 8–21. [Google Scholar] [CrossRef]
- Mohammed, I.N.; Tarboton, D.G. An examination of the sensitivity of the Great Salt Lake to changes in inputs. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Hakala, K. Climate Forcings on Groundwater Variations in Utah and the Great Basin. Master’s Thesis, Utah State University, Logan, UT, USA, 2014. [Google Scholar]
- Masbruch, M.D.; Rumsey, C.A.; Gangopadhyay, S.; Susong, D.D.; Pruitt, T. Analyses of infrequent (quasi-decadal) large groundwater recharge events in the northern Great Basin: Their importance for groundwater availability, use, and management. Water Resour. Res. 2016, 52, 7819–7836. [Google Scholar] [CrossRef]
- Ayers, J.; Ficklin, D.L.; Stewart, I.T.; Strunk, M. Comparison of CMIP3 and CMIP5 projected hydrologic conditions over the Upper Colorado River Basin. Int. J. Climatol. 2016, 36, 3807–3818. [Google Scholar] [CrossRef]
| RMSE | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ARMA | 5.0708 | 6.9829 | 6.9649 | 6.9612 | 6.945 | 6.9467 | 6.9728 | 6.9438 | 6.9472 | 6.9208 |
| SAR | 2.8673 | 4.4851 | 4.5344 | 4.319 | 4.1826 | 4.1037 | 4.318 | 5.1207 | 5.2668 | 5.2246 |
| SARX | 3.1274 | 4.3809 | 4.6646 | 4.157 | 3.7697 | 3.7116 | 4.1295 | 5.0421 | 5.1573 | 5.1757 |
| ARMAX | 2.877 | 4.3947 | 4.9787 | 5.1741 | 4.0544 | 3.9955 | 3.7328 | 4.4858 | 4.9159 | 6.2473 |
| SS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| ARMA | 0.4719 | −0.0107 | −0.0080 | 0.0029 | 0 | 0 | 0 | 0 | 0 | 0 |
| SAR | 0.8311 | 0.583 | 0.5727 | 0.6162 | 0.6373 | 0.651 | 0.6165 | 0.4562 | 0.4252 | 0.4301 |
| SARX | 0.7991 | 0.6022 | 0.5479 | 0.6444 | 0.7054 | 0.7145 | 0.6493 | 0.4727 | 0.4489 | 0.4407 |
| ARMAX | 0.83 | 0.5997 | 0.4849 | 0.4491 | 0.6592 | 0.6692 | 0.7134 | 0.5827 | 0.4993 | 0.1852 |
| RMSE | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| AR(19) | 0.5522 | 0.5374 | 0.547 | 0.4876 | 0.5062 | 0.4872 | 0.4805 | 0.4951 | 0.5087 | 0.4506 |
| ARMAX1 | 0.4152 | 0.4123 | 0.4079 | 0.4268 | 0.4297 | 0.4266 | 0.4316 | 0.4369 | 0.4315 | 0.4312 |
| ARMAX2 | 0.4153 | 0.419 | 0.4125 | 0.4197 | 0.4208 | 0.4181 | 0.4185 | 0.4231 | 0.4243 | 0.4265 |
| SS | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| AR(19) | 0.0181 | 0.0802 | 0.0541 | 0.2458 | 0.1811 | 0.235 | 0.2537 | 0.2091 | 0.1605 | 0.3391 |
| ARMAX1 | 0.445 | 0.4585 | 0.4739 | 0.4221 | 0.4099 | 0.4135 | 0.3977 | 0.3841 | 0.3959 | 0.3949 |
| ARMAX2 | 0.4448 | 0.4409 | 0.4621 | 0.4413 | 0.434 | 0.4367 | 0.4337 | 0.4223 | 0.416 | 0.4081 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plucinski, B.; Sun, Y.; Wang, S.-Y.S.; Gillies, R.R.; Eklund, J.; Wang, C.-C. Feasibility of Multi-Year Forecast for the Colorado River Water Supply: Time Series Modeling. Water 2019, 11, 2433. https://doi.org/10.3390/w11122433
Plucinski B, Sun Y, Wang S-YS, Gillies RR, Eklund J, Wang C-C. Feasibility of Multi-Year Forecast for the Colorado River Water Supply: Time Series Modeling. Water. 2019; 11(12):2433. https://doi.org/10.3390/w11122433
Chicago/Turabian StylePlucinski, Brian, Yan Sun, S.-Y. Simon Wang, Robert R. Gillies, James Eklund, and Chih-Chia Wang. 2019. "Feasibility of Multi-Year Forecast for the Colorado River Water Supply: Time Series Modeling" Water 11, no. 12: 2433. https://doi.org/10.3390/w11122433
APA StylePlucinski, B., Sun, Y., Wang, S.-Y. S., Gillies, R. R., Eklund, J., & Wang, C.-C. (2019). Feasibility of Multi-Year Forecast for the Colorado River Water Supply: Time Series Modeling. Water, 11(12), 2433. https://doi.org/10.3390/w11122433