Solution Approaches for the Management of the Water Resources in Irrigation Water Systems with Fuzzy Costs
Abstract
1. Introduction
1.1. Sustainability Concept in Water Systems
1.2. Political Context
1.3. Mathematical Programming Modelling Applied to Water Systems: Initial Overview
- Multistage stochastic programming: Some studies use this method. For example, the work in [21] developed an interval multistage water allocation model to optimize water allocation between different growth stages to obtain the maximum food production in reservoir irrigation systems characterized by inputs’ uncertainties. The study developed by [22] considered a fuzzy probability distribution based multistage stochastic robust programming method. This model supported regional water supply management. The developed model was applied to a water resources management system with three water users.
- Stochastic dynamic programming: Among the references analyzed and in order to show their applications, the work in [23] used stochastic dynamic programming to model a farmer’s choice whether to invest in a sprinkler irrigation system or in a more water efficient drip irrigation system under uncertainty. The work in [24] developed a stochastic dynamic programming model, but in this case, in the context of hydro-economic models to maximize irrigation benefits while minimizing the costs of power generation within a power market. The work in [25] also developed a stochastic dynamic programming model with fuzzy state variables for irrigation of multiple crops. This model, in which the reservoir storage and soil moisture of the crops are considered as fuzzy numbers and the reservoir inflow is considered as a stochastic variable, has the main objective of minimizing crop yield deficits, resulting in optimal water allocations to the crops by maintaining storage continuity and soil moisture balance.
- Inexact programming including fuzzy and interval based programming: The work in [26] formulated a fuzzy mathematical programming model for a multi-reservoir system applied to a three reservoir system in the Upper Cauvery River basin, South India. The study tried to minimize the sum of deviations of the irrigation withdrawals from their target demands, on a monthly basis, over a year. Another study developed an interval-fuzzy two stage stochastic quadratic programming model. The goal was to allocate the limited irrigation water to different crops, maximizing the net benefit under uncertainty and to analyze how water allocation schemes change under different climate change scenarios [27].
- Nonlinear programming: The work in [28] used a non-linear programming model to estimate farmers’ willingness-to-pay for irrigation water that maximizes revenue from crop production under different shortage levels. In this case, Monte Carlo simulation was implemented considering model parameters’ uncertainty to assess the variation of farmers’ willingness-to-pay and avoid water shortage [28]. Other authors used nonlinear programing for the optimization of profitability and productivity in an irrigation command area with conjunctive water use options [29].
- Multiobjective fuzzy linear programming: The work in [30] proposed a multiobjective fuzzy linear programming irrigation planning model for the evaluation of the management strategy in the case study of the Jayakwadi irrigation project, Maharashtra, India. Three conflicting objectives, net benefits, agricultural production, and labor employment, were considered in the irrigation planning scenario. However, the objectives pursued in this study are far from the main aim of the present research. In the same line, the work in [31] proposed a model of multiobjective fuzzy linear programming based on fuzzy parametric programming to solve the problem of optimal cropping pattern in an irrigation system. The objective of the irrigation planning model is to find out an optimal cropping pattern that maximizes simultaneously the net benefits, crop production, employment generation, and manure utilization.
1.4. Research Goals
2. Methodology
2.1. Formulation Model
- i ∈ I
- Procurement water sources of the water network
- m ∈ M
- Procurement methods
- t ∈ T
- Time periods; in this case, 8760 periods were considered (one year)
- k ∈ K
- Months in the year
- Set of time periods in month k (720 periods for months that have 30 days)
- dt
- Required demand in period t (in m3); it includes the evaporation, leakages, and non-measured volume of the water network; the data were obtained through the irrigation water manager
- CMit
- Maximum flow for source i in period t (in m3/h)
- CMTi
- Monthly maximum volume for source i (in m3)
- CHi,m
- Monthly available time for the procurement from source i with method m (in hours); CH is used when the water source requires grid consumption to procure it
- SMINt
- Safety stock of stored volume in period t (in m3)
- SMAXt
- Maximum stored volume in period t (in m3)
- Variable cost for source i with method m in period t (in €/m3)
- Fixed cost for source i with method m in period t (in €/m3)
- Storage cost in period t (in €/m3)
- Fixed cost for source i with method m over the planning horizon (in €/m3)
- St
- Storage in period t (in m3)
- Qimt
- Flow from source i with method m in period t (in m3/h)
- Yimt
- 1 if any amount of water is required from source i with method m in period t, and 0 otherwise
- Fim
- 1 if any procurement from source i with method m is placed over the planning horizon, and 0 otherwise
2.2. Solution Approaches
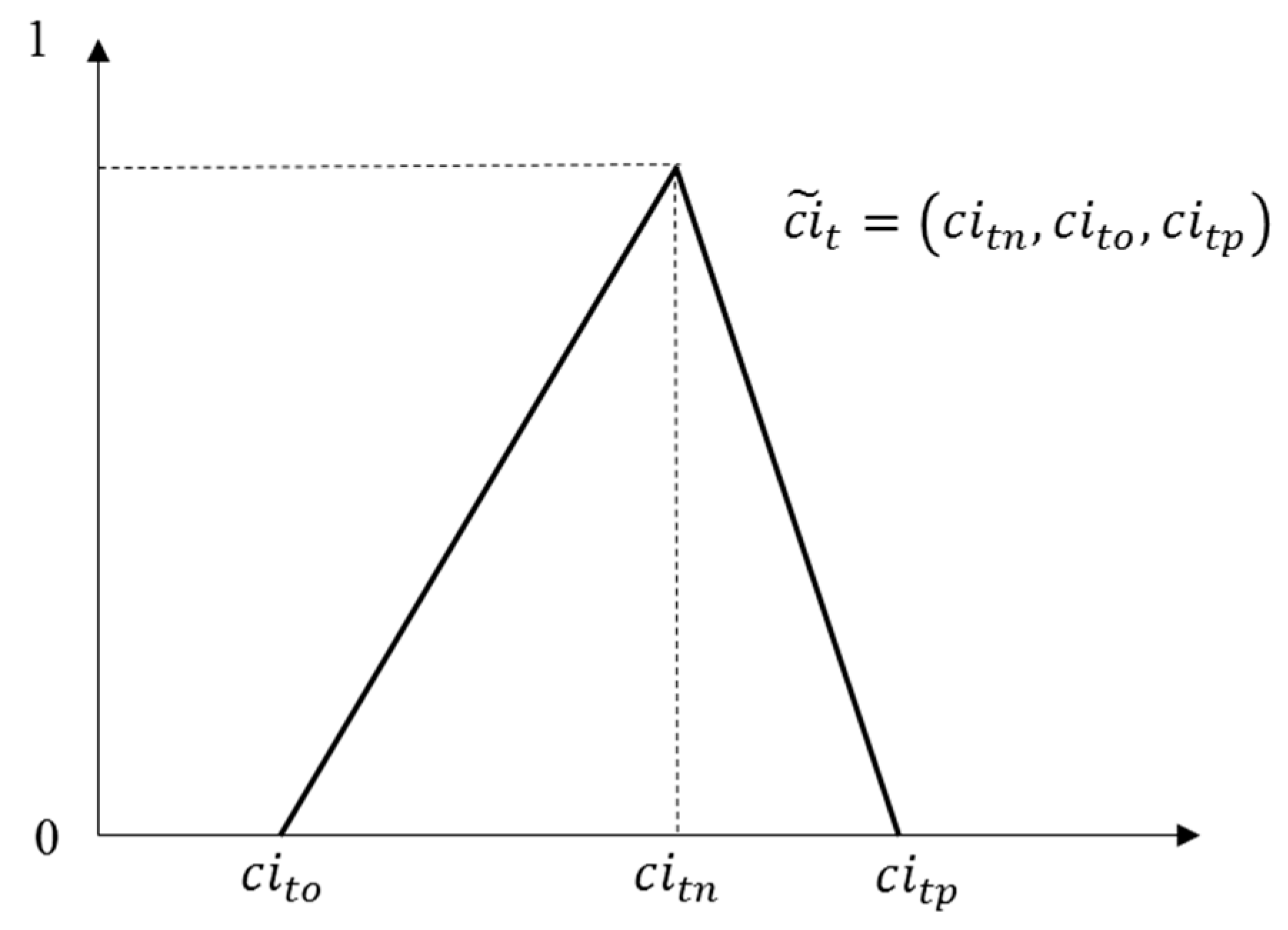
2.2.1. First Index of Yager
2.2.2. Third Index of Yager
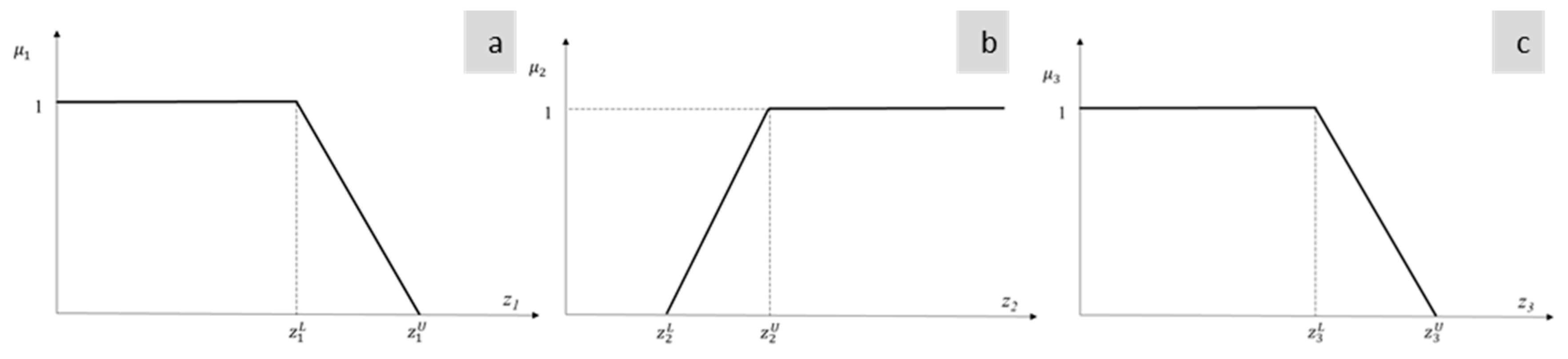
2.2.3. Lai and Hwang’s Approach
2.3. Application of the Solution Approaches
2.3.1. First Index of Yager
2.3.2. Third Index of Yager
2.3.3. Lai and Hwang’s Approach
2.3.4. The Zimmerman Solution Method
2.3.5. The Werners Solution Method
2.3.6. Selim and Ozkarahan’s Solution Method
2.3.7. Torabi and Hassini’s Solution Method
3. Results and Discussion
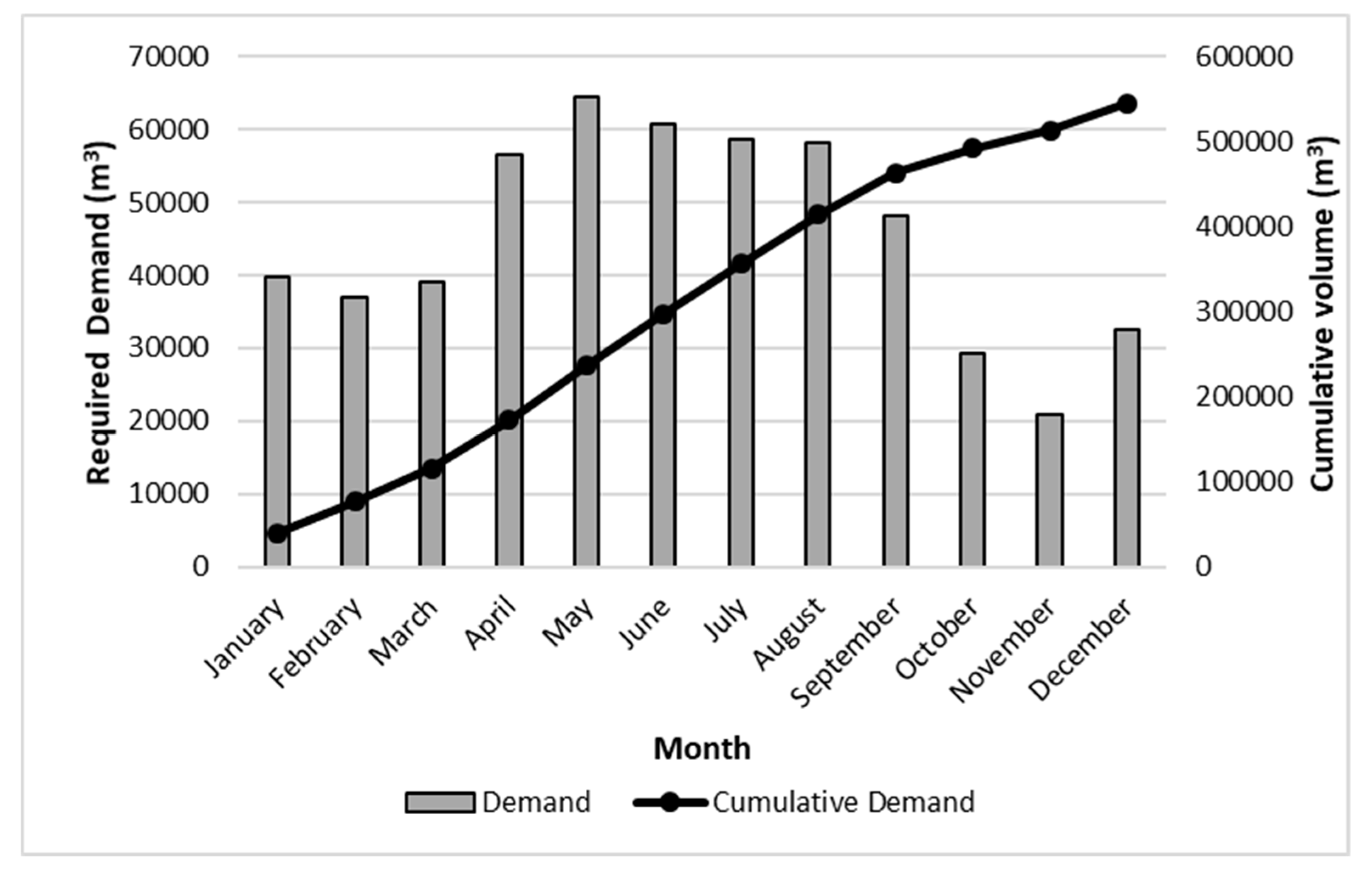
3.1. Case Study
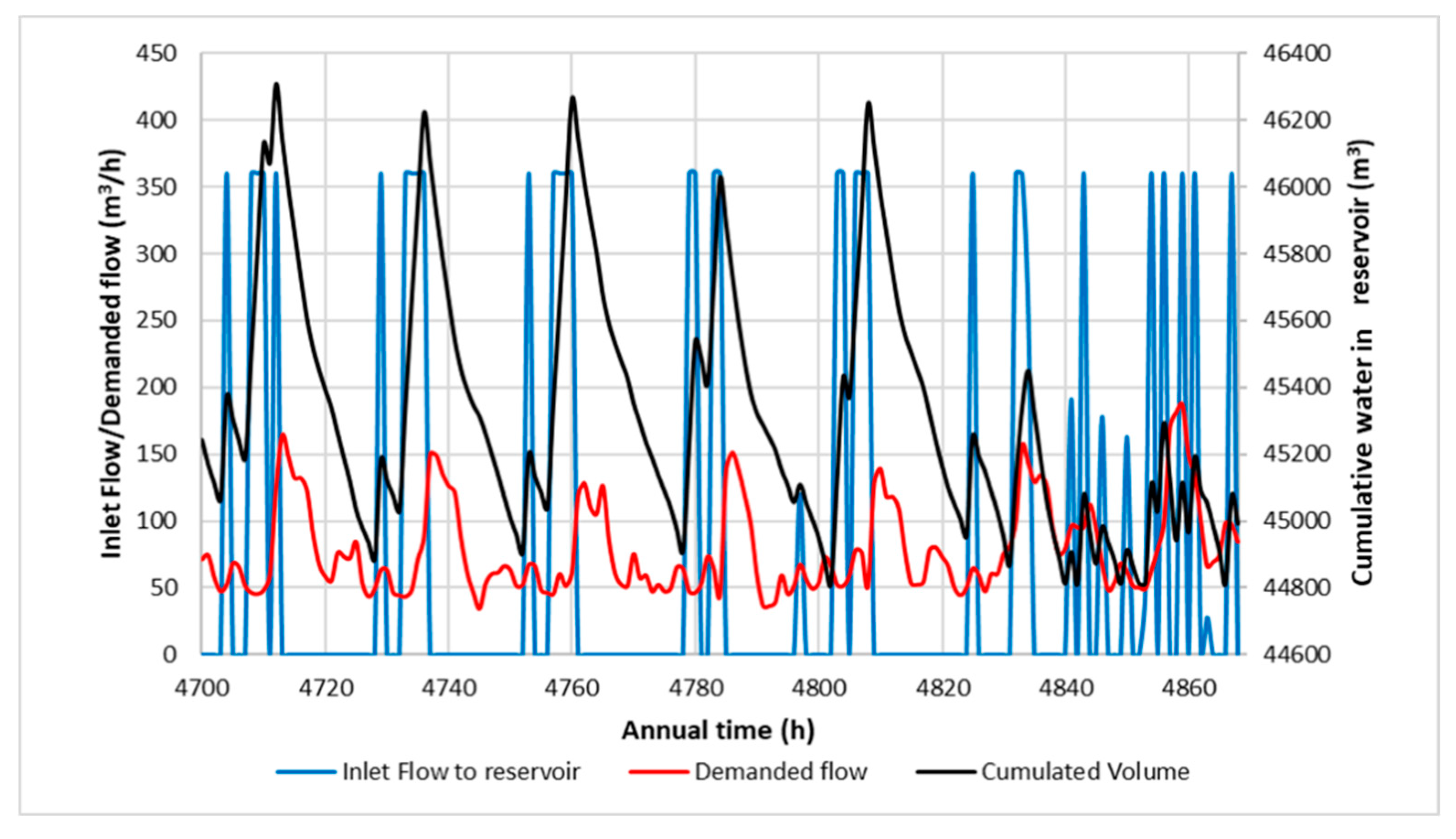
3.2. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Biswas, A.K. Integrated water resources management: A reassessment: A water forum contribution. Water Int. 2004, 29, 248–256. [Google Scholar] [CrossRef]
- Pahl-Wostl, C. Transitions towards adaptive management of water facing climate and global change. Water Resour. Manag. 2007, 21, 49–62. [Google Scholar] [CrossRef]
- Wu, K.K.; Zhang, L.P. Progress in the development of environmental risk assessment as a tool for decision-making process. J. Serv. Sci. Manag. 2014, 7, 131–144. [Google Scholar] [CrossRef][Green Version]
- Hernández-Bedolla, J.; Solera, A.; Paredes-Arquiola, J.; Pedro-Monzonís, M.; Andreu, J.; Sánchez-Quispe, S. The assessment of sustainability indexes and climate change impacts on integrated water resource management. Water 2017, 3, 213. [Google Scholar] [CrossRef]
- Hunink, J.; Simons, G.; Suárez-Almiñana, S.; Solera, A.; Andreu, J.; Giuliani, M.; Schasfoort, F. A simplified water accounting procedure to assess climate change impact on water resources for agriculture across different European river basins. Water 2019, 11, 1976. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; Ramos, H.R.; López Jiménez, P.A. Modeling irrigation networks for the quantification of potential energy recovering: A case study. Water 2016, 6, 234. [Google Scholar] [CrossRef]
- Corominas, J. Agua y energía en el riego, en la época de la sostenibilidad. Ing. Agua 2010, 17, 219–233. [Google Scholar] [CrossRef]
- Romero, L.; Pérez-Sánchez, M.; López Jiménez, P.A. Improvement of sustainability indicators when traditional water management changes: A case study in Alicante (Spain). AIMS Environ. Sci. 2017, 3, 502–522. [Google Scholar] [CrossRef]
- Davies, E.G.; Simonovic, S.P. Global water resources modeling with an integrated model of the social-economic-environmental system. Adv. Water Resour. 2011, 34, 684–700. [Google Scholar] [CrossRef]
- Alcamo, J.; Döll, P.; Henrichs, T.; Kaspar, F.; Lehner, B.; Rösch, T.; Siebert, S. Development and testing of the WaterGAP 2 global model of water use and availability. Hydrol. Sci. J. 2003, 48, 317–337. [Google Scholar] [CrossRef]
- Sanchis, R.; Poler, R. Enterprise resilience assessment—A quantitative approach. Sustainability 2019, 11, 4327. [Google Scholar] [CrossRef]
- Rahaman, M.M.; Varis, O. Integrated water resources management: Evolution, prospects and future challenges. Sustain. Sci. Pract. Policy. 2005, 1, 15–21. [Google Scholar] [CrossRef]
- Markantonis, V.; Arnaud, R.; Karabulut, A.; El Hajj, R.; Altinbilek, D.; Awad, I.; Brugemann, A.; Vangelis, C.; Mysiak, J.; Lamaddalena, N.; et al. Can the implementation of the water-energy-food nexus support economic growth in the Mediterranean region? The current status and the way forward. Front. Env. Sci. 2019, 7, 84. [Google Scholar] [CrossRef]
- Copeland, C. Energy Water Nexus: The Water Sector’s Energy Use; Congressional Research Service: Washington, DC, USA, 2014. [Google Scholar]
- Food and Agriculture Organization (FAO). Available online: www.fao.org (accessed on 2 September 2019).
- Tsur, Y. Water pricing. Agric. Appl. Econ. Assoc. 2019. [Google Scholar] [CrossRef]
- Schleich, J.; Hillenbrand, T. Water Demand Responds Asymmetrically to Rising and Falling Prices; No. S03/2019; Working Paper Sustainability and Innovation; Fraunhofer Institute for Systems and Innovation Research: Karlsruhe, Germany, 2019. [Google Scholar]
- Directive 2000/60/EC of the European Parliament and of the Council. Available online: https://eur-lex.europa.eu/eli/dir/2000/60/oj (accessed on 3 June 2019).
- Namany, S.; Al-Ansari, T.; Govindan, R. Sustainable energy, water and food nexus systems: A focused review of decision-making tools for efficient resource management and governance. J. Clean. Prod. 2019, 225, 610–626. [Google Scholar] [CrossRef]
- Archibald, T.W.; Marshall, S.E. Review of mathematical programming applications in water resource management under uncertainty. Env. Model. Assess. 2018, 23, 753–777. [Google Scholar] [CrossRef]
- Chen, S.; Shao, D.; Gu, W.; Xu, B.; Li, H.; Fang, L. An interval multistage water allocation model for crop different growth stages under inputs uncertainty. Agric. Water Manag. 2017, 186, 86–97. [Google Scholar] [CrossRef]
- Xie, Y.L.; Xia, D.H.; Huang, G.H.; Li, W.; Xu, Y. A multistage stochastic robust optimization model with fuzzy probability distribution for water supply management under uncertainty. Stoch. Env. Res. Risk. 2017, 31, 125–143. [Google Scholar] [CrossRef]
- Heumesser, C.; Fuss, S.; Szolgayová, J.; Strauss, F.; Schmid, E. Investment in irrigation systems under precipitation uncertainty. Water Resour. Manag. 2012, 26, 3113–3137. [Google Scholar] [CrossRef]
- Pereira-Cardenal, S.J.; Mo, B.; Riegels, N.D.; Arnbjerg-Nielsen, K.; Bauer-Gottwein, P. Optimization of multipurpose reservoir systems using power market models. J. Water Res. Plan. Man. 2015, 141, 8. [Google Scholar] [CrossRef]
- Kumari, S.; Mujumdar, P.P. Fuzzy set-based system performance evaluation of an irrigation reservoir system. J. Irrig. Drain. Eng. 2017, 143, 5. [Google Scholar] [CrossRef]
- Jairaj, P.G.; Vedula, S. Multireservoir system optimization using fuzzy mathematical programming. Water Resour. Manag. 2000, 14, 457–472. [Google Scholar] [CrossRef]
- Li, M.; Guo, P.; Singh, V.P.; Zhao, J. Irrigation water allocation using an inexact two-stage quadratic programming with fuzzy input under climate change. J. Am. Water Resour. 2016, 52, 667–684. [Google Scholar] [CrossRef]
- Bozorg-Haddad, O.; Malmir, M.; Mohammad-Azari, S.; Loáiciga, H.A. Estimation of farmers’ willingness to pay for water in the agricultural sector. Agric. Water Manag. 2016, 177, 284–290. [Google Scholar] [CrossRef]
- An-Vo, D.A.; Mushtaq, S.; Reardon-Smith, K. Estimating the value of conjunctive water use at a system-level using nonlinear programming model. J. Econ. Soc. Policy 2014, 17, 1–20. [Google Scholar]
- Raju, K.S.; Duckstein, L. Multiobjective fuzzy linear programming for sustainable irrigation planning: An Indian case study. Soft Comput. 2003, 7, 412–418. [Google Scholar] [CrossRef]
- Regulwar, D.G.; Gurav, J.B. Sustainable irrigation planning with imprecise parameters under fuzzy environment. Water Resour. Manag. 2012, 26, 3871–3892. [Google Scholar] [CrossRef]
- Mula, J.; Poler, R.; García, J.P. Capacity and material requirement planning modelling by comparing deterministic and fuzzy models. Int. J. Prod. Res. 2008, 6, 5589–5606. [Google Scholar] [CrossRef]
- Díaz-Madroñero, M.; Mula, J.; Jiménez, M.; Peidro, D. A rolling horizon approach for material requirement planning under fuzzy lead times. Int. J. Prod. Res. 2017, 55, 2197–2211. [Google Scholar] [CrossRef]
- Mula, J.; Díaz-Madroñero, M. Solution approaches for material requirement planning* with fuzzy costs. In Industrial Engineering: Innovative Networks; Sethi, S., Bogataj, M., Ros-McDonnell, L., Eds.; Springer: Berlin, Germany, 2012; pp. 349–357. [Google Scholar]
- Mula, J.; Poler, R.; Garcia, J.P. MRP with flexible constraints: A fuzzy mathematical programming approach. Fuzzy Sets Syst. 2006, 157, 74–97. [Google Scholar] [CrossRef]
- Mula, J.; Poler, R.; Garcia-Sabater, J.P. Material requirement planning with fuzzy constraints and fuzzy coefficients. Fuzzy Sets Syst. 2007, 158, 783–793. [Google Scholar] [CrossRef]
- Díaz-Madroñero, M.; Mula, J.; Jiménez, M. Fuzzy goal programming for material requirements planning under uncertainty and integrity conditions. Int. J. Prod. Res. 2014, 52, 6971–6988. [Google Scholar] [CrossRef]
- Peidro, D.; Díaz-Madroñero, M.; Mula, J. An Interactive fuzzy multi-objective approach for operational transport planning in an automobile supply chain. WSEAS Trans. Inf. Sci. Appl. 2010, 7, 283–294. [Google Scholar]
- Pérez-Sánchez, M.; Díaz-Madroñero Boluda, F.M.; López Jiménez, P.A.; Mula, J. Mathematical programming model for procurement selection in water irrigation systems. A case study. J. Eng. Sci. Technol. Rev. 2017, 6, 146–153. [Google Scholar] [CrossRef]
- Herrera, F.; Verdegay, J.L. Three models of fuzzy integer linear programming. Eur. J. Oper. Res. 1995, 83, 581–593. [Google Scholar] [CrossRef]
- Herrera, F.; Verdegay, J.L. Fuzzy boolean programming problems with fuzzy costs: A general study. Fuzzy Set Syst. 1996, 81, 57–76. [Google Scholar] [CrossRef]
- Alavidoost, M.H.; Babazadeh, H.; Sayyari, S.T. An interactive fuzzy programming approach for bi-objective straight and U-shaped assembly line balancing problem. Appl. Soft Comput. 2016, 40, 221–235. [Google Scholar] [CrossRef]
- Yager, R.R. Ranking fuzzy subsets over the unit interval. In Proceedings of the IEEE Conference on. Decision and Control, San Diego, CA, USA, 10–12 January 1979; pp. 1435–1437. [Google Scholar]
- Torabi, S.A.; Hassini, E. An interactive possibilistic programming approach for multiple objective supply chain master planning. Fuzzy Sets Syst. 2008, 159, 193–214. [Google Scholar] [CrossRef]
- Yager, R.R. A procedure for ordering fuzzy subsets of the unit interval. Inf. Sci. 1981, 24, 143–161. [Google Scholar] [CrossRef]
- Lai, Y.J.; Hwang, C.L. A new approach to some possibilistic linear programming problems. Fuzzy Sets Syst. 1992, 49, 121–133. [Google Scholar] [CrossRef]
- Zimmermann, H.J. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets Syst. 1978, 1, 45–55. [Google Scholar] [CrossRef]
- Werners, B. Aggregation models in mathematical programming. In Mathematical Models for Decision Support; Mitra, G., Greenberg, H.J., Lootsma, F.A., Rijckaert, M.J., Zimmermann, H.-J., Eds.; Springer: Berling/Heidelberg, Germany, 1988; pp. 295–305. [Google Scholar]
- Selim, H.; Ozkarahan, I. A supply chain distribution network design model: An interactive fuzzy goal programming-based solution approach. Int. J. Adv. Manuf. Technol. 2008, 36, 401–418. [Google Scholar] [CrossRef]
- Bellman, R.; Zadeh, L. Decision making in a fuzzy environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Maximal Software Incorporation. MPL Modeling System, Release 5.0; Maximal Software Incorporation: Arlington, VA, USA, 2016. [Google Scholar]
- Gurobi Optimization, Incorporation. Gurobi Optimizer Reference Manual, Release 7.5.2; Gurobi Optimization: Beaverton, OR, USA, 2017. [Google Scholar]
| Keywords | And “Water” | And “Irrigation” | Number of Publications Per Year and “Irrigation” Limited to Related Areas | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Total | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | |||
| “mathematical model” | 238,864 | 14,810 | 403 | 11 | 6 | 9 | 12 | 13 | 10 | 10 | 8 | 11 | 15 | 6 |
| “mathematical modelling” | 18,655 | 1862 | 60 | 1 | 1 | 2 | 3 | 5 | 1 | 3 | 2 | 1 | ||
| “mathematical programming” | 11,092 | 643 | 150 | 4 | 8 | 10 | 6 | 8 | 6 | 4 | 10 | 9 | 10 | 9 |
| “mathematical optimisation” | 2630 | 276 | 10 | 2 | 1 | 1 | ||||||||
| “fuzzy mathematical programming” | 362 | 12 | 4 | 1 | ||||||||||
| Source | Method | Price |
|---|---|---|
| (€/m3) | ||
| Source 1 | Fixed | 0.25 |
| Source 2 | Fixed | 0.35 |
| Source 3 | Fixed | 0.60 |
| Source 4 | Variable | − |
| P1 | 0.56 | |
| P2 | 0.50 | |
| P3 | 0.35 | |
| P4 | 0.30 | |
| P5 | 0.20 | |
| P6 | 0.12 | |
| Source 5 | Variable | − |
| P1 | 0.70 | |
| P2 | 0.65 | |
| P3 | 0.49 | |
| P4 | 0.42 | |
| P5 | 0.35 | |
| P6 | 0.25 |
| Hour | Month | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| January | February | March | April | May | 1–15 June | 16–30 June | July | August | September | October | November | December | |
| 0 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 |
| 1 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 |
| 2 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 |
| 3 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 |
| 4 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 |
| 5 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 |
| 6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 |
| 7 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 | P6 |
| 8 | P2 | P2 | P4 | P5 | P5 | P4 | P2 | P2 | P6 | P4 | P5 | P4 | P2 |
| 9 | P2 | P2 | P4 | P5 | P5 | P3 | P2 | P2 | P6 | P4 | P5 | P4 | P2 |
| 10 | P1 | P1 | P4 | P5 | P5 | P3 | P2 | P2 | P6 | P4 | P5 | P4 | P1 |
| 11 | P1 | P1 | P4 | P5 | P5 | P3 | P1 | P1 | P6 | P4 | P5 | P4 | P1 |
| 12 | P1 | P1 | P4 | P5 | P5 | P3 | P1 | P1 | P6 | P4 | P5 | P4 | P1 |
| 13 | P2 | P2 | P4 | P5 | P5 | P3 | P1 | P1 | P6 | P4 | P5 | P4 | P2 |
| 14 | P2 | P2 | P4 | P5 | P5 | P3 | P1 | P1 | P6 | P4 | P5 | P4 | P2 |
| 15 | P2 | P2 | P4 | P5 | P5 | P4 | P1 | P1 | P6 | P4 | P5 | P4 | P2 |
| 16 | P2 | P2 | P3 | P5 | P5 | P4 | P1 | P1 | P6 | P3 | P5 | P3 | P2 |
| 17 | P2 | P2 | P3 | P5 | P5 | P4 | P1 | P1 | P6 | P3 | P5 | P3 | P2 |
| 18 | P1 | P1 | P3 | P5 | P5 | P4 | P1 | P1 | P6 | P3 | P5 | P3 | P1 |
| 19 | P1 | P1 | P3 | P5 | P5 | P4 | P2 | P2 | P6 | P3 | P5 | P3 | P1 |
| 20 | P1 | P1 | P3 | P5 | P5 | P4 | P2 | P2 | P6 | P3 | P5 | P3 | P1 |
| 21 | P2 | P2 | P3 | P5 | P5 | P4 | P2 | P2 | P6 | P3 | P5 | P3 | P2 |
| 22 | P2 | P2 | P4 | P5 | P5 | P4 | P2 | P2 | P6 | P4 | P5 | P4 | P2 |
| 23 | P2 | P2 | P4 | P5 | P5 | P4 | P2 | P2 | P6 | P4 | P5 | P4 | P2 |
| Source | Hourly Capacity (m3) CMit | Monthly Capacity (m3) CMTit |
|---|---|---|
| 1 | 120 | 40,000 |
| 2 | 306 | 500,000 |
| 3 | 324 | 75,000 |
| 4 | 360 | 75,000 |
| 5 | 450 | 125,000 |
| Hours of Water Service Per Month | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Source | Method | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 2 | 132 | 120 | 0 | 0 | 0 | 0 | 286 | 0 | 0 | 0 | 0 | 126 |
| 4 | 3 | 220 | 200 | 0 | 0 | 0 | 0 | 66 | 0 | 0 | 0 | 0 | 210 |
| 4 | 4 | 0 | 0 | 126 | 0 | 0 | 126 | 0 | 0 | 120 | 0 | 126 | 0 |
| 4 | 5 | 0 | 0 | 210 | 0 | 0 | 210 | 0 | 0 | 200 | 0 | 210 | 0 |
| 4 | 6 | 0 | 0 | 0 | 336 | 336 | 0 | 0 | 0 | 0 | 352 | 0 | 0 |
| 4 | 7 | 392 | 352 | 408 | 384 | 408 | 384 | 392 | 744 | 400 | 392 | 384 | 456 |
| 5 | 2 | 132 | 120 | 0 | 0 | 0 | 0 | 286 | 0 | 0 | 0 | 0 | 126 |
| 5 | 3 | 220 | 200 | 0 | 0 | 0 | 0 | 66 | 0 | 0 | 0 | 0 | 210 |
| 5 | 4 | 0 | 0 | 126 | 0 | 0 | 126 | 0 | 0 | 120 | 0 | 126 | 0 |
| 5 | 5 | 0 | 0 | 210 | 0 | 0 | 210 | 0 | 0 | 200 | 0 | 210 | 0 |
| 5 | 6 | 0 | 0 | 0 | 336 | 336 | 0 | 0 | 0 | 0 | 352 | 0 | 0 |
| 5 | 7 | 392 | 352 | 408 | 384 | 408 | 384 | 392 | 744 | 400 | 392 | 384 | 456 |
| First Index of Yager | Third Index of Yager | Lai and Hwang Approach | ||||
|---|---|---|---|---|---|---|
| Zimmerman’s Approach | Werners’ Approach | Selim and Ozkarahan’s Approach | Torabi and Hassini’s Approach | |||
| Total costs (z) | 285,753 | 284,076 | - | - | - | - |
| Most possible total costs (z1) | - | - | 278,579 | 278,567 | 278,450 | 278,531 |
| Most optimistic total costs (z2) | - | - | 236,792 | 236,782 | 236,683 | 236,752 |
| Most pessimistic total costs (z3) | - | - | 348,224 | 348,209 | 348,063 | 348,164 |
| Computational Time | - | 30% | 294% | 350% | 322% | 229% |
| Source | Method | Annual Volume (m3/Year) | % Use with Respect to Annual Capacity of Each Water Source Used |
|---|---|---|---|
| First Index of Yager | |||
| 4 | 7 | 347,743 | 38.64% |
| Third Index of Yager | |||
| 4 | 7 | 347,743 | 38.64% |
| Zimmerman’s approach | |||
| 1 | 1 | 36 | 0.01% |
| 4 | 7 | 347,743 | 38.64% |
| Werners’ approach | |||
| 1 | 1 | 2565 | 0.53% |
| 2 | 1 | 343,111 | 5.72% |
| 3 | 1 | 1797 | 0.20% |
| Selim and Ozkarahan’s approach | |||
| 1 | 1 | 4489 | 0.94% |
| 2 | 1 | 951 | 0.02% |
| 4 | 7 | 346,457 | 38% |
| Torabi and Hassini’s approach | |||
| 1 | 1 | 1970 | 0.41% |
| 2 | 1 | 5454 | 0.09% |
| 4 | 7 | 340,049 | 37.78% |
| First Index of Yager | Third Index of Yager | Lai and Hwang Approach | ||||
|---|---|---|---|---|---|---|
| Zimmerman’s Approach | Werners’ Approach | Selim and Ozkarahan’s Approach | Torabi and Hassini’s Approach | |||
| Constraints | 455,654 | 455,654 | 455,661 | 455,661 | 455,661 | 455,661 |
| Variables | 96,372 | 96,372 | 96,376 | 96,379 | 96,379 | 96,376 |
| Integers | 43,812 | 43,812 | 43,812 | 43,812 | 43,812 | 43,812 |
| Nonzeros | 2,417,737 | 2,417,737 | 2,803,234 | 2,803,237 | 2,803,237 | 2,803,234 |
| Density | 0.006% | 0.006% | 0.006% | 0.006% | 0.006% | 0.006% |
| Iterations | 19,875 | 19,858 | 68,620 | 36,858 | 35,569 | 34,532 |
| Solution time (s) | 22 | 28 | 85 | 97 | 91 | 76 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanchis, R.; Díaz-Madroñero, M.; López-Jiménez, P.A.; Pérez-Sánchez, M. Solution Approaches for the Management of the Water Resources in Irrigation Water Systems with Fuzzy Costs. Water 2019, 11, 2432. https://doi.org/10.3390/w11122432
Sanchis R, Díaz-Madroñero M, López-Jiménez PA, Pérez-Sánchez M. Solution Approaches for the Management of the Water Resources in Irrigation Water Systems with Fuzzy Costs. Water. 2019; 11(12):2432. https://doi.org/10.3390/w11122432
Chicago/Turabian StyleSanchis, Raquel, Manuel Díaz-Madroñero, P. Amparo López-Jiménez, and Modesto Pérez-Sánchez. 2019. "Solution Approaches for the Management of the Water Resources in Irrigation Water Systems with Fuzzy Costs" Water 11, no. 12: 2432. https://doi.org/10.3390/w11122432
APA StyleSanchis, R., Díaz-Madroñero, M., López-Jiménez, P. A., & Pérez-Sánchez, M. (2019). Solution Approaches for the Management of the Water Resources in Irrigation Water Systems with Fuzzy Costs. Water, 11(12), 2432. https://doi.org/10.3390/w11122432








