1. Introduction
Travel times of soil water contain useful information about flowpaths, water sources and sinks as well as about mixing between old (pre-event) and new (event) water in a catchment storage system [
1]. The dynamics of soil water at the catchment and hillslope scales is not well understood due to the enormous heterogeneity of soil characteristics and a wide variety of physical processes involved. The runoff and soil water mixing processes become even more complex for hillslopes with preferential flowpaths. Subsurface stormflow in mountain hillslopes is known to be highly variable in both space and time [
2,
3,
4]; such variability has a significant effect on resulting travel times. Water residence and travel times in soils are of key importance for the reliable description of biogeochemical transformations of dissolved substances (such as dissolved organic carbon, nutrients, and contaminants).
In this context, it is important to distinguish between residence times and travel times. Travel (transit) time is defined as the elapsed time between entry and exit of an individual macroscopic particle of water at the respective boundaries of a flow system [
5], while residence time refers to a time spent by particles in a system, thus determining the age of water within the reservoir [
6].
Most recent studies showed that catchment mean residence times fall in the range from <1 to 5 years e.g., [
7,
8,
9,
10], depending on hydrogeological settings of the catchments (and thus on travel pathways and storage capacities). McGuire et al. [
11] demonstrated that residence times are controlled by catchment topography rather than total area. The mean residence time of hillslope soil water, estimated by Stewart and McDonnell [
12], ranged from 13 to 63 days for different hillslope locations and depths. Kabeya et al. [
13] showed mean residence times for soil water in 1–5 months range. Vitvar and Balderer [
14] estimated a mean residence time of 200 days for soil water in a forest lysimeter. Using steady-state assumption and long-term annual catchment water balance, Matsutani et al. [
15] evaluated the mean residence time of soil water to be about 10 months. Sprenger et al. [
16] highlighted the role of interfaces between hydrological compartments (e.g., soil–atmosphere and soil–groundwater) on travel times of water.
Beside mean travel or residence times, the travel time distribution is also of interest. If an environmental tracer (e.g., water stable isotope O-18) was applied uniformly in the form of an instantaneous unit pulse (the Dirac impulse) over the catchment or hillslope surface, the breakthrough curve of the tracer at the catchment or hillslope outlet would represent the travel time distribution, i.e., the travel time probability density function [
5]. Such distribution is affected by the variability of the flow velocity field in soils, different flow path lengths, and hydrodynamic dispersion e.g., [
17].
The travel time distribution is often used as a fundamental metrics of the catchment/hillslope hydrological response, providing information about flow paths, storages and sources of water [
5,
18]. McGuire et al. [
19] showed that subsurface storage, mixing assumptions, and water table dynamics were the most important controls on the distribution of travel times. The mean travel time of a particle can be calculated as the first moment of the travel time distribution or the average arrival time of the particle at the catchment/hillslope outlet. From the conceptual point of view, travel time distributions are usually considered as time invariant and spatially lumped catchment characteristics [
5].
The tracer application in the form of the Dirac impulse over the entire catchment area is difficult under real conditions [
20]. Therefore, monitoring of isotopes of water in precipitation and in different spatial compartments of catchments serves as a common approach to the estimation of travel times e.g., [
21,
22,
23,
24]. The travel time estimation is often based on the analysis of the transformation of isotopic input signals (in precipitation) into output signals (in soil pore water and in streamflow). However, this approach fails when the signals are highly erratic in time as in cases of highly structured hillslope soils with preferential pathways exhibiting rapid and short-lived runoff responses [
25]. When lumped convolution approaches are applied a prior assumption about the type of travel time distribution needs to be made. Common distributions are piston, exponential, exponential-piston, and dispersion models. Beside lumped convolution approaches used by Malozsewski and Zuber [
21], storage selection models were proposed and developed recently e.g., [
18,
26,
27]. Instead of a preselected type of travel time distribution, storage selection models use predefined storage functions [
28,
29]. In the above mentioned approaches, subsurface flow patterns and flow pathways are not explicitly considered to define travel time distributions.
Alternatively, travel time distributions can be evaluated by models integrating the dynamics of subsurface water flow and solute transport e.g., [
30,
31,
32,
33]. Fiori and Russo [
34] evaluated the variability of soil hydraulic characteristics in a hillslope mantle to obtain the resulting travel time distribution. Using a fully distributed hydrological model coupled with a conservative tracer transport component, Remondi et al. [
35] highlighted a considerable variability of travel times in catchments with contrasting climates and the pronounced effect of catchment topography on the inferred travel time distributions. Ameli et al. [
36] used a physically based subsurface flow model coupled with a particle movement module to assess hillslope travel time distributions. They showed that the vertical change of saturated hydraulic conductivity and porosity significantly affected the shape of hillslope travel time distributions. For the model evaluation of travel times, hydrodynamic mixing, consisting of molecular diffusion and mechanical dispersion, plays a crucial role. Reliable and independent estimates of longitudinal and transverse dispersivities, governing dispersive fluxes, are difficult to obtain under field conditions [
37]. Cardenas and Jiang [
30] showed that the enhanced dispersion leads to earlier arrival times causing skewed travel time distributions toward early arrivals.
Stewart and McDonnell [
12] recognized that hillslope residence times might be significantly affected by preferential flow effects. Klaus and McDonnell [
38] showed that the type of sampling method (e.g., suction cups, zero tension lysimeters, or soil core samples) may change the interpretation of isotopic signals in soils with preferential pathways. As a result, residence times evaluated using lumped approaches can be biased since the preferential flow component is not accounted for. In contrast, preferential flow effects can be taken into account when applying physically based models. For instance, Larsbo [
39] presented an event-based one-dimensional travel time model involving preferential flow, in which the effects of initial water content, rainfall intensity and duration were considered.
In our previous studies, a two-dimensional dual-continuum model was used to analyze the subsurface runoff dynamics at the hillslope site under study. Dusek and Vogel [
40] compared the predicted stormflow fluxes and hillslope soil water pressures with observed data, while Dusek and Vogel [
41] analyzed the threshold behavior of hillslope response to rainfall. Dusek and Vogel [
42] focused on the transport of natural oxygen-18 isotope in water (O-18) and compared the model predictions with the observed isotopic contents in stormflow and in soil pore water. The O-18 transport was affected by significant mixing of event water originating from different rainfall episodes. Nevertheless, travel time distributions were not sought in these studies.
In the present study, seasonal and episodal soil water travel time distributions are evaluated for the hillslope site of interest using the same two-dimensional flow and transport model as in our previous studies. The model, previously validated on the observed subsurface discharge and O-18 data, was used to simulate the hillslope hydrological responses and tracer breakthroughs resulting from a short-lived surface pulse of a fictious conservative tracer (approximating the Dirac impulse). The simulation was repeated for three consecutive growing seasons and nine selected rainfall–runoff events. The main objectives of the study were: (i) to evaluate the travel time distributions for different hillslope discharge processes, namely subsurface stormflow, deep percolation, and transpiration, (ii) to assess the role of transpiration when evaluating mean residence times and median travel times at the episodal and seasonal time scales, and (iii) to explore the possibility of constructing the time invariant master travel time distribution for stormflow to facilitate comparisons with other hillslopes.
3. Model Application
3.1. Model Representation of Stormflow, Deep Percolation, and Transpiration
The hillslope discharge at Tomsovka occurs at the respective boundaries of the hillslope segment —in the form of stormflow and deep percolation—as well as from the root zone—via plant transpiration. The water uptake by plant roots is represented by the sink term S in Equations (5) and (6). Direct evaporation from the soil surface is rendered insignificant by dense vegetation cover.
Subsurface stormflow, i.e., saturated flow of water above the soil–bedrock interface is represented by Darcian flow in the preferential flow domain of the dual-continuum system, Equations (5) and (6). Preferential flow at Tomsovka is activated only occasionally (several times a year) during major rainfall–runoff events. There are two possible mechanisms of preferential flow activation: (i) The soil-surface activation mechanism occurs when the infiltration capacity of the soil matrix at the soil surface is exceeded during extreme rainfall events and the excess water is directed to the preferential flow domain. (ii) The soil-base activation mechanism occurs when the soil matrix near the soil–bedrock interface becomes saturated—triggering the transfer of water from the soil matrix to the preferential flow domain. The soil-surface activation mechanism is rare at Tomsovka because of high saturated hydraulic conductivity of the soil matrix. It is mostly the soil-base activation mechanism that leads to the initiation of lateral preferential flow along the soil–bedrock interface regarded as stormflow.
The deep percolation component of the hillslope discharge is in our model associated with Darcian flow across the soil–bedrock interface taking place in the soil matrix domain. The intensity of the deep percolation fluxes is controlled by the abruptly decreasing hydraulic conductivity below the soil–bedrock interface (
Table 1).
3.2. Geometric, Material and Boundary Conditions for the Soil Water Flow Model
Details about the application of the S2D model at Tomsovka were presented in our previous studies [
40,
41,
42]. The daily potential evapotranspiration intensities were estimated using the Penman–Monteith equation [
54], based on the observed micrometeorological data. The uptake of water by plant roots was described using the approach of Feddes et al. [
55]. The vertical distribution of the root water uptake intensity in the soil profile was assumed to be constant in the upper 20 cm layer, decreasing linearly to zero between 20 and 70 cm [
25].
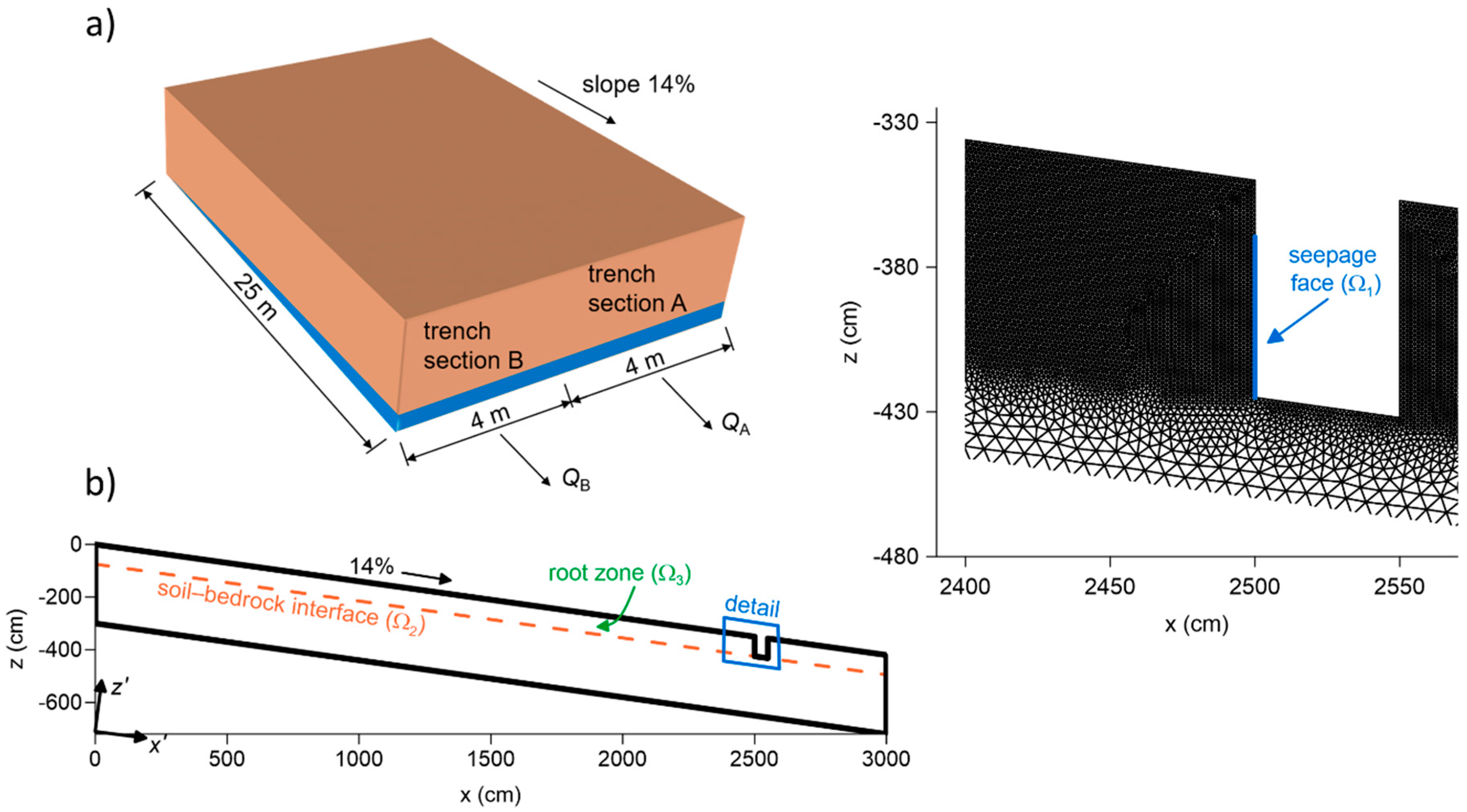
The hillslope segment was represented by a 30 m long and 3 m deep two-dimensional vertical cross-section with a constant slope of 14% (
Figure 1). The hillslope length contributing to subsurface discharge was 25 m. The two-dimensional flow domain was discretized using finite element mesh consisting of more than 250,000 triangular elements. Identical boundary conditions were used for both flow domains of the dual-continuum system, i.e., the preferential flow domain and the soil matrix domain.
The following boundary conditions were prescribed at the respective parts of the flow domains: (i) atmospheric boundary condition at the soil surface, (ii) seepage face boundary condition at the upslope face of the experimental trench, (iii) unit hydraulic gradient condition at the bottom boundary of the flow domain, (iv) no-flow boundary condition at the vertical upslope side of the flow domain, (v) seepage face boundary conditions at the vertical downslope side of the flow domain.
Hydraulic properties of the soil and weathered bedrock layers were described using the modified van Genuchten model [
56,
57,
58]. Soil hydraulic parameters and transfer term parameters were taken from our previous studies [
25,
40,
41]. The hydraulic parameters are shown in
Table 1. The volumetric fraction of the preferential flow domain
wf was set to 7% at the soil surface and 5% at the depth of 70 cm, with a linear variation between the two endpoints.
The increased lateral conductivity of the network of preferential pathways was represented by an increased conductivity anisotropy ratio in the soil profile (0–70 cm). The anisotropy ratio
Kx’x’/
Kz’z’ of the hydraulic conductivity tensor of the preferential flow domain in respect to principal directions
x’ and
z’ was set equal to ten. Although no direct determination of the lateral hydraulic conductivity was made, this assumption was confirmed by a sensitivity study of lateral conductivity, carried out using a diffusion wave model [
59,
60], and by a comparative study between runoff predictions obtained with the diffusion wave model and the two-dimensional model [
40].
3.3. Simulation Scenarios
To study the travel time distributions defined by Equation (4), two types of tracer transport simulations were performed: (i) short-term episodal tracer breakthrough simulations focusing on major rainfall–runoff episodes and (ii) long-term seasonal flow and transport simulations. In both cases, a fictitious conservative tracer, entering the hillslope surface in the form of a nearly instantaneous pulse at the beginning of the simulated period, was considered. The pulse was designed to play the role of the Dirac delta function as required by Equation (2).
The instantaneous input pulse of the tracer was approximated by a uniform tracer application over the contributing hillslope length of 25 m, entering the soil profile with a one-hour pulse of rainfall, assuming the tracer mass of M = 25 kg. The applied tracer mass was identical among the scenarios.
A zero-concentration initial condition was assumed at the beginning of each rainfall–runoff episode or growing season. A flux concentration (third-type) boundary condition was used at the soil surface. A zero-concentration gradient was used at the upslope face of the experimental trench and at the bottom boundary, allowing the tracer to leave the simulated domain freely with the discharging water. At the vertical upslope and downslope sides of the computational domain, zero-flux and zero concentration gradient boundary conditions were prescribed, respectively. According to Equations (7) and (8), the transport of tracer was subject to advection, hydrodynamic dispersion, root water uptake, and mass exchange between soil matrix and preferential flow domains. The uptake of tracer by plant roots was controlled by the soil water uptake, Equations (7) and (8).
The molecular diffusion coefficient was set equal to 2 cm
2 d
−1; this value represents the self-diffusion of water considered for transport of stable isotope O-18 in our previous studies. Longitudinal and transversal dispersivities of 20 cm and 5 cm, respectively, were applied [
42].
3.4. Episodal Simulations
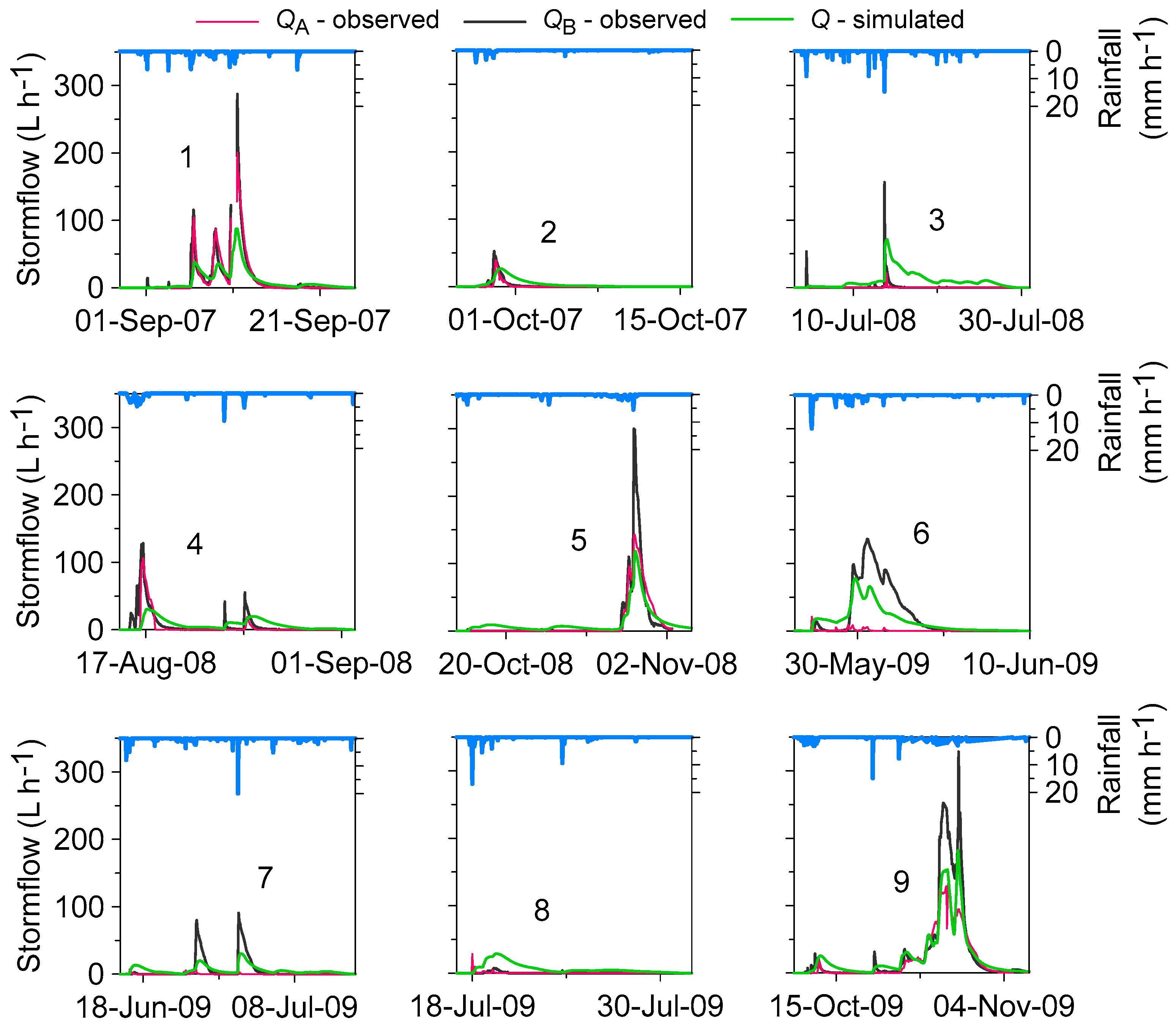
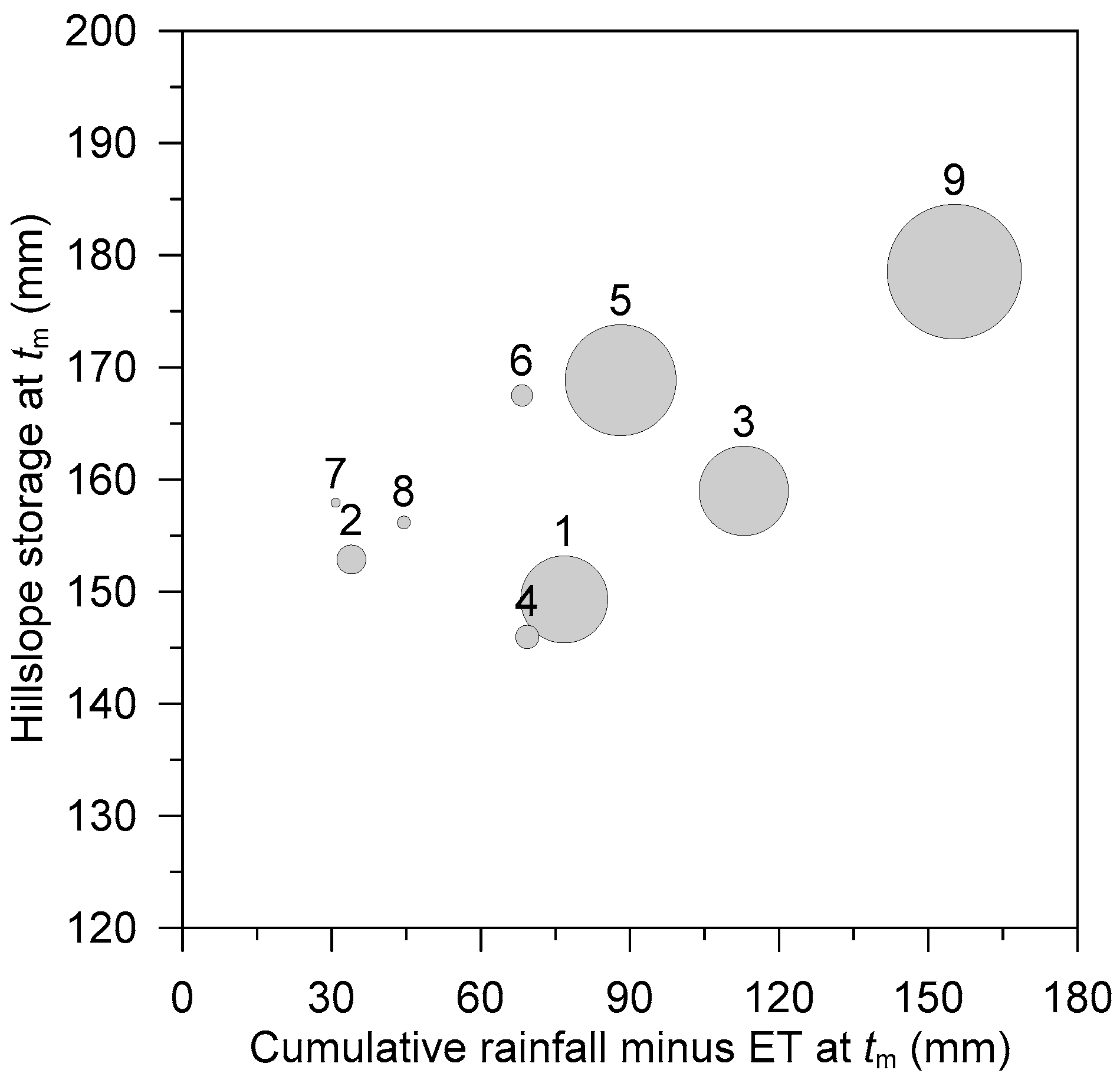
Nine significant rainfall–runoff episodes, observed at Tomsovka over the period from May 2007 to November 2009, were selected for the episodal tracer breakthrough simulations (
Figure 2). The episodes were characterized by a continuous subsurface hillslope discharge (stormflow) lasting more than 2 days. Three episodes (2, 3, and 8) had relatively small measured stormflow volumes (<0.9 m
3, i.e., <9 mm of the equivalent runoff height), while the remaining six episodes (i.e., 1, 4, 5, 6, 7, and 9) were characterized by at least 2.9 m
3 (29 mm) stormflow volume (
Figure 2). The largest stormflow volume was observed during Episode 9, when trench sections A and B showed hillslope discharge of 13.0 m
3 (130 mm) and 19.8 m
3 (198 mm), respectively.
Comparison of predicted subsurface stormflow intensities with the fluxes observed in the trench sections A and B at the Tomsovka hillslope was reported by Dusek and Vogel [
40,
42]. Their results are shown in
Figure 2. A reasonable agreement was also obtained for the comparison of observed and simulated natural O-18 contents in stormflow and in pore water (not shown in this paper).
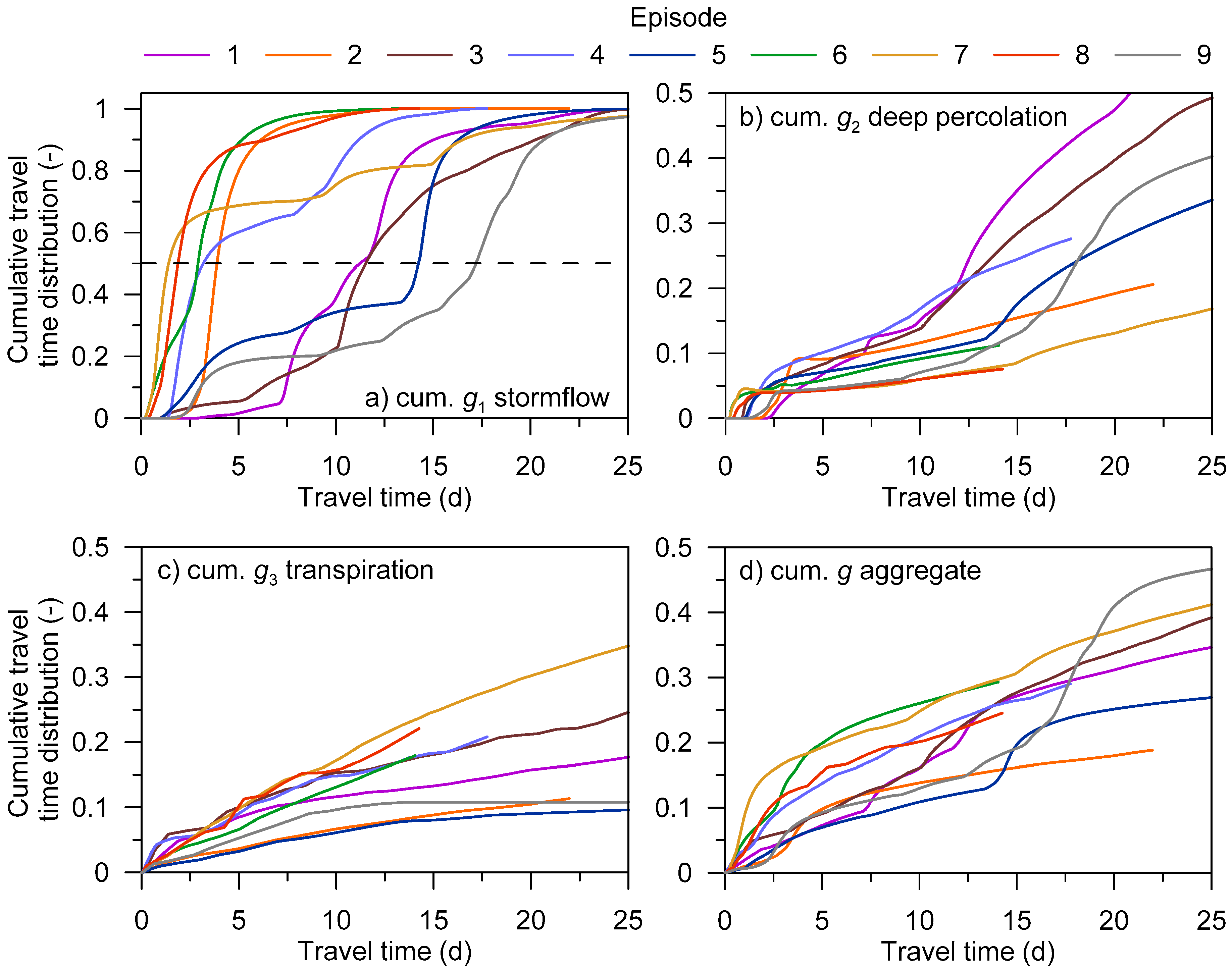
Since the stormflow is a process with a well-defined beginning and end, the travel time distribution g1 sums to unity by the end of each episode. The travel time distributions g2 and g3 sum to unity much later as the respective discharge processes continue beyond the end of the event. Due to this, the episodal tracer masses M2 and M3 for deep percolation and transpiration were estimated based on the seasonal simulations. When calculating g2 and g3, the tracer masses M2 and M3 in Equation (4) were determined by dividing the remaining tracer mass at the end of the episode (i.e., the amount M − M1) between deep percolation and transpiration in a ratio obtained from the respective seasonal mass balance.
3.5. Seasonal Simulations
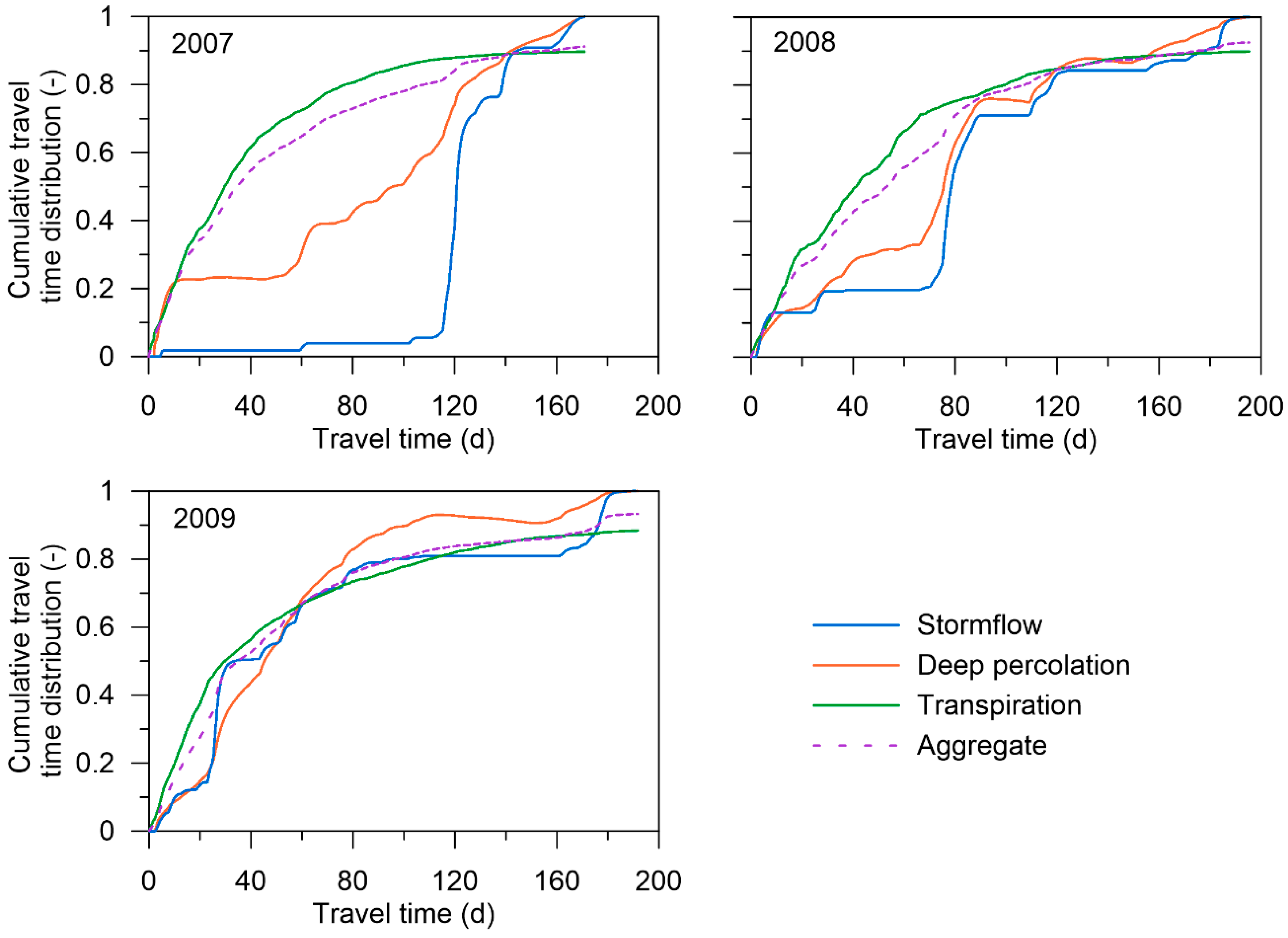
The seasonal tracer transport simulations were carried out for growing seasons 2007, 2008, and 2009. In this case, the tracer input pulse was introduced at the beginning of each growing season. While the cumulative transpiration was similar among the seasons, season 2009 was characterized by a larger rainfall input (874 mm) than season 2008 (724 mm) and 2007 (634 mm). Besides the total rainfall fallen during each growing season, temporal distribution of rainfall played an important role in the initiation of hillslope discharge. Rainfall was clustered in many short periods during 2009 season, which resulted in greater hillslope discharge compared to seasons 2007 and 2008.
5. Summary and Conclusions
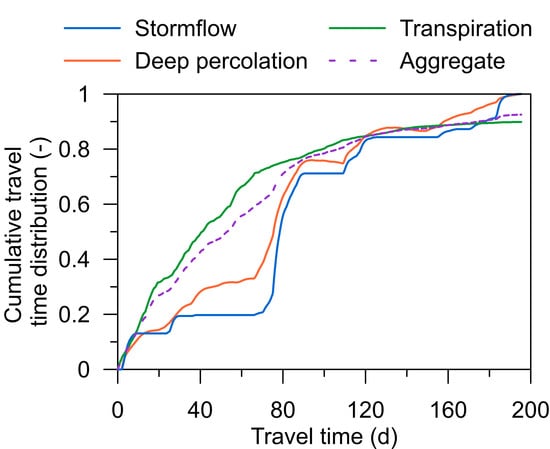
A two-dimensional dual-continuum model was used to evaluate the travel time distributions of water through a forest hillslope exhibiting significant lateral preferential flow effects. The breakthroughs of a fictious tracer, entering the soil profile in the form of the Dirac impulse, were analyzed and the associated travel time distributions were estimated at both episodal and seasonal time scales. The modeling approach applied allowed us to evaluate the partial travel time distributions for the relevant hillslope discharge processes, namely subsurface stormflow, deep percolation and transpiration as well as the aggregate travel time distributions characterizing the combination of all discharge processes. The numerical experiments were performed for three growing seasons and major rainfall–runoff episodes. The episodes differed in temporal rainfall patterns and initial distributions of soil water within the hillslope.
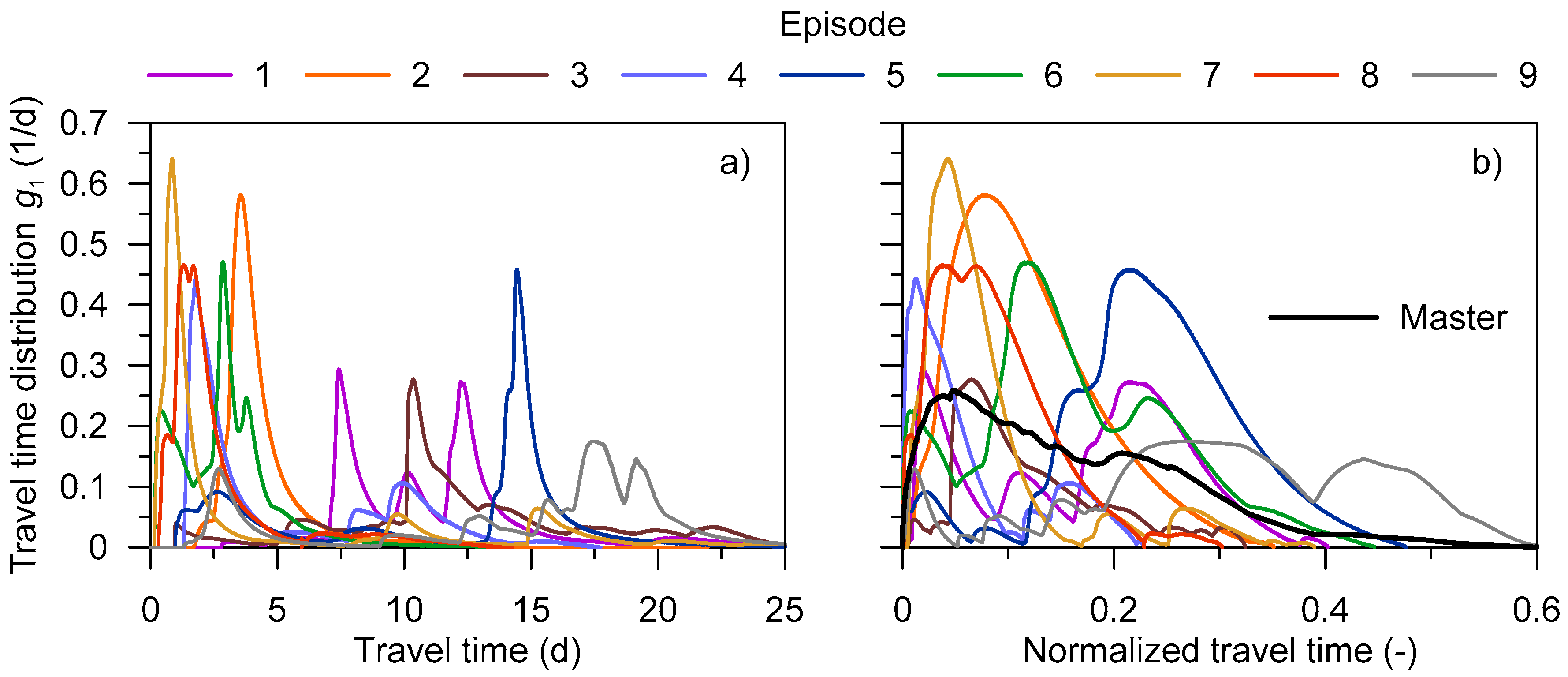
The obtained episodal travel time distributions suggest a quick hydrological response of the hillslope to rainfall, which can be attributed to the inclusion of preferential flow component in the model. The variability of the travel time distributions was found to be controlled by the meteorological conditions during the rainfall–runoff episodes and antecedent soil moisture distribution prior to the episodes. The flow-corrected time projection allowed as to construct master travel time distribution for stormflow, which can be used to compare the hydrological response of the hillslope of interest with that of other hillslopes.
The episodal median travel times of subsurface stormflow ranged from 1 to 17 days for the selected rainfall–runoff episodes. The results indicated a weak relationship between stormflow travel times and hillslope water storages. The seasonal aggregate median travel time (for all discharge processes combined) was estimated in the range of 30–46 days.
Transpiration was shown to have significant impact on the estimated seasonal as well as episodal aggregate travel time distributions. Transpiration had to be also considered in the calculations of mean residence times as it represents a significant part of the water balance. The mean residence times ranged between 29 and 37 days for the three seasons considered.
Once validated on experimental observations, the numerical model offers a valuable tool for the evaluation of soil water travel times in hillslopes. For instance, the flux partitioning in the subsurface, reflected in median travel times of the different discharge processes, may be used for the quantification of biogeochemical transformations of dissolved organic compounds. The partial travel time distributions associated with the different discharge mechanisms provide meaningful information for the catchment runoff modeling.