Modeling Travel Time Distributions of Preferential Subsurface Runoff, Deep Percolation and Transpiration at A Montane Forest Hillslope Site
Abstract
:1. Introduction
2. Materials and Methods
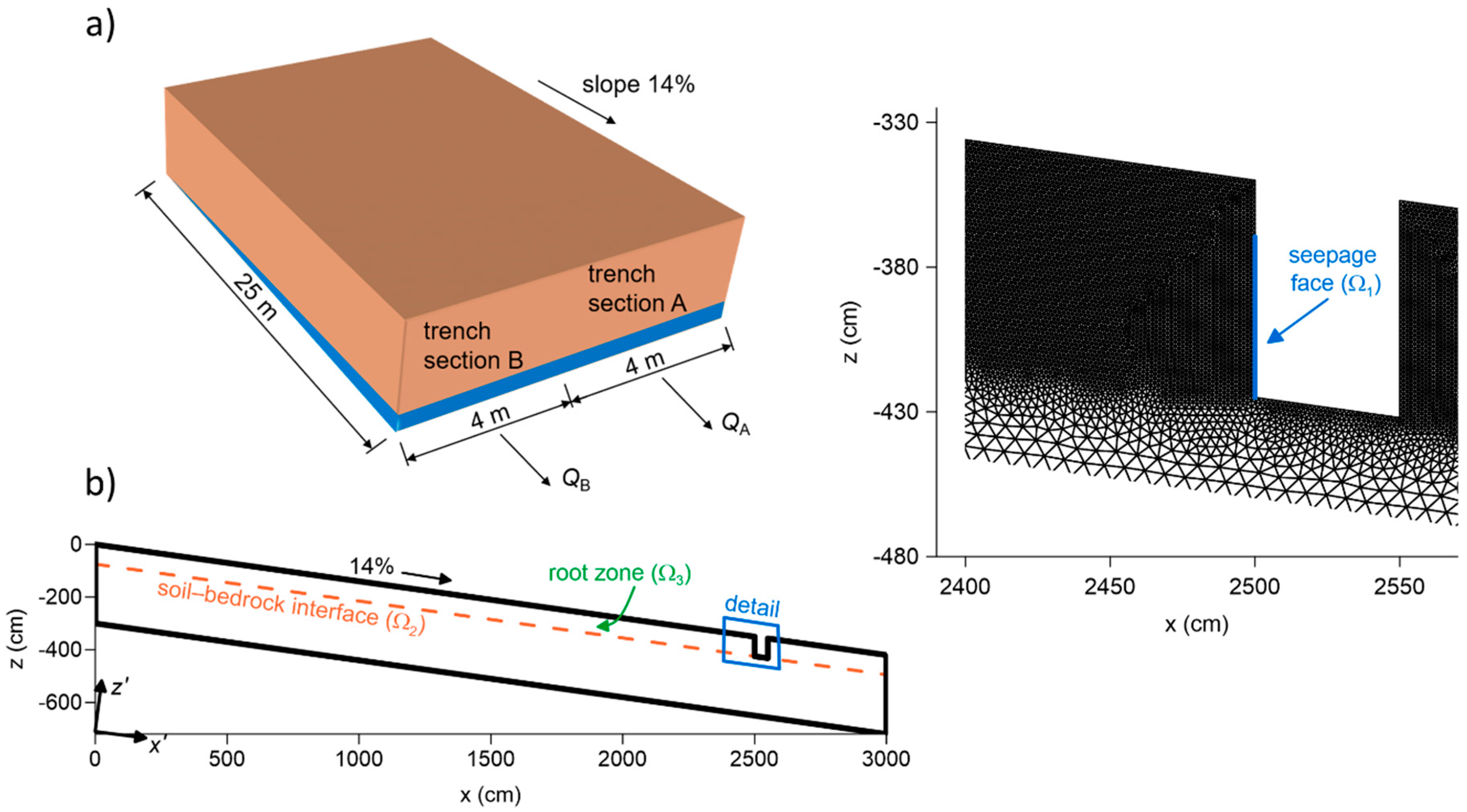
2.1. Study Site
2.2. Mean Residence Time
2.3. Travel Time Distributions
2.4. Two-Dimensional Flow and Transport Model
3. Model Application
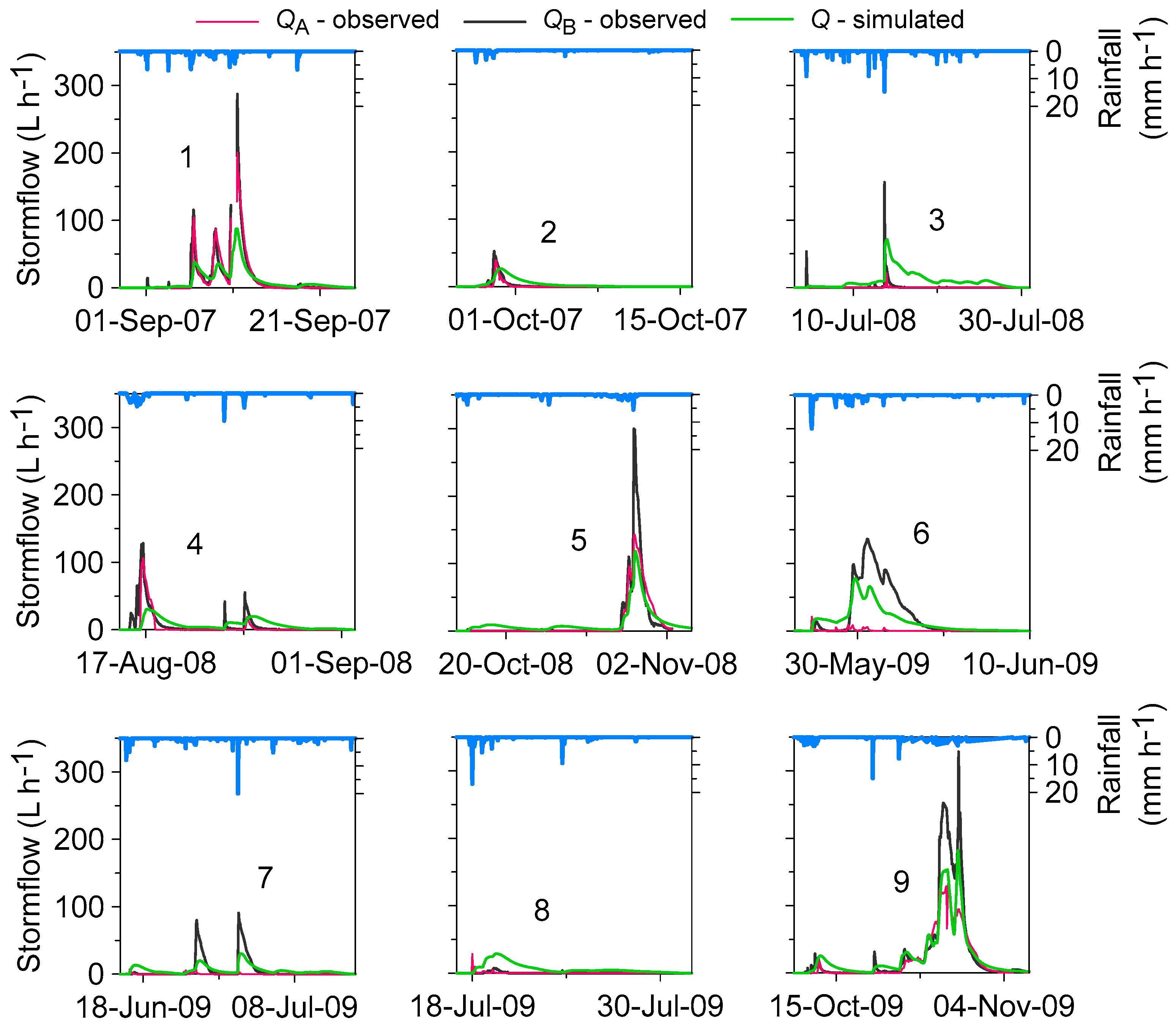
3.1. Model Representation of Stormflow, Deep Percolation, and Transpiration
3.2. Geometric, Material and Boundary Conditions for the Soil Water Flow Model
3.3. Simulation Scenarios
3.4. Episodal Simulations
3.5. Seasonal Simulations
4. Results and Discussion
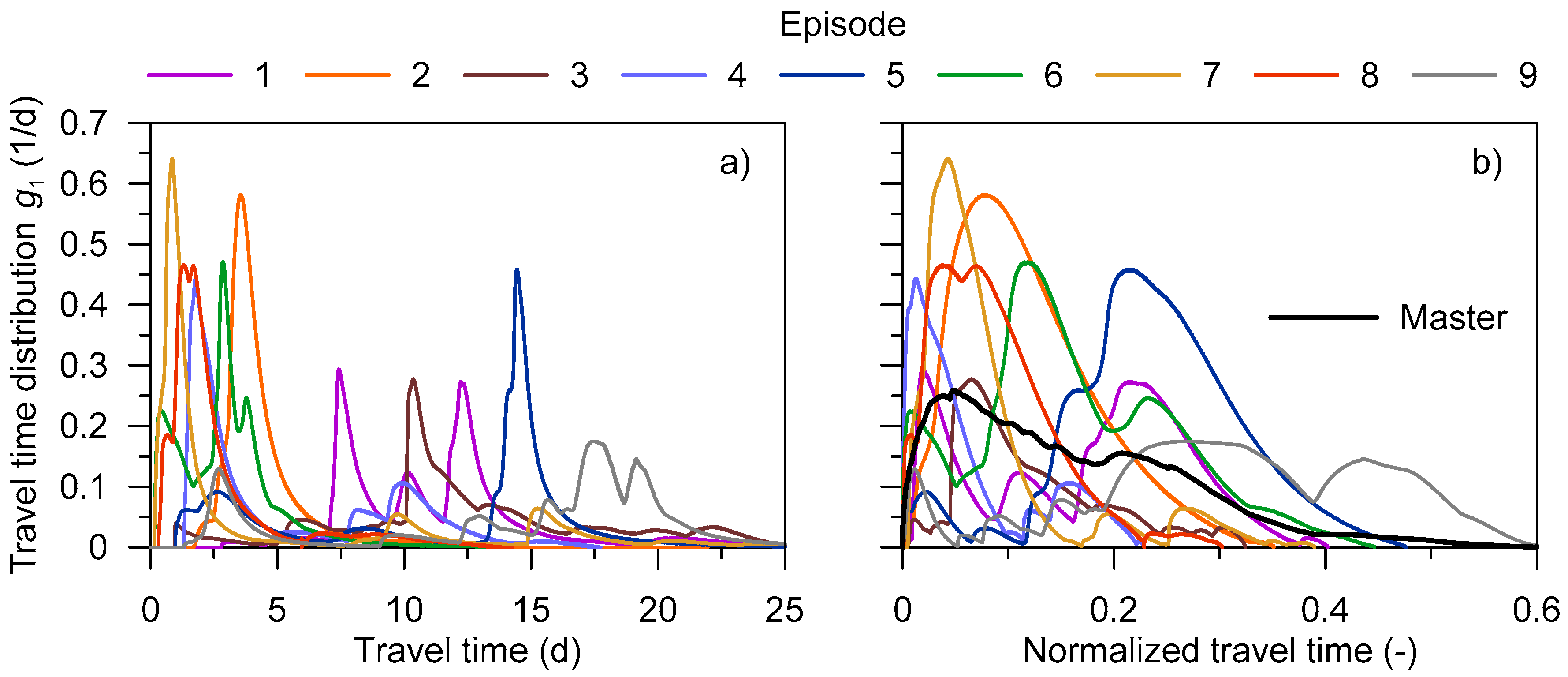
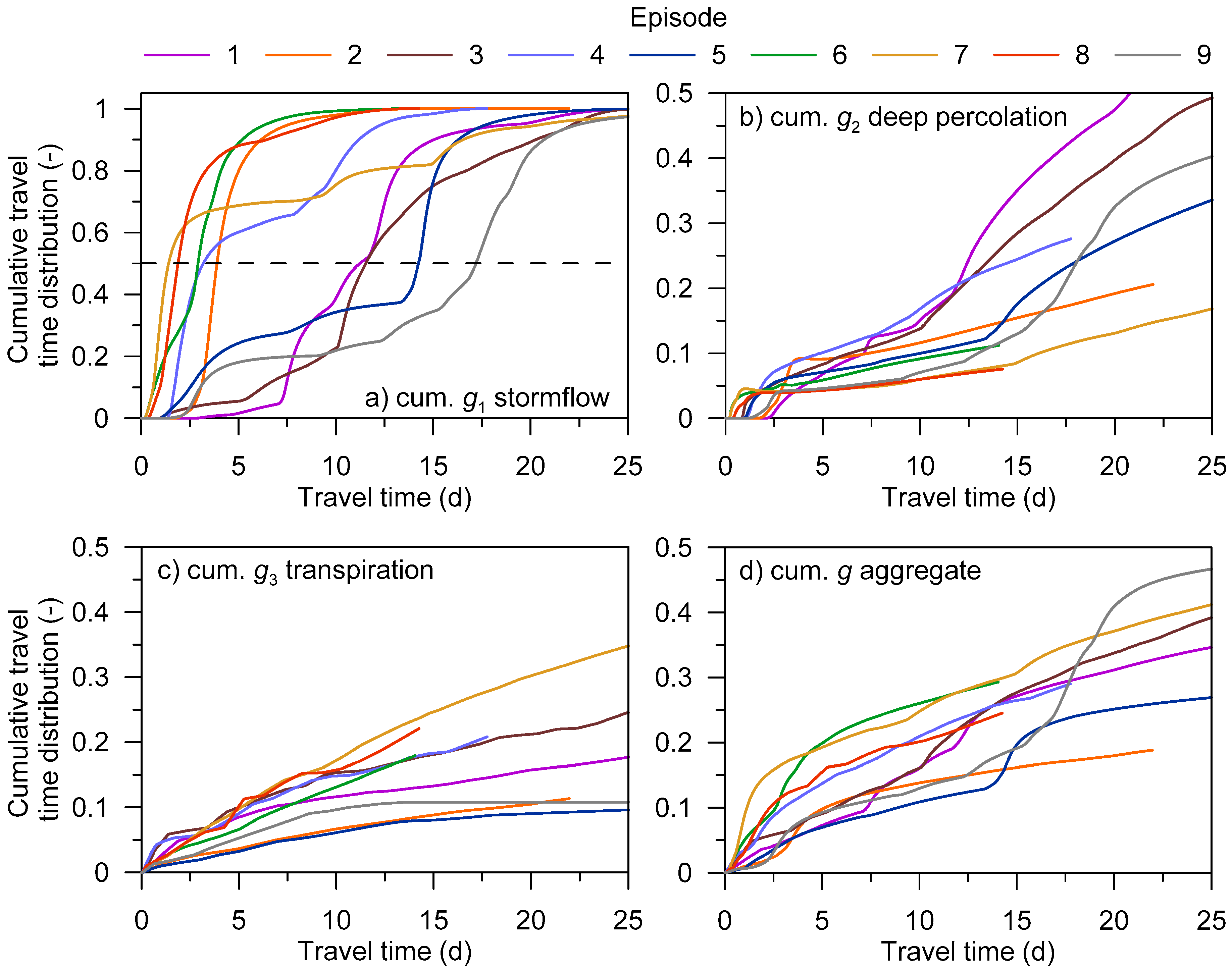
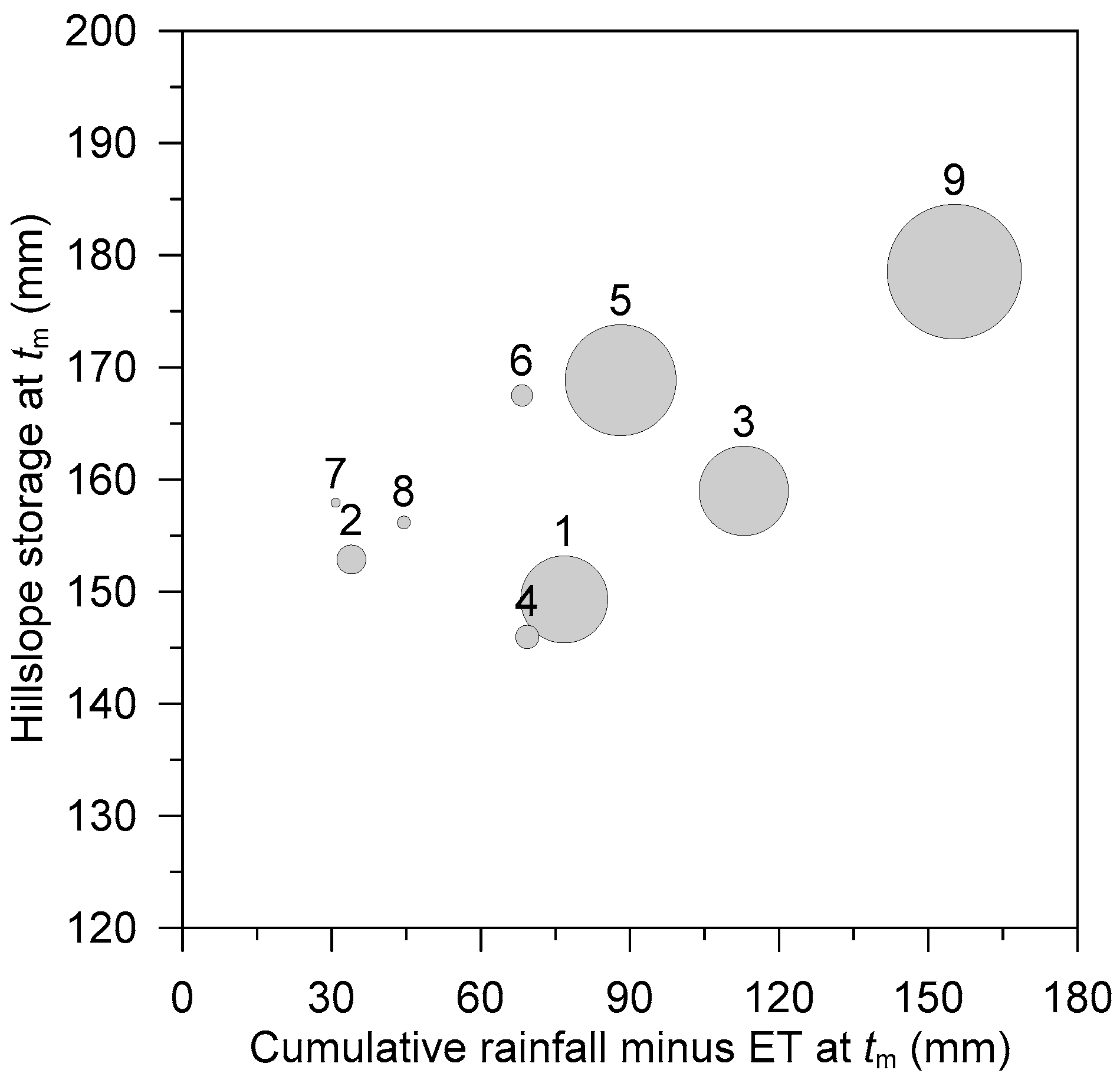
4.1. Episodal Travel Time Distributions
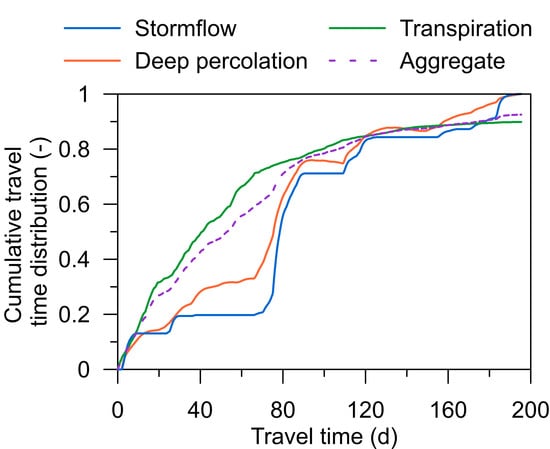
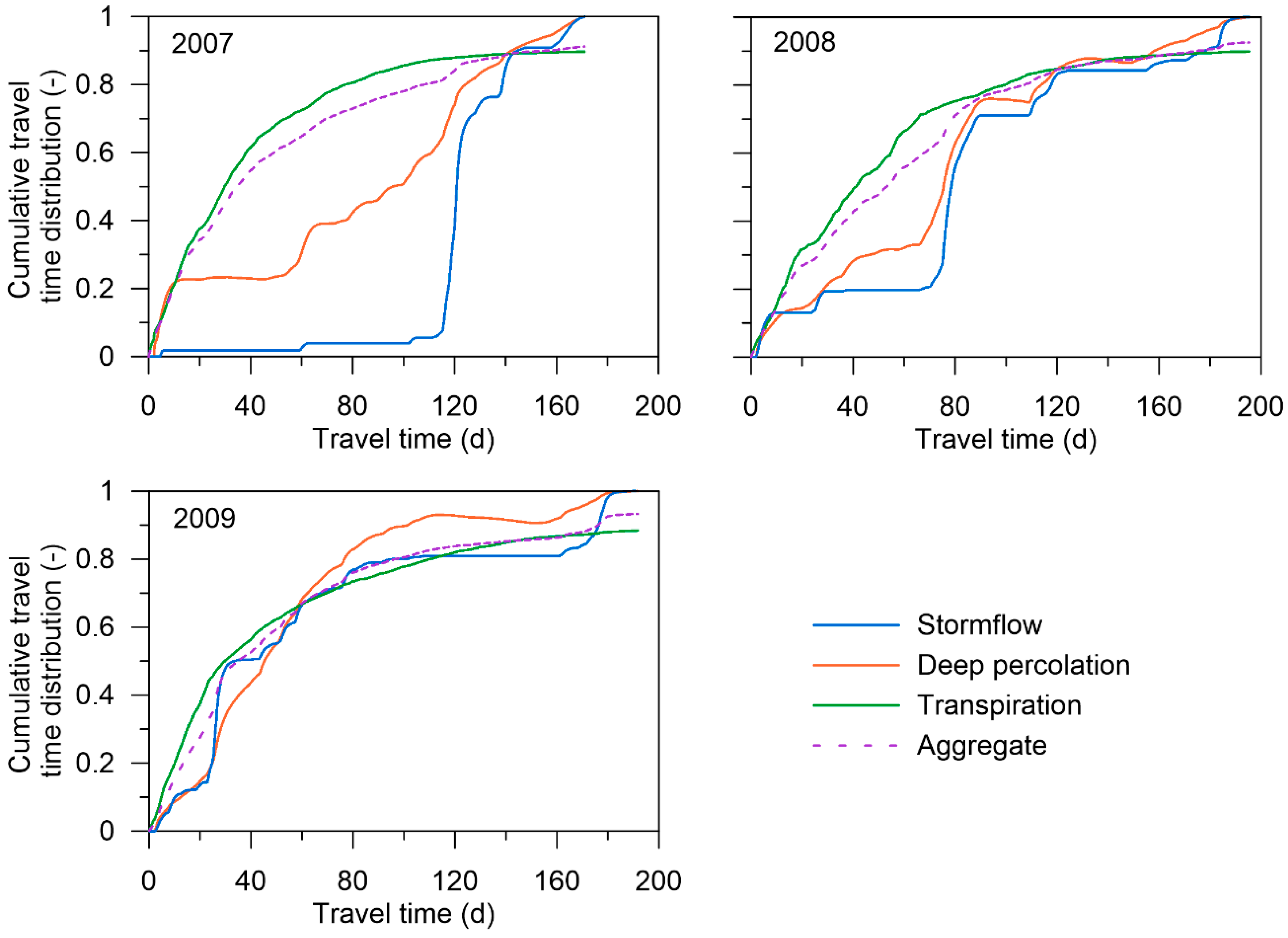
4.2. Seasonal Soil Water Balance, Residence Times, and Travel Time Distributions
4.3. Tracer Mass Partitioning
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Danesh-Yazdi, M.; Klaus, J.; Condon, L.E.; Maxwell, R.M. Bridging the gap between numerical solutions of travel time distributions and analytical storage selection functions. Hydrol. Process. 2018, 32, 1063–1076. [Google Scholar] [CrossRef]
- Woods, R.; Rowe, L. The changing spatial variability of subsurface flow across a hillside. J. Hydrol. 1996, 5, 51–86. [Google Scholar]
- Weiler, M.; McDonnell, J.J.; Tromp-van Meerveld, I.; Uchida, T. Subsurface stormflow. In Encyclopedia of Hydrological Sciences; Anderson, M.G., Ed.; John Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
- Bachmair, S.; Weiler, M. Interactions and connectivity between runoff generation processes of different spatial scales. Hydrol. Process. 2014, 28, 1916–1930. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J. A review and evaluation of catchment transit time modeling. J. Hydrol. 2006, 330, 543–563. [Google Scholar] [CrossRef]
- Rodhe, H. Modeling biogeochemical cycles. In Earth System Science; Elsevier Academic Press: London, UK, 2000; pp. 62–84. [Google Scholar]
- Asano, Y.; Uchida, T.; Ohte, N. Residence times and flow paths of water in steep unchannelled catchments, Tanakami, Japan. J. Hydrol. 2002, 261, 173–192. [Google Scholar] [CrossRef]
- Kabeya, N.; Shimizu, A.; Tamai, K.; Iida, S.; Shimizu, T. Transit times of soil water in thick soil and weathered gneiss layers using deuterium excess modelling. In Conceptual and Modelling Studies of Integrated Groundwater, Surface Water, and Ecological Systems (IAHS Publ. 345); Abesser, C., Naütman, G., Hill, M.C., Blöshl, G., Laksmanan, E., Eds.; IAHS Press: Wallingford, UK, 2011; pp. 163–168. [Google Scholar]
- Kim, S.; Jung, S. Estimation of mean water transit time on a steep hillslope in South Korea using soil moisture measurements and deuterium excess. Hydrol. Process. 2014, 28, 1844–1857. [Google Scholar] [CrossRef]
- Onderka, M.; Chudoba, V. The Wavelets show it—The transit time of water varies in time. J. Hydrol. Hydromech. 2018, 66, 295–302. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J.; Weiler, M.; Kendall, C.; McGlynn, B.L.; Welker, J.M.; Seibert, J. The role of topography on catchment-scale water residence time. Water Resour. Res. 2005, 41, W05002. [Google Scholar] [CrossRef]
- Stewart, M.K.; McDonnell, J.J. Modeling base-flow soil-water residence times from deuterium concentrations. Water Resour. Res. 1991, 27, 2681–2693. [Google Scholar] [CrossRef]
- Kabeya, N.; Katsuyama, M.; Kawasaki, M.; Ohte, N.; Sugimoto, A. Estimation of mean residence times of subsurface waters using seasonal variation in deuterium excess in a small headwater catchment in Japan. Hydrol. Process. 2007, 21, 308–322. [Google Scholar] [CrossRef]
- Vitvar, T.; Balderer, W. Estimation of mean water residence times and runoff generation by180 measurements in a Pre-Alpine catchment (Rietholzbach, Eastern Switzerland). Appl. Geochem. 1997, 12, 787–796. [Google Scholar] [CrossRef]
- Matsutani, J.; Tanaka, T.; Tsujimura, M. Residence times of soil, ground, and discharge waters in a mountainous headwater basin, central Japan, traced by tritium. In Tracers in Hydrology; International Association for Hydrological Science: Yokohama, Japan, 1993; pp. 57–63. [Google Scholar]
- Sprenger, M.; Stumpp, C.; Weiler, M.; Aeschbach, W.; Allen, S.T.; Benettin, P.; McDonnell, J.J. The demographics of water: A review of water ages in the critical zone. Rev. Geophys. 2019, 57, 800–834. [Google Scholar] [CrossRef]
- Hrachowitz, M.; Benettin, P.; van Breukelen, B.M.; Fovet, O.; Howden, N.J.; Ruiz, L.; Wade, A.J. Transit times—The link between hydrology and water quality at the catchment scale. WIREs Water 2016, 3, 629–657. [Google Scholar] [CrossRef]
- Botter, G.; Bertuzzo, E.; Rinaldo, A. Catchment residence and travel time distributions: The master equation. Geophys. Res. Lett. 2011, 38, L11403. [Google Scholar] [CrossRef]
- McGuire, K.J.; Weiler, M.; McDonnell, J.J. Integrating tracer experiments with modeling to assess runoff processes and water transit times. Adv. Water Resour. 2007, 30, 824–837. [Google Scholar] [CrossRef]
- Rodhe, A.; Nyberg, L.; Bishop, K. Transit times for water in a small till catchment from a step shift in the Oxygen 18 content of the water input. Water Resour. Res. 1996, 32, 3497–3511. [Google Scholar] [CrossRef]
- Maloszewski, P.; Zuber, A. Determining the turnover time of groundwater systems with the aid of environmental tracers: 1. Models and their applicability. J. Hydrol. 1982, 57, 207–231. [Google Scholar] [CrossRef]
- Tetzlaff, D.; Malcolm, I.A.; Soulsby, C. Influence of forestry, environmental change and climatic variability on the hydrology, hydrochemistry and residence times of upland catchments. J. Hydrol. 2007, 346, 93–111. [Google Scholar] [CrossRef]
- Stumpp, C.; Maloszewski, P. Quantification of preferential flow and flow heterogeneities in an unsaturated soil planted with different crops using the environmental isotope δ18O. J. Hydrol. 2010, 394, 407–415. [Google Scholar] [CrossRef]
- Sanda, M.; Vitvar, T.; Kulasova, A.; Jankovec, J.; Cislerova, M. Run-off formation in a humid, temperate headwater catchment using a combined hydrological, hydrochemical and isotopic approach (Jizera Mountains, Czech Republic). Hydrol. Process. 2014, 28, 3217–3229. [Google Scholar] [CrossRef]
- Vogel, T.; Sanda, M.; Dusek, J.; Dohnal, M.; Votrubova, J. Using oxygen-18 to study the role of preferential flow in the formation of hillslope runoff. Vadose Zone J. 2010, 9, 252–259. [Google Scholar] [CrossRef]
- Klaus, J.; Chun, K.P.; McGuire, K.J.; McDonnell, J.J. Temporal dynamics of catchment transit times from stable isotope data. Water Resour. Res. 2015, 51, 4208–4223. [Google Scholar] [CrossRef]
- Rinaldo, A.; Benettin, P.; Harman, C.; Hrachowitz, M.; McGuire, K.; van der Velde, Z.; Bertuzzo, E.; Botter, G. Storage selection functions: A coherent framework for quantifying how catchments store and release water and solutes. Water Resour. Res. 2015, 51, 4840–4847. [Google Scholar] [CrossRef]
- van der Velde, Y.; Heidbüchel, I.; Lyon, S.W.; Nyberg, L.; Rodhe, A.; Bishop, K.; Troch, P.A. Consequences of mixing assumptions for time-variable travel time distributions. Hydrol. Process. 2015, 29, 3460–3474. [Google Scholar] [CrossRef]
- Benettin, P.; Soulsby, C.; Birkel, C.; Tetzlaff, D.; Botter, G.; Rinaldo, A. Using SAS functions and high-resolution isotope data to unravel travel time distributions in headwater catchments. Water Resour. Res. 2017, 53, 1864–1878. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Jiang, X.-W. Groundwater flow, transport, and residence times through topography-driven basins with exponentially decreasing permeability and porosity. Water Resour. Res. 2010, 46, W11538. [Google Scholar] [CrossRef]
- Molénat, J.; Gascuel-Odoux, C.; Aquilina, L.; Ruiz, L. Use of gaseous tracers (CFCs and SF6) and transit-time distribution spectrum to validate a shallow groundwater transport model. J. Hydrol. 2013, 480, 1–9. [Google Scholar] [CrossRef]
- Heße, F.; Zink, M.; Kumar, R.; Samaniego, L.; Attinger, S. Spatially distributed characterization of soil-moisture dynamics using travel-time distributions. Hydrol. Earth Syst. Sci. 2017, 21, 549–570. [Google Scholar] [CrossRef]
- Kuppel, S.; Tetzlaff, D.; Maneta, M.P.; Soulsby, C. EcH2O-iso 1.0: Water isotopes and age tracking in a process-based, distributed ecohydrological model. Geosci. Model Dev. 2018, 11, 3045–3069. [Google Scholar] [CrossRef]
- Fiori, A.; Russo, D. Travel time distribution in a hillslope: Insight from numerical simulations. Water Resour. Res. 2008, 44, W12426. [Google Scholar] [CrossRef]
- Remondi, F.; Botter, M.; Burlando, P.; Fatichi, S. Variability of transit time distributions with climate and topography: A modelling approach. J. Hydrol. 2019, 569, 37–50. [Google Scholar] [CrossRef]
- Ameli, A.A.; Amvrosiadi, N.; Grabs, T.; Laudon, H.; Creed, I.F.; McDonnell, J.J.; Bishop, K. Hillslope permeability architecture controls on subsurface transit time distribution and flow paths. J. Hydrol. 2016, 543, 17–30. [Google Scholar] [CrossRef]
- Vanderborght, J.; Vereecken, H. Review of dispersivities for transport modeling in soils. Vadose Zone J. 2007, 6, 29–52. [Google Scholar] [CrossRef]
- Klaus, J.; McDonnell, J.J. Hydrograph separation using stable isotopes: Review and evaluation. J. Hydrol. 2013, 505, 47–64. [Google Scholar] [CrossRef]
- Larsbo, M. An episodic transit time model for quantification of preferential solute transport. Vadose Zone J. 2011, 10, 378–385. [Google Scholar] [CrossRef]
- Dusek, J.; Vogel, T. Modeling subsurface hillslope runoff dominated by preferential flow: One-vs. two-dimensional approximation. Vadose Zone J. 2014, 13. [Google Scholar] [CrossRef]
- Dusek, J.; Vogel, T. Hillslope-storage and rainfall-amount thresholds as controls of preferential stormflow. J. Hydrol. 2016, 534, 590–605. [Google Scholar] [CrossRef]
- Dusek, J.; Vogel, T. Hillslope hydrograph separation: The effects of variable isotopic signatures and hydrodynamic mixing in macroporous soil. J. Hydrol. 2018, 563, 446–459. [Google Scholar] [CrossRef]
- Sanda, M.; Cislerova, M. Transforming hydrographs in the hillslope subsurface. J. Hydrol. Hydromech. 2009, 57, 264–275. [Google Scholar] [CrossRef]
- Dohnal, M.; Dusek, J.; Vogel, T. The impact of the retention curve hysteresis on prediction of soil water dynamics. J. Hydrol. Hydromech. 2006, 54, 258–268. [Google Scholar]
- Dohnal, M.; Dusek, J.; Vogel, T.; Herza, J.; Tacheci, P. Analysis of soil water response to grass transpiration. Soil Water Res. 2006, 1, 85–98. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill Book Co.: Singapore, 1988. [Google Scholar]
- Zuber, A. On the interpretation of tracer data in variable flow systems. J. Hydrol. 1986, 86, 45–57. [Google Scholar] [CrossRef]
- Heidbüchel, I.; Troch, P.A.; Lyon, S.W.; Weiler, M. The master transit time distribution of variable flow systems. Water Resour. Res. 2012, 48, W06520. [Google Scholar] [CrossRef] [Green Version]
- Vogel, T.; Gerke, H.H.; Zhang, R.; van Genuchten, M.T. Modeling flow and transport in a two-dimensional dual-permeability system with spatially variable hydraulic properties. J. Hydrol. 2000, 238, 78–89. [Google Scholar] [CrossRef]
- Gerke, H.H.; van Genuchten, M.T. A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 1993, 29, 305–319. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Materials; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Gerke, H.H.; Dusek, J.; Vogel, T.; Köhne, J.M. Two-dimensional dual permeability analyses of a bromide tracer experiment on a tile-drained field. Vadose Zone J. 2007, 6, 651–667. [Google Scholar] [CrossRef]
- Dusek, J.; Gerke, H.H.; Vogel, T. Surface boundary conditions in two-dimensional dual-permeability modeling of tile drain bromide leaching. Vadose Zone J. 2008, 7, 1287–1301. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and surface temperature. Q. J. R. Meteorol. Soc. 1981, 107, 1–27. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water use and Crop Yield; Simul. Monogr., Cent. for Agric. Publ. and Doc.: Wageningen, The Netherlands, 1978; p. 189. [Google Scholar]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Vogel, T.; Cislerova, M. On the reliability of unsaturated hydraulic conductivity calculated from the moisture retention curve. Transp. Porous Media 1988, 3, 1–15. [Google Scholar] [CrossRef]
- Vogel, T.; van Genuchten, M.T.; Cislerova, M. Effect of the shape of soil hydraulic properties near saturation on numerical simulation of variably-saturated flow. Adv. Water Resour. 2000, 24, 133–144. [Google Scholar] [CrossRef]
- Dusek, J.; Vogel, T.; Dohnal, M.; Gerke, H.H. Combining dual-continuum approach with diffusion wave model to include a preferential flow component in hillslope scale modeling of shallow subsurface runoff. Adv. Water Resour. 2012, 44, 113–125. [Google Scholar] [CrossRef]
- Dusek, J.; Vogel, T.; Sanda, M. Hillslope hydrograph analysis using synthetic and natural oxygen-18 signatures. J. Hydrol. 2012, 475, 415–427. [Google Scholar] [CrossRef]
- Heidbüchel, I.; Troch, P.A.; Lyon, S.W. Separating physical and meteorological controls of variable transit times in zero-order catchments. Water Resour. Res. 2013, 49, 7644–7657. [Google Scholar] [CrossRef]
- Sprenger, M.; Seeger, S.; Blume, T.; Weiler, M. Travel times in the vadose zone: Variability in space and time. Water Resour. Res. 2016, 52, 5727–5754. [Google Scholar] [CrossRef] [Green Version]
| Depth | θr | θs | α | n | Ks | hs | |
|---|---|---|---|---|---|---|---|
| (cm) | (cm3 cm−3) | (cm3 cm−3) | (cm−1) | (-) | (cm d−1) | (cm) | |
| SM | 0–8 | 0.20 | 0.55 | 0.050 | 2.00 | 567 | 0.00 |
| 8–20 | 0.20 | 0.54 | 0.050 | 1.50 | 67 | −0.69 | |
| 20–70 | 0.20 | 0.49 | 0.020 | 1.20 | 17 | −1.48 | |
| 70–75 | 0.20 | 0.41 | 0.020 | 1.20 | 1.3 | −1.88 | |
| 75–300 | 0.00 | 0.21 | 0.020 | 1.20 | 0.4 | −2.61 | |
| PF | 0–70 | 0.01 | 0.60 | 0.050 | 3.00 | 5000 | 0.00 |
| 70–300 | 0.01 | 0.60 | 0.050 | 3.00 | 0.4 | 0.00 |
| Episode | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Episode Duration (d) | 27 | 22 | 26 | 18 | 26 | 14 | 32 | 14 | 33 |
| tm (d) | 11.2 | 3.9 | 11.5 | 3.2 | 14.2 | 2.9 | 1.4 | 1.9 | 17.2 |
| Season | 2007 | 2008 | 2009 |
| Season Duration (d) | 171 | 191 | 191 |
| Observed Rainfall (mm) | 634 | 724 | 874 |
| Stormflow (mm) | 97 | 169 | 301 |
| Deep Percolation (mm) | 76 | 125 | 182 |
| Transpiration (mm) | 429 | 438 | 396 |
| Initial Storage (mm) | 106 | 145 | 145 |
| Final Storage (mm) | 138 | 137 | 140 |
| Season | 2007 | 2008 | 2009 |
| Net Water Input (mm) | 205 | 286 | 478 |
| Stormflow (%) | 5.0 | 12.8 | 23.5 |
| Deep Percolation (%) | 9.9 | 13.5 | 18.8 |
| Transpiration (%) | 76.3 | 66.2 | 51.0 |
| Residual (%) | 8.8 | 7.5 | 6.7 |
| Season | 2007 | 2008 | 2009 |
| Stormflow (d) | 120.9 | 78.5 | 33.5 |
| Deep Percolation (d) | 95.8 | 75.5 | 35.4 |
| Transpiration (d) | 26.4 | 35.4 | 23.5 |
| Aggregate (d) | 30.4 | 46.2 | 30.1 |
| Episode | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Net Water Input (mm) | 121 | 28 | 130 | 91 | 102 | 80 | 77 | 36 | 260 |
| Stormflow (%) | 14.9 | 7.2 | 13.6 | 8.7 | 14.5 | 16.4 | 18.8 | 9.4 | 32.5 |
| Deep Percolation (%) | 7.0 | 2.5 | 8.9 | 5.1 | 6.0 | 3.5 | 6.3 | 2.5 | 11.6 |
| Transpiration (%) | 13.7 | 9.2 | 18.0 | 15.1 | 6.6 | 9.4 | 21.0 | 12.6 | 4.4 |
| Residual (%) | 64.4 | 81.2 | 59.5 | 71.0 | 72.8 | 70.7 | 53.9 | 75.5 | 51.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dusek, J.; Vogel, T. Modeling Travel Time Distributions of Preferential Subsurface Runoff, Deep Percolation and Transpiration at A Montane Forest Hillslope Site. Water 2019, 11, 2396. https://doi.org/10.3390/w11112396
Dusek J, Vogel T. Modeling Travel Time Distributions of Preferential Subsurface Runoff, Deep Percolation and Transpiration at A Montane Forest Hillslope Site. Water. 2019; 11(11):2396. https://doi.org/10.3390/w11112396
Chicago/Turabian StyleDusek, Jaromir, and Tomas Vogel. 2019. "Modeling Travel Time Distributions of Preferential Subsurface Runoff, Deep Percolation and Transpiration at A Montane Forest Hillslope Site" Water 11, no. 11: 2396. https://doi.org/10.3390/w11112396
APA StyleDusek, J., & Vogel, T. (2019). Modeling Travel Time Distributions of Preferential Subsurface Runoff, Deep Percolation and Transpiration at A Montane Forest Hillslope Site. Water, 11(11), 2396. https://doi.org/10.3390/w11112396