Evolution Pattern of Tailings Flow from Dam Failure and the Buffering Effect of Debris Blocking Dams
Abstract
1. Introduction
2. Model and Computational Method
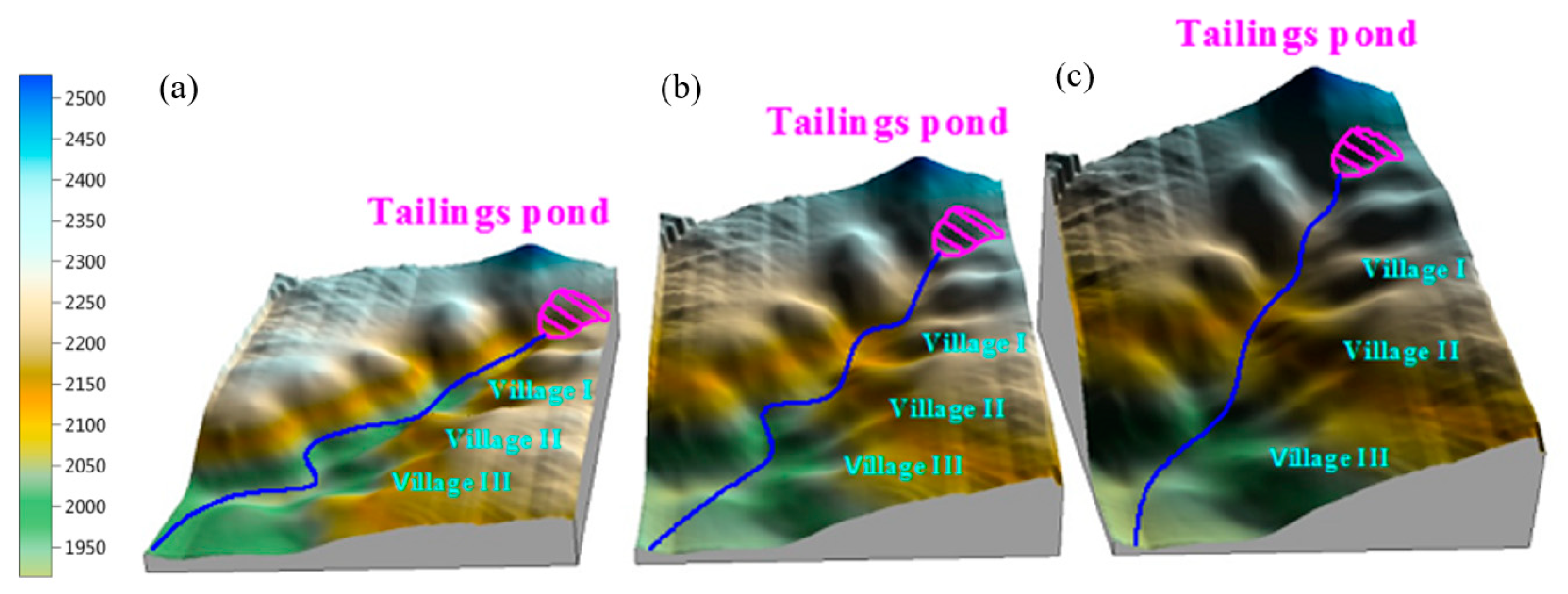
2.1. Simulation Model and Boundary Conditions
2.2. Computational Parameters
3. Results and Discussion
3.1. Various Downstream Riverbed Slope Conditions
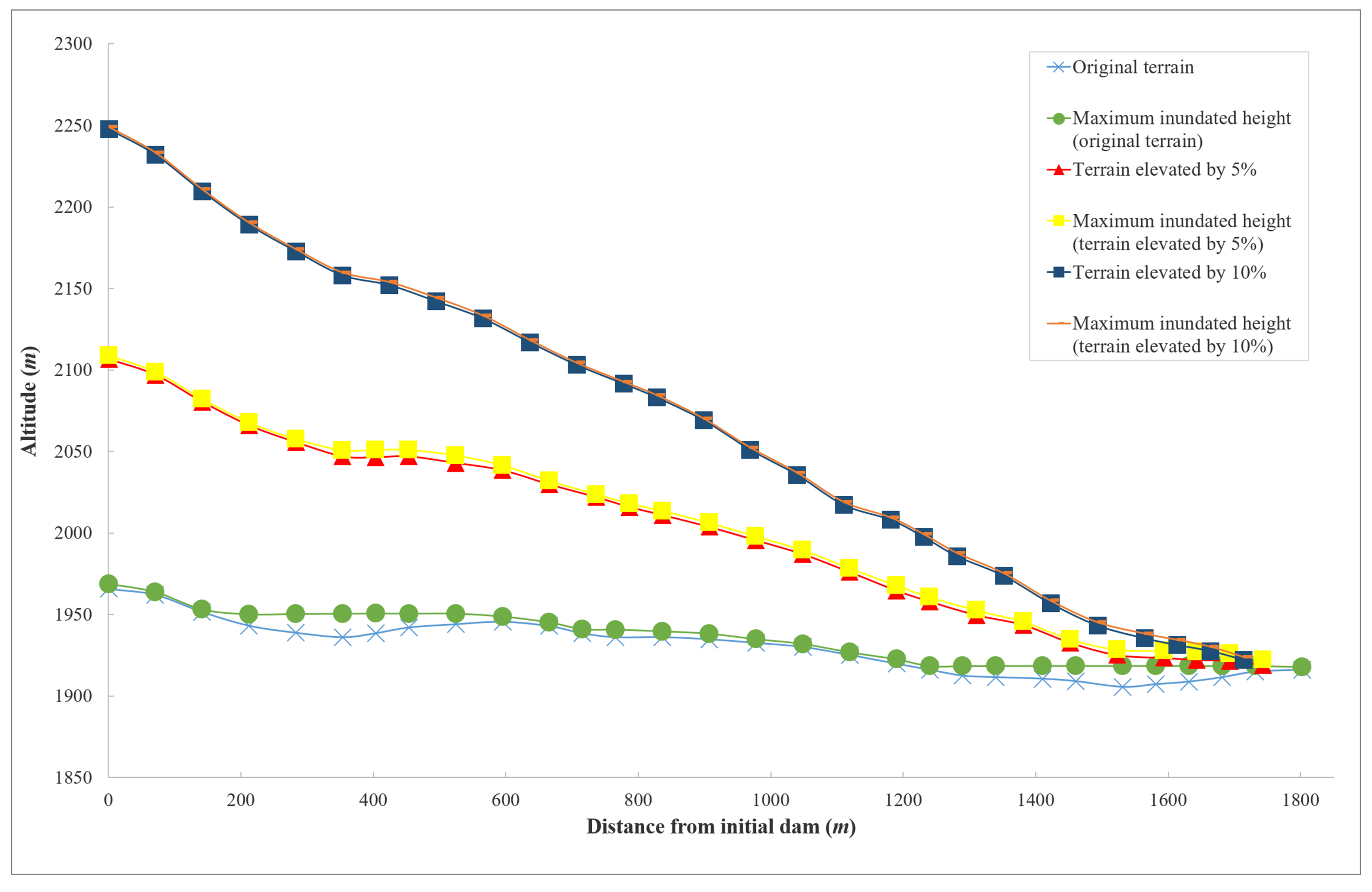
3.1.1. Flow Depth of Leaked Tailings
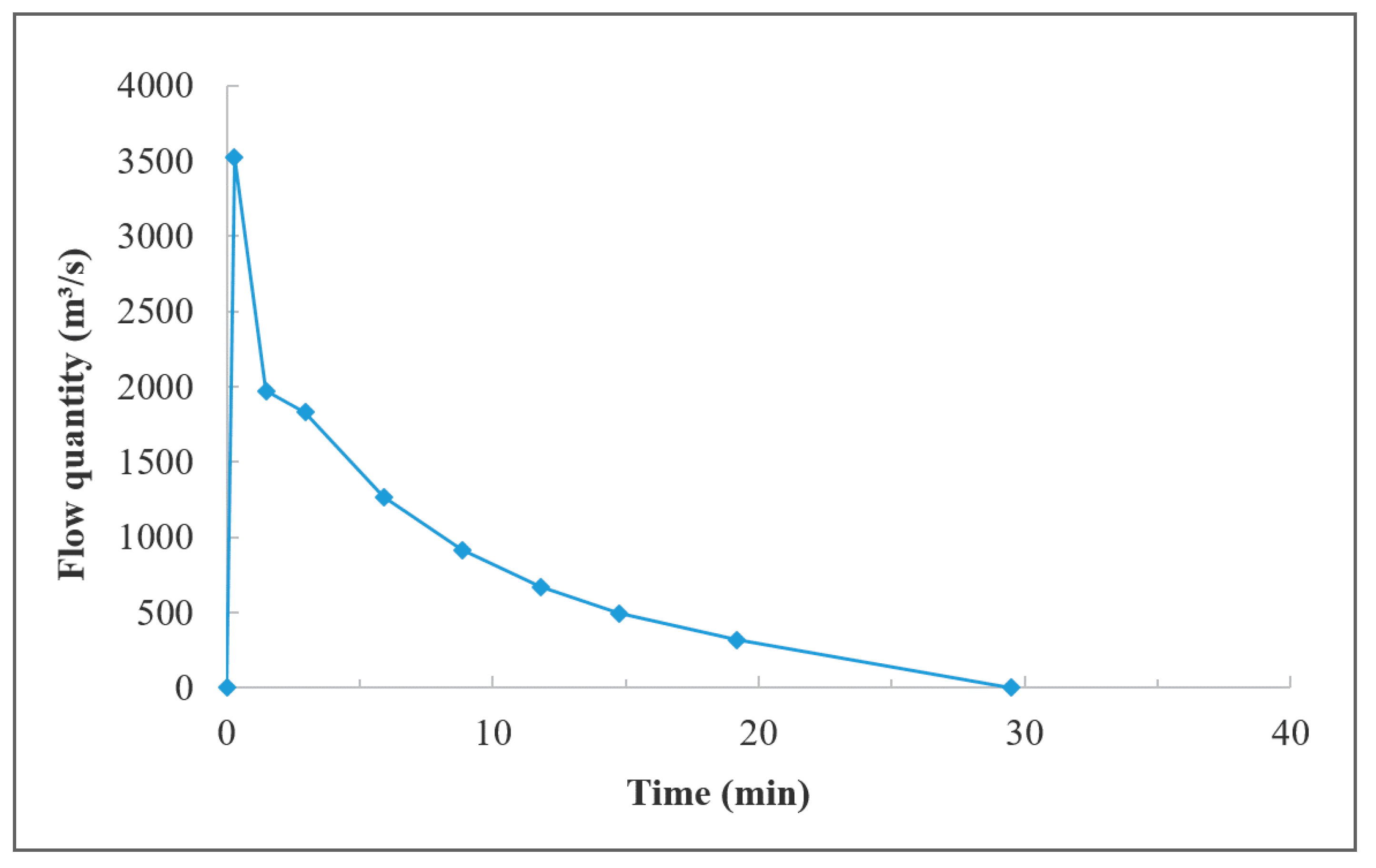
3.1.2. Flow Rate of Leaked Tailings
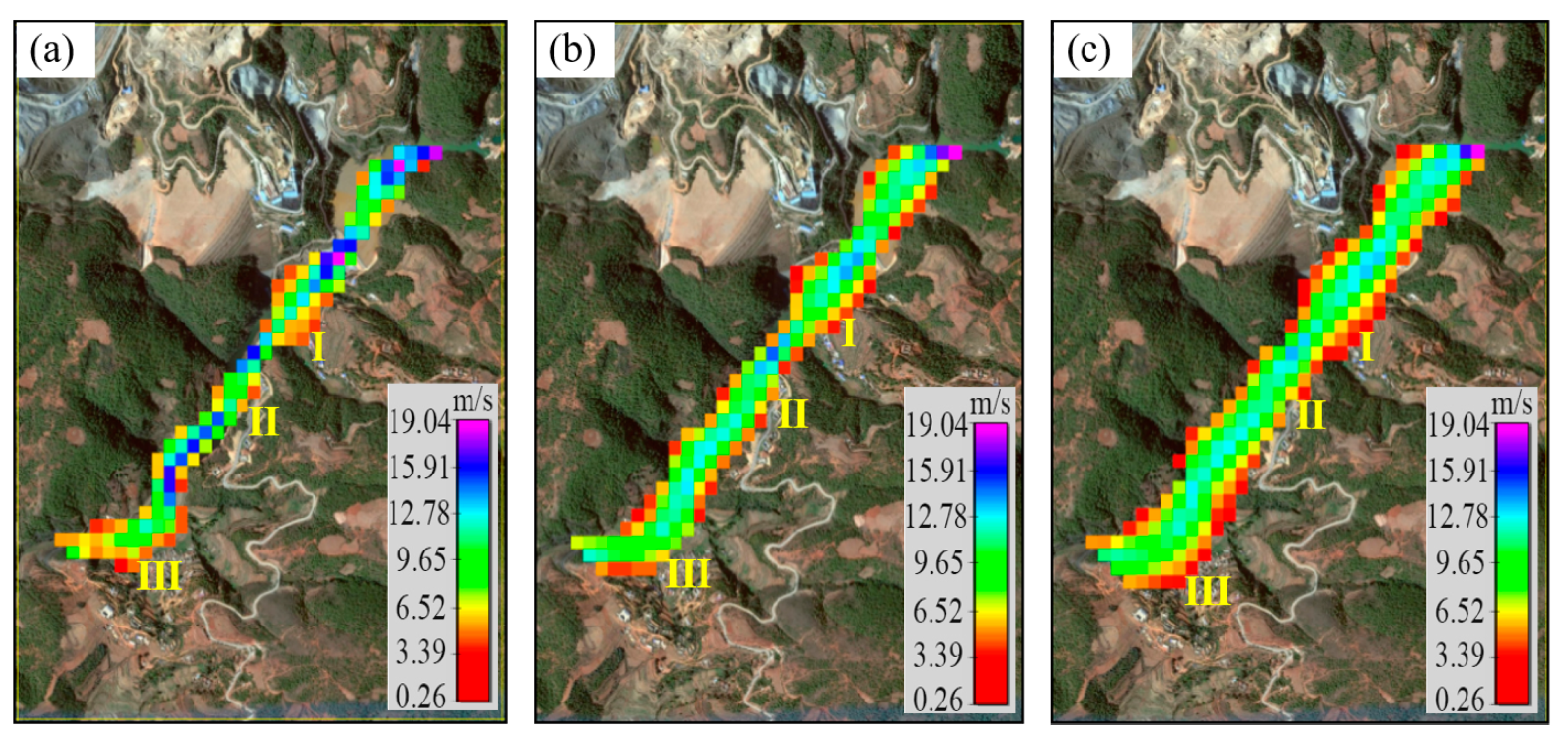
3.1.3. Impact Force of Leaked Tailings Flow
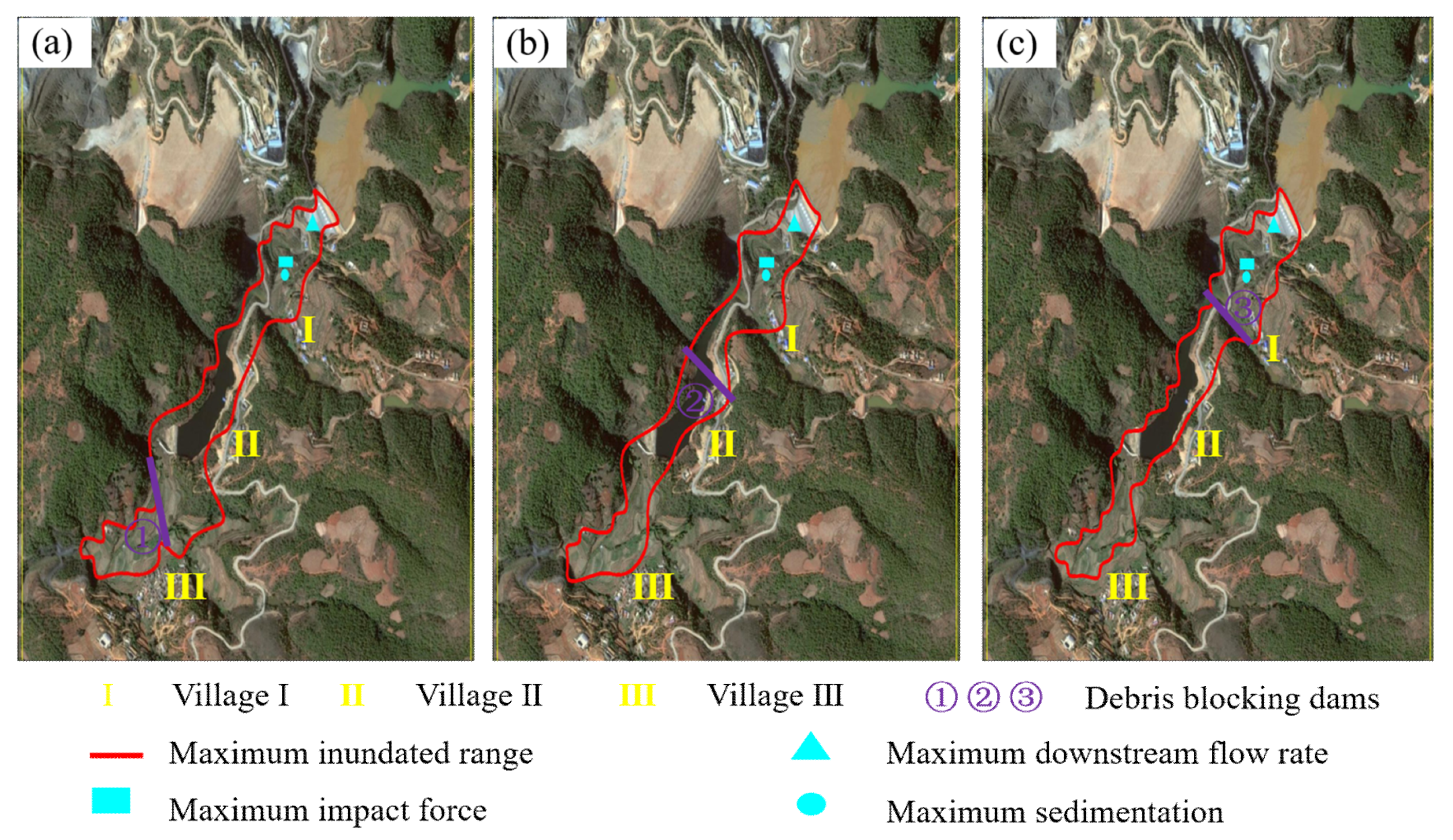
3.2. Effects of Debris Blocking Dam on Tailings Flow
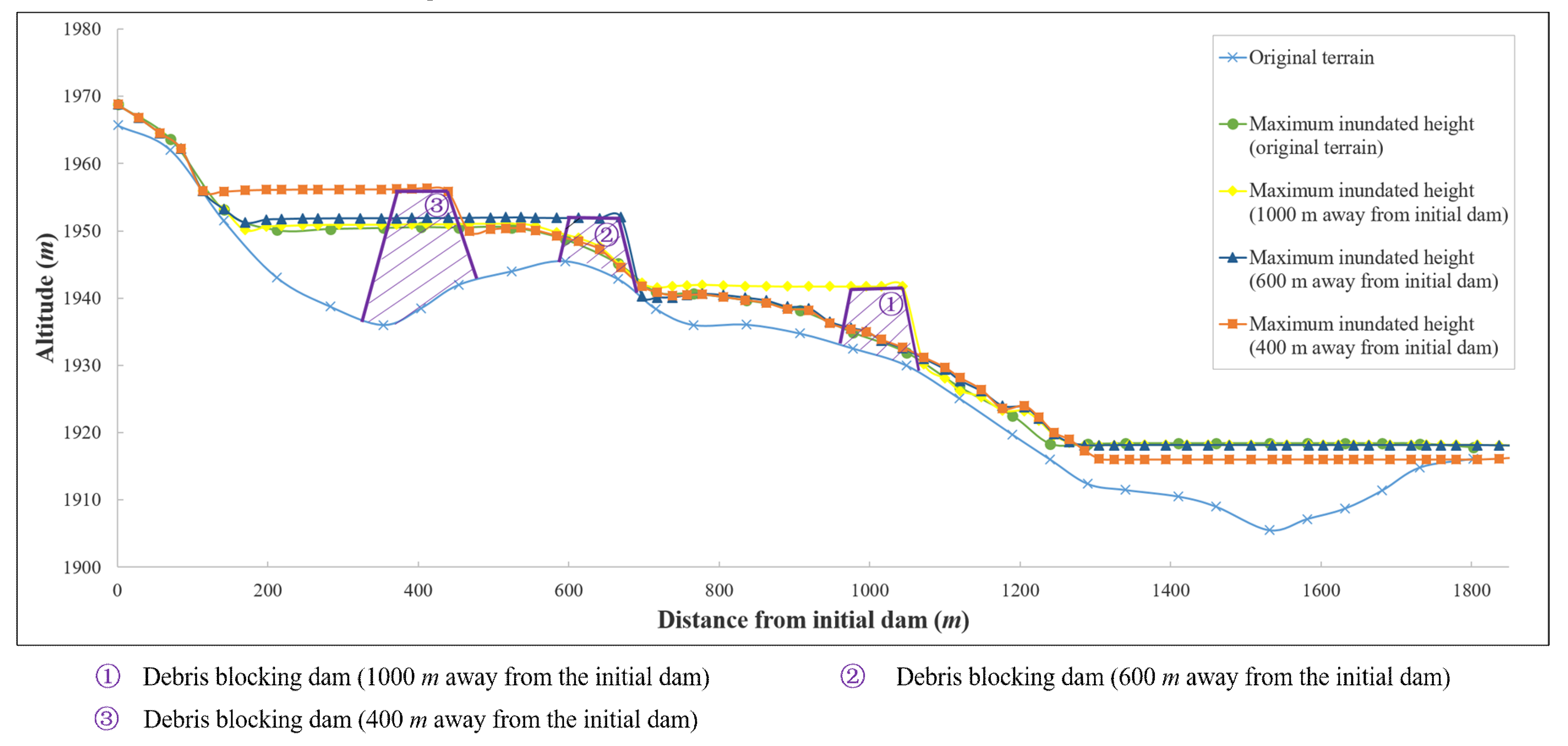
3.2.1. Flow Depth of Leaked Tailings
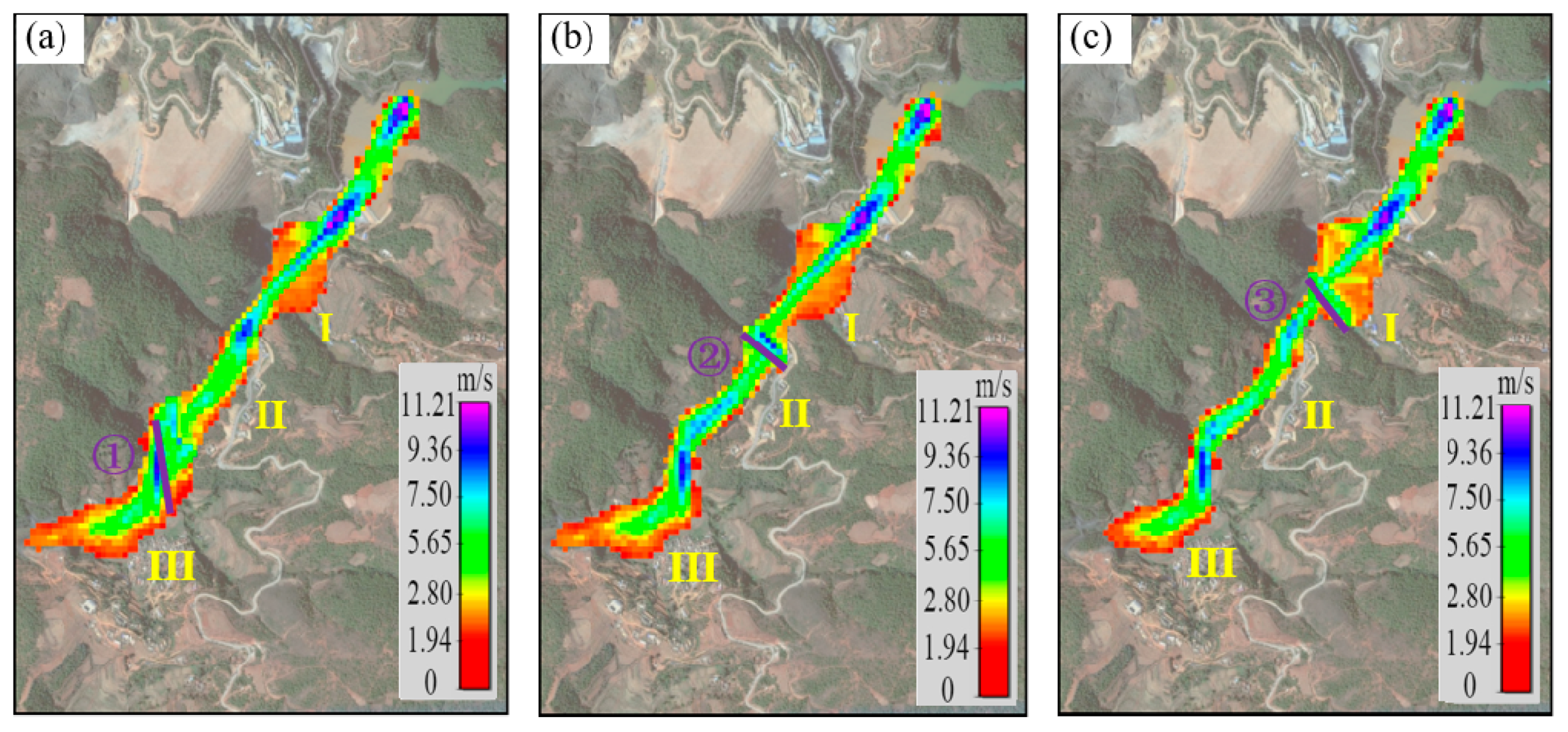
3.2.2. Flow Rate of Leaked Tailings
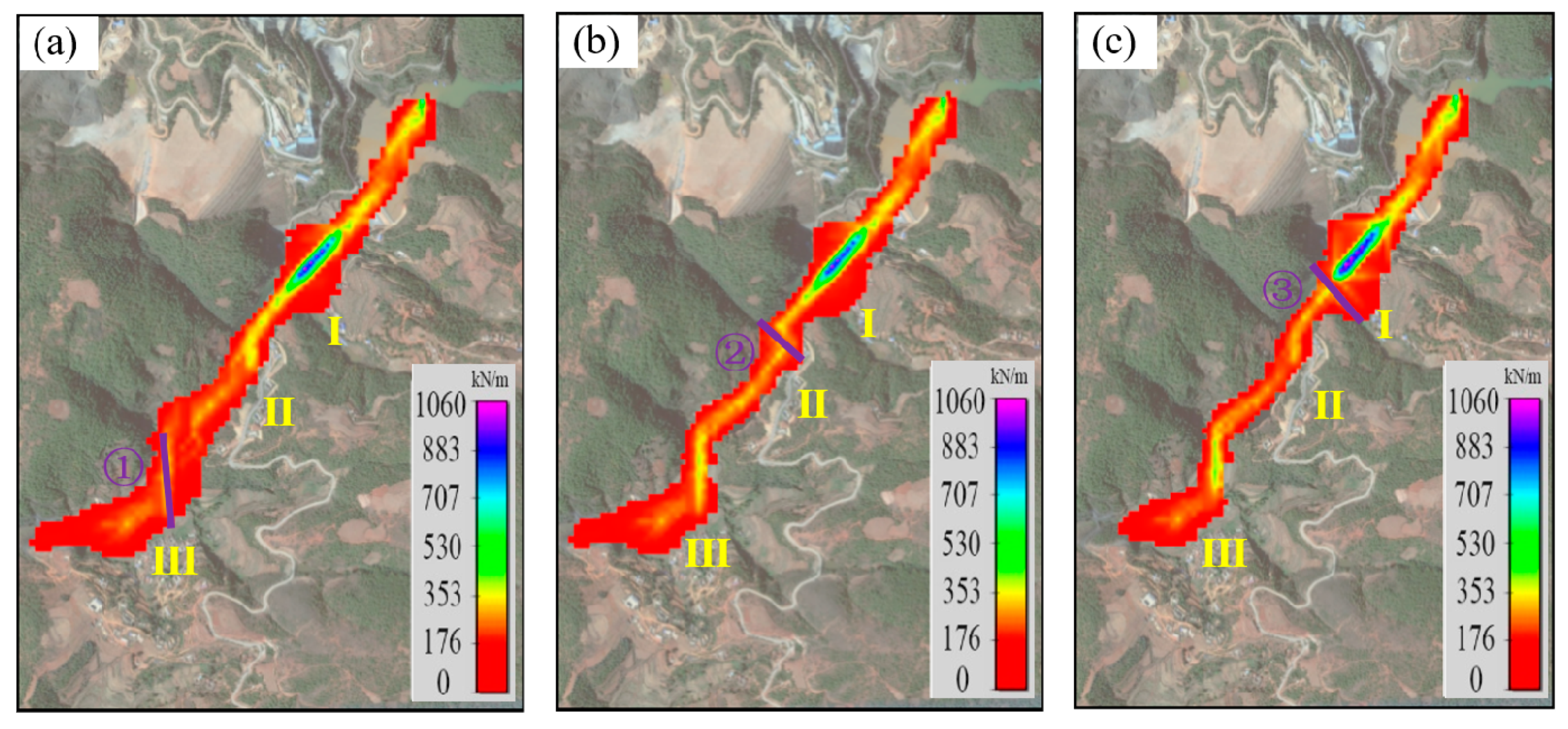
3.2.3. Impact Force of Leaked Tailings Flow
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yin, G.; Li, G.; Wei, Z.; Wan, L.; Shui, G.; Jing, X. Stability analysis of a copper tailings dam via laboratory model tests: A Chinese case study. Miner. Eng. 2011, 24, 122–130. [Google Scholar] [CrossRef]
- Mura, J.C.; Gama, F.F.; Paradella, W.R.; Negrão, P.; Carneiro, S.; De Oliveira, C.G.; Brandão, W.S. Monitoring the Vulnerability of the Dam and Dikes in Germano Iron Mining Area after the Collapse of the Tailings Dam of Fundão (Mariana-MG, Brazil) Using DInSAR Techniques with TerraSAR-X Data. Remote Sens. 2018, 10, 1507. [Google Scholar] [CrossRef]
- Sun, E.; Zhang, X.; Li, Z. The internet of things (IOT) and cloud computing (CC) based tailings dam monitoring and pre-alarm system in mines. Saf. Sci. 2012, 50, 811–815. [Google Scholar] [CrossRef]
- Azam, S. Tailings dam failure: A review of the last one hundred years. Geotech. News 2010, 28, 50–53. [Google Scholar]
- Zhou, X.; Cheng, H. Stability analysis of three-dimensional seismic landslides using the rigorous limit equilibrium method. Eng. Geol. 2014, 174, 87–102. [Google Scholar] [CrossRef]
- Parbhakar-Fox, A.; Glen, J.; Raimondo, B. A Geometallurgical Approach to Tailings Management: An Example from the Savage River Fe-Ore Mine, Western Tasmania. Minerals 2018, 8, 454. [Google Scholar] [CrossRef]
- Wang, K.; Yang, P.; Hudson-Edwards, K.A.; Lyu, W.; Yang, C.; Jing, X. Integration of DSM and SPH to Model Tailings Dam Failure Run-Out Slurry Routing Across 3D Real Terrain. Water 2018, 10, 1087. [Google Scholar] [CrossRef]
- Jia, T.; Wang, R.; Fan, X.; Chai, B. A Comparative Study of Fungal Community Structure, Diversity and Richness between the Soil and the Phyllosphere of Native Grass Species in a Copper Tailings Dam in Shanxi Province, China. Appl. Sci. 2018, 8, 1297. [Google Scholar] [CrossRef]
- Wang, X.; Zhan, H.; Wang, J.; Li, P. The Stability of Tailings Dams under Dry-Wet Cycles: A Case Study in Luonan, China. Water 2018, 10, 1048. [Google Scholar] [CrossRef]
- Ismet, C. Guest editorial-Special issue on dynamic failures in underground mines. Int. J. Min. Sci. Technol. 2018, 28, 719–720. [Google Scholar] [CrossRef]
- Aly, A.; Keizo, U.; Yang, Q. Assessment of 3D Slope Stability Analysis Methods Based on 3D Simplified Janbu and Hovland Methods. Int. J. Geomech. 2012, 12, 81–89. [Google Scholar]
- Santamarina, C.J.; Torres-Cruz, L.A.; Bachus, R.C. Why coal ash and tailings dam disasters occur. Science 2019, 364, 526–528. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.; Mei, G. Statistical analysis of tailings pond accidents and cause analysis of dam failure. China Saf. Sci. J. 2014, 24, 70–76. (In Chinese) [Google Scholar]
- Wei, Z.; Yin, G.; Wang, J.; Wan, L.; Li, G. Design, construction and management of tailings storage facilities for surface disposal in China: case studies of failures. Waste Manage Res. 2013, 31, 106–112. [Google Scholar] [CrossRef] [PubMed]
- Rico, M.; Benito, G.; Díez-Herrero, A. Floods from tailings dam failures. J. Hazard. Mater. 2008, 154, 79–87. [Google Scholar] [CrossRef]
- Peng, K.; Zhou, J.; Zou, Q.; Zhang, J.; Wu, F. Effects of stress lower limit during cyclic loading and unloading on deformation characteristics of sandstones. Constr. Build. Mater. 2019, 217, 202–215. [Google Scholar] [CrossRef]
- Roussel, N.; Stefani, C.; Leroy, R. From mini-cone test to Abrams cone test: Measurement of cement-based materials yield stress using slump tests. Cem. Concr. Res. 2005, 35, 817–822. [Google Scholar] [CrossRef]
- Hu, J.; Liu, C.; Li, Q.; Shi, X. Molecular simulation of thermal energy storage of mixed CO2/IRMOF-1 nanoparticle nanofluid. Int. J. Heat Mass Tran. 2018, 125, 1345–1348. [Google Scholar] [CrossRef]
- Tian, S.; Chen, J. Multi-hierarchical fuzzy judgment and nested dominance relation of the rough set theory-based environmental risk evaluation for tailings reservoirs. J. Cent. South Univ. 2015, 22, 4797–4806. [Google Scholar] [CrossRef]
- Deng, D.; Li, L.; Wang, J.; Zhao, L. Limit equilibrium method for rock slope stability analysis by using the Generalized Hoek–Brown criterion. Int. J. Rock Mech. Min. 2016, 89, 176–184. [Google Scholar]
- Jing, X.; Chen, Y.; Xie, D.; Williams, D.J.; Wu, S.; Wang, W.; Yin, T. The Effect of Grain Size on the Hydrodynamics of Mudflow Surge from a Tailings Dam-Break. Appl. Sci. 2019, 9, 2474. [Google Scholar] [CrossRef]
- Zheng, B.; Zhang, D.; Liu, W.; Yang, Y.; Yang, H. Use of Basalt Fiber-Reinforced Tailings for Improving the Stability of Tailings Dam. Materials 2019, 12, 1306. [Google Scholar] [CrossRef] [PubMed]
- Dutto, P.; Stickle, M.M.; Pastor, M.; Manzanal, D.; Yague, A.; Moussavi Tayyebi, S.; Lin, C.; Elizalde, M.D. Modelling of fluidised geomaterials: The case of the Aberfan and the Gypsum tailings impoundment flowslides. Materials 2017, 10, 562. [Google Scholar] [CrossRef] [PubMed]
- Marsooli, R.; Wu, W. 3-D finite-volume model of dam-break flow over uneven beds based on VOF method. Adv. Water Resour. 2014, 70, 104–117. [Google Scholar] [CrossRef]
- Zhang, L.; Tian, S.; Peng, T. Molecular Simulations of Sputtering Preparation and Transformation of Surface Properties of Au/Cu Alloy Coatings Under Different Incident Energies. Metals 2019, 9, 259. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency. Numerical Models Meeting Minimum Requirement of National Flood Insurance Program 2010. Available online: http://www.fema.gov (accessed on 10 January 2019).
- FLO-2D Software Inc. FLO-2D Users Manual; Version 2018, 06; FLO-2D Software Inc.: Nutrioso, AZ, USA, 2018. [Google Scholar]
- Hübl, J.; Steinwendtner, H. Two-dimensional simulation of two viscous debris flows in Austria. Phys. Chem. Earth 2001, 26, 639–644. [Google Scholar] [CrossRef]
- Du, X.; Sun, S.; Zhao, Z.; Qin, L. Research on Engineering Control Effect on Hongchun Gully Debris Based on FLO-2D Model. Earth Environ. 2016, 44, 376–381. (In Chinese) [Google Scholar]
- Pashias, N. A fifty cent rheometer for yield stress measurement. J. Rheol. 1996, 40, 1179. [Google Scholar] [CrossRef]
- Alhasan, Z.; Jandora, J.; Riha, J. Comparison of specific sediment transport rates obtained from empirical formulae and dam breaching experiments. Environ. Fluid Mech. 2016, 16, 1–23. [Google Scholar] [CrossRef]
- Gawu, S.K.; Fourie, A.B. Assessment of the modified slump test as a measure of the yield stress. Can. Geotech. J. 2004, 41, 39–47. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, Z.; Li, Q.; Guo, X. Sequential dam break simulation and risk analysis of earth-rock dams of cascade reservoirs. J. Hydroelectr. Eng. 2018, 37, 65–73. [Google Scholar]
- Tian, S.; Chen, J.; Dong, L. Rock strength interval analysis using theory of testing blind data and interval estimation. J. Cent. South Univ. 2017, 24, 168–177. [Google Scholar] [CrossRef]
- Mizani, S. Rheology of Thickened Gold Tailings for Surface Deposition. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2010. [Google Scholar]
- Zhou, Y.; Li, Q.; Wang, Q. Energy Storage Analysis of UIO-66 and Water Mixed Nanofluids: An Experimental and Theoretical Study. Energies 2019, 12, 2521. [Google Scholar] [CrossRef]
- Zhang, P.; Ma, J.; Shu, H.; Wang, G. Numerical simulation of erosion and deposition debris flow based on FLO-2D model. J. Lanzhou Univ. Nat. Sci. 2014, 50, 363–368. (In Chinese) [Google Scholar]
- Okuda, S.; Okunishi, K.; Suwa, H. Observation of Debris Flow at Kamikamihori Valley of Mt. Yakedake. In Proceedings of the 3rd Meeting of IGU Commission on Field Experiment in Geomorphology, Kyoto, Japan, 24–30 August 1980; pp. 116–139. [Google Scholar]
- Li, J.; Luo, D. The Formation and Characteristics of Mudflow and Flood in the Mountain Area of the Dachao River and Its Prevention. Z. Geomorphol. N.F. 1981, 25, 470–484. [Google Scholar]
- Nam, D.H.; Kim, M.I.; Kang, D.H.; Kim, B.S. Debris Flow Damage Assessment by Considering Debris Flow Direction and Direction Angle of Structure in South Korea. Water 2019, 11, 328. [Google Scholar] [CrossRef]


| Simulation Parameters | Values | |
|---|---|---|
| Fluid relative density (g/cm3) | 1.8 | |
| Retardation coefficient of laminar flow | 2285 | |
| Manning coefficient in passage zone | 0.05 | |
| Parameters of yield stress coefficients | 0.128 | |
| 12 | ||
| Parameters of viscous force coefficients | 0.0473 | |
| 21 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Tian, S.; Hu, B.; Xu, Z.; Chen, J.; Kong, X. Evolution Pattern of Tailings Flow from Dam Failure and the Buffering Effect of Debris Blocking Dams. Water 2019, 11, 2388. https://doi.org/10.3390/w11112388
Wang G, Tian S, Hu B, Xu Z, Chen J, Kong X. Evolution Pattern of Tailings Flow from Dam Failure and the Buffering Effect of Debris Blocking Dams. Water. 2019; 11(11):2388. https://doi.org/10.3390/w11112388
Chicago/Turabian StyleWang, Guangjin, Sen Tian, Bin Hu, Zhifa Xu, Jie Chen, and Xiangyun Kong. 2019. "Evolution Pattern of Tailings Flow from Dam Failure and the Buffering Effect of Debris Blocking Dams" Water 11, no. 11: 2388. https://doi.org/10.3390/w11112388
APA StyleWang, G., Tian, S., Hu, B., Xu, Z., Chen, J., & Kong, X. (2019). Evolution Pattern of Tailings Flow from Dam Failure and the Buffering Effect of Debris Blocking Dams. Water, 11(11), 2388. https://doi.org/10.3390/w11112388






