Assessment of Sediment Transport Functions with the Modified SWAT-Twn Model for a Taiwanese Small Mountainous Watershed

Abstract

In Taiwan, the steep landscape and highly vulnerable geology make it difficult to predict soil erosion and sediment transportation via variable transport conditions. In this study, we integrated the Taiwan universal soil loss equation (TUSLE) and slope stability conditions in the soil and water assessment tool (SWAT) as the SWAT-Twn model to improve sediment simulation and assess the sediment transport functions in the Chenyulan watershed, a small mountainous catchment. The results showed that the simulation of streamflow was satisfactory for calibration and validation. Before model calibration and validation for sediment, SWAT-Twn with default sediment transport method performed better in sediment simulation than the official SWAT model (version 664). The SWAT-Twn model coupled with the simplified Bagnold equation could estimate sediment export more accurately and significantly reduce the overestimated sediment yield by 65.7%, especially in highly steep areas. Furthermore, five different sediment transport methods (simplified Bagnold equation with/without routing by particle size, Kodoatie equation, Molinas and Wu equation, and Yang sand and gravel equation) were evaluated. It is suggested that modelers who conduct sediment studies in the mountainous watersheds with extreme rainfall conditions should adjust the modified universal soil loss equation (MUSLE) factors and carefully evaluate the sediment transportation equations in SWAT.

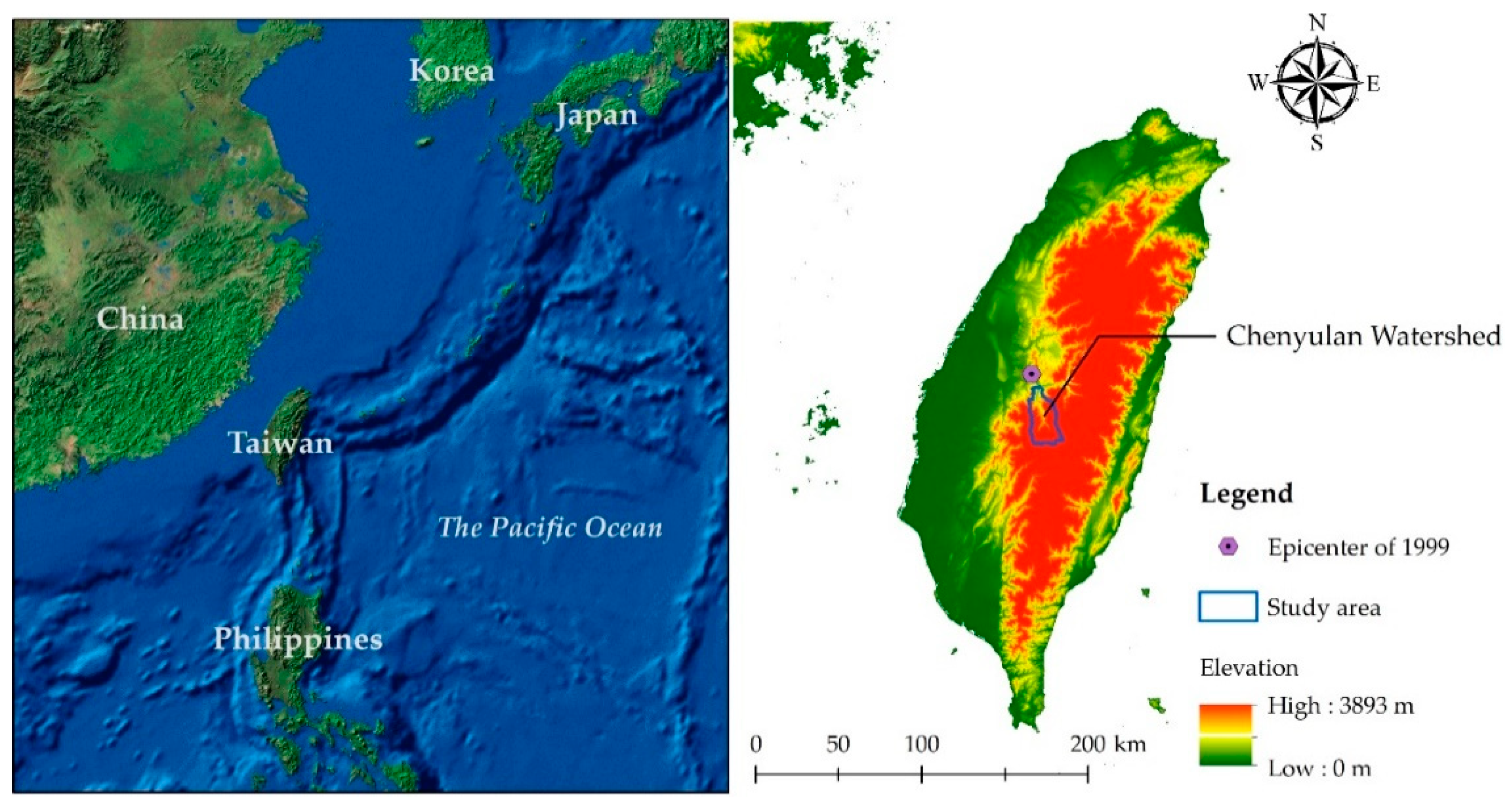
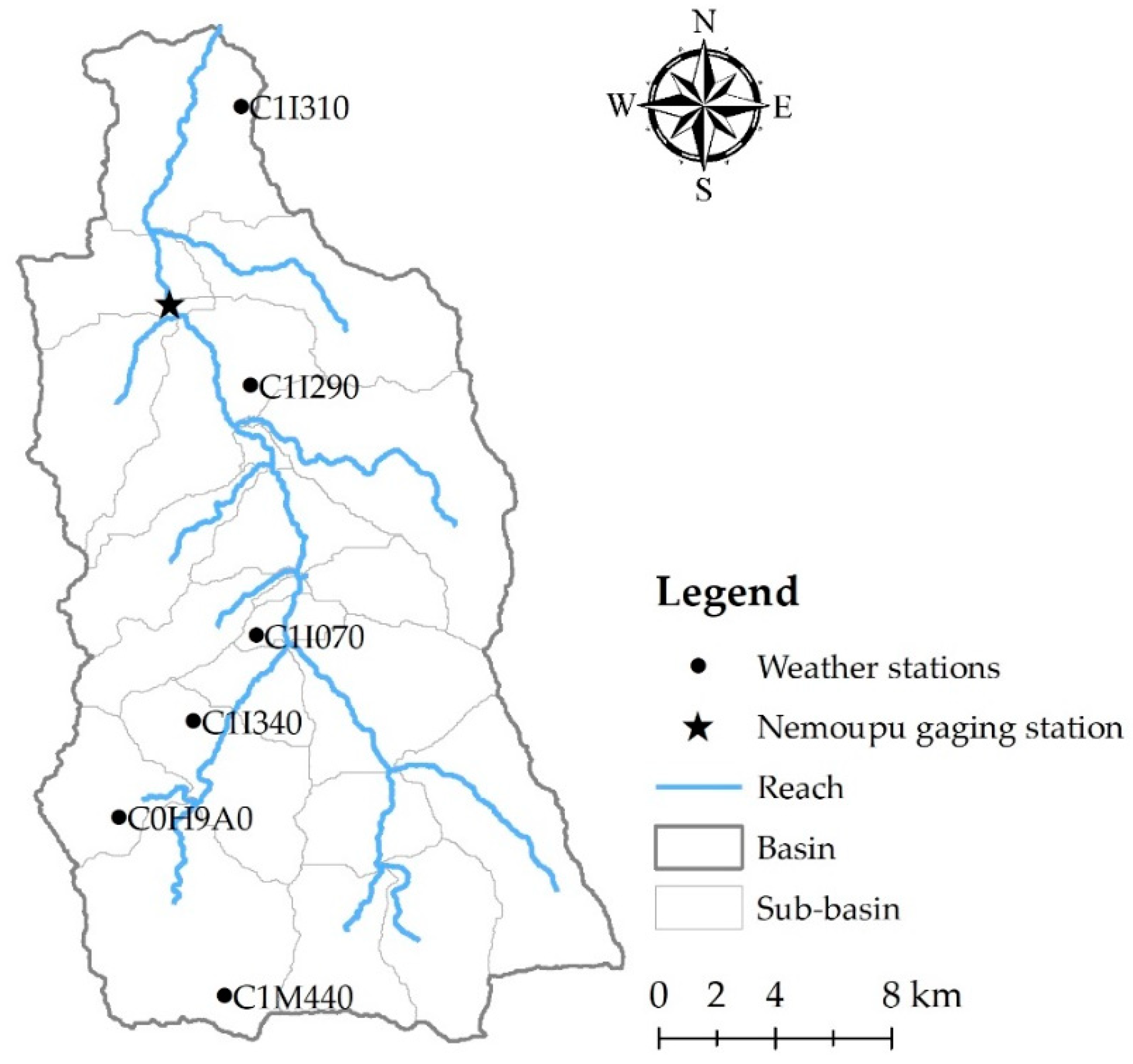
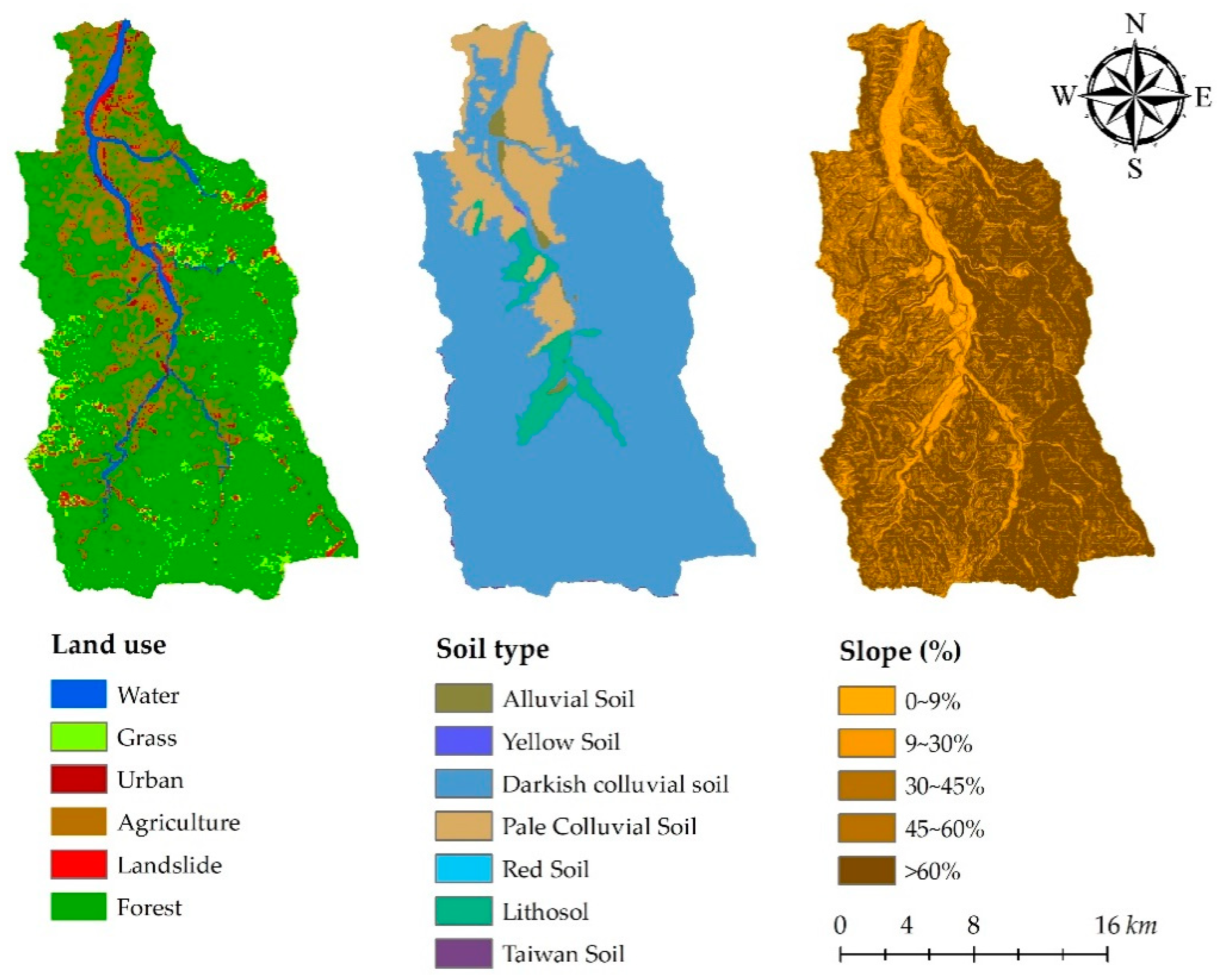
1. Introduction

The amount and occurrence time of sediment export from the watersheds are mainly caused by different types of soil erosion, such as channel bed and bank erosion, overland surface erosion, and glacier erosion [1]. As soil erosion causes shear stress by rainfall, surface runoff brings most sediment yields from the overland eroded soil and then is usually transported to the downstream [2]. Moreover, extreme natural disturbances (i.e., typhoons, earthquakes, landslides, and floods) also play as the trigger for abnormal sediment yields in some regions [3], and further change the characteristics of sediment yields and sediment transports in watersheds [4]. Many studies have indicated that climate change has caused higher rainfall intensity and annual precipitation, leading to increases in sediment yields and soil erosion rates [5].

In order to comprehensively quantify the impacts of rainfall, soil erodibility, land use cover, topography, and support practice to sediment yields, the universal soil loss equation (USLE) [6] and the modified universal soil loss equation (MUSLE) [7] have been developed. These two empirical equations have been used to estimate the soil loss in watersheds worldwide [8]. Some other physically-based erosion models were developed in the past decades, such as those used in ANSWERS (Areal Nonpoint Source Watershed Environmental Response Simulation) [9], EPIC (Environmental Policy Integrated Climate) model [10], WEPP (Water Erosion Prediction Project) [11], and EUROSEM (European Soil Erosion Model) [12]. The main difference between MUSLE and USLE is that USLE uses rainfall as an indicator of erosive energy, while MULSE uses the amount of runoff to simulate erosion and sediment yield. Sadeghi et al. [8] reviewed 49 papers of MUSLE application worldwide, and presented that most of MUSLE studies were to estimate the sediment yield on a storm basis (73.91%), monthly basis (2.17%), and annual basis (17.39%), while other applications of MUSLE (6.53%) were studied in soil erosion in storm-wise scale, pollutant estimation, and return periods of annual sediment yield. Therefore, MUSLE can better simulate the sediment yields during single storms with a low level of estimation error [13]. Since USLE and MUSLE were developed based on experiment watersheds in the U.S., [8] indicated that MUSLE would have huge errors without the calibration but can present reliable results for sediment yield on a storm basis after calibration, especially when it is applied under appropriate conditions (i.e., rangeland watersheds, similar climatic conditions as the USA) similar to where the original model was developed.

The process of erosion is usually described in three stages, which are detachment, transport and deposition; and four main types, which are sheet, rill, gully and in-stream erosion [14]. Sheet erosion and rill erosion are often classified as overland flow erosion caused by raindrop or overland flow [2,15]. Both types of erosions are usually considered together in erosion modelling. Gully erosion is the removal of soil along the channels of concentrated flow and is controlled by the thresholds related to slope and catchment area [2]. In-stream erosion involves the direct removal of sediment from stream beds and stream banks, especially during high flow periods huge amount of sediment transported through the stream network originates from the stream channel [14]. Erosion/sediment transport models can be categorized into three types: empirical model, conceptual model, and physics-based model [14]. The empirical models, the simplest ones, are based on the statistical observations of experiment areas in response to the characteristics of sediment transport [16], while conceptual models usually represent the catchment as a series of internal storages with parameters values determined through calibration against observed data [17]. Physics-based models integrate some fundamental physical equations, such as the equations of conservation of mass and momentum for flow, and those equations for sediment [14]. Compared to physics-based models and more complex conceptual models, which usually lack of sufficient spatially distributed input data, empirical and conceptual models are suggested to be combined for presenting the event responsiveness and sensitivity to climate variability [14].

The soil and water assessment Tool (SWAT) is a semi-distributed hydrological watershed model, which can simulate water balance, plant growth, and transport of sediment, nutrients, heavy metals and pesticides. The SWAT model has been used worldwide for simulating the impact of climate change and land use change on streamflow, sediment and nutrients exports, and best management practices (BMPs) on watershed responses in different countries [18,19,20]. Generally, the SWAT model performed well for simulating streamflow, sediment and nutrient exports at various spatio-temporal scales. MUSLE plays an important role of the simulation of continuous sediment loads [21]. Sediment transport is often called total sediment load, which is the sum of bed load and suspended load. The sediment transport is generally modeled through the sediment flow caused by overland flow and the channel erosion [22]. Some studies indicated unsatisfactory sediment simulation of the SWAT model. Addis et al. [23] used the SWAT model to simulate discharge and sediment transport at a small mountainous catchment in Ethiopian plateau, and showed that SWAT performed well for discharge but overestimated daily sediment transport with NSE = 0.07 and −1.76 for calibration and validation, respectively, mainly due to insufficient observed data and the heavy rainfall during simulation period. Bressiani et al. [24] indicated that the SWAT model was suitable for sediment simulation in most areas in Brazil and suggested the change in transmission of sediment should be reflected in the current SWAT version.

As the sediment transport and sediment concentration can affect the nutrient and turbidity in water, the estimation of sediment transport or sediment concentration need to be more reasonable. Arnold et al. [25] advised that SWAT users need to calibrate the discharge and sediment transport or concentration sequentially before simulating the nutrients. However, extreme rainfalls in Taiwan result in serious debris flows and landslides, making it more difficult to simulate the sediment transport in the river. As the runoff and sediment hazards in Taiwan are increasing, Lee et al. [26] indicated that the runoff and sediment yield would increase with the storm events and become more frequently occurred, especially in the small mountainous catchments. Chiu et al. [27] simulated the sediment yield in the Shihmen reservoir in Taiwan, and revealed that natural distributions (i.e., typhoon, storm, and earthquake) have become an important potential source of sediment yield. Therefore, Chang et al. [28] suggested that landslide should be considered in the model to simulate more accurate and reasonable sediment exports. In order to more accurately simulate the sediment transport and sediment yields in a small mountainous watershed in Taiwan, we aim to: (1) integrate Taiwan universal soil loss equation (TUSLE) and the landslide area-volume estimation equation into the SWAT model (version 664) as SWAT-Twn model; (2) examine five sediment transport methods in the SWAT model; (3) provide the calibration and validation experience of sediment transport simulation for the SWAT users.

2. Materials and Methods

2.1. Study Area and Data

The Chenyulan watershed, located in central Taiwan, has an area of 448 km² with the elevation ranging from 292 m to 3893 m (Figure 1). The Chenyulan watershed has steep terrain that is 49.74% of the total area with slopes steeper than 60%. Typhoons averagely hit Taiwan for 3–4 times in a year, leading large amounts of flow and sediment in the watersheds. Especially in 1996 and 2009, Typhoon Herb and Typhoon Morakot have brought more than 2000 mm of accumulated rainfall in two days, resulting in 3370 m³/s and 1860 m³/s of peak discharge and daily average streamflow, respectively. Moreover, extremely high sediment concentration of 98,499 mg/L was observed at Nemoupu station in the Chenyulan watershed when Typhoon Morakot occurred in 2009. During the study period (2004–2015), several typhoons that influenced the watershed have been recorded (

Table 1. Top 10 typhoons that influenced the study area during 2004–2015.

Rank	Typhoon	Occurred Period	Accumulated Precipitation (mm)	Weather Station
1	Morakot	5–10 August 2009	1953	C1M440
2	Matmo	21–23 July 2014	1136	C1M440
3	Sinlaku	11–16 September 2008	1072.5	C0H9A0
4	Mindulle	28 June–3 July 2004	774.5	C0H9A0
5	Krosa	4–10 October 2007	771	C0H9A0
6	Haitang	16–20 July 2005	760.5	C0H9A0
7	Saola	30 July–3 August 2012	693.5	C1I310
8	Sepat	16–19 August 2007	660.5	C1M440
9	Soulil	11–13 July 2013	624.5	C0H9A0
10	Jangmi	26–29 September 2008	593	C0H9A0

(Source: Typhoon Database, Central Weather Bureau, Taiwan [31]).

). Moreover, in 1999, the Chi-Chi earthquake of 7.3 Richter magnitude scale occurred in central Taiwan (Figure 1) and has seriously influenced the watershed landscape to become more fragile and sensitive [29,30].

The environmental data required for the SWAT model include: the digital elevation model (DEM), weather, observed streamflow and sediment concentration, land use and soil data. Moreover, the model simulation can be more precisely to represent the characteristics of the watershed by adding detailed information, such as point source pollutants, reservoirs, agriculture management scenarios [32,33,34,35,36,37]. The DEM data was available from Taiwan Geospatial One Stop (TGOS) [38]. We collected the data (i.e., precipitation, temperature, solar radiation, relative humidity, wind speed) of six weather stations in the watershed during 2003—2015 from the Taiwan Data Bank of Atmospheric and Hydrologic Research (DBAR) [39] (Figure 2). Some precipitation data missing during typhoons were replaced by the typhoon database of Taiwan Central Weather Bureau [31]. The observed daily streamflow and sediment concentration data during 2004–2015 were collected from the annual Hydrological Year Book of Taiwan Republic of China [40]. Most of the gages in the Chenyulan watershed seriously lack in measured data, and the Nemoupu gage is the only station that has complete data from 2004 to 2015 (Figure 2). The measured data during 2004–2009 and 2010–2015 were used for model calibration and validation, respectively. Since the sediment data were not measured continuously for every day, the sediment rating curve was first established to estimate the daily sediment concentration and loads for the model calibration and validation.

The land use data were collected form Second Land Use Survey in 2006 from [41] (Figure 3). Forest and agricultural lands are the two major land uses in the watershed, occupying 74.46% and 14.05% of the total area, respectively. The landslide area was set as barren (land use code in SWAT: BARR), accounting for 2.89% of total area. Soil data was collected from [42]. Approximately 82% of the total area has not been surveyed, thus it was assumed to be darkish colluvial soil in this study [30]. The pale colluvial clay accounts for 12% of the study area. The slope was calculated from the DEM data through the GIS spatial analysis tool. The slope was divided into five classes (0–9%, 9–30%, 30–45%, 45–60%, >60%), occupying 3.29%, 12.25%, 15.1%, 19.62%, and 49.74% of the total area, respectively.

2.2. SWAT Model

2.2.1. Model Description

The soil and water assessment tool (SWAT) model, a semi-distributed watershed-based hydrological model, was developed by the Agricultural Research Service, United States Department of Agriculture in 1994 [43]. The model can simulate the hydrological processes and sediment/nutrient transports at various spatio-temporal scales. In the SWAT model, several sub-basins are first delineated by setting the stream outlets (Figure 2), and further a unique combination of land use, soil and slope forms the basic modeling unit, called the hydrologic response unit (HRU). In this study, a total of 1173 HRUs of 23 sub-basins in the Chenyulan watershed were delineated (Figure 4).

The SWAT model simulates the surface runoff by using the curve number method, developed by the U.S. Soil Conservation Service (SCS). The SCS curve number equation is as follows:

$${\mathrm{Q}}_{\mathrm{surf}}=\frac{{\left({\mathrm{R}}_{\mathrm{day}}-{\mathrm{I}}_{\mathrm{a}}\right)}^2}{\left({\mathrm{R}}_{\mathrm{day}}-{\mathrm{I}}_{\mathrm{a}}\right)+\mathrm{S}}$$

(1)

where Q_surf is surface runoff (mm); R_day is daily precipitation (mm); I_a is the initial loss of surface water storage, interception, and percolation (mm); S is retention parameter (mm), which changes with soil type, land use and slope.

In SWAT model, infiltration is calculated by the Green and Ampt infiltration method. For evapotranspiration, three methods of evaporation estimation can be selected, including FAO Penman–Monteith, Hargreaves and Priestly-Taylor method. The hydrologic process is calculated by Equation (2).

$${\mathrm{S}}_{\mathrm{t}}={\mathrm{S}}_0+{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{t}}{\mathrm{R}}_{\mathrm{day}}-{\mathrm{Q}}_{\mathrm{surf}}-{\mathrm{E}}_{\mathrm{a}}-{\mathrm{W}}_{\mathrm{seep}}-{\mathrm{Q}}_{\mathrm{gw}}$$

(2)

where S_t is soil water content (mm); S₀ is initial soil water content (mm); R_day is the daily precipitation (mm); Q_surf is the daily surface runoff (mm); E_a is the daily evapotranspiration (mm); W_seep is the daily percolation (mm); Q_gw is the daily baseflow (mm)_. In SWAT, the soil water content is calculated for different layers defined by the users, and 50% of the evaporative demand is extracted from the top 10 mm of soil [44].

SWAT model uses the modified universal soil loss equation (MUSLE) to estimate soil loss at the HRU scale.

$$\mathrm{S}=11.8\times {\left({\mathrm{Q}}_{\mathrm{surf}}\times \mathrm{q}\times \mathrm{A}\right)}^{0.56}\times \mathrm{K}\times \mathrm{C}\times \mathrm{P}\times \mathrm{LS}\times \mathrm{CFRG}$$

(3)

where S is soil erosion (t); Q_surf is surface runoff (mm/ha); q is peak runoff (m³/s); A is the area of HRU (ha); K is the soil erodibility factor; C is the USLE land use/cover management factor; P is the USLE support practice factor; LS is the topographic factor; CFRG is the coarse fragment factor, which is calculated as the function of percent rock in the first soil layer. CFRG value equals 1 when there is no rock in the first soil layer. A higher percent of rock will result in smaller CFRG value and less soil loss.

2.2.2. Sediment Transport Methods

There are five sediment transport methods in SWAT model (version 664), which are the simplified Bagnold method with/without routing by particle size, Kodoatie method, Molinas and Wu method, and the Yang sand and gravel method. These methods can be applied for rivers of various river bed materials.

• Simplified Bagnold equation (EQN0 and EQN1):

The Bagnold method is the default method in SWAT model. The maximum sediment concentration is calculated as follows.

$${\mathrm{conc}}_{\mathrm{sed},\mathrm{ch},\mathrm{mx}}={\mathrm{c}}_{\mathrm{sp}}·{\mathrm{v}}_{\mathrm{ch},\mathrm{pk}}{}^{\mathrm{spexp}}$$

(4)

where ${\mathrm{conc}}_{\mathrm{sed},\mathrm{ch},\mathrm{mx}}$ is the maximum sediment concentration (t/m³); ${\mathrm{c}}_{\mathrm{sp}}$ is linear coefficient; ${\mathrm{v}}_{\mathrm{ch},\mathrm{pk}}$ is peak flow velocity (m/s); spexp is exponential coefficient.

In EQN0, as the default and only one sediment transport method in SWAT 2005 version, the bed load is limited by the channel cover and erodibility factors, and the sediment carried by channel is always near the calculated maximum transport capacity [44]. Moreover, it does not keep track of sediment pools in various particle sizes. Thus, EQN1, additional stream power equation in SWAT 2016 version, has been incorporated with physics-based approach for channel erosion.

• Kodoatie equation (EQN2):

The Kodoatie equation is an optimized sediment transport equation, based on the non-linear sediment equation [45] and the field observation data.

$${\mathrm{conc}}_{\mathrm{sed},\mathrm{ch},\mathrm{mx}}=\left(\frac{\mathrm{a}·{\mathrm{v}}_{\mathrm{ch}}{}^{\mathrm{b}}·{\mathrm{y}}^{\mathrm{c}}·{\mathrm{S}}^{\mathrm{d}}}{{\mathrm{Q}}_{\mathrm{in}}}\right)·\left(\frac{\mathrm{W}+{\mathrm{W}}_{\mathrm{btm}}}{2}\right)$$

(5)

where ${\mathrm{conc}}_{\mathrm{sed},\mathrm{ch},\mathrm{mx}}$ is the maximum sediment concentration (tons/m³); ${\mathrm{v}}_{\mathrm{ch}}$ is mean flow velocity (m/s); y is mean flow depth (m); S is energy slope (m/m); Q_in is water entering the reach (m³); a, b, c and d are regression coefficients for different bed materials; W is channel width at the water level (m); W_btm is bottom width of the channel (m).

• Molinas and Wu equation (EQN3):

Molinas and Wu [46] developed the sediment transport equation based on the universal stream power for rivers of large sand bed. The sediment weight concentration is calculated as follows.

$${\mathrm{C}}_{\mathrm{w}}={\mathrm{M}\mathsf{\Psi }}^{\mathrm{N}}$$

(6)

where C_w is sediment concentration by weight; Ψ is universal stream power; M and N are coefficients. The universal stream power (Ψ) is calculated as follows.

$$\mathsf{\Psi }={\left\{\left({\mathrm{S}}_{\mathrm{g}}-1\right)·\mathrm{g}·\mathrm{depth}·{\mathsf{\omega }}_{50}·\left[{\log }_{10}\left(\frac{\mathrm{depth}}{{\mathrm{D}}_{50}}\right)\right]\right\}}^{0.5}$$

(7)

where S_g is relative density of solid (2.65); g is acceleration of gravity (9.81 m/s²); depth is flow depth (m); ${\mathsf{\omega }}_{50}$ is fall velocity of median size particles (m/s); D₅₀ is median sediment size.

• Yang sand and gravel equation (EQN4):

Developed by Yang [47], the sediment weight concentration was calculated based on the sediment size (D₅₀), unit stream power (V_chS), shear velocity (${\mathrm{V}}_{*}$), fall velocity (${\mathsf{\omega }}_{50}$), and kinematic viscosity (υ). The equations are separated for sand and gravel bed material shown as follows.

Sand equation for median size (D₅₀) less than 2 mm,

$$\begin{array}{cc}\hfill \log {\mathrm{C}}_{\mathrm{w}}& =5.435-0.286\log \frac{{\mathsf{\omega }}_{50}{\mathrm{D}}_{50}}{\mathsf{\upsilon }}-0.457\log \frac{{\mathrm{V}}_{*}}{{\mathsf{\omega }}_{50}}\hfill \\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left(1.799-0.409\log \frac{{\mathsf{\omega }}_{50}{\mathrm{D}}_{50}}{\mathsf{\upsilon }}-0.314\log \frac{{\mathrm{V}}_{*}}{{\mathsf{\omega }}_{50}}\right)\log \left(\frac{{\mathrm{V}}_{\mathrm{ch}}\mathrm{S}}{{\mathsf{\omega }}_{50}}-\frac{{\mathrm{V}}_{\mathrm{cr}}\mathrm{S}}{{\mathsf{\omega }}_{50}}\right)\hfill \end{array}$$

(8)

Gravel equation for median size (D₅₀) between 2 mm and 10 mm,

$$\begin{array}{cc}\hfill \log {\mathrm{C}}_{\mathrm{w}}& =6.681-0.633\log \frac{{\mathsf{\omega }}_{50}{\mathrm{D}}_{50}}{\mathsf{\upsilon }}-4.816\log \frac{{\mathrm{V}}_{*}}{{\mathsf{\omega }}_{50}}\hfill \\ & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\left(2.784-0.305\log \frac{{\mathsf{\omega }}_{50}{\mathrm{D}}_{50}}{\mathsf{\upsilon }}-0.282\log \frac{{\mathrm{V}}_{*}}{{\mathsf{\omega }}_{50}}\right)\log \left(\frac{{\mathrm{V}}_{\mathrm{ch}}\mathrm{S}}{{\mathsf{\omega }}_{50}}-\frac{{\mathrm{V}}_{\mathrm{cr}}\mathrm{S}}{{\mathsf{\omega }}_{50}}\right)\hfill \end{array}$$

(9)

where C_w is weight concentration (ppm); ${\mathsf{\omega }}_{50}$ is fall velocity of the median size sediment (m/s); υ is kinematic viscosity (m²/s); ${\mathrm{V}}_{*}$ is shear velocity (m/s); V_ch is mean channel velocity (m/s); V_cr is critical velocity (m/s); S is energy slope (m/m).

2.3. Taiwan Universal Soil Loss Equation (TUSLE)

In order to present the characteristics of Taiwan soil, we applied the Taiwan universal soil loss equation (TUSLE) [48], revised from the universal soil loss equation (USLE) in the SWAT model. The factor adjustments are shown as follows.

• Soil erodibility factor (K)

The adjusted K factors were based on the soil survey in Taiwan conducted by [49,50]. The K values in the study area range from 0.13 to 0.40 (

Table 2. K factor used in the Chenyulan watershed.

Soil Type	Alluvial Soil	Lithosol	Darkish Colluvial Soil	Red Soil	Pale Colluvial Soil	Taiwan Clay	Yellow Soil
K factor	0.4	0.3	0.36	0.13	0.19	0.2	0.29

), and higher value indicates the soil layer is easier to erode.

• Rainfall erosivity factor (R)

The R factor in USLE is calculated by 30-min maximum rainfall intensity and rainfall kinetic energy [6]. Since the R factor of USLE is complicated to calculate, Chen et al. [48] estimated the R factor for TUSLE by the regression equation developed by the U.S. Department of Agriculture, Agriculture Research Service (Equation (10)) [48].

$${\mathrm{R}}_{\mathrm{eq}}=-823.8+5.213{\mathrm{P}}_{\mathrm{r}}$$

(10)

where R_eq is rainfall erosivity factor; P_r is annual precipitation (mm).

In MUSLE, the rainfall erosivity factor is replaced by the runoff factor as the runoff factor could better represent the surface runoff and overland sediment transport characteristics [7]. Thus, in this study, we calculated the runoff factor (R) in MUSLE, instead of the rainfall erosivity factor (R_eq).

$$\mathrm{R}=11.8{\left(\mathrm{Q}·\mathrm{q}·\mathrm{A}\right)}^{0.56}$$

(11)

where R is runoff factor; Q is surface runoff (mm/ha); q is peak runoff (m³/s); A is the area of catchment (ha).

• Cover and management factor (C)

The C factor was estimated by non-linear equation with the normalized difference vegetation index (NDVI) to avoid overestimating the C values of area with low soil erosion rate [51] (

Table 3. Normalized difference vegetation index (NDVI)-calculated weighted C value for different land uses.

NDVI-Calculated C	Number of Grids
	Grass	Forest	Agriculture	Landslide
0.01	3914	61,334	0	0
0.1	3049	67,819	8463	707
0.2	8417	153,468	26,007	2362
0.3	4120	59,365	14,141	1590
0.4	4084	56,689	17,422	2793
1	0	0	9205	8026
Weighted C	0.2	0.2	0.4	0.7
SWAT Default C	0.003	0.001	0.2	0.2

).

$$\mathrm{NDVI}\ge 0,\mathrm{C}={\left(\frac{1-\mathrm{NDVI}}{2}\right)}^{1+\mathrm{NDVI}}$$

(12)

$$\mathrm{NDVI}<0,\{\begin{array}{c}\mathrm{Building}\mathrm{or}\mathrm{non}-\mathrm{exposed}\mathrm{ground}, \mathrm{C}=0.01\\ \mathrm{Barren}, \mathrm{C}=1.0\end{array}$$

(13)

• Topographic factor (LS)

Wischmeier and Smith [52] established the LS equation (Equation (14)) as the product of L factor (Equation (15)) and S factor. In the SWAT model, the exponential factor (m) in the L factor equation is defined as Equation (16) [44], while TUSLE adopted the classification suggested by [52] that the exponential factor (m) varies with the slope, where m = 0.5, 0.4, 0.3 and 0.2 is used for the average slope greater than 5%, between 3–5%, between 1–3%, and less than 1%, respectively. Thus, TUSLE can increase the underestimated L factor at flatter slope and reduce the overestimated L factor at a steeper slope (Figure 5a). McCool et al. [53] indicated that Wischmeier and Smith’s [52] topographic factor equation could only be suitable for the slope from 0.1% to 18%, and developed S factor equation (Equations (17) and (18)) to more reasonably predict soil loss at steep topography. The comparison of S factor by [52,53] (Figure 5b) showed that the equation would overestimate S factor in areas of steeper slope. Therefore, we combined the L factor equation with m values from TUSLE and the S factor equation by [53] to calculate the LS factor.

$$\mathrm{LS}={\left(\frac{\mathrm{X}}{22.13}\right)}^{\mathrm{m}}\left(0.0654+4.56\sin \theta +65.4{\sin }^2\theta \right)$$

(14)

$$\mathrm{L}={\left(\frac{\mathrm{X}}{22.13}\right)}^{\mathrm{m}}$$

(15)

$$\mathrm{m}=0.6\times \left(1-{\mathrm{e}}^{-35.835*\theta }\right)$$

(16)

where X = slope length (m), m = exponential factor.

$$\mathrm{S}=10.8\sin \theta +0.03,\theta <9\%$$

(17)

$$\mathrm{S}={\left(\frac{\sin \theta }{0.0896}\right)}^{0.6},\theta \ge 9\%$$

(18)

where S is the slope factor of HRUs in MUSLE, $\theta$ is the slope of HRUs.

2.4. Calculation of Landslide Volume

The Chenyulan watershed has suffered by several severe natural disasters, such as Typhoon Herb (in 1996), 921 earthquake (in 1999), and Typhoon Morakot (in 2009), resulting in significant landslides, debris flows, change in landslide characteristics of central Taiwan [4]. Many studies have conducted the survey of landslide characteristic changed after the 921 earthquake [26,27,54,55,56,57]. Due to the lack of landslide calculation in the SWAT model, we integrated the landslide estimation equation developed by [28] into the SWAT model. The landslide volume was calculated by using the correlation between the landslide area and volume (R² = 0.79) (Equation (19)).

$$\ln \left(\mathrm{V}\right)=0.687\ln \left(\mathrm{A}\right)+2.326$$

(19)

where V is estimated landslide volume (m³); A is landslide area (m²).

It was reported that the percentage of landslide and debris flow in total sediment load would be greater than 60% when the daily cumulative precipitation is higher than 350 mm [58]. Therefore, the landslide volume estimation is triggered only when the daily precipitation exceeds 350 mm. The landslide area is read into the transformed landslide volume estimate equation as follows (Equation (20)).

$$\mathrm{V}={\mathrm{e}}^{2.326}·{\mathrm{A}}^{0.687}$$

(20)

In this study, the landslide area was identified by the land use survey map. The landslide volume is calculated by Equation (19), and then added into the sediment yields of HRUs.

2.5. Model Calibration and Validation

We applied the SWAT-CUP (SWAT Calibration Uncertainty Program) [59] for model sensitivity analysis, calibration and validation. In SWAT-CUP, parameter uncertainty can be analyzed by using Sequential Uncertainty Fitting version 2 (SUFI2), Generalized Likelihood Uncertainty Estimation (GLUE), Particle Swarm Optimization (PSO), Parameter Solution (ParaSol), or Marko Chain Monte Carlo (MCMC). Each uncertainty analysis method can run multiple simulations and find the ranges of best parameters for the study project. Parameters at any particular sub-basin, land use, soil, slope, and even HRU can be individually calibrated to reflect the unique spatial characteristics.

Among these uncertainty analysis methods, SUFI2, ParaSol and GLUE are easier to calibrate the parameters [59]. It is suggested that 3000, 7500, 10,000, 100,000, and 45,000 times of simulation are needed for SUFI2, ParaSol, GLUE, PSO, and MCMC, respectively, in order to get satisfactory simulation results [59]. SUFI2 method was selected in this study as it requires the least number of simulations. In sensitivity analysis, p-value is used to distinguish whether parameters are sensitive or not. Parameters that have p-value smaller than or equal to 0.05 are considered as sensitive parameters for further calibration [59]. After sensitivity analysis, the selection of calibrated ranges and fitted values of the parameters are identified based on the statistical criteria (i.e., R², NSE, PBIAS, and RSR), suggested by [60] with the model performance standards (

Table 4. Statistical criteria for model performance [60].

Model Performance	NSE	PBIAS (%)			RSR
		Flow	Sediment	Nutrient
Very Good	0.75 < NSE ≤ 1.00	|PBIAS| < 10	|PBIAS| < 15	|PBIAS| < 25	0.00 ≤ RSR ≤ 0.50
Good	0.65 < NSE ≤ 0.75	10 ≤ |PBIAS| < 15	15 ≤ |PBIAS| < 30	25 ≤ |PBIAS| < 40	0.50 < RSR ≤ 0.60
Satisfactory	0.5 < NSE ≤ 0.65	15 ≤ |PBIAS| < 25	30 ≤ |PBIAS| < 55	40 ≤ |PBIAS| < 70	0.60 < RSR ≤ 0.70
Unsatisfactory	NSE ≤ 0.5	|PBIAS| ≥ 25	|PBIAS| ≥ 55	|PBIAS| ≥ 70	RSR > 0.70

).

R² is the coefficient of determination, presenting the linear correlation between simulated and observed data. The value of R² closer to 1 indicates a higher correlation.

$${\mathrm{R}}^2=\frac{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i^{sim}-Y^{mean}\right)}^2}{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i^{obs}-Y^{mean}\right)}^2}$$

(21)

where Y^sim is the simulated data; Y^obs is observed data; Y^mean is the average of observation.

Nash–Sutcliffe efficiency (NSE) presents the residuals of measured data [61], and the value ranges from −∞ to 1. NSE value that equals 1, indicates the simulation is same as the observation, while NSE > 0.5 is acceptable for SWAT model performance [60].

$$\mathrm{NSE}=1-\left[\frac{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i^{obs}-Y_i^{sim}\right)}^2}{{{\displaystyle \sum }}_i^n{\left(Y_i^{obs}-Y^{mean}\right)}^2}\right]$$

(22)

Percent bias (PBIAS) presents whether the simulated data are overestimated or underestimated. When PBIAS is greater than 0, the simulation is underestimated [62].

$$\mathrm{PBIAS}(\%)=\frac{{{\displaystyle \sum }}_{i=1}^n\left(Y_i^{obs}-Y_i^{sim}\right)}{{{\displaystyle \sum }}_{i=1}^n{Y}_i^{obs}}\times 100$$

(23)

RMSE-observation standard deviation ratio (RSR) is the ratio between root mean square error and standard deviation. The smaller the RSR is, the better simulation performance is [63].

$$\mathrm{RSR}=\frac{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i^{obs}-Y^{sim}\right)}^2}}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(Y_i^{obs}-Y^{mean}\right)}^2}}$$

(24)

2.6. Sediment Load Estimation

In order to calibrate the daily sediment load, we estimated the observed daily sediment load by using the sediment rating curve, which describes the relationship between sediment concentration and water discharge. Since the Chenyulan watershed is a small mountainous watershed in Asia, we adopted the sediment rating curve method suggested by [64], who conducted studies in small mountainous watersheds in Japan.

We collected discontinuous data of sediment concentration and corresponding instant streamflow at the Nemoupu gauging station from 2004 to 2015 with a total of 338 data points. Both streamflow and sediment concentration data were first converted into logarithm and fitted with the linear regression model. A good relationship (r = 0.75) between sediment concentration and streamflow was found (Figure 6). Thus, the sediment rating curve was used for estimating the daily mean sediment concentration with the observed daily streamflow data, and the estimated daily sediment load could be further calculated.

3. Results

In this study, we compared three SWAT models, which are the official SWAT 2016 (version 664), SWAT-TUSLE and SWAT-Twn. The SWAT-TUSLE was modified with TUSLE which calculates C factor based on NDVI and L factors based on the slope. The SWAT-Twn was the integration of SWAT-TUSLE and landslide volume equation. Since we did not modify the streamflow-related equations in SWAT, the streamflow simulations are the same for all these three models. We first calibrated the official SWAT 2016 model for daily streamflow and compared the performance of sediment load simulations from SWAT 2016, SWAT-TUSLE, and SWAT-Twn.

3.1. Model Calibration and Validation for Streamflow

The observed streamflow from 2004 to 2015 was used for model calibration and validation. The streamflow-related parameters for calibration were referred to the previous study [30]. The parameters include curve number (CN2), plant uptake compensation factor (EPCO), surface runoff lag time (SURLAG), baseflow alpha factor (ALPHA_BF), effective hydraulic conductivity in main channel alluvium (CH_K2), and Manning’s “n” value for the main channel (CH_N2). In addition, we included Manning’s “n” value for the tributary channel (CH_N1) and effective hydraulic conductivity in tributary channel alluvium (CH_K1) as they are also sensitive in this study. In order to differentiate the characteristics of the parameters in various land use, slope, and soil, some parameters (i.e., CN2, ALPHA_BF, CH_K1, CH_K2, CH_N1, CH_N2, CH_K1) were individually calibrated for specific land use, slop and soil.

Table 5. Calibration results for streamflow.

Parameter	Unit	Class 1	Default	Calibrated Value
				Fitted	Min.	Max.
CN2	-	FRST	60	37 (−38.3%)	35 (−41.9%)	57 (−4.7%)
		RNGE	69	42 (−38.9%)	39 (−44.1%)	61 (−12.1%)
		AGRL	77	47 (−38.9%)	43 (−44.1%)	68 (−12.1%)
EPCO	-	All	1	0.34	0.10	0.44
SURLAG	-	All	4	20.77	3.24	23.11
ALPHA_BF	1/day	Downstream	0.048	0.31	0.18	0.53
		Sub. mean slope > 60%		0.38	0.06	0.43
CH_K2	mm/h	Downstream	0	543.86	427.89	811.25
		Sub. mean slope > 60%	0	546.43	386.38	744.02
		Head stream	0	515.61	293.20	579.25
CH_N2	-	Sub. mean slope > 60%	0.014	0.13	0.10	0.25
		Head stream		0.37	0.24	0.46
CH_K1	-	Downstream	0	58.88	53.76	161.54
CH_N1	-	Sub. mean slope > 60%	0.014	11.02	2.52	11.08

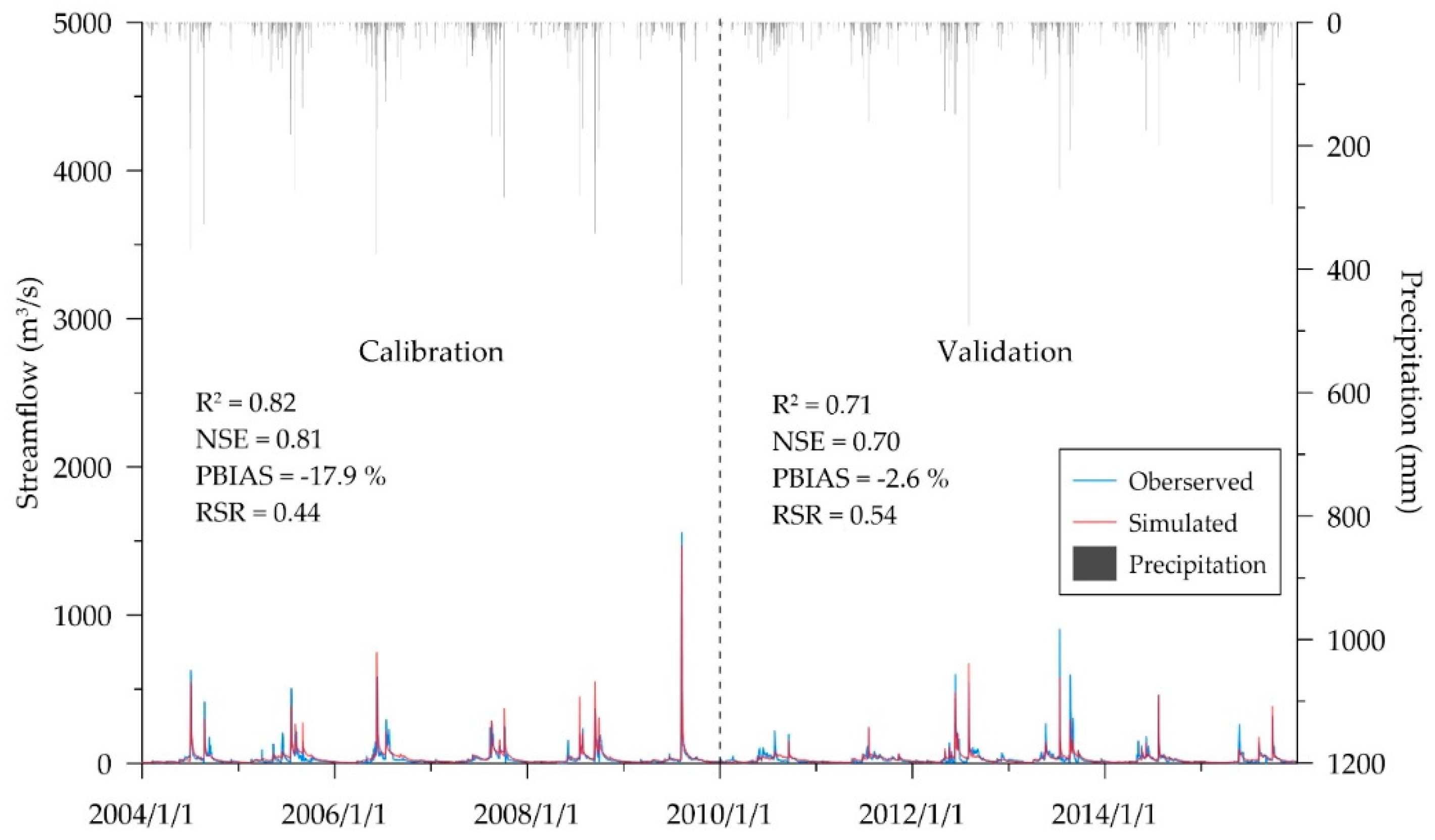
¹ FRST, RNGE, AGRL denote forest, grassland, agricultural land, respectively; three groups of sub-basin by slope are downstream (sub-basin no. 1–3, 5–7, 9–11, 13–15), sub-basin mean slope that greater than 60% (sub-basin no. 4, 8, 12, 16, 18, 19) and head stream (sub-basin no. 17, 20–23).

shows the calibrated ranges and fitted parameter values for daily streamflow simulation. The model did satisfactory and good performance for the calibration and validation, respectively (Figure 7), indicating the fitted streamflow parameters in model could well reflect the runoff characteristics of the Chenyulan watershed.

3.2. Comparison of SWAT 2016 and Modified SWAT Models

After calibrating the daily streamflow, we compared the uncalibrated simulated sediment yields from SWAT 2016, SWAT-TUSLE, and SWAT-Twn to quantify the impacts of using TUSLE and landslide volume equation on sediment yields at HRU and watershed levels (

Table 6. Sediment yields at hydrologic response unit (HRU) level.

Land Use	Sediment Yield (t/ha)			Difference (%)
	SWAT 2016	SWAT-TUSLE	SWAT-Twn	SWAT-TUSLE	SWAT-Twn
Urban	315.8	130.3	130.3	−58.7	−58.7
Agricultural land	1201.0	1196.0	1196.0	−0.4	−0.4
Forest	212.6	724.4	724.4	240.7	240.7
Grassland	271.1	933.1	933.1	244.2	244.2
Landslide	5461.6	1949.1	6872.3	−64.3	25.8

and

Table 7. Sediment yields at watershed level.

Year	Sediment Yield (t/ha)			Difference (%)
	SWAT 2016	SWAT-TUSLE	SWAT-Twn	SWAT-TUSLE	SWAT-Twn
2004	838	1335	1411	59.2	68.3
2005	756	1295	1320	71.3	74.6
2006	1028	1574	1635	53.1	59.0
2007	671	1133	1164	68.7	73.3
2008	1111	1561	1623	40.5	46.2
2009	746	1336	1382	79.2	85.3
Average	858	1372	1422	59.9	65.7

). It should be noted that we only used the sediment yield data during the streamflow calibration period because the fitted parameter values during validation period are different than those during calibration period. However, the range of parameter values are the same for both calibration and validation periods, and the simulation results can reflect the model uncertainty. Thus, we used the simulated sediment yield data during the calibration period (2004–2009) with calibrated fitted streamflow-related parameters and default sediment-related parameters to demonstrate the difference driven by different models.

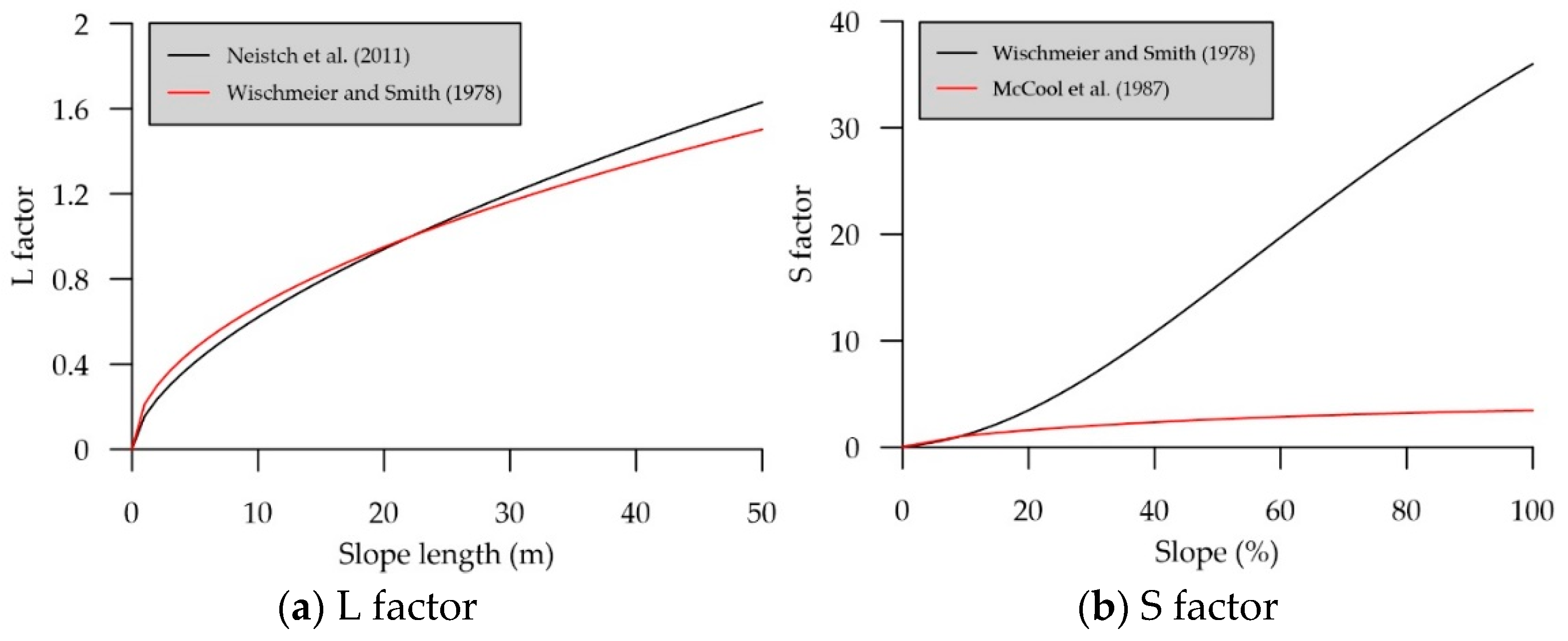
The major differences between SWAT 2016 and the two other modified SWAT (SWAT-TUSLE and SWAT-Twn) are the LS factor, which has more influence in steep slope areas (slope > 9%), and the C factor, which was calculated by NDVI resulting various C factor values for different land uses. There were 77.12% and 80.29% of urban and agricultural lands located in areas with steeper slope (slope > 9%). Therefore, with unchanged C factor for urban, sediment yield from urban had decreased by approximate 60% due to the modified LS factors in TUSLE (Table 6). However, sediment yields from agricultural lands did not change significantly by modified SWAT models. It was because the C factor calculated by NDVI is doubled than the SWAT default value (Table 3), compensating the decrease in sediment yields by modified LS factor in TUSLE. Besides urban and agricultural lands, significant changes in sediment yields from forest, grassland and landslide were found. Although LS factors could influence the sediment yields, the C factor of forest and grassland which were changed from 0.001–0.003 to 0.2, played an important role in increases in sediment yields.

In the SWAT-Twn model, the landslide volume estimation is activated when the daily precipitation reaches over 350 mm. It should be noted that landslide volume estimation is only applied to the landslide area, not other land uses. It is obvious that sediment yields from landslide area increased significantly when the landslide volume estimation was activated in SWAT-Twn. Moreover, since forest is the main land use occupying 74.46% of the watershed and the NDVI-calculated C factor of forest is greater than SWAT default C factor, the annual sediment yields from the watershed were increased by 59.9% and 65.7% by SWAT-TUSLE and SWAT-Twn, respectively (Table 7). The increase of 5.8% of sediment yield by SWAT-Twn was due to landslide volume estimation at the landslide areas. It shows that landslide volume estimation should be considered as the major contribution to sediment yields.

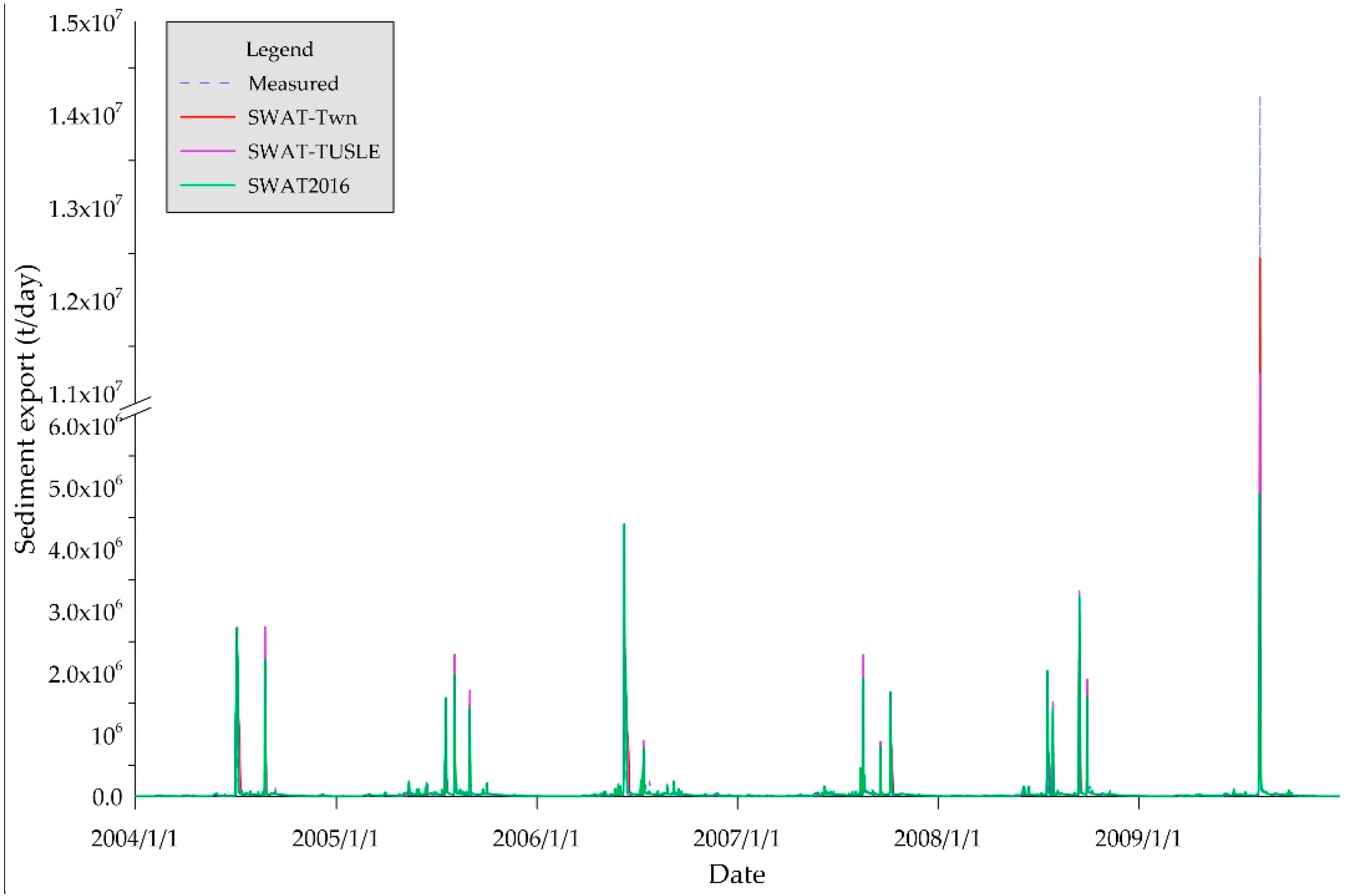
Before calibrating the sediment, these models overestimated the daily sediment load in terms of great positive PBIAS values (Figure 8). However, SWAT-TUSLE and SWAT-Twn performed better than SWAT 2016 in terms of greater R², NSE and smaller RSR, especially the SWAT-Twn performance had better statistical criteria values (R² = 0.74, NSE = 0.66, RSR = 0.58). Therefore, we used SWAT-Twn for further sediment calibration and validation.

3.3. Model Calibration and Validation for Sediment

The SWAT-Twn model was calibrated and validated for sediment loads with five different sediment transport methods (i.e., EQN0–4). The calibration (2004–2009) and validation (2010–2015) periods for sediment loads were the same as those for streamflow. First, the sensitivity analyses for sediment parameters for different sediment transport methods were examined (

Table 8. The sensitivity analysis of sediment-related parameters (p-value < 0.05).

Parameter	File Name	EQN0	EQN1	EQN2	EQN3	EQN4
SPCON	*.bsn	V	V
SPEXP	*.bsn	V	V
PRF_BSN	*.bsn	V	V
ADJ_PKR	*.bsn	V			V	V
CH_COV1	*.rte			V 3	V 3	V 3
CH_BNK_D50 1	*.rte					V 3
CH_BED_D50 1	*.rte		V 2	V 3	V 3

¹ unit: μm; ² the parameter is sensitive for sub-basins with mean slope < 60%; ³ the parameter is sensitive for sub-basins with mean slope > 60%.

). A total of eight sediment-related parameters were identified as sensitive parameters. Four of these parameters (i.e., SPCON, SPEXP, PRF_BSN, ADJ_PKR) are estimated on basin level (*.bsn), meaning that the parameter values are fixed for the entire watershed; while the rest of parameters (i.e., CH_COV1, CH_BNK_D50, CH_BED_D50) are estimated on reach level (*.rch), which could be varied by spatial and slope conditions.

The linear parameter (SPCON), exponent parameter (SPEXP) and peak rate adjustment factor (PRF_BSN) are only activated for the simplified Bagnold equation (EQN0 and EQN1). The peak rate adjustment factor (ADJ_PKR) was found to be sensitive to EQN0, EQN3 and EQN4. In order to identify the difference in the reach-level parameters, we separated the watershed by slope of 60% as almost half (49.58%) of the Chenyulan watershed is at a slope greater than 60%.

The channel bank vegetation coefficient for shear stress (CH_COV1) at the sub-basins with mean slope greater than 60% was sensitive for EQN2, EQN3 and EQN4, indicating that the vegetation at steeper slope areas would have great influence on sediment load compared to that at flatter slope areas. The median particle diameter of channel bank (CH_BNK_D50) at steeper slope areas was only sensitive for EQN4, while the median particle diameter of channel bed (CH_BED_D50) were sensitive for EQN1, EQN2, and EQN3. It shows that the median particle diameter of channel bank or bed should be measured for increasing the accuracy of sediment simulation with EQN1-4. Although both EQN0 and EQN1 are simplified Bagnold stream power equations, the EQN0 (default in SWAT 2005 version) does not keep track of sediment pools in various particle sizes, while the EQN1 (additional stream power equation in SWAT 2016) has been incorporated with physics-based approach for channel erosion. Moreover, the simulation of channel erosion with EQN0 is not partitioned between stream bank and stream bed. Thus, both CH_BNK_D50 and CH_BED_D50 are not sensitive for EQN0, while the EQN1 was sensitive with bed erosion (CH_BED_D50).

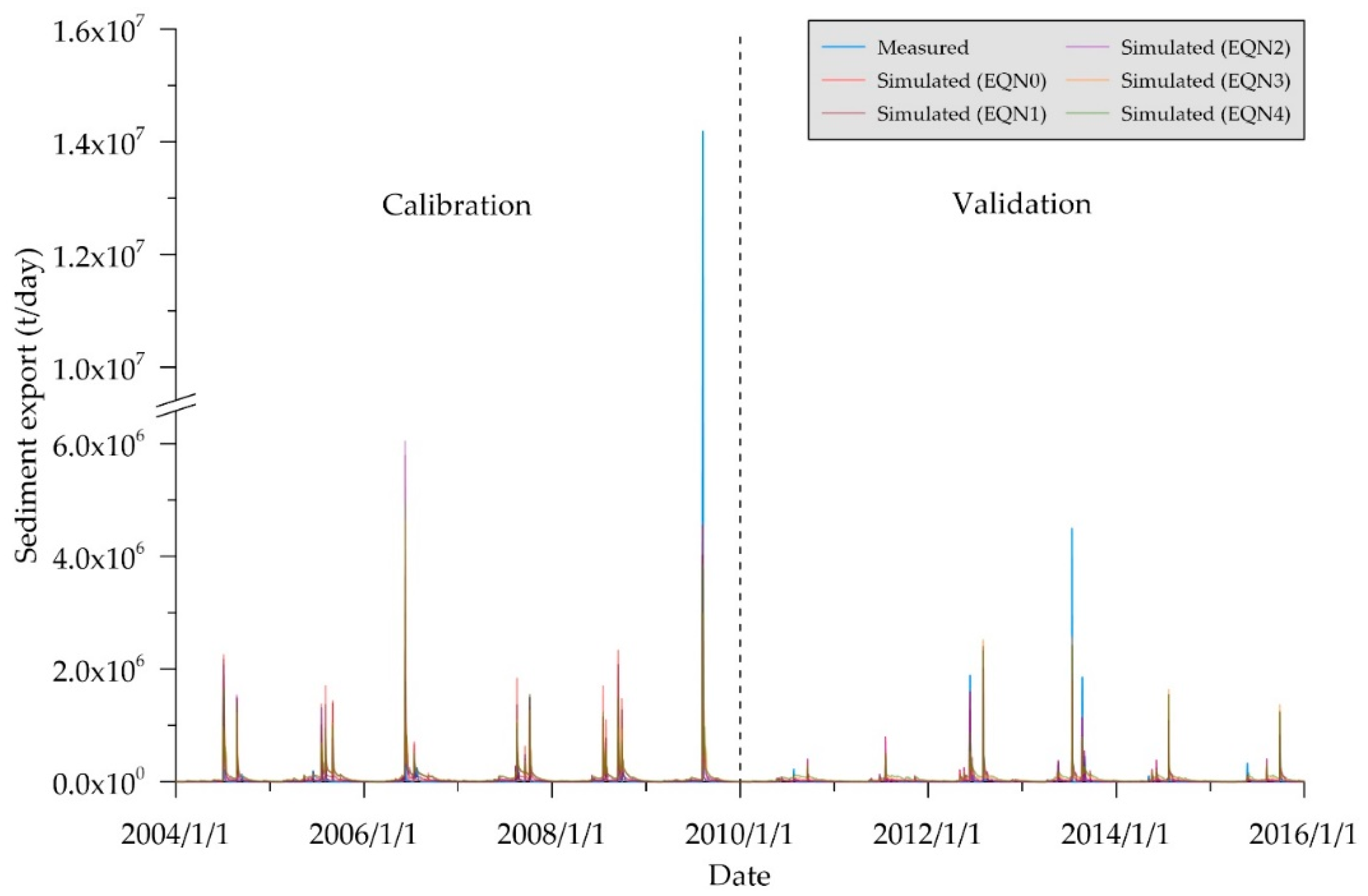
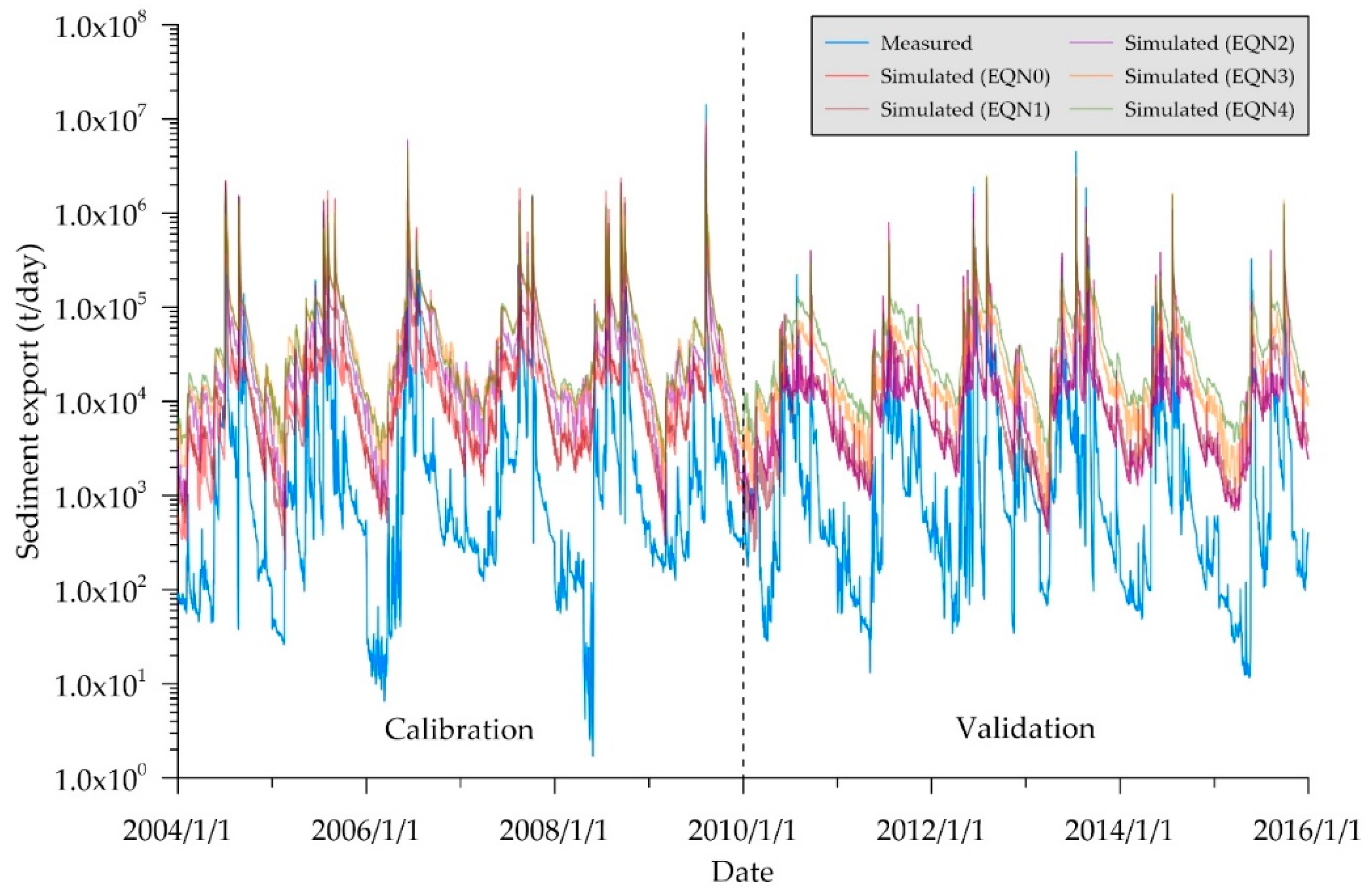
After identifying the sensitive parameters for those five sediment transport methods, the SWAT-Twn was calibrated and validated separately with each sediment transport method (

Table 9. Statistical results for sediment calibration and validation.

Statistical Parameter	EQN0		EQN1		EQN2		EQN3		EQN4
	Cal. 1	Val. 2	Cal.	Val.	Cal.	Val.	Cal.	Val.	Cal.	Val.
R2	0.74	0.55	0.66	0.66	0.24	0.57	0.28	0.58	0.34	0.57
NSE	0.73	0.73	0.65	0.65	0.22	0.22	0.25	0.25	0.31	0.31
PBIAS (%)	−89.8	−81.4	−116.8	−74.5	−164.1	−216.4	−226.5	−168.7	−240.8	−314.1
RSR	0.52	0.52	0.59	0.59	0.88	0.88	0.86	0.86	0.83	0.83

¹ Calibration; ² Validation.

and Figure 9). Generally, the simulation results by EQN0 and EQN1 were better than those by other sediment transport methods, in terms of R² and NSE greater than 0.5. It indicates that Bagnold equation is more suitable for the Chenyulan watershed. Moreover, the SWAT-Twn with EQN2, EQN3 or EQN4 was found to underestimate for peak flows and overestimate for low flows (Figure 9). Thus, the overestimated low flows at the most flow period resulted in great negative PBIAS values.

4. Discussion

4.1. Improvement of SWAT-Twn Model for Watershed Sediment Production

In the nearly-flat upland watersheds where surface runoff seldom occurs, sediment transported by surface runoff is usually significantly over predicted in a model [65]. Since the Chenyulan watershed is mountainous with hilly slope, modeling the sediment yield and transport responses with considering unique hydrological responses is important. Compared to SWAT 2016, the major modifications in SWAT-TUSLE are C factor and LS factor. The main land use in the Chenyulan watershed is forest, for which C factor is 0.2 by NDVI calculation and much greater than the SWAT default C factor (0.001). Although the decrease in LS factor would cause less sediment yields, the increase in sediment yield by the adjusted C factor was much greater than the decrease in sediment yield by the adjusted LS factor. Thus, it was found that some sub-basins (i.e., sub-basins no. 5, 8, 9, 12, 13, 16–19) where forest is dominated (>70%) generated more sediment yields (Figure 10 and

Table 10. Land use distribution (%) in sub-basins.

Sub-Basin	Area (km2)	Water	Grassland	Urban	Agricultural Land	Landslide	Forest
1	34.67	10.54	0	3.17	40.43	5.29	40.05
2	16.03	7.15	0	1.98	29.51	1.1	59.2
3	0.75	23.49	0	14.61	35.85	0	26.52
4	30.65	6.36	4.75	0.27	17.29	4.57	66.88
5	24.63	0.15	0	0.12	20.79	1.3	77.02
6	30.04	5.07	0.06	1.03	32.2	3.11	58.91
7	1.84	30.92	0	0	44.87	13.23	11.46
8	43.31	2.04	10.62	0.03	1.14	2.96	83.54
9	17.11	1.89	7.76	0.54	11.3	2.16	75.71
10	14.31	8.79	0.28	2.51	32.45	4.06	52.38
11	0.97	18.34	0	5.25	43.05	1.64	32.2
12	10.3	0	6.63	0	0.88	1.76	91.21
13	14.73	1.27	7.5	0	16.72	3.8	70.71
14	4.76	5.85	0	3.98	23.88	0.86	65.9
15	9.7	5.57	0	1.78	31.11	2.34	59.68
16	27.21	2.82	4.56	0.86	11.92	0.79	79.52
17	16	1.04	12.38	0	4.22	6.53	75.31
18	24.09	3.05	4.16	1.3	9.68	2.02	80.26
19	13.1	2.49	4.21	0	6.22	1.97	85.59
20	33.65	0.01	7.23	0	0.46	3.51	89
21	42.49	1.7	3.29	0.14	3.97	3.02	87.51
22	17.79	0	3.55	0	0.16	1.05	95.16
23	20.68	0	6.27	0	0	0.76	93.01

). Moreover, some agricultural-dominated (>30%) sub-basins (i.e., sub-basins no. 1, 3, 7, 10, 11 15) are mostly located in central and northern parts of the watershed, where slope is less steep. Thus, the adjusted LS factor has a relatively small impact on sediment yields from agricultural-dominated sub-basins. Great change in sediment yield was found in the south part of the watershed, where both forest and grassland are dominated, as the adjusted C factors of pasture and urban are greater than the SWAT default ones. Since the landslide volume equation is the additional improvement in SWAT-Twn from SWAT-TUSLE, the sediment yields by SWAT-Twn were increased by 2%, 40% and 3% in the sub-basins no. 1, 7, and 17, respectively, where the landslide area is greater than 5% of the sub-basin area.

4.2. Calibration with Different Sedmient Transport Methods

Based on the sensitivity analysis (Table 8), the calibrated values are listed in

Table 11. Calibrated sediment-related parameters for different sediment transport methods.

Parameter	EQN0	EQN1	EQN2	EQN3	EQN4
	Range (Fitted)	Range (Fitted)	Range (Fitted)	Range (Fitted)	Range (Fitted)
SPCON	0.01–0.10 (0.012)	0.01–0.10 (0.042)	-	-	-
SPEXP	1.02–1.20 (1.11)	1.00–1.40 (1.25)	-	-	-
PRF_BSN	1.00–1.20 (1.02)	0.80–1.20 (0.95)	-	-	-
ADJ_PKR	0.50–1.20 (0.61)	-	-	0.50–1.20(0.63)	0.50–1.50 (0.56)
CH_COV1	-	-	7.00-19.00 (10.51)	5.00–15.00 (0.13)	1.00–9.00 (1.70)
CH_BNK_D50 1	-	-	-	-	6500–9000 (7956.25)
CH_BED_D50 1	-	500–6000 (2411)	100–1800 (605.75)	350–1000 (377.63)	-

¹ unit: µm.

. For EQN0 and EQN1, the calibrated ranges and fitted values of SPCON, SPEXP and PRF_BSN are similar. Moreover, ADJ_PKR shows similar fitted value (0.56–0.63) and calibrated ranges (0.5–1.5) for EQN0, EQN3, and EQN4, indicating the characteristics of peak flow could be well represented in different sediment transport methods. For the simplified Bagnold method (EQN0 and EQN1), channel erodibility is controlled by the channel erodibility factor (CH_COV1) ranging from 0 to 1. The default value (0) indicates non-erosive channel, while the value of 1 indicates no resistance to erosion. However, CH_COV1, which is conceptually similar to the soil erodibility factor used in the USLE equation, was not sensitive and thus we used the default value for the simulation with EQN0 and EQN1. For other physics-based methods (EQN2-4), the channel erodibility is calculated by shear stress, and the CH_COV1 is defined as channel bank vegetation coefficient for estimating critical shear stress [66]. CH_COV1 is sensitive for EQN2, EQN3, and EQN4, however, the fitted values are quite different. The fitted CH_COV1 values indicate that the channel vegetation is between sparse trees (CH_COV1 = 5.40) and dense trees (CH_COV1 = 19.20), sparse trees, and grassy (CH_COV1 = 1.97) for EQN2, EQN3, and EQN4, respectively. The smaller the CH_COV1 value is, the greater the channel erodibility coefficient is [44]. Interestingly, the reflection of CH_COV1 on the channel erodibility is consistent with the suitability of using the Kodatie model (EQN2) for the stream bed material size ranging from silt to gravel, Molinas and Wu model (EQN3) for primarily sand size particles, and Yang sand and gravel model (EQN4) for primarily sand and gravel size particles.

Moreover, due to the lack of the information on channel materials, the calibrated median particle size diameter of channel bank sediment (CH_BNK_D50) or bed sediment (CH_BED_D50) showed various results among different sediment transport methods. For EQN1 and EQN4, the median size of bank and bed sediments were identified as mostly much greater than large aggregate (500 µm), thus the particle size distribution for D₅₀ (>2000 µm) assumed by SWAT is 15% of sand, 15% of silt, 5% of clay and 65% of gravel [44]. For EQN2, the calibrated CH_BED_D50 range is between 250 µm and 2000 µm, indicating the channels are characterized as medium to very coarse sand-bed materials [40]. Similarly, for EQN3, the fitted CH_BED_D50 value is between sand (200 µm) and large aggregate (500 µm) [44]. Therefore, for EQN2 and EQN3, the particle size distribution for D₅₀ (50 to 2000 µm) assumed by SWAT is 65% of sand, 15% of silt, 15% of clay and 5% of gravel.

In SWAT, the particle size distribution is usually used for estimating the bank and bed erosion, and the percentage of sediment (sand, silt, clay, gravel, small aggregate and large aggregate) that gets deposited, is calculated by the fall velocity of median size particle. The amount of sediment transported out of the reach is calculated as follows: Amount of total load entering the reach at the beginning of the time period minus the amount of total load deposited in the reach plus the amount of sediment due to bank and bed erosion in the reach. The total load in the reach considered includes bed and suspended load coming from the foregoing reaches, as well as suspended load originating from the soil erosion of the surrounding sub-basin. Thus, further improvements (i.e., the assumption of particle size distribution for bank and bed erosion, the calculation of fall velocity for wide range of particle size) need to be done to calculate more reliable and accurate sediment loads in SWAT.

4.3. Selection of a Suitable Sediment Transport Method

Due to the fact that sediment loads are extremely high during heavy rainfall events, the comparison between measured and simulated data in linear-scaled plot was difficult to identify their difference in sediment loads of low values. Therefore, we applied the logarithmic scale for the measured and simulated sediment data with different sediment transport methods and compared their statistical criteria (R² and PBIAS) during 2004–2016 (Figure 11 and

Table 12. Statistical results for simulated sediment loads in linear and logarithmic scales.

Method	Plot Scale	R2	PBIAS (%)
EQN0	Linear	0.71	−86.8
	Logarithmic	0.64	−34.3
EQN1	Linear	0.66	−101.6
	Logarithmic	0.68	−36.4
EQN2	Linear	0.28	−182.8
	Logarithmic	0.68	−48.6
EQN3	Linear	0.31	−205.7
	Logarithmic	0.64	−51.3
EQN4	Linear	0.37	−267.1
	Logarithmic	0.70	−55.4

). It should be noted that the simulation results are the same in Figure 9 and Figure 11. The simplified Bagnold method (EQN0 and EQN1) performed better for the low sediment loads with smaller PBIAS values. Although the model has been calibrated for sediment by SWAT-CUP, sediment loads are still overestimated for all sediment transport methods. It is because the SWAT-CUP model tends to adjust the parameters to meet the high observed sediment loads, but results in great PBIAS values. Thus, the SWAT model simulated high sediment loads better than the low sediment loads. Interestingly, when the measured and simulated sediment data are plotted in logarithmic scale, the R² values increase and PBIAS values decrease (Table 12). The greater improvement in the statistical criteria values shows the higher degree of overestimation when applying the Molinas and Wu model (EQN3) and Yang sand and gravel model (EQN4). By comparing the sediment load data in linear and logarithmic scales, we can better identify the suitable sediment transport method and suggest that further calibration and validation are needed for log-transformed simulated sediment data in the SWAT-CUP model.

5. Conclusions

The Chenyulan watershed has suffered from serious landslide and debris flow induced by heavy rainfall and typhoons. In this study, we integrated the TUSLE and landslide volume estimation into the SWAT model as SWAT-Twn. By evaluating the simulated sediment yields from different land uses, the importance of topographic (LS) factor and NDVI-calculated weighted C factor were identified and landslide volume estimation should be taken into concern. The examination of five different sediment transport methods revealed some important issues. First, the level of sensitivity of sediment-related parameters is different for those sediment transport methods, and parameters (i.e., CH_COV1, CH_BNK_D50, CH_BED_D50) that are estimated on each level, are suggested to be calibrated by spatial and slope conditions. Second, it is more accurate to investigate the channel vegetation (CH_COV1) and measure the particle sizes of channel bank and bed sediment (CH_BNK_D50 and CH_BED_D50). The calibrated parameter values by SWAT-CUP for different sediment transport methods may be misleading. Third, the particle size distribution assumed by SWAT is suggested to be an option that can be edited by users. Furthermore, the calculation of fall velocity is suggested to not be only limited for median particle size as it would be biased for channels of wide range of particle sizes. Last but not the least, like the streamflow simulation in SWAT and SWAT-CUP, an option for the user to compare and plot the sediment simulation in logarithmic scale would provide more insights into sediment calibration. In sum, the SWAT-Twn model performed better than SWAT 2016 and SWAT-TUSLE, as TUSLE calculated less sediment at steep area, resulting reasonable sediment export simulation at low flow condition and landslide volume estimation reflected the real situation. Additional improvements in SWAT and SWAT-CUP need to be made to better predict the sediment yields and loads at mountainous watersheds.