Characterization of the Groundwater Storage Systems of South-Central Chile: An Approach Based on Recession Flow Analysis
Abstract
:1. Introduction
2. Methods
2.1. Study Area and Hydrometeorological Data
2.2. Recession Flow Analysis
3. Results and Discussion
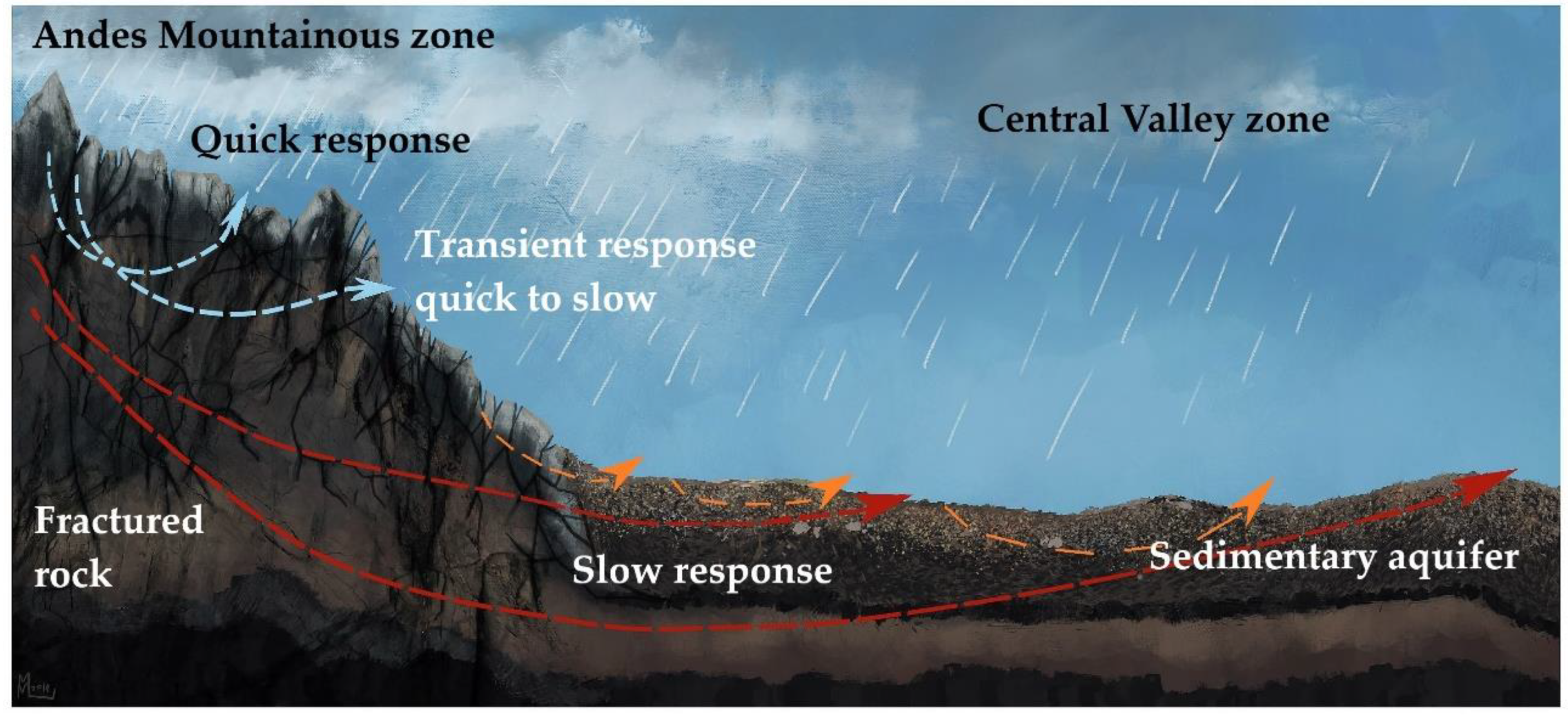
3.1. Recession Flow Behavior
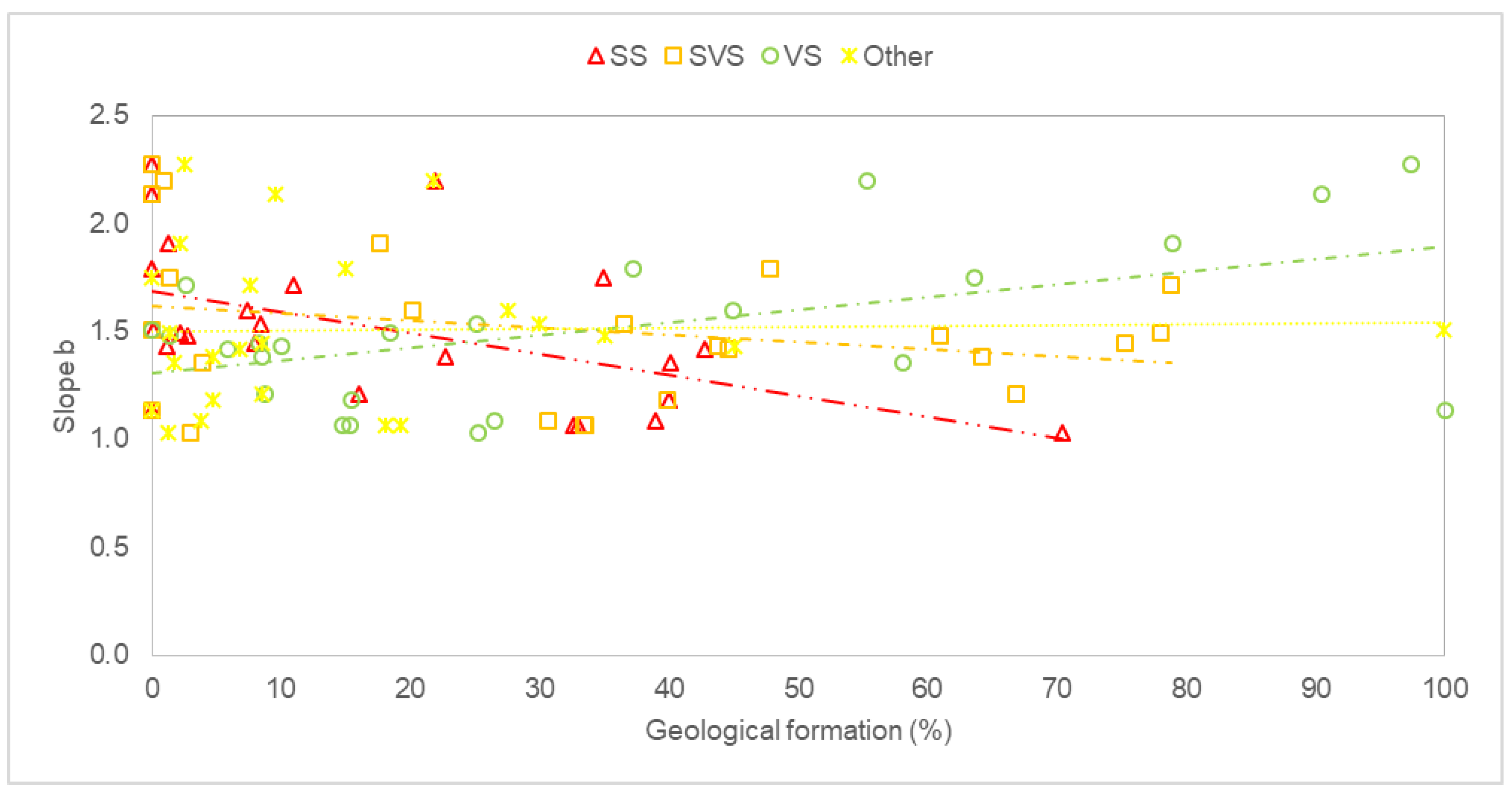
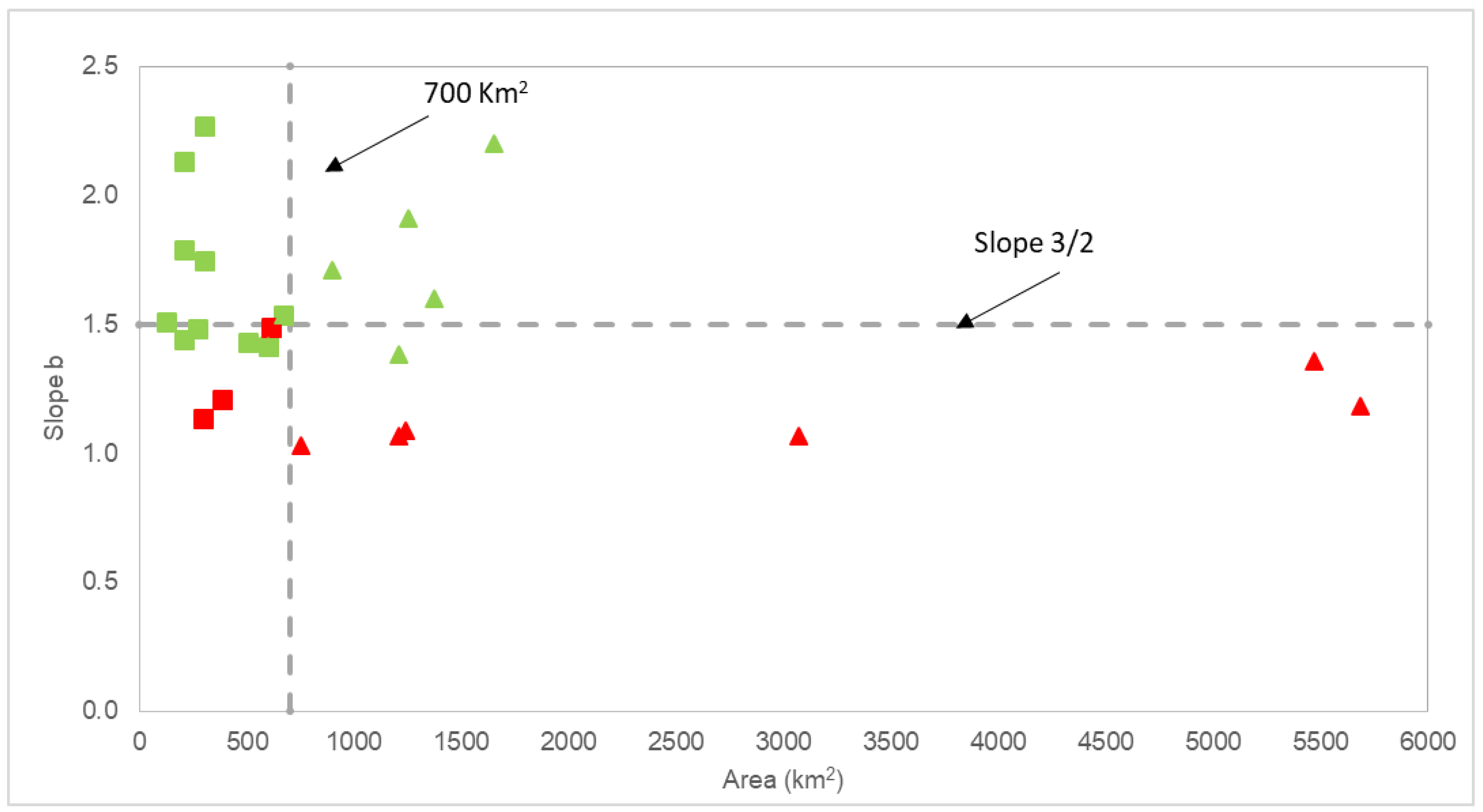
3.2. Predominant Drainage Process
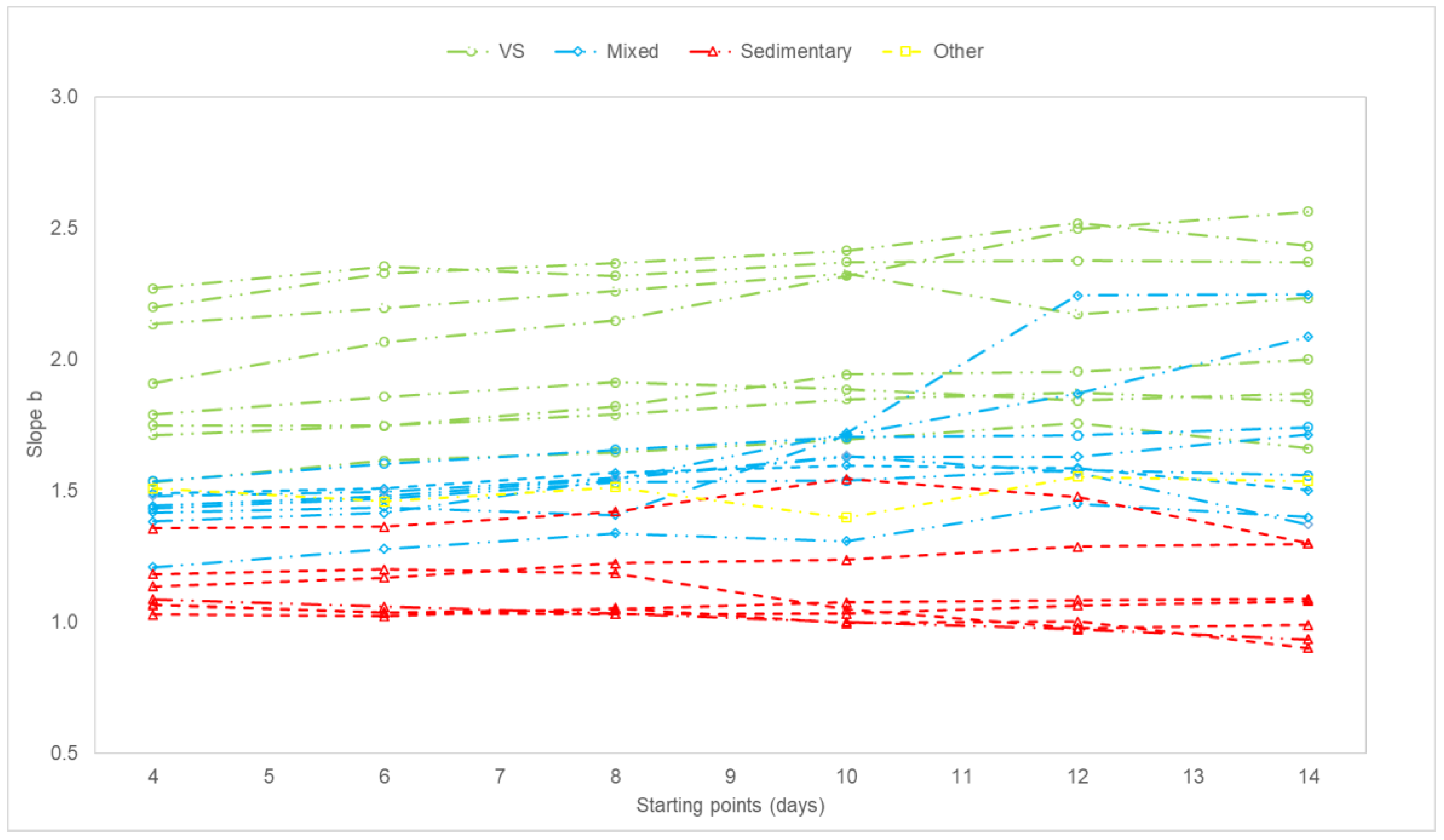
3.3. Does the Predominant Drainage Change?
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hood, J.L.; Roy, J.W.; Hayashi, M. Importance of groundwater in the water balance of an alpine headwater lake. Geophys. Res. Lett. 2006, 33, L13405. [Google Scholar] [CrossRef]
- Basile, H.; Seguis, L.; Hiderer, J.; Cohard, J.; Wubda, M.; Descloitres, M.; Benarrosh, N.; Boy, J. Water storage changes as a marker for base flow generation processes in a tropical humid basement catchment (Benin): Insights from hybrid gravimetry. Water Resour. Res. 2015, 51, 8331–8361. [Google Scholar]
- Thomas, B.F.; Vogel, R.M.; Kroll, C.N.; Famiglietti, J.S. Estimation of the baseflow recession constant under human interference. Water Resour. Res. 2013, 49, 7366–7397. [Google Scholar] [CrossRef]
- Stoelzle, M.; Weiler, M.; Stahl, K.; Morhard, A.; Schuetz, T. Is there a superior conceptual groundwater model structure for baseflow simulation? Hydrol. Process. 2015, 29, 1301–1313. [Google Scholar] [CrossRef]
- Brutsaert, W.; Nieber, J.L. Regionalized drought flow hydrographs froma mature glaciated plateau. Water Resour. Res. 1977, 13, 637–643. [Google Scholar] [CrossRef]
- Mendoza, G.F.; Steenhuis, T.S.; Walter, M.T.; Parlange, J.Y. Estimating basin-wide hydraulic parameters of a semi-arid mountainous watershed by recession-flow analysis. J. Hydrol. 2003, 279, 57–69. [Google Scholar] [CrossRef]
- Shaw, S.B.; Riha, S.J. Examining individual recession events instead of a data cloud: Using a modified interpretation of dQ/dt -Q streamflow recession in glaciated watersheds to better inform models of low flow. J. Hydrol. 2012, 434, 46–54. [Google Scholar] [CrossRef]
- Brutsaert, W. Long-term groundwater storage trends estimated from streamflow records: Climatic perspective. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Kirchner, J.W. Catchments as simple dynamical systems: Catchment characterization, rainfall-runoff modeling, and doing hydrology backward. Water Resour. Res. 2009, 45, W02429. [Google Scholar] [CrossRef]
- Ajami, H.; Troch, P.; Maddock, T., III; Meixner, T.; Eastoe, C. Quantifying mountain block recharge by means of catchment-scale storage-discharge relationships. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Dixon, H.; Murphy, M.; Sparks, S.; Chávez, R.; Naranjo, J.; Dunkley, P.; Young, S.; Gilbert, J.; Pringle, M. The geology of Nevados de Chillán volcano, Chile. Revis. Geol. Chile 1999, 26, 227–253. [Google Scholar] [CrossRef]
- Naranjo, J.; Gilbert, J.; Sparks, R. Geología del Complejo Volcánico Nevados de Chillán, Región del Biobío; Carta Geológica de Chile, Serie Geología Básica: Santiago, Chile, 2008. [Google Scholar]
- Muñoz, E.; Arumí, J.L.; Wagener, T.; Oyarzún, R.; Parra, V. Unraveling complex hydrogeological processes in Andean basins in South-Central Chile: An integrated assessment to understand hydrological dissimilarity. Hydrol. Process. 2016, 30, 4934–4943. [Google Scholar] [CrossRef]
- SERNAGEOMIN. Mapa Geológico de Chile: Versión Digital; Servicio Nacional de Geología y Minería (SERNAGEOMIN): La Serena, Chile, 2003; Volume 4. [Google Scholar]
- Pizarro, R.; Valdes, R.; García-Chevesich, P.; Vallejos, C.; Sangüesa, C.; Morales, C.; Balocchi, F.; Abarza, A.; Fuentes, R. Latitudinal Analysis of Rainfall Intensity and Mean Annual Precipitation in Chile. Chil. J. Agric. Res. 2012, 72, 252–261. [Google Scholar] [CrossRef] [Green Version]
- Bozkurt, D.; Rojas, M.; Boisier, J.P.; Valdivieso, J. Climate change impacts on hydroclimatic regimes and extremes over Andean basins in central Chile. Hydrol. Earth Syst. Sci. Discuss. 2017, 1–29. [Google Scholar] [CrossRef]
- Voeckler, H.; Allen, D.M. Estimating regional-scale fractured bedrock hydraulic conductivity using discrete fracture network (DFN) modeling. Hydrogeol. J. 2012, 20, 1081–1100. [Google Scholar] [CrossRef]
- Sánchez-Murillo, R.; Brooks, E.S.; Elliot, W.J.; Gazel, E.; Boll, J. Baseflow recession analysis in the inland Pacific Northwest of the United States. Hydrogeol. J. 2015, 23, 287–303. [Google Scholar] [CrossRef]
- Oyarzún, R.; Godoy, R.; Núñez, J.; Fairley, J.P.; Oyarzún, J.; Maturana, H.; Freixas, G. Recession flow analysis as a suitable tool for hydrogeological parameter determination in steep, arid basins. J. Arid Environ. 2014, 105, 1–11. [Google Scholar] [CrossRef]
- Vogel, R.; Kroll, C. Regional geohydrologic-geomorphic relationships for the estimation of low-flow statistics. Water Resour. Res. 1992, 28, 2451–2458. [Google Scholar]
- Szilagyi, J.; Parlange, M.B. Baseflow separation based on analytical solutions of the Boussinesq equation. J. Hydrol. 1998, 204, 251–260. [Google Scholar] [CrossRef] [Green Version]
- Brutsaert, W.; Lopez, J.P. Basin-scale geohydrologic drought flow features of riparian aquifers in the southern great plains. Water Resour. Res. 1998, 34, 233–240. [Google Scholar] [CrossRef]
- Malvicini, C.F.; Steenhuis, T.S.; Walter, M.T.; Parlange, J.Y.; Walter, M.F. Evaluation of spring flow in the uplands of Malatom, Leyte, Philippines. Adv. Water Resour. 2005, 28, 1083–1090. [Google Scholar] [CrossRef]
- Troch, P.A.; De Troch, F.P.; Brutsaert, W. Effective water-table depth to describe initial conditions prior to storm rainfall in humidregions. Water Resour. Res. 1993, 29, 427–434. [Google Scholar] [CrossRef]
- Arciniega-Esparza, S.; Breña-Naranjo, J.A.; Pedrozo-Acuña, A.; Appendini, C.M. HYDRORECESSION: A Matlab toolbox for streamflow recession analysis. Comput. Geosci. 2017, 98, 87–92. [Google Scholar] [CrossRef]
- Millares, A.; Polo, M.J.; Losada, M.A. The hydrological response of baseflow in fractured mountain areas. Hydrol. Earth Syst. Sci. 2009, 13, 1261–1271. [Google Scholar] [CrossRef]
- Falvey, M.; Garreaud, R. Wintertime Precipitation Episodes in Central Chile: Associated Meteorological Conditions and Orographic Influences. J. Hydrol. 2007, 8, 171–193. [Google Scholar] [CrossRef]
- Arumí, J.L.; Oyarzún, R.; Muñoz, E.; Rivera, D.; Aguirre, E. Caracterización de Dos Grupos de Manantiales en el Río Diguillín, Chile. Tecnol. Cienc. Agua 2014, 5, 151–158. [Google Scholar]
- Banks, E.W.; Simmons, C.; Love, A.; Cranswick, R.; Werner, A.; Bestland, E.; Wood, M.; Wilson, T. Fractured Bedrock and Saprolite Hydrogeologic Controls on Groundwater/Surface-Water Interaction: A Conceptual Model (Australia). Hydrogeol. J. 2009, 17, 1969–1989. [Google Scholar] [CrossRef]
- Staudinger, M.; Stahl, K.; Seibert, J.; Clark, M.P.; Tallaksen, M. Comparison of hydrological model structures based on recession and low flow simulations. Hydrol. Earth Syst. Sci. 2011, 15, 3447–3459. [Google Scholar] [CrossRef] [Green Version]
- Tallaksen, L. A review of baseflow recession analysis. J. Hydrol. 1995, 65, 349–370. [Google Scholar] [CrossRef]
- Moore, R. Storage-outflow modelling of streamflow recessions, with application to a shallow-soil forested catchment. J. Hydrol. 1997, 198, 260–270. [Google Scholar] [CrossRef]
- Parra, V.; Arumí, J.L.; Muñoz, E. Identifying a Suitable Model for Low-Flow Simulation in Watersheds of South-Central Chile: A Study Based on a Sensitivity Analysis. Water 2019, 11, 1506. [Google Scholar] [CrossRef]
- Chen, B.; Krajewski, W. Analysing individual recession events: Sensitivity of parameter determination to the calculation procedure. Hydrol. Sci. J. 2016, 61, 2887–2901. [Google Scholar] [CrossRef]
- Hailegeorgis, T.T.; Alfredsen, K.; Abdella, Y.S.; Kolberg, S. Evaluation of storage–discharge relationships and recession analysis-based distributed hourly runoff simulation in large-scale, mountainous and snow-influenced catchment. Hydrol. Sci. J. 2016, 61, 2872–2886. [Google Scholar] [CrossRef]
- Murgulet, D.; Murulet, V.; Spalt, N.; Douglas, A.; Hay, R.G. Impact of hydrological alterations on river-groundwater exchange and water quality in a semiarid area: Nueces River, Texas. Sci. Total Environ. 2016, 572, 595–607. [Google Scholar] [CrossRef]
- Uribe, H.; Arumí, J.L.; Gonzáles, L.; Salgado, L. Balances hidrológicos para estimar la recarga de acuíferos en el secano interior, Chile. Tecnol. Cienc. Agua 2003, 8, 17–28. [Google Scholar]
- Bergström, S. The HBV Model: Its Structure and Applications; Swedish Meteorological and Hydrological Institute: Norrköping, Sweden, 1992. [Google Scholar]
- Fenicia, F.; Savenije, H.; Matgen, P.; Pfister, L. Is the groundwater reservoir linear? Learning from data in hydrological modelling. Hydrol. Earth Syst. Sci. 2006, 10, 139–150. [Google Scholar] [CrossRef] [Green Version]
- Chapman, T. A comparison of algorithms for stream flow recession and baseflow separation. Hydrol. Process. 1999, 13, 701–714. [Google Scholar] [CrossRef]
- Gan, R.; Lou, Y. Using the nonlinear aquifer storage–discharge relationship to simulate the base flow of glacier- and snowmelt-dominated basins in Northwest China. Hydrol. Earth Syst. Sci. 2013, 17, 3577–3586. [Google Scholar] [CrossRef]
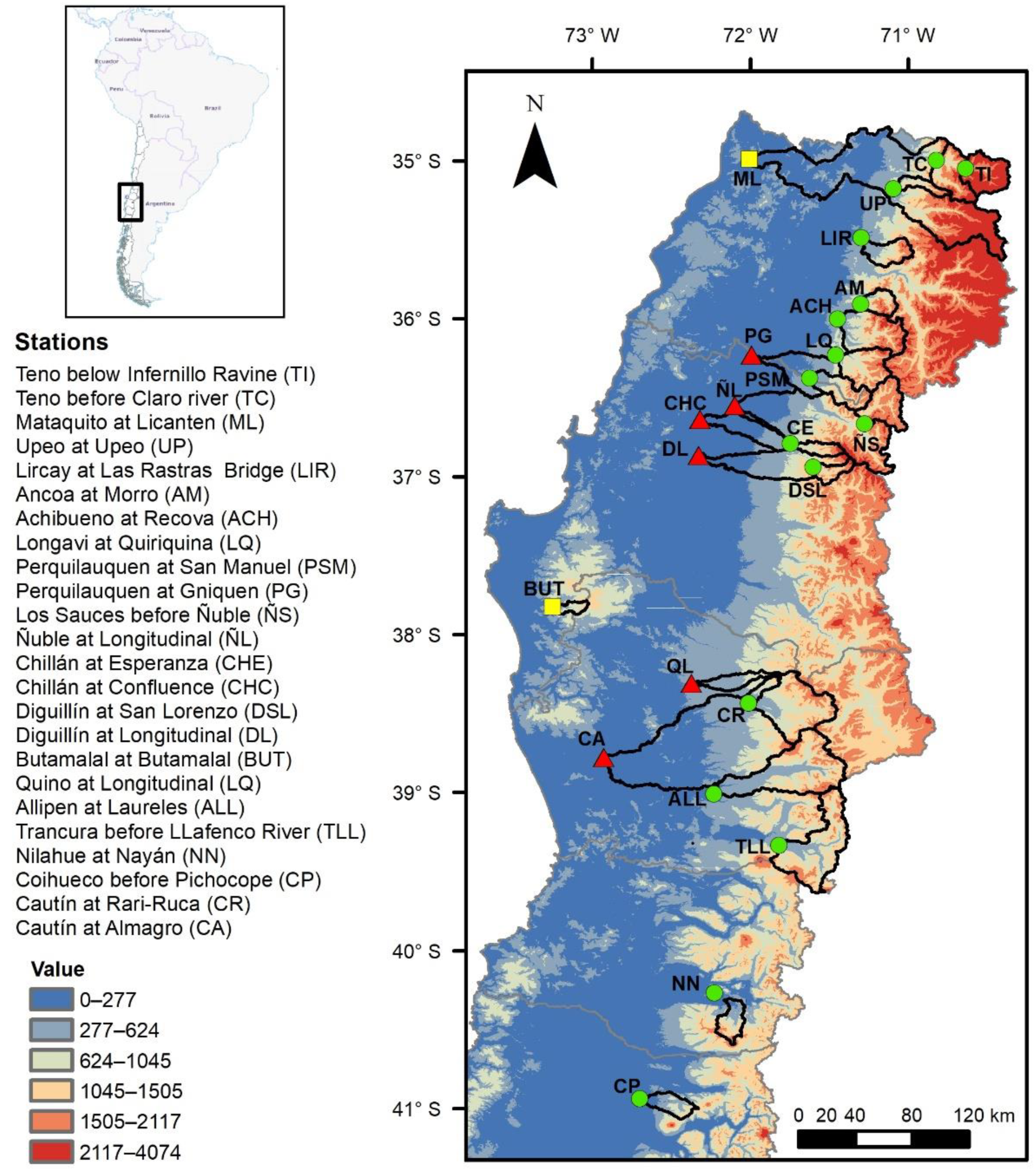
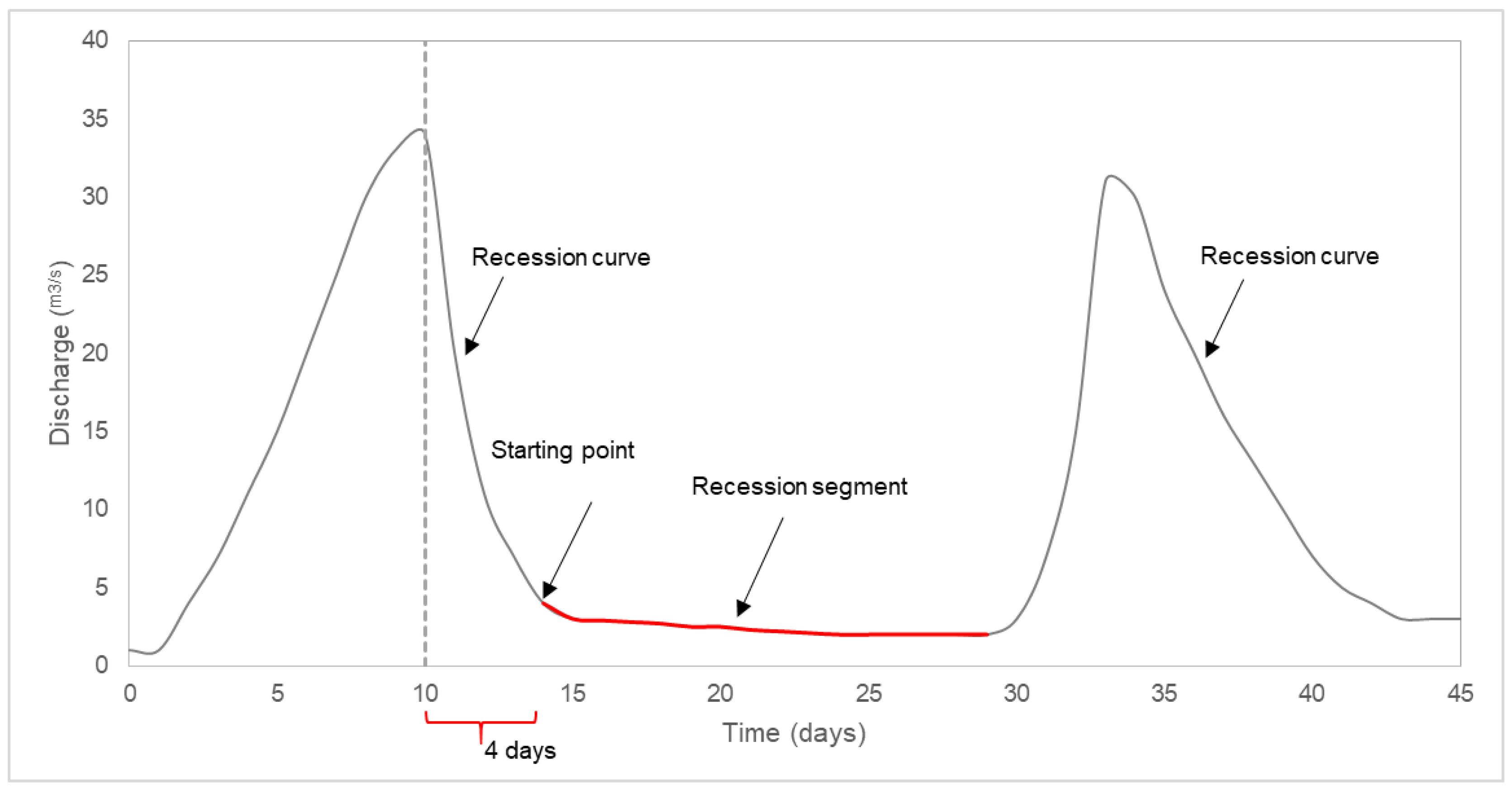
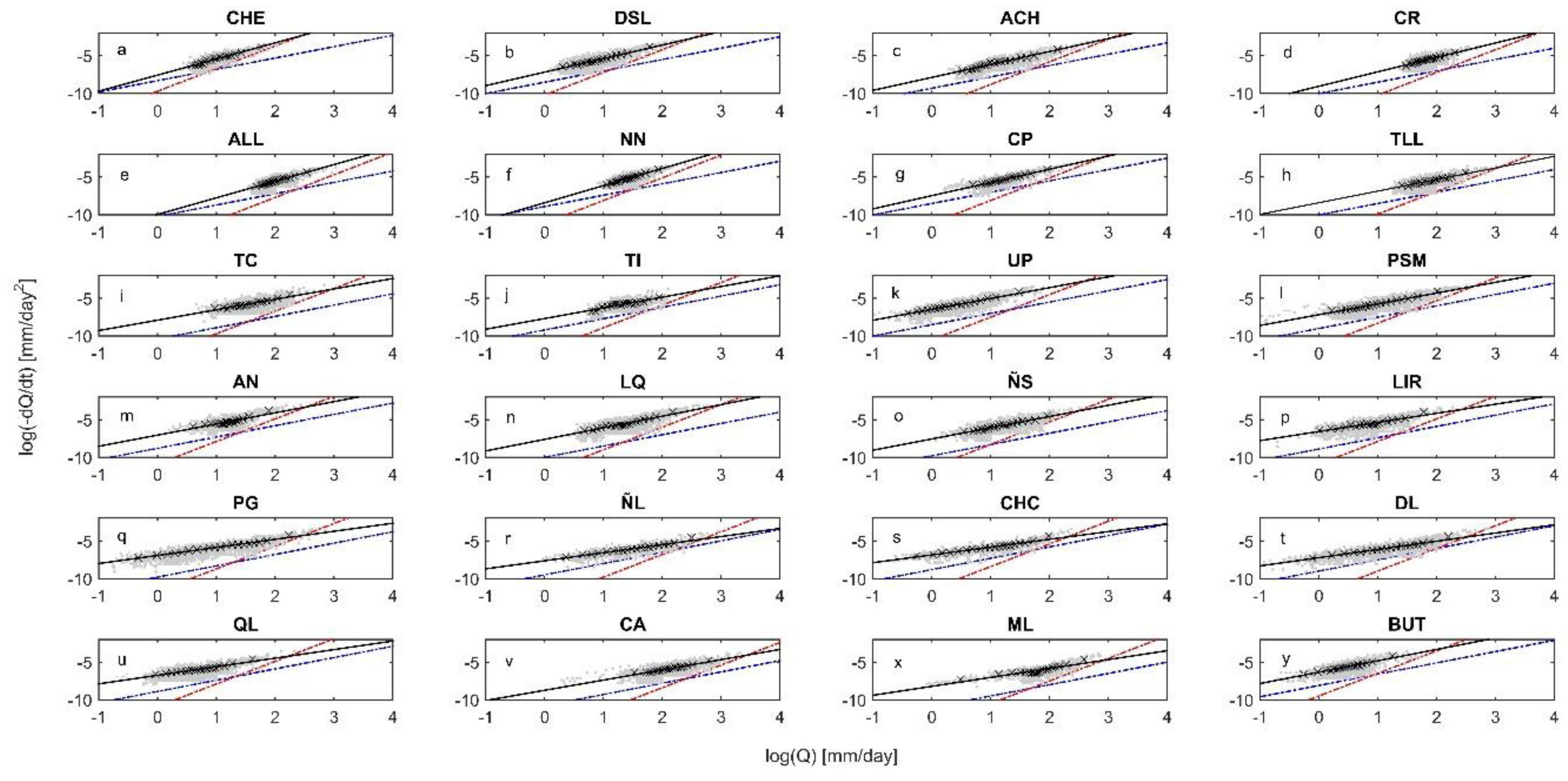
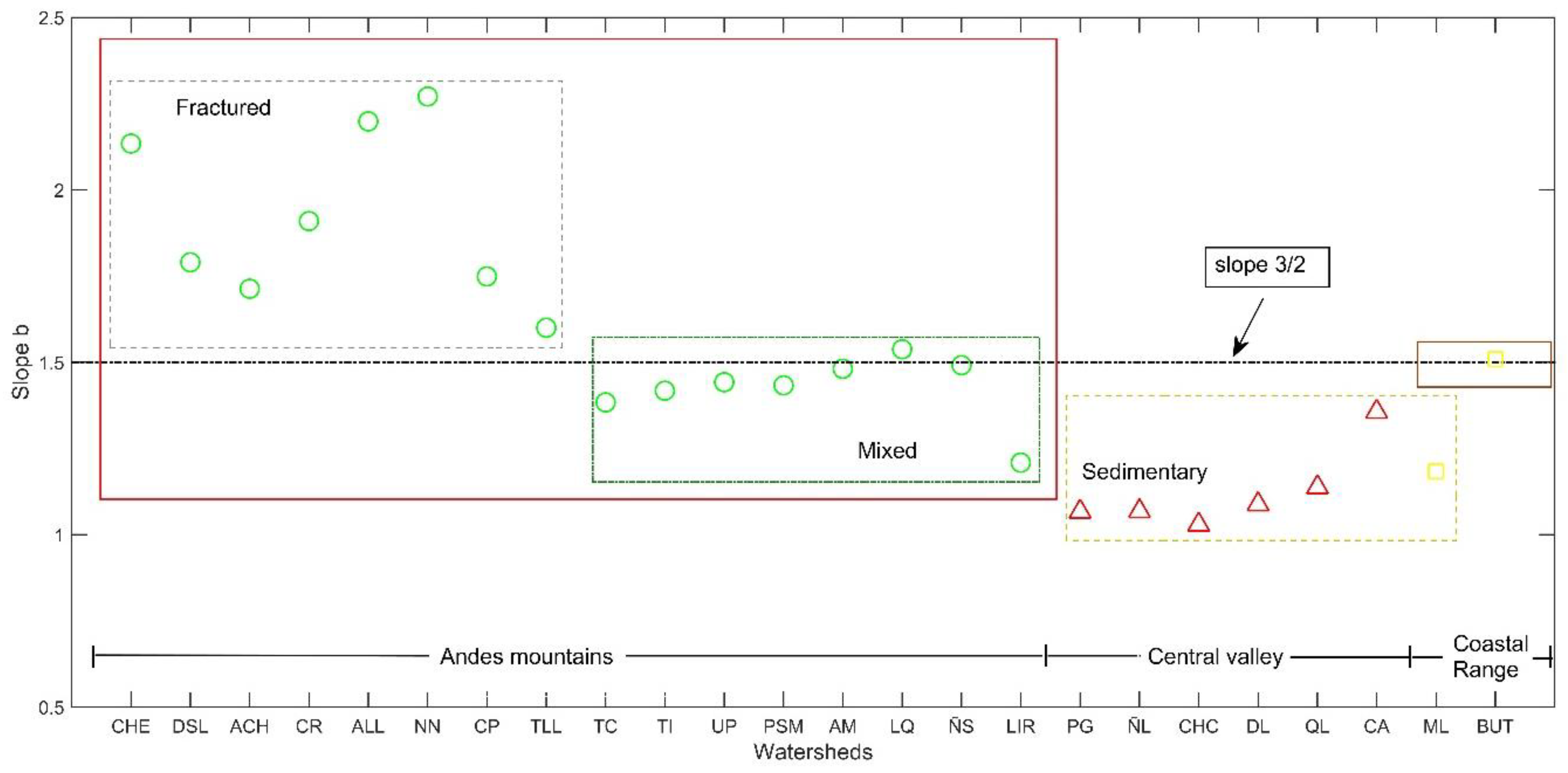

| Station ID | Area | Data Period | Geological Formation (%) | Relief (°) | Mean Annual Precipitation (mm) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Station | ID | (km2) | SS (%) | SVS (%) | VS (%) | IF (%) | MF (%) | AS | ||
| Chillan at Esperanza | CHE | 210 | 1960–2016 | 0.0 | 0.0 | 90.4 | 9.6 | 0.0 | 17.8 | 2200 |
| Diguillín at San Lorenzo | DSL | 207 | 1965–2016 | 0.0 | 47.9 | 37.2 | 14.9 | 0.0 | 23.6 | 2300 |
| Achibueno at the Recova | ACH | 899 | 1986–2016 | 11.0 | 78.8 | 2.6 | 7.6 | 0.0 | 20.1 | 2070 |
| Cautin at Rari-Ruca | CR | 1255 | 1985–2016 | 1.2 | 17.6 | 79.0 | 2.1 | 0.0 | 14.4 | 2330 |
| Río Allipen at Laureles | ALL | 1652 | 1985–2016 | 21.9 | 0.9 | 55.3 | 21.8 | 0.0 | 13 | 2294 |
| Nilahue at Nayan | NN | 304 | 1987–2016 | 0.0 | 0.0 | 97.4 | 2.6 | 0.0 | 11.7 | 2916 |
| Coihueco before Pichicope | CP | 303 | 1987–2016 | 34.9 | 1.4 | 63.7 | 0.0 | 0.0 | 11.0 | 2714 |
| Trancura before Llafenco river | TLL | 1374 | 1970–2016 | 7.4 | 20.2 | 44.9 | 27.5 | 0.0 | 17.0 | 2588 |
| Teno before Claro river | TC | 1206 | 1985–2016 | 22.7 | 64.2 | 8.5 | 4.7 | 0.0 | 22.2 | 1573 |
| Teno Bellow Infernillo Ravine | TI | 601 | 1985–2016 | 42.7 | 44.6 | 5.8 | 6.8 | 0.0 | 22.7 | 1622 |
| Upeo at Upeo | UP | 205 | 1980–2016 | 8.0 | 75.2 | 8.3 | 8.5 | 0.0 | 21.1 | 1354 |
| Perquilauquen at San Manuel | PSM | 504 | 1963–2016 | 1.2 | 43.7 | 10.0 | 45.1 | 0.0 | 18.5 | 2067 |
| Ancoa at Morro | AM | 273 | 1980–2016 | 2.8 | 60.9 | 1.3 | 35.0 | 0.0 | 23.6 | 1998 |
| Longaví at Quiriquina | LQ | 668 | 1966–2016 | 8.4 | 36.6 | 25.1 | 30.0 | 0.0 | 21.2 | 2270 |
| Los Sauces before Ñuble | ÑS | 610 | 1960–2016 | 2.2 | 78.0 | 18.4 | 1.4 | 0.0 | 20.0 | 2398 |
| Lircay at Las Rastras Bridge | LIR | 382 | 1985–2016 | 16.0 | 66.8 | 8.7 | 8.5 | 0.0 | 12.7 | 1621 |
| Perquilauquen at Gniquen | PG | 1205 | 1985–2016 | 32.6 | 33.4 | 14.8 | 19.3 | 0.0 | 11.0 | 1618 |
| Ñuble at Longitudinal | ÑL | 3069 | 1960–2016 | 33.0 | 33.5 | 15.4 | 18.1 | 0.0 | 14.5 | 1900 |
| Chillán to Confluencia | CHC | 754 | 1985–2016 | 70.4 | 3.0 | 25.3 | 1.3 | 0.0 | 10 | 1736 |
| Diguillin at Longitudinal | DL | 1239 | 1985–2016 | 39.0 | 30.7 | 26.5 | 3.8 | 0.0 | 8.1 | 1500 |
| Quino at Longitudinal | QL | 298 | 1969–2016 | 0.0 | 0.0 | 100.0 | 0.0 | 0.0 | 2.4 | 1850 |
| Cautin at Almagro | CA | 5470 | 1985–2016 | 40.1 | 3.9 | 58.1 | 1.0 | 0.7 | 6.0 | 1838 |
| Mataquito at Licanten | ML | 5688 | 1972–2016 | 40.0 | 39.8 | 15.5 | 4.0 | 0.7 | 11.2 | 1242 |
| Butamalal at Butamalal | BUT | 123 | 1985–2016 | 0.1 | 0.0 | 0.0 | 68.8 | 31.1 | 9.3 | 1483 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parra, V.; Arumí, J.L.; Muñoz, E.; Paredes, J. Characterization of the Groundwater Storage Systems of South-Central Chile: An Approach Based on Recession Flow Analysis. Water 2019, 11, 2324. https://doi.org/10.3390/w11112324
Parra V, Arumí JL, Muñoz E, Paredes J. Characterization of the Groundwater Storage Systems of South-Central Chile: An Approach Based on Recession Flow Analysis. Water. 2019; 11(11):2324. https://doi.org/10.3390/w11112324
Chicago/Turabian StyleParra, Víctor, José Luis Arumí, Enrique Muñoz, and Jerónimo Paredes. 2019. "Characterization of the Groundwater Storage Systems of South-Central Chile: An Approach Based on Recession Flow Analysis" Water 11, no. 11: 2324. https://doi.org/10.3390/w11112324
APA StyleParra, V., Arumí, J. L., Muñoz, E., & Paredes, J. (2019). Characterization of the Groundwater Storage Systems of South-Central Chile: An Approach Based on Recession Flow Analysis. Water, 11(11), 2324. https://doi.org/10.3390/w11112324





