Multifractal Analysis of River Networks in an Urban Catchment on the Taihu Plain, China
Abstract
:1. Introduction
2. Materials and Methods
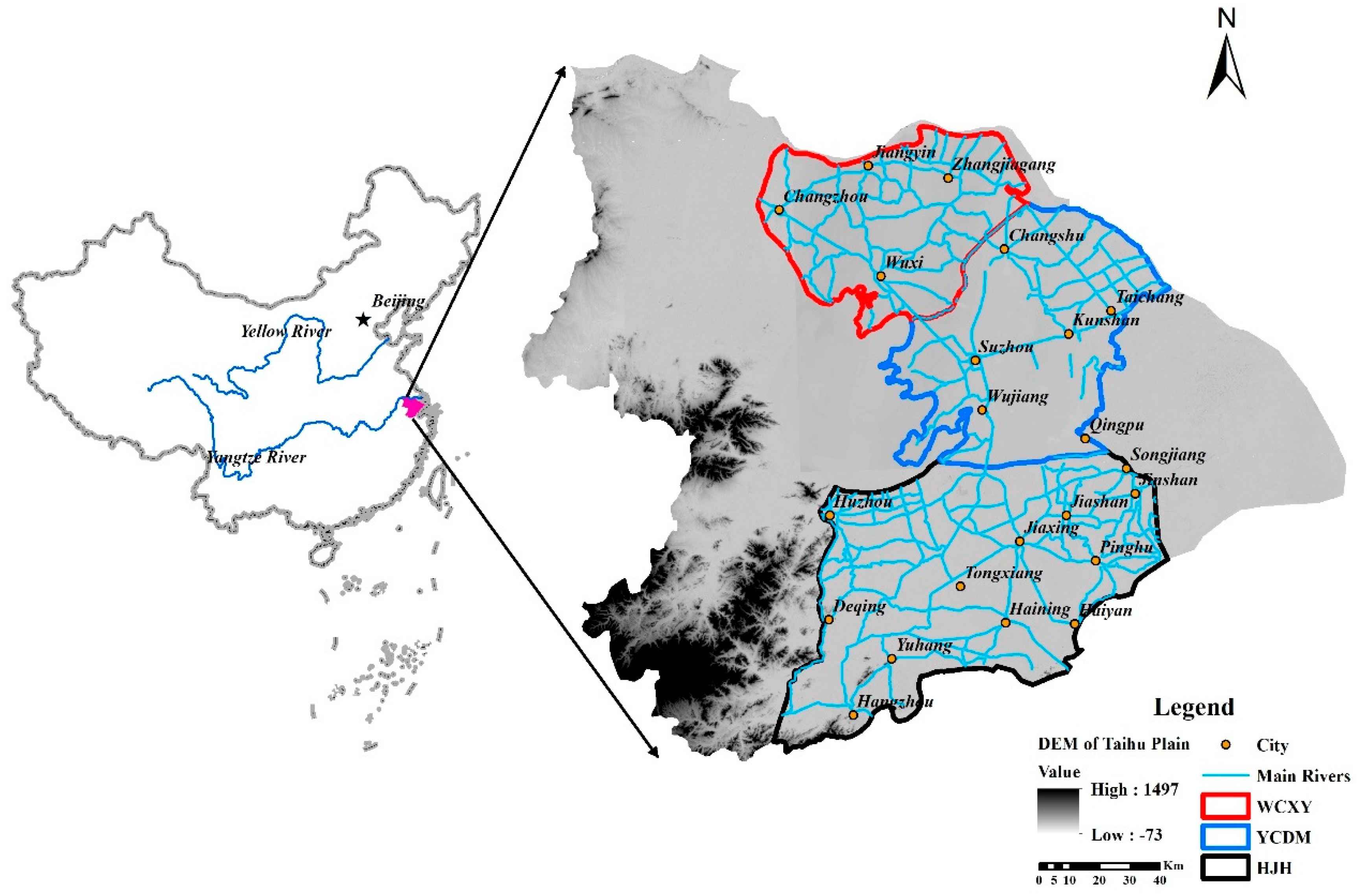
2.1. Study Area
2.2. Data Description
2.3. Methods
3. Results
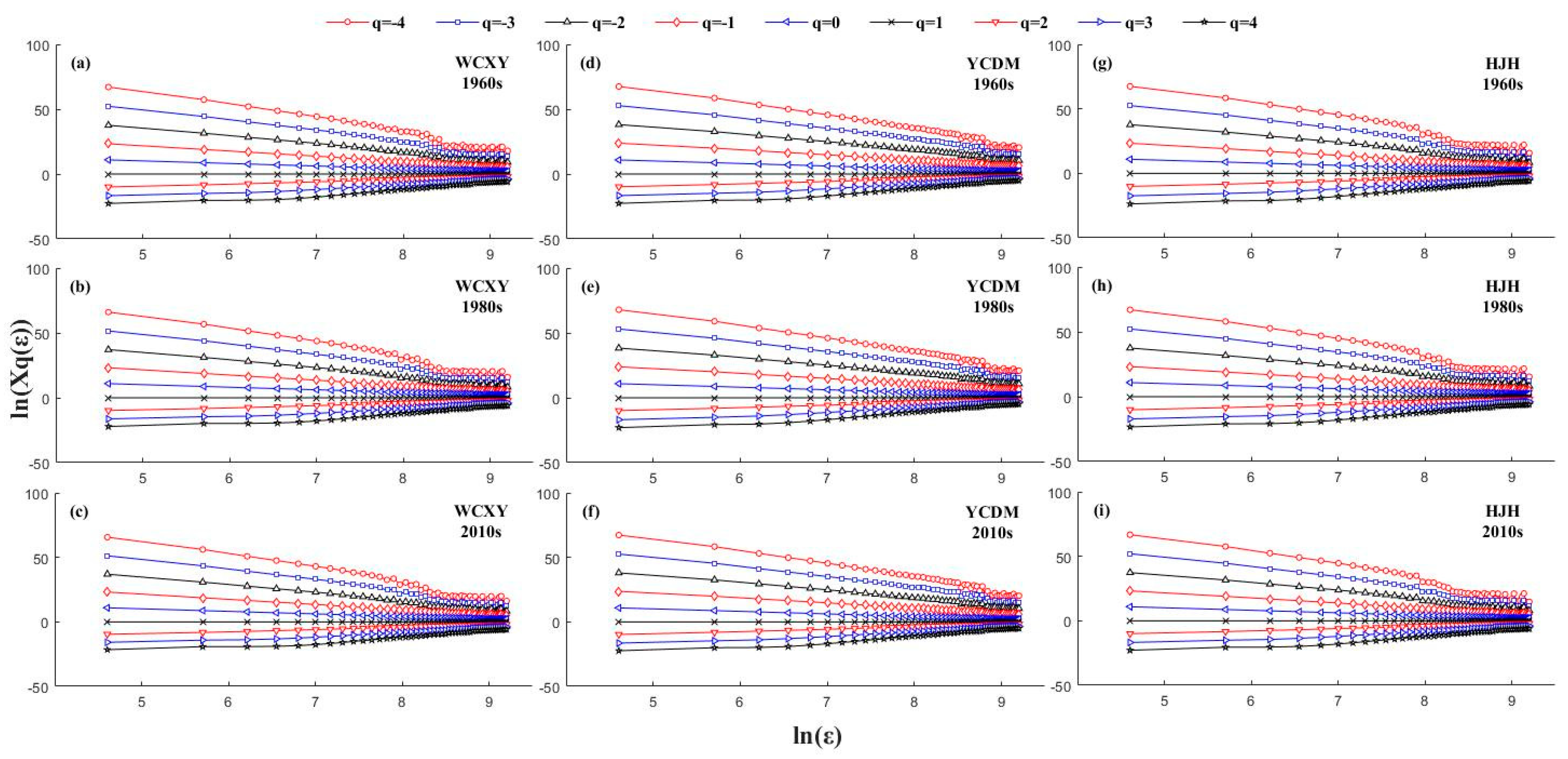
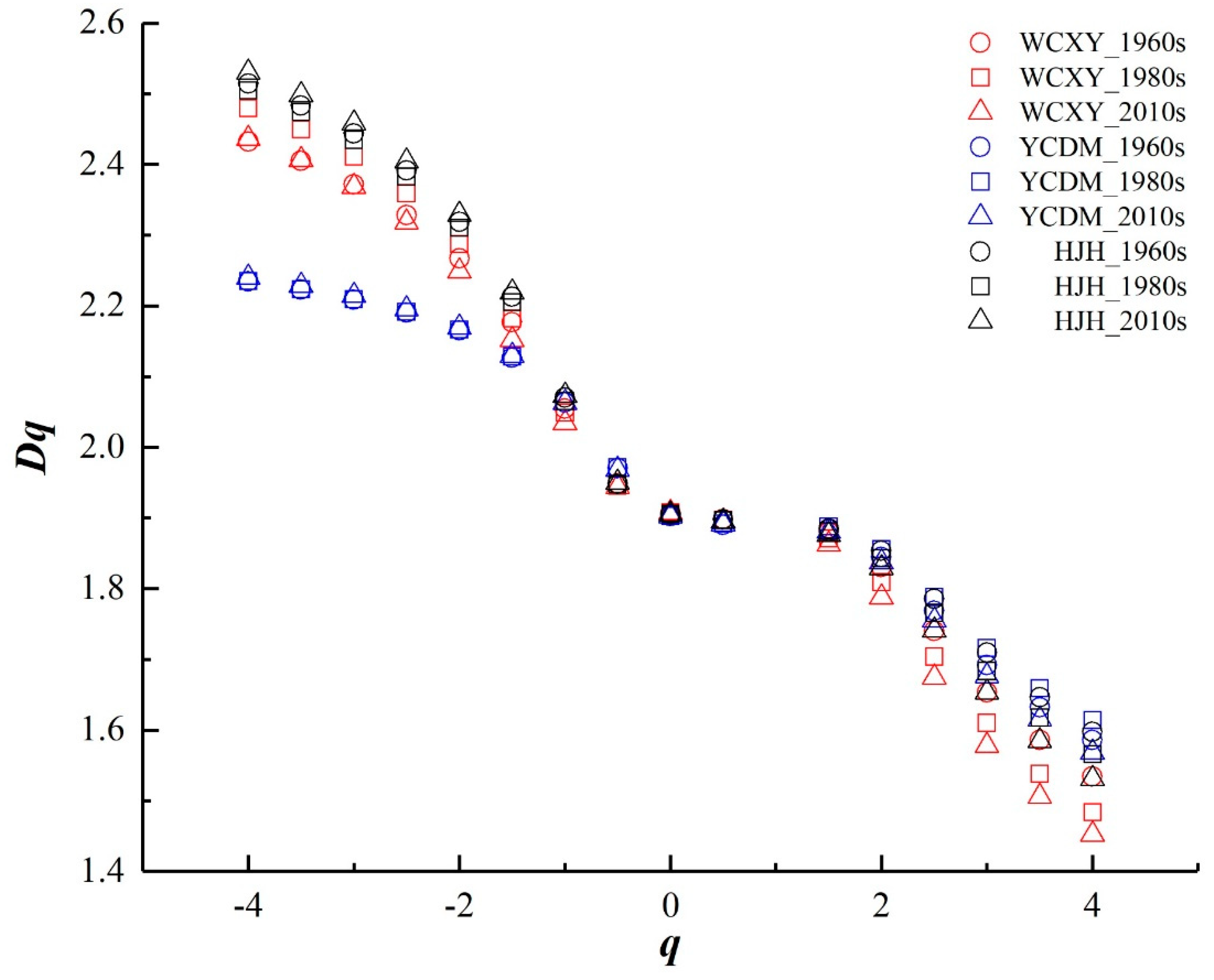
3.1. Determination of Multifractal Features
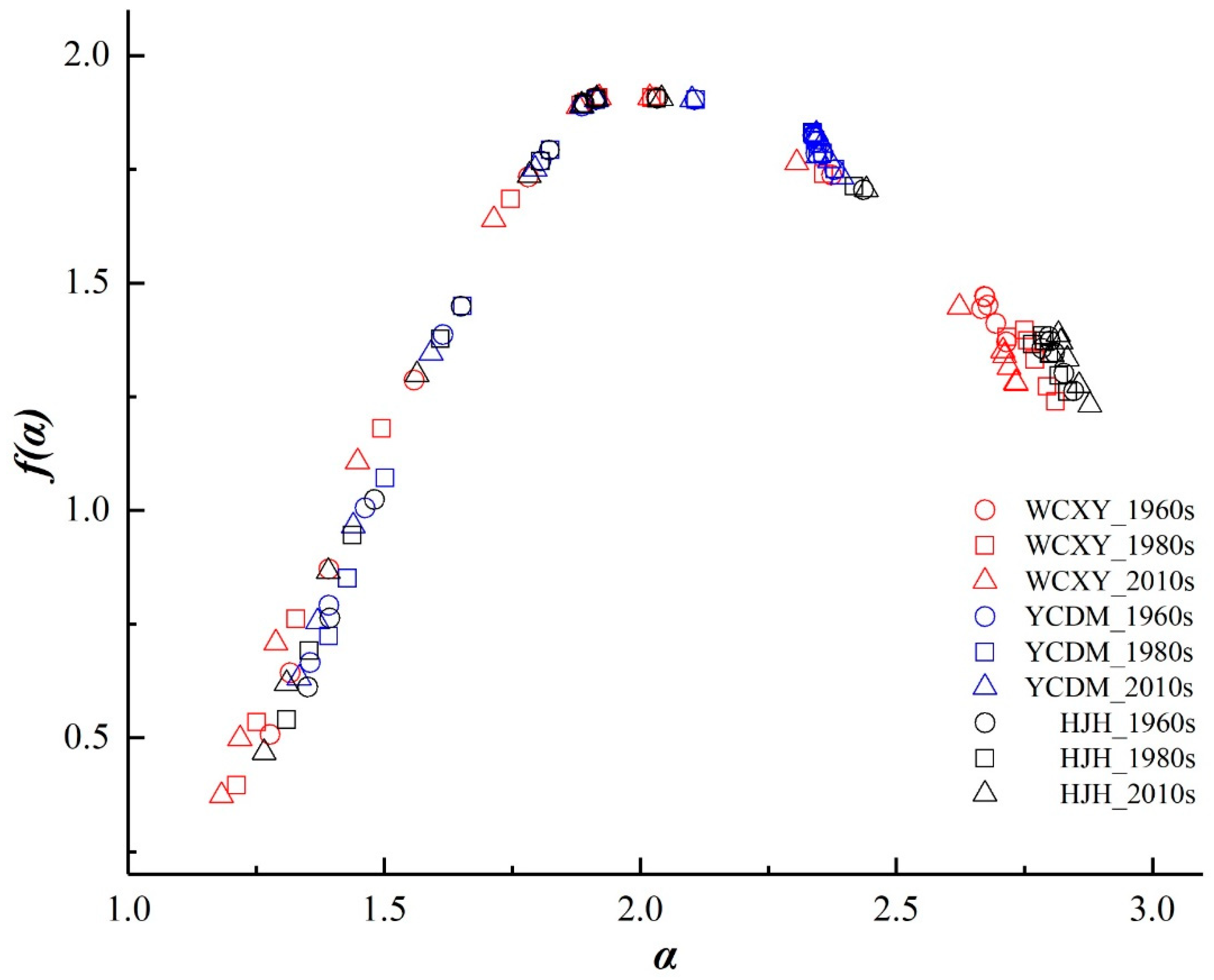
3.2. Multifractal Analysis
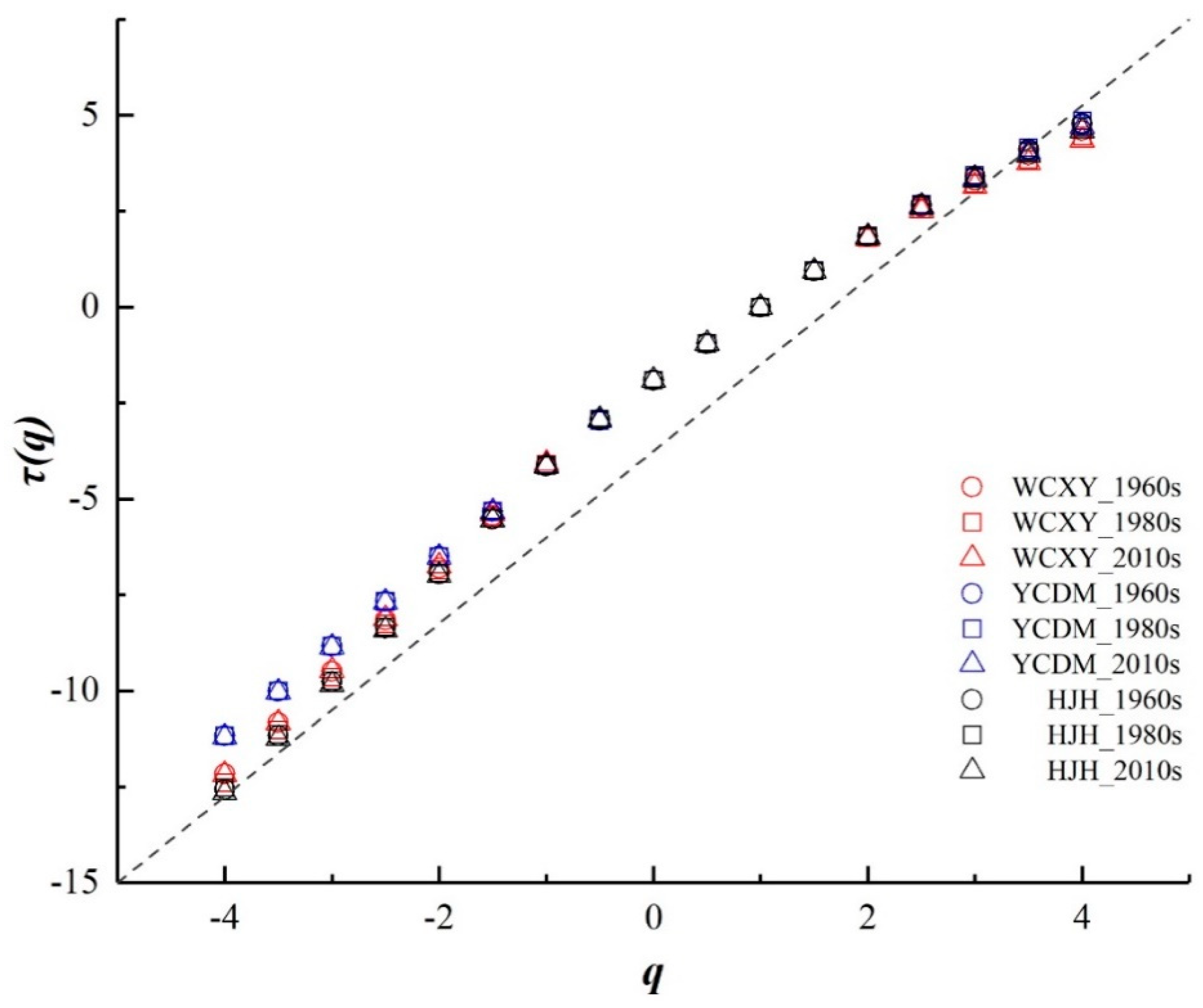
3.2.1. Multifractal Dimension Analysis
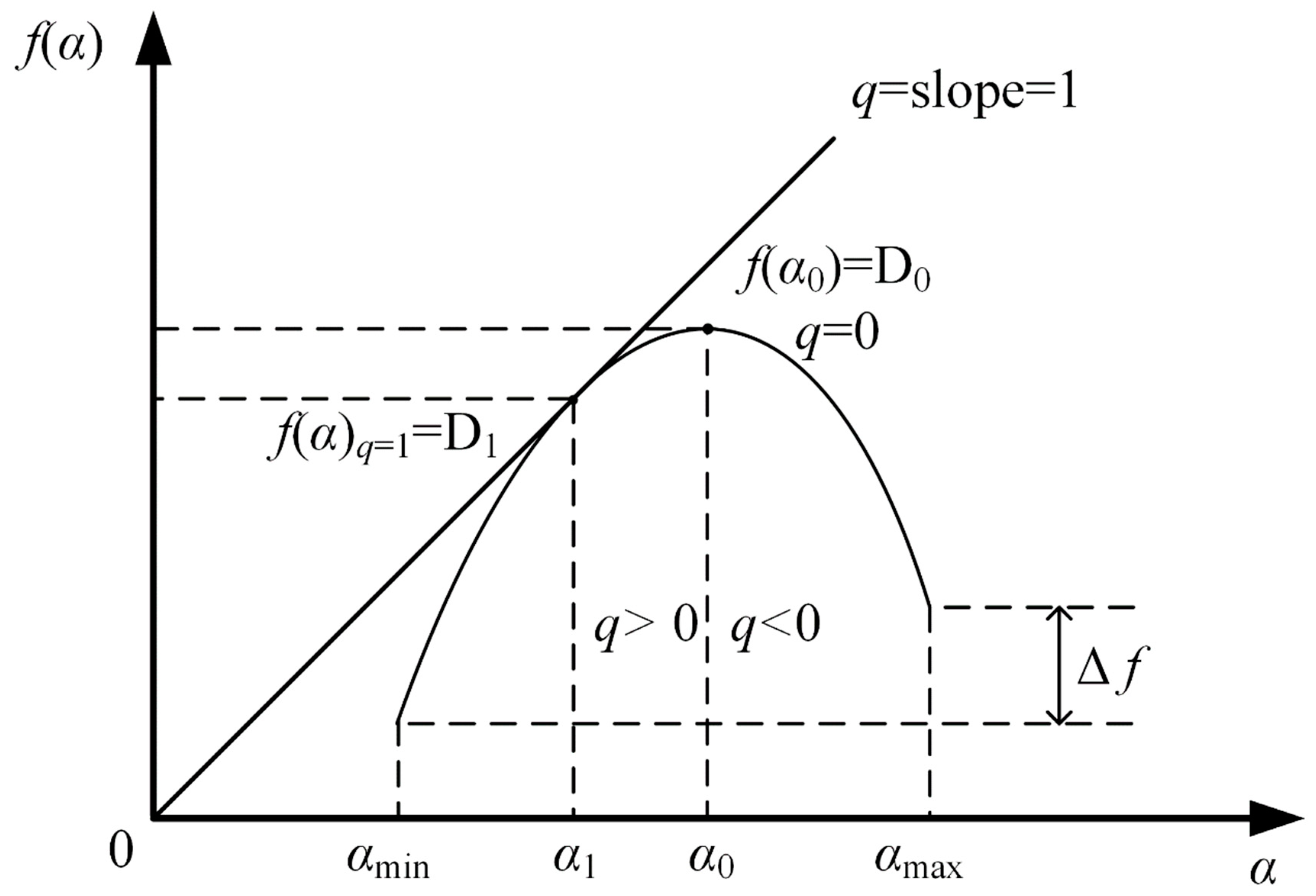
3.2.2. Multifractal Spectrum Analysis
4. Discussion
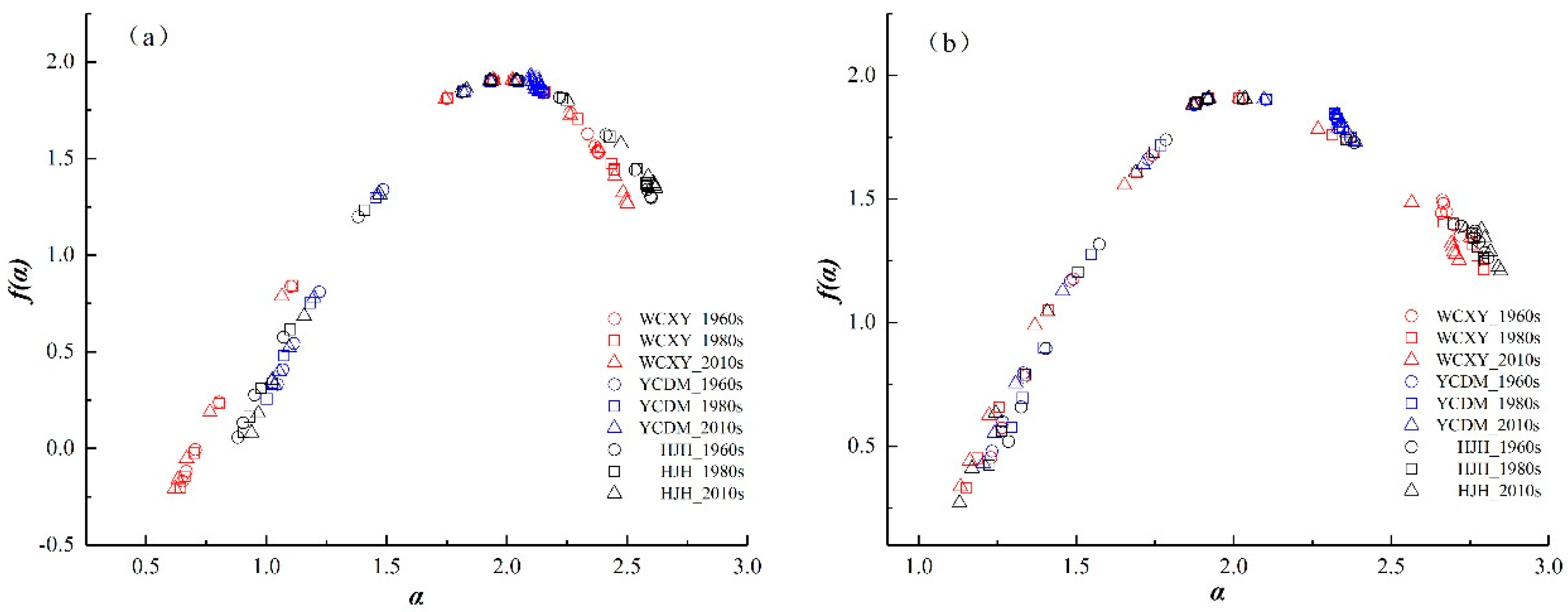
4.1. Multifractal Analysis of the Main Rivers and Tributaries
4.2. Multifractal Analysis of River Networks from Other Areas
4.3. Changes in River Networks and Urbanization
4.4. Limitations and Outlook
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Symbols and Abbreviations
| WCXY | the water conservancy region of Wuchengxiyu |
| YCDM | the water conservancy region of Yangchengdianmao |
| HJH | the water conservancy region of Hangjiahu |
| 3S | Remote sensing (RS), Geography information systems (GIS) and Global positioning systems (GPS) |
| DEM | the digital elevation model |
| DLG | the Digital Line Graphic |
| FSA | fixed size algorithms |
| E | the box size of the overlay network |
| Qi(ε) | the river distribution probability in box i of ε × ε grid |
| Mi(ε) | the overall length of the rivers in box i |
| M | the total length of the studied river networks |
| Xq(ε) | the partition function |
| N(ε) | the number of non-empty boxes covered the overall river networks of ε × ε grid |
| q∈(−∞, +∞) | the weight factor or probability moment |
| τ(q) | the mass exponent of the q power |
| Dq: | the multifractal dimension or generalized fractal dimension |
| A | singularity exponent |
| f(α) | the multifractal spectrum |
| ∆α | the variation of singularity component or the width of the multifractal spectrum |
| Δf | the heights variation of multifractal spectrum |
| determination coefficient of q = 0 | |
| TM | Landsat Thematic Mapper |
| Up | the ratio of non-agricultural population to total regional population |
| Ue | the ratio of non-agricultural GRDP (Gross Regional Domestic Product) to regional GRDP |
| AVG | the average of Up, Ue and Us |
| Rd (km/km2) | the river density |
| MIUH | the Multifractal Instantaneous Unit Hydrograph |
References
- Mandelbrot, B.B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef]
- Parisi, G.; Frisch, U. On the singularity structure of fully developed turbulence. In Turbulence and Predictability in Geophysical Fluid Dynamics; Proceedings of the International School of Physic Enrico Fermi: Amsterdam, The Netherlands, 1985; pp. 84–87. [Google Scholar]
- Liu, Y.Y.; Luo, X.S.; Chen, Q.B.; Wu, L. Application of multifractal spectrum in leaf images processing. Comput. Eng. Appl. 2008, 44, 190–192. [Google Scholar] [CrossRef]
- De Bartolo, S.G.; Gabriele, S.; Gaudio, R. Multifractal behaviour of river networks. Hydrol. Earth Syst. Sci. Discuss. 2000, 4, 105–112. [Google Scholar] [CrossRef] [Green Version]
- De Bartolo, S.G.; Gaudio, R.; Gabriele, S. Multifractal analysis of river networks: Sandbox approach. Water Resour. Res. 2004, 40, W02201. [Google Scholar] [CrossRef]
- De Bartolo, S.G.; Veltri, M.; Primavera, L. Estimated generalized dimensions of river networks. J. Hydrol. 2006, 322, 181–191. [Google Scholar] [CrossRef]
- He, L.H.; Zhao, H. The fractal dimension of river networks and its interpretation. Sci. Geogr. Sin. 1996, 16, 124–128. [Google Scholar] [CrossRef]
- La Barbera, P.; Rosso, R. On the fractal dimension of stream networks. Water Resour. Res. 1989, 25, 735–741. [Google Scholar] [CrossRef]
- Rosso, R.; Bacchi, B.; La Barbera, P. Fractal relation of mainstream length to catchment area in river networks. Water Resour. Res. 1991, 27, 381–387. [Google Scholar] [CrossRef]
- Nikora, V.I.; Sapozhnikov, V.B. River network fractal geometry and its computer simulation. Water Resour. Res. 1993, 29, 3569–3575. [Google Scholar] [CrossRef]
- Tarboton, D.G. Fractal river networks, Horton’s laws and Tokunaga cyclicity. J. Hydrol. 1996, 187, 105–117. [Google Scholar] [CrossRef]
- Li, M.; Zhu, L.R.; Long, H.Y. On fractal and multifractal properties for different types of landforms. Acta Geosci. Sin. 2003, 24, 237–242. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Li, Z.B.; Li, P.; Lu, K.X. Multifractal arithmethic for watershed topographic feature. Adv. Water Sci. 2009, 20, 385–391. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Zheng, T.T.; Wan, T.; Cheng, H.H.; Zhang, C. Analysis of Himalayas Mountains based on multifractal characteristics. J. Chongqing Technol. Bus. Univ. 2011, 28, 86–89. [Google Scholar] [CrossRef]
- Junior, O.C.; Guimaraes, R.; Freitas, L.; Gomes-Loebmann, D.; Gomes, R.A.; Martins, E.; RMontgomery, D. Urbanization impacts upon catchment hydrology and gully development using mutli-temporal digital elevation data analysis. Earth Surf. Process. Landf. 2010, 35, 611–617. [Google Scholar] [CrossRef]
- Wang, L.; Wang, K. Impacts of Dem Uncertainty on Estimated Surface Solar Radiation and Extracted River Network. Bull. Am. Meteorol. Soc. 2015, 96, 197–210. [Google Scholar] [CrossRef]
- Parmar, K.S.; Bhardwaj, R. Statistical, time series, and fractal analysis of full stretch of river Yamuna (India) for water quality management. Environ. Sci. Pollut. Res. 2015, 22, 397–414. [Google Scholar] [CrossRef]
- Donadio, C.; Magdaleno, F.; Mazzarella, A.; Kondolf, G.M. Fractal Dimension of the Hydrographic Pattern of Three Large Rivers in the Mediterranean Morphoclimatic System: Geomorphologic Interpretation of Russian (USA), Ebro (Spain) and Volturno (Italy) Fluvial Geometry. Pure Appl. Geophys. 2015, 172, 1975–1984. [Google Scholar] [CrossRef]
- Ariza-Villaverde, A.B.; Jiménez-Hornero, F.J.; Gutiérrez de Ravé, E. Influence of DEM resolution on drainage network extraction: A multifractal analysis. Geomorphology 2015, 241, 243–254. [Google Scholar] [CrossRef]
- Ariza-Villaverde, A.B.; Jiménez-Hornero, F.J.; Gutiérrez de, R. Multifractal analysis applied to the study of the accuracy of DEM-based stream derivation. Geomorphology 2013, 197, 85–95. [Google Scholar] [CrossRef]
- Fotherby, L.M. Valley confinement as a factor of braided river pattern for the Platte River. Geomorphology 2009, 103, 562–576. [Google Scholar] [CrossRef]
- Bergstrom, A.; McGlynn, B.; Mallard, J.; Covino, T. Watershed structural influences on the distributions of stream network water and solute travel times under baseflow conditions. Hydrol. Process 2016, 30, 2671–2685. [Google Scholar] [CrossRef]
- Rinaldo, A.; Rigon, R.; Banavar, J.R.; Maritan, A.; Rodriguez-Iturbe, I. Evolution and selection of river networks: Statics, dynamics, and complexity. Proc. Natl. Acad. Sci. USA 2014, 111, 2417–2424. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tonkin, J.D.; Altermatt, F.; Finn, D.S.; Heino, J.; Olden, J.D.; Pauls, S.U.; Lytle, D.A. The role of dispersal in river network metacommunities: Patterns, processes, and pathways. Freshw. Biol. 2018, 63, 141–163. [Google Scholar] [CrossRef]
- Deng, X.J.; Xu, Y.P.; Han, L.F. Impacts of human activities on the structural and functional connectivity of a river network in the taihu plain. Land Degrad. Dev. 2018, 29, 2575–2588. [Google Scholar] [CrossRef]
- López-Vicente, M.; Nadal-Romero, E.; Cammeraat, E.L.H. Hydrological connectivity does change over 70 years of abandonment and afforestation in the Spanish Pyrenees. Land Degrad. Dev. 2017, 28, 1298–1310. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, Y.; Wang, Z. Correlation between flood frequency and geomorphologic complexity of rivers network–A case study of Hangzhou China. J. Hydrol. 2015, 527, 113–118. [Google Scholar] [CrossRef]
- Men, K.P.; Zhu, S.D. The Ordered Network Structure and its Prediction for the Big Floods of the Changjiang River Basins. Z. Für Nat. A 2014, 68, 766–772. [Google Scholar] [CrossRef]
- Gregory, K.J. The human role in changing river channels. Geomorphology 2006, 79, 172–191. [Google Scholar] [CrossRef]
- Chin, A. Urban transformation of river landscapes in a global context. Geomorphology 2006, 79, 460–487. [Google Scholar] [CrossRef]
- Hooke, J.M. Human impacts on fluvial systems in the Mediterranean region. Geomorphology 2006, 79, 311–335. [Google Scholar] [CrossRef]
- Sear, D.A.; Newson, M.D. Environmental change in river channels: A neglected element. Towards geomorphological typologies, standards and monitoring. Sci. Total Environ. 2003, 310, 17–23. [Google Scholar] [CrossRef]
- Gaudio, R.; De Bartolo, S.G.; Primavera, L.; Veltri, M.; Gabriele, S. Procedures in multifractal analysis of river networks: A state of the art review. In the Basis of Civilization—Water Science Proceedings of the UNESCO/IAHS/IWHA symposium, Rome, Italy, 3–6 December 2003; IAHS Publication: Wallingford, UK, 2004; Volume 286, pp. 228–237. [Google Scholar]
- Kalantari, Z.; Ferreira, C.S.S.; Walsh, R.P.D.; Destouni, G. Urbanization development under climate change: Hydrological responses in a peri-urban Mediterranean catchment. Land Degrad. Dev. 2017, 28, 2207–2221. [Google Scholar] [CrossRef]
- Deng, X.J.; Xu, Y.P.; Han, L.F.; Song, S.; Yang, L.; Li, G.; Wang, Y.F. Impacts of Urbanization on River Systems in the Taihu Region, China. Water 2015, 7, 1340–1358. [Google Scholar] [CrossRef]
- Deng, X.J.; Xu, Y.P.; Han, L.F.; Li, G.; Wang, Y.F.; Xiang, J.; Xu, G.L. Spatial-temporal changes of river systems in Jiaxing under the background of urbanization. Acta Geogr. Sin. 2016, 71, 75–85. [Google Scholar] [CrossRef]
- Deng, X.J.; Xu, Y.P.; Han, L.F.; Yang, M.N.; Yang, L.; Song, S.; Li, G.; Wang, Y.F. Spatial-temporal evolution of the distribution pattern of river systems in the plain river network region of the Taihu Basin, China. Quat. Int. 2016, 392, 178–186. [Google Scholar] [CrossRef]
- Julian, J.P.; Wilgruber, N.A.; de Beurs, K.M.; Mayer, P.M.; Jawarneh, R.N. Long-term impacts of land cover changes on stream channel loss. Sci. Total Environ. 2015, 537, 399–410. [Google Scholar] [CrossRef]
- Han, L.F.; Xu, Y.P.; Yang, L.; Deng, X.J.; Hu, C.S.; Xu, G.L. Temporal and spatial change of stream structure in Yangtze River Delta and its driving forces during 1960s–2010s. Acta Geogr. Sin. 2015, 70, 819–827. [Google Scholar] [CrossRef]
- Elmore, A.J.; Kaushal, S.S. Disappearing headwaters: Patterns of stream burial due to urbanization. Front. Ecol. Environ. 2008, 6, 308–312. [Google Scholar] [CrossRef]
- Han, C.L.; Mao, Y. The structure characteristics and the functional variation of the river systems in Taihu Lake Catchment. J. Lake Sci. 1997, 9, 300–306. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Possible refinement of the lognormal hypothesis concerning the distribution of energy dissipation in intermittent turbulence. In Statistical Models and Turbulence; Rosenblatt, M., Van Atta Lect, C., Eds.; Springer: Berlin/Heidelberg, Germany, 1972; Volume 12, pp. 333–351. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Intermittent turbulence in self-similar cascades: Divergence of high moments and dimension of the carrier. J. Fluid Mech. 1974, 62, 331–358. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A 1986, 33, 1141–1151. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.Y.; Peng, N.; Liu, Y.S.; Nie, B.F. The Multifractal Research of River Watershed Geomorphology in Volcanic Region of Changbai Mountains. J. Cap. Norm. Univ. Nat. Sci. Ed. 2013, 34, 77–81. [Google Scholar] [CrossRef]
- Feder, J. Fractals; Plenum Press: New York, NY, USA, 1988. [Google Scholar]
- Aharony, A. Measuring multifractals. Phys. Nonlinear Phenom. 1989, 38, 1–4. [Google Scholar] [CrossRef]
- Falconer, K.J. Fractal Geometry: Mathematical Foundations and Applications; John Wiley: Hoboken, NJ, USA, 1990. [Google Scholar]
- Mach, J.; Mas, F.; Sague´s, F. Two representations in multifractal analysis. J. Phys. A Math. Gen. 1995, 28, 5607–5622. [Google Scholar] [CrossRef]
- Halsey, T.C.; Jensen, M.H.; Kadanoff, L.P.; Procaccia, I.; Shraiman, B.I. Stream construction characteristics in rapid urbanization area. Geogr. Res. 2008, 27, 1212–1220. [Google Scholar] [CrossRef]
- Lashermes, B.; Foufoula-Georgiou, E. Area and width functions of river networks: New results on multifractal properties. Water Resour. Res. 2007, 43, W09405. [Google Scholar] [CrossRef]
- Gaudio, R.; De Bartolo, S.G.; Primavera, L.; Gabriele, S.; Veltri, M. Lithologic control on the multifractal spectrum of river networks. J. Hydrol. 2006, 327, 365–375. [Google Scholar] [CrossRef]
- Dombrádi, E.; Timár, G.; Bada, G.; Cloetingh, S.; Horváth, F. Fractal dimension estimations of drainage network in the Carpathian–Pannonian system. Glob. Planet. Chang. 2007, 58, 197–213. [Google Scholar] [CrossRef]
- Shen, X.H.; Zou, L.J.; Zhang, G.F.; Su, N.; Wu, W.Y.; Yang, S.F. Fractal characteristics of the main channel of Yellow River and its relation to regional tectonic evolution. Geomorphology 2011, 127, 64–70. [Google Scholar] [CrossRef]
- Tian, S.M.; Su, X.H.; Wang, W.H.; Lai, R.X. Application of Fractal Theory in the River Regime in the Lower Yellow River. Appl. Mech. Mater 2012, 190–191, 1238–1243. [Google Scholar] [CrossRef]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. The fractal nature of river networks. Water Resour. Res. 1988, 24, 1317–1322. [Google Scholar] [CrossRef]
- Ijjasz-Vasquez, E.J.; Rodriguez-Iturbe, I.; Bras, R.L. On the multifractal characterization of river basins. Geomorphology 1992, 5, 297–310. [Google Scholar] [CrossRef]
- Claps, P.; Oliveto, G. Reexamining the determination of the fractal dimension of river networks. Water Resour. Res. 1996, 32, 3123–3135. [Google Scholar] [CrossRef]
- Kamer, Y.; Ouillon, G.; Sornette, D. Barycentric fixed-mass method for multifractal analysis. Phys. Rev. E 2013, 88, 022922. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.F.; Xu, Y.P.; Zhang, Q.Y.; Li, G.; Lei, C.G.; Yang, L.; Han, L.F.; Deng, X.J. Influence of stream structure change on regulation capacity of river networks in Taihu Lake Basin. Acta Geogr. Sin. 2016, 71, 449–458. [Google Scholar] [CrossRef]
- Gires, A.; Tchiguirinskaia, I.; Schertzer, D.; Ochoa Rodriguez, S.; Willems, P.; Ichiba, A.; Wang, L.; Pina, R.; Van Assel, J.; Bruni, G.; et al. Fractal analysis of urban catchments and their representation in semi-distributed models: Imperviousness and sewer system. Hydrol. Earth Syst. Sci. 2017, 21, 2361–2375. [Google Scholar] [CrossRef]
| Types | Orders | Widths | Graphical Representation | Main Functions | |
|---|---|---|---|---|---|
| Paper Topographic Map | Digital Line Graphics | ||||
| Main Rivers | 1st | >40 m | Double line rivers (>0.8 mm) | Planar canal, surface rivers and main channel | Discharge |
| 2nd | 20–40 m | Double line rivers (0.4–0.8 mm) | Planar canal, surface rivers and main channel | ||
| Tributaries | 3rd | 10–20 m | Wide single line rivers (0.3mm) | Linear surface rivers and main channel | Storage |
| 4th | <10 m | Narrow single line rivers (0.15mm) | Linear branch channel | ||
| Areas | Periods | D0 = f(α0) | α0 | αmin | αmax | f(αmin) | f(αmax) | △α | △f | |
|---|---|---|---|---|---|---|---|---|---|---|
| Wuchengxiyu (WCXY) | 1960s | 1.908 | 0.9976 | 2.031 | 1.278 | 2.716 | 0.508 | 1.370 | 1.438 | 0.862 |
| 1980s | 1.907 | 0.9976 | 2.022 | 1.212 | 2.811 | 0.396 | 1.239 | 1.599 | 0.843 | |
| 2010s | 1.908 | 0.9976 | 2.017 | 1.182 | 2.734 | 0.373 | 1.279 | 1.552 | 0.906 | |
| Yangchengdianmao (YCDM) | 1960s | 1.901 | 0.9977 | 2.049 | 1.356 | 2.379 | 0.666 | 1.748 | 1.023 | 1.082 |
| 1980s | 1.903 | 0.9977 | 2.048 | 1.392 | 2.380 | 0.724 | 1.750 | 0.988 | 1.026 | |
| 2010s | 1.903 | 0.9977 | 2.044 | 1.334 | 2.394 | 0.631 | 1.733 | 1.060 | 1.102 | |
| Hangjiahu (HJH) | 1960s | 1.905 | 0.9977 | 2.034 | 1.351 | 2.847 | 0.612 | 1.262 | 1.496 | 0.650 |
| 1980s | 1.905 | 0.9977 | 2.032 | 1.310 | 2.835 | 0.540 | 1.260 | 1.525 | 0.720 | |
| 2010s | 1.905 | 0.9976 | 2.041 | 1.266 | 2.878 | 0.468 | 1.232 | 1.612 | 0.764 |
| Areas | Periods | Entire Rivers | Main Rivers | Tributaries | Change Periods | Entire Rivers | Main Rivers | Tributaries | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| △α | △f | △α | △f | △α | △f | Change of △α/% | Change of △f /% | Change of △α /% | Change of △f /% | Change of △α/% | Change of △f /% | |||
| WCXY | 1960s | 1.438 | 0.862 | 1.727 | 1.700 | 1.489 | 0.898 | 1960s–1980s | 11.2 | −2.2 | 4.5 | −3.4 | 10.3 | −1.6 |
| 1980s | 1.599 | 0.843 | 1.804 | 1.642 | 1.643 | 0.884 | 1980s–2010s | −2.9 | 7.5 | 4.3 | −10.2 | −3.7 | 3.5 | |
| 2010s | 1.552 | 0.906 | 1.881 | 1.475 | 1.582 | 0.915 | 1960s–2010s | 7.9 | 5.1 | 8.9 | −13.2 | 6.2 | 1.9 | |
| YCDM | 1960s | 1.023 | 1.082 | 1.105 | 1.509 | 1.138 | 1.269 | 1960s–1980s | −3.4 | −5.2 | 4.0 | 4.9 | −5.4 | −7.4 |
| 1980s | 0.988 | 1.026 | 1.149 | 1.583 | 1.076 | 1.175 | 1980s–2010s | 7.3 | 7.4 | −4.3 | −4.0 | 9.7 | 10.9 | |
| 2010s | 1.060 | 1.102 | 1.100 | 1.519 | 1.180 | 1.303 | 1960s–2010s | 3.6 | 1.8 | −0.5 | 0.7 | 3.7 | 2.7 | |
| HJH | 1960s | 1.496 | 0.650 | 1.719 | 1.240 | 1.522 | 0.744 | 1960s–1980s | 1.9 | 10.8 | −2.4 | 2.5 | 3.5 | 10.9 |
| 1980s | 1.525 | 0.720 | 1.677 | 1.271 | 1.575 | 0.825 | 1980s–2010s | 5.7 | 6.1 | 0.2 | −0.4 | 9.1 | 13.7 | |
| 2010s | 1.612 | 0.764 | 1.680 | 1.266 | 1.719 | 0.938 | 1960s–2010s | 7.8 | 17.5 | −2.3 | 2.1 | 12.9 | 26.1 | |
| Urbanization Rate | Wuchengxiyu (WCXY) | Yangchengdianmao (YCDM) | Hangjiahu (HJH) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| △α | △f | Rd | △α | △f | Rd | △α | △f | Rd | |
| Up | 0.770 | 0.773 | 0.684 | 0.690 | 0.607 | 0.645 | 0.561 | 0.615 | 0.661 |
| Ue | 0.736 | 0.727 | 0.706 | 0.661 | 0.594 | 0.633 | 0.650 | 0.618 | 0.676 |
| Us | 0.809 | 0.749 | 0.834 | 0.680 | 0.605 | 0.642 | 0.690 | 0.817 | 0.865 |
| AVG | 0.772 | 0.750 | 0.741 | 0.677 | 0.602 | 0.640 | 0.634 | 0.683 | 0.734 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, J.; Xu, Y.; Yuan, J.; Wang, Q.; Wang, J.; Deng, X. Multifractal Analysis of River Networks in an Urban Catchment on the Taihu Plain, China. Water 2019, 11, 2283. https://doi.org/10.3390/w11112283
Xiang J, Xu Y, Yuan J, Wang Q, Wang J, Deng X. Multifractal Analysis of River Networks in an Urban Catchment on the Taihu Plain, China. Water. 2019; 11(11):2283. https://doi.org/10.3390/w11112283
Chicago/Turabian StyleXiang, Jie, Youpeng Xu, Jia Yuan, Qiang Wang, Jie Wang, and Xiaojun Deng. 2019. "Multifractal Analysis of River Networks in an Urban Catchment on the Taihu Plain, China" Water 11, no. 11: 2283. https://doi.org/10.3390/w11112283





